Академический Документы
Профессиональный Документы
Культура Документы
Aircraft Design Project-2 Eight Seater Short Range Business Jet Aircraft
Загружено:
Vignesh SelvarajАвторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Aircraft Design Project-2 Eight Seater Short Range Business Jet Aircraft
Загружено:
Vignesh SelvarajАвторское право:
Доступные форматы
vigneshaeronautical@gmail.
com
EIGHT SEATER SHORT RANGE BUSINESS JET
AN AIRCRAFT DESIGN
S.VIGNESH (30609101062)
P.VASANTHA PRABHU (30609101059)
J.SELVA KUMAR (30609101051)
N.VIGNESH (30609101061)
in partial fulfillm
BACHELOR OF ENGINEERING
JEPPIAAR ENGINEERING COLLEGE, CHENNAI 600 119
ANNA UNIVERSITY: CHENNAI 600 025
EIGHT SEATER SHORT RANGE BUSINESS JET
AIRCRAFT
AN AIRCRAFT DESIGN PROJECT-II REPORT
Submitted by
S.VIGNESH (30609101062)
P.VASANTHA PRABHU (30609101059)
J.SELVA KUMAR (30609101051)
N.VIGNESH (30609101061)
fulfillment for the award of the degree
of
BACHELOR OF ENGINEERING
in
AERONAUTICAL
JEPPIAAR ENGINEERING COLLEGE, CHENNAI 600 119
ANNA UNIVERSITY: CHENNAI 600 025
NOV/DEC 2012
P a g e | 1
EIGHT SEATER SHORT RANGE BUSINESS JET
JEPPIAAR ENGINEERING COLLEGE, CHENNAI 600 119
P a g e | 2
vigneshaeronautical@gmail.com
DEPARTMENT OF AERONAUTICAL ENGINEERING
JEPPIAAR ENGINEERING COLLEGE
ANNA UNIVERSITY, CHENNAI
BONAFIDE CERTIFICATE
Certified that this project report EIGHT SEATER SHORT RANGE
BUSINESS JET AIRCRAFT is a bonafide work of
__S.VIGNESH___________who carried out project under my supervision.
Submitted for the examination held on ____6.11.2012________
PROJECT GUIDE HEAD OF THE DEPARTMENT
INTERNAL EXAMINER EXTERNAL EXAMINER
P a g e | 3
vigneshaeronautical@gmail.com
ACKNOWLEDGEMENT
It gives us immense pleasure in expressing our sincere gratitude to
Honourable Dr.Jeppiaar, M.A., B.L., Ph.D., founder and Chairman of Jeppiaar
Engineering College for bestowing us with an opportunity to bring out this
project as a successful one.
We are very much grateful to our principal Dr.Susil Lal Das, M.Sc., Ph.D.,
for their encouragement and moral support.
We are very much indebted to Mr.G.Prabakaran (HOD) Aeronautical
Department for giving me his able support and encouragement.
At this juncture I must emphasis the point that this AIRCRAFT DESIGN
PROJECT-II would not have been possible without the highly informative and
valuable guidance by our respected preceptor (Ms. Puja Sunil and Ms. Usha
Bharathi), Mr. Balaraman whose vast knowledge and experience has must us go
about this project with great ease. We have great pleasure in expressing our sincere
& whole hearted gratitude to them. It is worth mentioning about my team mates,
friends and colleagues of the Aeronautical department, for extending their kind
help whenever the necessity arose. I thank one and all who have directly or
indirectly helped me in making this design project a great success.
P a g e | 4
vigneshaeronautical@gmail.com
ABSTRACT
The aim of this design project is to analysis an 8 Seater Short Range Executive Aircraft
by a structural analysis of Shear force and Bending moment. Have to design a more strength
aircraft by give the support of stringer, ribs, spar in Wing section and to give the support of
stinger, bulkhead, longer in Fuselage. The flying strength of aircraft is analysis by Vn diagram.
Then the Design of Miscellaneous Members of Wing Fuel Tank, Rib location and direction,
Empennage Design, Auxiliary Surfaces, Wing Fuselage Intersection, Flutter, Aileron Buzz and
Buffeting. Then the necessary graphs have to be plotted for further performance calculation.
Required diagrams are also drawn.
P a g e | 5
vigneshaeronautical@gmail.com
TABLE OF CONTENTS
TITLE PAGE
Abstract i
List of symbols iv
List of figures v
List of tables vi
List of Graphs vii
1 Introduction
1.1 Brief review of ADP - 1 1
1.2 Structural Design - Overview 2
2 V-n diagram 4
3 Structural Design of wing
3.1 Introduction 10
3.2 Air Inertia Load Estimation 11
3.3 Shear force & Bending moment Distribution 13
3.4 Material Selection 14
3.5 Wing Spar and Stringer Design 18
3.6 Shear flow Distribution 33
4
Structural Design of Fuselage
4.1 Design of fuselage
39
4.2 Stringer Design
39
4.3 Shear flow Distribution
43
4.4 Bulkhead design
46
P a g e | 6
vigneshaeronautical@gmail.com
5
Design of Miscellaneous Members
5.1 Wing Fuel Tank
47
5.2 Rib location and direction
48
5.3 Empennage Design
49
5.4 Auxiliary Surfaces
50
5.5 Wing Fuselage Intersection
52
5.6 Flutter
53
5.7 Aileron Buzz
54
5.8 Buffeting
55
6
Final design- three view diagram
56
7
Conclusion
57
Bibliography
58
Website reference
59
P a g e | 7
vigneshaeronautical@gmail.com
LIST OF SYMBOLS
A Total cross sectional area ft
2
A
SPAR
Cross sectional area of spar ft
2
A
fuselage
Cross sectional area of fuselage ft
2
a
t
Slope of the CL vs. curve for a horizontal tail. Deg
-1
a Distance of the front spar from the nose of the aircraft ft
b Distance of the rear spar from the nose of the aircraft ft
b Wing span ft
b
w
Width of the web Ft
b
f
Width of the flange Ft
C
wing
Chord of the actual wing Ft
C
elliptic
Chord of the elliptic wing Ft
C.G Centre of gravity Ft
g Acceleration due to gravity ft/s
2
D Drag Lb
E
Youngs modulus
lb/ft
2
FOS Factor of safety
F
tu
Tensile ultimate strength lb/ft
2
H Height of the C.G from the ground level Ft
i
w
Orientation of wing on fuselage Deg
I
xx
Second moment of area about X axis ft
4
Lw Local lift Lb
W
T.O
Takeoff weight Lb
W/S Wing loading lb/ft
2
y span location Ft
Angle of attack Deg
Turnover angle Deg
Density lb/ft
3
o
Density of air at sea level lb/ft
3
Bending stress lb/ft
2
P a g e | 8
vigneshaeronautical@gmail.com
LIST OF FIGURES
FIGURE TITLE PAGE NO.
1 Load on the aircraft 8
2 Typical V-n diagram 9
3 Final V-n diagram 14
4
Linear lift distribution
16
5 Elliptic Lift Distribution 17
6 Wing Separation Of Finite Section 22
7 Torque Distribution Over an Airfoil 26
8 Shear Center On The Chord 26
9 Wing Spar Arrangement 30
10 Different Spar Selection 31
11 Cross Section of Rear Spar 33
12 Cross Section of Middle Spar 35
13 Semimonocoque And Monocoque 39
14 Cross section Of Z-section 42
P a g e | 9
vigneshaeronautical@gmail.com
LIST OF TABLES
TABLE TITLE PAGE NO.
1 Specification of the Aircraft Design Project I 7
2 Load Factor 10
3 Velocity VS Load Factor 11
4 Load on Factor of safety 13
5 Span VS Linear Lift Distribution 17
6 Span VS Elliptic Lift Distribution 18
7 Span Vs Schrenk's value 18
8 Span Vs Load acting on wing 20
9 Centroid table 22
10 Span VS Shear Force 23
11 Span VS Bending Moment 23
12 Span wise VS Shear Force 25
13 Span wise VS Bending Moment0 25
14
Span wise VS Torque at Normal force
27
15
Spanwise VS Mean Aerodynamic Chord 28
16 Frontspar Centroid calculation table 33
17 Front Spar Bending Stress 34
18 Middle Spar Centroid Calculations 35
19 Middle Spar Bending Stress 36
20 Rear Spar Centroid Calculations 37
21 Rear Spar Bending Calculation 38
22 Fuselage Structure Analysis 41
23 Stringer Stress Tabulation 44
22 Weight, Moment, Shear Force, Bending Moment 45
P a g e | 10
vigneshaeronautical@gmail.com
LIST OF GRAPHS
GRAPHS TITLE PAGE NO.
1 Span VS Linear Lift Distribution 16
2 Span vs Elliptic lift Distribution 19
3 Span Vs Load acting on wing 20
4
Span Vs Fuel weight distribution
21
5 NET SHEAR FORCE vs BENDING MOMENT 25
6 Span wise VS Bending Moment 28
7 Span vs Net Torque Force 32
8 Stringer location in Fuselage 46
P a g e | 11
vigneshaeronautical@gmail.com
INTRODUCTION
Aircraft Design Project-II is a continuation of Aircraft Design Project-I. As mentioned in our
earlier project, Business jet, private jet or, colloquially, bizjet is a term describing a jet aircraft, usually
of smaller size, designed for transporting groups of up to 19 business people or wealthy individuals.
Business jets may be adapted for other roles, such as the evacuation of casualties or express parcel
deliveries, and a few may be used by public bodies, governments or the armed forces. The more formal
terms of corporate jet, executive jet, VIP transport or business jet tend to be used by the firms that build,
sell, buy and charter these aircraft. In our Aircraft Design Project-I, we have performed a rudimentary
analysis. We have carried out a preliminary weight estimation, power plant selection, aerofoil selection,
wing selection and aerodynamic parameter selection and analysis. Apart from the above mentioned, we
have also determined performance parameters such lift, drag, range, endurance, thrust and power
requirements.
Aircraft Design Project-II deals with a more in-depth study and analysis of aircraft performance
and structural characteristics. In the following pages we have carried out structural analysis of fuselage
and wings and the appropriate materials have been chosen to give our aircraft adequate structural
integrity. The flight envelope of our aircraft has also been established by constructing the V-n diagram.
We have also determined the landing gear position, retraction and other accompanying systems and
mechanisms. The study of all the above mentioned characteristics, has given us insight into the
complexity of designing a subsonic multi-role 8 seater business jet.
The specifications of the Aircraft design project-I as follows:
S.No DESIGN PARAMETER MAGNITUDE UNIT
1. Cruising speed 236.11 m/s
2. Wing span 12.84 m
3. Aircraft Length 19.5 m
4. Wing area 21.84 m
2
5. Height 4.8 m
1
P a g e | 12
vigneshaeronautical@gmail.com
6. Aspect ratio 7.55 (No unit)
7. Wing loading 585.89 Kg/m
2
8. Empty weight 7,296 Kg
9. Maximum take-off weight 1,25,568 N
10. Pay load 1280 kg
11. No. of engines 2 (No unit)
12. Thrust power 32.00 Kn
13. Range 5200 Km
14. Service ceiling 1,3700 M
15. Mach no. 0.715 (No unit)
16. Thrust/weight ratio 0.25 (No unit)
17. Gliding angle 4.23
o
18. Seating capacity 8 (No unit)
19. Fuselage 10.54 M
20. Take-off distance 1,007.46 M
21. Landing distance 710.3 M
22. Rate of climb 1.298 10
-3
m/s
P a g e | 13
vigneshaeronautical@gmail.com
LOADS ON THE AIRCRAFT:
The structure of an aircraft is required to support two classes of loads, first termed ground
loads, includes all loads encountered by the aircraft during movement or transportation on the
ground such as taxing, landing loads, towing etc, while the second is the air loads, comprises
loads imposed on the structure. The two classes of loads of loads may be still classified as
surface forces acting on the surface of the structure and body forces acting over the volume of
the structure. Basically all air loads are the resultant of the pressure distribution over the surfaces
of the skin produced by steady flight, maneuver or gust conditions. Generally these causes
bending, shear, torsion in all parts of the structure in addition to local normal pressure loads
imposed on the skin.
Ground loads encountered in landing and taxing subject the aircraft to concentrated shock
loads through the undercarriage system. The majority of the aircraft have their main
undercarriage located in the wings with nose wheel or tail wheel in the vertical plane of
symmetry. Clearly the position of the undercarriage should be in such a position so as to produce
minimum loads on the wing structure.
P a g e | 14
vigneshaeronautical@gmail.com
ESTIMATION OF V-N DIAGRAM
The control of weight in aircraft design is of extreme importance. Increase in weight
requires stronger structures to support them, which in turn lead to further increase in weight & so
on. Excess of structural weight means lesser amounts of payload, affecting the economic
viability of the aircraft.
Therefore there is need to reduce aircrafts weight to the minimum compatible with
safety. Thus to ensure general minimum standards of strength & safety, airworthiness regulations
lay down several factors which the primary structures of the aircraft must satisfy.
These are
1. LIMIT LOAD: the maximum load that the aircraft is expected to experience in normal
operation.
2. PROOF LOAD: product of the limit load and proof factor(1.0-1.25)
3. ULTIMATE LOAD : product of limit load and ultimate factor(1.0-1.5)
The aircrafts structure must withstand the proof load without detrimental distortion &
should not fail until the ultimate load has been achieved.
V-n Diagram:
A chart of Velocity versus load factor (V-n diagram) is another way of showing limits of
aircraft performance. It shows how much load factor can be safely achieved at different
airspeeds.
2
P a g e | 15
vigneshaeronautical@gmail.com
The maneuverability of the aircraft is also dictated by the loads falling on the structures
during the maneuvers. Both the aerodynamic and structural limitations for a given airplane are
illustrated in the V-n diagram, a plot of load factor versus flight velocity.
A V-n diagram is type of flight envelope for the aircraft establishing the maneuver boundaries.
The BCAR (British civil airworthiness requirements) has given the basic strength and
flight performance limits of various categories of the aircraft. They are listed below
Category Positive load factor (n
+
) Negative load factor(n
-
)
Normal 3.8 -1.5
Semi aerobatic 4.5 -2
Fully aerobatic 6 -3
Tabular column 2: LOAD FACTOR
The 8 seater executive aircraft comes under the normal category. Therefore the load
factor limits for the aircraft is 3.8 & -1.5.
The V-n diagram for the aircraft is drawn for the two cases namely,
1. Intentional maneuver( pilot induced maneuver )
2. Unintentional maneuver( gusts)
INTENTIONAL MANEUVER:
Intentional maneuvers are induced by the pilot during climb, pull up or pull down,
banking the plane etc...
The load factor is function of velocity. The expression relating the load factor and the
velocity is given by
n
max
= (
v
v
S
)
2
Where n
max
is the maximum load factor, V is the speed of the aircraft, V
s
is the stalling
speed of the aircraft.
The stalling speed of the aircraft V
s
2
=
2W
S
]
pC
L
max
V
s
= 59.197 m/s
P a g e | 16
vigneshaeronautical@gmail.com
For various values of V, n
max
is calculated and tabulated below,
Tab3. Velocity VS Load Factor
The cruising speed of the aircraft is 236.11 m/s.
The dive speed of the aircraft is the maximum speed of the aircraft. The dive speed is equal to
the sum of the cruising speed and 60 knots.
V
D
= 236.11 + 60 knots
= 236.11 +30.56 m/s
= 266.67 m/s
GUSTS:
The movement of air in turbulence is known as gusts. It produces changes in wing
incidence, thereby subjecting the aircraft to sudden or gradual increases or decreases in lift from
which normal accelerations result.
These may be critical for large, high speed aircraft and may possibly cause higher
loads than control initiated maneuvers.
Thus in the gust analysis, the change in load factor due to the gust is calculated. The
BCAR has given standard gust velocities for stall, cruise, dive speeds as 66, 50, 25 ft/s
V
N
max
=(
v
v
S
)
2
-0.25 29.598
-0.5 41.858
-0.75 51.256
-1 59.197
V
N
max
=(
v
v
S
)
2
4 118.394
3.8 115.396
3.5 110.74
3 102.53
2.5 93.599
2 83.71
1.5 72.501
1 59.197
P a g e | 17
vigneshaeronautical@gmail.com
respectively. The small change in load factor n due to the gust is calculated by assuming a
sharp gust.
The change in load factor n =
p
2()
Where density at cruising altitude,
a lift slope, in radians
U gust velocity in m/s
V velocity of the aircraft in m/s
W/S wing loading in N/m
2
In the above formula, gusts are assumed to be sharp but it is usually graded, hence
a relief factor called gust alleviation factor K is introduced in the term.
The value of the K is obtained from the book AIRPLANE AERODYNAMICS
AND PERFORMANCE by JAN ROSKAM
Where K =
0.88
5.3+u
, =
(WS)
pCgC
L
u
Where is the density, C is the mean aerodynamic chord, g is the acceleration due to gravity;
C
L
is the slope lift coefficient.
The C
L
(corrected for aspect ratio) is 0.0962/deg.
=
2 (WS)
pCgC
L
o
=
(25747.58)
(2.38849.811.70.157.3)
K =
0.88
5.3+u
=
0.8850.36
5.3+50.36
= 50.36
= == = 0.796 0.796 0.796 0.796
P a g e | 18
vigneshaeronautical@gmail.com
For STALL SPEED V= 59.197 m/s, U= 20m/s
n = K
pa0v
(WS)
=
0.7962.38840.157.32059.197
25747.58
n = 1.062
For CRUISE SPEED V=236.11 m/s, U= 15m/s
n = K
pa0v
(WS)
=
0.7962.38840.157.315236.11
25747.58
n = 2.725
For DIVE SPEED V= 266.67 m/s, U= 7.5 m/s
n = K
pa0v
(WS)
=
0.7962.38840.157.37.5266.67
25747.58
n = 1.794
K = Therefore n = K
pa0v
(WS)
P a g e | 19
vigneshaeronautical@gmail.com
V 1+ n 1- n
59.197 2.062 -0.062
236.11 3.725 -1.725
266.67 2.794 -1.794
Tab 4.load Factor of safety
P a g e | 20
vigneshaeronautical@gmail.com
STRUCTURAL ANALYSIS AND DESIGN OF WINGS
WING STRUCTURAL ANALYSIS:
The structural design of the wing requires a complete quantitative knowledge of the
different loads it will be subjected to during its flight regime. These loads can be briefly
classified as
1. Distributed loads - Loads such as aerodynamic loads, weight of the wing and weight of
fuel.
2. Concentrated loads Loads such as thrust, engine weight, landing gear weight and
armament weight.
LOADS ACTING ON WING:
As both the wings are symmetric, let us consider the starboard wing at first. There are three primary loads
acting on a wing structure in transverse direction which can cause considerable shear forces and bending moments
on it. They are as follows:
Lift force (given by Schrenks curve)
Self-weight of the wing
Weight of the power plant
Weight of the fuel in the wing
SCHRENKS CURVE:
Lift is a component of the resultant aerodynamic force acting at the centre of pressure of
an aerodynamic chord, along a direction perpendicular to the direction of the relative wind. At a
particular altitude and at a specific angle of attack, Lift varies along the wing span due to the
variation in chord length along the span. Schrenks curve defines this lift distribution over the
wing span of an aircraft. Since the wings of an aircraft are symmetrical about the longitudinal
axis, the Schrenks curve for the starboard wing alone can be obtained at first. This is given by
y= (
y
1
+y
2
2
)
where y
1
linear variation of lift along the wing semi-span
y
2
equivalent elliptic lift distribution along the wing semi-span
3
P a g e | 21
vigneshaeronautical@gmail.com
TO FIND y1:
Lift force is found along the line joining the aerodynamic centers of chords along the
wing span. Hence, the wing is rotated about the wing root so that the line joining the
aerodynamic centers becomes the horizontal line.
a=(
b
cos \
)
a=(
12.84
cos11
0
13
|
)
=6.55
Lift per unit length at wing root = C
L
0.5V
2
C
R
= 0.238840.51.4236.111
2
2.55
= 23766.98 N/m
Lift per unit length at wing tip = C
L
0.5V
2
C
t
=0.238840.51.4236.111
2
0.84
= 7829.12 N/m
6.55 m
Fig.4 Linear lift distribution
Area under trapezoid life distribution = 155673.719
Equation of linear lift distribution for starboard wing
Y1 = -1195.289x + 23766.98
Equation of linear lift distribution for port wing we have to replace x by x in general,
Y1 = 1195.289x + 23766.98
P a g e | 22
vigneshaeronautical@gmail.com
X Y
1
0 23766.98
1 22571.7
2 21376.42
3 20181.14
4 18985.86
5 17790.58
6 16595.3
6.55 15937.89
Tab5. Span VS Linear Lift Distribution
Graph.4 Span VS Linear Lift Distribution
Elliptic Lift Distribution:
Twice the area under the curve or line will give the lift which will be required to
overcome weight
Considering an elliptic lift distribution we get
L/2 = W/2 =
ab
1
4
Where b1 is Actual lift at root
A =
ab
1
4
And a is wing semi span
0
5000
10000
15000
20000
25000
0 1 2 3 4 5 6 6.55
L
I
N
E
A
R
L
I
F
T
D
I
S
T
R
I
B
U
T
I
O
N
SPAN (a)
Series1
Series2
P a g e | 23
vigneshaeronautical@gmail.com
Lift at Tip b = 15138.35 N/m
6.55 m
Fig 5. Elliptic Lift Distribution
Y
2
= 1155.60V42. 93 -x
2
x Y
2
0 15138.317
1 14960.852
2 14415.354
3 13457.142
4 11987.651
5 9779.05
6 6072.292
6.55 0
Tab 6: Span VS Elliptic Lift Distribution
15138.35 N/m
P a g e | 24
vigneshaeronautical@gmail.com
Construction of Schrenks Curve:
Schrenks Curve is given by
Y
1
+Y
2
=
1195.289 + 237.98+1155.
.
42.93-x
2
2
Y
1
+Y
2
= -597.64 x + 45489.019 + 1155.60 V42. 93 -x
2
x Y
1
+Y
2
0 19452.65
1 18766.28
2 17895.89
3 16819.14
4 15486.76
5 13784.82
6 11333.796
6.55 7968.95
Tab 7:SpanVsSchrenk's value
P a g e | 25
vigneshaeronautical@gmail.com
Graph 2: Span vs Elliptic lift Distribution
Load Estimation on wings
Description:
The solution methods which follow Eulers beam bending theory (/y=M/I=E/R) use the
bending moment values to determine the stresses developed at a particular section of the beam
due to the combination of aerodynamic and structural loads in the transverse direction. Most
engineering solution methods for structural mechanics problems (both exact and approximate
methods) use the shear force and bending moment equations to determine the deflection and
slope at a particular section of the beam. Therefore, these equations are to be obtained as
analytical expressions in terms of span wise location. The bending moment produced here is
about the longitudinal (x) axis.
Loads acting on wing:
As both the wings are symmetric, let us consider the starboard wing at first. There are
three primary loads acting on a wing structure in transverse direction which can cause
considerable shear forces and bending moments on it. They are as follows:
Lift force (given by Schrenks curve)
Self-weight of the wing
Weight of the power plant
Weight of the fuel in the wing
Self-Weight (y3): Self-weight of the wing,
W
wing
= 5548.06 kg 9.81
= 54426.46 N
P a g e | 26
vigneshaeronautical@gmail.com
W
port wing
=-27213.23 N
W
star board wing
= -27213.23 N
]
3
6.55
0
=]
k (x-(6.55))
3
3
6.55
0
y
3
= -290.52 (x-6.55)
2
x y
0 -12464.07
1 -8948.74
2 -6014.49
3 -3661.28
4 -1889.11
5 -697.97
6 87.88
6.55 0
Tab 8: SpanVs Load acting on wing
Graph 3: Span Vs Load acting on wing
P a g e | 27
vigneshaeronautical@gmail.com
Power Plant:
According to our design data, Our Aircraft power plant is attach to rear fuselage. So,
power plant calculation wont be calculated.
Fuel Weight Distribution:
W
f
= 23215.55
Consider as equation,
y
f
= 1902.91x-12464.07
2 -8658.25
3 -6755.35
4 -4852.43
5 -2949.52
Graph 4. Span Vs Fuel weight distribution
-10000
-9000
-8000
-7000
-6000
-5000
-4000
-3000
-2000
-1000
0
2 3 4 5 6 6.55
Fuel weight Distribution
P a g e | 28
vigneshaeronautical@gmail.com
SHEAR FORCE & BENDING MOMENT
SHEAR FORCE AND BENDING MOMENT DIAGRAMS OF A WING DUE
TO LOADS IN TRANSVERSE DIRECTION AT CRUISE CONDITION:
The solution methods which follow Euler's beam bending theory (/y=M/I=E/R) use the
bending moment values to determine the stresses developed at a particular section of the beam
due to the combination of aerodynamic and structural loads in the transverse direction. Most
engineering solution methods for structural mechanics problems (both exact and approximate
methods) use the shear force and bending moment equations to determine the deflection and
slope at a particular section of the beam. Therefore, these equations are to be obtained as
analytical expressions in terms of span wise location. The bending moment produced here is
about the longitudinal (x) axis.
As both the wings are symmetric, let us consider the starboard wing at first. There are
three primary loads acting on a wing structure in transverse direction which can cause
considerable shear forces and bending moments on it. They are as follows:
Lift force (given by Schrenk's curve)
Self-weight of the wing
Weight of the powerplant
S.No. Curve/Component Area/Structural weight (N) Centroid
1 Y
1
155673.719 5.458
2 Y
2
77896.859 2.781
3 Wing 54426.46 1.637
4 Fuel 23215.55 1.31
Tab 9: Centroid table
P a g e | 29
vigneshaeronautical@gmail.com
V=0
77836.859-54426.46-23215.55-V
A
= 0
V
A
= 194.85
M
A
= 0
M
A
+ (54426.4651.637)+(23215.551.31)-(155673.7195.458)-(77836.8592.781)
M
A
946622.97 = 0
M
A
= 946622.97
P a g e | 30
vigneshaeronautical@gmail.com
SHEAR FORCE
S.F
1
= -298.84 x
2
+ 45489.019 x + 577.8 V42. 93 -
2
- 42.903 Sin
-
1
x
.55
-290.52
x
3
3
+42. 9x +. 55 x
2
-194.85
SPAN Shear Force
0 -19625.79
1 -8113.17
2 1496.55
3 9203.37
4 15007.29
5 18908.31
6 20906.43
6.55 21194.28
Tab 10: Span VS Shear Force
BENDING MOMENT:
B.M = -199.21 x
3
+ 15163.006 x
2
+ 288.9 [x (xV42. 93 -
2
) + 42.903 Sin -1
x
.55
] + 385.2
(42.903- x
2
)
1.5
-290.52 (
x
4
12
+ 21.45 x
2
- 2.18 x
3
) + 94662.97
vigneshaeronautical@gmail.com
SPAN BENDING MOMENT
0 754870.44
1 1043525.353
2 1062831.914
3 1084364.515
4 1108829.591
5 1318721.935
6 1381469.212
6.55 943585.515
Tab 11 : Span VS Bending Moment
NET SHEAR FORCE AND BENDING MOMENT DIAGRAM:
Graph.5 NET SHEAR FORCE vs BENDING MOMENT
200000
400000
600000
800000
1000000
1200000
1400000
1600000
-8 -6 -4 -2
BENDING MOMENT
754870.44
1043525.353
1062831.914
1084364.515
1108829.591
1318721.935
1381469.212
943585.515
Tab 11 : Span VS Bending Moment
NET SHEAR FORCE AND BENDING MOMENT DIAGRAM:
Graph.5 NET SHEAR FORCE vs BENDING MOMENT
0
200000
400000
600000
800000
1000000
1200000
1400000
1600000
0 2 4 6 8
WING SPAN
BENDING
MOMENT
SHEAR FORCE
P a g e | 31
P a g e | 32
vigneshaeronautical@gmail.com
Shear force and bending moment diagrams due to loads along chordwise
direction at cruise condition:
Aerodynamic center- This is a point on the chord of an airfoil section where the bending
moment due to the components of resultant aerodynamic force (Lift and Drag) is constant
irrespective of the angle of attack. Hence the forces are transferred to this point for obtaining
constant Ma.c
Shear center- This is a point on the airfoil section where if a force acts, it produces only bending
and no twisting. Hence the force is transferred to this point and the torque is found.
Angle of Attack (max) = 15.0
0
, Angle of Attack (Zero lift) = -1.0
Cruise C
L
= 1.40 V = 236.11 m/s
= 0.23884 kg/m
3
C
D
= 0.0025
SHEAR FORCE BENDING MOMENT:
Co-efficient of force at normal direction
Cn = C
L
cos + C
D
sin
= 1.398
Co-efficient of force at Chordwise direction
C
C
= C
L
sin + C
D
cos
= 0.026
Therefore, Force per unit length= Cc0.5V
2
C
Force at Cr = 441.39 N/m
Force at Ct = 145.39 N/m
For Linear,
y = 23.05 x + 145.39 1
Shear Force:
Integrate Eqn. 1
] = 11. 525x
3
12.84
+145. 39 x
P a g e | 33
vigneshaeronautical@gmail.com
Span wise Shear force
0 0
1 156.915
2 336.88
3 539.895
4 765.96
5 1015.07
6 1287.24
7 1582.45
8 1900.72
9 2242.03
10 2606.40
11 2993.81
12 3404.28
12.84 3766.88
Tab 12: Span wise VS Shear Force
BENDING MOMENT:
] =
12.84
0
3.841 x
3
+72.69x
2
Span wise Bending moment
0 0
1 76.531
2 176.108
3 321.77
P a g e | 34
vigneshaeronautical@gmail.com
4 536.584
5 843.575
6 1265.796
7 1826.293
8 2548.112
9 3454.299
10 4567.9
11 5911.961
12 7509.528
12.84 9064.425
Tab 13: Span wise VS Bending Moment
Graph 6. Span wise VS Bending Moment
0
2000
4000
6000
8000
10000
12000
14000
CHORDWISE
BENDING MOMENT & SHEAR FORCE
BENDING
MOMENT
SHEAR
FORCE
P a g e | 35
vigneshaeronautical@gmail.com
TORQUE DUE TO NORMAL FORCES AND CONSTANT PITCHING
MOMENT AT CRUISE CONDITION:
Aerodynamic center- This is a point on the chord of an airfoil section where the bending
moment due to the components of resultant aerodynamic force (Lift and Drag) is constant
irrespective of the angle of attack. Hence the forces are transferred to this point for obtaining
constant M
a.c
Shear center- This is a point on the airfoil section where if a force acts, it produces only bending
and no twisting. Hence the force is transferred to this point and the torque is found
The lift and drag forces produce a moment on the surface of cross-section of the wing,
otherwise called a torque, about the shear center. Moment about the aerodynamic center gets
transferred to the shear center. The shear center on the chord under which it is locates.
Cruise condition (Normal Force)
T= C
n
V
2
c 0.034 C
P a g e | 36
vigneshaeronautical@gmail.com
= 1325.51 C
2
Where,
C chord
the equation for chord can also be represented in terms of x by taking C = mx +k,
C = 0.264 x +2.55
Therefore, Torque = 30.751x
3
+ 8418.46 x + 892.33 x
2
Span wise Torque at Normal force
0 0
1 9541.54
2 21052.24
3 34716.62
4 50719.18
5 69244.42
6 90476.85
7 114600.98
8 141801.31
9 172262.34
10 206168.6
11 243704.57
12 285054.76
12.84 322871.54
P a g e | 37
vigneshaeronautical@gmail.com
Tab 14:Span wise VS Torque at Normal force
TORQUE DUE TO CHORDWISE FORCE:
Torque per unit length T
2
= F
C
0
T
2
= 0
TORQUE DUE TO MEAN AERODYNAMIC CHORD:
Torque due to M
a.c
=
M
c.c
0.5V
2
CC
T
3
= -3347.9 C
2
T
3
= -77.671 x
3
- 21768.04 x- 2253.806 X
2
Span wise MEAN AERODYNAMIC CHORD
0 0
1 -24099.51
2 -53172.67
3 -87685.49
4 -128104.0
5 -174894.22
6 -228522.19
7 -289453.92
8 -358155.45
9 -435092.80
10 -520732.01
11 -615539.06
12 -719980.03
12.84 -815496.45
P a g e | 38
vigneshaeronautical@gmail.com
Tab 15: Spanwise VS Mean Aerodynamic Chord
NET TORQUE:
Then the different torque components are brought together in a same graph to make a
comparison
The net torque will be sum of all the above torques (i.e.) torques due to normal force, chordwise
force, powerplant and aerodynamic moment.
Graph.7 Span vs Net Torque Force
-1000000
-800000
-600000
-400000
-200000
0
200000
400000
1 2 3 4 5 6 7 8 9 10 11 12 13 14
Series1
Series2
Series3
P a g e | 39
vigneshaeronautical@gmail.com
LOAD ESTIMATION OF WINGS
WING STRUCTURAL LAYOUT
Specific Roles of Wing (Mainwing) Structure:
The specified structural roles of the wing (or main plane) are:
To transmit: wing lift to the root via the main span wise beam
Inertia loads from the power plants, undercarriage, etc., to the main beam.
Aerodynamic loads generated on the aerofoil, control surfaces & flaps to the main
beam.
To react against:
Landing loads at attachment points
Loads from pylons/stores
Wing drag and thrust loads
To provide:
Fuel tank age space
Torsional rigidity to satisfy stiffness and aero-elastic requirements.
To fulfill these specific roles, a wing layout will conventionally compromise:
Span wise members (known as spars or booms)
Chord wise members(ribs)
A covering skin
Stringers
P a g e | 40
vigneshaeronautical@gmail.com
Basic Functions of Wing Structural Members
The structural functions of each of these types of members may be considered independently as:
SPARS
Form the main span wise beam
Transmit bending and torsional loads
Produce a closed-cell structure to provide resistance to torsion, shear and tension loads.
In particular:
Webs resist shear and torsional loads and help to stabilize the skin.
Flanges - resist the compressive loads caused by wing bending.
SKIN
To form impermeable aerodynamics surface
Transmit aerodynamic forces to ribs & stringers
Resist shear torsion loads (with spar webs).
React axial bending loads (with stringers).
STRINGERS
Increase skin panel buckling strength by dividing into smaller length sections.
React axial bending loads
RIBS
Maintain the aerodynamic shape
Act along with the skin to resist the distributed aerodynamic pressure loads
Distribute concentrated loads into the structure & redistribute stress around any
discontinuities
Increase the column buckling strength of the stringers through end restraint
Increase the skin panel buckling strength.
SPAR DEFINITION:
The maximum bending moment from previous section was found to be as 2897784.51
Nm. Therefore we define 3 Spars with front spar at 15% of chord, middle spar at 45% of chord
and rear spar at 70% of chord. The position of the three spars from the leading edge of the root
chord is given below as follows:
P a g e | 41
vigneshaeronautical@gmail.com
Front spar - 15% of chord = 2.442 m
Middle spar - 45% of chord = 7.326 m
Rear spar - 70% of chord = 11.396 m
Bending moment M = Max BM * FOS * n
= 2897784.51 1.5 3.8
= 16517371.71Nm
The Structural load bearing members in the wing are the Spars and Stringers. The
bending moment carried by the Spars is 70% and that of Stringers is 30% of the total Bending
Moment.
Bending Moment taken by Spars is = 0.7 x 16517371.71 = 11562160.19 Nm
The cross section of the spar chosen here is an I-section
For each spar we are determining the following parameters:
A. Centroid
B. Moment of Inertia
C. Bending Moment
D. Bending Stress
vigneshaeronautical@gmail.com
FRONT SPAR:
Height of the spar = 38 cm
Breadth of the spar = 16 cm
Thickness of the spar = 4.5 cm
Fig 11: Cross Section of Rear Spar
To find out the centroid, the following
Element
Area(A)
(cm
2
)
x
(cm) (cm)
1 72 8 2.25
2 130.5 8
3 72 8 35.75
Total 274.5
Height of the spar = 38 cm
Breadth of the spar = 16 cm
Thickness of the spar = 4.5 cm
Fig 11: Cross Section of Rear Spar
To find out the centroid, the following calculations are made:
y
(cm)
Ax
(cm
3
)
Ay
(cm
3
)
Ax
2
(cm
4
)
Ay
2
(cm
4
)
2.25 576 162 4608 364.5
19 1044 2479.5 8352 47110.5
35.75 576 2574 4608 92020.5
2196 5215.5 17568 139495.5
P a g e | 42
Icx
(cm
4
)
Icy
(cm
4
)
121.5 1536
47110.5 9145.8 220.22
92020.5 121.5 1536
139495.5 9388.87 3292.22
P a g e | 43
vigneshaeronautical@gmail.com
Front Spar Calculations:
Centroid = X =
Ax
A
= 8 cm; Y=
Ay
A
= 19 cm
I
xx
= I
cx
+ Ay
2
AY
2
I
xx
= (9388.87) + (139495.5) (274.5)(19)
2
I
xx
= 49789.88 cm
4
I
yy
= I
cy
+ Ax
2
AX
2
I
yy
= (3292.22) + (17568) (274.5) (8)
2
I
yy
= 3292.22 cm
4
The FRONT SPAR carries 35 % of the BM carried by the Spars. Thus,
Front spar BM = 0.35 x 1156216019 N-cm
= 404675606.7 N cm
Front Spar Bending Stress:
Bending Stress,
z
= (
N
x
I
xx
)y
POINTS
COORDINATES (y)
(cm)
BENDING STRESS
(N/cm
2
)
A 19 154425.68
B 14.5 117851.18
C 14.5 117851.18
D -14.5 -117851.18
E -14.5 -117851.18
F -19 -154425.68
The bending stress at various points whose co-ordinates are determined with centroid as
the origin are calculated from above formula and tabulated.
vigneshaeronautical@gmail.com
MIDDLE SPAR:
Height of the spar = 41.6 cm
Breadth of the spar = 18 cm
Thickness of the spar = 5 cm
Fig 12: Cross Section of Middle Spar
Height of the spar = 41.6 cm
Breadth of the spar = 18 cm
Thickness of the spar = 5 cm
Fig 12: Cross Section of Middle Spar
P a g e | 44
P a g e | 45
vigneshaeronautical@gmail.com
To find out the centroid, the following calculations are made:
Element
Area(A)
(cm
2
)
x
(cm)
y
(cm)
Ax
(cm
3
)
Ay
(cm
3
)
Ax
2
(cm
4
)
Ay
2
(cm
4
)
Icx
(cm
4
)
Icy
(cm
4
)
1 90 9 2.5 810 225 7290 562.5 187.5 2430
2 158 9 20.8 1422 3286.4 12798 68357.12 13147.7 329.17
3 90 9 39.1 810 3519 7290 137592.9 187.5 2430
Total 338 3042 7030.4 27378 206512.5 13522.7 5189.17
Middle Spar Calculations
Centroid = X =
Ax
A
= 9 cm; Y=
Ay
A
= 20.8 cm
I xx = I
cx
+ Ay
2
AY
2
I xx = (13522.7) + (206512.5) (338) (20.8)2
I xx = 60467.7 cm
4
I
yy
= I
cy
+ Ax
2
AX
2
I
yy
= (5189.17) + (27378) (338) (9)
2
I yy = 5189.17 cm
4
The bending moment carried by the middle spar is 40% of the total bending moment
carried by the spars.
Middle Spar BM = 462486407.6 N-cm
Bending Stress,
z
= (
M
x
I
xx
)y
vigneshaeronautical@gmail.com
POINTS
COORDINATES (y)
A
B
C
D
E
F
The bending stress at various points whose co
the origin are calculated from above formula and
REAR SPAR
Height of the spar = 17.72 cm
Breadth of the spar = 7.6 cm
Thickness of the spar = 2.5 cm
COORDINATES (y)
(cm)
BENDING STRESS
(N/cm
2
)
20.8 159088.52
15.8 120846.09
15.8 120846.09
-15.8 -120846.09
-15.8 -120846.09
-20.8 -159088.52
The bending stress at various points whose co-ordinates are determined with centroid as
the origin are calculated from above formula and tabulated.
Height of the spar = 17.72 cm
Breadth of the spar = 7.6 cm
Thickness of the spar = 2.5 cm
P a g e | 46
ordinates are determined with centroid as
P a g e | 47
vigneshaeronautical@gmail.com
To find out the centroid, the following calculations are made:
Element
Area(A)
(cm
2
)
x
(cm)
y
(cm)
Ax
(cm
3
)
Ay
(cm
3
)
Ax
2
(cm
4
)
Ay
2
(cm
4
)
Icx
(cm
4
)
Icy
(cm
4
)
1 19 3.8 1.25 72.2 23.75 274.36 29.6875 9.896 91.45
2 31.8 3.8 8.86 120.84 281.748 459.19 2496.287 428.76 16.56
3 19 3.8 16.47 72.2 312.93 274.36 5153.957 9.896 91.45
Total 69.8 265.24 618.428 1007.9 7679.932 448.552 199.46
Rear Spar Calculations
Centroid = X =
Ax
A
= 3.8 cm; Y=
Ay
A
= 8.86 cm
I
xx
= I
cx
+ Ay
2
AY
2
I
xx
= (448.552) + (7679.932) (69.8) (8.86)
2
I
xx
= 2649.184 cm
4
I
yy
= I
cy
+ Ax
2
AX
2
I
yy
= (199.46) + (1007.9) (69.8) (3.8)
2
I
yy
= 199.46 cm
4
Rear Spar carries 25 % of the spar Bending Moments.
Bending Moment = 289054004.8 N-cm
Bending Stress,
z
= (
M
x
I
xx
)y
P a g e | 48
vigneshaeronautical@gmail.com
The bending stresses at various points are obtained as:
Rear Spar Bending
Stress POINTS
COORDINATES (y)
(cm)
BENDING STRESS
(N/cm2)
A 8.86 966719.74
B 6.36 693943.29
C 6.36 693943.29
D -6.36 -693943.29
E -6.36 -693943.29
F -8.86 -966719.74
The bending stress at various points whose co-ordinates are determined with Centroid as
the origin are calculated from above formula and tabulated.
vigneshaeronautical@gmail.com
STRUCTURAL ANALYSIS AND DESIGN OF FUSELAGE
FUSELAGE STRUCTURAL LAYOUT:
The fuselage is the main structure, or body, of the aircraft. It provides space for
personnel, cargo, controls, and most of the accessories. The power plant, wings,
landing gear are attached to it.
There are two general types of fuselage construction
designs. The welded steel truss was used in smaller Navy aircraft, and it is still being used in
some helicopters.
The monocoque design relies largely on the strength of the skin, or covering, to carry
various loads. The monocoque design may be divided into three classes
semimonocoque and reinforced shell.
Fig 13:Semimonocoque And Monocoque
STRUCTURAL ANALYSIS AND DESIGN OF FUSELAGE
FUSELAGE STRUCTURAL LAYOUT:
The fuselage is the main structure, or body, of the aircraft. It provides space for
personnel, cargo, controls, and most of the accessories. The power plant, wings, stabilizers, and
There are two general types of fuselage constructionwelded steel truss and monocoque
designs. The welded steel truss was used in smaller Navy aircraft, and it is still being used in
onocoque design relies largely on the strength of the skin, or covering, to carry
various loads. The monocoque design may be divided into three classes - monocoque,
semimonocoque and reinforced shell.
Fig 13:Semimonocoque And Monocoque
4
P a g e | 49
STRUCTURAL ANALYSIS AND DESIGN OF FUSELAGE
The fuselage is the main structure, or body, of the aircraft. It provides space for
stabilizers, and
welded steel truss and monocoque
designs. The welded steel truss was used in smaller Navy aircraft, and it is still being used in
onocoque design relies largely on the strength of the skin, or covering, to carry
monocoque,
P a g e | 50
vigneshaeronautical@gmail.com
The true monocoque construction uses formers, frame assemblies, and bulkheads to give
shape to the fuselage. However, the skin carries the primary stresses. Since no bracing
members are present, the skin must be strong enough to keep the fuselage rigid. The
biggest problem in monocoque construction is maintaining enough strength while
keeping the weight within limits.
Semimonocoque design overcomes the strength-to-weight problem of monocoque
construction. In addition to having formers, frame assemblies, and bulkheads, the
semimonocoque construction has the skin reinforced by longitudinal members.
The reinforced shell has the skin reinforced by a complete framework of structural
members.
Different portions of the same fuselage may belong to any one of the three classes. Most are
considered to be of semimonocoque-type construction.
The semimonocoque fuselage is constructed primarily of aluminum alloy, although steel
and titanium are found in high-temperature areas. Primary bending loads are taken by the
longerons, which usually extend across several points of support. The longerons are
supplemented by other longitudinal members known as stringers. Stringers are more numerous
and lightweight than longerons.
The vertical structural members are referred to as bulkheads, frames, and formers. The
heavier vertical members are located at intervals to allow for concentrated loads. These members
are also found at points where fittings are used to attach other units, such as the wings and
stabilizers.
The stringers are smaller and lighter than longerons and serve as fill-ins. They have some
rigidity but are chiefly used for giving shape and for attachment of skin. The strong, heavy
longerons hold the bulkheads and formers. The bulkheads and formers hold the stringers. All of
these join together to form a rigid fuselage framework. Stringers and longerons prevent tension
and compression stresses from bending the fuselage.
The skin is attached to the longerons, bulkheads, and other structural members and
carries part of the load. The fuselage skin thickness varies with the load carried and the stresses
sustained at particular location.
There are a number of advantages in using the semimonocoque fuselage.
The bulkhead, frames, stringers, and longerons aid in the design and construction of a
streamlined fuselage. They add to the strength and rigidity of the structure.
The main advantage of the semimonocoque construction is that it depends on many
structural members for strength and rigidity. Because of its stressed skin construction, a
semimonocoque fuselage can withstand damage and still be strong enough to hold
together.
P a g e | 51
vigneshaeronautical@gmail.com
Loads and its distribution:
To find out the loads and their distribution, consider the different cases. The main
components of the fuselage loading diagram are:
Weight of the fuselage
Engine weight
Weight of the horizontal and vertical stabilizers
Tail lift
Weight of crew, payload and landing gear
Systems, equipment, accessories
Symmetric flight condition, steady and level flight: (Downward forces negative) Values for the
different component weights are obtained from aerodynamic design calculations.
S.No.
Equipment and
Component
Length
from Ref.
point
Weight (N) Moment
Shear
Force
Bending
Moment
1 Nose 0.58 3933.81 2281.609 3933.81 2281.809
2 Pilot(2) 2.02 1962.00 3963.24 5895.81 6244.84
3 Cockpit 2.62 4944.24 12953.908 10840.05 19198.757
4 Wing 6.62 54426.46 360303.16 65266.51 379501.91
5 Passenger(3) 6.63 3237.30 21463.29 68503.81 400965.2
6 Passenger(3) 7.92 3237.30 25639.41 71741.11 426604.61
7 Passenger(2) 9.85 2060.10 20291.98 73801.21 446896.59
8 Crew(2) 10.32 2060.10 21260.23 75861.31 468156.82
9
Weight of
Fuselage Sheet
10.50 2000.68 21007.14 77861.99 489163.96
10 Power Plant 14.23 3937.83 56036.74 81799.92 545200.72
11 Horizontal Tail 17.10 13232.807 226280.9 95032.72 771481.607
12 Vertical tail 17.60 8971.34 157895.58 104004.06 929377.18
SHEAR FORCE AND BENDING MOMENT DIAGRAM
P a g e | 52
vigneshaeronautical@gmail.com
To determine the shear force and bending moment diagram for the wing we assume that the wing
is a cantilever beam with the root end fixed while the tail end is free.
For a cantilever beam the shear force is a given by,
Shear Force = Rx
Bending Moment =
Rx
2
2
Tabulation for the values of shear force and bending moment at various positions along the span
is as follows.
FUSELAGE STRUCTURAL ANALYSIS
0
20000
40000
60000
80000
100000
120000
0.58 2.02 2.62 6.62 6.63 7.92 9.85 10.32 10.5 14.23 17.1 17.6
S
h
e
a
r
f
o
r
c
e
Length from Ref. point
Graph 9. Length from Ref. point Vs Shear Force
0
100000
200000
300000
400000
500000
600000
700000
800000
900000
1000000
0.58 2.02 2.62 6.62 6.63 7.92 9.85 10.32 10.5 14.23 17.1 17.6
B
e
n
d
i
n
g
m
o
m
e
n
t
Leght from Ref. point
Graph 10. Lengtth from Ref. point Vs Bending Moment
P a g e | 53
vigneshaeronautical@gmail.com
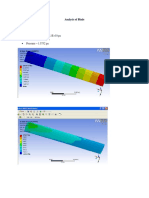
Structural analysis of fuselage like that of wing is of prime importance while designing
an aircraft. As the fuselage is the one which houses the pilot, the power plant and also part of the
payload its structural integrity is a matter of concern. While analyzing the fuselage structure the
section must be idealized. Idealization involves the conversion of a stringer and its
accompanying skin thickness into a concentrated mass known as a boom. The shear flow
analysis of the fuselage simulating flight conditions is shown below.
X
(m)
Y
(m)
1.005 0
0.985 0.26
0.88 0.48
0.72 0.72
0.48 0.88
0.26 0.985
0 1.005
-0.26 0.985
-0.48 0.88
-0.72 0.72
-0.88 0.48
-0.985 0.26
-1.005 0
-0.985 -0.26
-0.88 -0.48
-0.72 -0.72
-0.48 -0.88
-0.26 -0.985
0 -1.005
0.26 -0.985
0.48 -0.88
0.72 -0.72
0.88 -0.48
0.985 -0.26
1.005 0
vigneshaeronautical@gmail.com
The stringer used is of Z type. The following are its dimensions
Cross sectional area of each stringer is 100mm
Fig 14: Cross section of Z
-1.5 -1
Stringer location in Fuselage
type. The following are its dimensions
of each stringer is 100mm
2
Fig 14: Cross section of Z-section
-1.5
-1
-0.5
0
0.5
1
1.5
-0.5 0 0.5 1 1.5
Stringer location in Fuselage
P a g e | 54
1.5
P a g e | 55
vigneshaeronautical@gmail.com
The above stringer section is uniformly used throughout the fuselage as shown above in
order to provide the fuselage the required load carrying capacity. The diagram showed adjacent
is of the idealized fuselage structure. The idealization process is carried out in the following way.
STRESS ANALYSIS:
IDEALIZATION:
The boom 1 is given by
where,
B
1
Area of Boom 1
t
D
Thickness of skin panel
b Circumferential distance between 2 stringers
By Symmetry,
B
1
= B
9
, B
2
= B
8
, B
10
= B
16
, B
3
= B
7
, B
11
= B
15
, B
4
= B
6
= B
l2
= B
14
,B
5
= B
13
B
1
=100+ (0.651.37
10
6
6
) [2+(
4110
5500
)] + (0.651.37
10
6
6
)[2+(
4110
5500
)]
=815582.12
Similarly for boom 2 ,
B
2
= 815582.12 mm
2
Similarly B
3
= 815582.12 mm
2
, B4 =815582.12 mm
2
. We note that stringers 5 and 13 lie on the
neutral axis of the section and are therefore unstressed; the calculation of boom areas B
5
and B
13
does not then arise.
Thus, we have B
1
:B
16
= 815582.12 mm
2
P a g e | 56
vigneshaeronautical@gmail.com
We know that,
I
xx
= By
2
I
xx
1
= 24.67 m
4
; I
xx
2
= 13.77 m
4
; I
xx
3
= 6.12 m
4
; I
xx
S
= 1.11 m
4
Maximum bending moment = 2897784.51 Nm
Hence the Bending moment acting on the fuselage M = Max.B.M n FOS
=2897784.51 3.81.5
=16517371.71 Nm
I
xx
= 24.67 m
4
The value of stress acting is given by the expression:
= (
16517371.71 y
24.67
)
STRINGER/BOOM Y (m) STRESS x 10
6
(Nm
-2
)
1 5.5 3.68
2, 16 4.11 2.75
3, 15 2.74 1.83
4, 14 1.37 0.9
5, 13 0 0
6, 12 -1.37 -0.9
7, 11 -2.74 -1.83
8, 10 -4.11 -2.75
9 -5.5 -3.68
P a g e | 57
vigneshaeronautical@gmail.com
Design of Miscellaneous Members
Wing fuselage intersection
The 8 seater business jet aircraft has low wing configuration, thus the entire wing
structure continues in the way of airplane body.
Four pin design concept:
This concept is adopted as it is the most simple and straight forward method used in
Horizon 4000 transport, during 1950s. The lift and moment loads can be carried between the
wing and fuselage by simple shear on the four pins. The drag and thrust is taken by breather web.
This design allows the wing spar and fuselage bulkheads to deflect independently of each other
such that no spar moment is directly transferred to the bulkheads.
The wing-body juncture produces aerodynamic interference which in turn promotes flow
separation with its attendant higher drag and unsteady buffeting. This adverse pressure gradient
and consequent flow separation can be minimized using contoured surface called fillet.
Engine mount
An engine mount is a frame that supports the engine and holds it to the fuselage or
nacelle. Usually it is made of built up sheet metal, welded steel tubing. The turbofan engine,
HONEY WELL TFE731-20 is wing mounted. A typical turbofan engine installation for a
low wing aircraft configuration similar to that of this aircraft is shown below,
5
vigneshaeronautical@gmail.com
The pylon has three spars (longerons)
bulkheads, and is attached to the wing at four primary points. These are two mid
upper link and a diagonal brace (drag strut). The attachment pins are secured with fuse bolts
which are hollow carbon steel devices that have been heat treated to shear fail at a definite load.
In the landing break way condition (wheels
upper and lower links so that the pylon rotates around the mid
design provides considerable load path redundancy such that an upper link can fail, partially or
completely, and there is an alternate path
engine mounts.
The pylon has three spars (longerons) Upper, middle and lower- and three major
bulkheads, and is attached to the wing at four primary points. These are two mid-
upper link and a diagonal brace (drag strut). The attachment pins are secured with fuse bolts
which are hollow carbon steel devices that have been heat treated to shear fail at a definite load.
In the landing break way condition (wheels-up landing); the sequence is designed to fail the
upper and lower links so that the pylon rotates around the mid-spar and upward. The wing pylon
design provides considerable load path redundancy such that an upper link can fail, partially or
ere is an alternate path- lower diagonal brace. The below figure shows the
P a g e | 58
and three major
-spar fittings, an
upper link and a diagonal brace (drag strut). The attachment pins are secured with fuse bolts
which are hollow carbon steel devices that have been heat treated to shear fail at a definite load.
anding); the sequence is designed to fail the
spar and upward. The wing pylon
design provides considerable load path redundancy such that an upper link can fail, partially or
lower diagonal brace. The below figure shows the
P a g e | 59
vigneshaeronautical@gmail.com
Empennage Design
Horizontal Stabilizer:
The horizontal tail of the aircraft is conventional and consists of a fixed tail box. The
horizontal stabilizer is usually a two spar structure consisting of a Centre structural box section
and two outer sections. The stabilizer assembly is interchangeable (symmetrical airfoil section)
as a unit at the fuselage attach points and the outer sections are interchangeable at the attachment
to the center box.
The two basic horizontal stabilizer box constructions for modern transports are
1. Box constructions with spars, closer light rib spacing (usually less than 10 inches) and
surface (may be tapered skins) without stringer reinforcement. The feature of this design
is the low manufacturing cost and high torsional stiffness require by the flutter analysis.
2. Box construction with spar stronger ribs and surface skins with stringer reinforcements
(skin-stringer or integrally stiffened panels) is a lighter weight structure.
P a g e | 60
vigneshaeronautical@gmail.com
Vertical Stabilizer:
The structural design of the vertical stabilizer is essentially the same as for the horizontal
stabilizer is essentially the same as for horizontal stabilizers. The vertical stabilizer box is a two
or multi spar structure (general aviation airplanes usually use single spar design) with cover
panels (with or without ribs). The root of the box is terminated at the aft fuselage conjuncture
with fittings or splices.
P a g e | 61
vigneshaeronautical@gmail.com
WING FUEL TANKS:
In addition to providing the required strength and stiffness, the structural box almost
always has to provide fuel space. Integral tanks, as opposed to separate internally supported
types, are preferred since their use enables the maximum advantage to be taken of the available
volume. Integrally machined or moulded constructions, which use a small amount of large
components, are obviously an advantage since sealing is reduced to a minimum. The major
problem occurs at tank end ribs, particularly in the corners of the spar web and skins, and at
lower surface access panels. The corner difficulty is overcome by using special suitcase corner
fittings.
Access panels should be large enough for a person to get through so that the inside can be
inspected and resealed if necessary. On shallow section wings, the access has to be in the lower
surface so that the operator can work in an acceptable way even if the depth is insufficient to
climb in completely. Apart from the sealing problems, lower surface access panels are in what is
primarily a tension skin and so introduce stress concentrations in an area where crack
propagation is a major consideration. The access panels are arranged in a span-wise line so the
edge reinforcing can be continuous and minimum stress concentration due to the cut-outs.
Access panels are often designed to carry only shear and pressure loads, the wing bending being
reacted by the edge reinforcing members. A deep wing can avoid these problems by using upper
surface access panels but this is not a preferred aerodynamic solution.
AUXILIARY SURFACES
The structural layout of the auxiliary lifting surfaces is generally similar to that of the
wing but there are differences, in part due to the smaller size and in part due to the need to
provide hinges or supports. The latter implies that each auxiliary surface is a well-defined.
HINGED CONTROL SURFACES:
Conventional training edge control surfaces are almost invariably supported by a number
of discrete hinges, although continuous, piano type, hinges may be used for secondary tabs. To
some degree the number and location of the discrete hinges depends upon the length of the
control. The major points to be considered are:
The bending distortion of the control relative to the fixed surface must be limited so that
the nose of the control does mot fouls the fixed shroud.
The control hinge loads and the resulting shear forces and bending moments should be
equalized as far as is possible.
Structural failure of a single hinge should be tolerated unless each hinge is of fail-safe
design and can tolerate cracking one load path.
P a g e | 62
vigneshaeronautical@gmail.com
These points suggest the use of a relatively large number of discrete hinges but there are
difficulties associated with this solution there are the obvious loads likely to be induced in the
control by the distortion under load of the main surface to which it is attached may be significant.
These problems do not arise if only two hinge points are used as any span-wise distortion or
misalignment can be accommodated by designing one of the hinges so that it can rotate about a
vertical axis. When more than two hinges are used the floating hinge concept cannot fully
overcome the problems. However, it is possible to design the control surface so that it is flexible
in bending and indeed the more hinges there are the easier this is to accomplish. One hinge must
always be capable of reacting side loads in the plane of the control surface. The hinges are
supported near to the aft extremities of the main surface ribs.
PIVOTED CONTROL SURFACES
In certain high-performance aircraft, the whole of a stabilizing or control surface on one
side of the aircraft may be pivot about a point on its root chord. Clearly in this case, the structural
considerations are dominated by the need to react all the forces and moments at the pivot and
operating points. Thus the structural layout may consist of an integral root rib or pivot or stub
spar arrangement to which is attached a number of shear webs fanning out towards the
extremities of the surface, possibly in conjunction with full depth honeycomb. High skin shear
loading is inevitable due to the need to bring the loads to the two concentrated points. Shear
loads due to torsion may be limited by locating the operating point on the root rib some distance
away from the pivot.
Some designs incorporate the pivot into the moving surface with the support bearings on
the fuselage, while on others the pivot is attached to the fuselage and the bearings are in the
surface. The bearings should be as far apart as local geometry allows minimizing loads resulting
from the reaction of the surface bending moment.
HIGH LIFT SYSTEMS
There is a wide variety of leading and trailing edge high-lift systems. Some types are
simply hinged to the wing, but many require some degree of chord-wise extension. This can be
achieved by utilizing a linkage, a mechanism, a pivot located outside the aerofoil contour or,
perhaps most commonly, by some form of track. Trailing edge flaps may consist of two or more
separate chord-wise segments, or slats, to give a slotted surface and these often move on tracts
attached to the main wing structure.
The majority of flaps and slats are split into span wise segments of no greater lengths
than can be supported at two or three locations. As with control surfaces, the locations of the
support points are established so as to minimize local deformations since the various slots are
critical in determining the aerodynamic performance. Sometimes the actuation may be located at
P a g e | 63
vigneshaeronautical@gmail.com
a different pan wise position from the support points. This is often a matter of convenience,
layout clearances, and the like.
The structural design of flaps is similar to that of control surfaces but it s simpler as there
is no requirement for mass balance, the operating mechanisms normally being irreversible. On
large trailing edge flap components, there is often more than one spar member. Especially when
this assists in reacting the support or operating loading. There may be a bending stiffness
problem in the case of relatively small chord slat segments and full depth honey combs can be
used to deal with this. Figure shows a cross section of a typical slotted flap of metal construction
but the same layout applies if composite materials are used.
In many cases the slipstream or afflux from power plants impinges upon a flap and this is
likely to require special consideration in the design. Additional stiffness is not necessarily the
answer because acoustic fatigue characteristics are often worse at higher panel frequencies.
However the extensive local support offered by sandwich construction, either in panel or full
depth configuration, is usually beneficial. This leads naturally to the application of reinforced
plastic materials. Trailing edge flaps tends to be prone to damage by debris thrown up by the
landing gear and it may be desirable to use Kevlar or glass rather than carbon fibers for the lower
surface, but material compatibility needs to be considered.
ATTACHMENT OF LIFTING SURFACES
The joint of the fuselage with the wing is subjected to heavy load inputs and there is a
potential for considerable relative distortion. This distortion is usually accepted and the wing
centre box is built completely into the fuselage, the resulting constraint stresses being allowed
for. It is usual for the wing structure of large aircraft to include a production joint at the side of
the fuselage and this is virtual essential for swept wings.
It is sometimes possible to arrange the wing pick-ups as pivots on the neutral axis or set
them on swinging links. In this case, the relative motion is allowed to take place and there are no
induced stresses. Structural assembly of the wing to the fuselage is relatively simple.
Similar remarks also apply to the attachment of the horizontal stabilizer when the
incidence setting is fixed. If the surface is also used for trimming or control, some special
consideration is necessary in the location of the pivot and actuation fittings. These usually
require a relatively heavily loaded rib or a pair of ribs, and where possible at least one of the
attachment points should be close to the rib or spar intersection. It is desirable to arrange for the
lateral distance between the pivots to be as great as possible to minimize pivot loads resulting
from asymmetric span-wise loading. When the controls are manually operated, it is simplest if
the elevator-hinge line and pivot coincide.
Fins are usually built integrally with the rear fuselage. This is mainly due to the different
form of loading associated with the geometric asymmetry.
P a g e | 64
vigneshaeronautical@gmail.com
Flutter:
Flutter as the dynamic instability of an elastic body in an airstream. It is found most
frequently in aircraft structures subjected to large aerodynamic loads such as wings, tail units and
control surfaces.
Flutter occurs at a critical or flutters speed V
f
which in turn is defined as the lowest
airspeed at which a given structure will oscillate with sustained simple harmonic motion. Flight
at speeds below and above the flutter speed represents conditions of stable and unstable (that is
divergent) structural oscillation, respectively.
Generally, an elastic system having just one degree of freedom cannot be unstable unless
some peculiar mechanical characteristic exists such as a negative spring force or a negative
damping force. However, it is possible for systems with two or more degrees of freedom to be
unstable without possessing unusual characteristics. The forces associated with each individual
degree of freedom can interact, causing divergent oscillations for certain phase differences.
The flutter of a wing in which the flexural and torsional modes are coupled is an
important example of this type of instability. Some indication of the physical nature of wing
bendingtorsion-flutter may be had from an examination of aerodynamic and inertia forces
during a combined bending and torsional oscillation in which the individual motions are 90 out
of phase. In a pure bending or pure torsional oscillation the aerodynamic forces produced by the
effective wing incidence oppose the motion; the geometric incidence in pure bending remains
constant and therefore does not affect the aerodynamic damping force, while in pure torsion the
geometric incidence produces aerodynamic forces which oppose the motion during one-half of
the cycle but assist it during the other half so that the overall effect is nil. Thus, pure bending or
pure torsional oscillations are quickly damped out. This is not the case in the combined
oscillation when the maximum twist occurs at zero bending and vice versa; i.e. a 90 phase
difference.
The type of flutter described above, in which two distinctly different types of oscillating
motion interact such that the resultant motion is divergent, is known as classical flutter. Other
types of flutter, non-classical flutter, may involve only one type of motion. For example, stalling
flutter of a wing occurs at a high incidence where, for particular positions of the span wise axis
of twist, self-excited twisting oscillations occur which, above a critical speed, diverge.
Aileron Buzz:
Another non-classical form of flutter, aileron buzz, occurs at high subsonic speeds and is
associated with the shock wave on the wing forward of the aileron. If the aileron oscillates
downwards the flow over the upper surface of the wing accelerates, intensifying the shock and
P a g e | 65
vigneshaeronautical@gmail.com
resulting in a reduction in pressure in the boundary layer behind the shock. The aileron,
therefore, tends to be sucked back to its neutral position. When the aileron raises the shock
intensity reduces and the pressure in the boundary layer increases, tending to push the aileron
back to its neutral position.
At low frequencies these pressure changes are approximately 180 out of phase with the
aileron deflection and therefore become aerodynamic damping forces. At higher frequencies a
component of pressure appears in phase with the aileron velocity which excites the oscillation. If
this is greater than all other damping actions on the aileron a high frequency oscillation results in
which only one type of motion, rotation of the aileron about its hinge, is present, i.e. aileron
buzz. Aileron buzz may be prevented by employing control jacks of sufficient stiffness to ensure
that the natural frequency of aileron rotation is high.
Buffeting:
Buffeting is produced most commonly in a tail plane by eddies caused by poor airflow In
the wing wake striking the tail plane at a frequency equal to its natural frequency; a resonant
oscillation having one degree of freedom could then occur. The problem may be alleviated by
proper positioning of the tail plane and clean aerodynamic design.
P a g e | 66
vigneshaeronautical@gmail.com
P a g e | 67
vigneshaeronautical@gmail.com
CONCLUSION
In conclusion, the series of short range aircrafts incorporated many unique design of
future that was never seen on an operational aircraft. The design of these aircrafts points the way
for the design of future of very high mach airplanes.
The airplane has gone through many design modifications since its early conceptual
designs expected, among these was a growth in weight. The document to provide information on
the trends in various aircraft characteristics that may influence general long-term airport planning
and design.
These are strong indications that future trends could see the coexistence of very high
capacity aircraft modules of similar capacities for the long range/very long range operations.
Cargo payloads, which include mail, express and freight, are increasing in size and weight as
larger aircraft service with the airlines,
To ensure continued growth in payload and the profitability of cargo operations,
improvements in methods, equipment and terminal facilities will be required in order to reduce
cargo handling costs and aircraft ground time and to provide improved service for the shippers.
We have enough hard work for this design project. A design never gets completed in a
flutter sense but it is one step further towards ideal system. But during the design of this aircraft,
we learnt a lot about aeronautics and its implications when applied to an aircraft design.
7
P a g e | 68
vigneshaeronautical@gmail.com
BIBLIOGRAPHY
AIRPLANE AERODYNAMICS AND PERFORMANCE by JAN ROSKAM
E.F. Bruhn, Analysis and Design of Flight Vehicle Structures, Tristate Offset Co.,
1980.
Lloyd R. Jenkinson and James F.Marchman III., Aircraft Design project, Butterworth-
Heinemann., Burlington, 2003.
Anderson, John D., Jr:Aircraft Performance and Design, McGraw-Hill, Boston, 1999.
Megson, T.M.G; Aircraft Structures for Engineering Students, Edward Arnold, 1989
Peery, D.J. and Azar, J.J., Aircraft Structures, 2nd Edition, McGraw-Hill, New York,
1993.
McCornic, B.W, Aerodynamics, Aeronautics & Flight Mechanics. John Wiley, 1995.
G. Corning, Supersonic & Subsonic Airplane Design, II Edition, Edwards Brothers
Inc., Michigan, 1953.
Ira h. Abbott, Albert e. Von Doenhoff,and Louis S. Stivers, Jr,Summary of Airfoil
Data, National advisory committee for aeronautics, 1947.
John T.Lowry., Performance of Light Aircraft, American institute of aeronautics and
astronautics, Washington.D.C, 1935.
Dr.lng.S.F.Hoerner,Fluid Dynamic Drag,Hoerner fluid dynamics., 1992.
J.B. Russell, Performance and Stability of Aircraft. ISBN 0-340-63170-8. Arnold 1996.
Mark D. Ardema, Mark C. Chambers, Anthony P. Patron, Andrew S. Hahn, Hirokazu
Miura, and Mark D. Moore, Analytical Fuselage and Wing Weight Estimation of
Transport Aircraft,1996.
P a g e | 69
vigneshaeronautical@gmail.com
WEBSITE REFERENCE
http://www.worldofkrauss.com/
http://faculty.dwc.edu/sadraey/V-n%20diagram.pdf
http://www.aerostudents.com/files/aircraftStressAnalysisAndStructura
lDesign/reader.pdf
http://www.cta-dlr2009.ita.br/Proceedings/PDF/60272.pdf
http://www.emteq.com/aircraft-structural-analysis-modifications.php
http://www.biznet.org.au/member.asp?id=1094&pid=184
http://www.cp.berkeley.edu/cds_ucb/UCB-05100.pdf
http://www.aer.ita.br/~bmattos/download/fuselagem-design.pdf
http://adg.stanford.edu/aa241/fuselayout/sstfuse.html
http://www.mat.ethz.ch/news_events/archive/materialsday/matday01/
pdf/TempusMD.pdf
http://www.free-online-private-pilot-ground-school.com/aircraft-
structure.html
http://www.zenithair.com/stolch701/7-design-fuselage.html
http://www.nusil.com/products/engineering/aircraft/documents/Aircra
ft%20Selection%20Guide.pdf
http://www.scielo.oces.mctes.pt/pdf/ctm/v20n3-4/v20n3-4a11.pdf
http://www.faa.gov/library/manuals/aircraft/amt_handbook/media/FA
A-8083-30_Ch05.pdf
http://www.ppart.de/aerodynamics/profiles/NACA5.html
http://www.desktop.aero/appliedaero/airfoils1/airfoilgeometry.html
http://www.mh-aerotools.de/airfoils/jf_users_manual.htm
Вам также может понравиться
- Aircraft Design Project-1 (50 Seated Aircraft)Документ124 страницыAircraft Design Project-1 (50 Seated Aircraft)renjithrenju75% (4)
- Aircraft Design Project - Ii Heavy Business Jet: Jackson.J Iyyappan.P Velmurugan.P Vijay.UДокумент7 страницAircraft Design Project - Ii Heavy Business Jet: Jackson.J Iyyappan.P Velmurugan.P Vijay.UJackson JackОценок пока нет
- 400 Seater Passenger AircraftДокумент65 страниц400 Seater Passenger Aircraftganeshyams100% (1)
- Aircraft Design Project 2 PDFДокумент76 страницAircraft Design Project 2 PDFUma shree100% (3)
- Aircraft Design Project - 150 Seater Passenger AircraftДокумент118 страницAircraft Design Project - 150 Seater Passenger Aircraftsonusingh786775% (12)
- Adp 2 FinalДокумент70 страницAdp 2 Finalrahul_vh0% (2)
- Aerodynamics II NotesДокумент166 страницAerodynamics II NotesAlexShearОценок пока нет
- Aircraft Design Project - 280 Seat TransportДокумент108 страницAircraft Design Project - 280 Seat TransportNick Fisette75% (4)
- 2.shrenck's Curveschrenk Curve, Adp-2, Aircraft Design Project-2Документ3 страницы2.shrenck's Curveschrenk Curve, Adp-2, Aircraft Design Project-2Balaji Aero50% (2)
- Cargo Adp-2Документ100 страницCargo Adp-2Adrian James100% (3)
- Schrenk's Curve and V-N DiagramДокумент9 страницSchrenk's Curve and V-N DiagramLogesh Sadhasivam100% (1)
- Aircraft Design Project 2Документ117 страницAircraft Design Project 2Mahesh J Rao85% (13)
- Aircraft Design Project Eight Seater Short Range Business Jet AircraftДокумент119 страницAircraft Design Project Eight Seater Short Range Business Jet AircraftVignesh Selvaraj89% (9)
- Aircraft Design ReportДокумент91 страницаAircraft Design ReportGrassrehLeОценок пока нет
- Aircraft Design Project 2Документ80 страницAircraft Design Project 2Technology Informer90% (21)
- Gate Flight Mechanics by VayushastraДокумент36 страницGate Flight Mechanics by Vayushastraudaykumar100% (4)
- As-Ii Notes PDFДокумент218 страницAs-Ii Notes PDFJason Jeevan50% (2)
- Introduction To Aircraft Performance and Static StabilityДокумент36 страницIntroduction To Aircraft Performance and Static StabilityKaran GroverОценок пока нет
- AE8711 Aircraft Systems Laboratory Manual: Madha Engineering CollegeДокумент43 страницыAE8711 Aircraft Systems Laboratory Manual: Madha Engineering CollegeKishoremc100% (5)
- Aircraft Design Project1Документ30 страницAircraft Design Project1Playfull RivalОценок пока нет
- Aircraft Design Project-1Документ50 страницAircraft Design Project-1Ajith Kumar100% (2)
- Experimental Aerodynamics 2 Marks by Nambi RajanДокумент8 страницExperimental Aerodynamics 2 Marks by Nambi RajanNambi Rajan50% (2)
- ADP II - Vicky (Main)Документ70 страницADP II - Vicky (Main)thupten tsundueОценок пока нет
- Elements of Aeronautics NotesДокумент36 страницElements of Aeronautics NotesAnu AОценок пока нет
- Aircraft Structures II Laboratory Manual With Model Calculations and GraphsДокумент52 страницыAircraft Structures II Laboratory Manual With Model Calculations and GraphsTAMILSELVAM NALLUSAMY100% (10)
- Aircraft StabilityДокумент126 страницAircraft StabilitymunirnadirОценок пока нет
- Aircraft Design Project IДокумент74 страницыAircraft Design Project ISherlock HólmesОценок пока нет
- Megson Solution Manual Aircraft Structures CH01Документ13 страницMegson Solution Manual Aircraft Structures CH01Naveen Kumar83% (6)
- Aerodynamics-II Part B QuestionsДокумент7 страницAerodynamics-II Part B QuestionsAeronaughtycs Hamdan100% (1)
- AE 8504 Propulsion II 2 MarksДокумент20 страницAE 8504 Propulsion II 2 MarksBairaviPerumalVigneswaran100% (1)
- Aircraft Design Project - Phase 2Документ64 страницыAircraft Design Project - Phase 2Sultan BadhushaОценок пока нет
- Adp 1 FinalДокумент43 страницыAdp 1 Finalrahul_vh100% (1)
- Aircraft Design Project - 1Документ80 страницAircraft Design Project - 1Abhishekhari50% (2)
- 4.torque Diagram of The WingДокумент3 страницы4.torque Diagram of The WingBalaji AeroОценок пока нет
- As-Ii 2marksДокумент11 страницAs-Ii 2marksrobinston jeyasingh0% (1)
- Aircraft Design Project 2 Heavyweight CargoДокумент50 страницAircraft Design Project 2 Heavyweight Cargosanthoshsaba12345Оценок пока нет
- Anna University Propulsion - I Question PapersДокумент10 страницAnna University Propulsion - I Question Papersmurjass85Оценок пока нет
- AE8502 AIRCRAFT STRUCTURES II Unit IIДокумент24 страницыAE8502 AIRCRAFT STRUCTURES II Unit IIObli Kumaran L100% (1)
- Aerodynamics Question BankДокумент39 страницAerodynamics Question BankSeeandgrow ByabdulsamadОценок пока нет
- ASC-mod 3-Static Directional Stability and ControlДокумент16 страницASC-mod 3-Static Directional Stability and ControlJason JeevanОценок пока нет
- Aerodynamics - Problem Sheet Level 1Документ4 страницыAerodynamics - Problem Sheet Level 1Komal joshi100% (1)
- Anna University Chennai B.E Aerodynamics Question PapersДокумент3 страницыAnna University Chennai B.E Aerodynamics Question Papersabhishek_mahadevanОценок пока нет
- Mini Project Report V2.0 Updated 1Документ43 страницыMini Project Report V2.0 Updated 1Tanishq ShettyОценок пока нет
- 7 TH Sem AdpДокумент56 страниц7 TH Sem AdpJackson JackОценок пока нет
- Aircraft Structures 1 - 15AE54Документ161 страницаAircraft Structures 1 - 15AE54Jason Jeevan86% (7)
- Wa0007.Документ76 страницWa0007.Vasan VasanОценок пока нет
- 400 Seater Passenger AircraftДокумент65 страниц400 Seater Passenger AircraftSonu Raina MahiОценок пока нет
- Acknowledgment: Dr.V.K.Shanmuganathan (M.E, PH.D) (Head of Aeronautical Department) WhoДокумент50 страницAcknowledgment: Dr.V.K.Shanmuganathan (M.E, PH.D) (Head of Aeronautical Department) WhoJustin RajaОценок пока нет
- 2011 - Design and Wind Tunnel Tests of A Tiltwing UAVДокумент11 страниц2011 - Design and Wind Tunnel Tests of A Tiltwing UAVahmad.yasser123456Оценок пока нет
- Adp ProjectДокумент45 страницAdp Projectkavitha RavichandranОценок пока нет
- Horten Flying WingДокумент38 страницHorten Flying WingArtúr SzemánОценок пока нет
- FatigueДокумент6 страницFatigueEnriqueGDОценок пока нет
- Bezier CurveДокумент12 страницBezier CurveAnh NgoОценок пока нет
- ICAT-2019-09 STOL VTOL ComparisonДокумент20 страницICAT-2019-09 STOL VTOL ComparisonSergioОценок пока нет
- 100 Seater Aircraft ADP 2Документ76 страниц100 Seater Aircraft ADP 2Balasastha PОценок пока нет
- Contribution of Wing, Vertical Tail and Fuselage OnДокумент14 страницContribution of Wing, Vertical Tail and Fuselage OnMOHAMMED JAWADОценок пока нет
- Aerodynamic Optimization of WingsДокумент21 страницаAerodynamic Optimization of WingsMarcos SoarОценок пока нет
- Aeromodelling DesignДокумент70 страницAeromodelling DesignMayank AgrawalОценок пока нет
- Pitot Static Tube With Digital ManometerДокумент4 страницыPitot Static Tube With Digital ManometerVignesh SelvarajОценок пока нет
- Analysis of BladeДокумент3 страницыAnalysis of BladeVignesh SelvarajОценок пока нет
- 1200W Smoke Generator:: Technical DetailsДокумент1 страница1200W Smoke Generator:: Technical DetailsVignesh SelvarajОценок пока нет
- Vibration Exciter (2N To 100N) : Use ScenariosДокумент1 страницаVibration Exciter (2N To 100N) : Use ScenariosVignesh SelvarajОценок пока нет
- Linear Variable Differential TransformerДокумент1 страницаLinear Variable Differential TransformerVignesh SelvarajОценок пока нет
- Carbon PDFДокумент4 страницыCarbon PDFVignesh SelvarajОценок пока нет
- AA02 Supersonic Wind Tunnel ContinuousДокумент5 страницAA02 Supersonic Wind Tunnel ContinuousVignesh SelvarajОценок пока нет
- TicДокумент1 страницаTicVignesh SelvarajОценок пока нет
- Impact Testing Machine Make KedarДокумент3 страницыImpact Testing Machine Make KedarVignesh SelvarajОценок пока нет
- Service DetailsДокумент1 страницаService DetailsVignesh SelvarajОценок пока нет
- EI P L: Column Testing - Fixed-FixedДокумент3 страницыEI P L: Column Testing - Fixed-FixedVignesh SelvarajОценок пока нет
- Newton's RingДокумент7 страницNewton's RingReddyvari Venugopal100% (1)
- Member Management System - MMS User GuideДокумент11 страницMember Management System - MMS User GuideVignesh SelvarajОценок пока нет
- Form 1: Employee Personal Information Name of DepartmentДокумент12 страницForm 1: Employee Personal Information Name of DepartmentRajashree PatilОценок пока нет
- Achievements Summary-AadesДокумент1 страницаAchievements Summary-AadesVignesh SelvarajОценок пока нет
- Analysis of An Inflatable Gossamer Device To Efficiently De-OrbitДокумент100 страницAnalysis of An Inflatable Gossamer Device To Efficiently De-OrbitVignesh SelvarajОценок пока нет
- 1page 3Документ2 страницы1page 3Sajid MahmoodОценок пока нет
- Impact Test MachineДокумент2 страницыImpact Test MachineVignesh SelvarajОценок пока нет
- Pre CompДокумент33 страницыPre CompVignesh SelvarajОценок пока нет
- Vinayakar-Subramanyar ThuthiДокумент1 страницаVinayakar-Subramanyar ThuthiVignesh SelvarajОценок пока нет
- Sample Employment Application FormДокумент4 страницыSample Employment Application Formapi-296940651Оценок пока нет
- Quantitative AptitudeДокумент2 страницыQuantitative AptitudeSivakumar MОценок пока нет
- Vocab Spot CheckДокумент9 страницVocab Spot CheckMr. Yogesh RamaniОценок пока нет
- Drawing 1Документ1 страницаDrawing 1Vignesh SelvarajОценок пока нет
- Thulasi StotramДокумент2 страницыThulasi StotramVignesh SelvarajОценок пока нет
- ShivaДокумент6 страницShivaVignesh SelvarajОценок пока нет
- Sample Employment Application FormДокумент4 страницыSample Employment Application Formapi-296940651Оценок пока нет
- Optimization Formulations For Composite Structures Subjected To Compression LoadsДокумент2 страницыOptimization Formulations For Composite Structures Subjected To Compression LoadsVignesh SelvarajОценок пока нет
- Length-2.6 M Chord 0.15m No of Blade-5 Radius-1.2 M Max Torque - 150 N-M Rated Wind Speed-11 M/s Max Force - 500N, Operational Force-250 N NACA-4415Документ1 страницаLength-2.6 M Chord 0.15m No of Blade-5 Radius-1.2 M Max Torque - 150 N-M Rated Wind Speed-11 M/s Max Force - 500N, Operational Force-250 N NACA-4415Vignesh SelvarajОценок пока нет
- Product Perspective: XP Button, LV Button and VK FrameДокумент54 страницыProduct Perspective: XP Button, LV Button and VK FrameGokul krishnanОценок пока нет
- GGДокумент8 страницGGGaurav SharmaОценок пока нет
- (FreeCourseWeb - Com) 1493997599Документ386 страниц(FreeCourseWeb - Com) 1493997599MuruganandamGanesanОценок пока нет
- Compaction Factor ExperimentДокумент23 страницыCompaction Factor ExperimentYI HEN ONGОценок пока нет
- Ap T240 13Документ92 страницыAp T240 13mehdiОценок пока нет
- C ValueДокумент2 страницыC ValuePadmanabh Shetty0% (1)
- Delamination With AbaqusДокумент13 страницDelamination With AbaqusSchmetterling TraurigОценок пока нет
- BS en 00480-2-2006Документ14 страницBS en 00480-2-2006Shan Sandaruwan Abeywardene100% (1)
- Draft NADCAДокумент8 страницDraft NADCAPierre MackenzieОценок пока нет
- MT-LXX Parallel Manual PDFДокумент120 страницMT-LXX Parallel Manual PDFJunior Alexander Rodriguez Rodriguez0% (1)
- 20-F201007-SC-010 R0 - Design Calculation of Foam Tank and Fire Pump ShedДокумент187 страниц20-F201007-SC-010 R0 - Design Calculation of Foam Tank and Fire Pump ShedSaravan KumarОценок пока нет
- Roasting Matte To Nickel Oxide and MetalДокумент7 страницRoasting Matte To Nickel Oxide and MetalDavid SanchezОценок пока нет
- DNV RP F401Документ23 страницыDNV RP F401Christopher BlevinsОценок пока нет
- State Load Despatch Centre (SLDC), Patna: Bihar State Power Transmission Co. LTDДокумент10 страницState Load Despatch Centre (SLDC), Patna: Bihar State Power Transmission Co. LTDsldcОценок пока нет
- Intro Adobe Photoshop HandoutДокумент13 страницIntro Adobe Photoshop Handoutoyindamola ayobamiОценок пока нет
- Geomechanics: Figure 1 Geomechanics in Oil & Gas Industry (Source: Geomechanics Engineering)Документ2 страницыGeomechanics: Figure 1 Geomechanics in Oil & Gas Industry (Source: Geomechanics Engineering)ابوالحروف العربي ابوالحروفОценок пока нет
- Ratio Worksheet AKДокумент12 страницRatio Worksheet AKChika AuliaОценок пока нет
- 07a80809 OperationsresearchДокумент11 страниц07a80809 OperationsresearchSharanya ThirichinapalliОценок пока нет
- Opposite Corners CourseworkДокумент8 страницOpposite Corners Courseworkpqltufajd100% (2)
- Practical Exercise 2 - SolutionДокумент5 страницPractical Exercise 2 - SolutionmidoriОценок пока нет
- S/Mime (Secure/Multipurpose Internet Mail Extensions)Документ15 страницS/Mime (Secure/Multipurpose Internet Mail Extensions)Vishnupriya100% (1)
- QuesTeksFerriumC61C64andC6 PDFДокумент23 страницыQuesTeksFerriumC61C64andC6 PDFEmily MillerОценок пока нет
- Preboard Questions: Multiple ChoiceДокумент3 страницыPreboard Questions: Multiple ChoiceAlfredo CondeОценок пока нет
- DRK109A&B Touch-Screen Bursting Strength TesterДокумент2 страницыDRK109A&B Touch-Screen Bursting Strength Testermohamadreza1368Оценок пока нет
- Activity 2 Resultant Vector by Graphical MethodДокумент2 страницыActivity 2 Resultant Vector by Graphical MethodRick Ignacio0% (1)
- HAARPДокумент230 страницHAARPMartin hume100% (2)
- OSD PrintoutДокумент18 страницOSD PrintoutDSAO AmravatiОценок пока нет
- Astm D 3341Документ4 страницыAstm D 3341Manuel GuzmanОценок пока нет
- 12 Physics Exemplar PDFДокумент130 страниц12 Physics Exemplar PDFPRATIM SADHU100% (1)
- Chameleon ChipДокумент2 страницыChameleon ChipChetan KumarОценок пока нет