Lecture 2 SLOPE DEFLECTION

2005 Pearson Education South Asia Pte Ltd
1

STRUCTURAL ANALYSIS
VBB 2053

LECTURE 2

SLOPE-DEFLECTION METHOD
2
Learning Objectives
Learn to analyse statically indeterminate
structures using slope-deflection method.
Knowing the slope-deflection equations.
Discuss the application of slope-deflection
method to beams and frames.
3
Outline
Introduction to slope-deflection method.
General procedure of slope-deflection method
of analysis.
Derivation of slope-deflection equations.
Work examples on slope-deflection method of
analysis: beams and frames.
4
Statically Indeterminate
Structures: Method of Analysis
Analyzing any indeterminate structure, it is
necessary to satisfy:
Equilibrium Equilibrium is satisfied when the
reactive forces hold the structure at rest.
Compatibility Compatibility is satisfied when the
various segments of the structure fit together
without intentional breaks or overlaps.
Force-displacement This requirements depend
upon the way the material responds linear
elastic response.

5
Statically Indeterminate
Structures: Method of Analysis
There are two ways to analyze a statically
indeterminate structure
Force Method
Displacement Method

Force Method of Analysis
Identifying unknown redundant forces.
Satisfying structures compatibility equations.
This is done by expressing the displacements
in terms of the loads by using the load-
displacement relations.
The solution of the resultant equations yields
the redundant reactions, and then the
equilibrium equations are used to determine
the remaining reactions on the structure.
6
Displacement Method of Analysis
Satisfying equilibrium equations for the
structure.
Unknown displacements are written in terms
of the loads by using the load-displacement
relations, then solved for the displacements.
Once the displacement obtained, the
unknown loads are determined from the
compatibility equations using the load-
displacement relations.
7
Degree of Freedom
When a structure is loaded, the node will
undergo unknown displacements.
These displacements are referred to as the
degree of freedom. Specify degree of
freedom is a necessary 1
st
step when apply
displacement method.
In 3D, each node on a beam or frame can
have at most 3 linear displacements & 3
rotational displacements.
In 2D, each node can have at most 2 linear
displacements & 1 rotational displacement.
8
Degree of Freedom
The number of these unknowns are referred
to as the degree in which the structure is
kinematically indeterminate.

9
Any load applied to the beam
will cause node A to rotate.
Node B is completely restricted
from moving.
Hence, the beam has only one
unknown degree of freedom.
Therefore kinematically
indeterminate to 1
st
degree.
Degree of Freedom

10
The beam has nodes at A, B & C
There are 4 degrees of freedom
u
A
, u
B
, u
C
and A
C
.
It is kinematically indeterminate
to 4
th
degree.
The frame has 3 degrees of
freedom, u
B
, u
C
and A
B
.
It is kinematically indeterminate
to 3
rd
degree.
11
Slope-Deflection Method
The slope-deflection method uses displacements as
unknowns and is referred to as a displacement
method.
In the slope-deflection method, the moments at the
ends of the members are expressed in terms of
displacements and end rotations of these ends.
An important characteristic of the slope-deflection
method is that it does not become increasingly
complicated to apply as the number of unknowns in
the problem increases.
In the slope-deflection method the individual
equations are relatively easy to construct regardless
of the number of unknowns.

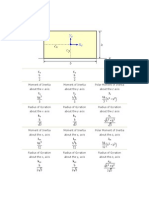
Derivation of Slope-Deflection
Equations
To derive the general form of the slope-deflection
equation, let us consider the typical span AB of the
continuous beam shown below when subjected to
arbitrary loading.

The slope-deflection equation
can be obtained using the
principle of superposition
By considering separately the
moments developed at each support due to
A
,
B
, ,
P.
Assume clockwise is positive.

13
Equations
Moment due to angular displacement at A,
A

To determine the moment M
AB
needed to cause this
displacement, we will use the conjugate beam method.

From which we obtain the following relationships.

A AB
L
EI 4
M u =
A BA
L
EI 2
M u =
0
3
L 2
L
EI
M
2
1
3
L
L
EI
M
2
1
0 M
BA AB
' A
=
(
|
.
|
\
|
|
.
|
\
|
=
0 L
3
L 2
L
EI
M
2
1
3
L
L
EI
M
2
1
0 M
A
AB BA
' B
= +
(
|
.
|
\
|
|
.
|
\
|
=
u
14
Equations
Moment due to angular displacement at B,
B

The applied moment M
BA
to the angular displacement
u
B
& the reaction moment M
AB
at the wall can be
related as:

B BA
L
EI 4
M u =
B AB
L
EI 2
M u =
Equations
Moment due to relative linear displacement,
If the far node B of the member is displaced relative to A, so that
the cord of the member rotates clockwise & yet both ends do not
rotate, then equal but opposite moment and shear reactions are
developed in the member.
Moment M can be related to the
displacement using conjugate
beam method.

15
( ) ( )
A
= = =
= A
(
=
2
BA AB
' B
L
EI 6
M M M
0
3
L
L
EI
M
2
1
3
L 2
L
EI
M
2
1
0 M
Equations
Moment due to loading (P or w)
These moments are called Fixed End Moment (FEM).
In general, linear and angular displacement of the nodes are
caused by loadings acting on the span of the member.
To develop the slope-deflection equation, we must transform
these span loadings into equivalent moment acting at the nodes
and then use the load-displacement relationships just derived.

16

17
Equations
Slope-Deflection Equation
The end moments due to each displacement and loadings are
added together, the resultant moments at the ends can be
written as:
M
AB
= M
A
+ M
B
+ M
+ M
load

18
0 FEM
L
3 2
L
2E M
0 FEM
L
3 2
L
2E M
BA A B BA
AB B A AB
= +
(
|
.
|
\
|
+
|
.
|
\
|
=
= +
(
|
.
|
\
|
+
|
.
|
\
|
=
I
I
Equations
The slope-deflection equations can be generalized as follows:

M
N
= internal moment in the near end of the span,
E = modulus of elasticity
k = span stiffness, k = I/L
u
N
, u
F
= near- and far-end slopes or angular displacements of the span
at the supports
= span rotation of its cord due to a linear displacement,
= A/L
FEM
N
= fixed end moment at the near end support.

19
| |
N F N N
FEM 3 2 Ek 2 M + + =
20
Pin supported end span
Sometimes an end span of a
beam or frame is supported by a
pin or roller at its far end.

The moment at the roller or pin is zero provided the angular
displacement at this support does not have to be determined.
Use the generalised slope-deflection equation, we have:

Since far end is pinned, FEM
F
= 0
FEM
N
can be obtained

| |
| | 0 3 2 Ek 2 0
FEM 3 2 Ek 2 M
F N
N F N N
+ + =
+ + =
21
Simplifying, we get:

Only applicable for end span with far end
pinned or roller supported
| |
N N N
FEM Ek 3 M + =
Work Example 1
Draw the shear & moment diagrams for the
beam shown below.

22
Work Example 2
Draw the shear & moment diagrams for the
beam shown below.

23
A
B
C
40 kN/m 60 kN
6 m
1 m 1 m
24
Analysis of Frames: No Sidesway
Slope-deflection method can also be used to analyse
frames.
A frame will not sidesway to the left or right provided it
is properly restrained.

25
Analysis of Frames: No Sidesway
No sidesway will occur in an unrestrained frame
provided it is symmetric with respect to both loading
and geometry.

26
Work Example 6: Frame With No
Sidesway
Determine the moments at each joint of the
frame shown below. EI is constant.
3 spans must be considered in this
case: AB, BC & CD

Step 1: FEM

m . kN 80
96
wL 5
FEM
m . kN 80
96
wL 5
FEM
2
CB
2
BC
+ = + =
= =
0 and 0 that Note
CD BC AB D A
= = = = =
27
Sidesway
Step 2: Slope-Deflection Equations

C DC
C CD
B C CB
C B BC
B BA
B AB
EI 1667 . 0 M
EI 333 . 0 M
80 EI 25 . 0 EI 5 . 0 M
80 EI 25 . 0 EI 5 . 0 M
EI 333 . 0 M
EI 1667 . 0 M
=
=
+ + =
+ =
=
=
| |
N F N N
FEM 3 2
L
I
E 2 M + +
|
.
|
\
|
=
28
Sidesway
Step 3: Equilibrium Equations
Moment equilibrium at joints B & C, we have:

Substitute M
BA
, M
BC
and M
CB
, M
CD
into above
equations, we get:

Solving simultaneously yields

80 EI 25 . 0 EI 833 . 0
80 EI 25 . 0 EI 833 . 0
B C
C B
= +
= +
0 M M ; 0 M
BC BA B
= + =
0 M M ; 0 M
CD CB C
= + =
EI
1 . 137

C B
= =
29
Sidesway
Step 4: Moment Calculation
Using these results, the reactions at the
ends of each member can be determined
using equations of equilibrium.
The moment diagram for the frame can
be drawn.

kNm 9 . 22 M
kNm 7 . 45 M
kNm 7 . 45 M
kNm 7 . 45 M
kNm 7 . 45 M
kNm 9 . 22 M
DC
CD
CB
BC
BA
AB
=
=
=
=
=
=
Sidesway
Determine the internal moments at each joint of the frame shown
below. The moment of inertia for each member is given in the
figure. Take E = 200 Gpa.
Take as self study at home.Refer to Hibbeler 7
th

edition, Example 11-6

30
4.5 m
30 kN
50 kN/m
A
B C E
D
2.4 m 2.4 m
3.6 m 320 (10
6
) mm
4

260 (10
6
) mm
4

1
6
0

(
1
0
6
)

m
m
4

80 (10
6
) mm
4

31
Analysis of Frames: Sidesway
A frame will sidesway when it or the loading acting on
it is nonsymmetric.
Consider the frame shown here.
The loading P causes an unequal
moments at joint B and C.
M
BC
tends to displace joint B to
the right.
M
CB
tends to displace joint C to
the left.
Since M
BC
> M
CB
, the net result is
a sidesway of both joint B & C to the right.
32
Analysis of Frames: Sidesway
When applying the slope-deflection equation to each
column, we must consider the column rotation ( =
A/L) as an unknown in the equation.
As a result, an extra equilibrium equation must be
included in the solution.
The techniques for solving problems for frames with
sidesway is best illustrated by work examples.
33
Work Example 8: Frame With
Sidesway
Determine the moments at each joint of the
frames shown below.
Ends A & D are fixed.
Sidesway occurs here.

AB
= A/4 (+ ve)

DC
= A/6 (+ ve)

AB
= (6/4)
DC

34
Sidesway
Slope-Deflection Equations

(6) ) 0 . 1 333 . 0 ( EI M
(5) ) 0 . 1 667 . 0 ( EI M
(4) ) 4 . 0 8 . 0 ( EI M
(3) ) 4 . 0 8 . 0 ( EI M
(2) ) 25 . 2 0 . 1 ( EI M
(1) ) 25 . 2 5 . 0 ( EI M
DC C DC
DC C CD
B C CB
C B BC
DC C BA
DC B AB
=
=
+ =
+ =
=
=
35
Sidesway
Equilibrium Equation
9 unknowns and 6 equations. Thus, we need 3
equilibrium equations.
2 moment equilibrium equations
for joints B & C.

Another equilibrium equation obtained from
summation of forces (entire frame) in x-direction,
since there is horizontal displacement A.

(7) 0 M M ; 0 M
BC BA B
= + =
(8) 0 M M ; 0 M
CD CB C
= + =
(9) 0 V V 200 ; 0 F
D A X
= =

36
Sidesway
Considering the free-body diagram of each column
separately.

(9) 0
6
M M
4
M M
200
6
M M
V 0 M
4
M M
V 0 M
CD DC BA AB
CD DC
D C
BA AB
A B
=
+
+
+
+
+
= =
+
= =
37
Sidesway
Substitute equation (2) and (3) into equation (7).
Substitute equation (4) and (5) into equation (8).
Equation (1), (2), (5) and (6) into equation (9).

Solve simultaneously, we have

48 . 208 EI
66 . 75 EI
78 . 243 EI
DC
C
B
=
=
=
38
Sidesway
Moment calculation
Using these results & solving for equation (1) to
(6)

kNm 183 M
kNm 158 M
kNm 158 M
kNm 225 M
kNm 225 M
kNm 347 M
DC
CD
CB
BC
BA
AB
=
=
=
=
=
=

Lecture 2 SLOPE DEFLECTION

Загружено:

Сведения о документе

Авторское право

Доступные форматы

Поделиться этим документом

Поделиться или встроить документ

Параметры публикации

Этот документ был вам полезен?

Это неприемлемый материал?

Авторское право:

Доступные форматы

Lecture 2 SLOPE DEFLECTION

Загружено:

Авторское право:

Доступные форматы

2005 Pearson Education South Asia Pte Ltd

2005 Pearson Education South Asia Pte Ltd

Вам также может понравиться