Академический Документы
Профессиональный Документы
Культура Документы
Chapter 03 Homework
Загружено:
Fatboy91Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Chapter 03 Homework
Загружено:
Fatboy91Авторское право:
Доступные форматы
3/3/2014
Chapter 3 Homework
Chapter 3 Homework
Due: 10:00pm on Friday, February 14, 2014
You will receive no credit for items you complete after the assignment is due. Grading Policy
Exercise 3.7
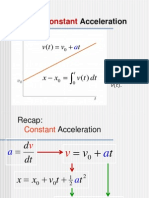
The coordinates of a bird flying in the xy-plane are given by
and = 1.2 m/s2 .
x(t) = t
and y(t) = 3.0m t2 , where = 2.4
m/s
Part A
Calculate the velocity vector of the bird as a function of time.
Give your answer as a pair of components separated by a comma. For example, if you think the x
component is 3t and the y component is 4t, then you should enter 3t,4t. Express your answer using two
significant figures for all coefficients.
ANSWER:
v (t)
2.4, 2.4t
m/s
Correct
Part B
Calculate the acceleration vector of the bird as a function of time.
Give your answer as a pair of components separated by a comma. For example, if you think the x
component is 3t and the y component is 4t, then you should enter 3t,4t. Express your answer using two
significant figures for all coefficients.
ANSWER:
a (t)
= 0,-2.4
m/s
Correct
Part C
Calculate the magnitude of the bird's velocity at
t = 2.0s
Express your answer using two significant figures.
ANSWER:
v
= 5.4
m/s
Correct
Typesetting math: 43%
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
1/21
3/3/2014
Chapter 3 Homework
Part D
Let the direction be the angle, that the vector makes with the +x-axis measured counterclockwise. Calculate the
direction of the bird's velocity at t = 2.0s.
Express your answer in degrees using two significant figures.
ANSWER:
= -63
Correct
Part E
Calculate the magnitude of the bird's acceleration at
t = 2.0s
Express your answer using two significant figures.
ANSWER:
2.4
m/s
Correct
Part F
Calculate the direction of the bird's acceleration at
t = 2.0s
ANSWER:
= -90
Correct
Part G
At
, is the bird speeding up, slowing down or moving at constant speed?
t = 2.0s
ANSWER:
speeding up
slowing down
moving at constant speed
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
2/21
3/3/2014
Chapter 3 Homework
Correct
Conceptual Problem about Projectile Motion
Learning Goal:
To understand projectile motion by considering horizontal constant velocity motion and vertical constant acceleration
motion independently.
Projectile motion refers to the motion of unpowered objects (called projectiles) such as balls or stones moving near the
surface of the earth under the influence of the earth's gravity alone. In this analysis we assume that air resistance can
be neglected.
An object undergoing projectile motion near the surface of the earth obeys the following rules:
1. An object undergoing projectile motion travels horizontally at a constant rate. That is, the x component of
its velocity, vx , is constant.
2. An object undergoing projectile motion moves vertically with a constant downward acceleration whose
magnitude, denoted by g, is equal to 9.80 m/s2 near the surface of the earth. Hence, the y component of
its velocity,
vy
, changes continuously.
3. An object undergoing projectile motion will undergo the horizontal and vertical motions described above
from the instant it is launched until the instant it strikes the ground again. Even though the horizontal and
vertical motions can be treated independently, they are related by the fact that they occur for exactly the
same amount of time, namely the time t the projectile is in the air.
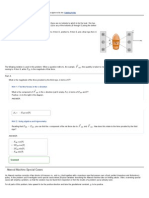
The figure shows the trajectory (i.e., the path) of a ball
undergoing projectile motion over level ground. The time
t0 = 0 s corresponds to the moment just after the ball is
launched from position x0 = 0 m and y 0 = 0 m. Its launch
velocity, also called the initial velocity, is v0 .
Two other points along the trajectory are indicated in the
figure.
One is the moment the ball reaches the peak of its
trajectory, at time t1 with velocity v1 . Its position at
this moment is denoted by
(x1 , y max )
(x1 , y 1 )
or
since it is at its maximum height.
The other point, at time t2 with velocity
v2
corresponds to the moment just before the ball strikes
the ground on the way back down. At this time its
position is (x2 , y 2 ) , also known as (xmax , y 2 ) since it is at its maximum horizontal range.
Projectile motion is symmetric about the peak, provided the object lands at the same vertical height from which is was
launched, as is the case here. Hence y 2 = y 0 = 0 m.
Part A
How do the speeds
v0
v1
, and v2 (at times
t0
t1
, and t2 ) compare?
ANSWER:
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
3/21
3/3/2014
Chapter 3 Homework
v0
v1
v2
>0
v0
v2
>
v1
=0
v0
v2
>
v1
>0
v0
>
v1
>
v2
>0
v0
>
v2
>
v1
=0
Correct
Here v0 equals
v2
by symmetry and both exceed v1 . This is because v0 and v2 include vertical speed as
well as the constant horizontal speed.
Consider a diagram of the ball at time t0 . Recall that t0 refers
to the instant just after the ball has been launched, so it is
still at ground level (x0 = y 0 = 0 m). However, it is already
moving with initial velocity v0 , whose magnitude is
v0 = 30.0 m/s and direction is = 60.0 degrees
counterclockwise from the positive x direction.
Part B
What are the values of the intial velocity vector components
vector components
a0,x
v 0,x
and v0,y (both in m/s) as well as the acceleration
and a0,y (both in m/s )? Here the subscript 0 means "at time t0 ."
2
Hint 1. Determining components of a vector that is aligned with an axis
If a vector points along a single axis direction, such as in the positive x direction, its x component will be its
full magnitude, whereas its y component will be zero since the vector is perpendicular to the y direction. If
the vector points in the negative x direction, its x component will be the negative of its full magnitude.
Hint 2. Calculating the components of the initial velocity
Notice that the vector v0 points up and to the right. Since "up" is the positive y axis direction and "to the
right" is the positive x axis direction,
As shown in the figure,
v 0,x
v0,x
v0,y
v0,x
and v0,y will both be positive.
, and v0 are three sides of a right triangle, one angle of which is . Thus
and v0,y can be found using the definition of the sine and cosine functions given below. Recall that
= 60.0 degrees
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
0 = 30.0 m/s
4/21
3/3/2014
Chapter 3 Homework
v 0 = 30.0 m/s
and
= 60.0 degrees
and note that
sin() =
cos() =
length of opposite side
length of hypotenuse
length of adjacent side
length of hypotenuse
v0,y
v0
v 0,x
v0
What are the values of v0,x and v0,y ?
Enter your answers numerically in meters per second separated by a comma.
ANSWER:
15.0,26.0
m/s
ANSWER:
30.0, 0, 0, 0
0, 30.0, 0, 0
15.0, 26.0, 0, 0
30.0, 0, 0, -9.80
0, 30.0, 0, -9.80
15.0, 26.0, 0, -9.80
15.0, 26.0, 0, +9.80
Correct
Also notice that at time t2 , just before the ball lands, its velocity components are v2,x
as always) and v2,y
= 26.0 m/s
(the same size but opposite sign from
v0,y
(the same
by symmetry). The
acceleration at time t2 will have components (0, -9.80 m/s ), exactly the same as at
2
= 15 m/s
t0
, as required by Rule
2.
The peak of the trajectory occurs at time t1 . This is the point where the ball reaches its maximum height y max . At the
peak the ball switches from moving up to moving down, even as it continues to travel horizontally at a constant rate.
Part C
What are the values of the velocity vector components
vector components
a1,x
v 1,x
and v1,y (both in m/s) as well as the acceleration
and a1,y (both in m/s )? Here the subscript 1 means that these are all at time t1 .
2
ANSWER:
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
5/21
3/3/2014
Chapter 3 Homework
0, 0, 0, 0
0, 0, 0, -9.80
15.0, 0, 0, 0
15.0, 0, 0, -9.80
0, 26.0, 0, 0
0, 26.0, 0, -9.80
15.0, 26.0, 0, 0
15.0, 26.0, 0, -9.80
Correct
At the peak of its trajectory the ball continues traveling horizontally at a constant rate. However, at this
moment it stops moving up and is about to move back down. This constitutes a downward-directed change in
velocity, so the ball is accelerating downward even at the peak.
The flight time refers to the total amount of time the ball is in the air, from just after it is launched (t0 ) until just before it
lands (t2 ). Hence the flight time can be calculated as t2 t0 , or just t2 in this particular situation since t0 = 0 .
Because the ball lands at the same height from which it was launched, by symmetry it spends half its flight time
traveling up to the peak and the other half traveling back down. The flight time is determined by the initial vertical
component of the velocity and by the acceleration. The flight time does not depend on whether the object is moving
horizontally while it is in the air.
Part D
If a second ball were dropped from rest from height
y max
, how long would it take to reach the ground? Ignore air
resistance.
Check all that apply.
Hint 1. Kicking a ball of cliff; a related problem
Consider two balls, one of which is dropped from rest off the edge of a cliff at the same moment that the
other is kicked horizontally off the edge of the cliff. Which ball reaches the level ground at the base of the cliff
first? Ignore air resistance.
Hint 1. Comparing position, velocity, and acceleration of the two balls
Both balls start at the same height and have the same initial y velocity (v0,y
= 0
) as well as the
same acceleration (a = g downward). They differ only in their x velocity (one is zero, the other
nonzero). This difference will affect their x motion but not their y motion.
ANSWER:
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
6/21
3/3/2014
Chapter 3 Homework
The ball that falls straight down strikes the ground first.
The ball that was kicked so it moves horizontally as it falls strikes the ground first.
Both balls strike the ground at the same time.
ANSWER:
t0
t1 t0
t2
t2 t1
t2 t0
2
Correct
In projectile motion over level ground, it takes an object just as long to rise from the ground to the peak as it
takes for it to fall from the peak back to the ground.
The range \texttip{R}{R} of the ball refers to how far it moves horizontally, from just after it is launched until just before it
lands. Range is defined as x_2 - x_0, or just \texttip{x_{\rm 2}}{x_2} in this particular situation since x_0 = 0.
Range can be calculated as the product of the flight time \texttip{t_{\rm 2}}{t_2} and the x component of the velocity
\texttip{v_{\mit x}}{v_x} (which is the same at all times, so v_x = v_{0,x}). The value of \texttip{v_{\mit x}}{v_x} can be
found from the launch speed \texttip{v_{\rm 0}}{v_0} and the launch angle \texttip{\theta }{theta} using trigonometric
functions, as was done in Part B. The flight time is related to the initial y component of the velocity, which may also be
found from \texttip{v_{\rm 0}}{v_0} and \texttip{\theta }{theta} using trig functions.
The following equations may be useful in solving projectile motion problems, but these equations apply only to a
projectile launched over level ground from position (x_0 = y_0 = 0) at time t_0 = 0 with initial speed \texttip{v_{\rm 0}}
{v_0} and launch angle \texttip{\theta }{theta} measured from the horizontal. As was the case above, \texttip{t_{\rm 2}}
{t_2} refers to the flight time and \texttip{R}{R} refers to the range of the projectile.
flight time: \large{t_2 = \frac{2 v_{0, y}}{g} = \frac{2 v_0 \sin(\theta)}{g}}
range: \large{R = v_x t_2 = \frac{v_0^2 \sin(2\theta)}{g}}
In general, a high launch angle yields a long flight time but a small horizontal speed and hence little range. A low launch
angle gives a larger horizontal speed, but less flight time in which to accumulate range. The launch angle that achieves
the maximum range for projectile motion over level ground is 45 degrees.
Part E
Which of the following changes would increase the range of the ball shown in the original figure?
Check all that apply.
ANSWER:
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
7/21
3/3/2014
Chapter 3 Homework
Increase \texttip{v_{\rm 0}}{v_0} above 30 \rm{m/s}.
Reduce \texttip{v_{\rm 0}}{v_0} below 30 \rm{m/s}.
Reduce \texttip{\theta }{theta} from 60 \rm{degrees} to 45 \rm{degrees}.
Reduce \texttip{\theta }{theta} from 60 \rm{degrees} to less than 30 \rm{degrees}.
Increase \texttip{\theta }{theta} from 60 \rm{degrees} up toward 90 \rm{degrees}.
Correct
A solid understanding of the concepts of projectile motion will take you far, including giving you additional
insight into the solution of projectile motion problems numerically. Even when the object does not land at the
same height from which is was launched, the rules given in the introduction will still be useful.
Recall that air resistance is assumed to be negligible here, so this projectile motion analysis may not be the
best choice for describing things like frisbees or feathers, whose motion is strongly influenced by air. The value
of the gravitational free-fall acceleration \texttip{g}{g} is also assumed to be constant, which may not be
appropriate for objects that move vertically through distances of hundreds of kilometers, like rockets or
missiles. However, for problems that involve relatively dense projectiles moving close to the surface of the
earth, these assumptions are reasonable.
Exercise 3.10
A daring 510-{\rm N} swimmer dives off a cliff with a running horizontal leap, as shown in the figure .
Part A
What must her minimum speed be just as she leaves the top of the cliff so that she will miss the ledge at the
bottom, which is 1.75 {\rm m} wide and 9.00 {\rm m} below the top of the cliff?
ANSWER:
v_0 = 1.29 {\rm m/s}
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
8/21
3/3/2014
Chapter 3 Homework
Correct
Exercise 3.12
A rookie quarterback throws a football with an initial upward velocity component of 15.9{\rm m/s} and a horizontal
velocity component of 19.9{\rm m/s} . Ignore air resistance.
Part A
How much time is required for the football to reach the highest point of the trajectory?
Express your answer using three significant figures.
ANSWER:
t_1 = 1.62 {\rm s}
Correct
Part B
How high is this point?
Express your answer using three significant figures.
ANSWER:
h = 12.9 {\rm m}
Correct
Part C
How much time (after it is thrown) is required for the football to return to its original level?
Express your answer using three significant figures.
ANSWER:
t_2 = 3.24 {\rm s}
Correct
Part D
How does this compare with the time calculated in part (a).
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
9/21
3/3/2014
Chapter 3 Homework
Express your answer using three significant figures.
ANSWER:
\large{\frac{t_2}{t_1}} = 2.00
Correct
Part E
How far has it traveled horizontally during this time?
Express your answer using three significant figures.
ANSWER:
x = 64.6 {\rm m}
Correct
Exercise 3.13
A car comes to a bridge during a storm and finds the bridge washed out. The driver must get to the other side, so he
decides to try leaping it with his car. The side the car is on is 22.4{\rm m} above the river, while the opposite side is a
mere 1.6{\rm m} above the river. The river itself is a raging torrent 57.0{\rm m} wide.
Part A
How fast should the car be traveling just as it leaves the cliff in order just to clear the river and land safely on the
opposite side?
ANSWER:
v_0 = 27.7 {\rm m/s}
Correct
Part B
What is the speed of the car just before it lands safely on the other side?
ANSWER:
v = 34.3 {\rm m/s}
Correct
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
10/21
3/3/2014
Chapter 3 Homework
Exercise 3.15
Inside a starship at rest on the earth, a ball rolls off the top of a horizontal table and lands a distance D from the foot of
the table. This starship now lands on the unexplored Planet X. The commander, Captain Curious, rolls the same ball off
the same table with the same initial speed as on earth and finds that it lands a distance 2.43 D from the foot of the
table.
Part A
What is the acceleration due to gravity on Planet X?
ANSWER:
g_{\rm X} = 1.66 {\rm m/s^2}
Correct
Exercise 3.19
In a carnival booth, you win a stuffed giraffe if you toss a quarter into a small dish. The dish is on a shelf above the point
where the quarter leaves your hand and is a horizontal distance of 2.1 {\rm m} from this point (the figure ). If you toss the
coin with a velocity of 6.4 {\rm{ m/s}} at an angle of 60 ^\circ
above the horizontal, the coin lands in the dish. You can
ignore air resistance.
Part A
What is the height of the shelf above the point where the quarter leaves your hand?
Express your answer using two significant figures.
ANSWER:
H = 1.5 {\rm m}
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
11/21
3/3/2014
Chapter 3 Homework
Correct
Part B
What is the vertical component of the velocity of the quarter just before it lands in the dish?
Express your answer using two significant figures.
ANSWER:
v_y = -0.89 {\rm m/s}
Correct
Problem 3.51
A jungle veterinarian with a blow-gun loaded with a tranquilizer dart and a sly 1.5-{\rm kg} monkey are each a height
25{\rm m} above the ground in trees a distance 70{\rm m} apart. Just as the hunter shoots horizontally at the monkey,
the monkey drops from the tree in a vain attempt to escape being hit.
Part A
What must the minimum muzzle velocity of the dart have been for the hunter to hit the monkey before it reached the
ground?
Express your answer using two significant figures.
ANSWER:
v = 31 {\rm m/s}
Correct
Circular Launch
A ball is launched up a semicircular chute in such a way that at the top of the chute, just before it goes into free fall, the
ball has a centripetal acceleration of magnitude 2 \texttip{g}{g}.
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
12/21
3/3/2014
Chapter 3 Homework
Part A
How far from the bottom of the chute does the ball land?
Your answer for the distance the ball travels from the end of the chute should contain \texttip{R}{R}.
Hint 1. Speed of ball upon leaving chute
How fast is the ball moving at the top of the chute?
Hint 1. Equation of motion
The centripetal acceleration for a particle moving in a circle is a_c = v^2/r, where \texttip{v}{v} is its
speed and \texttip{r}{r} is its instantaneous radius of rotation.
ANSWER:
\texttip{v}{v} = \sqrt{\left(2 g R\right)}
Incorrect; Try Again; 5 attempts remaining
Hint 2. Time of free fall
How long is the ball in free fall before it hits the ground?
Express the free-fall time in terms of \texttip{R}{R} and \texttip{g}{g}.
Hint 1. Equation of motion
There is constant acceleration due to gravity, so you can use the general expression
\large{y(t) = y_0 + v_{y0}t + \frac{a_y t^2}{2}}.
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
13/21
3/3/2014
Chapter 3 Homework
Write the values of \texttip{y_{\rm 0}}{y_0}, \texttip{v_{\rm y0}}{v_y0}, and \texttip{a_{\mit y}}{a_y}
(separated by commas) that are appropriate for this situation. Use the standard convention that
\texttip{g}{g} is the magnitude of the acceleration due to gravity. Take y = 0 at the ground, and take
the positive y direction to be upward.
ANSWER:
\texttip{y_{\rm 0}}{y_0}, \texttip{v_{\rm y0}}{v_y0}, \texttip{a_{\mit y}}{a_y} = 2 R,0,-g
Hint 2. Equation for the height of the ball
To find the time in free fall before the ball hits the ground, \texttip{t_{\rm f \hspace{1 pt}}}{t_f}, set the
general equation for the height equal to the height of the ground.
Answer in terms of \texttip{t_{\rm f \hspace{1 pt}}}{t_f}, \texttip{R}{R}, and \texttip{g}{g}.
ANSWER:
y(t_{\rm f \hspace{1 pt}})=0 = \large{2 R-\frac{g}{2} {t_{f}}^{2}}
ANSWER:
\texttip{t_{\rm f \hspace{1 pt}}}{t_f} = \large{2 \sqrt{\frac{R}{g}}}
Hint 3. Finding the horizontal distance
The horizontal distance follows from D = x(t_{\rm f \hspace{1 pt}}) = x_0 + v_{x0}t_{\rm f \hspace{1 pt}},
where x_0=0. \texttip{v_{\rm x0}}{v_x0} and \texttip{t_{\rm f \hspace{1 pt}}}{t_f} were found in Parts i and ii
respectively.
ANSWER:
\texttip{D}{D} = \large{\sqrt{19.6 R} \sqrt{\frac{4R}{9.8}}}
Correct
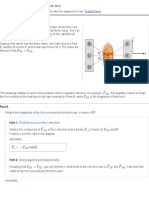
Direction of Acceleration of Pendulum
Learning Goal:
To understand that the direction of acceleration is in the direction of the change of the velocity, which is unrelated to the
direction of the velocity.
The pendulum shown makes a full swing from -\pi/4 to + \pi/4. Ignore friction and assume that the string is massless.
The eight labeled arrows represent directions to be referred to when answering the following questions.
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
14/21
3/3/2014
Chapter 3 Homework
Part A
Which of the following is a true statement about the acceleration of the pendulum bob, \texttip{\vec{a}}{a_vec}.
ANSWER:
\texttip{\vec{a}}{a_vec} is equal to the acceleration due to gravity.
\texttip{\vec{a}}{a_vec} is equal to the instantaneous rate of change in velocity.
\texttip{\vec{a}}{a_vec} is perpendicular to the bob's trajectory.
\texttip{\vec{a}}{a_vec} is tangent to the bob's trajectory.
Correct
Part B
What is the direction of \texttip{\vec{a}}{a_vec} when the pendulum is at position 1?
Enter the letter of the arrow parallel to \texttip{\vec{a}}{a_vec}.
Hint 1. Velocity at position 1
What is the velocity of the bob when it is exactly at position 1?
ANSWER:
\texttip{v_{\rm 1}}{v_1} = 0 {\rm m/s}
Correct
Hint 2. Velocity of bob after it has descended
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
15/21
3/3/2014
Chapter 3 Homework
What is the velocity of the bob just after it has descended from position 1?
ANSWER:
very small and having a direction best approximated by arrow D
very small and having a direction best approximated by arrow A
very small and having a direction best approximated by arrow H
The velocity cannot be determined without more information.
Correct
ANSWER:
H
Correct
Part C
What is the direction of \texttip{\vec{a}}{a_vec} at the moment the pendulum passes position 2?
Enter the letter of the arrow that best approximates the direction of \texttip{\vec{a}}{a_vec}.
Hint 1. Instantaneous motion
At position 2, the instantaneous motion of the pendulum can be approximated as uniform circular motion.
What is the direction of acceleration for an object executing uniform circular motion?
ANSWER:
C
Correct
We know that for the object to be traveling in a circle, some component of its acceleration must be pointing
radially inward.
Part D
What is the direction of \texttip{\vec{a}}{a_vec} when the pendulum reaches position 3?
Give the letter of the arrow that best approximates the direction of \texttip{\vec{a}}{a_vec}.
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
16/21
3/3/2014
Chapter 3 Homework
Hint 1. Velocity just before position 3
What is the velocity of the bob just before it reaches position 3?
ANSWER:
very small and having a direction best approximated by arrow B
very small and having a direction best approximated by arrow C
very small and having a direction best approximated by arrow H
The velocity cannot be determined without more information.
Hint 2. Velocity of bob at position 3
What is the velocity of the bob when it reaches position 3?
ANSWER:
\texttip{v_{\rm 3}}{v_3} = 0 {\rm m/s}
ANSWER:
F
Correct
Part E
As the pendulum approaches or recedes from which position(s) is the acceleration vector \texttip{\vec{a}}{a_vec}
almost parallel to the velocity vector \texttip{\vec{v}}{v_vec}.
ANSWER:
position 2 only
positions 1 and 2
positions 2 and 3
positions 1 and 3
Correct
Exercise 3.25
The earth has a radius of 6380 {\rm km} and turns around once on its axis in 24 {\rm h}.
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
17/21
3/3/2014
Chapter 3 Homework
Part A
What is the radial acceleration of an object at the earth's equator? Give your answer in {\rm{m/s}}^2.
ANSWER:
a_{\rm rad} = 3.40102 {\rm{m/s}}^2
Correct
Part B
What is the radial acceleration of an object at the earth's equator? Give your answer as a fraction of {\it g}.
ANSWER:
a_{\rm rad} = 3.40103 {\it g}
Correct
Part C
If a_{{\rm{rad}}} at the equator is greater than {\it g} , objects would fly off the earth's surface and into space. What
would the period of the earth's rotation have to be for this to occur?
ANSWER:
T = 5070 {\rm s}
Correct
Exercise 3.29
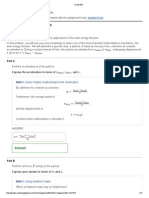
A Ferris wheel with radius 14.0 {\rm m} is turning about a horizontal axis through its center (the figure ). The linear speed
of a passenger on the rim is constant and equal to 6.40{\rm {\rm m/s}} .
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
18/21
3/3/2014
Chapter 3 Homework
Part A
What is the magnitude of the passenger's acceleration as she passes through the lowest point in her circular
motion?
ANSWER:
a = 2.93 {\rm m/s^2}
Correct
Part B
What is the direction of the passenger's acceleration as she passes through the lowest point in her circular motion?
ANSWER:
towards the center
outwards the center
Correct
Part C
What is the magnitude of the passenger's acceleration as she passes through the highest point in her circular
motion?
ANSWER:
a = 2.93 {\rm m/s^2}
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
19/21
3/3/2014
Chapter 3 Homework
Correct
Part D
What is the direction of the passenger's acceleration as she passes through the highest point in her circular
motion?
ANSWER:
towards the center
outwards the center
Correct
Part E
How much time does it take the Ferris wheel to make one revolution?
ANSWER:
T = 13.7 {\rm s}
Correct
Exercise 3.30
At its Ames Research Center, NASA uses its large 20-G centrifuge to test the effects of very large accelerations
(hypergravity) on test pilots and astronauts. In this device, an arm 8.84 {\rm m} long rotates about one end in a
horizontal plane, and the astronaut is strapped in at the other end. Suppose that he is aligned along the arm with his
head at the outermost end. The maximum sustained acceleration to which humans are subjected in this machine is
typically 12.5 {\it g}.
Part A
How fast must the astronaut's head be moving to experience this maximum acceleration?
ANSWER:
v = 32.9 {\rm m/s}
Correct
Part B
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
20/21
3/3/2014
Chapter 3 Homework
What is the difference between the acceleration of his head and feet if the astronaut is 2.00 {\rm m} tall?
ANSWER:
\Delta a = 27.7 {\rm m/s^2}
Correct
Part C
How fast in rpm \left( {\rm rev/min} \right) is the arm turning to produce the maximum sustained acceleration?
ANSWER:
\large{\frac{1}{T}} = 35.5 {\rm rpm}
Correct
Problem 3.88
A projectile is thrown from a point P. It moves in such a way that its distance from P is always increasing.
Part A
Find the maximum angle above the horizontal with which the projectile could have been thrown. You can ignore air
resistance.
ANSWER:
\phi = 70.5 ^\circ
Correct
Score Summary:
Your score on this assignment is 98.3%.
You received 13.77 out of a possible total of 14 points.
http://session.masteringphysics.com/myct/assignmentPrintView?assignmentID=2766014
21/21
Вам также может понравиться
- XX MP4Документ19 страницXX MP4abeck171383% (6)
- Chapter 04 HomeworkДокумент32 страницыChapter 04 HomeworkFatboy9181% (16)
- Mastering Physics 3Документ14 страницMastering Physics 3ozilla_26_me0% (4)
- Chapter 2 Homework Solutions with Velocity and Acceleration CalculationsДокумент18 страницChapter 2 Homework Solutions with Velocity and Acceleration CalculationsFatboy9183% (6)
- Mastering HW 1Документ29 страницMastering HW 1hieОценок пока нет
- Mastering Physics Ch14Документ12 страницMastering Physics Ch14apuszis100% (1)
- MasteringPhysics - Assignment 4 - Motion in 1-DДокумент6 страницMasteringPhysics - Assignment 4 - Motion in 1-DStrange Sht100% (3)
- MasteringPhysics - Assignment 4 - Motion in 2-DДокумент4 страницыMasteringPhysics - Assignment 4 - Motion in 2-DStrange Sht100% (1)
- Exercise 10.1 - Enhanced - With Solution: Pages 303 - 306Документ15 страницExercise 10.1 - Enhanced - With Solution: Pages 303 - 306Siva Ram100% (2)
- Chapter 08 HomeworkДокумент40 страницChapter 08 HomeworkFatboy9146% (24)
- Homework6 Chap5 PDFДокумент47 страницHomework6 Chap5 PDFFedaNahawi100% (30)
- Chapter 07 HomeworkДокумент30 страницChapter 07 HomeworkFatboy9188% (16)
- 7.4-7.5 HWДокумент12 страниц7.4-7.5 HWADVITH CHEGU40% (5)
- Chapter 14 and 15 HomeworkДокумент29 страницChapter 14 and 15 HomeworkFatboy91100% (4)
- The vector C⃗ is oriented at an angle φ counterclockwise from the positive x-axis. Therefore:C⃗ = ccos(φ), -csin(φДокумент15 страницThe vector C⃗ is oriented at an angle φ counterclockwise from the positive x-axis. Therefore:C⃗ = ccos(φ), -csin(φFatboy91100% (5)
- Skiladæmi 9 problem solutionsДокумент8 страницSkiladæmi 9 problem solutionsAl Maimun As SameeОценок пока нет
- CH 08 HWДокумент34 страницыCH 08 HWAbbas53% (47)
- Chapter 11 and 13 HomeworkДокумент31 страницаChapter 11 and 13 HomeworkFatboy91100% (18)
- MP2 DDДокумент30 страницMP2 DDabeck171344% (9)
- Chapter 06 Homework AssignmentДокумент15 страницChapter 06 Homework AssignmentMohammed ElnaggarОценок пока нет
- Mastering PhysicsДокумент10 страницMastering Physicsozilla_26_me100% (1)
- Boat Statics Forces SolvedДокумент67 страницBoat Statics Forces SolvedAliciaTorres0% (1)
- Understanding the Work Done by ForcesДокумент129 страницUnderstanding the Work Done by ForcesWALTER ANDRES CORDOBA CACEREОценок пока нет
- Chapter 09 HomeworkДокумент27 страницChapter 09 HomeworkFatboy9194% (17)
- Mastering Physics: CH 06Документ27 страницMastering Physics: CH 06Paulina Wetner75% (24)
- 17Документ46 страниц17physicsdocs90% (10)
- Mastering Physics 2Документ12 страницMastering Physics 2ozilla_26_me80% (5)
- Mastering Physics CH 04 HW College Physics I LCCCДокумент43 страницыMastering Physics CH 04 HW College Physics I LCCCSamuel100% (16)
- MasteringPhysics Homework 1Документ59 страницMasteringPhysics Homework 1Sarah Brown67% (24)
- Chapter 10 HomeworkДокумент32 страницыChapter 10 HomeworkFatboy9186% (22)
- Chapter 06 HomeworkДокумент14 страницChapter 06 HomeworkFatboy91100% (1)
- Chapter 08 Homework AssignmentДокумент20 страницChapter 08 Homework AssignmentMohammed Elnaggar100% (1)
- MasteringPhysics - Assignment 8 - Motion in 1-DДокумент4 страницыMasteringPhysics - Assignment 8 - Motion in 1-DStrange Sht100% (1)
- CH 07 HWДокумент27 страницCH 07 HWbbhughey1788% (16)
- MasteringPhysics: HomeworkДокумент5 страницMasteringPhysics: HomeworkEric JonesОценок пока нет
- HW 8 AnsДокумент14 страницHW 8 AnsKristin Dikiciyan100% (5)
- Mastering Physics CH 02 HW College Physics I LCCCДокумент33 страницыMastering Physics CH 02 HW College Physics I LCCCSamuel80% (15)
- PC1431 MasteringPhysics Assignment 6Документ16 страницPC1431 MasteringPhysics Assignment 6stpmoment33% (3)
- Chapter 05 Homework AssignmentДокумент21 страницаChapter 05 Homework AssignmentMohammed Elnaggar100% (2)
- CH 06 HWДокумент40 страницCH 06 HWAliciaTorres76% (33)
- HW 12Документ23 страницыHW 12Siva RamОценок пока нет
- Introduction To MasteringPhysicsДокумент17 страницIntroduction To MasteringPhysicsmasteringmastering123100% (3)
- WorkДокумент27 страницWorkLea Dominique Mangubat Fariola0% (2)
- CH 07 HW PDFДокумент36 страницCH 07 HW PDFShaya Nirenberg33% (3)
- 16Документ68 страниц16physicsdocs87% (23)
- Potential Energy Mastering PhysicsДокумент23 страницыPotential Energy Mastering PhysicsLea Dominique Mangubat Fariola0% (1)
- HW #3 - 2D Motion and Projectiles Mastering Physics AnswersДокумент41 страницаHW #3 - 2D Motion and Projectiles Mastering Physics AnswersQusizle72% (18)
- HW1 Mastering PhysicsДокумент16 страницHW1 Mastering Physicszmontgom183% (6)
- MasteringPhysics - Assignment 7 - Forces Part OneДокумент5 страницMasteringPhysics - Assignment 7 - Forces Part OneStrange Sht100% (1)
- Mastering Physics AnswersДокумент144 страницыMastering Physics Answerscuriousbookworm100% (2)
- Physics Chapter 7 AnswersДокумент26 страницPhysics Chapter 7 AnswersAbovethesystem100% (8)
- Projectile Motion Constant AccelerationДокумент7 страницProjectile Motion Constant AccelerationIrish MejiaОценок пока нет
- Projectile Motion in PhysicsДокумент9 страницProjectile Motion in Physicsdharul khairОценок пока нет
- Kinematics in Two and Three DimensionsДокумент7 страницKinematics in Two and Three DimensionsJhun Lerry TayanОценок пока нет
- ProjectilesДокумент5 страницProjectilesShinjiОценок пока нет
- KINEMATICSДокумент7 страницKINEMATICSJhane AlvaradoОценок пока нет
- Motion in Two or Three DimensionsДокумент58 страницMotion in Two or Three DimensionsMarc Howard Detera PanganibanОценок пока нет
- Week 6 Activity: Projectile Motion IIДокумент3 страницыWeek 6 Activity: Projectile Motion IIJ-heart Basabas MalpalОценок пока нет
- Motion Graphs and Kinematic EquationsДокумент45 страницMotion Graphs and Kinematic EquationsBrian NkhomaОценок пока нет
- Chapter 10 HomeworkДокумент32 страницыChapter 10 HomeworkFatboy9186% (22)
- Chapter 14 and 15 HomeworkДокумент29 страницChapter 14 and 15 HomeworkFatboy91100% (4)
- Chapter 11 and 13 HomeworkДокумент31 страницаChapter 11 and 13 HomeworkFatboy91100% (18)
- Chapter 09 HomeworkДокумент27 страницChapter 09 HomeworkFatboy9194% (17)
- Chapter 08 HomeworkДокумент40 страницChapter 08 HomeworkFatboy9146% (24)
- Chapter 06 HomeworkДокумент14 страницChapter 06 HomeworkFatboy91100% (1)
- Chapter 07 HomeworkДокумент30 страницChapter 07 HomeworkFatboy9188% (16)
- Soundproofing Plans Cost Comparison Under 40 CharactersДокумент2 страницыSoundproofing Plans Cost Comparison Under 40 CharactersFatboy91Оценок пока нет
- The vector C⃗ is oriented at an angle φ counterclockwise from the positive x-axis. Therefore:C⃗ = ccos(φ), -csin(φДокумент15 страницThe vector C⃗ is oriented at an angle φ counterclockwise from the positive x-axis. Therefore:C⃗ = ccos(φ), -csin(φFatboy91100% (5)
- Pokemon ListДокумент5 страницPokemon ListFatboy91Оценок пока нет
- Calculus II Course Notes (Traces of Surfaces)Документ6 страницCalculus II Course Notes (Traces of Surfaces)Emil James LadoresОценок пока нет
- Exercicios SuvorovДокумент56 страницExercicios SuvorovfnirneОценок пока нет
- 138 Machine Drawing: Revolved Sections Are Cross Sections of An Elongated Form or Object Rotated TowardДокумент6 страниц138 Machine Drawing: Revolved Sections Are Cross Sections of An Elongated Form or Object Rotated TowardbalajimeieОценок пока нет
- Kikoin, Kikoin - Senior Physics 1Документ254 страницыKikoin, Kikoin - Senior Physics 1Sashank VarmaОценок пока нет
- 07 JPNT Addhm f4 Modul1 Edit BaruДокумент9 страниц07 JPNT Addhm f4 Modul1 Edit BaruSivaneswary Premendran HometuitionОценок пока нет
- MIR - LML - Markushevich A. I. - Areas and LogarithmsДокумент76 страницMIR - LML - Markushevich A. I. - Areas and Logarithmsavast2008100% (5)
- Types of PendulumsДокумент10 страницTypes of PendulumsAdrian Arasu100% (1)
- Recalling Trigonometry FunctionsДокумент3 страницыRecalling Trigonometry FunctionsKetaks MooОценок пока нет
- TEST 12 (Basic Algebra & Arithmetic)Документ41 страницаTEST 12 (Basic Algebra & Arithmetic)Bblack DeathОценок пока нет
- 2006 Maths BДокумент24 страницы2006 Maths BAmeze UmaigbaОценок пока нет
- (Out of 100 Marks) : Mathematics (Paper 1)Документ28 страниц(Out of 100 Marks) : Mathematics (Paper 1)hope tugumeОценок пока нет
- Mensuration PDFДокумент19 страницMensuration PDFRakesh PradhanОценок пока нет
- WM DFJD ZVSR 3 Pu S0 Ym T9 WДокумент19 страницWM DFJD ZVSR 3 Pu S0 Ym T9 WRangeОценок пока нет
- Circle CompositesДокумент89 страницCircle Compositesshashikesh kumarОценок пока нет
- Complex Variable Lecture-7Документ14 страницComplex Variable Lecture-7Syed Afridi RahmanОценок пока нет
- Chapter 4: Stresses and Strains: Fundamentals of Machine Elements, 3 Ed. Schmid, Hamrock and Jacobson © 2014 CRC PressДокумент29 страницChapter 4: Stresses and Strains: Fundamentals of Machine Elements, 3 Ed. Schmid, Hamrock and Jacobson © 2014 CRC PressAlexDiazОценок пока нет
- Digos City National High School Math Summative TestДокумент3 страницыDigos City National High School Math Summative TestGary NugasОценок пока нет
- Sample Paper 1 Class 91636722674Документ4 страницыSample Paper 1 Class 91636722674MeenakshiSundareshОценок пока нет
- EG Question - Final - PrintДокумент9 страницEG Question - Final - PrintgandhiramОценок пока нет
- Inverse trigonometric functions worksheet solutionsДокумент5 страницInverse trigonometric functions worksheet solutionsAdesh KannaОценок пока нет
- SohcahtoaДокумент18 страницSohcahtoaASHWANI Raj100% (1)
- Vit MathsДокумент2 страницыVit Maths100marksОценок пока нет
- Word problem solving in maxima and minimaДокумент7 страницWord problem solving in maxima and minimaDronio Arao L-saОценок пока нет
- VC.09: Spherical Coordinates Literacy: S Cos R T Sin S Sin R T Cos S Sin R T S Z T S y T S XДокумент6 страницVC.09: Spherical Coordinates Literacy: S Cos R T Sin S Sin R T Cos S Sin R T S Z T S y T S XSri RaghavanОценок пока нет
- Area Roughing For ImpellersДокумент3 страницыArea Roughing For ImpellersDženana Delić - AgićОценок пока нет
- PG - Functional 3 - Spectral TheoryДокумент7 страницPG - Functional 3 - Spectral TheoryNirmal KumarОценок пока нет
- 11 Mathematics Imp ch3 1 PDFДокумент12 страниц11 Mathematics Imp ch3 1 PDFSangeetha ThyagarajanОценок пока нет
- CylinderДокумент5 страницCylinderuaarОценок пока нет
- Generalized Complex NumbersДокумент12 страницGeneralized Complex NumbersAnonymous MUhD413U6Оценок пока нет
- Mecanica Clasica - Deleanu DumitruДокумент137 страницMecanica Clasica - Deleanu DumitruAurora LotreanuОценок пока нет