Академический Документы
Профессиональный Документы
Культура Документы
1 s2.0 0022247X71901132 Main PDF
Загружено:
Seshu Kumar DamarlaОригинальное название
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
1 s2.0 0022247X71901132 Main PDF
Загружено:
Seshu Kumar DamarlaАвторское право:
Доступные форматы
JOURNAL
OF MATHEMATICAL
ANALYSIS
The Fractional
AND
APPLICATIONS
Derivative
MARVIN
34, 289-301 (1971)
Via Entire Functions
C. GAER*
University of Delaware, Newark, Delaware 19711
AND
L. A. RUBEL+
University of Illinois, Urbana, Illinois 61801
Submitted by R. P. Boas
INTRODUCTION
Let 9 be the class of functions, defined and analytic on a neighborhood
of the extended real line in the extended complex plane, that vanish at infinity.
We say that an entire function belongs to the Carlson class if it is of exponential type and if its rate of growth on the imaginary axis is less than V.
THEOREM 1, For eachf E F and each t E R, there exists a unique function
F(z : t) in the Carlson cZass,such that F(n : t) = f ()(t)/n!.
This result is simple to prove, but it has interesting implications. We are
led to define the fractional Taylor coefficients of order x off at t by F(z : t),
and therefore to define the fractional derivative f()(t) of any complex
order z # -1, -2, -3,... by f($)(t) = x! F(.z : t), where z! = r(z + 1).
This leads to a consistent theory of fractional differentiation and integration
for functions in the class S. If z = n is a nonnegative integer, then fez)
coincides with the ordinary n-th derivative off.
Our theory is connected with other theories of fractional differentiation,
We show that our fractional derivative coincides with the Weyl fractional
derivative for this class of functions, over a suitable range of z. Our fractional
derivative also coincides with the result of formal differentiation under the
integral sign in the Fourier transform representation, again for a suitable
* The research of this author was partially supported by a grant from the University
of Delaware Research Foundation. Parts of this paper appeared in the first authors
doctoral dissertation [3].
+ The research of this author was partially supported by a grant from the United
States Air Force Office of Scientific Research, Grant Number AF OSR 68 1499.
289
290
GAER AND RUBEL
range of z. The Fourier transforms of functions in 9 are characterized by
pairs of entire functions of exponential type back-to-back (see Definition
1.1). We write 9 = flG for this class of functions.
In Section 1 we sketch a proof of Theorem 1 and show the connections with
the Fourier transform and the Weyl integral. In Section 2, we study some of
the properties off tZ). In particular, we derive a new formula for the fractional
derivative of a product that is not a generalization of the Leibnitz formula.
It does not reduce to it even in the case of first-order differentiation, although
it gives the same numerical value, of course. In Section 3, we briefly discuss 9
as a convolution algebra.
1. CONNECTION
WITH
OTHER THEORIES
By standard contour bending, as found for example
in Buck [2] in a similar context, we get
Proof of Theorem 1.
;p
&
f(W)
j
r
(w
dw,
t)+1
where r = r, u C , where r,. and C are contours that wind once
around the singularities off in the upper and lower half-planes, respectively.
Defining
F(x : t) = - j
+(t) e-*E d6,
where
and where y is the image of r under the change of variable w - t = exp 5,
so that y is composed of two contours y+ and y- lying in the strip 1Im 5 / < 7~,
we obtain the required function F. The uniqueness ofF follows from Carlsons
theorem [l, p. 1531. A useful formula for F is
F(z : t) = - r
f(w)
277i .i r (w - ty+1
dw
(1.1)
where the principal branch of the logarithm is chosen.
It is an unfortunate fact that if z is not an integer, then F(z : t), as a function
of t, may fail to belong to 9 because of branch singularities.
1.1. Let f(w) = (i - w)-1 so that f E 9. We have
= (z- t)-tn+l). We make the guess F(z : t) = (i - t)-cz+l), with
EXAMPLE
f)(t)/n!
FRACTIONAL
291
DERIVATIVE
the principal branch of the logarithm. Since this F belongs to the Carlson
class and has the right values at the positive integers, it must be correct.
DEFINITION
1.1. Let 9 be the class of functions $(x) defined on
(- co, 0~))such that I$(x ) restricted to (0, co) is the restriction there of an
entire function #+ of exponential type that decays exponentially at CO,and
such that 4(x) restricted to (- CO,0) is the restriction there of an entire
function +- of exponential type that decays exponentially at - KI.
We say that + consists of two entire functions of exponential type back-toback. An example is (b(x) = e-lzl, whose Fourier transform, incidentally,
is f(x) = (1 + X2)-l.
THEOREM
1.1. 9 and 3 are reciprocal classes under Fourier transformation.
The proof involves only standard contour bending as in the proof in [I,
p. 1051of the Paley-Wiener theorem, and we omit it, after making the remark
that if f ~9, then f EL~(- co, oo), and f (t) - a(i - t)-l EP(-- co, CO) for
a suitable constant a.
THEOREM
1.2. &ppose
that
E 9,
with f = 4.
Then if Re x > -
1,
we have
f (j(x) = --&==g,I,
4(t) (-
it) e-izt dt,
where the branch cut for the logarithm is the negative imaginary
axis.
We sketch the proof. Let @+and @- be the Bore1 transforms of 4, and $- ,
and let 52, and JX be closed contours lying in the left and right half-planes,
respectively, surrounding the singularities of @+ and @- , respectively. That
is, Q+(w) is the analytic continuation of sr +(t) eetw dt, and
4+(4= & jQ+[E]
dw>
with similar relations between @- and #J- . Then we have
_ ei(n/2)z
F(z: x>= 32
\j D+(W) (W n-a
77 Q+
-I
s)_ D-(w) (w - i~)-~+l
h-(2+1)
dw
dw/ ,
where the branch of the logarithm is cut along the negative imaginary axis.
To prove this formula, it need only be verified for z = 1, 2, 3,... which is
GAER AND RUBEL
292
easy, and then be observed that F(x : x) belongs to the Carlson class, upon
which Theorem 1 assures its validity for all z. Now a direct computation
verifies the assertion of Theorem 1.2.
For f E g, we define the Weyl fractional integral of order /3by the customary formula
dt, P>a
fdx)=&jjs1,(x- W1f(t)
and the Weyl fractional derivative by
for n > Is.
THEOREM 1.3.
If f E 9, x E R, and /3 > 0, then
f (@(x) = f {@(x).
Proof.
Let f [al(x) be defined by
f v4
= gfh-B,(X)
n
for suitable n, where
co
fdt)
w + 1) aktk+O
= k&o IyK + 1 + /I)
if
f(t)
= J$ a#,
k-0
where these formulas hold for small complex values of t, and the principal
value of the logarithm is used. This is Hadamards version of fractional
differentiation. We have
fbl(4
1
= qsJ I o* (z - .)E-l f (u) du,
the path of integration being rectilinear, and (z - ~)s-l having its principal
value at the origin (see [4]). We prove our theorem by showing that
f [yx)
-f
(fl)(x) =
r(l
+ j3) sin 7+ O
f(w) (x - w)-@+l) dw
77
s -cc
==fBl(X) -fqv)
FRACTIONAL DERIVATIVE
293
if f E S, /3 > 0, and 0 < x < B, where B is the radius of convergence of the
power-series expansion off around 0. The second equality follows from the
definitions. Now Hardy and Littlewood [4] have shown that
P](5) = 2;
B, j,,f(w)
(w - ()-(B+l) dw,
where C, is a loop from w = 0 around w = 5 in the counterclockwise
direction, and where (w - [)-(a-i) has its principal value at the point of C,
on the radial line from w = 0 to w = 5. We will take 5 = x > 0. By contour
bending, we have
p](X)
=p2;I /j;- + j,,,i- jr+- s,\f(w)(w- x)-@*l)
dw,
from which the result follows on comparison with (1. I).
2. PROPERTIES OF THE FRACTIONAL DERIVATIVE
In this section we also use the notation Dz for fractional differentiation, so
that Dzf = f lz). It is quite easy to prove that fractional differentiation commutes with translation, and that if f E9, then
= f (z+n)(x) = Df (l(x),
Df(x)
Ifg =f(z),
n = 1, 2, 3,..., z # - I, - 2, - 3 ,.,..
wemaydefine
gcw) = f (z+w)
for w # - 1 - z, - 2 - z, - 3 - z ,... .
This leads to a consistent theory.
THEOREM 2. I.
If f E F then
$y+[f
Proof.
(y) -f
WI =
,:f (4 ds.
Writing f = $J^,we see by Fubinis theorem that
j: f (s) ds = --&
j:,
q%(t)(it)-1 (e-i*u - eeits) dt.
Nowfor-l<(z<O,weseethatfor-l<(t<l,
1q%(t)(- it) (rigt - e-tat)l < ( b(t) (- it)-l (civt - e-ist)l .
294
GAER AND RUBEL
We have, using Theorem 1.2,
f'"'(y) -f'"'(X)
= --Jig jIm f$(t)(- it)* (e-igt - e-izt) &
The first and third integrals converge for all x and depend continuously on a
since 4 is of exponential decay in both directions. By the Lebesgue dominated
convergence theorem,
Iim j
2+--l+
--1
#(t) (- it)* (e-ivt - e-izt) dt = jIl#(t)
(- it)-l (e-igt - &St) dt,
and the result follows.
THEOREM 2.2. Suppose that
g(x) =f(kx).
Then if k > 0,
~9,
that k is a real number, and that
G(z : t) = kF(z : kt),
where kz is defined by the principal
branch of the logarithm.
(2.1)
If k = - 1, then
G(z : t) = eZrriF*(z : t),
(2.2)
where F*(z : t) is de$ned as in (1. l), but using the branch of the logarithm cut
along [0, + co).
We omit the easy proof that proceeds by showing that the functions on the
right sides of Eqs. (2.1) and (2.2) belong to the Carlson class and have the
right values at z = 1, 2, 3,... .
The next theorem gives an interesting interpretation of the Taylor coefficients of negative integral order.
THEOREM 2.3.
If f E F with f (0) = 0 and if g(x) = f( l/x), then
G(x : 0) = - F(-
z : 0).
The proof simply involves a change of variables in Eq. (1. l), and we omit it.
THEOREM 2.4.
-p)/p.
Re.a>(l
Proof.
ties off
Suppose
that
Thenf(Z) E LP(-
f E 9,
that 0 < p < 03, and
co, 00). This result is sharp.
that
It will do no harm to suppose for simplicity that all the singularilie in the upper half-plane. We may enclose them with a circle
FRACTIONAL
295
DERIVATlVE
d = {zu : w = w,, + pei} that does not intersect R. We writeF,(x)
and also write x = OL+ ip. Then
= F(x : x),
=(&)jr, /jA.f(w)
exp[(8+1+$3)
Log(w
--x)1
dw1dx
x exp[PArg(w- 41p&I.
Since 1Arg(w - x)1 < n and 1f(w)1 is bounded on d, we can find an 44 < co
such that
(2~)~~(f(w)/p exp[j? Arg(w - x)] 6 &P/p
for w E d.
Hence
Since d is compact, there is a real number A > 0 such that for any fixed
WEA and for all xER,
A / w _ x I-W)
> 1w. + pei - x (-(a-t-l)
for all C$with - rr < 4 < r. Hence for some finite K > 0,
/IF, 11;< K jy, I w' - x I (ar+lkP
dx,
which converges when 01> (1 - p)/p, and the first part of the theorem is
proved. The sharpness of the result is proved by consideringf(x) = (; - x)-r
as in Example 1.1.
We now consider the fractional derivative of a product of two functions in
9. Formally, we will have
co
I
(fg) Cx)= go k!(zT A)!(f(x) g+(x) + p(X) g(x)}.
However, this formula requires strict interpretation,
integer.
especially if x is an
296
GAER AND RUBEL
We recall that the Mittag-Leffler star (ML-star) off is the region formed
by drawing rays from 0 through every singular point off and removing from
the complex plane the parts of the rays beyond these singular points. The
importance of the Mittag-Leffler summability method for our purpose is that
it sums the Taylor series off to f throughout the ML-star off, and uniformly
on compact subsets of it. By definition,
DEFINITION
2.1. Given f and g in 9, we say that f and g are MittagLeffler compatible if the singularities off lie in the ML-star of those of g,
and vice versa.
THEOREM
2.5. If h = fg, wheref and g are ML-compatible functions in St,
then
H(z : 0) = (ML) 5 [F(k : 0) G(z - k : 0)] + (ML) f [F(z - K : 0) G(R : O)].
k=O
k=O
Proof. The singularities of h lie in the union of the singularities off with
those ofg. By Eq. (1.1)
(2.3)
where I, represents two closed contours, not intersecting R, one in the upper
half-plane and one in the lower half-plane, enclosing the singularities off and
g. By contour bending, we can decompose r, into two sets of closed contours
represented by r, and I, , enclosing the singularities off and of g, respectively, and lying entirely in the ML-stars of g and off respectively. Equation
(2.3) can be written as
H(z : 0) = - &
jrDfw
dt - &
jryfw
d[.
(2.4)
Since I, is contained in the ML-star off, we see that for 4 in I, we have
FRACTIONAL
297
DERIVATIVE
and this holds uniformly. Letting H,(z) be the first of the integrals on the
right in Eq. (2.4), we have
[F(K : 0) G(z - k : O)].
= (ML) i
k=O
A similar computation holds for the second integral on the right in Eq. (2.4),
and the theorem is proved.
EXAMPLE 2.1. Let f and g be the ML-compatible functions in 9 given by
f(x) = (ein/* - x)-r and g(x) = (eirri2 - x)-r. Expanding f in a power series,
we have
f(E)
e-i(n+lh/4p
TL=O
and therefore, as in Example 1.1,
F(z
: 0) = e-iaPe-izq/4.
Similarly,
G(z : 0) = e-in/Q-i*n/2.
Letting h =
obtain
fg,
we compute H(z : 0) directly, using partial fractions to
1
W)
ei"/4(1
,i*/4)
f
[e-iw+lhr/2
n=.
e-i(n+lh/4]
5"
so that, as in Example 1.1,
f&f
: 0) = ei,4(1 - ei,4) {e--irfl/2e--in/2 - e-i*n/4e-in/4}.
(2.5)
GAER AND RUBEL
298
Now
(ML) 2 [F(K : 0) G(s - k : 0) + F(x - K : 0) G(k : 0)]
ILO
=
(ML)
(e-i?r/4e-ikn/4e-inj2e-ion/2
e-ix/4e-i(z-k)n/4e-i/2e-ik~/2)
k=O
(2.6)
_
&35,/4(ML)
(e-izn/2eikn/4
,-izn/4e-ikn/4}
k=O
e-izn12
=
&3n/4
!
1 -
eiv14
since (ML) CI==, an = (1 - a)- unless CA>, 1. It is easy now to check that
the right sides of Eqs. (2.5) and (2.6) are the same, thereby supporting
Theorem 2.5.
Theorem 2.5 unfortunately does not apply to two functionsf and g in 9
if the singularities of each do not lie in the ML-star of the other. The next
result holds in general, but is more complicated.
THEOREM 2.6. If h =
that whenever T > rO ,
H(z:O)=(ML)f$
fg, with f
and g in 3,
then there is a number 7. such
n=O .
Here, F(,z - R + n + l)jr(z
- k + 1) is shorthand for
(.z - k + 1) (Z + k + 2) ..+ (x - k + n)
and
r(k
is shorthand for (k + 1) (k + 2) ... (k + n).
Proof.
We have
f&z : 0) = (ML) 5 (TX=0
1) K)(z; T) $ ,
+ n + 1)
r(k + 1)
299
FRACTIONAL DERIVATIVE
where
@f : 4 = ; [wk7)1(0)
and
P)(x;
T) = g
Iqz : T),
where
&(X) = g(x - 4.
This is because K(z; T) is an analytic function of 7 for T E R since
I+?;
T)
= - &
j, ;$p
dw = - &
But by taking r large enough, we guarantee that
tible, so that Theorem 2.5 applies and gives us
K(z : T) = (ML) i
j,f(w)$z~,--
dw.
and g, are ML-compa-
[F(k : 0) G(.z - k : -
T)]
k=O
+ (ML) 2 [F(z - k : 0) G(k : - T)]
k=O
and the result is proved.
We conclude this section with a uniqueness result that follows directly from
[5, p. 1931and the fact that F belongs to the Carlson class.
THEOREM 2.7. If f E 9 and if A = {A, , A, , A, ,...} is a sequenceof numberswith0 <A, <A, <A, < .a*,such that D&I) > 1, and iffor some x0 E R,
f (A*)(xo) = 0 for all n = 0, 1, 2,..., then f (x) = 0 for all x.
Here DL is the logarithmic block density defined by
DL(A) = lim lim sup
a-Pm X-+rn
A(ax) - A(x)
log a
where
A(t) =
c f .
n,<t n
3. SOME PROPERTIES OF ?? AS A CONVOLUTION ALGEBRA
It is clear that 9 is closed under convolution since (f * g) = f ^g, and F
is closed under pointwise multiplication. The next result shows that the
hypothesis in the definition of 9 about $+ and 4- being of exponential type is
essential.
409/34/2-S
300
GAER AND RUBEL
EXAMPLE 3.1.
Let
and
for t > 0
for 1 < 0.
Then $ t 4 has no extension as an entire function. To see this, we write, for
x > 0,
(4 c I)) (x) = j:,
Z,!J(X
- t) t+(t) dt = 11 exp(-
= j: exp[-
e-(-t)) exp(-
et(e-3c- l)] dt = 1 + /:
et) dt
= B(x) + C(x).
Clearly, B(x) has a unique extension as an entire function, and C(x) can be
extended uniquely as an analytic function C(c) of 5 = s + it for s > 0.
Fixing t = n, we let y(s) = 1 + e-s-in = 1 - e@. Now y(s) -+ 0+ as s -+ Of.
Making the substitution u = et and writing C(y) for C(c), the integral now
takes the form
C(y) = jr
u--le--Y du.
It is clear now that C(y) + CCas y -+ O+, so that 5 = in is a singularity of
cw
We now consider the problem of convolution multipliers for 9.
THEOREM 3.1. Let m be a measurable function on (- co, co) such that
m * g = y5exists and such that # is again a member of 569
for each g in 8. Then,
module its values on a set of measure zero, m must be a member of 9.
Proof. Suppose m satisfies the hypotheses. Let g(x) = e-= if x > 0 and
g(x) = 0 if x < 0. Then g E 9 and hence, if x > 0,
+(x) = (m * g) (x) = s, g(x - Y) m(r) d. = (l,
is the right half of a function in 9. Hence
j:)
e-5-m(y)
dY
FRACTIONAL
DERIVATIVE
301
Applying the fundamental theorem of the calculus for Lebesgue integrals,
we have
44
= #+(x> + #+(x)
(a.e. * 3 0).
From the Polya representation theorem, we know (see [l, p. 771) that the
indicator diagram of #+ is the same in our case as that of z+!J+
. In particular,
where
h&+(0) = lim sup r-l log j #+(reis)i .
r-m
Hence
Thus m(x) is (a.e. x > 0) the restriction of an entire function of exponential
type that decays exponentially as x + + co. Essentially the same argument
holds for x < 0, so that m E B.
THEOREM 3.2. Let m be an element of L1(- co, co) such that for some one
g E 59, g not identically 0, m * g = 4 belongs again to 9. Then m E 9, module
its values on a set of measure 0.
Proof. We have m^g^ = *^ so that m is meromorphic on R. Actually,
mh is analytic on R since possible zeros of g^ on R must be zeros of +
there, of at most the same multiplicity since m^ is bounded. Also, mh has
at worst a pole at co, since g and tj^ are regular there. But m(x) + 0 as
x + f CL),by the Riemann-Lebesgue lemma, and hence mh E 3 so that
m E 9.
Perhaps it is true that if m is measurable and if m *g = $J exists and
belongs to 9 for some one g E 99such thatg^ has no zeros, then m must belong
to 9. The restriction that g^ have no zeros is essential. Otherwise, we could
choose m(t) = e-i(sot) where g^(x,) = 0.
REFERENCES
1. R. P. BOAS, JR., Entire Functions,
Academic Press, Inc., New York/London,
1954.
2. R. C. BUCK, A class of entire functions, Duke Math. f. 13 (1946), 541-559.
3. M. C. GAER, Fractional
Derivatives
and Entire Functions,
Ph.D. thesis, University of Illinois, Urbana. 1968.
4. G. H. HARDY AND J. E. LITTLEWOOD, Some properties of fractional integrals, II,
Math. 2. 34 (1931-32), 403-439.
5. P. MALLIAVIN
AND L. A. RUBEL, On small entire functions of exponential type with
given zeros, Bull. Sot. Math. France 89 (1961), 175-206.
Вам также может понравиться
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeОт EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeРейтинг: 4 из 5 звезд4/5 (5783)
- The Yellow House: A Memoir (2019 National Book Award Winner)От EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Рейтинг: 4 из 5 звезд4/5 (98)
- Never Split the Difference: Negotiating As If Your Life Depended On ItОт EverandNever Split the Difference: Negotiating As If Your Life Depended On ItРейтинг: 4.5 из 5 звезд4.5/5 (838)
- The Emperor of All Maladies: A Biography of CancerОт EverandThe Emperor of All Maladies: A Biography of CancerРейтинг: 4.5 из 5 звезд4.5/5 (271)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceОт EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceРейтинг: 4 из 5 звезд4/5 (890)
- The Little Book of Hygge: Danish Secrets to Happy LivingОт EverandThe Little Book of Hygge: Danish Secrets to Happy LivingРейтинг: 3.5 из 5 звезд3.5/5 (399)
- Team of Rivals: The Political Genius of Abraham LincolnОт EverandTeam of Rivals: The Political Genius of Abraham LincolnРейтинг: 4.5 из 5 звезд4.5/5 (234)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaОт EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaРейтинг: 4.5 из 5 звезд4.5/5 (265)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryОт EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryРейтинг: 3.5 из 5 звезд3.5/5 (231)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureОт EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureРейтинг: 4.5 из 5 звезд4.5/5 (474)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersОт EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersРейтинг: 4.5 из 5 звезд4.5/5 (344)
- The Unwinding: An Inner History of the New AmericaОт EverandThe Unwinding: An Inner History of the New AmericaРейтинг: 4 из 5 звезд4/5 (45)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyОт EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyРейтинг: 3.5 из 5 звезд3.5/5 (2219)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreОт EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreРейтинг: 4 из 5 звезд4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)От EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Рейтинг: 4.5 из 5 звезд4.5/5 (119)
- Proofs of Trigonometric Identities - WikipediaДокумент35 страницProofs of Trigonometric Identities - WikipediaChris BakamОценок пока нет
- 15 TrigonometryДокумент87 страниц15 TrigonometryTwinnie NddОценок пока нет
- 8) C2 Graphs of Trigonometric FunctionsДокумент27 страниц8) C2 Graphs of Trigonometric FunctionsAhmed KhalilОценок пока нет
- Exponents and Powers Worksheet-1 PDFДокумент2 страницыExponents and Powers Worksheet-1 PDFlperumalОценок пока нет
- Identity Theorem in Complex Analysis: Journal of Scientific ResearchДокумент4 страницыIdentity Theorem in Complex Analysis: Journal of Scientific ResearchNishan ChatterjeeОценок пока нет
- Very Short Answer Questions - Introduction To Trigonometry - Mathematics (Maths) Class 10 PDF DownloadДокумент9 страницVery Short Answer Questions - Introduction To Trigonometry - Mathematics (Maths) Class 10 PDF Downloadkrishnatsharma5432Оценок пока нет
- Multivariable Calculus 7th Edition Stewart Solutions ManualДокумент60 страницMultivariable Calculus 7th Edition Stewart Solutions Manualdecardbudgerowhln100% (22)
- 3.2 Sine, Cosine, Tangent (And Cosecant, Secant, Cotangent)Документ8 страниц3.2 Sine, Cosine, Tangent (And Cosecant, Secant, Cotangent)Orlando Medina SandovalОценок пока нет
- Csir Net Complex AnalysisДокумент259 страницCsir Net Complex Analysissourav ganguly100% (2)
- Derivatives of Exponential and Logarithmic Functions PDFДокумент11 страницDerivatives of Exponential and Logarithmic Functions PDFStevenzel Eala EstellaОценок пока нет
- Full Download Trigonometry 11th Edition Lial Solutions ManualДокумент36 страницFull Download Trigonometry 11th Edition Lial Solutions Manuallucas43mreed100% (28)
- Harmonic Functions and The Poisson IntegralДокумент8 страницHarmonic Functions and The Poisson IntegralehsanОценок пока нет
- MathemagicsДокумент71 страницаMathemagicsFevzi YasinОценок пока нет
- Fall Prep Session Materials 2014-15 DraftДокумент216 страницFall Prep Session Materials 2014-15 Draftapi-283319039Оценок пока нет
- reviewer-Math-9-Q4-2023-24 (1)Документ5 страницreviewer-Math-9-Q4-2023-24 (1)sinukshineОценок пока нет
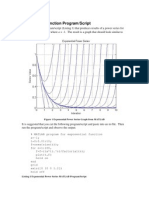
- Exponential Function ScriptДокумент1 страницаExponential Function ScriptyousufnetОценок пока нет
- Harmonic Function: TheoremДокумент11 страницHarmonic Function: TheoremKazi HabibaОценок пока нет
- MA (Improper Integrals & Comparison Test For Improper Integrals)Документ5 страницMA (Improper Integrals & Comparison Test For Improper Integrals)John ManciaОценок пока нет
- Trignometric Equations - 10Документ8 страницTrignometric Equations - 10rebel rocksОценок пока нет
- De Moivre's theorem for complex numbersДокумент260 страницDe Moivre's theorem for complex numbersMarioОценок пока нет
- Complex Number Assignment SolutionsДокумент3 страницыComplex Number Assignment SolutionsSrisai GaneshОценок пока нет
- Complex Analysis, Gamelin, II.6 Problems and SolutionsДокумент5 страницComplex Analysis, Gamelin, II.6 Problems and SolutionsC. Ephrem StuyvesantОценок пока нет
- Theorem:: 2.4.1 The Power FunctionДокумент12 страницTheorem:: 2.4.1 The Power FunctionMert AğaldayОценок пока нет
- Miscellaneous Exercise 2Документ11 страницMiscellaneous Exercise 2Asghar AliОценок пока нет
- Unit 2 PDFДокумент19 страницUnit 2 PDFSampath KumarОценок пока нет
- IIT-JEE 2019: Definite Integration Properties and IllustrationsДокумент5 страницIIT-JEE 2019: Definite Integration Properties and Illustrationsmehul yoОценок пока нет
- CALCUSДокумент5 страницCALCUSDevil KingОценок пока нет
- p3 Complex Numbers NotesДокумент12 страницp3 Complex Numbers NotesZira GreyОценок пока нет
- 5 Tough Solving Trig Problems SolutionsДокумент3 страницы5 Tough Solving Trig Problems SolutionsDal ChawalОценок пока нет
- Binomial TheoremДокумент132 страницыBinomial TheoremHemanth Kumar K SОценок пока нет