Академический Документы
Профессиональный Документы
Культура Документы
Trig Substitution
Загружено:
willygopeИсходное описание:
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Trig Substitution
Загружено:
willygopeАвторское право:
Доступные форматы
Simple trigonometric substitutions with broad results
Vardan Verdiyan, Daniel Campos Salas
Often, the key to solve some intricate algebraic inequality is to simplify it by
employing a trigonometric substitution. When we make a clever trigonometric sub-
stitution the problem may reduce so much that we can see a direct solution imme-
diately. Besides, trigonometric functions have well-known properties that may help
in solving such inequalities. As a result, many algebraic problems can be solved by
using an inspired substitution.
We start by introducing the readers to such substitutions. After that we present
some well-known trigonometric identities and inequalities. Finally, we discuss some
Olympiad problems and leave others for the reader to solve.
Theorem 1. Let , , be angles in (0, ). Then , , are the angles of a
triangle if and only if
tan
2
tan
2
+ tan
2
tan
2
+ tan
2
tan
2
= 1.
Proof. First of all note that if = = , then the statement clearly holds.
Assume without loss of generality that = . Because 0 < + < 2, it follows
that there exists an angle in (, ), say
, such that + +
= .
Using the addition formulas and the fact that tan x = cot
_
2
x
_
, we have
tan
2
= cot
+
2
=
1 tan
2
tan
2
tan
2
+ tan
2
,
yielding
tan
2
tan
2
+ tan
2
tan
2
+ tan
2
tan
2
= 1. (1)
Now suppose that
tan
2
tan
2
+ tan
2
tan
2
+ tan
2
tan
2
= 1, (2)
for some , , in (0, ).
We will prove that =
, and this will imply that , , are the angles of a
triangle. Subtracting (1) from (2) we get tan
2
= tan
2
. Thus
= k for
some nonnegative integer k. But
< , so it follows that k = 0.
That is =
, as desired.
Mathematical Reflections 6 (2007) 1
Theorem 2. Let , , be angles in (0, ). Then , , are the angles of a
triangle if and only if
sin
2
2
+ sin
2
2
+ sin
2
2
+ 2 sin
2
sin
2
sin
2
= 1.
Proof. As 0 < + < 2, there exists an angle in (, ), say
, such that
+ +
= . Using the product-to-sum and the double angle formulas we get
sin
2
2
+ 2 sin
2
sin
2
sin
2
= cos
+
2
_
cos
+
2
+ 2 sin
2
sin
2
_
= cos
+
2
cos
2
=
cos + cos
2
=
_
1 2 sin
2
2
_
+
_
1 2 sin
2
2
_
2
= 1 sin
2
2
sin
2
2
.
Thus
sin
2
2
+ sin
2
2
+ sin
2
2
+ 2 sin
2
sin
2
sin
2
= 1. (1)
Now suppose that
sin
2
2
+ sin
2
2
+ sin
2
2
+ 2 sin
2
sin
2
sin
2
= 1, (2)
for some , , in (0, ). Subtracting (1) from (2) we obtain
sin
2
2
sin
2
2
+ 2 sin
2
sin
2
_
sin
2
sin
2
_
= 0,
that is
_
sin
2
sin
2
__
sin
2
+ sin
2
+ 2 sin
2
sin
2
_
= 0.
The second factor can be written as
sin
2
+ sin
2
+ cos
2
cos
+
2
= sin
2
+ cos
2
,
which is clearly greater than 0. It follows that sin
2
= sin
2
, and so =
, showing
that , , are the angles of a triangle.
Mathematical Reflections 6 (2007) 2
Substitutions and Transformations
T1. Let , , be angles of a triangle. Let
A =
2
, B =
2
, C =
2
.
Then A+B+C = , and 0 A, B, C <
2
. This transformation allows us to switch
from angles of an arbitrary triangle to angles of an acute triangle. Note that
cyc(sin
2
= cos A), cyc(cos
2
= sin A), cyc(tan
2
= cot A), cyc(cot
2
= tan A),
where by cyc we denote a cyclic permutation of angles.
T2. Let x, y, z be positive real numbers. Then there is a triangle with sidelengths
a = x + y, b = y + z, c = z + x. This transformation is sometimes called Dual
Principle. Clearly, s = x+y+z and (x, y, z) = (sa, sb, sc). This transformation
already triangle inequality.
S1. Let a, b, c be positive real numbers such that ab + bc + ca = 1. Using the
function f : (0,
2
) (0, +), for f(x) = tan x, we can do the following substitution
a = tan
2
, b = tan
2
, c = tan
2
,
where , , are the angles of a triangle ABC.
S2. Let a, b, c be positive real numbers such that ab +bc +ca = 1. Applying T1
to S1, we have
a = cot A, b = cot B, c = cot C,
where A, B, C are the angles of an acute triangle.
S3. Let a, b, c be positive real numbers such that a + b + c = abc. Dividing by
abc it follows that
1
bc
+
1
ca
+
1
ab
= 1. Due to S1, we can substitute
1
a
= tan
2
,
1
b
= tan
2
,
1
c
= tan
2
,
that is
a = cot
2
, b = cot
2
, c = cot
2
,
where , , are the angles of a triangle.
S4. Let a, b, c be positive real numbers such that a + b + c = abc. Applying T1
to S3, we have
a = tan A, b = tan B, c = tan C,
Mathematical Reflections 6 (2007) 3
where A, B, C are the angles of an acute triangle.
S5. Let a, b, c be positive real numbers such that a
2
+ b
2
+ c
2
+ 2abc = 1. Note
that since all the numbers are positive it follows that a, b, c < 1. Usign the function
f : (0, ) (0, 1), for f(x) = sin
x
2
, and recalling Theorem 2, we can substitute
a = sin
2
, b = sin
2
, c = sin
2
,
where , , are the angles of a triangle.
S6. Let a, b, c be positive real numbers such that a
2
+b
2
+c
2
+2abc = 1. Applying
T1 to S5, we have
a = cos A, b = cos B, c = cos C,
where A, B, C are the angles of an acute triangle.
S7. Let x, y, z be positive real numbers. Applying T2 to expressions
_
yz
(x + y)(x + z)
,
_
zx
(y + z)(y + x)
,
_
xy
(z + x)(z + y)
,
they can be substituted by
_
(s b)(s c)
bc
,
_
(s c)(s a)
ca
,
_
(s a)(s b)
ab
,
where a, b, c are the sidelengths of a triangle. Recall the following identities
sin
2
=
_
(s b)(s c)
bc
, cos
2
=
_
s(s a)
bc
.
Thus our expressions can be substituted by
sin
2
, sin
2
, sin
2
,
where , , are the angles of a triangle.
S8. Analogously to S7, the expressions
x(x + y + z)
(x + y)(x + z)
,
y(x + y + z)
(y + z)(y + x)
,
z(x + y + z)
(z + x)(z + y)
,
can be substituted by
cos
2
, cos
2
, cos
2
,
where , , are the angles of a triangle.
Mathematical Reflections 6 (2007) 4
Further we present a list of inequalities and equalities that can be helpful in
solving many problems or simplify them.
Well-known inequalities
Let , , be angles of a triangle ABC. Then
1. cos + cos + cos sin
2
+ sin
2
+ sin
2
3
2
2. sin + sin + sin cos
2
+ cos
2
+ cos
2
3
3
2
3. cos cos cos sin
2
sin
2
sin
2
1
8
4. sin sin sin cos
2
cos
2
cos
2
3
3
8
5. cot
2
+ cot
2
+ cot
C
2
3
3
6. cos
2
+ cos
2
+ cos
2
sin
2
2
+ sin
2
2
+ sin
2
C
2
3
4
7. sin
2
+ sin
2
+ sin
2
cos
2
2
+ cos
2
2
+ cos
2
2
9
4
8. cot + cot + cot tan
2
+ tan
2
+ tan
2
3
Well-known identities
Let , , be angles of a triangle ABC. Then
1. cos + cos + cos = 1 + 4 sin
2
sin
2
sin
2
2. sin + sin + sin = 4 cos
2
cos
2
cos
2
3. sin 2 + sin 2 + sin 2 = 4 sin sin sin
4. sin
2
+ sin
2
+ sin
2
= 2 + 2 cos cos cos
For arbitrary angles , , we have
sin + sin + sin sin( + + ) = 4 sin
+
2
sin
+
2
sin
+
2
.
cos + cos + cos + cos( + + ) = 4 cos
+
2
cos
+
2
cos
+
2
.
Mathematical Reflections 6 (2007) 5
Applications
1. Let x, y, z be positive real numbers. Prove that
x
x +
_
(x + y)(x + z)
+
y
y +
_
(y + z)(y + x)
+
z
x +
_
(z + x)(z + y)
1.
(Walther Janous, Crux Mathematicorum)
Solution. The inequality is equivalent to
1
1 +
_
(x+y)(x+z)
x
2
1.
Beceause the inequality is homogeneous, we can assume that xy +yz +zx = 1.
Let us apply substitution S1: cyc(x = tan
2
), where , , are angles of a
triangle. We get
(x + y)(x + z)
x
2
=
_
tan
2
+ tan
2
_
_
tan
2
+ tan
2
_
tan
2
2
=
1
sin
2
2
,
and similar expressions for the other terms. The inequality becomes
sin
2
1 + sin
2
+
sin
2
1 + sin
2
+
sin
2
1 + sin
2
1,
that is
2
1
1 + sin
2
+
1
1 + sin
2
+
1
1 + sin
2
.
On the other hand, using the well-known inequality sin
2
+ sin
2
+ sin
2
3
2
and the Cauchy-Schwarz inequality, we have
2
9
(1 + sin
2
) + (1 + sin
2
) + (1 + sin
2
)
1
1 + sin
2
,
and we are done.
2. Let x, y, z be real numbers greater than 1 such that
1
x
+
1
y
+
1
z
= 2. Prove that
x 1 +
_
y 1 +
z 1
x + y + z.
(Iran, 1997)
Mathematical Reflections 6 (2007) 6
Solution. Let (x, y, z) = (a+1, b+1, c+1), with a, b, c positive real numbers.
Note that the hypothesis is equivalent to ab + bc + ca + 2abc = 1. Then it
suces to prove that
a +
b +
a + b + c + 3.
Squaring both sides of the inequality and canceling some terms yields
ab +
bc +
ca
3
2
.
Using substitution S5 we get (ab, bc, ca) = (sin
2
2
, sin
2
2
, sin
2
2
), where ABC
is an arbitrary triangle. The problem reduces to proving that
sin
2
+ sin
2
+ sin
2
3
2
,
which is well-known and can be done using Jensen inequality.
3. Let a, b, c be positive real numbers such that a + b + c = 1. Prove that
_
ab
c + ab
+
_
bc
a + bc
+
_
ca
b + ca
3
2
.
(Open Olympiad of FML No-239, Russia)
Solution. The inequality is equivalent to
ab
((c + a)(c + b)
+
bc
(a + b)(a + c)
+
_
ca
(b + c)(b + a)
3
2
.
Substitution S7 replaces the three terms in the inequality by sin
2
, sin
2
, sin
2
.
Thus it suces to prove sin
2
+ sin
2
+ sin
2
3
2
, which clearly holds.
4. Let a, b, c be positive real numbers such that (a + b)(b + c)(c + a) = 1. Prove
that
ab + bc + ca
3
4
.
(Cezar Lupu, Romania, 2005)
Solution. Observe that the inequality is equivalent to
_
ab
_
3
_
3
4
_
3
(a + b)
2
(b + c)
2
(c + a)
2
.
Mathematical Reflections 6 (2007) 7
Because the inequality is homogeneous, we can assume that ab + bc + ca = 1.
We use substitution S1: cyc(a = tan
2
), where , , are the angles of a
triangle. Note that
(a + b)(b + c)(c + a) =
_
cos
2
cos
2
cos
2
_
=
1
cos
2
cos
2
cos
2
.
Thus it suces to prove that
_
4
3
_
3
1
cos
2
2
cos
2
2
cos
2
2
,
or
4 cos
2
cos
2
cos
2
3
3
2
.
From the identity 4 cos
2
cos
2
cos
2
= sin + sin + sin , the inequality is
equivalent to
sin + sin + sin
3
3
2
.
But f(x) = sin x is a concave function on (0, ) and the conclusion follows
from Jensens inequality.
5. Let a, b, c be positive real numbers such that a + b + c = 1. Prove that
a
2
+ b
2
+ c
2
+ 2
3abc 1.
(Poland, 1999)
Solution. Let cyc
_
x =
_
bc
a
_
. It follows that cyc(a = yz). The inequality
becomes
x
2
y
2
+ y
2
z
2
+ x
2
z
2
+ 2
3xyz 1,
where x, y, z are positive real numbers such that xy +yz +zx = 1. Note that
the inequality is equivalent to
(xy + yz + zx)
2
+ 2
3xyz 1 + 2xyz(x + y + z),
or
3 x + y + z.
Applying substitution S1 cyc(x = tan
2
), it suces to prove
tan
2
+ tan
2
+ tan
2
3.
The last inequality clearly holds, as f(x) = tan
x
2
is convex function on (0, ),
and the conclusion follows from Jensens inequality.
Mathematical Reflections 6 (2007) 8
6. Let x, y, z be positive real numbers. Prove that
_
x(y + z) +
_
y(z + x) +
_
z(x + y) 2
(x + y)(y + z)(z + x)
x + y + z
(Darij Grinberg)
Solution. Rewrite the inequality as
x(x + y + z)
(x + y)(x + z)
+
y(x + y + z)
(y + z)(y + x)
+
z(x + y + z)
(z + x)(z + y)
2.
Applying substitution S8, it suces to prove that
cos
2
+ cos
2
+ cos
2
2,
where , , are the angles of a triangle. Using transformation T1 cyc(A =
2
),
where A, B, C are angles of an acute triangle, the inequality is equivalent to
sin A + sin B + sin C 2.
There are many ways to prove this fact. We prefer to use Jordans inequality,
that is
2
sin for all (0,
2
).
The conclusion immediately follows.
7. Let a, b, c be positive real numbers such that a +b +c +1 = 4abc. Prove that
1
a
+
1
b
+
1
c
3
1
ab
+
1
bc
+
1
ca
.
(Daniel Campos Salas, Mathematical Reections, 2007)
Solution. Rewrite the condition as
1
bc
+
1
ca
+
1
ab
+
1
abc
= 4.
Observe that we can use substitution S5 in the following way
_
1
bc
,
1
ca
,
1
ab
_
=
_
2 sin
2
2
, 2 sin
2
2
, 2 sin
2
2
_
,
Mathematical Reflections 6 (2007) 9
where , , are angles of a triangle. It follows that
_
1
a
,
1
b
,
1
c
_
=
_
2 sin
2
sin
2
sin
2
,
2 sin
2
sin
2
sin
2
,
2 sin
2
sin
2
sin
2
_
.
Then it suces to prove that
sin
2
sin
2
sin
2
+
sin
2
sin
2
sin
2
+
sin
2
sin
2
sin
2
3
2
sin
2
+ sin
2
+ sin
2
.
The right-hand side of the inequality is well known. For the left-hand side we
use trasnformation T2 backwards. Denote by x = s a, y = s b, z = s c,
where s is the semiperimeter of the triangle. The left-hand side is equivalent
to
x
y + z
+
y
x + z
+
z
x + y
3
2
,
which a famous Nesbitts inequality, and we are done.
8. Let a, b, c (0, 1) be real numbers such that ab + bc + ca = 1. Prove that
a
1 a
2
+
b
1 b
2
+
c
1 c
2
3
4
_
1 a
2
a
+
1 b
2
b
+
1 c
2
c
_
.
(Calin Popa)
Solution. We apply substitution S1 cyc(a tan
A
2
), where A, B, C are angles
of a triangle. Because a, b, c (0, 1), it follows that tan
A
2
, tan
B
2
, tan
C
2
(0, 1),
that is A, B, C are angles of an acute triangle. Note that
cyc
_
a
1 a
2
=
sin
A
2
cos
A
2
cos A
=
tan A
2
_
.
Thus the inequality is equivalent to
tan A + tan B + tan C 3
_
1
tan A
+
1
tan B
+
1
tan C
_
.
Now observe that if we apply transformation T1 and the result in Theorem
1, we get
tan A + tan B + tan C = tan Atan B tan C.
Hence our inequality is equivalent to
(tan A + tan B + tan C)
2
3 (tan Atan B + tan B tan C + tan Atan C) .
This can be written as
1
2
(tan Atan B)
2
+ (tan B tan C)
2
+ (tan C tan A)
2
0,
and we are done.
Mathematical Reflections 6 (2007) 10
9. Let x, y, z be positive real numbers. Prove that
_
y + z
x
+
_
z + x
y
+
_
x + y
z
16(x + y + z)
3
3(x + y)(y + z)(z + x)
.
(Vo Quoc Ba Can, Mathematical Reections, 2007)
Solution. Note that the inequality is equivalent to
cyc
(y + z)
(x + y)(z + x)
x(x + y + z)
4(x + y + z)
3
.
Let use transfromation T2 and substitution S8. We get
cyc
_
(y + z)
(x + y)(z + x)
x(x + y + z)
=
a
cos
2
= 4Rsin
2
_
,
and
4(x + y + z)
3
=
4R(sin + sin + sin )
3
,
where , , are angles of a triangle with circumradius R. Therefore it suces
to prove that
3
2
_
sin
2
+ sin
2
+ sin
2
_
sin
2
cos
2
+ sin
2
cos
2
+ sin
2
cos
2
.
Because f(x) = cos
x
2
is a concave function on [0, ], from Jensens inequality
we obtain
3
2
1
3
_
cos
2
+ cos
2
+ cos
2
_
.
Finally, we observe that f(x) = sin
x
2
is an increasing function on [0, ], while
g(x) = cos
x
2
is a decreasing function on [0, ]. Using Chebyschevs inequality,
we have
1
3
_
sin
2
+ sin
2
+ sin
2
__
cos
2
+ cos
2
+ cos
2
_
sin
2
cos
2
,
and the conclusion follows.
Mathematical Reflections 6 (2007) 11
Problems for independent study
1. Let a, b, c be positive real numbers such that a + b + c = 1. Prove that
a
b + c
+
b
c + a
+
c
a + b
_
3
2
.
(Romanian Mathematical Olympiad, 2005)
2. Let a, b, c be positive real numbers such that a + b + c = 1. Prove that
_
1
a
1
_
1
b
1 +
_
1
b
1
_
1
c
1 +
_
1
c
1
_
1
a
1 6
(A. Teplinsky, Ukraine, 2005)
3. Let a, b, c be positive real numbers such that ab + bc + ca = 1. Prove that
1
a + b
+
1
b + c
+
1
c + a
2 +
1
2
.
(Le Trung Kien)
4. Prove that for all positive real numbers a, b, c,
(a
2
+ 2)(b
2
+ 2)(c
2
+ 2) 9(ab + bc + ca).
(APMO, 2004)
5. Let x, y, z be positive real numbers such that
1
x
+
1
y
+
1
z
= 1. Prove that
x + yz +
x + yz +
x + yz
xyz +
x +
y +
z.
(APMO, 2002)
6. Let a, b, c be positive real numbers. Prove that
b + c
a
+
c + a
b
+
a + b
c
4
_
a
b + c
+
b
c + a
+
c
a + b
_
.
(Mircea Lascu)
7. Let a, b, c be positive real numbers, such that a + b + c =
abc. Prove that
ab + bc + ca 9(a + b + c).
(Belarus, 1996)
Mathematical Reflections 6 (2007) 12
8. Let a, b, c be positive real numbers. Prove that
b + c
a
+
c + a
b
+
a + b
c
+ 2
abc
(a + b)(b + c)(c + a)
2
(Bui Viet Anh)
9. Let a, b, c be positive real numbers such that a + b + c = abc. Prove that
(a 1)(b 1)(c 1) 6
3 10.
(Gabriel Dospinescu, Marian Tetiva)
10. Let a, b, c be nonnegative real numbers such that a
2
+b
2
+c
2
+abc = 4. Prove
that
0 ab + bc + ca abc 2.
(Titu Andreescu, USAMO, 2001)
REFERENCES
[1. ] Titu Andreescu, Zuming Feng, 103 Trigonometry Problems: From the Training
of the USA IMO Team, Birkhauser, 2004
[2. ] Titu Andreescu, Vasile Cirtoaje, Gabriel Dospinescu, Mircea Lascu - Old and
New Inequalities, GIL Publishing House, 2004
[3. ] Tran Phuong, Diamonds in Mathematical Inequalities, Hanoi Publishing House,
2007
[4. ] N.M. Sedrakyan Geometricheskie Neravenstva, Yerevan, 2004
[5. ] E. Specht, Collected Inequalities, http://www.imo.org.yu/othercomp/Journ/ineq.pdf
[6. ] H. Lee, Topics in Inequalities - Theorems and Techniques
[7. ] H. Lee, Inequalities through problems
[8. ] Crux Mathematicorum and Mathematical Mayhem (Canada)
Mathematical Reflections 6 (2007) 13
Вам также может понравиться
- Algebraic Inequalities: 1 The Rearrangement Inequality and Its Conse-QuencesДокумент23 страницыAlgebraic Inequalities: 1 The Rearrangement Inequality and Its Conse-QuencesFREDY POMA LIMAОценок пока нет
- Adrian Tang - Mixing Variable TechniqueДокумент4 страницыAdrian Tang - Mixing Variable TechniqueDijkschneier100% (4)
- MR5 ProblemsДокумент4 страницыMR5 Problemslovemath213Оценок пока нет
- Junior Problems: Mathematical Reflections (2018) 1Документ4 страницыJunior Problems: Mathematical Reflections (2018) 1StephenОценок пока нет
- 2012 Hs ContestДокумент7 страниц2012 Hs ContestJohn TafuiОценок пока нет
- Junior problems solved and exploredДокумент4 страницыJunior problems solved and exploredLêNhậtHoàng0% (1)
- MR 6 2017 ProblemsДокумент4 страницыMR 6 2017 ProblemsAlessandroОценок пока нет
- 2006 6 ProblemsДокумент4 страницы2006 6 ProblemsAn Phu PhamОценок пока нет
- MR Year 2006 Problem Column PDFДокумент218 страницMR Year 2006 Problem Column PDFMd Hajjul100% (1)
- MR6Документ5 страницMR6Zakaria KhayiouiОценок пока нет
- RMC2006Документ97 страницRMC2006calinenescu100% (1)
- Inequalities MarathonДокумент55 страницInequalities MarathonChuông GióОценок пока нет
- 2019 Hs ContestДокумент6 страниц2019 Hs ContestJohn TafuiОценок пока нет
- Mathematical Olympiad Math Olympiad TutorialsДокумент62 страницыMathematical Olympiad Math Olympiad TutorialsClaudio Perez100% (1)
- MR 3 2015 Problems 2Документ4 страницыMR 3 2015 Problems 2uthso royОценок пока нет
- Junior Math Problems and SolutionsДокумент4 страницыJunior Math Problems and SolutionsgrishaОценок пока нет
- MR 2 2016 ProblemsДокумент4 страницыMR 2 2016 Problemsuthso royОценок пока нет
- Mathematical Olympiad Problems and SolutionsДокумент13 страницMathematical Olympiad Problems and SolutionsGV Nguyen ChuОценок пока нет
- ARML Local 2019 ProblemsДокумент4 страницыARML Local 2019 ProblemsAndrew CourtneyОценок пока нет
- Greece JBMO TST Greece 1998 251Документ1 страницаGreece JBMO TST Greece 1998 251Biswarup BurmanОценок пока нет
- Canadian MO 1969-2019, Solutions From 1994 - 2019 PDFДокумент237 страницCanadian MO 1969-2019, Solutions From 1994 - 2019 PDFMuhammad Naufal FirdausОценок пока нет
- BulgarianMO1960 2008Документ104 страницыBulgarianMO1960 2008hungkgОценок пока нет
- Solving complex mathematical problemsДокумент4 страницыSolving complex mathematical problemsluatdhv4684Оценок пока нет
- 1989 Asian Pacific Mathematical Olympiad questionsДокумент36 страниц1989 Asian Pacific Mathematical Olympiad questionsS.M.A NahianОценок пока нет
- Smops 2016 Round 1Документ10 страницSmops 2016 Round 1dK GanОценок пока нет
- Mathematical Excalibur - Pole and Polar PDFДокумент4 страницыMathematical Excalibur - Pole and Polar PDFAlex YuОценок пока нет
- Number Theory Handout #6: 1 ProblemsДокумент2 страницыNumber Theory Handout #6: 1 ProblemsWalker KroubalkianОценок пока нет
- IMO 2015 ShorlistДокумент7 страницIMO 2015 ShorlistAxelОценок пока нет
- The Basics of Olympiad Number Theory: Author Justin Stevens Editor and L TEX Manager David AltizioДокумент44 страницыThe Basics of Olympiad Number Theory: Author Justin Stevens Editor and L TEX Manager David AltizioJustin StevensОценок пока нет
- Algebra Handout #6: 1 ProblemsДокумент2 страницыAlgebra Handout #6: 1 ProblemsWalker KroubalkianОценок пока нет
- Number Theory 3 Solutions UHSMCДокумент5 страницNumber Theory 3 Solutions UHSMCWalker KroubalkianОценок пока нет
- Euclid Combined Contest (CMC)Документ95 страницEuclid Combined Contest (CMC)Eric MooiОценок пока нет
- 2019 HSSolutionДокумент16 страниц2019 HSSolutionrizky rajendra anantadewaОценок пока нет
- MOTP Mock Soham Problems on Positive Reals, Digital Sums, Divisors & MoreДокумент1 страницаMOTP Mock Soham Problems on Positive Reals, Digital Sums, Divisors & MoreGunjan AggarwalОценок пока нет
- Rezolvari EGMO 2014 Ziua 1Документ9 страницRezolvari EGMO 2014 Ziua 1Raluca PantaziОценок пока нет
- Algebra Handout #5: 1 ProblemsДокумент2 страницыAlgebra Handout #5: 1 ProblemsWalker KroubalkianОценок пока нет
- Rice MathДокумент60 страницRice MathHarikrishna ShenoyОценок пока нет
- Croatia Team Selection Test 2008 106Документ1 страницаCroatia Team Selection Test 2008 106Biswarup BurmanОценок пока нет
- Geometric Inequalities (Akadii Slinko)Документ24 страницыGeometric Inequalities (Akadii Slinko)jvr84Оценок пока нет
- Book Homc2019 Đã Chuyển ĐổiДокумент208 страницBook Homc2019 Đã Chuyển ĐổißαϮMαn DОценок пока нет
- Geometry Handout 2: 1 ProblemsДокумент6 страницGeometry Handout 2: 1 ProblemsWalker KroubalkianОценок пока нет
- Extracted Pages From 250 Problems in Elementary Number Theory - Sierpinski (1970)Документ51 страницаExtracted Pages From 250 Problems in Elementary Number Theory - Sierpinski (1970)Pham Thi Thanh ThuyОценок пока нет
- Austrict 2020Документ16 страницAustrict 2020ferrousweiОценок пока нет
- MR5 2010 ProblemsДокумент4 страницыMR5 2010 ProblemsMuhammad Royyan ZahirОценок пока нет
- Number Theory Handout #8: 1 ProblemsДокумент2 страницыNumber Theory Handout #8: 1 ProblemsWalker KroubalkianОценок пока нет
- Algebra 1Документ6 страницAlgebra 1RonakPawarОценок пока нет
- Titu Andreescu - Interesting Mathematical Problems To Ponder - Titufall06 PDFДокумент4 страницыTitu Andreescu - Interesting Mathematical Problems To Ponder - Titufall06 PDFtheuОценок пока нет
- Mathematical Olympiad 2016 AnswersДокумент3 страницыMathematical Olympiad 2016 AnswersDhrubajyoti Ghosh100% (1)
- British Mathematical Olympiad Past PapersДокумент44 страницыBritish Mathematical Olympiad Past Papersspringfield1233% (3)
- No integer n satisfies harmonic series equalityДокумент25 страницNo integer n satisfies harmonic series equalityEmmyОценок пока нет
- MR Year 2014 Problem Column PDFДокумент188 страницMR Year 2014 Problem Column PDFMd HajjulОценок пока нет
- Inmo-Sol-2000 Previous Year Question Papers of Indian National Mathematical Olympiad (INMO) With SolutionsДокумент5 страницInmo-Sol-2000 Previous Year Question Papers of Indian National Mathematical Olympiad (INMO) With SolutionsAkshay PandeyОценок пока нет
- Inmo Sol 2000Документ5 страницInmo Sol 2000ashu_dwy8605Оценок пока нет
- CRMO-2015 Questions and SolutionsДокумент3 страницыCRMO-2015 Questions and SolutionssaswatОценок пока нет
- Split 4026815802256091763Документ5 страницSplit 4026815802256091763vidyakumari808940Оценок пока нет
- Junior Balkan Mathematical Olympiad Problems SolvedДокумент4 страницыJunior Balkan Mathematical Olympiad Problems SolvedTiến Việt PhạmОценок пока нет
- Enrichment Lectures 2007 Mathematical InequalitiesДокумент29 страницEnrichment Lectures 2007 Mathematical InequalitiesTho NguyenОценок пока нет
- EuclidДокумент4 страницыEuclidayoyaОценок пока нет
- Technical Analysis of Three Variable Inequalities TIV (Lionel Messi - Red3Документ34 страницыTechnical Analysis of Three Variable Inequalities TIV (Lionel Messi - Red3VanHieu1997Оценок пока нет
- Homc PDFДокумент14 страницHomc PDFAnonymous xFEpO2zBОценок пока нет
- Geometry BasicsДокумент2 страницыGeometry BasicswillygopeОценок пока нет
- A Tiling of The Plane With TrianglesДокумент6 страницA Tiling of The Plane With TriangleswillygopeОценок пока нет
- Putnam InequalitiesДокумент15 страницPutnam InequalitieswillygopeОценок пока нет
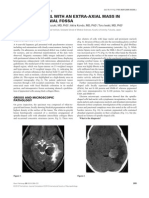
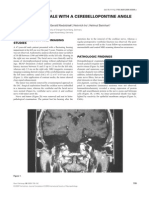
- A 45-Year Old Male With Left-Sided Hemihypesthesia: Clinical HistoryДокумент4 страницыA 45-Year Old Male With Left-Sided Hemihypesthesia: Clinical HistorywillygopeОценок пока нет
- 1009 Case 2Документ4 страницы1009 Case 2willygopeОценок пока нет
- 1109 Case 2Документ4 страницы1109 Case 2willygopeОценок пока нет
- 1109 Case 1Документ4 страницы1109 Case 1willygopeОценок пока нет
- Chords RegionsДокумент3 страницыChords RegionswillygopeОценок пока нет
- A 10-Year Old Girl With Neck Pain: Clinical HistoryДокумент4 страницыA 10-Year Old Girl With Neck Pain: Clinical HistorywillygopeОценок пока нет
- 1208 Case 2Документ4 страницы1208 Case 2willygopeОценок пока нет
- 1009 Case 1Документ4 страницы1009 Case 1willygopeОценок пока нет
- 1008 Case 2Документ4 страницы1008 Case 2willygopeОценок пока нет
- 1208 Case 1Документ2 страницы1208 Case 1willygopeОценок пока нет
- 1108 Case 1Документ2 страницы1108 Case 1willygopeОценок пока нет
- 1108 Case 2Документ4 страницы1108 Case 2willygopeОценок пока нет
- 0909 Case 2Документ2 страницы0909 Case 2willygopeОценок пока нет
- 0809 Case 2Документ4 страницы0809 Case 2willygopeОценок пока нет
- 1008 Case 1Документ4 страницы1008 Case 1willygopeОценок пока нет
- 0909 Case 1Документ4 страницы0909 Case 1willygopeОценок пока нет
- 0610case1 Metastatic MelanomaДокумент4 страницы0610case1 Metastatic MelanomawillygopeОценок пока нет
- 0709 Case 2Документ4 страницы0709 Case 2willygopeОценок пока нет
- A 7-Year-Old Boy Dying of Acute Encephalopathy: Case History Autopsy FindingsДокумент4 страницыA 7-Year-Old Boy Dying of Acute Encephalopathy: Case History Autopsy FindingswillygopeОценок пока нет
- 0609 Case 1Документ4 страницы0609 Case 1willygopeОценок пока нет
- 0609 Case 2Документ2 страницы0609 Case 2willygopeОценок пока нет
- 0409 Case 2Документ4 страницы0409 Case 2willygopeОценок пока нет
- 0410case1 GBM With PNETДокумент4 страницы0410case1 GBM With PNETwillygopeОценок пока нет
- 0510 Case 1Документ2 страницы0510 Case 1willygopeОценок пока нет
- 0509 Case 1Документ4 страницы0509 Case 1willygopeОценок пока нет
- A 24-Year-Old Male With Headaches: Clinical HistoryДокумент4 страницыA 24-Year-Old Male With Headaches: Clinical HistorywillygopeОценок пока нет
- Nymphomaniac: Vol. I: by Lars Von TrierДокумент57 страницNymphomaniac: Vol. I: by Lars Von TrierY LОценок пока нет
- MAX3-ONE THERMO-SVC Manual RT43ENSW5 XPEДокумент65 страницMAX3-ONE THERMO-SVC Manual RT43ENSW5 XPECesar Calderon Gr100% (2)
- The Generalized Correlation Method For Estimation of Time Delay-3c4Документ8 страницThe Generalized Correlation Method For Estimation of Time Delay-3c4Abin BabyОценок пока нет
- CORRELATION RANK COEFFICIENTДокумент23 страницыCORRELATION RANK COEFFICIENTSomhita Chakraborty100% (3)
- Atom ChemistryДокумент14 страницAtom ChemistryPriscilla TanОценок пока нет
- Optimal Diet and Furniture Shop ProductionДокумент7 страницOptimal Diet and Furniture Shop ProductionBeatriz ArevaloОценок пока нет
- L3 ProbabilityДокумент22 страницыL3 ProbabilitySidarthОценок пока нет
- Introduction To Social Return On InvestmentДокумент12 страницIntroduction To Social Return On InvestmentSocial innovation in Western Australia100% (2)
- Plan Clock ProjectДокумент2 страницыPlan Clock Projectapi-209169836Оценок пока нет
- Ratio Analysis of Financial StatementsДокумент34 страницыRatio Analysis of Financial StatementsShakti TandonОценок пока нет
- 19-20 Math Section A1 Answer KeyДокумент5 страниц19-20 Math Section A1 Answer KeyChad Aristo CHIMОценок пока нет
- VECV Infra NormsДокумент10 страницVECV Infra Normsvikrantnair.enarchОценок пока нет
- Basic Probability Part 6 PDFДокумент7 страницBasic Probability Part 6 PDFboss BossОценок пока нет
- 11 Abm Research g3Документ18 страниц11 Abm Research g3Ergil Villanueva RomualdoОценок пока нет
- Defense of Collection Cases Edelman, (2007)Документ43 страницыDefense of Collection Cases Edelman, (2007)Jillian Sheridan100% (2)
- Anodizing aluminium enhances corrosion resistanceДокумент49 страницAnodizing aluminium enhances corrosion resistanceAnwaar Ul HaqОценок пока нет
- As Sci 10 SLG Week 2 Quarter IiДокумент3 страницыAs Sci 10 SLG Week 2 Quarter IiDarwin BondocОценок пока нет
- WCB Fallers BuckersДокумент125 страницWCB Fallers BuckersMario FernandesОценок пока нет
- Sequences PDFДокумент26 страницSequences PDFcheng linОценок пока нет
- Test 1Документ12 страницTest 1kashif aliОценок пока нет
- MCS in NepalДокумент8 страницMCS in NepalSourabh InaniОценок пока нет
- Nelson2014 Hialuronidase em HematomasДокумент3 страницыNelson2014 Hialuronidase em HematomasPaula AzevedoОценок пока нет
- Johann Sebastian Bach Raaf Hekkema: Suites BWV 1007-1012Документ22 страницыJohann Sebastian Bach Raaf Hekkema: Suites BWV 1007-1012Stanislav DimОценок пока нет
- Knight EnchanterДокумент2 страницыKnight EnchanterGiampiero Magalli100% (1)
- Modeling of Hydro PlantДокумент57 страницModeling of Hydro Plantshift incharge ikhepОценок пока нет
- Sp1u C0Документ4 страницыSp1u C0Драган РодићОценок пока нет
- Test Your Knowledge: QuestionsДокумент5 страницTest Your Knowledge: QuestionsRITZ BROWNОценок пока нет
- CSI DHL Resilience360 Google Case Study enДокумент2 страницыCSI DHL Resilience360 Google Case Study enBona HarahapОценок пока нет
- Ista 2BДокумент5 страницIsta 2Bduygu9merve100% (1)
- Rothesay Castle and The Hovering HamДокумент7 страницRothesay Castle and The Hovering Hamgrahamsmithpr43zbОценок пока нет