Академический Документы
Профессиональный Документы
Культура Документы
Lecture Dynamics PDF
Загружено:
Ankan PalОригинальное название
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Lecture Dynamics PDF
Загружено:
Ankan PalАвторское право:
Доступные форматы
Batch: Jan - May 2008 R.
Ganesh Narayanan 1
Engineering Mechanics Dynamics
Instructor
R. Ganesh Narayanan
Department of Mechanical Engineering
IIT Guwahati
Batch: Jan - May 2008 R. Ganesh Narayanan 2
-These lecture slides were prepared and used by me to conduct lectures for 1
st
year
B. Tech. students as part of ME 101 Engineering Mechanics course at IITG.
- Theories, Figures, Problems, Concepts used in the slides to fulfill the course
requirements are taken from the following textbooks
- Kindly assume that the referencing of the following books have been done in this slide
- I take responsibility for any mistakes in solving the problems. Readers are requested
to rectify when using the same
- I thank the following authors for making their books available for reference
R. Ganesh Narayanan
1. Vector Mechanics for Engineers Statics & Dynamics, Beer & Johnston; 7
th
edition
2. Engineering Mechanics Statics & Dynamics, Shames; 4
th
edition
3. Engineering Mechanics Statics Vol. 1, Engineering Mechanics Dynamics Vol. 2,
Meriam & Kraige; 5
th
edition
4. Schaums solved problems series Vol. 1: Statics; Vol. 2: Dynamics, Joseph F. Shelley
R. Ganesh Narayanan 3
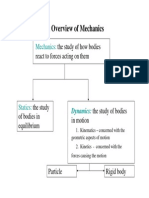
Dynamics Kinematics of particles
Analysis of bodies in motion
1) Kinematics
- study of the geometry of motion
- relate displacement, velocity, acceleration, and time without reference to
the source/cause of motion
2) Kinetics
- study of the relations existing between the forces acting on a body, the
mass of the body, and the motion of the body
- To predict the motion caused by given forces or to determine the forces
required to produce a given motion.
Rectilinear motion: position, velocity, and acceleration of a particle as it moves
along a straight line
Curvilinear motion: position, velocity, and acceleration of a particle as it moves
along a curved line
R. Ganesh Narayanan 4
Rectilinear motion of particle
Position
Position coordinate of a particle is defined by positive or negative distance
of particle from a fixed origin on the line.
The motion of a particle is known if the position
coordinate for particle is known for every value of
time t. Motion of the particle may be expressed in the
form of a function, e.g.,
3 2
6 t t x =
or in the form of a graph x vs. t.
R. Ganesh Narayanan 5
Velocity
Consider particle which occupies position P at time t
and P at t+t,
Average velocity
Instantaneous velocity
t
x
=
x
t
v
t
= =
0
lim
Instantaneous velocity may be positive or negative.
Magnitude of velocity is referred to as particle
speed.
From the definition of a derivative,
dt
dx
t
x
v
t
=
=
0
lim
e.g.,
2
3 2
3 12
6
t t
dt
dx
v
t t x
= =
=
R. Ganesh Narayanan 6
Consider particle with velocity v at time t and
v at t+t,
Instantaneous acceleration
t
v
a
t
= =
0
lim
Acceleration
From the definition of a derivative,
t t v
dv v
3 12 e.g.
2
2
t
dt
dv
a 6 12
= =
=
dt
x d
dt t
a
t
lim
2
0
= =
=
a = v (dv/dx)
R. Ganesh Narayanan 7
Motion curves
0 < t < 2
2< t < 4
4 < t < 6
t > 6
Particle is moving
in straight line only
and not along the
curves
R. Ganesh Narayanan 8
Motion of a particle is known if position is known for all time t
Typically, conditions of motion are specified by the type of
acceleration experienced by the particle. Determination of velocity
and position requires two successive integrations.
Acceleration given as a function of time, a = f(t):
( ) ( )
( )
( ) ( ) ( )
( ) ( )
( )
( ) ( ) ( )
= = = =
= = = = =
t t t x
x
t t t v
v
dt t v x t x dt t v dx dt t v dx t v
dt
dx
dt t f v t v dt t f dv dt t f dv t f a
dt
dv
0
0
0
0
0
0
0
0
Acceleration given as a function of position, a = f(x):
( )
( )
( )
( ) ( ) ( )
= = =
= = = = =
x
x
x
x
x v
v
dx x f v x v dx x f dv v dx x f dv v
x f
dx
dv
v a
dt
dv
a
v
dx
dt
dt
dx
v
0 0 0
2
0
2
1
2
2
1
or or
a = v (dv/dx)
dt = dx/v; Integration gives relation between x and t
Relate V-t; x-t
Relate V-x; x-t
R. Ganesh Narayanan 9
Acceleration given as a function of velocity, a = f(v):
( )
( ) ( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
( )
=
= = = =
=
= = = =
t v
v
t v
v
t x
x
t v
v
t t v
v
v f
dv v
x t x
v f
dv v
dx
v f
dv v
dx v f a
dx
dv
v
t
v f
dv
dt
v f
dv
dt
v f
dv
v f a
dt
dv
0
0 0
0
0
0
0
Relate v-t, x-v
R. Ganesh Narayanan 10
kv a =
Brake mechanism used to reduce gun recoil consists of
piston attached to barrel moving in fixed cylinder filled
with oil. As barrel recoils with initial velocity v
0
, piston
moves and oil is forced through orifices in piston,
causing piston and cylinder to decelerate at rate
proportional to their velocity.
Determine v(t), x(t), and v(x).
Integrate a = dv/dt = -kv to find v(t).
( )
( )
kt
v
t v
dt k
v
dv
kv
dt
dv
a
t t v
v
= = = =
0
0
ln
0
( )
kt
e v t v
=
0
R. Ganesh Narayanan 11
Integrate v(t) = dx/dt to find x(t).
( )
( )
( )
t
kt
t
kt
t x
kt
e
k
v t x dt e v dx
e v
dt
dx
t v
0
0
0
0
0
0
1
(
= =
= =
( ) ( )
kt
e
k
v
t x
= 1
0
Integrate a = v dv/dx = -kv to find v(x).
kx v v
dx k dv dx k dv kv
dx
dv
v a
x v
v
=
= = = =
0
0
0
kx v v =
0
R. Ganesh Narayanan 12
The motion of the slider A is defined by the relation
x= 500sinkt, where x and t are expressed in
millimeters and seconds, respectively, and k is a
constant. Knowing that k = 10 rad/s, determine the
position, the velocity, and the acceleration of slider A
when t = 0.05 s.
Beer/johnston, 11.3
x = 500sinkt
v = dx/dt = 500 k cos kt
a = dv/dt = -500k
2
sin kt
For k= 10 rad/s; t = 0.05s; kt = 0.5 rad
x = 500sinkt = 500 sin 0.5= 239.7 mm
v = dx/dt = 500 k cos kt = 4387.9 mm/s
a = dv/dt = -500k
2
sin kt = -23971 mm/s
2
R. Ganesh Narayanan 13
Beer/johnston, 11.20
The acceleration of a particle is defined by the relation a = k (1-e
-x
) where k is a
constant. Knowing that the velocity of the particle is v = +9 m/s when x = -3m and
that the particle comes to rest at the origin, determine (a) the value of k, (b) the
velocity of the particle when x = -2 m.
Limits: v = 9; x = -3, v = 0; x = 0
vdv = adx = k(1-e
-x
) dx
x: -3 -2 0
V: 9 find 0
a)
R. Ganesh Narayanan 14
At x = -2 m; v = 2.2440 (-2+e
2
-1)
1/2
= 4.70 m/s
x: -3 -2 0
V: 9 find 0
Implies at x = -2 m; v = + 4.70 m/s
Or limits can also be from
+9 to v & -3 to x
b)
R. Ganesh Narayanan 15
Beer/johnston, 11.23
The acceleration of slider A is defined by the relation
a= 2k k2v2, where a and v are expressed in m/s2
and m/s, respectively, and k is a constant. The system
starts at time t = 0 with x = 1.5 m and v = 0. Knowing
that x = 1.2 m when t = 0.2 s, determine the value of k.
At t = 0; x = 1.5 m, v = 0
At t = 0.2 s; x = 1.2 m, v = unknown; find k
We know limits for x, t & hence x, t should be related
Integrate this from 0 to t & 0 to v
R. Ganesh Narayanan 16
dx = vdt = -k sin (2kt) dt Relating x, t
Integrate this from x = 1.5 to 1.2 & t = 0 to 0.2
R. Ganesh Narayanan 17
Uniform rectilinear motion
For particle in uniform rectilinear motion, the acceleration is zero
and the velocity is constant.
vt x x
vt x x
dt v dx
v
dt
dx
t x
x
+ =
=
=
= =
0
0
0
0
constant
Earlier v was function of t
(This eqn can be used only if velocity is
said to be uniform)
R. Ganesh Narayanan 18
Uniformly Accelerated Rectilinear Motion
Here the acceleration of the particle is constant; e.g., free falling body
at v v
at v v dt a dv a
dt
dv
t v
v
+ =
= = = =
0
0
0
0
constant
( )
2
2
1
0 0
2
2
1
0 0
0
0 0
0
at t v x x
at t v x x dt at v dx at v
dt
dx
t x
x
+ + =
+ = + = + =
1)
2)
3)
( ) ( )
( )
0
2
0
2
0
2
0
2
2
1
2
constant
0 0
x x a v v
x x a v v dx a dv v a
dx
dv
v
x
x
v
v
+ =
= = = =
(These eqns can be used only if acceleration is said to be uniform)
R. Ganesh Narayanan 19
Motion of several particles
Particles moving along straight line, time
should be measured from same instant &
displacement should be measured from same
origin and in same line only
= =
A B A B
x x x
relative position of B with
respect to A
A B A B
x x x + =
= =
A B A B
v v v
relative velocity of B with
respect to A
A B A B
v v v + =
= =
A B A B
a a a
relative acceleration of B
with respect to A
A B A B
a a a + =
V
B/A
is +ve means B is moving in
positive direction when seen
from A
R. Ganesh Narayanan 20
Dependent motion
Motion of one particle depends on motion of other particle
Position of block B depends on position of block A. Since
rope is of constant length, sum of lengths of segments of
rope must be a constant.
= +
B A
x x 2
constant
Positions of three blocks are dependent.
= + +
C B A
x x x 2 2
constant
x
B
= -1/2 (x
A
)
These are linearly related positions
0 2 2 or 0 2 2
0 2 2 or 0 2 2
= + + = + +
= + + = + +
C B A
C B A
C B A
C B A
a a a
dt
dv
dt
dv
dt
dv
v v v
dt
dx
dt
dx
dt
dx
R. Ganesh Narayanan 21
An airplane begins its take-off run at A with zero
velocity and a constant acceleration a. Knowing that it
becomes airborne 30 s later at B and that the
distance AB is 823 m, determine (a) the acceleration
a, (b) the takeoff velocity vB.
Beer/Johnston, 11.33
Initial: VA = 0; xA = 0; uniform acceleration
V = VA + at = at; X = X0+V0t +1/2 at
2
= at
2
At B, XB = 823 m; t = 30 s => a = 2Xb/t
2
= 2(823)/30
2
= 1.83 m/s
2
V = 1.83 x 30 = 54.9 m/s
R. Ganesh Narayanan 22
A stone is dropped from well shaft. Three secs after the
stone is dropped, the sound of the stone hitting the
bottom of the shaft is heard. Find depth of the well.
Sound velocity = 1120 ft/s
Stone: x = g t
2
= (32.2) t
2
Sound: x1 = vt1 = 1120 t1
t+t1 = 3 sec => t1= 3-t
Also, x = x1
16.1t
2
= 1120 (3-t) => t = 2.89 s
t1 = 3-2.89 = 0.11 s
Depth of well, x = (32.2) 2.89
2
= 134 ft
Shelley
R. Ganesh Narayanan 23
Two rockets are launched at a fireworks performance. Rocket A
is launched with an initial velocity v0 and rocket B is launched
4 s later with the same initial velocity. The two rockets are
timed to explode simultaneously at a height of 73 m, as A is
falling and B is rising. Assuming a constant acceleration g =
9.81 m/s
2
determine (a) the initial velocity v0, (b) the velocity of
B relative to A at the time of the explosion.
Beer/Johnston, 11.40
Rocket A Rocket B
X = 0, v=v0, t = 0
vA =v0 gt
xA = v0 t-1/2 gt
2
X = 0, v=v0, t = tB = 4 s
VB = v0 g (t-tB)
xB = v0 (t-tB)-1/2 g (t-tB)
2
Explosion occurs at same height, xA = xB = 73 m, at t = tE (say)
R. Ganesh Narayanan 24
Substitute this V0 in XA at t = tE; solve for tE.
Solve for tE at tB = 4 s, xA = 73 m; g =9.81m/s
2
tE = 6.35 s
1)
2)
R. Ganesh Narayanan 25
Meriam/Kraige, 2/25
A
S
V0
A car is travelling at constant speed of 100 km/h.
when 6% incline is encountered, the driver does not
change the throttle setting and the car decelerates
at const. rate of (g sin). Find the speed of the car
a) 10 secs after passing point A, (b) s = 100 m
V0 = 100x5/18 = 27.77 m/s
a = -g sin = -9.81 sin (tan
-1
6/100) = -0.588 m/s
2
a) V = V0+at = 27.77-0.588 (10) = 21.9 m/s
b) V
2
= V0
2
+2a (s-s0) = 27.77
2
+2 (-0.588) (100) = 25.6 m/s
R. Ganesh Narayanan 26
Block C starts from rest and moves down with a constant
acceleration. Knowing that after block A has moved 0.5 m its
velocity is 0.2 m/s, determine (a) the accelerations of A and C, (b)
the velocity and the change in position of block B after 2 s.
Beer/Johnston, 11.48
+ve
Block/cable A: XA+(XA-XB) = Const;
2VA-VB = 0 => VA = VB/2; aA=aB/2
Block/cable B: 2XB+XC = const
2VB+VC = 0 => VC = -2 VB; aC = -2aB
a)
b)
R. Ganesh Narayanan 27
Collar A starts from rest at t = 0 and moves upward with a constant
acceleration of 9 cm/s2. Knowing that collar B moves downward with
a constant velocity of 45.7 cm/s, determine (a) the time at which the
velocity of block C is zero, (b) the corresponding position of block C.
Beer/Johnston, 11.59
xB
xA
xC
+ve
R. Ganesh Narayanan 28
R. Ganesh Narayanan 29
Curvilinear motion of particles
Particle moving along a curve other than a straight line is in curvilinear
motion. Position of particle here is defined by position vector.
Position vector of a particle at time t is defined by a vector between
origin O of a fixed reference frame and the position occupied by
particle.
Consider particle which occupies position P defined by r at time t and
P defined by r at t + t
v = lim
t-0
(r/t)
Tangent to particle
path; t becomes
smaller
Instantaneous velocity =
V=dr/dt
Magnitude of V, v = ds/dt = speed of particle
R. Ganesh Narayanan 30
x
y
z
v
V
Q
Q
v
x
y
z
v
Q
a
a = lim
t-0
v/t = dv/dt
Instantaneous acceleration =
R. Ganesh Narayanan 31
Derivative of vector functions
Let P be a vector function of scalar variable u,
( ) ( )
u
u P u u P
u
P
du
P d
u u
+
=
=
0 0
lim lim
Change in u defines the path traveled by particle
Derivative of vector sum,
( )
du
Q d
du
P d
du
Q P d
+ =
+
Derivative of product of scalar and vector functions,
( )
du
P d
f P
du
df
du
P f d
+ =
Derivative of scalar product and vector product,
( )
( )
du
Q d
P Q
du
P d
du
Q P d
du
Q d
P Q
du
P d
du
Q P d
+ =
+ =
R. Ganesh Narayanan 32
Rectangular components of vector components
When position vector of particle P is given by its
rectangular components,
k z j y i x r
+ + =
Velocity vector,
k v j v i v
k z j y i x k
dt
dz
j
dt
dy
i
dt
dx
v
z y x
+ + =
+ + = + + =
+ve value of vx indicates vector
component is towards right
Acceleration
vector,
2
2
k a j a i a
k
dt
z d
j
dt
y d
i
dt
x d
a
z y x
+ + =
+ + =
2 2 2
2
2
ax depends on t, x and/or vx only
R. Ganesh Narayanan 33
Movement of helicopter w.r.t. ship sailing in ocean
Ocean fixed frame of reference; ship moving frame of reference
Motion relative to frame in translation
Position vectors for particles A and B with respect to
the fixed frame of reference Oxyz are
.
and
B
A
r
r
Vector joining A and B defines the position of
B with respect to the moving frame Axyz and
r r r
A B A B
+ =
A B
r
velocity of B relative to A.
Differentiating twice,
acceleration of B relative
to A.
A B A B
v v v
+ =
A B A B
a a a
+ =
=
A B
v
=
A B
a
Absolute motion of B can be obtained by combining motion of A with relative
motion of B with respect to moving reference frame attached to A.
R. Ganesh Narayanan 34
A ski jumper starts with a horizontal take-off
velocity of 25 m/s and lands on a straight landing
hill inclined at 30. Determine (a) the time between
take-off and landing, (b) the length d of the jump,
(c) the maximum vertical distance between the
jumper and the landing hill.
Beer/Johnston, 11.99
a) t = 2V
0
tan 30/g = 2(25) tan 30/9.81 = 2.94 s
b) d = V
0
t/cos 30 = 25 (2.94)/cos 30 = 85 m
c) hmax = V
0
2
tan
2
30/2g = (25)
2
tan
2
30/2x9.81 = 10.62 m
R. Ganesh Narayanan 35
The three-dimensional motion of a particle is defined by the position vector
Determine the magnitudes of the velocity and acceleration of the particle. (The
space curve described by the particle is a conic helix).
Beer/Johnston
R. Ganesh Narayanan 36
A rocket runs out of fuel in the position shown and
continues in unpowered flight above the atmosphere. If
its velocity in this position is 600 m/s, find the maximum
height reached and time t to reach it.; g = 9.81 m/s2
30
600
Meriam/kraige, 2/68
Vy = Vy0+at = 600 sin 60-9.81t; t = 53 sec
Vy
2
= Vy
2
+2ay => 0 = (600 sin 60)
2
-2(9.81)y => y = 13761 m
At an intersection car A is traveling south with a
velocity of 40 km/h when it is struck by car B
traveling 30 north of east with a velocity of 48
km/h. Determine the relative velocity of car B with
respect to car A.
Beer/Johnston, 11.121
R. Ganesh Narayanan 37
R. Ganesh Narayanan 38
A = 80 km/h
B = 60 km/h
25
The velocities of commuter trains A and B are as
shown. Knowing that the speed of each train is constant
and that B reaches the crossing 10 min after A passed
through the same crossing, determine (a) the relative
velocity of B with respect to A, (b) the distance between
the fronts of the engines 3 min after A passed through
the crossing.
Find VB/A
Find
R. Ganesh Narayanan 39
Tangential & normal components of velocity and acceleration
e
n
= de
t
/ d
V =ve
t
V = ve
t
e
t
, e
n
are unit vectors
a = dV/dt = dv/dt (e
t
) + v de
t
/dt
a = dv/dt (e
t
) + v
2
/ (e
n
)
a
t
a
n
radius of curvature of the path followed
a
t
is +ve => increase in speed of particle => points in
direction of motion
a
n
always points along the radius of curvature
In plane:
R. Ganesh Narayanan 40
In space:
Relations for tangential and normal acceleration also
apply for particle moving along space curve.
v dv v dv
2 2
a
dt
a e e
dt
a
n t n t
= = + =
Plane containing tangential and normal unit vectors is
called the osculating plane.
Normal to the osculating plane is found from
Direction of e
n
is important
n t b
e e e
=
binormal e
normal principal e
b
n
=
=
Acceleration can be resolved into two components, one in tangential direction &
other in principal normal at P
R. Ganesh Narayanan 41
In cylindrical co-ordinates
Position vector,
k z e R r
R
+ =
Velocity vector,
k z e R e R
dt
r d
v
R
+ + = =
Acceleration vector,
a = dv/dt = (R-R
2
)e
R
+ (R+2R)e
+ z k
vr v
ar
a
R. Ganesh Narayanan 42
Rotation of the arm about O is defined by =
0.15t
2
where is in radians and t in seconds. Collar
B slides along the arm such that r = 0.9 - 0.12t
2
where r is in meters. After the arm has rotated
through 30
o
, determine (a) the total velocity of the
collar, (b) the total acceleration of the collar, and (c)
the relative acceleration of the collar with respect to
the arm.
Evaluate time t for = 30
o
.
s 869 . 1 rad 524 . 0 30
0.15
2
= = =
=
t
t
2
2
s m 24 . 0
s m 449 . 0 24 . 0
m 481 . 0 12 . 0 9 . 0
=
= =
= =
r
t r
t r
2
2
s rad 30 . 0
s rad 561 . 0 30 . 0
rad 524 . 0 15 . 0
=
= =
= =
t
t
R. Ganesh Narayanan 43
Calculate velocity and acceleration.
( )( )
r
r
r
v
v
v v v
r v
s r v
1 2 2
tan
s m 270 . 0 s rad 561 . 0 m 481 . 0
m 449 . 0
= + =
= = =
= =
&
&
= = 0 . 31 s m 524 . 0 v
( )( )
( )( ) ( )( )
r
r
r
a
a
a a a
r r a
r r a
1 2 2
2
2
2
2 2
2
tan
s m 359 . 0
s rad 561 . 0 s m 449 . 0 2 s rad 3 . 0 m 481 . 0
2
s m 391 . 0
s rad 561 . 0 m 481 . 0 s m 240 . 0
= + =
=
+ =
+ =
=
=
=
&
&
& &
&
& &
= = 6 . 42 s m 531 . 0 a
Motion of collar with respect to arm is rectilinear
motion
2
s m 240 . 0 = = r a
OA B
& &
R. Ganesh Narayanan 44
As cam A rotates, follower wheel B rolls without slipping on
the face of the cam. Knowing that the normal components of the
acceleration of the points of contact at C of the cam A and the
wheel B are 0.66 m/s2 and 6.8 m/s2, respectively, determine the
diameter of the follower wheel.
R. Ganesh Narayanan 45
The peripheral speed of the tooth of a 10-in.-diameter circular saw blade is 45 m/s when the
power to the saw is turned off. The speed of the tooth decreases at a constant rate, and the
blade comes to rest in 9 s. Determine the time at which the total acceleration of the tooth is
39 m/s 2.
For uniformly decelerated
motion
V0 = 45 m/s
R. Ganesh Narayanan 46
Kinetics of particles
Newtons first law and third law are sufficient for studying bodies at
rest (- statics) or bodies in motion with no acceleration
study of the relations existing between the forces acting on a body,
the mass of the body, and the motion of the body
When a body accelerates (change in velocity magnitude or direction),
Newtons second law is required to relate the motion of the body to the
forces acting on it
Newtons Second Law: If the resultant force acting on a particle is not
zero, the particle will have an acceleration proportional to the magnitude
of resultant and in the direction of the resultant.
Ist law: A particle remains at rest or continues to move with uniform velocity
(in a straight line with const. speed) if there is no unbalanced force acting on it
R. Ganesh Narayanan 47
Consider a particle subjected to constant forces,
m
a
F
a
F
a
F
mass, constant
3
3
2
2
1
1
= = = =
Characteristic of
particle considered
When a particle of mass m is acted upon by a force F, the
acceleration of the particle must satisfy
a m F
=
If force acting on particle is zero, particle will not accelerate, i.e., it will
remain stationary or continue on a straight line at constant velocity
Newtons Ist law
Magnitudes of F & a are proportional; F & a vectors are in
same direction
Body subjected to several forces, F = ma
R. Ganesh Narayanan 48
Linear momentum of a particle
Replacing the acceleration by the derivative of the velocity yield
( )
particle the of momentum linear
=
= =
=
L
dt
L d
v m
dt
d
dt
v d
m F
L - Same direction as that of velocity of particle mv (vector)
Mass is constant
L = mv => F = dL/dt
The rate of change of linear momentum (dL/dt) is zero when F = 0 => If
the resultant force acting on the particle is zero, linear momentum of the
particle L is constant, in magnitude and direction
This is called as Principle of conservation of momentum => another version
of Newtons 1
st
law
Unit: kg. (m/s)
R. Ganesh Narayanan 49
Equations of motion
Newtons second law provides
a m F
=
( ) ( )
z m F y m F x m F
ma F ma F ma F
k a j a i a m k F j F i F
z y x
z z y y x x
z y x z y x
= = =
= = =
+ + = + +
0 0 - W
For a projectile without air
resistance
For tangential and normal components,
2
v
m F
dt
dv
m F
ma F ma F
n t
n n t t
= =
= =
In rectangular components,
R. Ganesh Narayanan 50
Dynamic equilibrium
Alternate expression of Newtons second law,
ector inertial v a m
a m F 0
=
Particle is in equilibrium under given forces and inertia vector
called Dynamic equilibrium
In coplanar force system, all forces can be made into closed vector
polygon and can be solved (OR)
Sum of force components including inertia vector can be equated to zero
Fx = 0; Fy = 0
Rectangular components
R. Ganesh Narayanan 51
Tangential components can also be
used, -ma
t
& -ma
n
Tangential component: Measure of resistance of
particle to change in speed
Normal component: Tendency of particle to leave
its path
Inertia vectors or inertia forces are measure of resistance
that particles offer for motion
These forces are not considered like g, contact forces etc. and
hence dynamic equilibrium method is not used
R. Ganesh Narayanan 52
The two blocks shown start from rest. The horizontal
plane and the pulley are frictionless, and the pulley is
assumed to be of negligible mass. Determine the
acceleration of each block and the tension in the cord.
Beer/Johnston, 12.3
Write the kinematic relationships for the dependent motions and
accelerations of the blocks.
A B A B
a a x y
2
1
2
1
= =
Apply Newtons II law to blocks A, B, pulley C
Write equations of motion for blocks and pulley:
:
A A x
a m F =
( )
A
a T kg 100
1
=
:
B B y
a m F =
( )( ) ( )
( )
B
B
B B B
a T
a T
a m T g m
kg 300 - N 2940
kg 300 s m 81 . 9 kg 300
2
2
2
2
=
=
=
x
y
T2 = 2940-150 aA
R. Ganesh Narayanan 53
: 0 = =
C C y
a m F
0 2
1 2
= T T
Put T1, T2 in above equn., 2940-150aA-2 (100aA) = 0; aA = 8.4 m/s2
aB = 8.4/2 = 4.2 m/s2; T1 = 100 (8.4) = 840 N
T2 = 2 (840) 1680 N
R. Ganesh Narayanan 54
Beer/Johnston, 12.14
A B A light train made up of two cars is traveling at 88 km/h
when the brakes are applied to both cars. Knowing that car
A has a weight of 24947.56 kg and carB has a weight of
19958 kg and that the braking force is 31137.5 N on each
car, determine (a) the distance traveled by the train before it
comes to a stop, (b) the force in the coupling between the
cars while the train is slowing down.
88 km/h
Consider Fb as braking force
Fb
Find ax
(a) Relate ax to Xf by ax = v (dv/dx); Apply BCs and by integration of x
and v; Find Xf
Fb Fb
Fb
Fc
A
(b) Find Fc from this
R. Ganesh Narayanan 55
A 2-kg ball revolves in a horizontal circle as shown at a
constant speed of 1.5 m/s. Knowing that L = 600 mm,
determine (a) the angle that the cord forms with the
vertical, (b) the tension in the cord.
12.36
T
W
Fy = m (ay) = 0 =>T cos -w = 0
Fx = m (ax) => T sin = ma
ma
a is towards circle center = v
2
/ = v
2
/Lsin
Solve these equns. and get , t
R. Ganesh Narayanan 56
A curve in a speed track has a radius of 200 m and a rated
speed of 180 km/h. Knowing that a racing car starts
skidding on the curve when traveling at a speed of 320
km/h, determine (a) the banking angle , (b) the coefficient
of static friction between the tires and the track under the
prevailing conditions
12.53
Rated speed is the speed at which a car should travel if no lateral
friction force is to be exerted on its wheels
Put F=0 and find
Find from = F/N
w
N
F
X
Y
ma
R. Ganesh Narayanan 57
Angular momentum of particle
moment of momentum or the angular
momentum of the particle about O.
= =
V m r H
O
is perpendicular to plane containing
O
H V m r and
z y x
O
mv mv mv
z y x
k j i
H
=
We have Hx, Hy, Hz
Derivative of angular momentum with respect to time,
It follows from Newtons second law that the sum of the moments about O of
the forces acting on the particle is equal to the rate of change of the angular
momentum of the particle about O
=
=
+ = + =
O
O
M
F r
a m r V m V V m r V m r H
0
R. Ganesh Narayanan 58
Eqs of Motion in Radial & Transverse Components
( )
Consider particle at r and , in polar coordinates,
( )
r r m ma F
r
r
m ma F
r r
2
= =
= =
2
+
Motion under central force
When only force acting on particle is directed toward or
away from a fixed point O, the particle is said to be moving
under a central force.
Since the line of action of the central force passes
through O,
and 0
= =
O O
H M
O
constant
= =
H V m r
rmv sin = r
0
mv
0
sin
0
R. Ganesh Narayanan 59
The 2.7 kg collar B slides on the frictionless arm AA.
The arm is attached to drum D and rotates about O in
a horizontal plane at the rate = 0.8t,
where and t are expressed in rad/s and seconds,
respectively. As the arm-drum assembly rotates, a
mechanism within the drum releases cord so that the
collar moves outward from O with a constant speed of
0.457 m/s. Knowing that at t = 0, r = 0, determine the
time at which the tension in the cord is equal to the
magnitude of the horizontal force exerted on B by arm
AA.
dr/dt = r = 0.457 m/s; dr = 0.457 dt => r = 0.457t; r = 0
0
r
0
t
(
)
( )
r r m ma F
r
r
m ma F
r r
2
= =
= =
2
+
a
r
= -0.292 t
3
m/s2; a
= 1.09 m/s2
R. Ganesh Narayanan 60
T
Q
=
M a
r
M a
T = Q => -m a
r
= m a
0.292 t
3
= 1.09 => t = 1.66 s
R. Ganesh Narayanan 61
Previously, problems dealing with the motion of particles were
solved through the fundamental equation of motion, F = ma
We introduce two additional methods of analysis
Method of work and energy: directly relates force, mass, velocity
and displacement
Method of impulse and momentum: directly relates force, mass,
velocity, and time
Energy and momentum methods
R. Ganesh Narayanan 62
Work of the force is
dz F dy F dx F
ds F
r d F dU
z y x
+ + =
=
=
cos
Work of a force
Work is a scalar quantity, i.e., it has magnitude and sign but not direction.
force. length
Dimensions of work are Units are
( ) ( )( ) m 1 N 1 J 1 = joule
Work of finite displacement
Work of force of gravity
Work of the force exerted by a spring
Method of Work & energy
R. Ganesh Narayanan 63
Kinetic energy of particle
dv mv ds F
ds
dv
mv
dt
ds
ds
dv
m
dt
dv
m ma F
t
t t
=
= =
= =
Consider a particle of mass m acted upon by force, F
Integrating from A
1
to A
2
,
energy kinetic mv T T T U
mv mv dv v m ds F
v
v
s
s
t
= = =
= =
2
2
1
1 2 2 1
2
1
2
1
2
2
2
1
2
1
2
1
The work of the force F is equal to the change in kinetic energy
of the particle => Principle of work & energy
KE:
Unit: Nm or Joule
Scalar quantity
T
2
= T
1
+ U (1-2)
R. Ganesh Narayanan 64
To determine velocity of pendulum bob
at A
2
. Consider work & kinetic energy.
Force P acts normal to path and does no work.
gl v
v
g
W
Wl
T U T
2
2
1
0
2
2
2
2 2 1 1
=
= +
= +
T
2
T
1
Velocity found without determining expression for acceleration and
integrating
All quantities are scalars and can be added directly
Forces which do no work are eliminated from the problem.
Advantages:
R. Ganesh Narayanan 65
Principle of work and energy cannot be applied to
directly to determine the acceleration of the
pendulum bob
Calculating the tension in the cord requires
supplementing the method of work and energy with
an application of Newtons second law
As the bob passes through A
2
,
W
l
gl
g
W
W P
l
v
g
W
W P
a m F
n n
3
2
2
2
= + =
=
=
F
t
= m a
t
= 0
Problem with more particles: KE
can be obtained for each particle
separately and KE can be added for
all particles
T
1
+ U (1-2) = T
2
T arithmetic sum of the KEs of
particles involved; U (1-2) = work of
all the forces acting on the particles
R. Ganesh Narayanan 66
Power: Rate at which work is done
Power = dU/dt = F.dr/dt = F.v
Unit: Nm/s
Efficiency = Power output / Power input < 1
R. Ganesh Narayanan 67
Two blocks are joined by an inextensible cable as
shown. If the system is released from rest, determine
the velocity of block A after it has moved 2 m. Assume
that the coefficient of friction between block A and the
plane is
k
= 0.25 and that the pulley is weightless and
frictionless.
Apply the principle of work and energy separately to
blocks A and B.
( )( )
( )
( ) ( )
( ) ( )( ) ( )
2
2
1
2
2
1
2 2 1 1
2
kg 200 m 2 N 490 m 2
m 2 m 2 0
:
N 490 N 1962 25 . 0
N 1962 s m 81 . 9 kg 200
v F
v m F F
T U T
W N F
W
C
A A C
A k A k A
A
=
= +
= +
= = = =
= =
+ ve
R. Ganesh Narayanan 68
( )( )
( ) ( )
( ) ( )( ) ( )
2
2
1
2
2
1
2 2 1 1
2
kg 300 m 2 N 2940 m 2
m 2 m 2 0
:
N 2940 s m 81 . 9 kg 300
v F
v m W F
T U T
W
c
B B c
B
= +
= +
= +
= =
When the two relations are combined, the work of the cable forces cancel.
Solve for the velocity
( )( ) ( )( ) ( )
( )
2
2
1
2
2
1
kg 500 J 4900
kg 300 kg 200 m 2 N 490 m 2 N 2940
v
v
=
+ =
s m 43 . 4 = v
R. Ganesh Narayanan 69
A 2000-kg automobile starts from rest at point A on a
6 incline and coasts through a distance of 150 m to
point B. The brakes are then applied, causing the
automobile to come to a stop at point C, 20 m from
B. Knowing that slipping is impending during the
braking period and neglecting air resistance and
rolling resistance, determine (a) the speed of the
automobile at point B, (b) the coefficient of static
friction between the tires and the road
6
w
N
F
VA = 0; Vc = 0; w = 19620 N
U (A-B) = T
B
T
A
19620 (150) Sin 6 = (2000) (VB
2
)
VB =17.5 m/s
U (A-C) = T
C
T
A
19620 (170) Sin 6 F (20) = 0
19620 (170) Sin 6 19620 () cos 6 (20) = 0
= 0.89
R. Ganesh Narayanan 70
A 40.8 kg package is at rest on an incline when a constant
force P is applied to it. The coefficient of kinetic friction
between the package and the incline is 0.35. Knowing that the
speed of the package is 0.6m/s after it has moved 0.9 m up
the incline, determine the magnitude of the force P.
400
N
F = 0.35 N
20
50
P
T
1
= 0
N = 400 Cos 20 + P sin 50 Put N in U (1-2)
U (1-2) = T
2
T
1
=> P = 737.9 N
R. Ganesh Narayanan 71
Car B is towing car A with 4.6 m cable at a constant speed
of 9 m/s on an uphill grade when the brakes of car B are
fully applied causing it to skid to a stop. Car A, whose driver
had not observed that car B was slowing down, then strikes
the rear of car B. Neglecting air resistance and rolling
resistance and assuming a coefficient of kinetic friction of
0.9, determine the speed of car A just before the collision.
mg
F = 0.9 N
N = mg cos 5
0
F = 0.9 mg cos 5
=> d = 4.2 m
N
mg
Car B
Car A
For Car A: initial to contact
(-mg sin 5) (4.6+4.2) = m VA
2
(m) 9
2
=>
VA = 8.22 m/s
R. Ganesh Narayanan 72
Conservative forces
Potential energy
PE due to displacement; U (1-2) = Wy1 Wy2 = V1-V2
PE due to spring deformation; U (1-2) = k(x1)
2
k (x2)
2
Forces whose work done is independent of path followed; depends
only on initial and final positions => conservative forces
Concept of potential energy can be applied if the
work of the force is independent of the path
followed by its point of application.
( ) ( )
2 2 2 1 1 1 2 1
, , , , z y x V z y x V U =
For any conservative force applied on closed path
F. dr = 0
R. Ganesh Narayanan 73
Elementary work corresponding to displacement between two
neighboring points,
( ) ( )
( ) z y x dV
dz z dy y dx x V z y x V dU
, ,
, , , ,
=
+ + + =
du = -dv (x, y, z)
The elementary work of a
conservative force is exact
differential
V
z
V
y
V
x
V
F
dz
z
V
dy
y
V
dx
x
V
dz F dy F dx F
z y x
grad = |
\
|
=
|
\
|
= + +
r
Differential of a function
of several variables
Fx = -v/x; Fy = -v/y; Fz = -v/z
Depends only on position
of point of application
F = -grad V For conservative force
R. Ganesh Narayanan 74
Conservation of energy
U (1-2) = V1 V2; V POTENTIAL ENERGY
U (1-2) = T2 T1; T KINETIC ENERGY
V1 V2 = T2 T1
T1+V1 = T2+V2
When a particle moves under the action of conservative forces, the sum of
kinetic energy and potential energy of particle remains constant
T + V = CONSTANT = MECHANICAL ENERGY, E
R. Ganesh Narayanan 75
At A1; T1 = 0; V1 = Wl; T1 + V1 = Wl
At A2; T2 = (W/g) v2
2
= (W/g) (2gl) = Wl; V2 = 0
T2 + V2 = Wl
E = T + V = CONSTANT
Energy: A1 = only potential; A2 = Only kinetic
Only PE depends on elevation and not KE. So, speed is
same in A, A
R. Ganesh Narayanan 76
Particle will have same speed at A, B, C as long as weight of
particle and normal reaction of path are the two forces acting;
without friction
A B
C
Weight of particle, forces exerted by spring conservative
forces
Friction force => Non-conservative force; work done by friction
force can not be expressed as change in potential energy as it
depends on path followed by point of application
A mechanical system involving friction will have decrease in
total mechanical energy; dissipated as heat etc.
R. Ganesh Narayanan 77
A 20 N collar slides without friction along a vertical
rod as shown. The spring attached to the collar has an
undeflected length of 4 cm and a constant of 3 N/cm. If
the collar is released from rest at position 1, determine
its velocity after it has moved 6 cm. to position 2.
Position 1: ( )( )
0
0 cm N 24
cm N 24 cm 4 cm 8 cm / N 3
1
1
2
2
1
2
1
2
1
=
+ = + =
= = =
T
V V V
kx V
g e
e
PE:
KE:
Position 2:
( )( )
( )( )
2
2
2
2
2
1
2
2
2
2
1
2
2
2
1
10
20
2
1
cm N 66 120 54
cm N 120 cm 6 N 20
cm N 54 cm 4 cm 0 1 cm / N 3
v mv T
V V V
Wy V
kx V
g e
g
e
= =
= = + =
= = =
= = =
PE:
KE:
R. Ganesh Narayanan 78
Conservation of Energy:
cm N 66 cm N 24 0
2
2
2 2 1 1
= +
+ = +
v
V T V T
= s m 5 . 9
2
v
R. Ganesh Narayanan 79
A force P is slowly applied to a plate that is
attached to two springs and causes a deflection
x0. In each of the two cases shown, derive an
expression for the constant , ke in terms of k1
and k2 , of the single spring equivalent to the
given system, that is, of the single spring which
will undergo the same deflection x0 when
subjected to the same force P.
13.55
Series connection:
Force in both springs is the same = P
X0 = X1 + X2
P/Ke = P/K1 + P/K2
=> Ke = (K1.K2)/(K1+K2)
Parallel connection:
Deflection in both springs is the same = X0
P = P1 + P2 = K1 X0 + K2 X0
P = Ke X0 => Ke = K1 + K2
R. Ganesh Narayanan 80
A 750-g collar can slide along the horizontal rod
shown. It is attached to an elastic cord with an
undeformed length of 300 mm and a spring
constant of 150 N/m. Knowing that the collar is
released from rest at A and neglecting friction,
determine the speed of the collar (a) at B, (b) at E.
13.59
R. Ganesh Narayanan 81
R. Ganesh Narayanan 82
2.7 kg
K = 2627 N/m
A 2.7 kg collar can slide without friction on a vertical rod
and is held so it just touches an undeformed spring.
Determine the maximum deflection of the spring (a) if the
collar is slowly released until it reaches an equilibrium
position, (b) if the collar is suddenly released.
a) Collar in equilibrium
F = 0 => -26.5+2627X = 0
X
max
= 0.01 m
b) Collar in suddenly released
T1+V1 = T2+V2
0+0 = 0 + (-Wh+1/2x2627xh
2
)
h = 2 (26.5)/2627 = 0.02 m
R. Ganesh Narayanan 83
A spring is used to stop a 90.7 kg package which is moving
down a 20 incline. The spring has a constant k = 22 kN/m
and is held by cables so that it is initially compressed 15 cm.
Knowing that the velocity of the package is 2.4 m/s when it is
7.6 m from the spring and neglecting friction, determine the
maximum additional deformation of the spring in bringing
the package to rest.
Position 1 is at the top of the incline; position 2 is when the spring has maximum
deformation
T1 + V1 = T2 + V2
(90.7) (2.4) + [1/2 (22000) (0.15)
2
+ 890 (7.6+X) sin 20] =
0 + [0 + (22000) (X+0.15)
2
]
Where x = Deformation of the spring
Solving this, X = 0.367 m
R. Ganesh Narayanan 84
Method of impulse and momentum
Method of impulse and momentum: directly relates force, mass,
velocity, and time.
F = d (mv) / dt
Fdt = d (mv)
F dt = mv
2
- mv
1
t1
t2
mv
1
+ F dt = mv
2
t1
t2
Integral => Impulse
of force, F (Imp
1-2
)
Vector quantity;
Unit : N.s
Imp
1-2
= i F
X
dt + j F
y
dt + k F
z
dt, from t1 to t2
FX
t
t1 t2
R. Ganesh Narayanan 85
mv
1
+ F dt = mv
2
t1
t2
mv
1
+ Imp
1-2
= mv
2
The final momentum of the particle can be obtained by adding
vectorially its initial momentum and the impulse of the force
during the time interval.
Note: KE, work => scalar quantities; Momentum, impulse =>
vector quantities
R. Ganesh Narayanan 86
Several forces acting on one particle mv
1
+ Imp
1-2
= mv
2
Two or more particles
mv
1
+ Imp
1-2
= mv
2
Impulse of action and reaction forces exerted by particles cancel
out; Only the impulses of external forces need be considered
If sum of external forces is zero, then mv
1
= mv
2
. This says
that total momentum of the particles is conserved. (discussed later)
R. Ganesh Narayanan 87
Impulsive motion
Force acting on a particle during a very short time interval that is large
enough to cause a significant change in momentum is called an
impulsive force and resulting motion is called impulsive motion
When impulsive forces act on a particle,
2 1
v m t F v m
= +
When a baseball is struck by a bat, contact occurs over a short time
interval but force is large enough to change sense of ball motion
Non-impulsive forces are forces for which (F t) is small and
therefore, may be neglected; Eg., weight of body, spring force etc.
R. Ganesh Narayanan 88
Impulse motion of several particles
v
2
1
m
t F v m
= +
Second term involves only impulse and external forces
If all the external force are non-impulsive, then m v1 = m v2
This indicates that total momentum of particle is conserved, and
not energy; Eg., Two particles moving freely collide each other
R. Ganesh Narayanan 89
A 0.5 kg baseball is pitched with a velocity of 80 m/s.
After the ball is hit by the bat, it has a velocity of 120
m/s in the direction shown. If the bat and ball are in
contact for 0.15 s, determine the average impulsive
force exerted on the ball during the impact.
x
y
x component equation:
y component equation:
( ) ( ) ( )
N 58.42
40 cos 120
9.81
5 . 0
15 . 0 80
9.81
5 . 0
40 cos
2 1
=
= +
= +
x
x
x
F
F
mv t F mv
( ) ( )
N
21
.
26
40
sin
120
9.81
5 . 0
15 . 0
40 sin 0
2
=
=
= +
y
y
y
F
F
mv t F
F = 64.03 N; = 24.16
R. Ganesh Narayanan 90
The initial velocity of the block in position A is 9 m/s.
Knowing that the coefficient of kinetic friction
between the block and the plane is 0.30, determine the
time it takes for the block to reach B with zero
velocity, if (a) = 0, (b) =20.
A) = 0
t = 3.05 s
R. Ganesh Narayanan 91
b) = 20
t = 0.96 s
R. Ganesh Narayanan 92
18Mg 13Mg
72 km/hr A light train made of two cars travels at 72 km/h. The mass of
car A is 18 Mg and the mass of car B is 13 Mg. When the
brakes are suddenly applied, a constant braking force of 19
kN is applied to each car. Determine (a) the time required for
the train to stop after the brakes are applied, (b) the force in
the coupling between the cars while the train is slowing
down.
(a) Entire train: 72 km/h = 20 m/s
R. Ganesh Narayanan 93
b) Car A: mA = 18 Mg = 18x10
3
kg; t
1-2
= 16.32 s
R. Ganesh Narayanan 94
A 0.03 kg bullet is fired into an 3.6 kg wooden
block and becomes embedded in it. Knowing that
the block and bullet then move up the smooth
incline for 1.2 s before they come to a stop,
determine the magnitude of the initial velocity of
the bullet
(1)
R. Ganesh Narayanan 95
= 432 m/s
R. Ganesh Narayanan 96
Impact: Collision between two bodies which
occurs during a small time interval and during
which the bodies exert large forces on each other.
Line of Impact: Common normal to the surfaces
in contact during impact.
Central Impact: Impact for which the mass
centers of the two bodies lie on the line of impact;
otherwise, it is an eccentric impact..
Direct Central
Impact
Direct Impact: Impact for which the velocities of
the two bodies are directed along the line of
impact.
Oblique Central Impact
Oblique Impact: Impact for which one or both of
the bodies move along a line other than the line of
impact.
Impact
R. Ganesh Narayanan 97
Bodies moving in the same straight line, v
A
>v
B
.
Upon impact the bodies undergo a period of
deformation, at the end of which, they are in
contact and moving at a common velocity.
A period of restitution follows during which the
bodies either regain their original shape or remain
permanently deformed.
Wish to determine the final velocities of the
two bodies. The total momentum of the
two body system is preserved,
A second relation between the final velocities is
required.
Before impact
At maximum
deformation
After impact
VA VB
m
A
v
A
+ m
B
v
B
= m
A
v
A
+ m
B
v
B
(In scalar, same direction)
Direct central impact
R. Ganesh Narayanan 98
Period of deformation: u m Pdt v m
A A A
=
Period of restitution:
A A A
v m Rdt u m
=
During period of deformation, P is the impulse force exerted on A
by B
During period of restitution, R is the impulse force exerted on A by B
In general, R and P are different; Impulse of R < Impulse of P
1 0
= =
=
e
u v
v u
Pdt
Rdt
n restitutio of t coefficien e
A
A
Particle A
R. Ganesh Narayanan 99
Particle B
A similar analysis of particle B yields
B
B
v u
u v
e
=
Combining the relations leads to the desired
second relation between the final velocities.
( )
B A A B
v v e v v =
The relative velocity of two particles after impact can be obtained by
multiplying relative velocity of two particles before impact with e.
=> This property is used to find e of particles experimentally
m
A
v
A
+ m
B
v
B
= m
A
v
A
+ m
B
v
B
( )
B A A B
v v e v v =
+ ve sign = right motion
- ve sign = left motion
FINAL:
R. Ganesh Narayanan 100
m
A
v
A
+ m
B
v
B
= m
A
v
A
+ m
B
v
B
( )
B A A B
v v e v v =
1. Perfectly plastic impact, e =0 => v
B
= v
A
=> No period of restitution; Particles stay together after impact
Let v
B
= v
A
= v => m
A
v
A
+ m
B
v
B
= (m
A
+ m
B
) v ;
=> v can be solved
2. Perfectly elastic impact, e =1 => v
B
- v
A
= v
A
- v
B
=> Relative velocities before and after impact are equal; Impulses
received by each particle during period of deformation and
restitution are same; Particles move with same velocity but
opposite in nature
=> Total energy and total momentum conserved (not in general case)
=> v
A
and v
B
can be solved
R. Ganesh Narayanan 101
Oblique central impact
V
A
V
B
Velocities of particles are not directed along
the line of impact => Oblique impact
Final velocities V
A
and V
B
and directions
are un-known
n axis => along line of impact; t axis => common tangent
F t
-F t
Frictionless, smooth surface; Impulses due to internal forces
directed along the line of impact n axis
R. Ganesh Narayanan 102
1) Tangential component of momentum
for each particle considered separately
is conserved.
( ) ( ) ( ) ( )
t
B
t
B
t
A
t
A
v v v v
=
=
2) Normal component of total
momentum of the two
particles is conserved.
( ) ( ) ( ) ( )
n
B B
n
A A
n
B B
n
A A
v m v m v m v m
+
= +
3) Normal components of
relative velocities before and
after impact are related by the
coefficient of restitution.
( ) ( ) ( ) ( ) | |
n
B
n
A
n
A
n
B
v v e v v =
We have 4 independent equations to solve for components
of velocities of A and B after impact
Particles can move in space; no constraints
R. Ganesh Narayanan 103
One or two particles have constraints
Block constrained to move along horizontal
surface.
Final velocity of ball unknown in direction and magnitude
and unknown final block velocity magnitude. Three
equations required.
Impulses from internal forces
along the n axis and from external force
exerted by horizontal surface and directed
along the vertical to the surface.
F F
and
ext
F
R. Ganesh Narayanan 104
1) Tangential momentum of ball is
conserved.
( ) ( )
t
B
t
B
v v
=
2) Total horizontal momentum of block
and ball is conserved.
( ) ( ) ( ) ( )
x
B B A A
x
B B A A
v m v m v m v m
+
= +
3) Normal component of relative
velocities of block and ball are related
by coefficient of restitution.
( ) ( ) ( ) ( ) | |
n
B
n
A
n
A
n
B
v v e v v =
Not extension of central impact case
m
a
v
a
- Pdt cos = m
a
u; m
A
u - Rdt cos = m
A
v
A
Period of deformation Period of restitution
R. Ganesh Narayanan 105
1 0
= =
=
e
u v
v u
Pdt
Rdt
n restitutio of t coefficien e
A
A
Multiply all velocities by cos to obtain their projections on line of
impact
e = u
n
(v
A
)
n
/ (v
a
)
n
- u
n
Similar to the central impact case, e can be derived between
initial and final velocities
R. Ganesh Narayanan 106
A 20 Mg railroad car moving at a speed of 0.5 m/s to right collides
with a 35 Mg car which is at rest. If after collision 35 Mg car is
observed to move to the right at a speed of 0.3 m/s. find the coefft.
of restitution between the two cars
mAvA + mBvB = mAvA + mBvB
(20 x 0.5) + 0 = 20 x vA + (35 x 0.3)
vA = -0.025 m/s
( )
B A A B
v v e v v =
e = 0.3 (-0.025)/0.5-0 = 0.65
R. Ganesh Narayanan 107
The magnitude and direction of the velocities of
two identical frictionless balls before they strike
each other are as shown. Assuming e = 0.9,
determine the magnitude and direction of the
velocity of each ball after the impact.
( ) s m 0 . 26 30 cos = =
A
n
A
v v ( ) s m 0 . 15 30 sin = =
A
t
A
v v
( ) s m 0 . 20 60 cos = =
B
n
B
v v ( ) s m 6 . 34 60 sin = =
B
t
B
v v
( ) ( ) ( ) ( )
t
B
t
B
t
A
t
A
v v v v
=
=
We know that,
Find v
A
t,
v
B
t
( ) ( ) ( ) ( )
n
B B
n
A A
n
B B
n
A A
v m v m v m v m
+
= +
( ) ( ) ( ) ( ) | |
n
B
n
A
n
A
n
B
v v e v v =
Find v
A
n
& v
B
n
R. Ganesh Narayanan 108
Two steel blocks slide without friction on a horizontal surface;
immediately before impact their velocities are as shown.
Knowing that e = 0.75, determine (a) their velocities after
impact, (b) the energy loss during impact.
a) Put given input values and solve these two
equations; find final velocities
b) E = T1 T2
R. Ganesh Narayanan 109
Three methods for the analysis of kinetics problems:
- Direct application of Newtons second law
- Method of work and energy
- Method of impulse and momentum
Application of three methods
Select the method best suited for the problem or part of a
problem under consideration.
R. Ganesh Narayanan 110
(b) Pendulum A from A1 to A2: Apply conservation of energy
principle, find vA2 at A2
(c) A hits B: Total momentum of two pendulums is conserved; use
relation between relative velocities; find vA3, vB3 after impact
(d) B from B3 to B4: Apply conservation of energy principle to
pendulum B
(b) (c) (d)
R. Ganesh Narayanan 111
A 7.9 kg sphere A of radius 11.4 cm moving with a
velocity v0 of magnitude 1.8 m/s strikes a 0.73 kg
sphere B of radius 5 cm which was at rest. Both
spheres are hanging from identical light flexible
cords. Knowing that the coefficient of restitution is
0.8, determine the velocity of each sphere
immediately after impact.
Ball A
Ft
m
A
v
A
+
=
m
A
v
A
mAvA - Ft cos = mAvA
Ball B
Ft
=
m
B
v
B
Ft = mBvB
vA cos vB = e (-v
0
cos )
Solve three equns,
vA = +1.56 m/s; vB = 2.76 m/s
0.164
0.064
=22.9
R. Ganesh Narayanan 112
System of particles
Motion of large number of particles considered together
Application of Newtons second law for system of particles
Newtons second law for each particle P
i
in a
system of n particles,
( )
force effective
forces internal force external
1
1
=
= =
= +
= +
=
=
i i
ij i
i i i
n
j
ij i i i
i i
n
j
ij i
a m
f F
a m r f r F r
a m f F
Repeat this for n number of particles & will get n equations. The vectors m
i
a
i
are called effective forces of the particles; The external forces F
i
and internal
forces f
ij
acting on the various particles form a system equivalent to the
system of the effective forces m
i
a
i
.
R. Ganesh Narayanan 113
The external forces F
i
and internal forces f
ij
acting on the various particles
form a system equivalent to the system of the effective forces m
i
a
i
.
Summing over all the elements,
( ) ( ) ( )
= = = =
= = = =
= +
= +
n
i
i i i
n
i
n
j
ij i
n
i
i i
n
i
i i
n
i
n
j
ij
n
i
i
a m r f r F r
a m f F
1 1 1 1
1 1 1 1
R. Ganesh Narayanan 114
Since the internal forces occur in equal and opposite
collinear pairs, the resultant force and couple due to the
internal forces are zero,
( ) ( )
=
=
i i i i i
i i i
a m r F r
a m F
The system of the external forces acting on the particles and the
system of the effective forces of the particles are equipollent
NOTE: Equipollent system of vectors: F = F; Mo = Mo
R. Ganesh Narayanan 115
Linear & angular momentum
Linear momentum of the system of particles,
= =
=
= =
=
n
i
i i
n
i
i i
n
i
i i
a m v m L
v m L
1 1
1
Angular momentum about fixed point O of system of particles,
n
( )
( ) ( )
( )
=
= =
=
=
+ =
=
n
i
i i i
n
i
i i i
n
i
i i i O
i
i i i O
a m r
v m r v m r H
v m r H
1
1 1
1
F = L; Mo = Ho
Resultant of the external forces is equal to rate of change of linear momentum of the
system of particles; Moment resultant about fixed point O of the external forces is
equal to the rate of change of angular momentum of the system of particles
R. Ganesh Narayanan 116
Motion of the mass center of a system of particles
Mass center G of system of particles is defined by position vector
which satisfies
G
r
n
=
=
i
i i G
r m r m
1
Differentiating,
=
=
i
i i G
r m r m
1
n
= =
=
L v m v m
n
i
i i G
1
Differentiating,
= =
F L a m
G
This defines motion of mass center G of the
system of particles
Similarly angular momentum of a system of particles about mass
center can be obtained
R. Ganesh Narayanan 117
Conservation of momentum for a system of particles
If no external forces act on the particles of a system, then the linear
momentum and angular momentum about the fixed point O are conserved.
constant constant
0 0
= =
= = = =
O
O O
H L
M H F L
Concept of conservation of momentum also applies to the analysis of the
mass center motion
constant
= =
G
Constant
=
G
v
v m L
Similarly, H
G
= Constant
R. Ganesh Narayanan 118
Kinetic energy of system of particles
KE of system of particles is defined as sum of KEs of various
particles of the system
=
=
n
i
i i
v m T
1
2
2
1
It is convenient to consider separately the
motion of mass center G of the system and
the motion of the system relative to a moving
frame attached to G
=
+ =
n
i
i i G
v m v m
1
2
2
1
2
2
1
T
Kinetic energy is equal to kinetic energy of mass center
plus kinetic energy relative to the centroidal frame.
R. Ganesh Narayanan 119
Work-energy principle for system of particles
Principle of work and energy can be applied to each particle P
i
,
2 2 1 1
T U T = +
where represents the work done by the internal forces,
f
ij
and the resultant external force F
i
acting on P
i
.
2 1
U
Principle of work and energy can be applied to the entire system by
adding the kinetic energies of all particles and considering the
work done by all external and internal forces
Although f
ij
and f
ji
are equal and opposite, the work of these forces
will not, in general, cancel out.
If the forces acting on the particles are conservative, the work is
equal to the change in potential energy and
2 2 1 1
V T V T + = +
which expresses the principle of conservation of energy for the system of particles.
R. Ganesh Narayanan 120
Principle of impulse & momentum for system of particles
F = L; Mo = Ho
2 1
1 2
2
1
2
1
L dt F L
L L dt F
t
t
t
t
= +
=
2 1
1 2
2
1
2
1
H dt M H
H H dt M
t
t
O
t
t
O
= +
=
R. Ganesh Narayanan 121
2 1
1 2
2
1
2
1
L dt F L
L L dt F
t
t
t
t
= +
=
2 1
1 2
2
1
2
1
H dt M H
H H dt M
t
t
O
t
t
O
= +
=
The momenta of the particles at time t
1
and the impulse of the
forces from t
1
to t
2
form a system of vectors equipollent to the
system of momenta of the particles at time t
2
.
With no external forces acting, L
1
= L
2
; H
1
= H
2
The linear momentum & angular momentum of system of
particles are conserved
R. Ganesh Narayanan 122
Kinetics principles established so far were derived for
constant systems of particles, i.e., systems which neither
gain nor lose particles.
A large number of engineering applications require the
consideration of variable systems of particles, e.g., hydraulic
turbine, rocket engine, etc.
For analyses, consider auxiliary systems which consist of
the particles instantaneously within the system plus the
particles that enter or leave the system during a short time
interval. The auxiliary systems, thus defined, are constant
systems of particles.
Variable systems of particles
R. Ganesh Narayanan 123
System consists of a steady stream of particles against a vane or
through a duct.
The auxiliary system is a constant system of particles over t.
Define auxiliary system which includes particles which
flow in and out over t.
( ) | | ( ) | |
B i i A i i
t
t
v m v m t F v m v m
L dt F L
+ = + +
= +
2 1
2
1
dm
( )
A B
v v
dt
F
=
Steady stream of particles
Air flow
through duct
or blower
R. Ganesh Narayanan 124
Fluid Flowing Through a Pipe
Jet Engine
Fan
Fluid Stream Diverted by Vane
or Duct
Helicopter
Applications
R. Ganesh Narayanan 125
Systems gaining or losing mass
Define auxiliary system to include particles
of mass m within system at time t plus the
particles of mass m which enter the system
over time interval t.
The auxiliary system is a constant system of
particles.
2 1
2
1
L dt F L
t
t
= +
( ) ( )
v m v v m v m t F
a
+ + =
( ) | | ( )( )
v v m m t F v m v m
a
+ + = + +
negligible
u = v
a
- v
R. Ganesh Narayanan 126
m)
v m t F
( - =
u
F = m (dv/dt)-u (dm/dt)
F + u (dm/dt) = ma
In the case of losing mass case, rate of change of mass is negative
R. Ganesh Narayanan 127
A 20 N projectile is moving with a
velocity of 100 m/s when it explodes
into 5 and 15 N fragments.
Immediately after the explosion, the
fragments travel in the directions
A
=
45
o
and
B
= 30
o
. Determine the
velocity of each fragment.
x
y
R. Ganesh Narayanan 128
Write separate component equations for the conservation of linear
momentum.
x components:
( ) 100 20 30 cos 15 45 cos 5 = +
B A
v v
y components:
0 30 sin 15 45 sin 5 =
B A
v v
Solve the equations simultaneously for the
fragment velocities.
s m 6 . 97 s m 207 = =
B A
v v
( ) ( ) ( )
0
0
20 15 5 v g v g v g
v m v m v m
B A
B B A A
= +
= +
R. Ganesh Narayanan 129
Grain falls onto a chute at the rate of 240 N/s. It
hits the chute with a velocity of 20 m/s and leaves
with a velocity of 15 m/s. The combined weight of
the chute and the grain it carries is 600 N with the
center of gravity at G. Determine the reactions at C
and B.
The sum m
i
v
i
of the momenta of the particles supported by
the chute is same at t and t+t
kg/s 24
/s m 10
N/s 240
2
= =
t
m
R. Ganesh Narayanan 130
( ) ( ) ( ) = + +
10 sin
B y A
v m t B W C v m
( ) =
10 cos
B x
v m t C
= +
2 1
L dt F L
Apply impulse-momentum principle,
In x-axis:
In y-axis:
( ) ( )
( ) ( ) =
+ +
10 sin 12 10 cos 6
12 7 3
B B
A
v m v m
t B W v m
= +
2 , 1 , C C C
H dt M H
Put input values in three equations and solve for B, Cx, Cy
( )
584 .75 N 354 .5 432 .75 N B C i j = = +
r
r r
R. Ganesh Narayanan 131
A bullet is fired with a horizontal velocity of 500 m/s
through a 3-kg block A and becomes embedded in a
2.5-kg block B. Knowing that blocks A and B start
moving with velocities of 3 m/s and 5 m/s,
respectively, determine (a) the mass of the bullet, (b)
its velocity as it travels from block A to block B
(a) the mass of the bullet
mv
0
+m
A
(0)+m
B
(0) = mv
B
+m
A
v
A
+m
B
v
B
m = m
A
v
A
+m
B
v
B
/ (v
0
-v
b
) = (3) (3) + (2.5) (5) / (500-5) = 43.434 x10
-3
kg
(b) velocity as it travels from block A to block B
mv
0
+m
A
(0) = mv
1
+m
A
v
A
=> v
1
= mv
0
- m
A
v
A
/ m =
= 43.434 x10
-3
(500) (3) (3) / 43.434 x10
-3
= 292.8 m/s
R. Ganesh Narayanan 132
A system consists of three particles A, B, and C. We
know that WA = WB = 17.79 N and Wc = 124.55 N
and that the velocities of the particles, expressed in
m/s are, respectively, vA = 42i + 63j, vB = 42i +
63j, and vC = 9j 6k. Determine the angular
momentum H
O
of the system about O.
H
0
= ZERO
R. Ganesh Narayanan 133
In a game of pool, ball A is moving with a velocity v0 of
magnitude v0 = 4.57 m/s when it strikes balls B and C,
which are at rest and aligned as shown. Knowing that
after the collision the three balls move in the directions
indicated and assuming frictionless surfaces and perfectly
elastic impact (that is, conservation of energy), determine
the magnitudes of the velocities vA, vB and vC.
v0
vA
vB
vC
j
i
X-axis:
y-axis:
Find V
B
and V
c
in
terms of V
0
and V
A
Put V
B
and V
c
R. Ganesh Narayanan 134
The nozzle shown discharges a stream of water at a
flow rate Q= 1.8 m3/min with a velocity v of
magnitude 18.29 m/s. The stream is split into two
streams with equal flow rates by a wedge which is
kept in a fixed position. Determine the components
of the force exerted by the stream on the wedge.
Q = 1.8 m3/min = 0.03 m3/s
Impulse-momentum principle
m (v) + F t = m/2 (v1) + m/2 (v2)
F = m / t (1/2 v1+1/2 v2 v)
j
i
v1
v2
Velocity
vectors:
R. Ganesh Narayanan 135
F
F = - 117.17 i - 56.8 j N
R. Ganesh Narayanan 136
Sand falls from three hoppers onto a conveyor
belt at a rate of 40 kg/s for each hopper. The sand
hits the belt with a vertical velocity v1 = 3 m/s
and is discharged at A with a horizontal velocity
v2 = 4 m/s. Knowing that the combined mass of
the beam, belt system, and the sand it supports is
600 kg with a mass center at G, determine the
reaction at E.
F
E
a a a
a
4 2
h
W = mg = 600 x 9.81 = 5886 N
R = 4040 N (+)
R. Ganesh Narayanan 137
Kinematics of rigid bodies
relations between time and the positions, velocities, and accelerations of the
particles forming a rigid body.
Rectilinear translation
Curvilinear translation
Rotation about a fixed axis
Curvilinear translation rotation
(1)
(2)
(3)
Plane motion
R. Ganesh Narayanan 138
(4)
General Plane motion
(5) Motion about a fixed point
R. Ganesh Narayanan 139
(1) Translation
Consider rigid body in translation:
direction of any straight line inside the body is constant,
all particles forming the body move in parallel lines.
For any two particles in the body,
A B A B
r r r
+ =
All particles have the same velocity.
v v
A B
=
Differentiating with respect to time,
A A B A B
r r r r
= + =
r
B/A
= 0
Differentiating with respect to time again,
All particles have the same acceleration.
A B
a a
=
R. Ganesh Narayanan 140
When a rigid body is in translation, all the points of the body
have the same velocity and same acceleration at any given instant
In curvilinear translation, the velocity and acceleration change in
direction and in magnitude at every instant; In rectilinear
translation, velocity, acceleration direction are same during entire
motion
v v
A B
=
A B
a a
=
R. Ganesh Narayanan 141
(2) Rotation About a Fixed Axis: Velocity & Acceleration
Consider rotation of rigid body about a fixed
axis AA
The length s of the arc described by P when the
body rotates through ,
( ) ( )
( )
sin sin lim
sin
0
r
t
r
dt
ds
v
r BP s
t
=
= =
= =
r
dt
r d
V
= =
Vector direction along the rotation
axis AA, angular velocity
R. Ganesh Narayanan 142
Differentiating to determine the acceleration,
( )
v r
dt
d
dt
r d
r
dt
d
r
dt
d
dt
v d
a
+ =
+ =
= =
Angular acceleration,
a = x r + x ( x r)
Tangential
acceleration
component
Radial
acceleration
component
R. Ganesh Narayanan 143
Equations Defining the Rotation of a Rigid Body About a Fixed Axis
d
d
dt
d
dt
d
d
dt
dt
d
= = =
= =
2
2
or
v = dx/dt
a = d
2
x/dt
2
a = v (dv/dx)
Uniform Rotation, = 0:
t + =
0
Uniformly Accelerated Rotation, = constant:
( )
0
2
0
2
2
2
1
0 0
0
2
+ =
+ + =
+ =
t t
t
x = x
0
+ vt
v = v
0
+ at
x = x
0
+ v
0
t + at
2
v
2
= v
0
2
+ 2a (x-x
0
)
Equns. Can be used only
when = 0 & constant
R. Ganesh Narayanan 144
The rectangular block shown rotates about the diagonal
OA with a constant angular velocity of 6.76 rad/s.
Knowing that the rotation is counterclockwise as viewed
from A, determine the velocity and acceleration of point
B at the instant shown.
Angular velocity.
Velocity of point B.
vB = x R
B/O
= (i + 6.24j + 2.4 k) x (0.127i + 0.396j)
= -0.95i + 0.305j 0.396 k m/s
Acceleration of point B.
aB =vB = -3.2 i 1.88j + 6.23k m/s
2
R. Ganesh Narayanan 145
The assembly shown consists of two rods and a
rectangular plate BCDE which are welded together.
The assembly rotates about the axis AB with a constant
angular velocity of 10 rad/s. Knowing that the rotation
is counterclockwise as viewed from B, determine the
velocity and acceleration of corner E.
Find r
B/A
, r
E/B
Find angular velocity vector; = (r
B/A
/ l
AB
)
1) v
E
= x r
E/B
; 2) a
E
= x v
E
R. Ganesh Narayanan 146
Ring B has an inner radius r2 and hangs from the
horizontal shaft A as shown. Shaft A rotates with a
constant angular velocity of 25 rad/s and no slipping
occurs. Knowing that r1 = 1.27 cm, r2 = 6.35 cm, and
r3 = 8.9 cm, determine (a) the angular velocity of ring
B, (b) the acceleration of the points of shaft A and ring
B which are in contact, (c) the magnitude of the
acceleration of a point on the outside surface of ring B.
R. Ganesh Narayanan 147
R. Ganesh Narayanan 148
(3) General Plane Motion
General plane motion is neither a translation nor a rotation.
General plane motion can be considered as the sum of a
translation and rotation.
Displacement of particles A and B to A
2
and B
2
can
be divided into two parts:
- translation to A
2
and
- rotation of about A
2
to B
2
1
B
1
B
R. Ganesh Narayanan 149
Absolute and Relative Velocity in Plane Motion
Any plane motion can be replaced by a translation of an arbitrary reference
point A and a simultaneous rotation about A.
A B A B
v v v
+ =
r v
A B
=
r v
A B A B
=
A B A B
r v v
+ =
Absolute and Relative Velocity in Plane Motion
R. Ganesh Narayanan 150
Assuming that the velocity v
A
of end A is known, wish to determine the
velocity v
B
of end B and the angular velocity in terms of v
A
, l, and .
The direction of v
B
and v
B/A
are known. Complete the velocity diagram.
tan
tan
A B
A
B
v v
v
v
=
=
cos
cos
l
v
l
v
v
v
A
A
A B
A
=
= =
Point A as reference
R. Ganesh Narayanan 151
Point B as reference
Selecting point B as the reference point and solving for the velocity v
A
of end A
and the angular velocity leads to an equivalent velocity triangle.
v
A/B
has the same magnitude but opposite sense of v
B/A
. The sense of the
relative velocity is dependent on the choice of reference point.
Angular velocity of the rod in its rotation about B is the same as its rotation
about A. Angular velocity is not dependent on the choice of reference point.
R. Ganesh Narayanan 152
The crank AB has a constant clockwise angular
velocity of 2000 rpm.
For the crank position indicated, determine (a) the
angular velocity of the connecting rod BD, and (b)
the velocity of the piston P.
The velocity is obtained from the crank rotation data.
B
v
r
( ) ( )( ) s rad 4 . 209 in. 3
s rad 4 . 209
rev
rad 2
s 60
min
min
rev
2000
= =
=
|
\
|
|
|
\
|
|
\
|
=
AB B
AB
AB v
The velocity direction is as shown.
= 628.3 in/s
= =
95 . 13
in. 3
sin
in. 8
40 sin
The direction of the absolute velocity is horizontal.
The direction of the relative velocity is
perpendicular to BD. Compute the angle between the
horizontal and the connecting rod from the law of sines.
D
v
B D
v
R. Ganesh Narayanan 153
=
sin76.05
s in. 3 . 628
50 sin 95 . 53 sin
B D
D
v
v
s in. 9 . 495
s ft 6 . 43 s in. 4 . 523
=
= =
B D
D
v
v s ft 6 . 43 = =
D P
v v
s rad 0 . 62
in. 8
s in. 9 . 495
=
= =
=
l
v
l v
B D
BD
BD B D
( )
k
BD
s rad 0 . 62
=
R. Ganesh Narayanan 154
Instantaneous Center of Rotation in Plane Motion
Plane motion of all particles in a slab can always be
replaced by the translation of an arbitrary point A and a
rotation about A with an angular velocity that is
independent of the choice of A.
The same translational and rotational velocities at A are
obtained by allowing the slab to rotate with the same
angular velocity about the point C on a perpendicular to
the velocity at A.
The velocity of all other particles in the slab are the same
as originally defined since the angular velocity and
translational velocity at A are equivalent.
As far as the velocities are concerned, the slab seems to
rotate about the instantaneous center of rotation C.
R. Ganesh Narayanan 155
How to obtain instantaneous center of rotation
Fig. 1
Fig. 2
If the velocity at two points A and B are known, the
instantaneous center of rotation lies at the intersection
of the perpendiculars to the velocity vectors through A
and B . (fig. 1)
If the velocity vectors at A and B are perpendicular to
the line AB, the instantaneous center of rotation lies at
the intersection of the line AB with the line joining the
extremities of the velocity vectors at A and B. (fig. 2)
If the velocity vectors are parallel, the instantaneous
center of rotation is at infinity and the angular velocity
is zero. (fig. 1)
If the velocity magnitudes are equal, the instantaneous
center of rotation is at infinity and the angular velocity
is zero. (fig. 2)
R. Ganesh Narayanan 156
The particle at the center of rotation has zero velocity.
The particle coinciding with the center of rotation changes with
time and the acceleration of the particle at the instantaneous center
of rotation is not zero.
The acceleration of the particles in the slab cannot be determined
as if the slab were simply rotating about C.
The trace of the locus of the center of rotation on the body
is the body centrode and in space is the space centrode.
R. Ganesh Narayanan 157
The crank AB has a constant clockwise angular
velocity of 2000 rpm.
For the crank position indicated, determine (a)
the angular velocity of the connecting rod BD,
and (b) the velocity of the piston P.
vB = 628.3 in/s; = 13.95
The instantaneous center of rotation is at the
intersection of the perpendiculars to the velocities
through B and D.
= =
= + =
05 . 76 90
95 . 53 40
D
B
=
sin50
in. 8
95 . 53 sin 05 . 76 sin
CD BC
in. 44 . 8 in. 14 . 10 = = CD BC
Same problem
R. Ganesh Narayanan 158
Determine the angular velocity about the center of
rotation based on the velocity at B.
( )
in. 10.14
s in. 3 . 628
= =
=
BC
v
BC v
B
BD
BD B
s rad 0 . 62 =
BD
Calculate the velocity at D based on its rotation about
the instantaneous center of rotation.
( ) ( )( ) s rad 0 . 62 in. 44 . 8 = =
BD D
CD v
s ft 6 . 43 s in. 523 = = =
D P
v v
R. Ganesh Narayanan 159
Absolute and Relative Acceleration in Plane Motion
Absolute acceleration of a particle of the slab,
A B A B
a a a
+ =
Relative acceleration associated with rotation about A includes
tangential and normal components,
A B
a
r
( )
n
( )
( )
2
r a
r a
n
A B
t
A B
=
=
( )
A B A B
A B
t
A B
r a
r a
2
=
=
t
( ) ( )
A B
n
A B A
A B A B
a a a
a a a
+ + =
+ =
R. Ganesh Narayanan 160
Rate of Change With Respect to a Rotating Frame
Frame OXYZ is fixed.
Frame Oxyz rotates about fixed
axis OA with angular velocity
Vector function varies
in direction and magnitude.
( )
t Q
With respect to the rotating Oxyz frame,
k Q j Q i Q Q
z y x
+ + =
( )
k Q j Q i Q Q
z y x
Oxyz
+ + =
With respect to the fixed OXYZ frame,
( )
dk/dt Q
dj/dt Q
di/dt Q k Q j Q i Q Q z
y
x z y x
OXYZ
+
+
+ + + =
( )
k Q j Q i Q Q
z y x
Oxyz
+ + =
Represent velocity of particle, xQ
If were fixed within Oxyz then is
equivalent to velocity of a point in a rigid body
attached to Oxyz and
Q
( )
OXYZ
Q
Q
dk/dt
Q
z
= +
dj/dt Q di/dt Q
y x
+
Rate of change of Q depends on frame of reference
R. Ganesh Narayanan 161
With respect to the fixed OXYZ frame,
( ) ( )
Q Q Q
Oxyz OXYZ
+ =
This relation is useful to find rate of change of Q w.r.t. fixed
frame of reference OXYZ when Q is defined by its components
along the rotating frame Oxyz
R. Ganesh Narayanan 162
Coriolis Acceleration
Frame OXY is fixed and frame Oxy rotates with angular
velocity .
r
Position vector for the particle P is the same in both
frames but the rate of change depends on the choice of
frame.
P
r
The absolute velocity of the particle P is,
( )
( )
Oxy OXY P
r r r v
+ = =
The absolute acceleration of the particle P is,
a
p
= v
p
= xr + xr + d/dt [(r)
Oxy
]
( ) ( )
Q Q Q
Oxyz OXYZ
+ =
( )
( )
Oxy OXY P
r r r v
+ = =
a
p
= x r + x ( x r) + 2 x (r)
Oxy
+ (r)
Oxy
R. Ganesh Narayanan 163
a
p
= x r + x ( x r) + 2 x (r)
Oxy
+ (r)
Oxy
a = x r + x ( x r)
Coriolis
acceleration, a
c
Two vectors are normal to each other, 2v
Oxy
R. Ganesh Narayanan 164
Disk D of the Geneva mechanism rotates with
constant counterclockwise angular velocity
D
=
10 rad/s.
At the instant when = 150
o
, determine (a) the
angular velocity of disk S, and (b) the velocity of
pin P relative to disk S.
Direction of velocity of P with respect to S is parallel
to slot.
From the law of cosines,
mm 1 . 37 551 . 0 30 cos 2
2 2 2 2
= = + = r R Rl l R r
From the law of sine,
=
= 4 . 42
742 . 0
30 sin
sin
30 sin
R
sin
r
Magnitude and direction of absolute velocity of pin P are
calculated from radius and angular velocity of disk D.
( )( ) s mm 500 s rad 10 mm 50 = = =
D P
R v
R. Ganesh Narayanan 165
The absolute velocity of the point P may be written as
s P P P
v v v
+ =
( )
( )
Oxy OXY P
r r r v
+ = =
s
s rad 08 . 4
=
= = 6 . 17 30 4 . 42 90
The interior angle of the vector triangle is
( )
mm 1 . 37
s mm 2 . 151
s mm 2 . 151 6 . 17 sin s mm 500 sin
= =
= = =
s s
P P
r
v v
( ) = = 6 . 17 cos s m 500 cos
P s P
v v
Coriolis acceleration, ac = 2
s
v
p/s
= 2 (4.08) (477) = 3890 mm/s
2
( )
v
s P
=
4 . 42 s m 477
R. Ganesh Narayanan 166
Kinetics of rigid bodies
Equations of Motion for a Rigid Body
relations between the forces acting on a rigid body, the shape and mass of the
body, and the motion produced.
Consider a rigid body acted upon by several external
forces.
Assume that the body is made of a large number of
particles.
For the motion of the mass center G of the body
with respect to the Newtonian frame Oxyz,
a m F
=
For the motion of the body with respect to the
centroidal frame Gxyz,
G G
H M
=
O
o
H M
= == =
R. Ganesh Narayanan 167
System of external forces is equipollent to the
system consisting of
. and
G
H a m
R. Ganesh Narayanan 168
Angular Momentum of a Rigid Body in Plane Motion
Consider a rigid slab in plane motion.
Angular momentum of the slab may be
computed by
( )
( ) | |
( )
I
m r
m r r
m v r H
i i
n
i
i i i
n
i
i i i G
=
=
=
=
2
1
1
MI of slab about centroidal
axis perpendicular to slab
After differentiation,
I I H
G
= =
H
G
Results are also valid for plane motion of bodies which are symmetrical with
respect to the reference plane; Results are not valid for asymmetrical bodies
or three-dimensional motion.
R. Ganesh Narayanan 169
Plane Motion of a Rigid Body: DAlemberts Principle
I M a m F a m F
G y y x x
= = =
Motion of a rigid body in plane motion is
completely defined by the resultant and moment
resultant about G of the external forces.
The external forces and the collective effective forces of the slab particles are
equipollent (reduce to the same resultant and moment resultant) and equivalent
(have the same effect on the body).
dAlemberts Principle: The external forces acting on a rigid
body are equivalent to the effective forces of the various
particles forming the body.
R. Ganesh Narayanan 170
The most general motion of a rigid body that is symmetrical with respect to
the reference plane can be replaced by the sum of a translation and a
centroidal rotation.
Translation Centroidal rotation
R. Ganesh Narayanan 171
Problems in motion of rigid bodies
I M a m F a m F
G y y x x
= = =
The fundamental relation between the forces acting on a rigid body in plane
motion and the acceleration of its mass center and the angular acceleration
of the body is illustrated in a free-body-diagram equation.
The techniques for solving problems of static equilibrium may be applied to
solve problems of plane motion by utilizing dAlemberts principle, or
principle of dynamic equilibrium
dAlemberts principle
R. Ganesh Narayanan 172
At a forward speed of 30 m/s, the truck brakes
were applied, causing the wheels to stop rotating.
It was observed that the truck to skidded to a stop
in 200 m. Determine the magnitude of the normal
reaction and the friction force at each wheel as
the truck skidded to a stop.
External forces Effective forces
( )
( ) m 200 2
s
m
30 0
2
2
0
2
0
2
a
x x a v v
+
|
\
|
=
+ =
assuming uniform acceleration
s
m
25 . 2 = a
2
Equns of motion.
0 = + W N N
B A
( )
=
eff
y y
F F
=> F
A
+ F
B
=
K
W
( )
=
eff
x x
F F
=
a m F F
B A 229 . 0
9.81
25 .
2
= = =
g
a
k
( ) =
a g W W
k
R. Ganesh Narayanan 173
( )
=
eff
A A
M M
( ) ( ) ( )
W N
g
a W
a
g
W
W N
a m N W
B
B
B
650 . 0
4 5
12
4 5
12
1
m 4 m 12 m 5
=
|
\
|
+ = |
\
|
+ =
= +
W N W N
B A
350 . 0 = =
( ) W N N
A rear
350 . 0
2
1
2
1
= = W N
rear
175 . 0 =
( ) W N N
V front
650 . 0
2
1
2
1
= =
W N
front
325 . 0 =
W F
rear
04 . 0 =
W F
front
07 . 0 =
( )( )
W N F
rear k rear
175 . 0 229 . 0
= =
( )( )
W N F
front k front
325 . 0 229 . 0
= =
R. Ganesh Narayanan 174
A 20 kg cabinet is mounted on casters that allow it to
move freely ( = 0) on the floor. If a 100 N force is
applied as shown, determine (a) the acceleration of the
cabinet, (b) the range of values of h for which
the cabinet will not tip.
0.9 m
G
0.6 m
h
100 N
G
ma
a) acceleration: ( )
=
eff
x x
F F
100 = m a => 100/m = a Find a
(b) For tipping to impend
A B
Find h
For tipping to impend
Find h
R. Ganesh Narayanan 175
A 10-kg uniform disk is placed in contact with an
inclined surface and a constant 11 N m couple M is
applied as shown. The weight of the link AB is
negligible. Knowing that the coefficient of kinetic
friction at D is 0.4, determine (a) the angular
acceleration of the disk, (b) the force in the link AB.
B
W = 10 x 9.81 = 98.1
F
AC
N
0.4N
11 Nm
M
B
= I
G
= m r
2
11 - (0.4N )(0.225) = (10) (0.225)
2
= 0.25313
( )
=
eff
y y
F F
11 - (0.4x115.9)(0.225) = 0.25313 => = 2.25 rad/s
2
( )
=
eff
x x
F F => F
AC
+ 0.4N sin 30 N cos 30 = 0; F
AC
= 77.2 N
R. Ganesh Narayanan 176
Constrained Plane Motion
Most engineering applications involve rigid
bodies which are moving under given constraints,
e.g., cranks, connecting rods, and non-slipping
wheels.
Constrained plane motion: motions with definite
relations between the components of acceleration
of the mass center and the angular acceleration of
the body.
Solution of a problem involving constrained
plane motion begins with a kinematic analysis.
e.g., given , , and , find P, N
A
, and N
B
.
- kinematic analysis yields
- application of dAlemberts principle yields
P, N
A
, and N
B
.
. and
y x
a a
R. Ganesh Narayanan 177
1) Non-centroidal rotation
Noncentroidal rotation: motion of a body is constrained
to rotate about a fixed axis that does not pass through its
mass center.
Kinematic relation between the motion of the mass
center G and the motion of the body about G,
2
r a r a
n t
= =
R. Ganesh Narayanan 178
The kinematic relations are used to eliminate
from equations derived from
dAlemberts principle or from the method of
dynamic equilibrium.
n t
a a and
R. Ganesh Narayanan 179
2) Rolling motion
For a balanced disk constrained to
roll without sliding,
r a r x = =
Rolling, no sliding:
N F
s
r a =
Rolling, sliding impending:
N F
s
= r a =
Rotating and sliding:
N F
k
= r a,
independent
Same as block not sliding; F has to
be found out independent of N, i.e.
only from figure shown
a r
R. Ganesh Narayanan 180
A sphere of weight Wis released with no initial
velocity and rolls without slipping on the incline.
Determine: a) the minimum value of the
coefficient of friction, b) the velocity of G after
the sphere has rolled 10 m and c) the velocity of G
if the sphere were to move 10 m down a
frictionless incline.
With the linear and angular accelerations related, solve
the three scalar equations derived from the free-body-
equation for the angular acceleration and the normal
and tangential reactions at C.
( )
=
eff
C C
M M
( ) ( )
( ) ( )
|
\
|
+ |
\
|
=
+ =
+ =
2
2
5
2
5
2
sin
r
g
W
r r
g
W
mr r mr
I r a m r W
r
g
7
sin 5
=
R. Ganesh Narayanan 181
( )
7
30 sin m/s 10 5
7
30 sin 5
2
= =
g
r a
2
m/s 57 . 3 = a
( )
=
eff
x x
F F
W W F
g
g
W
a m F W
143 . 0 30 sin
7
2
7
sin 5
sin
= =
=
=
( )
=
eff
y y
F F
W W N
W N
866 . 0 30 cos
0 cos
= =
=
Calculate the friction coefficient required for the
indicated tangential reaction at C.
W
W
N
F
N F
s
s
866 . 0
143 . 0
= =
=
165 . 0 =
s
R. Ganesh Narayanan 182
Calculate the velocity after 10 m of uniformly
accelerated motion.
( )
( )( ) m 10 m/s 57 . 3 2 0
2
2
0
2
0
2
+ =
+ = x x a v v
m/s 4 . 71
=
v
Assuming no friction, calculate the linear acceleration and the
corresponding velocity after 10 m.
( )
=
eff
x x
F F
( )
2 2
m/s 5 30 sin m/s 10
sin
= =
|
\
|
= =
a
a
g
W
a m W
( )
( )( ) m 10 m/s 5 2 0
2
2
0
2
0
2
+ =
+ = x x a v v
m/s 100 = v
r
R. Ganesh Narayanan 183
Plane Motion of Rigid Bodies:
Energy and Momentum Methods
Principle of Work and Energy for a Rigid Body
Assume that the rigid body is made of a large
number of particles.
2 2 1 1
T U T = +
=
2 1
, T T
=
2 1
U
initial and final total kinetic energy of
particles forming body
total work of internal and external forces
acting on particles of body.
Internal forces between particles A and B are equal
and opposite.
Therefore, the net work of internal forces is zero.
In general, small displacements of the particles A
and B are not equal but the components of the
displacements along AB are equal.
R. Ganesh Narayanan 184
Work of a force during a displacement of its point of application,
( )
= =
2
1
2
1
cos
2 1
s
s
A
A
ds F r d F U
F F
and
M
Consider the net work of two forces
forming a couple of moment during a
displacement of their points of application.
( )
1 2
2 1
2
1
=
=
M
d M U
if M is constant.
d M
d Fr ds F
r d F r d F r d F dU
=
= =
+ =
2
2 1 1
R. Ganesh Narayanan 185
Forces acting on rigid bodies which do no work:
Forces applied to fixed points:
- reactions at a frictionless pin when the supported body rotates about
the pin.
Forces acting in a direction perpendicular to the displacement of their
point of application:
- reaction at a frictionless surface to a body moving along the
surface
- weight of a body when its center of gravity moves horizontally
Friction force at the point of contact of a body rolling without sliding
on a fixed surface.
( ) 0 = = = dt v F ds F dU
c C
R. Ganesh Narayanan 186
Kinetic Energy of a Rigid Body in Plane Motion
Consider a rigid body of mass m in plane motion.
2
2
1
2
2
1
v m v m T
i i
+ =
( )
2
2
1
2
2
1
2 2
2
1
2
2
1
I v m
m r v m
i i
+ =
+ =
KE of motion
mass center of
body
KE of motion of
particle in
GXY frame
KE associated with
the motion of the
mass center G
KE associated with
the rotation of the
body about G
Centroidal rotation, ZERO
Pure translation, ZERO
Consider a rigid body rotating about a fixed axis
through O.
( ) ( )
2
2
1
2 2
2
1
2
2
1
2
2
1
O
i i i i i i
I
m r r m v m T
=
+ + =
R. Ganesh Narayanan 187
Systems of Rigid Bodies
For problems involving systems consisting of several rigid bodies, the
principle of work and energy can be applied to each body.
We may also apply the principle of work and energy to the entire system,
2 2 1 1
T U T = +
= arithmetic sum of the kinetic energies of
all bodies forming the system
= work of all forces acting on the various
bodies, whether these forces are internal
or external to the system as a whole.
2 1
,T T
2 1
U
For problems involving pin connected members, blocks and pulleys
connected by inextensible cords, and meshed gears,
- internal forces occur in pairs of equal and opposite forces
- points of application of each pair move through equal distances
- net work of the internal forces is zero
- work on the system reduces to the work of the external forces
R. Ganesh Narayanan 188
Conservation of Energy
Expressing the work of conservative forces as a change in
potential energy, the principle of work and energy becomes
2 2 1 1
V T V T + = +
In the plane motion of rigid body, the KE of the body should include both
translational and rotational terms
Power = rate at which work is done
For a body acted upon by force and moving with velocity ,
For a rigid body rotating with an angular velocity and acted
upon by a couple of moment parallel to the axis of rotation,
r
M
r
M
dt
d M
dt
dU
= = = Power
Power
F
v F
dt
dU
= =
Power
v
R. Ganesh Narayanan 189
Each of the two slender rods has a mass of 6 kg.
The system is released from rest with = 60
o
.
Determine a) the angular velocity of rod AB
when = 20
o
, and b) the velocity of the point D
at the same instant.
Consider a system consisting of the two rods. With
the conservative weight force,
2 2 1 1
V T V T + = +
2
1 1
=
Wy V
V
2
=2Wy
2
( )( ) ( ) ( )( ) ( )
2
2
2
1
2
12
1
2
2
1
2
12
1
2
2
1
2
12
1
2
2
1
2
12
1
2
520 . 1
281 . 0 522 . 0 6 281 . 0 375 . 0 6
=
+ + + =
+ + + =
BD BD BD AB AB AB
I v m I v m T
T
1
= 0
Put v1, v2, T1, T2 in energy conservation equation, find
AB
From this , find v
D
R. Ganesh Narayanan 190
Each of the gears A and B has a weight of 2.3 kg and a
radius of gyration of 10.2 cm, while gear C has a weight of
11.3 kg and a radius of gyration of 19 cm. A couple M of
magnitude 9.15 Nm is applied to gear C. Determine (a) the
number of revolutions of gear C required for its angular
velocity to increase from 100 to 450 rpm, (b) the
corresponding tangential force acting on gear A.
100 rpm for gear C:
Find T1
A
, T1
B
, T1
C
; Find total T = T1
A
+ T1
B
+ T1
C
;
Here, T1
A
= I
A
2
= (mk
2
)
2
; SIMILARLY for B, C
Find
B
,
c
,
B,
c
by:
450 rpm for gear C:
Find T2
A
, T2
B
, T2
C
; Find total T = T2
A
+ T2
B
+ T2
C
Work of couple, U(1-2) = M
C
Find
C
from T1+U(1-2) = T2; then find
A
APPLY WORK-ENERGY PRINCIPLE for gear A, find M
A
; then find F
t
= M
A
/r
A
R. Ganesh Narayanan 191
Principle of Impulse and Momentum
Method of impulse and momentum:
- well suited to the solution of problems involving time and velocity
- the only practicable method for problems involving impulsive
motion and impact.
System Momenta
1
+ System External Imp
1-2
= System Momenta
2
R. Ganesh Narayanan 192
v m m v L
i i
r
r
r
= =
The momenta of the particles of a system may be reduced to a vector
attached to the mass center equal to their sum,
i i i G
m v r H
r r
r
=
and a couple equal to the sum of their moments about the mass center,
I H
G
=
r
For the plane motion of a rigid slab or of a rigid body symmetrical with
respect to the reference plane,
V
i
(m
i
)
Pi =
L = mv
G
H
G
= I
R. Ganesh Narayanan 193
Principle of impulse and momentum for the plane motion of a rigid slab
or of a rigid body symmetrical with respect to the reference plane
expressed as a free-body-diagram equation,
Results in three equations of motion:
- summing and equating momenta and impulses in the x and y directions
- summing and equating the moments of these vectors with respect to any
given point
R. Ganesh Narayanan 194
Noncentroidal rotation
- Equating the moments of the momenta and impulses
about O,
2 1
2
1
O
t
t
O O
I dt M I = +
R. Ganesh Narayanan 195
System of rigid bodies
Motion of several rigid bodies can be analyzed by applying the
principle of impulse and momentum to each body separately.
For problems involving no more than three unknowns, it may be
convenient to apply the principle of impulse and momentum to the
system as a whole.
For each moving part of the system, the diagrams of momenta should
include a momentum vector and/or a momentum couple.
Internal forces occur in equal and opposite pairs of vectors and hence of
impulse of internal forces can be omitted
R. Ganesh Narayanan 196
When the sum of the angular impulses pass through O, the
linear momentum may not be conserved, yet the angular
momentum about O is conserved,
( ) ( )
2
0
1
0
H H =
When no external force acts on a rigid body or a system of rigid
bodies, the system of momenta at t
1
is equipollent to the system
at t
2
. The total linear momentum and angular momentum about
any point are conserved,
( ) ( )
2
0
1
0
H H =
2 1
L L
r r
=
Conservation of momentum principle
R. Ganesh Narayanan 197
mm 80 kg 3
mm 200 kg 10
= =
= =
B B
A A
k m
k m
The system is at rest when a moment
of is applied to gear B.
Neglecting friction, a) determine the
time required for gear B to reach an
angular velocity of 600 rpm, and b) the
tangential force exerted by gear B on
gear A.
m N 6 = M
( )
( ) ( )( )
s N 2 . 40
s rad 1 . 25 m kg 400 . 0 m 250 . 0
0
2
=
=
=
Ft
Ft
I Ftr
A A A
moments about A:
moments about B:
( )
( ) ( )
( )( ) s rad 8 . 62 m kg 0192 . 0
m 100 . 0 m N 6
0
2
2
=
= +
Ft t
I Ftr Mt
B B B
t = 0.871 s
F (0.871) = 40.2 => F = 46.2 N
R. Ganesh Narayanan 198
A sphere of radius r and weight W with an initial clockwise
angular velocity
0
is placed in the corner formed by the
floor and a vertical wall. Denoting by
k
the coefficient of
kinetic friction at A and B, derive an expression for the
time required for the sphere to come to rest.
G
A
I
1
G
A
N
A
t
k
N
A
t
N
B
t
k
N
B
t
wt
G
A
I
2
= 0
+
= B
In X dirn.: 0 +
k
N
A
t - N
B
t = 0; In Y dirn.: 0 wt + N
a
t +
k
N
B
t = 0
Find N
B
and N
A
from these equations
I
1
k
N
A
tr
k
N
B
tr = 0 => from this find t by sub. N
A
and N
B
R. Ganesh Narayanan 199
A 15-g magnet D is released from rest in the position
shown, falls a distance of 320 mm, and becomes
attached at A to the 200-g steel bar AB. Assuming
that the impact is perfectly plastic, determine the
angular velocity of the bar and the velocity of the
magnet immediately after the impact.
m
D
v
0
c
+
c
Fdt
=
m
D
v
A
c
I
About C: m
D
v
0
(0.3) = m
D
v
A
(0.3) + I
0.015 (V
0
) (0.3) = 0.015 (V
A
) (0.3) + I
Conservation of energy: T1+V1 = T2+V2 =>
0 + (0.015) (9.81) (0.32) = (0.015) (V0
2
) + 0
V
0
= 2.5057 m/s
V
A
= (0.3)
R. Ganesh Narayanan 200
0.015 (V
0
) (0.3) = 0.015 (V
A
) (0.3) + I
0.015 (2.5057) (0.3) = 0.015 (0.3) (0.3) + 1/12 (0.2) (0.6)
2
=> = 1.53 rad/s
V
A
= V
D
= (0.3) = 0.3 X 1.53 = 0.46 m/s
R. Ganesh Narayanan 201
Eccentric Impact
( ) ( )
n
B
n
A
u u
r r
=
Period of deformation Period of restitution
= dt R Impulse
r
= dt P Impulse
r
Principle of impulse and momentum is supplemented by
( ) ( )
( ) ( )
n
B
n
A
n
A
n
B
v v
v v
dt P
dt R
n restitutio of t coefficien e
=
= =
r
r
R. Ganesh Narayanan 202
A 0.05-N bullet is fired into the side of a 20-N
square panel which is initially at rest. Determine
a) the angular velocity of the panel immediately
after the bullet becomes embedded and b) the
impulsive reaction at A, assuming that the bullet
becomes embedded in 0.0006 s.
Moment about A, impulse principle in x-direction, y-direction;
I = 1/6 (20/9,81)(18)
2
; v2 = (9)
2
=> Find
2
, V
2
Find Ax, Ay by sub. V2, t in above equns.
R. Ganesh Narayanan 203
Member ABC has a weight of 2.27 kg and is attached
to a pin support at B. A 0.68 kg sphere D strikes end C
of member ABC with a vertical velocity v1 of 9 ft/s.
Knowing that L = 30 in. and that the coefficient of
restitution between the sphere and member ABC is
0.5, determine immediately after the impact (a) the
angular velocity of member ABC, (b) the velocity of
the sphere.
Impact condition
Kinematics
About B:
Put data in and v
D
, find and v
D
R. Ganesh Narayanan 204
In a game of pool, ball A is rolling without slipping with a velocity
v0 as it hits obliquely ball B, which is at rest. Denoting by r the
radius of each ball and by
k
the coefficient of kinetic friction
between the balls and the table surface, and assuming perfectly
elastic impact, determine (a) the linear and angular velocity of each
ball immediately after the impact, (b) the velocity of ball B after it
has started rolling uniformly.
During impact: write impulse momentum principle for ball A and B separately
Find V
A
, V
B
,
A
,
B
After impact: write impulse momentum principle for ball B after impact, find V
B
R. Ganesh Narayanan 205
Kinetics of rigid body in 3D
G G
H M
a m F
&
r r
r
r
=
=
The fundamental relations developed for
the plane motion of rigid bodies may also
be applied to the general motion of three
dimensional bodies.
r
r
I H
G
= The relation which was used
to determine the angular momentum of a
rigid slab is not valid for general three
dimensional bodies and motion.
R. Ganesh Narayanan 206
Rigid Body Angular Momentum in Three Dimensions
Angular momentum of a body about its mass center,
( ) ( ) | |
= =
=
n
i
i i i
n
i
i i i G
m r r m v r H
1 1
r r r r r
r
z z y zy x zx z
z yz y y x yx y
z xz y xy x x x
I I I H
I I I H
I I I H
+ =
+ =
+ =
The relations show that the operation which transforms the vector
into the vector H
G
is characterized by the array of moments and
products of inertia
|
|
|
\
|
+
+
+
z zy zx
yz y yx
xz xy x
I I I
I I I
I I I
Inertia tensor at mass
center of the body
R. Ganesh Narayanan 207
With respect to the principal axes of inertia,
|
|
|
\
|
z
y
x
I
I
I
0 0
0 0
0 0
Select axis GXY called principal axes of inertia on which
all products of inertia are zero
Principal centroidal MI of the body
z z z y y y x x x
I H I H I H
= = =
The angular momentum of a rigid body and
its angular velocity have the same direction
if, and only if, is directed along a principal
axis of inertia.
G
H
r
r
r
R. Ganesh Narayanan 208
Angular momentum of body constrained to rotate about fixed point
z z y zy x zx z
z yz y y x yx y
z xz y xy x x x
I I I H
I I I H
I I I H
+ =
+ =
+ =
the angular momentum may be computed directly
from the moments and products of inertia with
respect to the Oxyz frame.
( )
( ) | |
=
=
=
=
n
i
i i i
n
i
i i O
m r r
m v r H
1
1
r r r
r r
r
MIs and product of MIs are computed w.r.t. Oxyz centered at O
R. Ganesh Narayanan 209
Principle of Impulse and Momentum
The principle of impulse and momentum can be applied directly to the
three-dimensional motion of a rigid body,
Syst Momenta
1
+ Syst Ext Imp
1-2
= Syst Momenta
2
The free-body diagram equation is used to develop component and
moment equations.
For bodies rotating about a fixed point, eliminate the impulse of the
reactions at O by writing equation for moments of momenta and
impulses about O.
R. Ganesh Narayanan 210
Kinetic Energy of a Rigid Body in Plane Motion
Consider a rigid body of mass m in plane motion.
2
2
1
2
2
1
v m v m T
i i
+ =
( )
2
2
1
2
2
1
2 2
2
1
2
2
1
I v m
m r v m
i i
+ =
+ =
KE of motion
mass center of
body
KE of motion of
particle in
GXY frame
KE associated with
the motion of the
mass center G
KE associated with
the rotation of the
body about G
Centroidal rotation, ZERO
Pure translation, ZERO
Consider a rigid body rotating about a fixed axis
through O.
( ) ( )
2
2
1
2 2
2
1
2
2
1
2
2
1
O
i i i i i i
I
m r r m v m T
=
+ + =
R. Ganesh Narayanan 211
Kinetic Energy of body in 3D
Kinetic energy of particles forming rigid body,
) 2 2
2 (
2 2 2
2
1
2
2
1
1
2
2
1
2
2
1
1
2
2
1
2
2
1
x z zx z y yz
y x xy z z y y x x
n
i
i i
n
i
i i
I I
I I I I v m
m r v m
v m v m T
+ + + =
+ =
+ =
=
=
r r
If the axes correspond instantaneously with the
principle axes,
) (
2 2 2
2
1
2
2
1
z z y y x x
I I I v m T
+ + + =
With these results, the principles of work and
energy and conservation of energy may be applied
to the three-dimensional motion of a rigid body.
R. Ganesh Narayanan 212
Kinetic energy of a rigid body with a fixed point,
) 2 2
2 (
2 2 2
2
1
x z zx z y yz
y x xy z z y y x x
I I
I I I I T
+ + =
If the axes Oxyz correspond instantaneously with
the principle axes Oxyz,
) (
2 2 2
2
1
z z y y x x
I I I T
+ + =
KE w.r.t fixed point
R. Ganesh Narayanan 213
A thin homogeneous square plate of mass m and side a is
welded to a vertical shaft AB with which it forms s an angle
of 45. Knowing that the shaft rotates with a constant angular
velocity , determine the angular momentum H
A
of the plate
about point A.
A X
Y
Y
Y
Z
Z
45
YZ as principal axes
Y
=
Y
cos 45;
z
=
z
sin 45
x
= 0
R. Ganesh Narayanan 214
A 4.5 kg rod of uniform cross section is used to form the shaft shown. Knowing that
the shaft rotates with a constant angular velocity 12 rad/s, determine (a) the angular
momentum HG of the shaft about its mass center G
m = 4.5 kg
z z y zy x zx z
z yz y y x yx y
z xz y xy x x x
I I I H
I I I H
I I I H
+ =
+ =
+ =
Find these values by evaluating Ix, Ixy, Ixz
R. Ganesh Narayanan 215
Mass Moment of Inertia
For a body of mass m the resistance to rotation
about the axis AA is
inertia of moment mass dm r
m r m r m r I
= =
+ + + =
2
2
3
2
2
2
1
L
Moment of inertia with respect to the y coordinate
axis is
( )
+ = = dm x z dm r I
y
2 2 2
Similarly, for the moment of inertia with respect to
the x and z axes,
( )
( )
+ =
+ =
dm y x I
dm z y I
z
x
2 2
2 2
R. Ganesh Narayanan 216
Generalizing for any axis AA and a parallel centroidal
axis,
2
md I I + =
Parallel axes theorem
The definition of the mass products of inertia of a
mass is an extension of the definition of product of
inertia of an area
x z m I dm zx I
z y m I dm yz I
y x m I dm xy I
x z zx
z y yz
y x xy
+ = =
+ = =
+ = =
R. Ganesh Narayanan 217
Rigid body motion in three dimension
G G
H M
a m F
&
r r
r
r
=
=
valid
Angular momentum and its rate of change are
taken with respect to centroidal axes GXYZ of
fixed orientation.
Define rate of change of change of with
respect to the rotating frame,
G
H
r
( ) k H j H i H H
z y x
Gxyz
G
r
&
r
&
r
&
&
r
+ + =
Then,
( )
r
r r r
&
r
&
r
= + =
G
Gxyz
G G
H H H
R. Ganesh Narayanan 218
( )
G
Gxyz
G G
H H M
r r
&
r r
+ =
With and Gxyz chosen to correspond
to the principal axes of inertia,
r
r
=
( )
( )
( )
y x y x z z z
x z x z y y y
z y z y x x x
I I I M
I I I M
I I I M
=
=
=
&
&
&
Eulers Equations:
We know for principal axes of inertia of the body,
H
G
= I
X
X
i + I
y
y
j + I
z
z
k & substituting this in above equn.
F
x
= m a
x
; F
y
= m a
y
; F
z
= m a
z
Six equations define the rigid body motion in 3D
Scalar form
R. Ganesh Narayanan 219
For a rigid body rotation around a fixed point,
( )
O
Oxyz
O
O O
H H
H M
r r
&
r
r r
+ =
=
w.r.t rotating
frame of reference
w.r.t fixed frame
of reference
For a rigid body rotation around a fixed axis,
z z yz y xz x
I H I H I H = = =
( )
( )
( )
( ) ( )
2
i I j I k I j I i I
k I j I i I k
k I j I i I
H H M
yz xz z yz xz
z yz xz
z yz xz
O
Oxyz
O O
r r
r
r r
r
r r
r
&
r
r r
r
r
&
r r
+ + + =
+ +
+ =
+ =
Angular velocity of
rotating frame Oxyz
z z y zy x zx z
z yz y y x yx y
z xz y xy x x x
I I I H
I I I H
I I I H
+ =
+ =
+ =
R. Ganesh Narayanan 220
In scalar form,
z z
xz yz y
yz xz x
I M
I I M
I I M
=
+ =
+ =
2
2
When the forces applied to a body are known, and can be obtained from
last equation and sub. in first two equations. These equns. and three resultant
force equations can be used to find reactions at the bearings A, B.
F
x
= m a
x
; F
y
= m a
y
; F
z
= m a
z
If symmetrical with respect to the xy plane,
z z y x
I M M M = = =
0 0
If not symmetrical, the sum of external moments
will not be zero, even if = 0,
0
2 2
= = =
z xz y yz x
M I M I M
R. Ganesh Narayanan 221
Rod AB with weight W = 40 N is pinned at A to a vertical
axle which rotates with constant angular velocity 15 rad/s.
The rod position is maintained by a horizontal wire BC.
Determine the tension in the wire and the reaction at A.
G G
H M
a m F
&
r r
r
r
=
=
( )
eff
A A
M M
=
r r
( ) ( ) ( )
( ) ( )K K T
K I J J I I T J
r r
r r r r r r r
4 . 2078 6228 80 93 . 6
4 . 2078 1800 46 . 3 40 2 93 . 6
+ =
+ = +
N 1210 = T
( )
eff
F F
=
r r
I J I K A J A I A
Z Y X
r r r r r r
1800 40 1210 = + +
( ) ( )J I A
r r r
N 40 N 590 + =
H
G
= (H
G
)
GXYZ
+ xH
G
H
G
= I
X
X
i + I
y
y
j + I
z
z
k
ma = m(-r
2
)
R. Ganesh Narayanan 222
A homogeneous 3.6 kg disk is mounted on the horizontal shaft AB. The plane of the
disk forms a 20 angle with the yz plane as shown. Knowing that the shaft rotates
with a constant angular velocity of magnitude 10 rad/s, determine the dynamic
reactions at points A and B.
z
y
x
R. Ganesh Narayanan 223
A
Z
= 0
A = -1.836 N; B = 1.836 N
R. Ganesh Narayanan 224
Motion of a Gyroscope: Eulerian Angles
A gyroscope consists of a rotor with its mass center fixed in space but which
can spin freely about its geometric axis and assume any orientation.
R. Ganesh Narayanan 225
R. Ganesh Narayanan 226
From a reference position with gimbals and a
reference diameter of the rotor aligned, the
gyroscope may be brought to any orientation
through a succession of three steps:
a) rotation of outer gimbal through about AA
b) rotation of inner gimbal through about BB
c) rotation of the rotor through about CC
, , and are called the Eulerian angles and
spin of rate
nutation of rate
precession of rate
=
=
=
&
&
&
At that instant
R. Ganesh Narayanan 227
= - sin i + j + ( + cos )k
H
O
= - I sin i + I j + I ( + cos )k
( ) ( )
( ) ( )
( )
cos
cos sin cos sin
cos cos 2 sin
2
& &
& & & & & &
& & & & & & &
+ =
+ +
=
+ + +
dt
d
I M
I I M
I I M
z
y
x
I MI of the rotor about its spin axis; I MI about transverse axis through O
R. Ganesh Narayanan 228
A uniform thin disk of 15.2 cm diameter is attached to the
end of a rod AB of negligible mass which is supported by a
ball-and-socket joint at point A. Knowing that the disk is
observed to precess about the vertical axis AC at the
constant rate of 36 rpm in the sense indicated and that its
axis of symmetry AB forms an angle = 60 with AC,
determine the rate at which the disk spins about rod AB.
x
z
R. Ganesh Narayanan 229
Ay
Ax
C sin
mg
Find I/m and I/m
Put r = 0.076 m; = 60; c = 0.61 m; = 36 rpm = 3. 769 rad/s
in above equn.
= 306.9 rad/s
R. Ganesh Narayanan 230
A homogeneous sphere of radius c = 40 mm is attached as shown
to a cord AB. The cord forms an angle = 30 with the vertical and
is observed to precess at the constant rate = 5 rad/s about the
vertical through A. Determine the angle that the diameter BC
forms with the vertical, knowing that the sphere (a) has no spin, (b)
spins about its diameter BC at the rate = 30 rad/s, (c) spins about
BC at the rate = 30 rad/s.
R. Ganesh Narayanan 231
Find I, I and put in above equn.
R. Ganesh Narayanan 232
M = I x p
Gyroscope: simplified analysis
Symmetrical rotor rotating about z-
axis with large angular velocity p
known as SPIN VELOCITY; Two
forces F applied to form a couple
M with relatively low angular
velocity known as
PRECESSION VELOCITY
R. Ganesh Narayanan 233
The turbine rotor in a ships power plant has
a mass of 1000kg, with center of mass at G
and a radius of gyration of 200 mm. The
rotor shaft is mounted in bearings A and B
with its horizontal axis as shown and turns
CCW at speed of 5000 rev/min when
viewed from stern. Find the vertical
components of the bearing reactions at A,
B if the ship is making a turn to port of 400
mm radius at speed of 25 knots (1 knot =
0.514 m/s).
R1, R2 => Reactions by bearings
R =>Reaction by gyroscope effect
M => Pointing towards B; so at B,
R points upwards and downwards at
A.
R. Ganesh Narayanan 234
RA = R1 - R; RB = R2 + R
Precession velocity, = v/r = 25 (0.514)/400 = 0.03215 rad/s
M = I x p
1500 (R) = 1000 (0.2)
2
(0.03215) [5000(2)/60] =>
R = 449 N
R1 = 5890 N; R2 = 3920 N
RA = 5440 N; RB = 4370 N
Вам также может понравиться
- Differential Transformation Method for Mechanical Engineering ProblemsОт EverandDifferential Transformation Method for Mechanical Engineering ProblemsОценок пока нет
- Dynamics Lecture Accl-VelocityДокумент18 страницDynamics Lecture Accl-VelocityAbhijeeth Nagaraj100% (4)
- Lagrange Equation 1Документ32 страницыLagrange Equation 1Gthulasi78Оценок пока нет
- Vibrations 2dofДокумент29 страницVibrations 2dofbhukthaОценок пока нет
- Important QuestionsДокумент8 страницImportant QuestionsdineshbabuОценок пока нет
- Midterm MECE303 M 2 11 SampleДокумент2 страницыMidterm MECE303 M 2 11 SamplePplegal PplegalpplegalОценок пока нет
- Dynamics KinematicsДокумент32 страницыDynamics Kinematicsวอ แวณОценок пока нет
- Mechanism DesignДокумент30 страницMechanism DesignBivas Panigrahi0% (1)
- Introduction To Mechanism and KinematicsДокумент17 страницIntroduction To Mechanism and Kinematicsfieramina83% (6)
- Solucionario Berr Chapter13Документ38 страницSolucionario Berr Chapter13Johan Andres Arenas0% (1)
- Theory of Machine Unit 1Документ122 страницыTheory of Machine Unit 1Deepak PrajapatОценок пока нет
- Vibration: (BDA31103) Multi-Degree of FreedomДокумент65 страницVibration: (BDA31103) Multi-Degree of FreedomhildaОценок пока нет
- Mechanical Vibrations: Why Do We Study ?Документ27 страницMechanical Vibrations: Why Do We Study ?sagar kumarОценок пока нет
- Kinematics of Particles (Ch1 Dynamics Chapter 11 Beer7)Документ43 страницыKinematics of Particles (Ch1 Dynamics Chapter 11 Beer7)Er Shankar Singh Dhami100% (3)
- Two Lecture VibrationДокумент12 страницTwo Lecture VibrationUjjawal GuptaОценок пока нет
- 4 Bar Mechanism PDFДокумент3 страницы4 Bar Mechanism PDFSagar Dutt MathurОценок пока нет
- Straight Line MechanismsДокумент2 страницыStraight Line MechanismsكنوزخطابОценок пока нет
- Dynamics - Chapter 16 (Beer7)Документ39 страницDynamics - Chapter 16 (Beer7)api-3709496100% (4)
- Class Robotics Unit3Документ97 страницClass Robotics Unit3Senthilkumaar JS100% (1)
- Random VibrationsДокумент20 страницRandom VibrationsVivek PandeyОценок пока нет
- 1406 Advanced Kinematics and Dynamics of MachineryДокумент13 страниц1406 Advanced Kinematics and Dynamics of MachineryChiranjeev JainОценок пока нет
- Dynamics 15 LectureДокумент106 страницDynamics 15 Lecturelalo RodriguezОценок пока нет
- Application Differential EquationДокумент37 страницApplication Differential EquationNida KhairiyahОценок пока нет
- Notes-Unit-1 - 1d Kinematics StudentДокумент12 страницNotes-Unit-1 - 1d Kinematics StudenttrucksrcoolОценок пока нет
- 27-11 Mechanical Vibration (ME)Документ3 страницы27-11 Mechanical Vibration (ME)Mahir MahmoodОценок пока нет
- Mechanical Vibration NotesДокумент56 страницMechanical Vibration NotesYadanaОценок пока нет
- 2 Marks Question & AnswerДокумент9 страниц2 Marks Question & AnswerShanmuga PriyaОценок пока нет
- Stress Strain DiagramДокумент4 страницыStress Strain DiagramMartine CastroОценок пока нет
- Solved Problems: Single Degree Free VibrationДокумент14 страницSolved Problems: Single Degree Free Vibrationprem adhikariОценок пока нет
- 2D Motion of A Particle Using Plan-Polar Coordinates: Velocity ComponentsДокумент71 страница2D Motion of A Particle Using Plan-Polar Coordinates: Velocity Componentssharwan sharmaОценок пока нет
- Robotics (17ME2504A) Unit IV Manipulator KinematicsДокумент32 страницыRobotics (17ME2504A) Unit IV Manipulator KinematicsNani PusuluriОценок пока нет
- FrictionДокумент62 страницыFrictionchellamvОценок пока нет
- 1-Basic ConceptsДокумент47 страниц1-Basic Conceptsjaved hussainОценок пока нет
- Basu-Fem Notes Me623Документ210 страницBasu-Fem Notes Me623Subhradeep ChatterjeeОценок пока нет
- BMMV3043 TutorialДокумент4 страницыBMMV3043 TutorialKartik KrisnianОценок пока нет
- Rotational MotionДокумент4 страницыRotational MotionWraith KingОценок пока нет
- 2 Wave EquationДокумент34 страницы2 Wave EquationSandeep Chaudhary100% (1)
- Mechanical Properties of MaterialsДокумент53 страницыMechanical Properties of MaterialsfanaОценок пока нет
- Seminar Report1Документ9 страницSeminar Report1Abhilash JhaОценок пока нет
- Jacobians-Differential KinematicsДокумент62 страницыJacobians-Differential KinematicsChay Tick FeiОценок пока нет
- Lagrange Equations: Use Kinetic and Potential Energy To Solve For Motion!Документ32 страницыLagrange Equations: Use Kinetic and Potential Energy To Solve For Motion!Ribal KhreisОценок пока нет
- 05 Question Bank Fo RMV Unit V Continuous Systems 06 05 2018 Additional PDFДокумент4 страницы05 Question Bank Fo RMV Unit V Continuous Systems 06 05 2018 Additional PDFNABIL HUSSAIN0% (1)
- Kinematics of MechanicsДокумент34 страницыKinematics of MechanicsErasmo Israel Garcia Ochoa100% (1)
- Kinematics and Dynamics of Machinery Lab ManualДокумент63 страницыKinematics and Dynamics of Machinery Lab ManualsaranОценок пока нет
- D-H Problems PDFДокумент9 страницD-H Problems PDFkrupachariОценок пока нет
- r05320305 Design of Machine Members IIДокумент11 страницr05320305 Design of Machine Members IISrinivasa Rao G100% (4)
- FemДокумент10 страницFemSeenu CnuОценок пока нет
- Holonomic and Nonholonomic ConstraintsДокумент20 страницHolonomic and Nonholonomic Constraintsoltinn0% (1)
- Fourier TransformДокумент16 страницFourier TransformManish Kumar MouryaОценок пока нет
- Hamiltonian PDFДокумент64 страницыHamiltonian PDFAnnaОценок пока нет
- Chapter - 11 - Forced Vibration Single Degree of Freedom SystemsДокумент19 страницChapter - 11 - Forced Vibration Single Degree of Freedom SystemsRakesh BhaskerОценок пока нет
- Dynamics Lecture2 General Curvilinear Motion - Rectangular Components and Projectile MotionДокумент41 страницаDynamics Lecture2 General Curvilinear Motion - Rectangular Components and Projectile MotionJJ Enzon100% (1)
- PhysicsДокумент11 страницPhysicsEthylОценок пока нет
- Chapter 12-15Документ59 страницChapter 12-15Abdulaziz FarhanОценок пока нет
- Problems Lesson 1 (Kinematics)Документ18 страницProblems Lesson 1 (Kinematics)Gabrielgarcy12Оценок пока нет
- Impulse MomentumДокумент29 страницImpulse MomentumpinkysushuОценок пока нет
- Kinematics of A Particle AllДокумент160 страницKinematics of A Particle AllaychiluhimhailuОценок пока нет
- Chapter II (Compatibility Mode)Документ160 страницChapter II (Compatibility Mode)Biruk TemesgenОценок пока нет
- Kinematics Using Vector Analysis: Standard CompetencyДокумент18 страницKinematics Using Vector Analysis: Standard CompetencyYasheive saadiОценок пока нет
- Topic 3 - Kinematics CurveДокумент30 страницTopic 3 - Kinematics CurveBoodjieh So ImbaОценок пока нет
- Gamma-Aminobutyric AcidДокумент12 страницGamma-Aminobutyric AcidAnkan PalОценок пока нет
- Mesalazine: Mesalazine (INN, BAN), Also Known As Mesalamine (USAN) or 5-Aminosalicylic AcidДокумент4 страницыMesalazine: Mesalazine (INN, BAN), Also Known As Mesalamine (USAN) or 5-Aminosalicylic AcidAnkan PalОценок пока нет
- Mefenamic Acid Is A Non-SteroidalДокумент4 страницыMefenamic Acid Is A Non-SteroidalAnkan PalОценок пока нет
- Praziquantel - Wikipedia, The Free EncyclopediaДокумент6 страницPraziquantel - Wikipedia, The Free EncyclopediaAnkan PalОценок пока нет
- Pyridine - Wikipedia, The Free EncyclopediaДокумент15 страницPyridine - Wikipedia, The Free EncyclopediaAnkan Pal100% (1)
- Fusidic Acid - Wikipedia, The Free EncyclopediaДокумент6 страницFusidic Acid - Wikipedia, The Free EncyclopediaAnkan PalОценок пока нет
- 6th Central Pay Commission Salary CalculatorДокумент15 страниц6th Central Pay Commission Salary Calculatorrakhonde100% (436)
- PhysicsДокумент28 страницPhysicsAniket DeyОценок пока нет
- Levofloxacin - Wikipedia, The Free EncyclopediaДокумент19 страницLevofloxacin - Wikipedia, The Free EncyclopediaAnkan PalОценок пока нет
- What Are Bacteria - Streptococcus FaecalisДокумент3 страницыWhat Are Bacteria - Streptococcus FaecalisAnkan PalОценок пока нет
- Differences Between Generations of CephalosporinsДокумент3 страницыDifferences Between Generations of CephalosporinsAnkan PalОценок пока нет
- Ofloxacin - Wikipedia, The Free EncyclopediaДокумент20 страницOfloxacin - Wikipedia, The Free EncyclopediaAnkan PalОценок пока нет
- Abstract AlgebraДокумент3 страницыAbstract AlgebraAnkan PalОценок пока нет
- Pin Racking Mech U-PowerДокумент2 страницыPin Racking Mech U-PowerAnkan PalОценок пока нет
- C-POWER ACB For DC ApplicationДокумент4 страницыC-POWER ACB For DC ApplicationAnkan PalОценок пока нет
- PIN New FSD Connector 20122010Документ1 страницаPIN New FSD Connector 20122010Ankan PalОценок пока нет
- Important Instructions To Examiners:: Maharashtra State Board of Technical Education (ISO/IEC - 27001 - 2013 Certified)Документ15 страницImportant Instructions To Examiners:: Maharashtra State Board of Technical Education (ISO/IEC - 27001 - 2013 Certified)Mohit D MoreОценок пока нет
- MTV310 Chapter3-1 CompleteДокумент5 страницMTV310 Chapter3-1 CompleteThabiso MashigoОценок пока нет
- Thermodynamics QuestionsДокумент2 страницыThermodynamics QuestionssreyaОценок пока нет
- Moving Man SimulationДокумент12 страницMoving Man SimulationAlexa AquinoОценок пока нет
- Opensource - Electrical Machines Part 2Документ9 страницOpensource - Electrical Machines Part 2Mohammad Sharid S. SchuckОценок пока нет
- Convert Ion MeasurementДокумент2 страницыConvert Ion MeasurementSayed MachfudОценок пока нет
- Stem - Physics 2 CGДокумент15 страницStem - Physics 2 CGVictoria Mabini100% (7)
- Surface Areas and VolumesДокумент63 страницыSurface Areas and Volumesnirvana.7Оценок пока нет
- Engi 9113 (2020) - Final Exam SolutionДокумент10 страницEngi 9113 (2020) - Final Exam SolutionReza AsakerehОценок пока нет
- Fiz Uis f4p1Документ12 страницFiz Uis f4p1Adibah AliasОценок пока нет
- Weight CalculatorДокумент2 страницыWeight Calculatorfarooqui rehmatОценок пока нет
- Electrical Thumb Rules (Part 3)Документ3 страницыElectrical Thumb Rules (Part 3)Himdad TahirОценок пока нет
- Lab ManualДокумент5 страницLab ManualAnonymous 5etAwAM3LT100% (1)
- Introduction To Electricity and Magnetism: Project PHYSNET Physics Bldg. Michigan State University East Lansing, MIДокумент6 страницIntroduction To Electricity and Magnetism: Project PHYSNET Physics Bldg. Michigan State University East Lansing, MIp_k_soni_iit_physicsОценок пока нет
- Phy 11L Finals: - Multiple Choice. Choose The CorrectДокумент3 страницыPhy 11L Finals: - Multiple Choice. Choose The CorrectMerlin MendozaОценок пока нет
- Motion Question AnswersДокумент11 страницMotion Question Answerspiyush_2189Оценок пока нет
- Volume K1Документ88 страницVolume K1salbiah_ibrОценок пока нет
- Fundamentals of Biomechanics 4.3Документ199 страницFundamentals of Biomechanics 4.3Maggie-Louise BellamyОценок пока нет
- Course Outline Applied Physics PDFДокумент2 страницыCourse Outline Applied Physics PDFMuhammad UmerОценок пока нет
- 10 - Accesorios de Los Transformadores (Parte2)Документ63 страницы10 - Accesorios de Los Transformadores (Parte2)LOURDES JANNETH LIMON ROMEROОценок пока нет
- Chapter 14 Kinetics of Particle - Work & EnergyДокумент37 страницChapter 14 Kinetics of Particle - Work & Energyحزيفہ اعظمОценок пока нет
- Idoc - Pub Astm TablesДокумент253 страницыIdoc - Pub Astm TablesShekhar SumanОценок пока нет
- Admmodule Stem Gp12v Ia 8 9Документ26 страницAdmmodule Stem Gp12v Ia 8 9Diana Silva Hernandez100% (2)
- Svcma Course Material ModifiedДокумент46 страницSvcma Course Material Modifiedsai manoharОценок пока нет
- Conservation Equations For Mass Momentum and EnergyДокумент12 страницConservation Equations For Mass Momentum and Energypuja kochОценок пока нет
- Physics UnitsДокумент5 страницPhysics UnitsGopan KrishnanОценок пока нет
- Profexam 115Документ3 страницыProfexam 115eiufjojОценок пока нет
- Liquid Scale reading = Liquid density, ρ specific gravity, S Water Engine Oil Glycerol corn OilДокумент14 страницLiquid Scale reading = Liquid density, ρ specific gravity, S Water Engine Oil Glycerol corn OiltareqОценок пока нет
- A Design Methodology of Resonant LLC DC-DC ConverterДокумент10 страницA Design Methodology of Resonant LLC DC-DC ConverterArsalan AtharОценок пока нет
- Supercoductivity, Its Type and ApplicationsДокумент8 страницSupercoductivity, Its Type and ApplicationsRahul YadavОценок пока нет