Академический Документы
Профессиональный Документы
Культура Документы
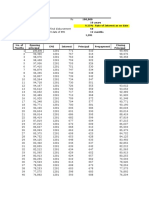
Time Value of Money
Загружено:
mohitash23Исходное описание:
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Time Value of Money
Загружено:
mohitash23Авторское право:
Доступные форматы
What Is Time Value? If you're like most people, you would choose to receive the $10,000 now.
After all, three years is a long time to wait. Why would any rational person defer payment into the future when he or she could have the same amount of money now? For most of us, taking the money in the present is just plain instinctive. So at the most basic level, the time value of money demonstrates that, all things being equal, it is better to have money now rather than later. But why is this? A $100 bill has the same value as a $100 bill one year from now, doesn't it? Actually, although the bill is the same, you can do much more with the money if you have it now because over time you can earn more interest on your money. Back to our example: by receiving $10,000 today, you are poised to increase the future value of your money by investing and gaining interest over a period of time. For Option B, you don't have time on your side, and the payment received in three years would be your future value. To illustrate, we have provided a timeline:
If you are choosing Option A, your future value will be $10,000 plus any interest acquired over the three years. The future value for Option B, on the other hand, would only be $10,000. So how can you calculate exactly how much more Option A is worth, compared to Option B? Let's take a look. SEE: Internal Rate Of Return: An Inside Look Future Value Basics If you choose Option A and invest the total amount at a simple annual rate of 4.5%, the future value of your investment at the end of the first year is $10,450, which of course is calculated by multiplying the principal amount of $10,000 by the interest rate of 4.5% and then adding the interest gained to the principal amount: Future value of investment at end of first year: = ($10,000 x 0.045) + $10,000 = $10,450 You can also calculate the total amount of a one-year investment with a simple manipulation of the above equation: Original equation: ($10,000 x 0.045) + $10,000 = $10,450 Manipulation: $10,000 x [(1 x 0.045) + 1] = $10,450 Final equation: $10,000 x (0.045 + 1) = $10,450 The manipulated equation above is simply a removal of the like-variable $10,000 (the principal amount) by dividing the entire original equation by $10,000.
If the $10,450 left in your investment account at the end of the first year is left untouched and you invested it at 4.5% for another year, how much would you have? To calculate this, you would take the $10,450 and multiply it again by 1.045 (0.045 +1). At the end of two years, you would have $10,920: Future value of investment at end of second year: = $10,450 x (1+0.045) = $10,920.25 The above calculation, then, is equivalent to the following equation: Future Value = $10,000 x (1+0.045) x (1+0.045) Think back to math class and the rule of exponents, which states that the multiplication of like terms is equivalent to adding their exponents. In the above equation, the two like terms are (1+0.045), and the exponent on each is equal to 1. Therefore, the equation can be represented as the following: We can see that the exponent is equal to the number of years for which the money is earning interest in an investment. So, the equation for calculating the three-year future value of the investment would look like this:
This calculation shows us that we don't need to calculate the future value after the first year, then the second year, then the third year, and so on. If you know how many years you would like to hold a present amount of money in an investment, the future value of that amount is calculated by the following equation: SEE:Accelerating Returns With Continuous Compounding Present Value Basics If you received $10,000 today, the present value would of course be $10,000 because present value is what your investment gives you now if you were to spend it today. If $10,000 were to be received in a year, the present value of the amount would not be $10,000 because you do not have it in your hand now, in the present. To find the present value of the $10,000 you will receive in the future, you need to pretend that the $10,000 is the total future value of an amount that you invested today. In other words, to find the present value of the future $10,000, we need to find out how much we would have to invest today in order to receive that $10,000 in the future. To calculate present value, or the amount that we would have to invest today, you must subtract the (hypothetical) accumulated interest from the $10,000. To achieve this, we can discount the future payment amount ($10,000) by the interest rate for the period. In essence, all you are doing is rearranging the future value equation above so that you may
solve for P. The above future value equation can be rewritten by replacing the P variable with present value (PV) and manipulated as follows:
Let's walk backwards from the $10,000 offered in Option B. Remember, the $10,000 to be received in three years is really the same as the future value of an investment. If today we were at the two-year mark, we would discount the payment back one year. At the twoyear mark, the present value of the $10,000 to be received in one year is represented as the following: Present value of future payment of $10,000 at end of year two:
Note that if today we were at the one-year mark, the above $9,569.38 would be considered the future value of our investment one year from now. Continuing on, at the end of the first year we would be expecting to receive the payment of $10,000 in two years. At an interest rate of 4.5%, the calculation for the present value of a $10,000 payment expected in two years would be the following: Present value of $10,000 in one year:
Of course, because of the rule of exponents, we don't have to calculate the future value of the investment every year counting back from the $10,000 investment at the third year. We could put the equation more concisely and use the $10,000 as FV. So, here is how you can calculate today's present value of the $10,000 expected from a three-year investment earning 4.5%:
So the present value of a future payment of $10,000 is worth $8,762.97 today if interest rates are 4.5% per year. In other words, choosing Option B is like taking $8,762.97 now and then investing it for three years. The equations above illustrate that Option A is better not only because it offers you money right now but because it offers you $1,237.03 ($10,000 - $8,762.97) more in cash! Furthermore, if you invest the $10,000 that you receive from Option A, your choice gives you a future value that is $1,411.66 ($11,411.66 - $10,000) greater than the future value of Option B. SEE: Economics And The Time Value Of Money Present Value of a Future Payment Let's add a little spice to our investment knowledge. What if the payment in three years is more than the amount you'd receive today? Say you could receive either $15,000 today or $18,000 in four years. Which would you choose? The decision is now more difficult. If
you choose to receive $15,000 today and invest the entire amount, you may actually end up with an amount of cash in four years that is less than $18,000. You could find the future value of $15,000, but since we are always living in the present, let's find the present value of $18,000 if interest rates are currently 4%. Remember that the equation for present value is the following:
In the equation above, all we are doing is discounting the future value of an investment. Using the numbers above, the present value of an $18,000 payment in four years would be calculated as the following: Present Value
From the above calculation we now know our choice is between receiving $15,000 or $15,386.48 today. Of course we should choose to postpone payment for four years! The Bottom Line These calculations demonstrate that time literally is money - the value of the money you have now is not the same as it will be in the future and vice versa. So, it is important to know how to calculate the time value of money so that you can distinguish between the worth of investments that offer you returns at different times. Read more: http://www.investopedia.com/articles/03/082703.asp#ixzz2KQXa1ncl
Calculating The Present And Future Value Of Annuities September 03 2010| Filed Under Annuity, Formulas, Personal Finance, Retirement, Savings At some point in your life you may have had to make a series of fixed payments over a period of time - such as rent or car payments - or have received a series of payments over a period of time, such as bond coupons. These are called annuities. If you understand the time value of money and have an understanding of future and present value you're ready to learn about annuities and how their present and future values are calculated. (To read
more on this subject, see Understanding The Time Value Of Money and Continuously Compound Interest.) What Are Annuities? Annuities are essentially series of fixed payments required from you or paid to you at a specified frequency over the course of a fixed period of time. The most common payment frequencies are yearly (once a year), semi-annually (twice a year), quarterly (four times a year) and monthly (once a month). There are two basic types of annuities: ordinary annuities and annuities due. Ordinary Annuity: Payments are required at the end of each period. For example, straight bonds usually pay coupon payments at the end of every six months until the bond's maturity date. Annuity Due: Payments are required at the beginning of each period. Rent is an example of annuity due. You are usually required to pay rent when you first move in at the beginning of the month, and then on the first of each month thereafter. Since the present and future value calculations for ordinary annuities and annuities due are slightly different, we will first discuss the present and future value calculation for ordinary annuities. Watch: What is An Annuity Calculating the Future Value of an Ordinary Annuity If you know how much you can invest per period for a certain time period, the future value of an ordinary annuity formula is useful for finding out how much you would have in the future by investing at your given interest rate. If you are making payments on a loan, the future value is useful for determining the total cost of the loan. Let's now run through Example 1. Consider the following annuity cash flow schedule:
In order to calculate the future value of the annuity, we have to calculate the future value of each cash flow. Let's assume that you are receiving $1,000 every year for the next five years, and you invested each payment at 5%. The following diagram shows how much you would have at the end of the five-year period:
Since we have to add the future value of each payment, you may have noticed that, if you have an ordinary annuity with many cash flows, it would take a long time to calculate all the future values and then add them together. Fortunately, mathematics provides a formula that serves as a short cut for finding the accumulated value of all cash flows received from an ordinary annuity:
C = Cash flow per period i = interest rate n = number of payments If we were to use the above formula for Example 1 above, this is the result: = $1000*[5.53] = $5525.63 Note that the one cent difference between $5,525.64 and $5,525.63 is due to a rounding error in the first calculation. Each of the values of the first calculation must be rounded to the nearest penny - the more you have to round numbers in a calculation the more likely rounding errors will occur. So, the above formula not only provides a short-cut to finding FV of an ordinary annuity but also gives a more accurate result. (Now that you know how to do these on your own, check out our Future Value of an Annuity Calculator for the easy method.) Calculating the Present Value of an Ordinary Annuity If you would like to determine today's value of a series of future payments, you need to use the formula that calculates the present value of an ordinary annuity. This is the formula you would use as part of a bond pricing calculation. The PV of ordinary annuity calculates the present value of the coupon payments that you will receive in the future. For Example 2, we'll use the same annuity cash flow schedule as we did in Example 1. To obtain the total discounted value, we need to take the present value of each future payment and, as we did in Example 1, add the cash flows together.
Again, calculating and adding all these values will take a considerable amount of time, especially if we expect many future payments. As such, there is a mathematical shortcut we can use for PV of ordinary annuity. C = Cash flow per period i = interest rate n = number of payments The formula provides us with the PV in a few easy steps. Here is the calculation of the annuity represented in the diagram for Example 2: = $1000*[4.33]
= $4329.48 Not that you'd want to use it now that you know the long way to get present value of an annuity, but just in case, you can check out our Present Value of an Annuity Calculator. Calculating the Future Value of an Annuity Due When you are receiving or paying cash flows for an annuity due, your cash flow schedule would appear as follows:
Since each payment in the series is made one period sooner, we need to discount the formula one period back. A slight modification to the FV-of-an-ordinary-annuity formula accounts for payments occurring at the beginning of each period. In Example 3, let's illustrate why this modification is needed when each $1,000 payment is made at the beginning of the period rather than the end (interest rate is still 5%):
Notice that when payments are made at the beginning of the period, each amount is held for longer at the end of the period. For example, if the $1,000 was invested on January 1st rather than December 31st of each year, the last payment before we value our investment at the end of five years (on December 31st) would have been made a year prior (January 1st) rather than the same day on which it is valued. The future value of annuity formula would then read:
Therefore, = $1000*5.53*1.05 = $5801.91 Check out our Future Value Annuity Due Calculator to save some time. Calculating the Present Value of an Annuity Due For the present value of an annuity due formula, we need to discount the formula one period forward as the payments are held for a lesser amount of time. When calculating the present value, we assume that the first payment was made today. We could use this formula for calculating the present value of your future rent payments as specified in a lease you sign with your landlord. Let's say for Example 4 that you make your first rent payment at the beginning of the month and are evaluating the present value of your five-month lease on that same day. Your present value calculation would work as follows:
Of course, we can use a formula shortcut to calculate the present value of an annuity due:
Therefore, = $1000*4.33*1.05 = $4545.95 Recall that the present value of an ordinary annuity returned a value of $4,329.48. The present value of an ordinary annuity is less than that of an annuity due because the further back we discount a future payment, the lower its present value: each payment or cash flow in ordinary annuity occurs one period further into future. Check out our Present Value Annuity Due Calculator. Conclusion Now you can see how annuity affects how you calculate the present and future value of any amount of money. Remember that the payment frequencies, or number of payments, and the time at which these payments are made (whether at the beginning or end of each payment period) are all variables you need to account for in your calculations.
Вам также может понравиться
- The Yellow House: A Memoir (2019 National Book Award Winner)От EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Рейтинг: 4 из 5 звезд4/5 (98)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeОт EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeРейтинг: 4 из 5 звезд4/5 (5794)
- The Little Book of Hygge: Danish Secrets to Happy LivingОт EverandThe Little Book of Hygge: Danish Secrets to Happy LivingРейтинг: 3.5 из 5 звезд3.5/5 (400)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureОт EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureРейтинг: 4.5 из 5 звезд4.5/5 (474)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryОт EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryРейтинг: 3.5 из 5 звезд3.5/5 (231)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceОт EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceРейтинг: 4 из 5 звезд4/5 (895)
- Team of Rivals: The Political Genius of Abraham LincolnОт EverandTeam of Rivals: The Political Genius of Abraham LincolnРейтинг: 4.5 из 5 звезд4.5/5 (234)
- Never Split the Difference: Negotiating As If Your Life Depended On ItОт EverandNever Split the Difference: Negotiating As If Your Life Depended On ItРейтинг: 4.5 из 5 звезд4.5/5 (838)
- The Emperor of All Maladies: A Biography of CancerОт EverandThe Emperor of All Maladies: A Biography of CancerРейтинг: 4.5 из 5 звезд4.5/5 (271)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaОт EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaРейтинг: 4.5 из 5 звезд4.5/5 (266)
- The Unwinding: An Inner History of the New AmericaОт EverandThe Unwinding: An Inner History of the New AmericaРейтинг: 4 из 5 звезд4/5 (45)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersОт EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersРейтинг: 4.5 из 5 звезд4.5/5 (345)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyОт EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyРейтинг: 3.5 из 5 звезд3.5/5 (2259)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreОт EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreРейтинг: 4 из 5 звезд4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)От EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Рейтинг: 4.5 из 5 звезд4.5/5 (121)
- Module 5 Using Mathematical TechniquesДокумент57 страницModule 5 Using Mathematical Techniquessheryl_morales100% (5)
- Chapter Two: The Financial Statement Auditing EnvironmentДокумент34 страницыChapter Two: The Financial Statement Auditing EnvironmentKookies4Оценок пока нет
- EconomicsДокумент50 страницEconomicshiteshrao810Оценок пока нет
- Step by Step Procedure To Solve Pension ProblemДокумент5 страницStep by Step Procedure To Solve Pension ProblemgcrajasekaranОценок пока нет
- Cumulative FD - Non-Cumulative Fixed DepositДокумент10 страницCumulative FD - Non-Cumulative Fixed Depositconfirm@Оценок пока нет
- Diaz vs. Secretary of Finance (G.R. No. 193007, July 19, 2011)Документ3 страницыDiaz vs. Secretary of Finance (G.R. No. 193007, July 19, 2011)EvangerylОценок пока нет
- Trends and Technology Timeline 2010Документ1 страницаTrends and Technology Timeline 2010Lynda KosterОценок пока нет
- Application Form Self Help Groups For PrintoutДокумент5 страницApplication Form Self Help Groups For Printoutnilya7081Оценок пока нет
- Recipe For Indices and Forex InvestingДокумент84 страницыRecipe For Indices and Forex InvestingAbdulafees Abdullahi Adebayo100% (4)
- Introduction To Financial DerivativesДокумент80 страницIntroduction To Financial Derivativessnehakopade0% (1)
- PRQZ 2Документ31 страницаPRQZ 2Yashrajsing LuckkanaОценок пока нет
- Full Download Fundamentals of Corporate Finance Asia Global 2nd Edition Ross Solutions ManualДокумент36 страницFull Download Fundamentals of Corporate Finance Asia Global 2nd Edition Ross Solutions Manualempiercefibberucql19100% (36)
- Civil Engineering Thumb RuleДокумент28 страницCivil Engineering Thumb Rulecivilsadiq100% (16)
- Revati Krishna CV (1) - 1Документ2 страницыRevati Krishna CV (1) - 1shivram.antallkoОценок пока нет
- Loan CalculatorДокумент5 страницLoan CalculatorHema Kumar Hema KumarОценок пока нет
- Bubble and Bee Lecture TemplateДокумент2 страницыBubble and Bee Lecture TemplateMavin JeraldОценок пока нет
- SAMPLE HOURLY: Personnel Activity Report (Time & Effort Report)Документ1 страницаSAMPLE HOURLY: Personnel Activity Report (Time & Effort Report)phaser2k10Оценок пока нет
- Brain Drain Is The Emigration of Highly Trained or Intelligent People From A Particular CountryДокумент3 страницыBrain Drain Is The Emigration of Highly Trained or Intelligent People From A Particular CountrydivyanshОценок пока нет
- CA Power of Attorney FORM & Info 87-68.200Документ29 страницCA Power of Attorney FORM & Info 87-68.200JugyОценок пока нет
- Corporations Statutes and RegulationsДокумент246 страницCorporations Statutes and Regulationsddreifuerst1984Оценок пока нет
- Mzalendo Trust Analysis of The Finance Bill 2023 CQMBHGNДокумент16 страницMzalendo Trust Analysis of The Finance Bill 2023 CQMBHGNRaoОценок пока нет
- Nikl Metals WeeklyДокумент7 страницNikl Metals WeeklybodaiОценок пока нет
- Multiple Choice Questions (MCQ) : Finance and Accounts DivisionДокумент9 страницMultiple Choice Questions (MCQ) : Finance and Accounts DivisionKawoser AhammadОценок пока нет
- Albuquerque Journal Homestyle 01/06/2017Документ15 страницAlbuquerque Journal Homestyle 01/06/2017Albuquerque JournalОценок пока нет
- ch07 - Intermediate Acc IFRS (Cash and Receivable)Документ104 страницыch07 - Intermediate Acc IFRS (Cash and Receivable)irma cahyani kawiОценок пока нет
- Bret 7 UДокумент31 страницаBret 7 UQuint WongОценок пока нет
- PT 2 Question Paper Class 8 Maths 2021-22Документ2 страницыPT 2 Question Paper Class 8 Maths 2021-22Neha BansalОценок пока нет
- Pre-Feasibility Study of The Iloilo Central Business District Revitalization ProjectДокумент46 страницPre-Feasibility Study of The Iloilo Central Business District Revitalization ProjectCarl100% (3)
- Manoj Batra 120 MCQДокумент14 страницManoj Batra 120 MCQAjay BalachandranОценок пока нет
- Development Project ProposalДокумент8 страницDevelopment Project Proposalnickdash09100% (1)