Академический Документы
Профессиональный Документы
Культура Документы
Quantum Cromodynamics - Keith Ellis
Загружено:
Sebastián Felipe Mantilla SerranoАвторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Quantum Cromodynamics - Keith Ellis
Загружено:
Sebastián Felipe Mantilla SerranoАвторское право:
Доступные форматы
Quantum Chromodynamics
Keith Ellis
Fermilab, February 2005
Lecture 1: QCD:Asymptotic freedom and infrared safety
QCD Lagrangian
Gauge Invariance
Feynman rules
Running coupling
-function
Non-perturbative QCD and infra-red divergences.
R.K.Ellis, Fermilab, February 2005
Lagrangian of QCD
Feynman rules for perturbative QCD follow from Lagrangian
1 =
1
4
F
A
A
+
X
avours
q
a
(i,D m)
ab
q
b
+1
gaugexing
F
A
is eld strength tensor for spin-1 gluon eld ,
A
,
F
A
,
A
,
A
gf
ABC
,
B
,
C
Capital indices A, B, C run over 8 colour degrees of freedom of the gluon eld. Third
non-Abelian term distinguishes QCD from QED, giving rise to triplet and quartic gluon
self-interactions and ultimately to asymptotic freedom.
QCD coupling strength is
S
g
2
/4. Numbers f
ABC
(A, B, C = 1, ..., 8) are
structure constants of the SU(3) colour group. Quark elds q
a
(a = 1, 2, 3) are in triplet
colour representation. D is covariant derivative:
(D
)
ab
=
ab
+ ig
t
C
,
C
ab
(D
)
AB
=
AB
+ ig(T
C
,
C
)
AB
R.K.Ellis, Fermilab, February 2005 1
t and T are matrices in the fundamental and adjoint representations of SU(3), respectively:
[t
A
, t
B
] = if
ABC
t
C
, [T
A
, T
B
] = if
ABC
T
C
where (T
A
)
BC
= if
ABC
. We use the metric g
= diag(1,1,1,1) and set
h = c = 1. ,D is symbolic notation for
. Normalisation of the t matrices is
Tr t
A
t
B
= T
R
AB
, T
R
=
1
2
.
Colour matrices obey the relations:
X
A
t
A
ab
t
A
bc
= C
F
ac
, C
F
=
N
2
1
2N
Tr T
C
T
D
=
X
A,B
f
ABC
f
ABD
= C
A
CD
, C
A
= N
Thus C
F
=
4
3
and C
A
= 3 for SU(3).
R.K.Ellis, Fermilab, February 2005 2
Gauge invariance
QCD Lagrangian is invariant under local gauge transformations. That is, one can redene quark
elds independently at every point in space-time,
q
a
(x) q
t
a
(x) = exp(it (x))
ab
q
b
(x) (x)
ab
q
b
(x)
without changing physical content.
Covariant derivative is so called because it transforms in same way as eld itself:
D
q(x) D
t
q
t
(x) (x)D
q(x) .
(omitting the colour labels of quark elds from now on). Use this to derive transformation
property of gluon eld ,
D
t
q
t
(x) = (
+ igt ,
t
)(x)q(x)
(
(x))q(x) + (x)
q(x) + igt ,
t
(x)q(x)
where t ,
P
A
t
A
,
A
. Hence
t ,
t
= (x)t ,
1
(x) +
i
g
(
(x))
1
(x) .
R.K.Ellis, Fermilab, February 2005 3
Transformation property of gluon eld strength F
is
t F
(x) t F
t
(x) = (x)F
(x)
1
(x) .
Contrast this with gauge-invariance of QED eld strength. QCD eld strength is not gauge
invariant because of self-interaction of gluons. Carriers of the colour force are themselves
coloured, unlike the electrically neutral photon.
Note there is no gauge-invariant way of including a gluon mass. A term such as
m
2
,
is not gauge invariant. This is similar to QED result for mass of the photon. On the other hand
quark mass term is gauge invariant.
R.K.Ellis, Fermilab, February 2005 4
Feynman rules
Use free piece of QCD Lagrangian to obtain inverse quark and gluon propagators.
Quark propagator in momentum space obtained by setting
= ip
for an incoming
eld. Result is in Table 1. The i prescription for pole of propagator is determined by
causality, as in QED.
Gluon propagator impossible to dene without a choice of gauge. The choice
1
gaugexing
=
1
2
,
A
2
denes covariant gauges with gauge parameter . Inverse gluon propagator is then
(2)
AB, ]
(p) = i
AB
p
2
g
(1
1
)p
.
(Check that without gauge-xing term this function would have no inverse.) Resulting
propagator is in the table. = 1 (0) is Feynman (Landau) gauge.
R.K.Ellis, Fermilab, February 2005 5
R.K.Ellis, Fermilab, February 2005 6
Gauge xing explicitly breaks gauge invariance. However, in the end physical results will be
independent of gauge. For convenience, we usually use Feynman gauge.
In non-Abelian theories like QCD, covariant gauge-xing term must be supplemented by a ghost
term which we do not discuss here. Ghost eld, shown by dashed lines in the above table, cancels
unphysical degrees of freedom of gluon which would otherwise propagate in covariant gauges.
Propagators determined from S, interactions from S.
R.K.Ellis, Fermilab, February 2005 7
Alternative choice of gauge
An alternative choice of gauge xing is provided by the axial gauges which are xed in terms of
another vector which we denote by b
1
gauge-xing
=
1
2
,
A
2
,
The advantage of the axial class of gauge is that ghost elds are not required. However one pays
for this simplicity because the gluon propagator is more complicated. The inverse propagator is
(2)
AB, ]
(p) = i
AB
p
2
g
+
1
.
The inverse of this matrix gives the gauge boson propagator,
(2)
BC, ]
(p) =
BC
i
p
2
2
4
g
+
b
+ p
b p
(b
2
+ p
2
)p
(b p)
2
3
5
.
Notice the new singularities at b p = 0.
R.K.Ellis, Fermilab, February 2005 8
What are the properties of these gauges which make them interesting? Let us specialize to the
case = 0, b
2
= 0, (light-cone gauge).
(2)
BC,]
(p) =
BC
i
p
2
d
(p, b)
where
d
= g
+
b
+ p
b p
.
In the limit p
2
0 we nd that
b
(p, b) = 0, p
(p, b) = 0 .
Only two physical polarization states, orthogonal to b and p, propagate. For this reason these
classes of gauges are called physical gauges. In the p
2
0 limit we may decompose the
numerator of the propagator into a sum over two polarizations:
d
=
X
i
(i)
(p)
(i)
(p) .
In addition to the constraint
(i)
(p)p
= 0, which is always true, in an axial gauge we have
the further constraint
(i)
(p)b
= 0.
R.K.Ellis, Fermilab, February 2005 9
Running coupling
Consider dimensionless physical observable R which depends on a single large energy scale,
Q m where m is any mass. Then we can set m 0 (assuming this limit exists), and
dimensional analysis suggests that R should be independent of Q.
This is not true in quantum eld theory. Calculation of R as a perturbation series in the coupling
S
= g
2
/4 requires renormalization to remove ultraviolet divergences. This introduces a
second mass scale point at which subtractions which remove divergences are performed.
Then R depends on the ratio Q/ and is not constant. The renormalized coupling
S
also
depends on .
But is arbitrary! Therefore, if we hold bare coupling xed, R cannot depend on . Since R
is dimensionless, it can only depend on Q
2
/
2
and the renormalized coupling
S
. Hence
2
d
d
2
R
Q
2
2
,
S
2
+
2
R = 0 .
R.K.Ellis, Fermilab, February 2005 10
Introducing
= ln
Q
2
, (
S
) =
2
2
,
we have
+ (
S
)
R = 0.
This renormalization group equation is solved by dening running coupling
S
(Q):
=
Z
S
(Q)
S
dx
(x)
,
S
()
S
.
Then
S
(Q)
= (
S
(Q)) ,
S
(Q)
S
=
(
S
(Q))
(
S
)
.
and hence R(Q
2
/
2
,
S
) = R(1,
S
(Q)). Thus all scale dependence in R comes from
running of
S
(Q).
We shall see QCD is asymptotically free:
S
(Q) 0 as Q . Thus for large Q we can
safely use perturbation theory. Then knowledge of R(1,
S
) to xed order allows us to predict
variation of R with Q.
R.K.Ellis, Fermilab, February 2005 11
Beta function
Running of the QCD coupling
S
is determined by the function, which has the expansion
(
S
) = b
2
S
(1 + b
t
S
) +c(
4
S
)
b =
(11C
A
2N
f
)
12
, b
t
=
(17C
2
A
5C
A
N
f
3C
F
N
f
)
2(11C
A
2N
f
)
,
where N
f
is number of active light avours. Terms up to c(
5
S
) are known.
R.K.Ellis, Fermilab, February 2005 12
Roughly speaking, quark loop diagram (a) contributes negative N
f
term in b, while gluon loop
(b) gives positive C
A
contribution, which makes function negative overall.
QED function is
QED
() =
1
3
2
+ . . .
Thus b coecients in QED and QCD have opposite signs.
From previous section,
S
(Q)
= b
2
S
(Q)
h
1 + b
t
S
(Q)
i
+c(
4
S
).
Neglecting b
t
and higher coecients gives
S
(Q) =
S
()
1 +
S
()b
, = ln
Q
2
.
As Q becomes large,
S
(Q) decreases to zero: this is asymptotic freedom. Notice that sign of
b is crucial. In QED, b < 0 and coupling increases at large Q.
Including next coecient b
t
gives implicit equation for
S
(Q):
b =
1
S
(Q)
S
()
+ b
t
ln
S
(Q)
1 + b
t
S
(Q)
b
t
ln
S
()
1 + b
t
S
()
R.K.Ellis, Fermilab, February 2005 13
What type of terms does the solution of the renormalization group equation take into account
in the physical quantity R?
Assume that R has perturbative expansion
R =
S
+c(
2
S
)
Solution R(1,
S
(Q)) can be re-expressed in terms of
S
():
R(1,
S
(Q)) =
S
()
X
j=0
(1)
j
(
S
()b)
j
=
S
()
h
1
S
()b +
2
S
()(b)
2
+ . . .
i
Thus there are logarithms of Q
2
/
2
which are automatically resummed by using the running
coupling. Neglected terms have fewer logarithms per power of
S
.
R.K.Ellis, Fermilab, February 2005 14
Lambda parameter
Perturbative QCD tells us how
S
(Q) varies with Q, but its absolute value has to be obtained
from experiment. Nowadays we usually choose as the fundamental parameter the value of the
coupling at Q = M
Z
, which is simply a convenient reference scale large enough to be in the
perturbative domain.
Also useful to express
S
(Q) directly in terms of a dimensionful parameter (constant of
integration) :
ln
Q
2
2
=
Z
S
(Q)
dx
(x)
=
Z
S
(Q)
dx
bx
2
(1 + b
t
x + . . .)
.
Then (if perturbation theory were the whole story)
S
(Q) as Q . More generally,
sets the scale at which
S
(Q) becomes large.
In leading order (LO) keep only rst -function b:
S
(Q) =
1
b ln(Q
2
/
2
)
(LO).
R.K.Ellis, Fermilab, February 2005 15
In next-to-leading order (NLO) include also b
t
:
1
S
(Q)
+ b
t
ln
b
t
S
(Q)
1 + b
t
S
(Q)
= b ln
Q
2
.
This can be solved numerically, or we can obtain an approximate solution to second order in
1/ log(Q
2
/
2
):
S
(Q) =
1
b ln(Q
2
/
2
)
"
1
b
t
b
ln ln(Q
2
/
2
)
ln(Q
2
/
2
)
#
(NLO).
This is Particle Data Group (PDG) denition.
Note that depends on number of active avours N
f
. Active means m
q
< Q. Thus for
5 < Q < 175 GeV we should use N
f
= 5. See ESW for relation between s for dierent
values of N
f
.
R.K.Ellis, Fermilab, February 2005 16
Measurements of
S
are reviewed in ESW. A more recent compilation from hep-ex/0407021 is
shown above. Evidence that
S
(Q) has a logarithmic fall-o with Q is persuasive.
R.K.Ellis, Fermilab, February 2005 17
S
at m
Z
jets & shapes 161 GeV
jets & shapes 172 GeV
0.08 0.10 0.12 0.14
___ _ ((( (SSS S ))) )
s Z
o-decays [LEP]
xF [i -DIS]
F [e-, -DIS]
[ decays
K(Z --> had.) [LEP]
e e [m ]
+
had
_
e e [jets & shapes 35 GeV]
+
_
m(pp --> jets)
pp --> bb X
0
QQ + lattice QCD
DIS [GLS-SR]
2
3
pp, pp --> a X
DIS [Bj-SR]
e e [jets & shapes 58 GeV]
+
_
jets & shapes 133 GeV
e e [jets & shapes 22 GeV]
+
_
e e [jets & shapes 44 GeV]
+
_
e e [m ]
+
had
_
jets & shapes 183 GeV
DIS [pol. strct. fctn.]
jets & shapes 189 GeV
e e [scaling. viol.]
+
_
jets & shapes 91.2 GeV
e e F
+
_
2
a
e e [jets & shapes 14 GeV]
+
_
e e [4-jet rate]
+
_
jets & shapes 195 GeV
jets & shapes 201 GeV
jets & shapes 206 GeV
DIS [ep > jets]
S
(M
Z
) = 0.1182 0.0027, hep-ex/0407021, (2004)
R.K.Ellis, Fermilab, February 2005 18
Non-perturbative QCD
Corresponding to asymptotic freedom at high momentum scales, we have infra-red slavery:
S
(Q) becomes large a low momenta, (long distances). Perturbation theory is not reliable for
large
S
, so non-perturbative methods, (e.g. lattice) must be used.
Important low momentum scale phenomena
Connement: partons (quarks and gluons) found only in colour singlet bound states, hadrons,
size 1 fm. If we try top separate them it becomes energetically favourable to create extra
partons from the vacuum.
Hadronization: partons produced in short distance interactions re-organize themselves to
make the observed hadrons.
R.K.Ellis, Fermilab, February 2005 19
Infrared divergences
Even in high-energy, short-distance regime, long-distance aspects of QCD cannot be ignored.
Soft or collinear gluon emission gives infrared divergences in PT. Light quarks (m
q
)
also lead to divergences in the limit m
q
0 (mass singularities).
Spacelike branching: gluon splitting on incoming line (a)
p
2
b
= 2E
a
E
c
(1 cos ) 0 .
Propagator factor 1/p
2
b
diverges as E
c
0 (soft singularity) or 0 (collinear or
mass singularity). If a and b are quarks, inverse propagator factor is
p
2
b
m
2
q
= 2E
a
E
c
(1 v
a
cos ) 0 ,
Hence E
c
0 soft divergence remains; collinear enhancement becomes a divergence
R.K.Ellis, Fermilab, February 2005 20
as v
a
1, i.e. when quark mass is negligible. If emitted parton c is a quark, vertex
factor cancels E
c
0 divergence.
Timelike branching: gluon splitting on outgoing line (b)
p
2
a
= 2E
b
E
c
(1 cos ) 0 .
Diverges when either emitted gluon is soft (E
b
or E
c
0) or when opening angle
0. If b and/or c are quarks, collinear/mass singularity in m
q
0 limit. Again,
soft quark divergences cancelled by vertex factor.
Similar infrared divergences in loop diagrams, associated with soft and/or collinear
congurations of virtual partons within region of integration of loop momenta.
Infrared divergences indicate dependence on long-distance aspects of QCD not correctly
described by PT. Divergent (or enhanced) propagators imply propagation of partons over
long distances. When distance becomes comparable with hadron size 1 fm, quasi-free
partons of perturbative calculation are conned/hadronized non-perturbatively, and apparent
divergences disappear.
Can still use PT to perform calculations, provided we limit ourselves to two classes of
observables:
Infrared safe quantities, i.e. those insensitive to soft or collinear branching. Infrared
divergences in PT calculation either cancel between real and virtual contributions or
are removed by kinematic factors. Such quantities are determined primarily by hard,
short-distance physics; long-distance eects give power corrections, suppressed by inverse
powers of a large momentum scale.
R.K.Ellis, Fermilab, February 2005 21
Factorizable quantities, i.e. those in which infrared sensitivity can be absorbed into an
overall non-perturbative factor, to be determined experimentally.
In either case, infrared divergences must be regularized during PT calculation, even though
they cancel or factorize in the end.
Gluon mass regularization: introduce nite gluon mass, set to zero at end of calculation.
However, as we saw, gluon mass breaks gauge invariance.
Dimensional regularization: analogous to that used for ultraviolet divergences, except we
must increase dimension of space-time, = 2
D
2
< 0. Divergences are replaced by
powers of 1/.
R.K.Ellis, Fermilab, February 2005 22
Recap
QCD is an SU(3) gauge theory of quarks (3 colours) and gluons (8 colours,selnteracting)
Renormalization of dimensionless observables depending on a single large scale implies that
the scale dependence enters through the running coupling.
Asymptotic freedom implies that IR-safe quantities can be calculated in perturbation theory.
(M
Z
) : 0.118 in ve avour MS-renormalization scheme.
Perturbative QCD has infrared singularities due to collinear or soft parton emission. We can
calculate infra-red safe or factorizable quantities in perturbation theory.
R.K.Ellis, Fermilab, February 2005 23
Вам также может понравиться
- Optics - Benjamin Crowell 5 of 6Документ114 страницOptics - Benjamin Crowell 5 of 6Nige Danton100% (2)
- Helmholtz DecompositionДокумент4 страницыHelmholtz DecompositionSebastián Felipe Mantilla SerranoОценок пока нет
- Integral and Comparison TestsДокумент12 страницIntegral and Comparison TestsSebastián Felipe Mantilla SerranoОценок пока нет
- Fuchs and The Theory of Differentian EquationsДокумент26 страницFuchs and The Theory of Differentian EquationsSebastián Felipe Mantilla SerranoОценок пока нет
- Exp3 Photoelectric EffectДокумент18 страницExp3 Photoelectric EffectRitzyAmorM.EctinОценок пока нет
- Minimal SU (5) GUTДокумент2 страницыMinimal SU (5) GUTSebastián Felipe Mantilla SerranoОценок пока нет
- Helmholtz DecompositionДокумент4 страницыHelmholtz DecompositionSebastián Felipe Mantilla SerranoОценок пока нет
- Standard Model LagrangianДокумент2 страницыStandard Model LagrangianSebastián Felipe Mantilla SerranoОценок пока нет
- RiemannSurfacesMiniNotes W12Документ25 страницRiemannSurfacesMiniNotes W12Sebastián Felipe Mantilla SerranoОценок пока нет
- Step IДокумент8 страницStep IhmphryОценок пока нет
- Effect of Physical Activity On KneesДокумент11 страницEffect of Physical Activity On KneesGus LudlowОценок пока нет
- Jackson - Classical Electrodynamics 3rd EditionДокумент833 страницыJackson - Classical Electrodynamics 3rd EditionDeb Goldberg95% (19)
- Standard Model LagrangianДокумент2 страницыStandard Model LagrangianSebastián Felipe Mantilla SerranoОценок пока нет
- Minimal SU (5) GUTДокумент2 страницыMinimal SU (5) GUTSebastián Felipe Mantilla SerranoОценок пока нет
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeОт EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeРейтинг: 4 из 5 звезд4/5 (5782)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceОт EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceРейтинг: 4 из 5 звезд4/5 (890)
- The Yellow House: A Memoir (2019 National Book Award Winner)От EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Рейтинг: 4 из 5 звезд4/5 (98)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureОт EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureРейтинг: 4.5 из 5 звезд4.5/5 (474)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaОт EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaРейтинг: 4.5 из 5 звезд4.5/5 (265)
- The Little Book of Hygge: Danish Secrets to Happy LivingОт EverandThe Little Book of Hygge: Danish Secrets to Happy LivingРейтинг: 3.5 из 5 звезд3.5/5 (399)
- Never Split the Difference: Negotiating As If Your Life Depended On ItОт EverandNever Split the Difference: Negotiating As If Your Life Depended On ItРейтинг: 4.5 из 5 звезд4.5/5 (838)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryОт EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryРейтинг: 3.5 из 5 звезд3.5/5 (231)
- The Emperor of All Maladies: A Biography of CancerОт EverandThe Emperor of All Maladies: A Biography of CancerРейтинг: 4.5 из 5 звезд4.5/5 (271)
- Team of Rivals: The Political Genius of Abraham LincolnОт EverandTeam of Rivals: The Political Genius of Abraham LincolnРейтинг: 4.5 из 5 звезд4.5/5 (234)
- The Unwinding: An Inner History of the New AmericaОт EverandThe Unwinding: An Inner History of the New AmericaРейтинг: 4 из 5 звезд4/5 (45)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersОт EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersРейтинг: 4.5 из 5 звезд4.5/5 (344)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyОт EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyРейтинг: 3.5 из 5 звезд3.5/5 (2219)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreОт EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreРейтинг: 4 из 5 звезд4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)От EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Рейтинг: 4.5 из 5 звезд4.5/5 (119)
- Podkletnov 2001 Paper With Giovanni ModaneseДокумент39 страницPodkletnov 2001 Paper With Giovanni ModaneseNullpunktsenergieОценок пока нет
- p6 DownloadДокумент51 страницаp6 DownloadJohn Adams VillamoranОценок пока нет
- Ground State Wave Function and Energy of The Lithium AtomДокумент15 страницGround State Wave Function and Energy of The Lithium AtomMohammedHejaziОценок пока нет
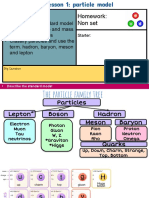
- Particle Molecule AtomДокумент3 страницыParticle Molecule AtomGermaeGonzalesОценок пока нет
- QCL Lecture LongДокумент160 страницQCL Lecture Longss626Оценок пока нет
- OU Open University SM358 2013 Exam SolutionsДокумент54 страницыOU Open University SM358 2013 Exam Solutionssam smith100% (3)
- Jack Sarfatti - Zero Point Energy, Star Gates & Warp Drive (2002)Документ32 страницыJack Sarfatti - Zero Point Energy, Star Gates & Warp Drive (2002)theherbsmith100% (1)
- Quantum Harmonic Oscillator GuideДокумент33 страницыQuantum Harmonic Oscillator GuideAlanoud AllaОценок пока нет
- Ta-Pei Cheng, Ling-Fong Li-Gauge Theory of Elementary Particle Physics Problems and Solutions-Oxford University Press (2000)Документ315 страницTa-Pei Cheng, Ling-Fong Li-Gauge Theory of Elementary Particle Physics Problems and Solutions-Oxford University Press (2000)Johan Renzo Salazar Malpartida100% (2)
- 03 Atomic StructureДокумент68 страниц03 Atomic StructureSUJATA SAHUОценок пока нет
- Failure of Classical MechanicsДокумент25 страницFailure of Classical MechanicsRasikh JalalОценок пока нет
- Electron Configurations GuideДокумент10 страницElectron Configurations GuideMonish KarakampalleОценок пока нет
- Wave-Particle Duality - WikipediaДокумент16 страницWave-Particle Duality - WikipediaRafih YahyaОценок пока нет
- Structure of the AtomДокумент29 страницStructure of the AtomSayantan MukherjeeОценок пока нет
- Particle model and forces explainedДокумент85 страницParticle model and forces explainedJustCallMeLarryОценок пока нет
- Report On ICM Project: Rutherford ScatteringДокумент10 страницReport On ICM Project: Rutherford ScatteringSaurabh KumarОценок пока нет
- Structure of An Atom Revision PaperДокумент5 страницStructure of An Atom Revision PaperZoe Kim ChinguwaОценок пока нет
- Quigg NotesДокумент87 страницQuigg NotesRohit DhirОценок пока нет
- Problem Solutions Becker String TheoryДокумент129 страницProblem Solutions Becker String Theorybanedog100% (2)
- KДокумент32 страницыKFathimath SajahathОценок пока нет
- Orca Manual 4 2 1Документ1 048 страницOrca Manual 4 2 1Daniel100% (1)
- As CT2 - Mechanics, Waves and QuantumДокумент9 страницAs CT2 - Mechanics, Waves and QuantumShabbir H. KhanОценок пока нет
- Atomic structure key conceptsДокумент27 страницAtomic structure key conceptsPriyanuj Bora50% (2)
- Blackbody Radiation and Photon Gas PropertiesДокумент26 страницBlackbody Radiation and Photon Gas PropertiesIca LubisОценок пока нет
- Quantum Field Theory AnomaliesДокумент91 страницаQuantum Field Theory AnomaliesrafitikiОценок пока нет
- Review 3 SolutionsДокумент17 страницReview 3 SolutionsAnonymous 7CxwuBUJz3Оценок пока нет
- Physics 215 - Quantum Mechanics 1 Assignment 5: Problem 1Документ11 страницPhysics 215 - Quantum Mechanics 1 Assignment 5: Problem 1SäntiiäGo Burgös PuëntësОценок пока нет
- Lesson Plan of Atomic Structure Grade IxДокумент3 страницыLesson Plan of Atomic Structure Grade IxKhadija0% (1)
- Ramsauer-Townsend Effect PDFДокумент3 страницыRamsauer-Townsend Effect PDFmisanthropoОценок пока нет
- MIT6 701S10 Notes by Marc BaldoДокумент261 страницаMIT6 701S10 Notes by Marc BaldoAlfredo Rico GuzmánОценок пока нет