Review of Lecture 2

The expectation value of an operator is the average of repeated measurements on an ensemble of

identically prepared particles.
Expectation value of position x:
_
`

x =

x|(x, t)|
2
dx
Expectation value of momentum p:
_
`

p = m
dx
dt
=i h

x
dx
Expectation value of a generic operator Q(x, p):
_
`

Q(x, p) =

x,
h
i

dx
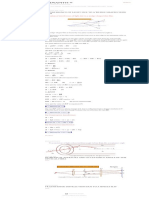
The Uncertainty Principle
Classically, we see no problem with measuring both the position and momentum of a particle
to arbitrary precision; doing so would essentially correspond to reducing the slightly spread-out
wave of the second plot to a localized spike and measuring the particles momentum to similar
precision. Quantum mechanics, on the other hand, says particles behave like waves, in the sense
that they are represented by a wavefunction that solves the wave equation. To account for the
wave-like nature of quantum systems, deBroglie formulated a relation between the wavelength
of a particle and its momentum:
the de Broglie formula:
_
`

p =
h

=
2 h

This means that for quantum mechanical systems, a spread in wavelength corresponds to a spread
in momentum. Using this fact in combination with the graphs above, this means the more well-
dened the position, the more spread out the wavelength, and hence, by the deBroglie relation,
the more spread out the momentum. Here spread refers to the fact that measurements on iden-
tically prepared systems do not yield identical results. This relationship between the spread of
measurements of position and momentum can be written quantitatively as the
Heisenberg uncertainty principle:
_
`

h
2
What this means in practice is that if you identically prepare many individual quantum mechanical
systems to be well-localized in space, the measured positions of these systems will be very similar
in value ( will be a localized spike), but if you measure the momentum of these identically
prepared systems, the values will be widely spread.
17
The Time-independent Schrdinger equation
How does one solve the Schrdinger equation?
Stationary states: We assume that the potential V is independent of time. In this case, the Schrdinger
equation can be solved by the method of separation of variables. We will look for the solutions
that are simple products:
For such separable solutions
18
This can only be true if both sides are constant. We will call the separation constant E.
We will consider how to solve the time-independent equation for various simple potentials. But
rst,
Why would we want to nd separable solutions?
1. They are stationary states, i.e. the probability density does not depend on time:
The time-dependence cancels out.
The same thing happens when you calculate the expectation value of any dynamic variable:
Every expectation value is constant in time, so we can drop and use in place of .
19
2. They are the states of denite total energy
In classical mechanics, the total energy is the Hamiltonian:
The expectation value of the total energy is
20
If = 0 every measurement of the total energy is certain to return the value E for these states.
3. The general solution is a linear combination of separable solutions.
As we will discover later, the time-independent Schrdinger equation yields a collection of solu-
tions (
1
(x),
2
(x),
3
(x), . . .), each with its value of the separation constant (E
1
, E
2
, . . .). Thus
there is a different wave function for each allowed energy:
Any linear combination of solutions of the Schrdinger equation is a solution. Thus a general
solution can be constructed as
where the constants c
n
are found by tting to the initial conditions.
Note that although the
n
are stationary states, the general solution is not necessarily stationary,
because the energies are different for different
n
and the exponentials do not necessarily cancel
when you calculate ||
2
.
21
The innite square well
A particle in this potential is completely free, except at the two ends, where an innite force
prevents it from escaping.
Lets solve the Schrdinger equation!
First, we seek stationary states
We need to solve the time-independent Schrdinger equation
to nd (x).
Outside of the well, (x) = 0.
Inside the well, where V = 0, the time-independent Schrdinger equation becomes:
We introduce k

2mE
h
and write
where A and B are arbitrary constants, generally obtained from boundary conditions.
22
What are the boundary conditions for (x)? Usually, both (x) and
d
dx
are continuous (to be
proved later), but where V only (x) is continuous.
Continuity of (x) requires that
Now we can nd out something about A and B.
Therefore, the distinct solutions are
and thus quantum particles in the innite square well cannot have just any energy it has to be one
of these special allowed values.
23
Now, we nd A by normalizing (x):
Global phase carries no signicance in quantum mechanics, since we always take ||
2
, so we can
pick the positive root.
These solutions look like:
24
The set of functions
n
(x) has the following properties:
1. They are alternately even and odd:
1
is even,
2
is odd, etc.
2. As you go up in energy, each successive state has one more node (zero-crossing).
3. They are mutually orthogonal, i.e.
We can combine orthogonality and normalization into a single statement:
We say that functions
n
(x) are orthonormal.
4. They are complete, in the sense that any other function, f (x), can be expressed as a linear
combination of them:
The coefcients c
n
can be evaluated using
Fouriers trick:
_

25