Академический Документы
Профессиональный Документы
Культура Документы
Fluid Flow in Solidification 2
Загружено:
Anonymous T02GVGzBИсходное описание:
Оригинальное название
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Fluid Flow in Solidification 2
Загружено:
Anonymous T02GVGzBАвторское право:
Доступные форматы
Graduate Institute of Ferrous Technology, POSTECH
Rongshan Qin (R. S. Qin)
15. Fluid flow in solidification 2
15.1 Governing equation for fluid flow
Motion of fluid is governed by a set of equations called the Navier-Stokes
equations. These equations are derived by Navier in 1831, and more rigorously
by Stokes in 1845. The Navier-Stokes equations describe the physics of a large
number of phenomena, for examples, blood flow in vessels and pollution
spreading. Its importance in alloy solidification has been promoted by the
recently developed semisolid metal processing technology.
To demonstrate the derivation of the Navier-Stokes equations we consider an
infinitesimal volume of fluid as illustrated in figure 1. The derivations are based
on conservations of mass, momentum and energy.
Figure 1. An infinitesimal volume of fluid considered here
Conservation of mass
The principle of the mass conservation states that mass cannot be created or
disappeared in the infinitesimal volume. The rate at which mass changes within
the volume = The rate at which mass enters or leaves the volume through its six
boundaries.
Graduate Institute of Ferrous Technology, POSTECH
Rongshan Qin (R. S. Qin)
The mass within the volume = z y x , where xyz is the volume and is
the average density in the infinitesimal volume.
The rate at which mass changes within the volume
( )
( )
t
z y x
t
z y x
=
Suppose that the fluid flows with a velocity of z w y v x u V + + =
r
, the rate at which
mass moves through boundary
1 z y u S V = =
1 1 1 1 1
r r
The negative appears from the definition of that the flow-in is positive and is
opposite to the surface normal. The rate at which mass moves through other
boundaries are:
2: z y u S V = =
2 2 2 2 2
r r
3: z x v S V = =
3 3 3 3 3
r r
4: z x v S V = =
4 4 4 4 4
r r
5: y x w S V = =
5 5 5 5 5
r r
6: y x w S V = =
6 6 6 6 6
r r
The mass conservation gives
( ) ( ) ( ) ( ) y x w y x w z x v z x v z y u z y u
t
z y x =
5 5 6 6 3 3 4 4 1 1 2 2
( )
( ) ( ) ( )
(
=
z
w w
y
v v
x
u u
z y x
5 5 6 6 3 3 4 4 1 1 2 2
(15.1)
Because the considered volume is infinitesimal, equation (15.1) reduces into
( ) ( ) ( ) ( ) V w
z
v
y
u
x t
r
(15.2)
Or the continuity equation
( ) 0 = +
V
t
r
(15.3)
Graduate Institute of Ferrous Technology, POSTECH
Rongshan Qin (R. S. Qin)
Conservation of momentum
Fluid can be continuously deformed when a shear stress is applied. The stress is
identified by two subscripts such as
xy
, where the first subscript indicates the
plane on which they act and the second subscript identifies the direction of the
force associated with the force.
xy
implies that the plane is normal to the x-axis
and the shear force is pointing in the y-direction. The total stress requires three
pieces of information (its magnitude, its direction and the plane on which it acts)
to completely specify it. For Newtonian flow where stress and strain rate has
linear relationship is expresses as
y
u
yx
= (15.4)
Stokes extended Newton's idea from simple 1-D flow to 3D flow. He developed
the following relations, collectively known as Stokes relations.
(15.5)
The conservation of the momentum states that the change of the momentum in
the volume equals to the net rate of momentum enters or leaves the volume +
forces acting on the control volume. We consider the momentum change along x
direction firstly.
Graduate Institute of Ferrous Technology, POSTECH
Rongshan Qin (R. S. Qin)
The rate of change of momentum in the volume ( ) z y x u
t
=
The rate at which u-momentum enters through those boundaries are:
1. z y u u
1 1 1
2. z y u u
2 2 2
3. z x v u
3 3 3
4. z x v u
4 4 4
5. y x w u
5 5 5
6. y x w u
6 6 6
The pressure force acting on left and right boundaries are
1. z y P
2. z y P
The viscous forces on boundaries are
1. z y
xx
1
2. z y
xx
2
3. z x
yx
3
4. z x
yx
4
5. y x
zx
5
6. y x
zx
6
Summing up these contributions, dividing through x y x and taking the
assumption of infinitesimal volume, it has:
( ) ( ) ( ) ( )
z y x z
uw
y
uv
x
P uu
t
u
zx
yx
xx
+
+
(15.6)
With same algorithm, we can obtain
Graduate Institute of Ferrous Technology, POSTECH
Rongshan Qin (R. S. Qin)
( ) ( ) ( ) ( )
z y x z
vw
x
vu
y
P vv
t
v
zy yy xy
+
+
(15.7)
and
( ) ( ) ( ) ( )
z y x y
wv
x
wu
z
P ww
t
w
zz
yz
xz
+
+
(15.8)
Conservation of energy
The conservation of energy, or the first law of thermodynamics, states that: The
rate at which the total energy (i.e. internal + kinetic) increases within a volume
equals to the rate at which the energy enters into the volume + the rate at which
work is done on the system (via surface and body) + the rate at which heat is
generated or sunk. The mass specific energy is defined as
( ) ( )
2 2 2 2 2 2
2
1
2
1
w v u CT w v u e E + + + = + + + = (15.9)
where e is the mass specific internal energy and C is the specific heat capacity.
The rate at which total energy increases within the volume
( )
z y x
t
E
The rate of energy enters and leaves the boundaries of the volume are:
1. z y E u
1 1 1
2. z y E u
2 2 2
3. z x E v
3 3 3
4. z x E v
4 4 4
5. y x E w
5 5 5
6. y x E w
6 6 6
Totally as
( ) ( ) ( )
z y x
z
wE
y
vE
x
uE
|
|
\
|
At the surfaces of the control volume, there are pressure and viscous forces that
do work on the fluid, as the fluid particles cross the boundary. For examples, on
face 1, the pressure forces and viscous forces may be expressed as
Graduate Institute of Ferrous Technology, POSTECH
Rongshan Qin (R. S. Qin)
( ) z y z y x x P
xz xy xx
. The fluid velocity at this boundary is z w y v x u + + . The
rate at which work is done by the surface forces acting on surface 1 is
( ) z y w v u Pu
xz xy xx
Summation of all six boundaries and considering of the infinitesimal volume gives
( ) ( ) ( )
(
x
v u w Pw
y
w u v Pv
x
w v u Pu
z y x
zy zx zz yz yx yy xz xy xx
The rate of work done by body force z g y g x g g
z y x
+ + =
r
is
z y x
wg vg ug + +
The rate at which heat flows across a surface of unit area is proportional to the
negative of the temperature gradient normal to this surface. As we learned before,
the heat conduction effects at all six boundaries are
(
(
(
(
\
|
|
|
\
|
\
|
z
z
T
k
y
y
T
k
x
x
T
k
z y x
The heat generation and sinking rate is
z
q
y
q
x
q
z
y
x
Summing up all the terms we get the energy equation.
( ) ( ) ( ) ( ) ( ) ( ) ( )
z
wP
y
vP
x
uP
z
wE
y
vE
x
uE
t
E
( ) ( ) ( )
z
w v u
y
w v u
x
w v u
zz zy zx yz yy yx xz xy xx
+ +
+
+ +
+
+ +
=
Graduate Institute of Ferrous Technology, POSTECH
Rongshan Qin (R. S. Qin)
( ) ( ) ( )
z
q
y
q
x
q
wg vg ug
z
z T k
y
y T k
x
x T k
z
y
x
z y x
+ + +
(
+
(15.10)
15.2 Temperature distribution for planar coquette flow
Consider a case as illustrated in figure 2. The bottom and top plates are at
temperature of T1 and T2, respectively. The top plate is moving at the velocity V.
The pressure gradient satisfies 0 / = dx dP . We can solve the temperature
distribution in the fluid between the plates, and compute the rate at which heat is
transferred from the hot plate to the cold plate, as follows.
Figure 2. Temperature between moving heat plates
The energy equation for this case is obtained by reducing of equation (15.10)
( ) ( ) ( ) ( ) ( )
y
vP
x
uP
y
vE
x
uE
t
E
( ) ( )
( ) ( )
(
+
+
+
=
y
y T k
x
x T k
y
v u
x
v u
yy yx xy xx
For our parallel flow, we can set /x =0 and v = 0. For the case where 0 / = dx dP ,
the velocity profile is linear. One has
Graduate Institute of Ferrous Technology, POSTECH
Rongshan Qin (R. S. Qin)
When these expressions are substituted into the energy equation, and when all
x-derivatives are set to zero, and when v is set to zero, the following form results.
Integrating the above equation twice, we get
where C and D are constants of integration. These constants may be found by
applying the boundary condition T= T1 at y=0, and T = T2 at y= h. The final form
is
The first two terms in the above expression are linear in y, and model the effect
of conduction on the temperature distribution. The third term models the effect of
heat generation due to viscous work.
References
1. http://www.ae.gatech.edu/labs/windtunl/classes/hispd/hispd06/ns_eqns.html
2. http://www.allstar.fiu.edu/AERO/Flow2.htm
Вам также может понравиться
- Full Elementary Aerodynamics Course by MITДокумент158 страницFull Elementary Aerodynamics Course by MIT34plt34Оценок пока нет
- The Plasma Dispersion Function: The Hilbert Transform of the GaussianОт EverandThe Plasma Dispersion Function: The Hilbert Transform of the GaussianРейтинг: 5 из 5 звезд5/5 (1)
- δ F δm g, where: Forces acting on a differential element of fluidДокумент8 страницδ F δm g, where: Forces acting on a differential element of fluidsuwashacharyaОценок пока нет
- 1 Basic Equations of Hydromechanics: 1.1 General Transport EquationДокумент16 страниц1 Basic Equations of Hydromechanics: 1.1 General Transport EquationRaed NagmОценок пока нет
- FEM FullДокумент423 страницыFEM FullHarish LambadiОценок пока нет
- Chapter 8 Navier-Stokes EquationДокумент16 страницChapter 8 Navier-Stokes EquationSyahiran SalehОценок пока нет
- Laws of Fluid MotionДокумент12 страницLaws of Fluid Motiondist2235Оценок пока нет
- 3.1 Flow of Invisid and Homogeneous Fluids: Chapter 3. High-Speed FlowsДокумент5 страниц3.1 Flow of Invisid and Homogeneous Fluids: Chapter 3. High-Speed FlowspaivensolidsnakeОценок пока нет
- CH 2 - Wave Propagation in Viscous Fluid PDFДокумент20 страницCH 2 - Wave Propagation in Viscous Fluid PDFRhonda BushОценок пока нет
- Chapter8 Latest Combined ComplejoДокумент49 страницChapter8 Latest Combined ComplejoLuis Carlos Gonzales RengifoОценок пока нет
- Ch. IV Differential Relations For A Fluid Particle: V (R, T) I U X, Y, Z, T J V X, Y, Z, T K W X, Y, Z, TДокумент12 страницCh. IV Differential Relations For A Fluid Particle: V (R, T) I U X, Y, Z, T J V X, Y, Z, T K W X, Y, Z, TAditya GargОценок пока нет
- Fundamental Notions of Viscous Fluid MechanicsДокумент63 страницыFundamental Notions of Viscous Fluid Mechanicsbakri10101Оценок пока нет
- Chapter 3: Basic Elements Section 3 1: Preliminaries (Review of Section 3.1: Preliminaries (Review of Solid Mechanics)Документ52 страницыChapter 3: Basic Elements Section 3 1: Preliminaries (Review of Section 3.1: Preliminaries (Review of Solid Mechanics)Prakash KancharlaОценок пока нет
- Stresses in LiquidsДокумент9 страницStresses in LiquidsAl-Kawthari As-SunniОценок пока нет
- ST VenantДокумент18 страницST VenantgelicabalticaОценок пока нет
- Ecuatiile Saint Venant PDFДокумент18 страницEcuatiile Saint Venant PDFvale1127Оценок пока нет
- A9 PDFДокумент2 страницыA9 PDFdoraОценок пока нет
- Fluid Rotation: Figure. Rectangular Fluid Particle With Two Instantaneous PerpendicularДокумент10 страницFluid Rotation: Figure. Rectangular Fluid Particle With Two Instantaneous PerpendicularEmreОценок пока нет
- Navier Stokes EquationsДокумент17 страницNavier Stokes EquationsAlice LewisОценок пока нет
- 3 1 IrrotДокумент4 страницы3 1 IrrotShridhar MathadОценок пока нет
- fl3 Navier StokesДокумент6 страницfl3 Navier Stokesrahpooye313Оценок пока нет
- Radial Viscous Flow Between Two Parallel Annular PlatesДокумент12 страницRadial Viscous Flow Between Two Parallel Annular PlatesKyi Htin PawОценок пока нет
- Inviscid Fluid FlowДокумент22 страницыInviscid Fluid FlowmiladОценок пока нет
- Fluid NotesДокумент11 страницFluid NotesDeeptanshu ShuklaОценок пока нет
- Chee 331 Notes On Fluid IzationДокумент21 страницаChee 331 Notes On Fluid Ization0721673895Оценок пока нет
- Class 6 - Eqns of MotionДокумент37 страницClass 6 - Eqns of MotionverbicarОценок пока нет
- Esci342 Lesson07 Continuity EquationДокумент8 страницEsci342 Lesson07 Continuity EquationMohamed Abd El-MoniemОценок пока нет
- Basic Fluid Dynamics: Yue-Kin Tsang February 9, 2011Документ12 страницBasic Fluid Dynamics: Yue-Kin Tsang February 9, 2011alulatekОценок пока нет
- Stokes Drag FormulaДокумент4 страницыStokes Drag FormulaAjith KrishnanОценок пока нет
- Daniel Spirn and J. Douglas Wright - Linear Dispersive Decay Estimates For Vortex Sheets With Surface TensionДокумент27 страницDaniel Spirn and J. Douglas Wright - Linear Dispersive Decay Estimates For Vortex Sheets With Surface TensionPonmijОценок пока нет
- Derivation of The Navier-Stokes Equations, and Implications For Groundwater FlowДокумент20 страницDerivation of The Navier-Stokes Equations, and Implications For Groundwater FlowsuryaОценок пока нет
- A Brief Introduction To Atmospheric Dynamics: J. H. Lacasce, UioДокумент61 страницаA Brief Introduction To Atmospheric Dynamics: J. H. Lacasce, UioyyasamannОценок пока нет
- Chap3 Differential Eqns ZSJДокумент55 страницChap3 Differential Eqns ZSJNaresh SuwalОценок пока нет
- Corr Halle PaperДокумент14 страницCorr Halle PaperAntonio Martín AlcántaraОценок пока нет
- Lin Stab AnalysisДокумент7 страницLin Stab AnalysisMohammad RameezОценок пока нет
- Calculatioyjrtfgjdof Revolution With ArbitraryДокумент12 страницCalculatioyjrtfgjdof Revolution With ArbitrarySmileОценок пока нет
- 1.7 The Lagrangian DerivativeДокумент6 страниц1.7 The Lagrangian DerivativedaskhagoОценок пока нет
- A Derivation of The Navier-Stokes Equations: Neal ColemanДокумент7 страницA Derivation of The Navier-Stokes Equations: Neal ColemanEmmanuel IgweОценок пока нет
- Chap 4 Sec2 PDFДокумент15 страницChap 4 Sec2 PDFteknikpembakaran2013Оценок пока нет
- Flow in A Mixed Compression Intake With Linear and Quadratic ElementsДокумент10 страницFlow in A Mixed Compression Intake With Linear and Quadratic ElementsVarun BhattОценок пока нет
- 1 Navier StokesДокумент12 страниц1 Navier StokesShaurya SethОценок пока нет
- Chapter 2 - The Equations of MotionДокумент12 страницChapter 2 - The Equations of MotionAravind SankarОценок пока нет
- Differential Equations For Fluid MotionДокумент29 страницDifferential Equations For Fluid MotionLameuneОценок пока нет
- The Momentum EquationДокумент11 страницThe Momentum EquationLutfi IsmailОценок пока нет
- Lecture Notes Fluid Dynamics - Problems - LatexДокумент50 страницLecture Notes Fluid Dynamics - Problems - LatexDikaОценок пока нет
- Non-Local Continuum Mechanics and Fractional Calculus: K.A. LazopoulosДокумент5 страницNon-Local Continuum Mechanics and Fractional Calculus: K.A. Lazopoulosrs0004Оценок пока нет
- Introduction To Basic Principles of Fluid MechanicsДокумент11 страницIntroduction To Basic Principles of Fluid MechanicsNoureldin YosriОценок пока нет
- Chap 4 Sec1 PDFДокумент15 страницChap 4 Sec1 PDFteknikpembakaran2013Оценок пока нет
- 348 Term Paper ForemanДокумент9 страниц348 Term Paper ForemanSamuel Alfred ForemanОценок пока нет
- HydrodynamicsДокумент9 страницHydrodynamicsOur SalahEddineОценок пока нет
- Basic Equations of Fluid Mechanics: Dr.-Ing. Naseem UddinДокумент19 страницBasic Equations of Fluid Mechanics: Dr.-Ing. Naseem UddindabeeraliОценок пока нет
- Unsteady Rotor-Stator Interaction in A Low Pressure Centrifugal CompressorДокумент6 страницUnsteady Rotor-Stator Interaction in A Low Pressure Centrifugal CompressorbaubaumihaiОценок пока нет
- Mathematical Description of Conservation Equations Involving An InterfaceДокумент16 страницMathematical Description of Conservation Equations Involving An InterfaceeustaccoОценок пока нет
- Governing Equations For Fluid Motion: K W J V I U VДокумент16 страницGoverning Equations For Fluid Motion: K W J V I U VKelvin SudaniОценок пока нет
- CE374-Ch2a - Ek (Compatibility Mode)Документ59 страницCE374-Ch2a - Ek (Compatibility Mode)Ruben Edhino Vicente DueñasОценок пока нет
- En0175 07 PDFДокумент6 страницEn0175 07 PDFThangadurai Senthil Ram PrabhuОценок пока нет
- Ns EquationsДокумент9 страницNs EquationsTahok24Оценок пока нет
- Fluid Mechanics Formulas ShortcutsДокумент15 страницFluid Mechanics Formulas Shortcuts9444583008Оценок пока нет
- Fluidsnotes PDFДокумент81 страницаFluidsnotes PDFMohammad irfanОценок пока нет
- Lecture 12 BДокумент1 страницаLecture 12 BAnonymous T02GVGzBОценок пока нет
- Lecture13 14Документ2 страницыLecture13 14Anonymous T02GVGzBОценок пока нет
- Burdukova Et Al. 2006. Effect of CMC and PH On The Rheology of Suspensions of Isotropic and Anisotropic MineralsДокумент15 страницBurdukova Et Al. 2006. Effect of CMC and PH On The Rheology of Suspensions of Isotropic and Anisotropic MineralsAnonymous T02GVGzBОценок пока нет
- Lecture 12Документ1 страницаLecture 12Anonymous T02GVGzBОценок пока нет
- Lecture 12 AДокумент1 страницаLecture 12 AAnonymous T02GVGzBОценок пока нет
- Chapter 14 CДокумент8 страницChapter 14 CAnonymous T02GVGzBОценок пока нет
- Lecture 7Документ2 страницыLecture 7Anonymous T02GVGzBОценок пока нет
- Exploration Analysis: Evaluation of Geochemical Data C. JДокумент2 страницыExploration Analysis: Evaluation of Geochemical Data C. JAnonymous T02GVGzBОценок пока нет
- Chapter Outline: Failure Fracture: How Do Materials Break?Документ9 страницChapter Outline: Failure Fracture: How Do Materials Break?Anonymous T02GVGzBОценок пока нет
- Copper Flotation: Metals and Minerals IndustryДокумент2 страницыCopper Flotation: Metals and Minerals IndustryAnonymous T02GVGzBОценок пока нет
- Viscosity and Thermodynamics 2004Документ14 страницViscosity and Thermodynamics 2004Anonymous T02GVGzBОценок пока нет
- GJmatДокумент2 страницыGJmatAnonymous T02GVGzBОценок пока нет
- Solidification Processing: Lecture 10: Thermodynamics 3Документ17 страницSolidification Processing: Lecture 10: Thermodynamics 3Anonymous T02GVGzBОценок пока нет
- Case Study: Flow Models: 16.1 Lattice-Gas Automata ModelДокумент9 страницCase Study: Flow Models: 16.1 Lattice-Gas Automata ModelAnonymous T02GVGzBОценок пока нет
- Kinetics of Solidification 3: 13.1 Solid-Liquid Interface StructureДокумент7 страницKinetics of Solidification 3: 13.1 Solid-Liquid Interface StructureAnonymous T02GVGzBОценок пока нет
- Lecture 11Документ18 страницLecture 11Anonymous T02GVGzBОценок пока нет
- Fluid Flow in Solidification 1Документ7 страницFluid Flow in Solidification 1Anonymous T02GVGzBОценок пока нет
- Phase Field Models: Graduate Institute of Ferrous Technology, POSTECH Rongshan Qin (R. S. Qin)Документ10 страницPhase Field Models: Graduate Institute of Ferrous Technology, POSTECH Rongshan Qin (R. S. Qin)Anonymous T02GVGzBОценок пока нет
- Heat Transfer: Graduate Institute of Ferrous Technology, POSTECH Rongshan Qin (R. S. Qin)Документ8 страницHeat Transfer: Graduate Institute of Ferrous Technology, POSTECH Rongshan Qin (R. S. Qin)Anonymous T02GVGzBОценок пока нет
- Projectile Motion: Launching Things Into The Air: Section 4Документ24 страницыProjectile Motion: Launching Things Into The Air: Section 4keinwayОценок пока нет
- Pelton Wheel ExperimentДокумент7 страницPelton Wheel ExperimentCaleb KreegerОценок пока нет
- Crompton PaperДокумент7 страницCrompton PaperMuhammad Tayyab ZahoorОценок пока нет
- Problem Set 1 SolutionsДокумент5 страницProblem Set 1 SolutionssagarnitishpirtheeОценок пока нет
- Mechanics Level 3Документ40 страницMechanics Level 3greycouncilОценок пока нет
- Tutorial - Lecture 5 SolutionsДокумент10 страницTutorial - Lecture 5 SolutionsBastián Olfos MárquezОценок пока нет
- Chapter 11Документ49 страницChapter 11je steanОценок пока нет
- Engg Mechanics Ques BankДокумент68 страницEngg Mechanics Ques BankUtkalОценок пока нет
- Orbital Mechanics: Faraz AhmedДокумент8 страницOrbital Mechanics: Faraz AhmedHemendra PrasannaОценок пока нет
- Architectural AcousticsДокумент172 страницыArchitectural AcousticsMarnie B. Gutib100% (2)
- Newton's Laws of Motion Exercise PDFДокумент2 страницыNewton's Laws of Motion Exercise PDFwolfretonmathsОценок пока нет
- 11 TH PhysicsДокумент56 страниц11 TH PhysicsSammy GaurОценок пока нет
- Work Power and EnergyДокумент33 страницыWork Power and EnergyYfel UndagОценок пока нет
- V 2 Chap 1Документ34 страницыV 2 Chap 1guruvashisthaОценок пока нет
- Damped Harmonic Oscillators-1Документ11 страницDamped Harmonic Oscillators-1Shivam PandeyОценок пока нет
- UNIT-II-Quantum MechanicsДокумент9 страницUNIT-II-Quantum MechanicsGopichand surupulaОценок пока нет
- N. F. Mott - Elements of Wave MechanicsДокумент172 страницыN. F. Mott - Elements of Wave Mechanicsmasaud rejaliОценок пока нет
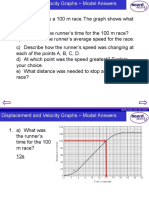
- P1c Displacement Time and Velocity Time Graphs Worksheet MSДокумент17 страницP1c Displacement Time and Velocity Time Graphs Worksheet MSDiamondОценок пока нет
- C-Band Wavelengths List and Codes: C C C C CДокумент2 страницыC-Band Wavelengths List and Codes: C C C C CPhyo Zin AungОценок пока нет
- KINEMATICSДокумент22 страницыKINEMATICSHemanth MadduriОценок пока нет
- CH 33Документ30 страницCH 33Phang MakhandaОценок пока нет
- As GCE Physics A 2823 01 June 2006 Question PaperДокумент12 страницAs GCE Physics A 2823 01 June 2006 Question PaperMitul KaziОценок пока нет
- 9 A Student Is Playing A Game With Some Empty Tins.: Turn OverДокумент3 страницы9 A Student Is Playing A Game With Some Empty Tins.: Turn OverYu SunОценок пока нет
- Axial Flow in Annulus With Rotating CylinderДокумент13 страницAxial Flow in Annulus With Rotating CylinderBrandonОценок пока нет
- Conceptual Questions:: University of Zambia School of Natural Sciences Department of PhysicsДокумент2 страницыConceptual Questions:: University of Zambia School of Natural Sciences Department of PhysicsAngel JereОценок пока нет
- SoundДокумент38 страницSoundthinkiitОценок пока нет
- Projectiles ws2 PDFДокумент2 страницыProjectiles ws2 PDFAnandraj GovindarajОценок пока нет
- Concentric Annular Flow With Centerbody Rotation of A Newtonian and A Shear-Thinning LiquidДокумент7 страницConcentric Annular Flow With Centerbody Rotation of A Newtonian and A Shear-Thinning LiquidHicham HichamОценок пока нет
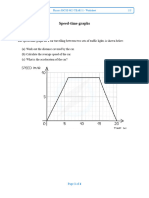
- Session 1 - Speed-Time Graph Worksheet - For StudentДокумент4 страницыSession 1 - Speed-Time Graph Worksheet - For StudentSelvenОценок пока нет
- Chapter Practice Problems-1: FiitjeeДокумент4 страницыChapter Practice Problems-1: FiitjeeullasagwОценок пока нет
- Giza: The Tesla Connection: Acoustical Science and the Harvesting of Clean EnergyОт EverandGiza: The Tesla Connection: Acoustical Science and the Harvesting of Clean EnergyОценок пока нет
- A Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and ScienceОт EverandA Beginner's Guide to Constructing the Universe: The Mathematical Archetypes of Nature, Art, and ScienceРейтинг: 4 из 5 звезд4/5 (51)
- Dark Matter and the Dinosaurs: The Astounding Interconnectedness of the UniverseОт EverandDark Matter and the Dinosaurs: The Astounding Interconnectedness of the UniverseРейтинг: 3.5 из 5 звезд3.5/5 (69)
- Knocking on Heaven's Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern WorldОт EverandKnocking on Heaven's Door: How Physics and Scientific Thinking Illuminate the Universe and the Modern WorldРейтинг: 3.5 из 5 звезд3.5/5 (64)
- Summary and Interpretation of Reality TransurfingОт EverandSummary and Interpretation of Reality TransurfingРейтинг: 5 из 5 звезд5/5 (5)
- The End of Everything: (Astrophysically Speaking)От EverandThe End of Everything: (Astrophysically Speaking)Рейтинг: 4.5 из 5 звезд4.5/5 (157)
- Midnight in Chernobyl: The Story of the World's Greatest Nuclear DisasterОт EverandMidnight in Chernobyl: The Story of the World's Greatest Nuclear DisasterРейтинг: 4.5 из 5 звезд4.5/5 (410)
- A Brief History of Time: From the Big Bang to Black HolesОт EverandA Brief History of Time: From the Big Bang to Black HolesРейтинг: 4 из 5 звезд4/5 (2193)
- The Holographic Universe: The Revolutionary Theory of RealityОт EverandThe Holographic Universe: The Revolutionary Theory of RealityРейтинг: 4.5 из 5 звезд4.5/5 (77)
- The Magick of Physics: Uncovering the Fantastical Phenomena in Everyday LifeОт EverandThe Magick of Physics: Uncovering the Fantastical Phenomena in Everyday LifeОценок пока нет
- Lost in Math: How Beauty Leads Physics AstrayОт EverandLost in Math: How Beauty Leads Physics AstrayРейтинг: 4.5 из 5 звезд4.5/5 (125)
- Quantum Spirituality: Science, Gnostic Mysticism, and Connecting with Source ConsciousnessОт EverandQuantum Spirituality: Science, Gnostic Mysticism, and Connecting with Source ConsciousnessРейтинг: 4 из 5 звезд4/5 (6)
- Bedeviled: A Shadow History of Demons in ScienceОт EverandBedeviled: A Shadow History of Demons in ScienceРейтинг: 5 из 5 звезд5/5 (5)
- The Power of Eight: Harnessing the Miraculous Energies of a Small Group to Heal Others, Your Life, and the WorldОт EverandThe Power of Eight: Harnessing the Miraculous Energies of a Small Group to Heal Others, Your Life, and the WorldРейтинг: 4.5 из 5 звезд4.5/5 (54)
- The Beginning of Infinity: Explanations That Transform the WorldОт EverandThe Beginning of Infinity: Explanations That Transform the WorldРейтинг: 5 из 5 звезд5/5 (60)
- Quantum Physics: What Everyone Needs to KnowОт EverandQuantum Physics: What Everyone Needs to KnowРейтинг: 4.5 из 5 звезд4.5/5 (49)
- Quantum Physcis for Beginners: An Easy Guide for Discovering the Hidden Side of Reality One Speck at a TimeОт EverandQuantum Physcis for Beginners: An Easy Guide for Discovering the Hidden Side of Reality One Speck at a TimeОценок пока нет
- Vibration and Frequency: How to Get What You Want in LifeОт EverandVibration and Frequency: How to Get What You Want in LifeРейтинг: 4.5 из 5 звезд4.5/5 (13)
- Hyperspace: A Scientific Odyssey Through Parallel Universes, Time Warps, and the 10th DimensionОт EverandHyperspace: A Scientific Odyssey Through Parallel Universes, Time Warps, and the 10th DimensionРейтинг: 4.5 из 5 звезд4.5/5 (3)
- Packing for Mars: The Curious Science of Life in the VoidОт EverandPacking for Mars: The Curious Science of Life in the VoidРейтинг: 4 из 5 звезд4/5 (1396)
- The Simulated Multiverse: An MIT Computer Scientist Explores Parallel Universes, The Simulation Hypothesis, Quantum Computing and the Mandela EffectОт EverandThe Simulated Multiverse: An MIT Computer Scientist Explores Parallel Universes, The Simulation Hypothesis, Quantum Computing and the Mandela EffectРейтинг: 4.5 из 5 звезд4.5/5 (20)
- Transform Your Life And Save The World: Through The Dreamed Of Arrival Of The Rehabilitating Biological Explanation Of The Human ConditionОт EverandTransform Your Life And Save The World: Through The Dreamed Of Arrival Of The Rehabilitating Biological Explanation Of The Human ConditionРейтинг: 5 из 5 звезд5/5 (2)
- Let There Be Light: Physics, Philosophy & the Dimensional Structure of ConsciousnessОт EverandLet There Be Light: Physics, Philosophy & the Dimensional Structure of ConsciousnessРейтинг: 4.5 из 5 звезд4.5/5 (57)