EXPLICIT RIEMANNIAN MANIFOLDS WITH

UNEXPECTEDLY BEHAVING CENTER OF MASS

CARLA CEDERBAUM AND CHRISTOPHER NERZ
Abstract. The (relativistic) center of mass of an asymptotically at Rie-
mannian manifold is often dened by certain surface integral expressions eval-
uated along a foliation of the manifold near innity, e. g. by Arnowitt, Deser,
and Misner (ADM). There are also what we call abstract denitions of the
center of mass in terms of a foliation near innity itself, going back to the
constant mean curvature (CMC-) foliation studied by Huisken and Yau; these
give rise to surface integral expressions when equipped with suitable systems
of coordinates. We discuss subtle asymptotic convergence issues regarding the
ADM- and the coordinate expressions related to the CMC-center of mass. In
particular, we give explicit examples demonstrating that both can diverge
in a setting where Einsteins equation is satised. Furthermore, we illustrate
the phenomenon by providing analogous examples in Newtonian gravity. Our
examples conict with some results in the literature.
1. Introduction and general considerations
Isolated gravitating systems are individual or clusters of stars, black holes, or
galaxies that do not interact with any matter or gravitational radiation outside
the system under consideration. Intuitively, they should have a (total) mass and
a (total) center of mass. We will demonstrate how delicately dierent notions of
(total) center of mass described in the literature depend on the decay of the matter
near innity, i. e. far away from the main constituents of the system.
Let us begin by stating (somewhat vague) denitions of isolated gravitating
systems to be made precise in Sections 3 and 4. Isolated gravitating systems have
been studied intensively both in Newtonian gravity (NG) and general relativity
(GR). In Newtonian gravity, an isolated gravitating system is described by a matter
density function : R
3
[0, ) that decays suitably fast at innity. It is useful to
introduce the Newtonian potential U solving the Poisson equation
U = 4 in R
3
, (1)
U 0 as r ,
where we have set the gravitational constant G to 1. U inherits its decay from .
In general relativity, isolated gravitating systems are modeled as asymptotically
at 3-dimensional Riemannian manifolds (M
3
, g) equipped with a symmetric (0, 2)-
tensor eld K suitably decaying at innity in the asymptotic end of the manifold.
In addition, an isolated gravitating system carries a suitably decaying mass density
Date: December 24, 2013.
This material is based upon work supported by the National Science Foundation under Grant
No. 0932078 000, while the authors were in residence at the Mathematical Science Research Insti-
tute in Berkeley, California, during the fall semester 2013.
1
a
r
X
i
v
:
1
3
1
2
.
6
3
9
1
v
1


[
m
a
t
h
.
A
P
]


2
2

D
e
c

2
0
1
3
2 CARLA CEDERBAUM AND CHRISTOPHER NERZ
function : M
3
R as well as a suitably decaying momentum density 1-form J.
and J are usually assumed to satisfy the dominant energy condition
[J[ (2)
on M
3
, where [ [ denotes the tensor norm induced by g. (M
3
, g) can be pictured
as a Riemannian submanifold or time-slice of a Lorentzian spacetime (M
4
, g). K
then arises as the induced second fundamental form. In this view, and J arise
as the time-time and the time-space components of the energy-momentum tensor
T of general relativity, respectively. The relativistic spacetime (M
4
, g) must satisfy
Einsteins equation
Ric
1
2
Rg = 8T, (3)
where we have set both the gravitational constant G and speed of light c to 1. Ric
and R denote the Ricci and scalar curvature of the Lorentzian metric g, respectively.
Applying the Gau-Mainardi-Codazzi equations to (M
3
, g) (M
4
, g), Einsteins
equation (3) implies the Einstein constraint equations
R [K[
2
+ (trK)
2
= 16 (4)
div(K trK g) = 8J. (5)
Here, tr and div denote the trace and the divergence with respect to g, respectively.
Collecting all the above pieces of information, we say that an isolated gravitating
system in GR is a so-called initial data set (M
3
, g, K, , J) of suitable decay and
satisfying (4) and (5). However, many properties of initial data sets (M
3
, g, K, , J)
such as e. g. mass and center of mass can be dened using only the Riemannian vari-
ables (M
3
, g) and we will frequently switch back and forth between the initial data
and the Riemannian perspectives. Also, we will explicitly denote the asymptotical
coordinate chart whenever it seems helpful.
This paper is concerned with delicate decay considerations related to the (total)
center of mass (CoM) of isolated gravitating systems in GR and NG, the latter
being regarded as an indicator of phenomena and an incubator for ideas. At the
same time, we will illustrate some more or less well-known analogies between the
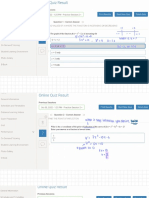
notions of center of mass in NG and GR, see Figure 1. When considering the
center of mass, we will always implicitly or explicitly assume that the related mass
is strictly positive. This is both a technical (as many denitions of center of mass
divide by the mass) and a physically reasonable assumption.
In NG, the mass and the center of mass of an isolated gravitating system are
conventionally determined by volume integrals of the matter density and the
weighted position vector x over the entire space R
3
, respectively, see (7) and
(8). The question whether the center of mass is well-dened thus depends on
the integrability properties of x in the sense of indenite Riemann integrals (in
spherical polars). On the other hand, as is essentially a divergence by (1), the
volume integrals for mass and center of mass can be rewritten in terms of surface
integrals at innity, see Section 3.
When an isolated gravitating system is modeled as an initial data set in GR, its
(total) relativistic mass, the so-called ADM-mass introduced by Arnowitt, Deser,
and Misner [ADM61], is given by a surface integral expression at innity, see (9).
The ADM-mass is known to asymptotically correspond to the volume integral over
the scalar curvature R in a sense made precise e. g. by Bartnik [Bar86]. Namely,
EXPLICIT RIEM. MFLDS. WITH UNEXPECTEDLY BEHAVING CENTER OF MASS 3
for any C
2
-asymptotically Schwarzschildean Riemannian manifold (M
3
, g, x) the
ADM-mass m
ADM
converges if and only if the volume integral

RdV
is nite (when taken over a suitable neighborhood of innty). This volume integral is
conceptually related to the Newtonian mass volume integral via (4). In the context
of static isolated gravitating systems with compactly supported matter, the rst
author dened a pseudo-Newtonian (quasi-local and total) mass such that the total
pseudo-Newtonian mass coincides with the ADM-mass of the system. Moreover,
the pseudo-Newtonian and thus the ADM-mass converges to the Newtonian mass as
c which provides further support for the relativistic concept of mass [Ced12,
Chap. 4, 6].
Let us proceed to discuss the (total) center of mass of an isolated gravitating
system in GR. First, let us remark that the contemporary literature knows several
denitions of such a center. One of the natural asymptotic decay conditions is to be
asymptotic to the Riemannian Schwarzschild metric, see Section 2. Several authors
dene the center of mass of an initial data set (M
3
, g, K, , J) as a foliation near
innity of the corresponding Riemannian manifold with total mass m > 0. We
will call such denitions abstract to contrast what we call coordinate denitions of
center of mass, see below.
The rst such denition was given by Huisken and Yau [HY96], who dened
the CMC-center of mass to be the unique foliation near innity by closed, sta-
ble surfaces with constant mean curvature. This was motivated by an idea of
Christodoulou and Yau [CY88]. Lamm, Metzger, and Schulze [LMS11] subsequent-
ly used a unique foliation by spheres of Willmore type. In the static case with
compactly supported matter, the rst author used level-sets of the static lapse
function to dene an abstract center of mass. As discussed in Section 3, we can
interpret the foliation near innity by level sets of the Newtonian potential as an
abstract center of mass in NG in the same spirit [Ced12, Chap. 3, 5], cf. Figure 1.
Chen, Wang, and Yau recently suggested a new denition of (quasi-local and
total) center of mass of isolated gravitating systems which is constructed from
optimal isometric embeddings into Minkowski spacetime [CWY13, Def. 3.2].
Other denitions of a relativistic CoM assign a specic center of mass vector
z R
3
to an isolated gravitating system. The vector z can be pictured to describe
a point in the target R
3
of the asymptotically at coordinate chart. The specic
vector z in the various constructions depends on the choice of coordinates near
innity (i. e. in the asymptotically at end of the manifold) at least a priori. In
particular, the CoM vectors z transform appropriately under Euclidean motions
applied to the chosen asymptotic coordinates. To distinguish such denitions from
the abstract denitions described above, we will call them coordinate centers of
mass.
The most important coordinate centers of mass in view of this paper are the
(coordinate) ADM- and the coordinate CMC-center of mass. The ADM-center
goes back to Arnowitt, Deser, and Misner [ADM61] and is constructed in close
analogy to the ADM-mass, see Denition 4.4. The coordinate CMC-center of mass
is constructed from the abstract CMC-center and was suggested by Huisken and
Yau [HY96] as a Euclidean center of the CMC-foliation, see Denition 4.2. Other
4 CARLA CEDERBAUM AND CHRISTOPHER NERZ
coordinate CoM notions have been suggested by Corvino and Schoen [CS06] and
by Huang [Hua10].
It is well-known that the coordinate CMC-center of mass of a given asymptot-
ically Schwarzschildean Riemannian manifold (M
3
, g, x) coincides with its ADM-
center of mass if the scalar curvature R is asymptotically even in the chosen co-
ordinates x, see Huang [Hua10] and Eichmair and Metzger [EM12]. This asymp-
totic evenness is summarized in the Regge-Teitelboim conditions and has a parallel
in the Newtonian context, see Section 3. The second author generalized this re-
sult, eliminating the Regge-Teitelboim conditions, and showed that asymptotically
Schwarzschildean Riemannian manifolds (M
3
, g, x) have a well-dened ADM-center
if and only if their coordinate CMC-center is well-dened (in the given asymptotic
coordinates x). Whenever one and thus both of them are well-dened, they coincide
[Ner13, Cor. 3.8].
The ADM-center of mass is known to asymptotically correspond to the volume
integral of the scalar curvature R integrated against x, i. e. for any C
2
-asymptotically
Schwarzschildean Riemannian manifold (M
3
, g, x) the ADM-center of mass z
ADM
converges if and only if the volume integral

RxdV
is nite (when taken over a suitable neighborhood of innty), see Corvino and
Wu [CW08], Denition 2.3, and page 14. This is true in particular if the Regge-
Teitelboim conditions are satised. As for the ADM-mass, this volume integral is
conceptually related to the Newtonian one via (4).
Again in the context of static isolated gravitating systems with compactly sup-
ported matter, the rst author dened a pseudo-Newtonian (quasi-local and total)
coordinate center of mass and proved that it coincides with the coordinate CMC-
and ADM-centers of mass (in appropriate geometric asymptotic coordinates). The
coordinate pseudo-Newtonian and thus the coordinate CMC- and ADM-center of
mass converges to the Newtonian one in the Newtonian limit c [Ced12,
Chap. 4, 6] which further justies the relativistic denitions.
We provide explicit examples of isolated gravitating systems of critical decay
for which the various coordinate centers of mass do not converge. The decay as-
sumptions we make fall within the category of metrics studied by Huisken and Yau
[HY96] and Metzger [Met07] who prove existence of the abstract CMC-center of
mass under stronger and weaker asymptotic conditions, respectively. They do not
satisfy the Regge-Teitelboim conditions. While the Euclidean centers of the leaves
of the CMC-foliation near innity stay bounded as asserted in [HY96, Proof of
Thm 5.1], they conict with the convergence to a coordinate CMC-center of mass
stated in [HY96, Thm 4.2].
The rst class of examples is derived from an understanding of the time evolu-
tion of the leaves of the CMC-foliation established by the second author in [Ner13,
Thm 3.1]. Here, we modify the Riemannian Schwarzschild metric by a term of the
form f(r) Y = O(r
2
), where f is a suitably chosen function and Y is the York
tensor introduced by York [Yor79] when considering the ADM-linear momentum.
Relying on the techniques developed in [Ner13], we nd that the Euclidean coor-
dinate centers of the CMC-leaves oscillate as the surfaces approach innity, see
Section 5. In this setting, we use an articial spacetime which probably has no
EXPLICIT RIEM. MFLDS. WITH UNEXPECTEDLY BEHAVING CENTER OF MASS 5
physical signicance; in particular, we do not specify the remaining data (K, , J)
needed to represent an initial data set.
The second class of examples arise as time-slices in the Schwarzschild space-
time (6), in particular as graphs over the canonical time-slice t = 0. As the
Schwarzschild spacetime satises the Einstein vacuum equation i. e. Equation (3)
with T 0 and hence 0, J 0 , and thus also the dominant energy condition
(2), these examples do seem physically relevant. However, the time-slices we study
may seem somewhat articial and denitely do not correspond to a conventional
family of observers near innity, see Section 6.
Structure of the paper. In Section 2, we introduce the relevant notations
and dene the asymptotic decay we will work with. In Section 3, we quickly review
the relevant facts and denitions from Newtonian gravity. We then discuss the
delicate inuence of the decay of the matter density of an isolated gravitating
system on the convergence of the center of mass (volume integral). The discussed
results are well-known; however, we provide explicit examples which will enable us
to highlight the similarities to the relativistic situation. The rst class of examples
is presented in Section 5, the second class in Section 6. We summarize the examples
and the dierent notions of mass and center of mass discussed in this paper on p. 15.
Acknowledgment. The authors thank Gerhard Huisken for helpful discussions.
2. Notation and decay conditions
The contemporary literature knows several dierent types of decay conditions
for isolated gravitating systems. We will use pointwise assumptions. Others as-
sume Sobolev regularity, i. e. they assume that g
m
g and g lie in specic
weighted Sobolev spaces
1
or satisfy certain symmetry conditions such as the Regge-
Teitelboim conditions
2
. We note that the decay assumptions satised by our exam-
ples are stronger, in particular the corresponding Sobolev assumptions hold. We
expect that our examples can be generalized to higher dimensions n 3.
We use the following O-notation corresponding to pointwise inequalities.
Notation 2.1. Let (M
3
, g) be a Riemannian manifold, R
0
> 0 a xed radius, and
x : M
3
L R
3
B
R0
(

0) a chart on M
3
outside a compact set L M
3
. For
s R, f, h C
0
(M
3
L), we write f = h + O(r
s
), if there is constant C such that
[f h[ C r
s
in M
3
L, where r(x)
.
.= [x[ denotes the Euclidean distance to the coordinate
origin. Similarly, we write f = h + O
k
(r
s
) if f, h C
k
(M
3
L) and s R satisfy

(f h)
x

O
_
r
s||
_
[[ k.
We will use the same notation for tensor elds, replacing partial by covariant deriva-
tives. Moreover, we will use this notation in the context of foliations near innity,
replacing the radial coordinate by the foliation parameter.
1
see for example Huang, Schoen, and Wang [HSW11, Thm 1, Thm 2]
2
see for example Huang [Hua10] or Eichmair and Metzger [EM12]
6 CARLA CEDERBAUM AND CHRISTOPHER NERZ
Let us now quickly recall the Schwarzschild spacetime. The Schwarzschild space-
time is the oldest known non-trivial solution of the (vacuum) Einstein equations
(3). It describes the spacetime exterior region of a spherically symmetric star or
a spherically symmetric black hole. In the context of isolated gravitating systems,
one mostly considers the Riemannian Schwarzschild time-slice t = 0.
Denition 2.2 (Schwarzschild spacetime). Let m > 0. The Schwarzschild space-
time (
m
M,
m
g) of mass m is dened by
m
M
.
.= R(R
3
B
m
2
(

0)) and
m
g
.
.=
_
1
m
2r
1 +
m
2r
_
2
dt
2
+
m
g, with
m
g
.
.=
_
1 +
m
2r
_
4
, (6)
where t is the time-coordinate and denotes the Euclidean metric on R
3
. The
metric
m
g is called the (Riemannian) Schwarzschild metric of mass m. The function
m
N
.
.=
1
m
2r
1 +
m
2r
is called the (Schwarzschild) lapse function.
It is well-known that (
m
M,
m
g) solves the vacuum Einstein equations, that the
ADM-mass of
m
g is equal to the parameter m, and that the scalar curvature
m
R of
m
g is 0 (and hence even in any system of asymptotic coordinates).
As there are dierent denitions of asymptotically Schwarzschildean Riemann-
ian manifolds, we now describe the asymptotic assumptions we make.
Denition 2.3 (C
k
-asymptotically Schwarzschildean Riemannian manifolds). Let
> 0. A triple (M
3
, g, x) is called C
k
-asymptotically Schwarzschildean of order
1 + with deviation B, if (M
3
, g) is a smooth manifold, B is a symmetric tensor
eld on M
3
, and x : M
3
L R
3
is a chart of M
3
outside a compact set L such
that
g =
m
g +B + O
k
_
r
2
_
with B = O
k
_
r
1
_
where k 2 and r : M
3
L (0, ) : p [x(p)[ is the Euclidean distance to the
coordinate origin.
3. The center of mass in Newtonian gravity
Isolated gravitating systems are systems with matter distributions that decay
suitably fast at innity. In NG, the relevant decaying quantity is the matter density
: R
3
[0, ) of the system (at one instant of time). Alternatively, one can ask
for suitable decay of the Newtonian potential U solving the Poisson equation (1).
The total mass m of the system is then given by the volume integral
m
.
.=

R
3
dV, (7)
while the total center of mass z of the system is dened as the volume integral
z
.
.=
1
m

R
3
xdV, (8)
whenever the system is non-empty, i. e. m > 0. Clearly, the mass and center of mass
integrals converge only when decays suitably fast, e. g. when decays faster than
EXPLICIT RIEM. MFLDS. WITH UNEXPECTEDLY BEHAVING CENTER OF MASS 7
r
4
. Alternatively, they converge when decays faster than r
3
and is asymptoti-
cally even in the sense that its odd part

odd
(x)
.
.=
(x) (x)
2
decays faster than r
4
while its even part

even
(x)
.
.=
(x) +(x)
2
need not. In terms of the O-notation introduced in Section 2, this can be rephrased
as follows.
Proposition 3.1. Let > 0. Let : R
3
[0, ) be a Newtonian matter density
such that = O(r
3
) as r and assume that its mass satises m > 0. The
corresponding center of mass is well-dened (in the sense of indenite Riemann
integrals in spherical polars) provided that

odd
= O
_
r
4
_
.
Proof. When = O(r
4
), the claim follows from Lebesgues theorem on domi-
nated convergence. Otherwise, we compute

B
R
(0)
xdV =

B
R
(0)

odd
xdV +

B
R
(0)

even
xdV
=

B
R
(0)

odd
xdV +

0,
for all R > 0, where B
R
(0) denotes the open ball of radius R centered at the origin.
Using the assumption of asymptotic evenness, we nd that the right hand side of
this converges as R , again by Lebesgues theorem. This implies that the
center of mass is well-dened.
In particular, non-empty isolated Newtonian systems with even matter density
(i. e.
odd
0) or even purely radial matter density = (r) have a well-dened
center of mass under the weaker decay condition = O(r
3
). This corresponds
to a similar asymptotic evenness condition in the context of GR, the so-called
Regge-Teitelboim conditions, see p. 5.
Our matter becomes more delicate when = O(r
4
): While the center of mass
can still converge in this case e. g. if is even or purely radial or has compact
support , it need not as the example

u
: R
3
[0, ) : x
1
r
4
_
[u[ +
x u
r
_
demonstrates
3
. Here, u R
3
0 is an arbitrary xed vector and x u denotes the
Euclidean dot product. This divergence eect is well-known in probability theory.
To further the analogy between NG and GR, it is useful to rewrite the volume
integrals dening mass and center of mass of a system with density in terms of
surface integrals using the Newtonian potential U via the Poisson equation (1).
3
In fact, this matter density is not well-dened at the coordinate origin. The described eect
however persists when it is multiplied by a cut-o function cutting out a ball centered at the
coordinate origin and equal to 1 in a neighborhood of .
8 CARLA CEDERBAUM AND CHRISTOPHER NERZ
Following [Ced12, Chap. 4], we dene the quasi-local Newtonian mass and center
of mass of a closed orientable surface R
3
as
m
N
()
.
.=
1
4

dA,
z
N
()
.
.=
1
4 m
N
()

_
U

x U
x

_
dA,
where dA is the area measure induced by the Euclidean metric and is the (Eu-
clidean) outer unit normal to . In the denition of z
N
(), we implicitly assume
that m
N
() ,= 0. These surface integral expressions are related to the volume inte-
grals for m and z via (1) by the divergence theorem and Greens formula, respec-
tively. Again by the divergence theorem, (1), and 0, one sees that m
N
() 0
for all . Whenever decays as in Proposition 3.1, m
N
(S
2
r
) and z
N
(S
2
r
) converge
to m and z as r , respectively.
Finally, the standard asymptotic expansion of the Newtonian potential U,
U =
m
r

mz x
r
3
+ O
2
_
r
3
_
ensures that the level sets of U foliate a neighborhood of innity when m ,= 0. More-
over, the leaves which are called equipotential surfaces become asymptotically
round spheres centered at z, [Ced12, p. 48]. We will a-historically call this foliation
the abstract Newtonian center of mass in analogy to the abstract CMC-center of
mass discussed in the introduction and in Section 4.
4. The center of mass in general relativity
The ADM-mass m of an isolated gravitating system in general relativity is de-
ned as follows.
Denition 4.1 (ADM-mass). The ADM-mass m of a C
k
-asymptotically Schwarz-
schildean Riemannian manifold (M
3
, g, x) of order 1 + for any > 0 is dened
by
m
ADM
.
.=
1
16
lim
r
3

i,j=1

S
2
r
(

0)
_
g
jj
x
i

g
ij
x
i
_
x
i
r
dA, (9)
where dA denotes the measure induced on the coordinate sphere S
2
r
(

0) by the
Euclidean metric .
The precise asymptotic decay necessary for dening the ADM-mass was discussed
by Bartnik [Bar86] and Chrusciel [Chr88]; the decay we assume here is by far more
restrictive. We will abbreviate the ADM-mass of a system (M
3
, g, x) by m and
will from now on assume that it is strictly positive.
We will now introduce the notion of the Euclidean coordinate center of a surface.
In Euclidean geometry, any closed surface R
3
has a Euclidean coordinate
center z
E
() dened by
z
i
.
.=

x
i
dA
.
.=
1
[[

x
i
dA, (10)
EXPLICIT RIEM. MFLDS. WITH UNEXPECTEDLY BEHAVING CENTER OF MASS 9
where dA denotes the measure induced on by the Euclidean metric . Picking a
xed system of asymptotically Schwarzschildean coordinates x : M
3
L R
3
of
(M
3
, g), this denition can be extended to closed surfaces M
3
L. We will
also call these Euclidean centers and denote them by z
E
(). Following Huisken
and Yau [HY96, Thm 4.2], we dene:
Denition 4.2 (Coordinate center of a foliation). Let

0
be a foliation near
innity of a C
k
-asymptotically Schwarzschildean Riemannian manifold (M
3
, g, x).
Let

z
E
denote the Euclidean coordinate center of the leaf

. The coordinate
center z of the foliation

0
is given by
z
.
.= lim

z
E
in case the limit exists.
Note that each

z
E
depends on the choice of asymptotic coordinates x. So does
the question of whether the limit exists.
Remark 4.3. In principle, we could use the non-Euclidean coordinate center instead
of the Euclidean one as these centers are asymptotically identical along a foliation
with r = + O(

), i. e.
1

A(

x d

A =

z
E
+ O
_

_
if r = + O
_

_
,
where

A denotes the measure on

induced by the metric g. As is does not make
a dierence, we will stick with the easier concept of Euclidean centers.
The rst geometric foliation used for the denition of a center of mass is the
foliation of (M
3
, g) near innity by stable spheres with constant mean curvature
introduced by Huisken and Yau. Existence and uniqueness of this so-called CMC-
foliation was rst proved by Huisken and Yau [HY96] in dimension three for C
4
-
asymptotically Schwarzschildean Riemannian manifolds of order 1 + = 2. Sub-
sequently, Metzger [Met07], Huang [Hua10] and Eichmair and Metzger [EM12]
weakened the decay and regularity assumptions on the metric. In particular, such
a CMC-foliation exists and is unique for any C
2
-asymptotically Schwarzschildean
Riemannian manifold of order 1+ > 1. In the following, we will call the coordinate
center of the CMC-foliation of (M
3
, g) with respect to coordinates x the coordinate
CMC-center of mass of (M
3
, g, x) (whenever it exists).
The ADM-center of mass is dened as follows [ADM61].
Denition 4.4 (ADM-center of mass). The ADM-center of mass z
ADM
R
3
of a C
k
-asymptotically Schwarzschildean Riemannian manifold (M
3
, g, x) of order
1 + > 0 is dened by
(z
ADM
)
i
.
.=
1
16m
lim
r
3

j=1

S
2
r
(0)
_
x
i
_
g
jk
x
j

g
jj
x
k
_

_
g
ij
x
j
r
g
jj
x
i
r
__
dA,
where all indices are raised and lowered with respect to the Euclidean metric .
It is well-known that the coordinate CMC-center of mass converges and coin-
cides with the ADM-center of mass, if the Regge-Teitelboim conditions hold, i. e. if
(in particular) the scalar curvature is asymptotically even, see Huang [Hua10] and
Eichmair and Metzger [EM12]. As proven by the second author [Ner13, Cor. 4.2],
10 CARLA CEDERBAUM AND CHRISTOPHER NERZ
the same is true in the setting of a C
2
-asymptotically Schwarzschildean Riemann-
ian manifold without symmetry assumptions on the scalar curvature , if the
coordinate CMC- or the ADM-center of mass converges.
5. Divergent examples related to motion
In this section, we construct examples of asymptotically Schwarzschildean Rie-
mannian manifolds (M
3
, g, x) for which the coordinate CMC-center of mass is not
well-dened, i. e. the Euclidean centers of the leaves

,

z
E
, do not converge along
the CMC-foliation. Therefore, the ADM-center of mass is not well-dened either
[Ner13, Cor. 4.2]. These examples are constructed in the following way: We be-
gin with the Riemannian Schwarzschild manifold (R
3
0,
m
g) of mass m > 0, see
Denition 2.2, perturb the metric by an arbitrary symmetric tensor eld B and cal-
culate the change of the constant mean curvature surfaces under this perturbation.
Then, we choose explicit tensors B such that the Euclidean coordinate center sof
the CMC-surfaces do not converge to a point in R
3
, i. e. such that the coordinate
CMC-center of mass is not well-dened.
Let B = O
2
(r
1
) be a symmetric tensor eld on M
3 .
.= R
3
B
R
(

0) for some
>
1
/2 and dene interpolating Riemannian metrics
t
g
.
.=
m
g 2t B, such that
the deviations B of the constructed metrics are given by
t
B = 2t B. By [Met07,
Thm 6.4], there exists a foliation

of M
3
by spheres

t
with constant mean
curvature
2
/ +
4m
/
2
with respect to
t
g. Let

t
z
E
R
3
denote the Euclidean
coordinate center of

t
, see (10).
Remark 5.1. Again, we could use the non-Euclidean coordinate centers instead of
the Euclidean ones as the CMC-leaves are almost asymptotically concentric [Ner13,
Sec. 2], in the sense that r = + O(

). In particular,

t
z
i
.
.=
_

t
z
E
_
i
=
1

t
A(

t
)

x
i
d

t
A+ O
_

1
_
,
where

t
A denotes the measure on

t
induced by the metric
t
g.
It is shown by the second author [Ner13, Thm 3.1] that these Euclidean coordi-
nate centers evolve in the following way:
Corollary 5.2 ([Ner13, Corollary of Thm 3.1]). For the outer unit normal of

t

with respect to the Euclidean metric, the asymptotic identity

t
z
i
t
=
1
8m

ij

j
+
ij

kl
,k

l
_
dA+ O
_

_
(11)
holds, where
.
.= trB B and tr denotes the trace with respect to the Euclidean
metric.
Remark 5.3. We recall that the ADM-linear momentum

P
ADM
R
3
of a suitably
decaying initial data set (M
3
, g, K, , J) is dened by
_

P
ADM
_
i
=
1
8m
lim

S
2

(0)

ij
x
j
r
dA,
where = trKg K is the momentum tensor eld of the initial data set [ADM61].
EXPLICIT RIEM. MFLDS. WITH UNEXPECTEDLY BEHAVING CENTER OF MASS 11
Thus, the rst part of the integral in (11) has to be understood as an approximate
linear momentum, while the second part is an error term due to the approximation.
This is explained in more detail in [Ner13, Remark 3.2].
By [Met07, Thm 1.1] and De Lellis and M uller [DLM05], we know furthermore
that the CMC-surface

t
is a graph of a function

t
H
1
(S
2

t
z)) over S
2

t
z) with
||
H
1
(S
2

(
t
z))
= O(r

), where we dropped the index E for notational convenience.

In particular,

t
z
i
t
=
1
8m

S
2

(
t
z)
_

ij
t

j
+
ij

kl
,k

l
_
dA+ O
_

_
, (12)
where

t
(x) =
(x
t
z)
/|x
t
z| denotes the outer unit normal of S
2

t
z) with respect
to the Euclidean metric. We know that

0
z = 0, since
t=0
g =
m
g is the Riemannian
Schwarzschild metric, in particular [

t
z
i
[ = O(
1
) by assumption on B = O
2
(r

)
and (12). Thus, we conclude

t
z
i
t
=
1
8m

S
2

0)
_

ij
x
j
r
+
ij

kl
,k
x
j
r
x
l
r
_
dA+ O
_

_
if we assume B = O
2
(r
1
). By a simple integration, the identity

t
z
i
=
t
2
2m

S
2

0)
_

ij
x
j
r
+
ij

kl
,k
x
j
r
x
l
r
_
dA+ O
_

_
(13)
holds asymptotically for any B = O
2
(r
1
). Thus, the CMC-center of mass is
well-dened if and only if (13) converges for . Let us now choose suitable
tensor elds B = O
2
(r
1
) to get the desired examples. Motivated by Yorks
example of a momentum tensor eld Y = O

(r
2
) with prescribed ADM-linear
momentum

P R
3
[Yor79, Chap. 6], we dene B
.
.= f(r) Y = O
k
(r
1
) for an
arbitrary function f = O
k
(r
1
) with k 2. Recall that the York tensor is given
by
Y
ij
(x)
.
.=
3
2r
2
_
P
i
x
j
r
+
x
i
r
P
j
P
k
x
k
r
_

ij

x
i
x
j
r
2
__
. (14)
Again, we raise and lower indices with respect to the Euclidean metric. We nd
tr B = O
k
(r
2
) and

t
z
E
=
t
2
(3f() +f

() )

P
m
+ O
_

_
.
Therefore, we conclude that
t
z
.
.= lim

t
z =
t

P
2m
lim

_
3f() +f

()
_
,
whenever this limit exists. In particular, by choosing t = 1 as well as the specic
functions f(r)
.
.= sin ( ln r) and f(r)
.
.= r
1
with (
1
/2, 1), we get examples of
C

-asymptotically Schwarzschildean manifolds (R

3
B
R
(0), g, x) of order 2 and
2, respectively, for which the coordinate CMC-center of mass (and therefore the
ADM-center of mass) do not exist. For f(r) = sin ( ln r), the Euclidean centers of
the leaves

of the CMC-foliation oscillate as . This conicts with [HY96,
Thm 4.2]. However, they are bounded as asserted by [HY96, Proof Thm 5.1].
12 CARLA CEDERBAUM AND CHRISTOPHER NERZ
When f(r) = r
1
, the Euclidean centers of the leaves

of the CMC-foliation are
unbounded; but we note that the decay conditions of [HY96] are violated.
Let us now summarize the above discussion, see also Figure 1.
Example 5.4 (Divergent CoM 1). Let m, > 0 and let Y be the York-tensor
dened in (14) for some

0 ,=

P R
3
. Let
f :
_
m
2
,
_
R : r sin(ln r) or f :
_
m
2
,
_
R : r r
1
.
Set
f
g
.
.=
m
g+f(r) Y so that
f
g =
m
g+O

(r
2
) or
f
g =
m
g+O

(r
1
), respectively,
on M
3 .
.= R
3
B
m/2
(

0). Neither the coordinate CMC-center of mass nor the ADM-

center of mass of (M
3
,
f
g) are well-dened.
6. Divergent examples in the Schwarzschild spacetime
The second class of examples of asymptotically Schwarzschildean Riemannian
manifolds or initial data sets arises as time-slices of the Schwarzschild spacetime
(
m
M,
m
g), see 2.2. As the eects we exploit have nothing to do with spherical sym-
metry or staticity, similar examples can be constructed in many spacetimes (e. g. in
any static one with compactly supported or suitably decaying matter distribution).
Clearly, the center of mass of the canonical time-slice t = 0 is the coordinate
origin, z
ADM
= z
CMC
=

0. Other time-slices of the Schwarzschild spacetime can
serve as a guideline for better understanding how dierent families of observers near
innity perceive the spacetime and its center of mass, in particular.
Here, we will focus on what we call graphical time-slices
T
M
3
arising as the
graph of a smooth function T : R
3

0 R over the canonical time-slice (in

time-direction), i. e.
T
M
3
.
.= t = T(x).
To most easily comply with the asymptotic decay conditions necessary for existence
and uniqueness of the CMC-foliation, we will assume that T = O
k
(r
0
) as r ,
with k 3. Let y
i .
.= x
i
[T
M
3 denote the induced coordinates on
T
M
3
. In those
coordinates, the metric
T
g induced on
T
M
3
reads
T
g
ij
.
.=
T
g
_

y
i ,
y
j
_
=
m
g(
x
i ,
x
j )
m
N
2
T
,i
T
,j
=
.
.
m
g
ij

m
N
2
T
,i
T
,j
with
m
N is as in Denition 2.2. Here and in the following, we will only use partial
derivatives with respect to the (spacetime) coordinates x
i
; partial derivatives with
respect to the coordinates y
i
adapted to the time-slice
T
M
3
will be expressed in
terms of partial derivatives with respect to x
i
via

y
i =
x
i +T
,i

t
.
A straightforward computation shows that (R
3

0,
T
g, y ) is C
k1
-asymptotically
Schwarzschildean of order 1 + = 2 with deviation
T
B
.
.= T
,i
T
,j
.
Moreover, the ADM-mass of (R
3

0,
T
g, y ) is m. To reduce notational complexity,
we will drop the left upper index m and understand all covariant derivatives and
EXPLICIT RIEM. MFLDS. WITH UNEXPECTEDLY BEHAVING CENTER OF MASS 13
norms to be with respect to the metric
m
g unless stated otherwise. The future unit
normal
T
n of
T
M
3
(
m
M,
m
g) is
T
n =

t
+N
2
T
N
_
1 N
2
[T[
2
,
where and [[ denote the covariant derivative and the norm induced on R
3

0 by
the metric
m
g, respectively. Accordingly, the second fundamental form of
T
M
3

(
m
M,
m
g) is given by
T
K
ij
=
T
,i
N
,j
+N
,i
T
,j
+N
2
ij
T N
3
[T[
2
T
,i
T
,j
_
1 N
2
[T[
2
,
where
2
T denotes the covariant Hessian of T with respect to
m
g. From this, one
computes that the ADM-linear momentum

P
ADM
of
T
M
3
vanishes (see Remark
5.3), so that the ADM-energy-momentum-4-vector of (
T
M
3
,
T
g,
T
K) coincides with
the one of the canonical time-slice. Moreover, the ADM-angular momentum of
(
T
M
3
,
T
g,
T
K) vanishes as will be discussed elsewhere. Also, the induced mean
curvature
T
H =
T
tr
T
K satises
T
H =

T +
m
r
2

T
x
r
+ O
k2
_
r
3
_
which means that the maximal slicing condition
T
H = 0 implies

T = O
k2
(r
3
).
From T = O
k
(r
0
), we deduce that the maximal slicing condition implies T =
O
k
(r
1
) by the faster fall-o trick of the rst author [Ced12, Thm 1.4.10].
When evaluating the ADM-center of mass surface integral from Denition 4.4
on a nite coordinate sphere with respect to the y-coordinates in
T
M
3
, we nd
_
T
z
_
S
2
r
_

0
___
l
=
1
16m
3

i,j=1

S
2
r
(

0)
_
(B
ij,i
B
ii,j
)
x
j
x
l
r

_
B
il
x
i
r
B
ii
x
l
r
_
+ O
k2
_
r
3
_
_
dA(x)
=
1
16m

S
2
r
(

0)
_
(divB)()x
l
(trB)x
l
B
_
,

x
l
_
+ trB
l
_
dA(x)
+ O
_
r
1
_
,
where and div are the Euclidean unit normal to S
2
r
(

0) and the Euclidean diver-

gence, respectively. We dropped the left upper index T on the deviation
T
B for
notational convenience and because this formula in fact applies to any deviation
B = O
k
(r
2
) with k 2, see also (12) where B = 2tB. As discussed in Section
1, Corvino and Wu [CW08] observed that the ADM-surface integrals correspond
to volume integrals over Rx. Here, this can be explicitly seen by applying the
Euclidean divergence theorem:
T
z
_
S
2
r
_

0
__
=
T
z
_
S
2
R0
_

0
__
+
1
16m

Br(

0)\B
R
0
(

0)
div(divB trB) x dV
+ O
_
r
1
_
14 CARLA CEDERBAUM AND CHRISTOPHER NERZ
for any xed R
0
> 0. In terms of T, this reads
T
z
_
S
2
r
_

0
__
=
T
z
_
S
2
R0
_

0
__
+
1
16m

Br(

0)\B
R
0
(

0)
_
(T)
2

2
T

2
_
x dV (15)
+ O
_
r
1
_
.
In particular, if T gives rise to maximal slicing and thus as discussed above satises
T = O
k
(r
1
) with k 3, the ADM- and thus also the coordinate CMC-center of
mass converges. It is hence impossible to construct examples of maximally sliced
time-slices with diverging center of mass.
To construct an example with diverging center of mass, we pick
T : R
3

0
_
R : x sin(ln r) +
u x
r
= O

_
r
0
_
for a xed vector

0 ,= u R
3
. One computes from (15) that
T
z
_
S
2
r
_

0
__
=
T
z
_
S
2
R0
_

0
__

1
3m
(cos(ln r) cos(ln R
0
))u
which diverges as r . Hence, the ADM- and thus also the coordinate CMC-
center diverge [Ner13, Cor. 4.2].
Finally, let us summarize the above discussion, see also Figure 1.
Example 6.1 (Divergent CoM 2). Let m > 0 and let
T : R
3

0
_
R : x sin(ln r) +
u x
r
for a xed vector

0 ,= u R
3
. Let
T
g be the metric induced on
T
M
3
= t = T(x) by
the Schwarzschild spacetime (
m
M,
m
g). Then neither the coordinate CMC-center
of mass nor the ADM-center of mass of (
T
M
3
,
T
g) are well-dened.
EXPLICIT RIEM. MFLDS. WITH UNEXPECTEDLY BEHAVING CENTER OF MASS 15
mass and CoM expressions NG, s. Sec. 3 GR, s. Sec. 4
mass surface integrals m
N
() m
ADM
(S
2
r
)
mass volume integrals

dV

R dV
total mass m m
ADM
CoM surface integrals z
N
() z
ADM
(S
2
r
), z
E
()
CoM volume integrals

x dV

Rx dV
total coordinate CoM z z
ADM
= z
CMC
abstract center of mass level sets of U CMC-foliation
sucient decay for = O(r
4
) R = O(r
4
)
convergence of the CoM U =
m
r
+ O2(r
2
) e. g. gij =
m
gij +O2(r
2
)
critical order = O(r
4
) R = O(r
4
)
of decay U =
m
r
+ O2(r
2
) e. g. gij =
m
gij +O2(r
2
)
traditional decay asymptotic evenness Regge-Teitelboim
assumption conditions
explicit examples
u
(x) =
1
r
4
(|u| +
x u
r
) g =
m
g + sin ( ln r) Y
with diverging CoM with

0 = u R
3
with Y York tensor, Sec. 5
and graph in
Schwarzschild spacetime:
t = T(x) = sin ( ln r) +
x u
r
with

0 = u R
3
, Sec. 6
Figure 1. Dierent expressions for mass and center of mass in
Newtonian gravity (NG) and general relativity (GR) as well as
decay considerations ( > 0).
m
g is the Riemannian Schwarzschild
metric of mass m > 0.
16 CARLA CEDERBAUM AND CHRISTOPHER NERZ
References
[ADM61] Arnowitt, Richard ; Deser, Stanley ; Misner, Charles W.: Coordinate Invariance and
Energy Expressions in General Relativity. In: Phys. Rev. 122 (1961), Nr. 3, S. 9971006
[Bar86] Bartnik, Robert: The Mass of an Asymptotically Flat Manifold. In: Communications
on Pure and Applied Mathematics 39 (1986), S. 661693. http://dx.doi.org/10.1002/
cpa.3160390505. DOI 10.1002/cpa.3160390505
[Ced12] Cederbaum, Carla: The Newtonian Limit of Geometrostatics, FU Berlin, Diss., 2012.
arXiv:1201.5433v1
[Chr88] Chr usciel, Piotr T.: On the invariant mass conjecture in general relativity. In: Com-
munications in Mathematical Physics 120 (1988), 233-248. http://dx.doi.org/10.1007/
BF01217963. ISSN 00103616
[CS06] Corvino, Justin ; Schoen, Richard M.: On the asymptotics for the vacuum Einstein
constraint equations. In: Journal of Dierential Geometry 73 (2006), Nr. 2, S. 185217
[CW08] Corvino, Justin ; Wu, Haotian: On the center of mass of isolated systems. In: Class.
Quantum Grav. 25 (2008), S. 118
[CWY13] Chen, Po-Ning ; Wang, Mu-Tao ; Yau, Shing-Tung: Quasilocal angular momentum
and center of mass in general relativity. (2013). arXiv:1312.0990v1
[CY88] Christodoulou, Demetrios ; Yau, Shing-Tung: Some remarks on the quasi-local mass.
In: Mathematics and general relativity (Santa Cruz, CA, 1986) Bd. 71. Providence, RI :
Amer. Math. Soc., 1988, S. 914
[DLM05] De Lellis, Camillo ; M uller, Stefan: Optimal rigidity estimates for nearly umbilical
surfaces. In: Journal of Dierential Geometry 69 (2005), Nr. 1, S. 075110
[EM12] Eichmair, Michael ; Metzger, Jan: Unique isoperimetric foliations of asymptotically at
manifolds in all dimensions. In: Inventiones mathematicae (2012), S. 140
[HSW11] Huang, Lan-Hsuan ; Schoen, Richard ; Wang, Mu-Tao: Specifying angular momentum
and center of mass for vacuum initial data sets. In: Communications in Mathematical
Physics 306 (2011), Nr. 3, S. 785803
[Hua10] Huang, Lan-Hsuan: Foliations by Stable Spheres with Constant Mean Curvature for
isolated systems with general asymptotics. In: Communications in Mathematical Physics
300 (2010), Nr. 2, S. 331373
[HY96] Huisken, Gerhard ; Yau, Shing-Tung: Denition of Center of Mass for Isolated Physical
Systems and Unique Foliations by Stable Spheres with Constant Mean Curvature. In:
Invent. Math. 124 (1996), S. 281311
[LMS11] Lamm, Tobias ; Metzger, Jan ; Schulze, Felix: Foliations of asymptotically at man-
ifolds by surfaces of Willmore type. In: Mathematische Annalen 350 (2011), Nr. 1, S.
178
[Met07] Metzger, Jan: Foliations of asymptotically at 3-manifolds by 2-surfaces of prescribed
mean curvature. In: Journal of Dierential Geometry 77 (2007), Nr. 2, S. 201236
[Ner13] Nerz, Christopher: Time evolution of ADM and CMC center of mass in general relativity.
(2013). tbp
[Yor79] York, J. W. Jr.: Kinematics and dynamics of general relativity. In: Smarr, L. L. (Hrsg.):
Sources of Gravitational Radiation, 1979, S. 83126
Mathematisches Institut, Universit at T ubingen, Auf der Morgenstelle 10, 72076
T ubingen, Germany
E-mail address: cederbaum@math.uni-tuebingen.de
Mathematisches Institut, Universit at T ubingen, Auf der Morgenstelle 10, 72076
T ubingen, Germany
E-mail address: Christopher.Nerz@phoenixes.de