1

2. FUNCIONES
2.1 CONCEPTO Y OPERACIONES CON FUNCIONES

Mara Concepcin Gonzlez Enrquez

Definicin. Sean B A y dos subconjuntos de nmeros reales, una funcin
f de B A en es una regla de correspondencia que asigna a cada
elemento de A un nico elemento de B .
Lo que se denota por B A f :


Es funcin Es funcin


No es funcin

Al conjunto A se le llama dominio de la funcin y al conjunto B se le
llama codominio, contradominio o recorrido de la funcin.

Sea Domf A x = a ) ( x f y = se le llama la imagen de x bajo la funcin,
Y al conjunto { } A x x f y B y = algn para ) ( : se le llama la Imagen de f.
Esto es, { } A x x f y B y = = algn para ) ( : Imagen(f)

Ejemplo. En la figura representamos una funcin
A
f
B

A
f
B

A
f
B

2


En esta funcin identificamos { } 7 , 3 , 2 = = Domf A ,
{ } 20 , 8 , 5 , 1 , 0 , 3 = = Codomf B ; regla de correspondencia 1 3 ) ( = = x x f y ;
{ } 20 , 5 , 8 Imagen(f) = .
Como 8 ) 3 ( = f decimos que 8 es la imagen de 3 bajo la funcin.

La variable que recorre todos los elementos del dominio, se denota por x
y se llama la variable libre, la variable que toma los valores resultantes de
aplicar la funcin se llama variable dependiente la cual se denota con y .
As tenemos ) ( x f y = .

Ejemplo. Cuando el dominio de la funcin es finito se puede escribir como
conjunto de parejas ordenadas
{ } ) 8 , 0 ( ), 3 , 4 ( ), 0 , 3 ( ), 8 , 2 ( = f
Tenemos que { } { } 8 , 3 , 0 y 4 , 2 , 0 , 3 = = Codomf Domf

Ejemplos.
1. Z Z f : tal que 1 3 ) ( + = k k f
2. N Z f : tal que
2
) 1 ( ) ( + = k k f
3. { } R R f 2 / 1 : tal que
x
x
x f
2 1
1
) (

+
=

El dominio de una funcin puede depender de que la regla de
correspondencia est bien definida, como es el caso en que se involucran
denominadores o races de orden par en dicha correspondencia, tambin si
la funcin representa una variable concreta en un fenmeno fsico.

Ejercicio. Determine el dominio de las siguientes funciones:
i)
2
25 8 ) ( x x x f =
0 25
2
x
2
25 x 5 5 x
Por lo tanto | | 5 , 5 = Domf

A
f
B

2
3
7

5
8
20
1
0
3
3
ii) 2 5 1 ) ( + = x x f
0 2 5 x 5 / 2 x
Por lo tanto |

= ,
5
2
Domf
iii)
1
1
) (
2

=
x
x f
0 1
2
> x 1
2
> x x x < < 1 o 1
Por la tanto ( ) ( ) = , 1 1 , U Domf
iv)
40 3
2
) (
2

+
=
x x
x
x f
) 8 )( 5 ( 0 40 3
2
+ = = x x x x
Por lo tanto { } 8 , 5 = R Domf

Nombramos algunas funciones bsicas.

Funcin constante cero: con dominio R y contradominio R , la
denotamos R R
R
: 0 cuya regla de correspondencia es 0 ) ( 0 = x
R
para
todo R x

Funcin constante uno: con dominio R y contradominio R , la denotamos
R R
R
: 1 cuya regla de correspondencia es 1 ) ( 1 = x
R
para todo R x

Funcin Identidad: con dominio R y contradominio R , la denotamos
R R I
R
: o simplemente
R
I cuya regla de correspondencia es
x x I
R
= ) (
Tambin podemos tener variantes de la funcin identidad
A
I donde A sea
un subconjunto de R

OPERACIONES DE FUNCIONES
- Suma
- Multiplicacin
- Divisin
- Composicin

Definicin. Sean ) ( y ) ( x g x f dos funciones se define:
La SUMA: ) )( ( x g f +
Domg Domf g f Dom I = + ) ( y
Regla de correspondencia ) ( ) ( ) )( ( x g x f x g f + = +

Ejemplo. 1 2 ) ( y 3 ) (
2
+ = = x x g x x x f
4
Tenemos: |

= = ,
2
1
) ( y ) ( g Dom R f Dom
|

=
|

= = + ,
2
1
,
2
1
) ( I I R Domg Domf g f Dom
Y 1 2 3 ) )( (
2
+ + = + x x x x g f .
Si aplicamos a un nmero especfico como:
5 1 ) 2 ( 2 ) 2 ( y 2 ) 2 ( 3 2 ) 2 (
2
= + = = = g f
Luego 5 2 ) 2 )( ( + = + g f

Propiedades de la suma de funciones.
Para funciones h g f y , se satisfacen:
i) ) )( ( ) )( ( x f g x g f + = +
ii) ) ( ) ( h g f h g f + + = + +
iii) Existe una funcin constante cero 0 tal que
f f = + 0
iv) Para cada funcin f existe su inverso aditivo f
Tal que 0 ) ( = + f f

Ejemplo. Verifique ) ( ) ( h g f h g f + + = + + con las funciones
{ } ) 8 , 0 ( ), 3 , 4 ( ), 0 , 3 ( ), 8 , 2 ( = f { } ) 6 , 1 ( ), 1 , 2 ( ), 2 , 3 ( ), 5 , 0 ( = g
{ } ) 7 , 0 ( ), 4 , 2 ( ), 1 , 3 ( = h
Tenemos que
{ } { } { } 2 , 0 , 3 y 1 , 2 , 3 , 0 y , 4 , 2 , 0 , 3 = = = Domh Domg Domf

Por lo que { } 2 , 0 , 3 ) ( = = + + Domh Domg Domf h g f Dom I I

Luego { } ) 13 , 0 ( ), 2 , 3 ( ), 7 , 2 ( = + g f
Y { } ) 20 , 0 ( ), 3 , 3 ( ), 3 , 2 ( ) ( = + + h g f (1)

Por otro lado { } ) 12 , 0 ( ), 3 , 3 ( ), 5 , 2 ( = + h g
Y { } ) 20 , 0 ( ), 3 , 3 ( ), 3 , 2 ( ) ( = + + h g f (2)

De (1) y (2) concluimos ) ( ) ( h g f h g f + + = + +


Definicin. Sean ) ( y ) ( x g x f dos funciones se define:
La MULTIPLICACION: ) )( ( x fg
Domg Domf fg Dom I = ) ( y
Regla de correspondencia ) ( ) ( ) )( ( x g x f x fg =

5
Ejemplo. 1 2 ) ( y 3 ) (
2
+ = = x x g x x x f
Tenemos: |

= = ,
2
1
) ( y ) ( g Dom R f Dom
|

= |

= = ,
2
1
,
2
1
) ( I I R Domg Domf fg Dom
Y 1 2 ) 3 ( ) )( (
2
+ = x x x x fg .
Si aplicamos a un nmero especfico como:
5 1 ) 2 ( 2 ) 2 ( y 2 ) 2 ( 3 2 ) 2 (
2
= + = = = g f
Luego 5 2 ) 2 )( ( = fg

Propiedades de la multiplicacin de funciones:
Para funciones h g f y , se satisfacen:
i) ) )( ( ) )( ( x gf x fg =
ii) ) ( ) ( gh f h fg =
iii) Existe una funcin constante uno
R
1 tal que
1 1 1 = = f f
R R


Todas las propiedades de las funciones de reales a reales se deducen de las
propiedades y axiomas de los nmeros reales, como se mostrar en la
siguiente propiedad. Para que dos funciones sean iguales deben ser iguales
los dominios y las reglas de correspondencia.

Propiedad distributiva de las funciones:
fh fg h g f + = + ) (
Demostracin.
{ } ) ( ) ( ) (
) ( ) ( )) ( (
h Dom g Dom f Dom
h g Dom f Dom h g f Dom
I I
I
=
+ = +

{ } { } ) ( ) ( ) ( ) ( h Dom f Dom g Dom f Dom I I I =
) (
) ( ) (
fh fg Dom
fh Dom fg Dom
+ =
= I

Usando las definiciones de dominio de la suma y de la multiplicacin de
funciones as como la propiedad distributiva de la interseccin de conjuntos
en el tercer paso.
Ahora, las reglas de correspondencia: como ) ( ), ( ), ( x h x g x f son nmeros
reales
( )
)) ( ) ( )(( (
)) )( )(( ( ) ( ) ( (
x h x g x f
x h g x f x h g f
+ =
+ = +

) ( ) ( ) ( )( ( x h x f x g x f + = Ax. distributividad de reales
) )( ( ) )( ( x fh x fg + =

Por lo tanto fh fg h g f + = + ) (
6
Ejemplo. Verifique fh fg h g f + = + ) ( con las funciones
{ } ) 3 , 4 ( ), 0 , 3 ( ), 8 , 2 ( = f { } ) 6 , 4 ( ), 1 , 2 ( ), 2 , 3 ( = g
{ } ) 4 , 4 ( ), 4 , 2 ( ), 1 , 3 ( = h
Tenemos que
{ } Domh Domg Domf = = = 4 , 2 , 3
Por lo que
{ } )) ( ( ) ( ) ( 4 , 2 , 3 ) ( h g f Dom h g Dom fh Dom fg Dom + = + = = =
Luego
{ } ) 2 , 4 ( ), 5 , 2 ( ), 3 , 3 ( = + h g
Y { } ) 6 , 4 ( ), 40 , 2 ( ), 0 , 3 ( ) ( = + h g f (1)

Por otra parte
{ } ) 18 , 4 ( ), 0 , 3 ( ), 8 , 2 ( = fg { } ) 12 , 4 ( ), 0 , 3 ( ), 32 , 2 ( = fh
Y { } ) 6 , 4 ( ), 0 , 3 ( ), 40 , 2 ( = + fh fg (2)

De (1) y (2) concluimos fh fg h g f + = + ) (

Definicin. Sean ) ( y ) ( x g x f dos funciones se define:
La DIVISIN: ) )( / ( x g f
{ } 0 ) ( : ) / ( = x g Domg Domf x g f Dom I y
Regla de correspondencia ) ( / ) ( ) )( / ( x g x f x g f =

Ejemplo. 1 2 ) ( y 3 ) (
2
+ = = x x g x x x f
Tenemos:
|

= = ,
2
1
) ( y ) ( g Dom R f Dom
|

= |

= ,
2
1
,
2
1
I I R Domg Domf
Como se debe tener 0 ) ( x g y 0
2
1
= |

\
|
g
|

\
|
= ,
2
1
) / ( g f Dom
Y
1 2
3
) )( / (
2
+

=
x
x x
x g f .
Si aplicamos a un nmero especfico como:
5 1 ) 2 ( 2 ) 2 ( y 2 ) 2 ( 3 2 ) 2 (
2
= + = = = g f
Luego
5
2
) 2 )( / (

= g f

Ejemplo. Con las funciones { } ) 3 , 4 ( ), 0 , 3 ( ), 8 , 2 ( = f { } ) 6 , 4 ( ), 0 , 2 ( ), 2 , 3 ( = g
Realice ) )( / ( x g f
7
Tenemos que
{ } Domg Domf = = 4 , 2 , 3
Luego { } { } 4 , 3 0 ) ( : ) / ( = = x g Domg Domf x g f Dom I
El 2 se quita porque 0 ) 2 ( = g

Y
)
`

\
|
=
2
1
, 4 ), 0 , 3 (
g
f


Definicin. Sean ) ( y ) ( x g x f dos funciones se define:
La COMPOSICION: ) )( ( x f g o
{ } Domg x f Domf x f g Dom = ) ( : ) ( o y
Regla de correspondencia )) ( ( ) )( ( x f g x f g = o

Ejemplo. x x x g x x f + = + = ) ( y 6 4 ) ( realice ) )( ( x f g o
Tenemos: | ) = = , 0 ) ( y ) ( g Dom R f Dom
{ }
| ) { } + =
=
, 0 ) 6 4 ( : ) (
) ( : ) (
x R x f g Dom
Domg x f Domf x f g Dom
o
o

Esto nos lleva a las condiciones equivalentes siguientes:
x x x +
2
3
4 6 6 4 0
Por lo tanto |

= ,
2
3
) ( f g Dom o
Luego para la regla de correspondencia


Comparemos el ejemplo anterior con el siguiente:

Ejemplo. x x x g x x f + = + = ) ( y 6 4 ) ( realice ) )( ( x g f o
Tenemos: | ) = = , 0 ) ( y ) ( g Dom R f Dom
{ }
| ) { } | ) = + =
=
, 0 ) ( : , 0 ) (
) ( ) ( : ) ( ) (
x R x x x g f Dom
f Dom x g g Dom x g f Dom
o
o


Luego para la regla de correspondencia
( ) ( ) 6 4 4 6 4 )) ( ( ) )( ( + + = + + = + = = x x x x x x f x g f x g f o

Como observamos de los dos ejemplos anteriores
6 4 4 ) )( ( 6 6 4 4 ) )( ( + + = + + + = x x x g f x x x f g o o

Con esto afirmamos que la composicin de funciones no es conmutativa

6 4 6 4 ) 6 4 ( ) )( ( + + + = + = x x x g x f g o
8
Ejemplo. 1 2 ) ( y 3 ) (
2
+ = = x x g x x x f
Tenemos: |

= = ,
2
1
) ( y ) ( g Dom R f Dom


Esto nos lleva a las condiciones siguientes:
x x 3
2
1
2

4
9
3
4
9
2
1
2
+ + x x
2
2
3
4
7
|

\
|
x
2
7
2
3
o
2
3
2
7
x x

2
3
2
7
o
2
3
2
7
+ + x x
( | | ) =
|
|

+
(

\
|



, 2.8 17 . 0 , ,
2
7 3
2
7 3
,
17 . 0 o 2.8
U U
x x

Por lo tanto ( | | ) =
|
|

+
(

\
|

= , 2.8 17 . 0 , ,
2
7 3
2
7 3
, ) ( U U o f g Dom
Y 1 6 2 1 ) 3 ( 2 ) 3 ( )) ( ( ) )( (
2 2 2
+ = + = = = x x x x x x g x f g x f g o .

Si aplicamos a un nmero especfico como: 3 = x
0 ) 3 ( 3 3 ) 3 (
2
= = f
Luego 1 1 1 ) 0 ( 2 ) 0 ( )) 3 ( ( ) 3 )( ( = = + = = = g f g f g o


Ejemplo. 1 2 ) ( y 3 ) (
2
+ = = x x g x x x f
Tenemos: |

= = ,
2
1
) ( y ) ( g Dom R f Dom
{ }
)
`

+ |

=
=
R x x g f Dom
Domf x g Domg x g f Dom
1 2 : ,
2
1
) (
) ( : ) (
o
o

Como 1 2 + x siempre es un nmero real,
|

= ,
2
1
) ( g f Dom o
Y ( ) ( ) ( ) 1 2 3 1 2 1 2 3 1 2 1 2 )) ( ( ) )( (
2
+ + = + + = + = = x x x x x f x g f x g f o .
{ }
)
`

=
=
,
2
1
3 : ) (
) ( : ) (
2
x x R x f g Dom
Domg x f Domf x f g Dom
o
o
9
Vemos 1 2 3 1 2 ) )( ( 1 6 2 ) )( (
2
+ + = + = x x x g f x x x f g o o

Si aplicamos a un nmero especfico como: 3 = x
7 1 ) 3 ( 2 ) 3 ( = + = g
Luego 7 3 7 7 3 1 ) 3 ( 2 ) 7 ( )) 3 ( ( ) 3 )( ( = + = = = f g f g f o

Propiedad asociativa de la composicin de funciones:
Para funciones h g f y , se satisface:
) ( ) ( f g h f g h o o o o =
Demostracin.
{ } ) ( ) ( : ) ) (( g h Dom x f Domf x f g h Dom o o o =
{ } Domh x f g g Dom x f Domf x = )) ( ( : ) ( ) ( : (1)

{ }
{ } Domh x f g f g Dom x
Domh x f g f g Dom x f g h Dom
=
=
)) ( ( : ) (
) )( ( : ) ( )) ( (
o
o o o o

{ } Domh x f g g Dom x f Domf x = )) ( ( : ) ( ) ( : (2)
Comparamos (1) y (2) y concluimos que
)) ( ( ) ) (( f g h Dom f g h Dom o o o o =
Ahora, las reglas de correspondencia;
Del lado izquierdo:
))) ( ( (
)) ( )( (( ) )( ) ((
x f g h
x f g h x f g h
=
= o o o

Del lado derecho:
))) ( ( (
)) )( (( ) ))( ( (
x f g h
x f g h x f g h
=
= o o o

Por lo tanto ) ( ) ( f g h f g h o o o o = .

Ejemplo. { } ) 1 , 3 )( 3 , 2 ( ), 2 , 1 ( = f , { } ) 1 , 3 )( 2 , 2 ( ), 3 , 1 ( = g , { } ) 2 , 3 )( 3 , 2 ( ), 1 , 1 ( = h
Formamos las funciones
{ } ) 3 , 3 )( 1 , 2 ( ), 2 , 1 ( = f g o
{ } ) 2 , 3 )( 1 , 2 ( ), 3 , 1 ( ) ( = f g h o o
{ } ) 1 , 3 )( 3 , 2 ( ), 2 , 1 ( = g ho
{ } ) 2 , 3 )( 1 , 2 ( ), 3 , 1 ( ) ( = f g h o o
Verificamos que ) ( ) ( f g h f g h o o o o =

Definicin. Sea B A f : una funcin, una funcin A B g : se llama
i) Inversa derecha de f , si
A
I f g = o
ii) Inversa izquierda de f , si
B
I g f = o
Si A B g : satisface las dos condiciones anteriores se llama simplemente
la inversa de f , y se denota
1
= f g . Tambin se dice que f es
10
invertible.

Nota: la definicin anterior es de la inversa de una funcin para la
operacin de composicin de funciones, no inversa para la multiplicacin
de funciones.
No todas las funciones poseen inversa para la composicin de funciones,
ms adelante veremos el criterio que debe satisfacer una funcin para tener
inversa.

Ejemplo. { } 7 , 2 , 3 = A , { } 9 , 7 , 8 = B con las siguientes funciones
B A f : { } ) 7 , 7 )( 8 , 2 ( ), 9 , 3 ( = f y
A B g : { } ) 3 , 9 )( 7 , 7 ( ), 2 , 8 ( = g
Satisfacen: { }
A
I f g = = ) 7 , 7 )( 2 , 2 ( ), 3 , 3 ( o
{ }
B
I g f = = ) 9 , 9 )( 7 , 7 ( ), 8 , 8 ( o

Por lo tanto g es la inversa de f para la composicin de funciones.

Otras funciones bsicas:
Funcin valor absoluto: con dominio R y contradominio R cuya regla
de correspondencia es

<

= =
0 si
0 si
) (
x x
x x
x x f

Funcin mximo entero menor o igual: con dominio R y contradominio
Z , la denotamos | | Z R : _ cuya regla de correspondencia es
| | { } x k Z k mximo x = : para todo R x .
Ejem. | | 3 4 . 3 = , | | 3 7 . 3 = , | | 0 5 . 0 = , | | 0 8 . 0 = , 1
3
1
=
(

, | | 2 2 . 1 =

CLASIFICACION DE FUNCIONES
- Constantes
c x f = ) (
- Lineales
b ax x f + = ) (
- Cuadrticas
c bx ax x f + + =
2
) (
- Polinomiales

n
n o
x a x a x a a x f + + + + = K
2
2 1
) (
- Racionales

m
m o
n
n o
x b x b x b b
x a x a x a a
x f
+ + + +
+ + + +
=
K
K
2
2 1
2
2 1
) (

11
- Algebraicas
La regla de correspondencia involucra algn exponente fraccionario
de la variable independiente
4 2 ) ( + = x x f
3 2
1
3
) (

=
x
x
x f
- Seccionadas
Seccionan el dominio con diferentes reglas de correspondencia
x x f = ) ( | | x x f = ) (
- Trigonomtricas
x x x x x senx x f csc , sec , cot , tan , cos , ) ( =
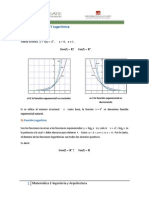
- Exponenciales

x
a x f = ) ( con 0 > a
- Logartmicas
x x f
b
log ) ( = con 0 > b

Veamos el planteamiento de ciertos problemas los cuales son modelados
por alguna funcin.

Ejemplo. Los que somos usuarios del servicio de transporte del metro,
pagamos el boleto a $3 sin importar el nmero de estaciones que nos
traslademos, es decir, tenemos una funcin cuyo dominio es el nmero
de estaciones que recorremos n y el codominio consta del nmero 3.
Tenemos entonces una funcin constante 3 ) ( = n f .

Ejemplo. Si consideramos las tarifa que se le paga a un taxista, se le
paga una cuota llamada banderazo $6, luego por cada kilmetro de
recorrido se cobra una cuota, digamos $5. Si x es la variable
independiente y representa el nmero de kilmetros de nuestro recorrido
la tarifa a pagar est dada por x x T 5 6 ) ( + = . Este ejemplo de una funcin
lineal.

Ejemplo. Se desea construir una caja sin tapa a partir de una lmina que
mide 90x40 cm. Cortando en las esquinas un cuadrado de lado x y
luego doblando las pestaas hacia arriba. Determine una funcin que
represente el volumen de la caja en funcin de la longitud x .

12


La caja tiene las dimensiones x 2 90 de largo, x 2 40 de ancho y x de
altura, por lo que escribimos el volumen en funcin de x como
x x x x V
x x x x x x x x V
3600 260 4 ) (
) 4 180 80 3600 ( ) 2 40 )( 2 90 ( ) (
2 3
2
+ =
+ = =

La cual es una funcin polinomial de grado 3.

Ejemplo. Se necesita conectar una lnea telefnica entre dos pueblos A
y B situados en lados opuestos de un ro. El ancho del ro es de 700 m.
y la distancia de los pueblos es de 1800 m a lo largo del ro. Tender el
cable por tierra tiene un costo C por m. Y un costo de 2C si se tiende
abajo del agua. Si la lnea sigue la orilla del ro x m, y luego atraviesa
abajo del agua hasta el otro pueblo, determine una funcin que
represente el costo de la lnea dependiendo de la variable x .


El recorrido del cableado consta de dos tramos, el tramo recto que tiene
longitud x y el tramo de la diagonal al pasar por el agua, del cual
podemos medir su longitud aplicando el teorema de Pitgoras,

transformando en kilmetros las longitudes.
2 2
) 8 . 1 ( ) 7 . 0 ( x +
A
B
x
1800
700
x 1800
x
x
90
40
x 2 90
x 2 40
x
x
13
Cada una de estas longitudes se multiplican por su costo
correspondiente y la suma de esas expresiones nos da la funcin
2 2
) 8 . 1 ( ) 7 . 0 ( 2 ) ( x C Cx x f + + =
Aqu C es una constante y obtuvimos una funcin algebraica.

Ejemplo. Se disea una lata cilndrica para comercializar 800 ml de un
refresco. Escribir una funcin que exprese el rea de material necesario
para construirla tal que dependa del radio r de la lata.


Recordamos que el volumen de un cilindro es 8 . 0
2
= = r h V y el rea del
cilindro es
2
2 ) 2 ( r h r A + = .
Como el volumen es constante, podemos despejar de su expresin la altura
2
8 . 0
r
h

= y sustituimos en la expresin del rea para que quede en funcin
de una sola variable, que en este caso es el radio,
r
r
r
r
r
r
r r h r A
3
2 2
2
2
2 6 . 1
2
) 8 . 0 ( 2
2
8 . 0
2 2 ) 2 (




+
= + = + |

\
|
= + =
Lo cual nos da una funcin racional.

Ejemplo. Se construir una canaleta para captar agua de lluvia a partir de
una lmina de largo L y ancho M, dar una funcin que exprese el
volumen de la canaleta dependiendo del ngulo con el cual se dobla la
lmina en tres partes iguales la longitud M.


L
M
3 / M
3 / M
3 / M
x
h
r
h
14
El volumen de la canaleta esta determinado por su el largo de la lmina, el
cual, es una constante y por el rea de la seccin transversal la cual forma
un trapecio.
En el trapecio consideramos las variables h x, y del tringulo rectngulo
que forman, tenemos las relaciones siguientes:
3 / M
x
Hip
CO
sen = = ,
3 /
cos
M
h
Hip
CA
= =
De estas despejamos h x, respectivamente:
3
Msen
x = ,
3
cos M
h =
Sabemos que el rea de un trapecio est dada por
2
) ( h b B
A
+
=
Donde la base mayor en este caso es
3
2
M
x B + =
La base menor es
3
M
b = , y la altura es
3
cos M
h = ; las cuales las
sustituimos en la expresin del rea y obtenemos
|

\
|
|

\
|
+ + =
+
=
3
cos
3 3
2
2
1
2
) ( M M M
x
h b B
A
Luego sustituimos
3
Msen
x = y simplificamos
) cos cos (
9
3
cos
3 3
cos
3
2
3
2
2
1
) (
2



+ =
|

\
|
|

\
| +
= |

\
|
|

\
|
+ =
sen
M
M M Msen M M Msen
A

En este ejemplo obtuvimos una funcin que involucra funciones
trigonomtricas.

Ejemplo. En un caf-internet se cobra $10 los primeros 20 minutos y $0.2
cada minuto extra. Escriba una funcin que represente el monto a pagar por
el servicio cuando se usa t minutos.
Tenemos que si 20 0 t , se paga $10 y para
t < 20 , se pagar t t t ) 2 . 0 ( 6 4 ) 2 . 0 ( 10 ) 2 . 0 )( 20 ( 10 + = + = +
La funcin es del tipo seccionada y la podemos escribir como

<

+
=
t
t
t
t f
20 si
20 0 si
) 2 . 0 ( 6
10
) (


2.2 Funciones inyectivas, suprayectivas y biyectivas.
Son diferentes clases de funciones con propiedades especiales.

15
Definicin. Una funcin B A f : se llama inyectiva si siempre que
2 1
a a se tiene que ) ( ) (
2 1
a f a f .

En forma equivalente usando la contrapuesta: B A f : es una funcin,
inyectiva Si ) ( ) (
2 1
a f a f = implica que
2 1
a a = .

Funcin Inyectiva Funcin No Inyectiva

Ejemplos.
1. Z Z f : tal que 1 3 ) ( + = k k f
Si ) ( ) (
2 1
k f k f = ,
1 3 1 3
2 1
+ = + k k

2 1
3 3 k k =

2 1
k k =
As f si es inyectiva.

2. N Z f : tal que
2
) 1 ( ) ( + = k k f
No es inyectiva porque 16 ) 1 3 ( ) 3 (
2
= + = f y 16 ) 1 5 ( ) 5 (
2
= + = f sin
embargo 5 3 .

3. { } R R f 2 / 1 : tal que
x
x
x f
2 1
1
) (

+
=
Si ) ( ) (
2 1
x f x f = ,

2
2
1
1
2 1
1
2 1
1
x
x
x
x

+
=

+
, de donde
) 2 1 )( 1 ( ) 2 1 )( 1 (
1 2 2 1
x x x x + = + , haciendo operaciones

1 2 1 2 2 2 1 1
2 2 1 2 2 1 x x x x x x x x + = +

1 2 2 1
2 2 x x x x =

2 1
3 3 x x =

2 1
x x =
As f es inyectiva.

4. { } ) 7 , 7 )( 8 , 2 ( ), 9 , 3 ( = f es inyectiva

A
f
B

A
f
B

16
5. { } ) 4 , 4 ( ), 5 , 7 ( ), 4 , 2 ( ), 0 , 3 ( = g no es inyectiva


Definicin. Una funcin B A f : se llama suprayectiva o sobreyectiva si
para cada B b existe A a tal que ) (a f b = .

En trminos de la imagen de f , podemos decir que B A f : es una
funcin suprayectiva o sobreyectiva si B f = Im

Funcin No sobreyectiva Funcin sobreyectiva

Ejemplos.
1. Z Z f : tal que 1 3 ) ( + = k k f
Esta funcin no es sobreyectiva sobre Z B = .
Como conjunto de parejas f se escribe como
{ } K K ) 10 , 3 ( ), 7 , 2 ( ), 4 , 1 ( ), 1 , 0 ( ), 2 , 1 ( ), 5 , 2 ( ), 8 , 3 ( = f
De donde observamos que algunos enteros no son imagen de algn
elemento, como lo son: K , 2 , 3 , 7
Podemos formalizar esta afirmacin como sigue:
Dado cualquier Z m , encontrar Z k tal que 1 3 ) ( + = = k k f m , de
aqu despejamos,
3
1
=
m
k , esto dice que el entero 1 m debe ser
divisible entre tres, lo cual no ocurre para toda m .

Una funcin est determinada por su dominio, codominio y regla de
correspondencia

2. R R f : tal que 1 3 ) ( + = x x f si es sobreyectiva.

3. { } { } 2 / 1 2 / 1 : R R f tal que
x
x
x f
2 1
1
) (

+
=
Dado { } 2 / 1 R y , encontrar { } 2 / 1 R x tal que
x
x
x f y
2 1
1
) (

+
= = ,
entonces
A
f
B

A
f
B

17

1 ) 2 1 (
1 2
1 2
1 ) 2 1 (
= +
= +
+ =
+ =
y y x
y xy x
x xy y
x x y


y
y
x
2 1
1
+

= con 2 / 1 y
Es decir, se puede encontrar x para cualquier 2 / 1 y , por lo tanto f
es sobreyectiva

4. { } 7 , 2 , 3 = A , { } 9 , 7 , 8 = B
B A f : { } ) 7 , 7 )( 8 , 2 ( ), 9 , 3 ( = f es suprayectiva

5. { } 7 , 2 , 3 = A , { } 9 , 7 , 8 = B
B A g : { } ) 7 , 7 ( ), 8 , 2 ( ), 7 , 3 ( = g no es suprayectiva


Definicin. Una funcin B A f : se llama biyectiva, si f es inyectiva
y es sobreyectiva

No biyectiva No biyectiva

No biyectiva biyectiva

Ejemplo. { } { } 2 6 : R R f tal que
x
x
x f

=
6
1 2
) (
f es inyectiva:
A
f
B

A
f
B

A
f
B

A
f
B

18
Si ) ( ) (
2 1
a f a f = entonces
2
2
1
1
6
1 2
6
1 2
a
a
a
a

Lo cual implica




f es suprayectiva:
Para { } 6 R y encontrar { } 2 R x tal que

x
x
x f y

= =
6
1 2
) (

Intentamos despejar x

2
2
1 6
) 2 ( 2 1 6
1 2 6
1 2 ) 6 (

+
+
=
+ = + = +
=
=
y
y
y
x
y x xy x y
x xy y
x x y


Por lo tanto
x
x
x f

=
6
1 2
) ( si es biyectiva

Ejemplo. Z N f : tal que
(

=
2
) 1 ( ) (
k
k f
k
es biyectiva
Si ponemos dos imgenes iguales
(

=
(

2
) 1 (
2
) 1 (
m k
m k
ambas deben ser positivas o ambas negativas, es decir
m k, deben ser ambos pares o ambos impares
Caso: son pares t m s k 2 , 2 = =
| | | | m k t s t s
t s m k
= = =
(

=
(

=
(

2
2
2
2

2 2


Caso: son impares 1 2 , 1 2 + = + = t m s k
m k t s t s
t s m k
= =
(

+ =
(

+
(

+
=
(

=
(

2
1
2
1

2
1 2
2
1 2

2 2

Por lo tanto f es inyectiva
2 1
2 1
1 2 1 2 2 2 1 1
1 2 2 1
11 11
6 2 12 6 2 12
) 6 )( 1 2 ( ) 6 )( 1 2 (
a a
a a
a a a a a a a a
a a a a
=
=
+ = +
=
19
Es til observar el comportamiento en algunos nmeros naturales
{ } K ), 2 , 5 ( ), 2 , 4 ( ), 1 , 3 ( ), 1 , 2 ( ), 0 , 1 ( = f
Podemos ver que los pares van a nmeros positivos y que los impares van a
nmeros negativos
Tambin de los positivos en la imagen se observa que provienen de su
doble, entonces
si Z m y 0 > m , sea N m k = 2 y satisface
| | m m
m k
k f
m k
= =
(

=
(

=
2
2
) 1 (
2
) 1 ( ) (
2

Para el otro caso
si Z m y 0 m , sea N m k + = 1 2 y satisface
m m
m k
k f
m k
=
(

+ =
(

+
=
(

=
+
2
1
2
1 2
) 1 (
2
) 1 ( ) (
1 2

Por lo tanto f es suprayectiva
Por lo tanto f es biyectiva


Propiedades de funciones inyectivas, suprayectivas y biyectivas.

Proposicin. Si B A f : y C B g : son funciones inyectivas, entonces
la composicin C A f g : o es inyectiva.
Demostracin.
Sean A a a
2 1
y tales que ) )( ( ) )( (
2 1
a f g a f g o o =
Entonces )) ( ( )) ( (
2 1
a f g a f g = por definicin de composicin de funciones,
Luego como g es inyectiva, se tiene ) ( ) (
2 1
a f a f = ,
Y tambin f es inyectiva, por lo que
2 1
a a =
Por lo tanto f g o es inyectiva.

Ejemplo. { {{ { } }} } ) 5 , 3 ( ), 2 , 1 ( = == = f inyectiva, { {{ { } }} } ) 8 , 5 ( ), 8 , 2 ( = == = g no inyectiva,
{ {{ { } }} } ) 8 , 3 ( ), 8 , 1 ( = == = f g o no inyectiva.

Ejemplo. { {{ { } }} } ) 3 , 3 ( ), 3 , 2 ( ), 2 , 1 ( = == = f no inyectiva, { {{ { } }} } ) 4 , 3 ( ), 6 , 2 ( = == = g inyectiva,
{ {{ { } }} } ) 4 , 3 ( ), 4 , 2 ( ), 6 , 1 ( = == = f g o no inyectiva.

Ejemplo. { } ) 2 , 3 ( ), 1 , 2 ( ), 3 , 1 ( = f inyectiva, { } ) 3 , 3 ( ), 1 , 2 ( ), 2 , 1 ( = g inyectiva,
{ } ) 1 , 3 ( ), 2 , 2 ( ), 3 , 1 ( = f g o inyectiva.

Proposicin. Sean B A f : y C B g : funciones, si C A f g : o es
inyectiva, entonces f es inyectiva.
Demostracin.
Sean A a a
2 1
y tales que ) ( ) (
2 1
a f a f =
20
aplicando la funcin g de ambos lados )) ( ( )) ( (
2 1
a f g a f g = o
) )( ( ) )( (
2 1
a f g a f g o o =
Como f g o es inyectiva, se tiene
2 1
a a =
Por lo tanto f es inyectiva.

Ejemplo. { {{ { } }} } ) , ( ), , ( f b e a f = == = inyectiva, { {{ { } }} } ) , ( ), , ( ), , ( m k m f d e g = == = no
inyectiva,
{ {{ { } }} } ) , ( ), , ( m b d a f g = == = o inyectiva.

Proposicin. Si B A f : y C B g : son funciones sobreyectivas,
entonces la composicin C A f g : o es sobreyectiva.
Demostracin.
Consideramos cualquier C c
Como g es sobreyectiva, existe algn B b tal que ) (b g c = ,
Luego para dicha B b , como f es sobreyectiva, existe A a tal que
) (a f b = ,
Sustituyendo esta expresin de b en ) (b g c = , tenemos, )) ( ( a f g c = , con
lo cual concluimos que para C c , existe A a tal que )) ( ( a f g c = o
) )( ( a f g c o = , es decir, f g o es sobreyectiva.

Ejemplo. Para los siguientes ejemplos consideramos { {{ { } }} } 3 , 2 , 1 = == = = == = B A

{ {{ { } }} } ) 3 , 3 ( ), 3 , 2 ( ), 2 , 1 ( = == = f no suprayectiva, { {{ { } }} } ) 2 , 2 ( ), 2 , 1 ( ), 1 , 3 ( = == = g no suprayectiva,
{ {{ { } }} } ) 2 , 3 ( ), 2 , 2 ( ), 1 , 1 ( = == = f g o no suprayectiva.

{ {{ { } }} } ) 1 , 3 ( ), 1 , 2 ( ), 3 , 1 ( = == = f no suprayectiva, { {{ { } }} } ) 1 , 2 ( ), 2 , 1 ( ), 3 , 3 ( = == = g suprayectiva,
{ {{ { } }} } ) 2 , 3 ( ), 2 , 2 ( ), 3 , 1 ( = == = f g o no suprayectiva.

{ } ) 1 , 3 ( ), 2 , 2 ( ), 3 , 1 ( = f suprayectiva, { {{ { } }} } ) 1 , 2 ( ), 2 , 1 ( ), 3 , 3 ( = == = g suprayectiva,
{ } ) 2 , 3 ( ), 1 , 2 ( ), 3 , 1 ( = f g o suprayectiva.

Proposicin. Sean B A f : y C B g : funciones, si C A f g : o es
sobreyectiva, entonces g es sobreyectiva.
Demostracin.
Consideramos cualquier C c
Como f g o es sobreyectiva, existe algn A a tal que
)) ( ( ) )( ( a f g a f g c = = o , tomamos ) (a f b = , B b y satisface
)) ( ( ) ( a f g b g c = =
Por lo tanto g es sobreyectiva.

21
Ejemplo. Sean { {{ { } }} } b a A , = == = , { {{ { } }} } l h e B , , = == = y { {{ { } }} } k m C , = == =
{ {{ { } }} } ) , ( ), , ( h b e a f = == = no es suprayectiva { {{ { } }} } ) , ( ), , ( ), , ( k l k h m e g = == = es suprayectiva
{ {{ { } }} } ) , ( ), , ( k b m a f g = == = o es suprayectiva.

Corolario. Si B A f : y C B g : son funciones biyectivas, entonces
la composicin C A f g : o es biyectiva.

Definicin. Sea B A f : una funcin, una funcin A B g : se llama
i) Inversa derecha de f , si
A
I f g = o
ii) Inversa izquierda de f , si
B
I g f = o

Ejemplo. Para { } { } 4 , 6 , 3 y 5 , 3 , 2 = = B A
{ } ) 3 , 5 ( ), 4 , 3 ( ), 6 , 2 ( = f Y { } ) 5 , 3 ( ), 3 , 4 ( ), 2 , 6 ( = g
Se satisface que
{ }
A
I f g = = ) 5 , 5 ( ), 3 , 3 ( ), 2 , 2 ( o y { }
B
I g f = = ) 3 , 3 ( ), 4 , 4 ( ), 6 , 6 ( o
Por lo que g es inversa derecha e inversa izquierda de f .

Proposicin. Sea B A f : una funcin, si f tiene inversa derecha
1
g e
inversa izquierda
2
g , entonces
2 1
g g = .
Demostracin.
Por hiptesis
A
I f g = o
1
y
B
I g f =
2
o
2
2
2 1
2 1
1 1
) (
) (
g
g I
g f g
g f g
I g g
A
B
=
=
=
=
=
o
o o
o o
o


Definicin. Sea B A f : una funcin, si f tiene inversa derecha e
inversa izquierda, por la proposicin anterior son iguales, entonces se dice
que f es invertible, y su inversa se denota por
1
f .

Nota:
1
f satisface que
A
I f f =

o
1
y
B
I f f =
1
o

Existe una relacin muy importante entre funciones biyectivas y funciones
invertibles, como se enuncia enseguida.

Proposicin. Una funcin B A f : es biyectiva si y solo si es
invertible.
Demostracin.
)
22
Suponemos B A f : biyectiva, y definimos una funcin A B g : de la
siguiente forma:
Para B b , como f es sobreyectiva, existe A a tal que ) (a f b = y
definimos a b g = ) (
g es una funcin bien definida, ya que si a b g = ) ( y a b g = ) ( , segn
nuestra definicin: ) (a f b = y ) (a f b = pero como f es inyectiva, a a = .

Luego g es inversa derecha e inversa izquierda de f puesto que:
Para A a , ) ( ) ( )) ( ( ) )( ( a I a b g a f g a f g
A
= = = = o y
Para B b , ) ( ) ( )) ( ( ) )( ( b I b a f b g f b g f
B
= = = = o
Por lo tanto f tiene funcin inversa, que es g , es decir f es invertible.

)
Suponemos que f es invertible,
Es decir existe A B g : tal que
A
I f g = o y
B
I g f = o , de aqu ,
Si ) ( ) (
2 1
a f a f = , entonces )) ( ( )) ( (
2 1
a f g a f g = o
) )( ( ) )( (
2 1
a f g a f g o o =
) ( ) (
2 1
a I a I
A A
=
2 1
a a =
Y f resulta inyectiva.

Tambin para cualquier B b , A a b g = ) ( , luego
b b I b g f a f
B
= = = ) ( )) ( ( ) (
Esto quiere decir que f es sobreyectiva. As f es biyectiva.

Ejemplo. { } { } 0 5 : R R f tal que
10 2
1
) (

=
x
x f
f es inyectiva:
Si ) ( ) (
2 1
a f a f = entonces
10 2
1
10 2
1
2 1

=
a a

Lo cual implica



f es suprayectiva:
Para { } 0 R y encontrar { } 5 R x tal que
10 2
1

=
x
y
2 1
2 1
2 1
2 2
10 2 10 2
a a
a a
a a
=
=
=
23

Intentamos despejar x



Lo cual est bien definido siempre que 0 y , lo cual se consider en
La condicin { } 0 R y
Podemos concluir que la funcin es biyectiva y por el teorema, es
invertible.

Encontrando la inversa de la funcin:
Del hecho de que la funcin es sobreyectiva, tenemos en el despeje

y
y
x
2
10 1+
= , concluimos, cambiando el nombre de la variable en la
expresin, que
x
x
x f
2
10 1
) (
1
+
=

Verificamos que es la inversa:
Primero

|

\
|

\
|

+
=
|

\
|

=
=

10 2
1
2
10 2
1
10 1
10 2
1
)) ( ( ) )( (
1
1 1
x
x
x
f
x f f x f f o

Para simplificar la expresin multiplicamos numerador y
denominador por

{ }
) (
2
2
2
10 10 2
10 2
10 2
10 2
1
2
10 2
1
10 1
5
x I x
x x
x
x
x
x
R
= = =
+
=

\
|

|
|

\
|
|

\
|

+

Segundo
)) ( ( ) )( (
1 1
x f f x f f

= o
|

\
| +
=
x
x
f
2
10 1

y
y
x
y
y
y
x
y
x
2
10 1
10 1
10
1
2
1
10 2
+
=
+
= + =
=
24

10
2
10 1
2
1

\
| +
=
x
x


Simplificamos la expresin

{ }
) (
10 10 1
10
10 1
1
10
2
10 1
2
1
0
x I x
x x
x
x
x
x
x
R
= =
+
=
|

\
| +
=
|

\
| +

Por lo tanto
x
x
x f
2
10 1
) (
1
+
=

si es la inversa de f

Ejemplo. Z Z f : tal que
( (( (

( (( (



= == =
2
) (
k
k f
No es inyectiva y si es sobreyectiva:
| || | | || | | || | | || | 3 5 . 3
2
7
) 7 ( 3 3
2
6
) 6 ( = == = = == =
( (( (

( (( (



= == = = == = = == = = == =
( (( (

( (( (



= == = f f pero 7 6
Para cualquier Z m , Z m 2 satisface | || | | || | m m
m
m f = == = = == =
( (( (

( (( (



= == =
2
2
) 2 (
Ahora Z Z g : tal que k k g 2 ) ( = == = es inversa izquierda de f :
| || | | || | k k
k
k f k g f k g f = == = = == =
( (( (

( (( (



= == = = == = = == =
2
2
) 2 ( )) ( ( ) )( ( o ,
Pero g no es inversa derecha de f :
Par un entero impar 1 2 + ++ + = == = m k
) ( ) (
1 2 2 ) (
2
1
2
1 2
)) 1 2 ( ( ) )( (
k I f g
k m m m g m g
m
g m f g k f g
Z

= == = + ++ + = == = = == =
( (( (

( (( (



+ ++ + = == =
( (( (

( (( (


+ ++ +
= == = + ++ + = == =
o
o

Por lo tanto la funcin no es invertible.

Ejemplo. Encuentre la inversa de la funcin x x g = 6 3 ) ( y demuestre
que lo es.
El dominio de la funcin es ( | 6 , , como 3 6 3 x , el codominio es
( | 3 , , entonces ( | ( | 6 , 3 , :
1

g

Haciendo x y = 6 3 y despejamos
y x = 3 6 ,
2
) 3 ( 6 y x = ,
2
) 3 ( 6 y x = ,
2
6 9 6 y y x + = , 3 6
2
+ = y y x
Proponemos 3 6 ) (
2 1
+ =

x x x g
Ahora verificamos las condiciones

( ) x g
x g g x g g
=
=

6 3
)) ( ( ) )( (
1
1 1
o

25
( ) ( )
) (
3 6 6 18 ) 6 ( 6 6 9
3 6 3 6 6 3
2
x I x
x x x
x x
= =
+ + =
+ =



( )
( )
) (
) 3 ( 3
3 3
) 3 ( 3
9 6 3
3 6 6 3
3 6 6 3
3 6
)) ( ( ) )( (
2
2
2
2
2
1 1
x I x
x
x
x
x x
x x
x x
x x g
x g g x g g
= =
=
=
=
+ =
+ + =
+ =
+ =
=

o

Nota. Como ( | 3 , ) (
1
=

g Dom tenemos 3 x , 0 3 x y x x = 3 3

Contar los elementos de un conjunto en la prctica, consiste en dar una
funcin biyectiva entre los elemento de conjunto y un conjunto de la forma
{ } n , , 2 , 1 K para algn N n .

Definicin. La cardinalidad de un conjunto A se define como el nmero
de elementos que tiene el conjunto y se denota por A

La cardinalidad de un conjunto puede ser finita o infinita.

Un conjunto es de cardinalidad finita si se puede dar una funcin
biyectiva entre los elemento de conjunto y un conjunto de la forma
{ } n , , 2 , 1 K para algn N n ; en caso contrario se dice que tiene
cardinalidad infinita.

Los conceptos de funciones inyectivas, sobreyectivas, biyectivas nos
ayudan a comparar las cardinalidades de dos conjuntos.

Se B A f : una funcin, si f es inyectiva, entonces la cardinalidad de
A es menor o igual que la cardinalidad de B ; B A
26

Se B A f : una funcin, si f es sobreyectiva, entonces la cardinalidad
de A es mayor o igual que la cardinalidad de B ; B A

Se B A f : una funcin, si f es biyectiva, entonces la cardinalidad de
A igual a la cardinalidad de B ; B A = .


Por lo tanto sin conocer explcitamente la cardinalidad de un conjunto,
podemos comparar su cardinalidad con la de otro conjunto, proporcionando
una funcin entre dichos conjuntos con alguna caracterstica inyectiva,
sobreyectiva o biyectiva.

Ejemplo. En un saln de clases podemos saber si la cantidad de alumnos es
la misma que la de bancas, observando si hay bancas desocupadas, o si hay
alumnos de pe, o ninguna de las dos posibilidades.

Una caracterstica de los conjuntos infinitos es que algunos de sus
subconjuntos son comparables con ellos mismos en cardinalidad, lo cual no
lo satisfacen los conjuntos finitos.

A
f
B

A
f
B

A
f
B

27
Ejemplo. Los naturales N si consideramos el subconjunto de los
naturales pares
P
N , podemos dar una funcin biyectiva entre los dos
conjuntos:
P
N N f : tal que n n f 2 ) ( =
es decir hay la misma cantidad de nmeros naturales que de naturales pares

Sabemos que tanto el conjunto de nmeros naturales como el conjunto de
los nmeros reales son infinitos, es decir su cardinalidad es infinita. En
matemticas avanzadas se puede probar que no se puede dar ninguna
funcin biyectiva de los naturales a los reales, por lo que diferenciamos dos
clases de conjuntos infinitos:



Los conjuntos infinitos numerables son aquellos que se pueden poner en
biyeccin con el conjunto de los nmeros naturales N .

Ejemplos. Los enteros, los impares, los racionales.

Los conjuntos infinitos no numerables son aquellos que se pueden poner
en biyeccin con el conjunto de los nmeros reales R .

Ejemplos. Los intervalos abiertos, intervalos cerrados, intervalos infinitos
de nmeros reales.

Ejemplo. La funcin | || | | || | | || | | || | 4 , 1 5 , 2 : f tal que
3
13
3
5
) ( = == = x x f es
biyectiva y muestra que ambos intervalos | | | | 4 , 1 y 5 , 2 tienen la misma
cantidad de elementos.

Ejemplo. | | | | 1 , 0 , : b a f tal que
a b
a x
x f

= ) (
Es una funcin biyectiva.

Ejemplo. | || | | || | | || | | || | b a f , 1 , 0 : tal que x a b a x f ) ( ) ( + ++ + = == =
Es la inversa del ejemplo anterior

Ejemplo. | || | | || | | || | | || | d c b a f , , : tal que ) ( ) ( a x
a b
c d
c x f


+ ++ + = == =
Infinitos Conjuntos
Numerables Infinitos Numerables No Infinitos
28
Es una funcin biyectiva.

Tambin es buen ejercicio contar todas las funciones que se pueden definir
de un conjunto a otro, y las que son inyectivas o sobreyectivas o biyectivas.

Ejemplo. { } { } u i B o e a A , y , , = = cuntas funciones se pueden definir de
B A en , cuntas son inyectivas, cuntas sobreyectivas y cuntas
biyectivas?
Podemos en listar las 8 2
3
= funciones

A 1
f
2
f
3
f
4
f
5
f
6
f
7
f
8
f
a i i i i u u u u
e i u i u u i u i
o i i u u u u i i

No hay funciones inyectivas, hay seis funciones suprayectivas, no hay
funciones biyectivas.

Ejemplo. { } { } t q p B s r A , , y , = = cuntas funciones se pueden definir de
B A en , cuntas son inyectivas, cuntas sobreyectivas y cuntas
biyectivas?
Podemos en listar las 9 3
2
= funciones

A 1
f
2
f
3
f
4
f
5
f
6
f
7
f
8
f
9
f
r
p p p q q q
t t t
s
p q
t
p q
t
p q
t

Hay seis funciones inyectivas, no hay funciones suprayectivas, no hay
funciones biyectivas

Ejemplo. { } { } k n m B c b a A , , y , , = = cuntas funciones se pueden definir de
B A en , cuntas son inyectivas, cuntas sobreyectivas y cuntas
biyectivas?
En este caso hay 27 3
3
= funciones, seis de las cuales son biyectivas y las
restantes no son ni inyectivas ni suprayectivas por qu?
Enlistamos las biyectivas

A 1
f
2
f
3
f
4
f
5
f
6
f
a m m n n k k
b n k m k m n
c k n k m n m
29


BIBLIOGRAFIA:
1. Swokowsky, Cole. Algebra y trigonometra con Geometra
Analtica. Grupo Edidtorial Iberoamrica
2. Haaser, LaSalle, Sullivan. Anlisis Matemtico. Vol. 1 Ed. Trillas
3. Spivak Michael. Clculus. Ed. Reverte.