GRILLAGE ANALYSIS OF COMPOSITE CONCRETE SLAB ON

STEEL BEAMS WITH PARTIAL INTERACTION

Prof. Dr. Husain M. Husain
1
, Dr. Ali N. Attiyah
2
and Jenan Niamah Yasser
3
ABSTRACT: The resent study is !on!erned "ith the #eha$ior of a !omosite stru!ture
made u of a !on!rete sla# !onne!ted to steel #eams in t"o dire!tions #y shear !onne!tors #y
ta%in& into !onsideration the linear a!tion of shear !onne!tors in the for!e'sli relationshi.
The &rilla&e or &rid frame"or% method as simlified method of analysis is used in this study
to study sli, defle!tion and stresses !aused #y moments from alied normal loads. A
method is su&&ested to deri$e the re(uired se!tion ri&idities )the fle*ural and torsional
ri&idities+ of the &rilla&e mem#ers from the !omosite a!tion of the indi$idual &rilla&e
!omosite mem#ers. Desi&n !harts are !onstru!ted for estimatin& the er!enta&e de!rease in
fle*ural ri&idity of ea!h !omosite mem#er "ith artial shear !onne!tion. ,t "as found for a
!omosite stru!ture analy-ed #y &rilla&e mem#ers, the effe!ti$e "idth of ea!h mem#er
should #e used to !al!ulate the fle*ural ri&idity of that mem#er. Also Poissons ratio effe!t
"as in!luded in the !al!ulation of the fle*ural ri&idities of the &rilla&e mem#ers. .ffe!t on
defle!tions #y trans$erse shearin& for!es "as found to #e small and thus it !an #e ne&le!ted
)er!enta&e differen!es is less than 11./ 0+.
1. Introduction
Each different building material has a special prominent quality which distinguishes it
from other materials. There is no material that can provide all the structural
requirements. This is the reason of using different materials that can be arranged in an
optimum geometric configuration, with the aim that only the desirable property of
each material will be utilized by virtue of its designated position. The structure is then
known as a composite structure, and the relevant method of building as composite
construction.
The composite concrete slab-on-steel beam structure consists of three major structural
elements, namely a reinforced concrete slab resting on longitudinal and transverse
steel beams, which interact, compositely with the slab by means of mechanical shear
connectors. The analysis of composite beams and their behavior assuming linear and
nonlinear material and shear connector behavior has been in general based on an
approach initiated by ewmark, !iess and "iest in #$%#
&#'
. The equilibrium and
compatibility equations for an element of the beam were reduced to a single second
1+ 1ni$ersity of Ti%reet , 2olle&e of .n&ineerin& , 2i$il Deartment.
2+ 1ni$ersity of 3ufa , 2olle&e of .n&ineerin& , 2i$il Deartment.
3+ 1ni$ersity of 3ufa , 2olle&e of .n&ineerin& , 2i$il Deartment.
#
order differential equation in terms of either the resultant a(ial force in the )concrete*
flange or the interface slip. !olution for the a(ial force or the interface slip was
substituted back into the basic equilibrium and compatibility equations, which could
then be solved to give the displacements and the strains throughout the beam. That
approach was initially based on linear material and shear connector behavior.
+n the method suggested for the present study, the composite structure is idealized as a
grillage, the grillage mesh is assumed to be coincident with the center-lines of the
main steel beams. The concrete slab and the steel beams are assumed to behave in the
elastic range and the force- slip behavior of the shear connectors is linear. To use the
T-beam approach, the concept of the effective width is used which refers to a fictitious
width of the slab that when acted on by the actual ma(imum stress the slab would
have the same static equilibrium effect as the e(isting variable stress. The effective
width is affected by various factors, such as the type of loading, the boundary
conditions at the supports and the ratio of beam spacing to span ,-.
&/'
.
0ohnson )#$1%*
&2'
proposed a partial interaction theory for simply supported composite
beams, in which the analysis was based on elastic theory. 3ennedy, 4race, and
!oliman )#$5$*
&6'
presented an e(perimental study that was conducted on three
composite bridge models each subjected to one- vehicle load. 0asim )#$$6*
&%'
presented
a method of analysis which depended on elastic theory. +n that analysis he adopted
same assumptions of ewmark
&#'
.
2. Assumptions of the Grillage Analogy
The grillage analogy involves the representation of effectively a three- dimensional
composite structure by a two- dimensional assemblage of discrete one- dimensional
interconnected beams in bending and torsion. +n analysis, the following assumptions
are introduced7
#- 8oncrete and steel are linearly elastic materials. The concrete slab is assumed
to be able to sustain sufficient tension such that no tensile cracks develop in
this part. The distribution of strains through the depth of each component is
linear.
/- The longitudinal and transverse steel beams are assumed rigidly connected
)welded connections*.
/
2- The shear connection between the two components is continuous along the
length. The discrete deformable connectors with equal moduli and uniform
spacing are assumed to be replaced by a medium of negligible thickness.
9riction and bond effects between the two components are neglected.
6- The amount of slip permitted by the connector is directly proportional to the
force transmitted through the connector.
%- :t every section of the composite beams, each component deflects the same
amount. o separation is assumed to occur.
3. Evaluation of Elastic Section Rigidities of Grillage Memers
The idealization of a composite slab;beam structure by an equivalent grillage requires
the evaluation of the elastic section rigidities of the grillage members. The elastic
rigidities of these members should be derived from the section properties of the actual
composite slab;beam structure so that an adequate picture for the composite section
behavior under the applied loadings can be obtained from the equivalent grillage. The
elastic section rigidities required for the sections of the equivalent composite grillage
members are as follows7
#-,ending )or fle(ural* rigidity )E+*. /-Torsional rigidity )40*. 2-!hearing
rigidity )4:
v
*.
<erein, suggestions are presented for these quantities and adopted in this work.
3.1 !ending "or #le$ural% rigidity&
9le(ural rigidities of the equivalent grillage members play an important role in the
calculation of deflections and in the distribution of moments. +n analyzing the
composite slab-beam structure by the grillage analogy, the fle(ural rigidities of the
composite members are derived from partial interaction theory. 4enerally, two factors
)besides the partial interaction effect* must also be considered in the calculation of the
fle(ural rigidity of the grillage members. These factors are due to the shear lag and
=oisson>s ratio effects. !hear lag effects can be included by using the effective width
concept. The two;dimensional confining effect of =oisson?s ratio can be considered
by dividing the modulus of elasticity of concrete E
#
by )#-@
/
*.The interaction
phenomenon can be illustrated from the discussion of the lower and upper limits of
behavior of composite beams, i.e., no interaction and complete )or full* interaction,
2
respectively. The analysis and fle(ural rigidity will be carried out on the basis of
elastic theory.
Asually, the interaction between steel and concrete is incomplete due to the
occurrence of slip. +t produces a discontinuity in the strain distribution at the interface
where appreciable strain difference. The neutral a(is of the slab is closer to the beam
and that of the beam is closer to the slab, when compared with the no- interaction
case. The result of the partial interaction is the partial development of the compressive
force in the concrete slab and tensile force in the steel beam. This leads to less
ultimate load than that resisted when complete interaction e(ists. =artial interaction is
the usual practical case in the design and analysis of composite structures.
: large number of research studies have been devoted to calculate the deflections of
composite beams with partial shear interaction.
The solution submitted by 0asim
&%'
for the final form of the governing equation for a
composite beam by using 9ourier series method will be adopted in the present study to
calculate the fle(ural rigidity of composite sections for simply supported beams under
different loading cases.
1niformly Distri#uted 4oad
9or the case of uniformly distributed load on a simply supported beam the solution for
the ma(imum deflection is7

( )
1
]
1

+ + 3 sinh 3 tanh 3 cosh #

3
#
/
#
3 %
8 /6
#
y
y
/
2
f
p

)#*
Bhere

/
/
f
. w
256
%
y
C the mid-span deflection of composite beam with full shear
connection D w is the displacement in z-direction, . is the span length, E
/
is the
modulus of elasticity of steel, + is the moment of inertia of the transformed fully
composite section about the elastic neutral a(is assuming uncracked section, y
p
is the
mid-span deflection of composite beam with partial shear connection,
6
( )
( )
( ) ( )
/ / # #
/ / # #
/ / # #
/
/ #
/ #
/ #
/
#/
2
. .
. . .
. . 6
# #
+

+
+

,
_

h h 2
2
t
t
and
/
. 8
3
#

.
)/*
Bhere 8
#/
is the depth of center of gravity of steel beam below mid-plane of slab, +
#
,
+
#t
and +
/
are the moments of inertia of concrete slab about its own centroid,
transformed area of concrete about its own centroid, steel beam about its own
centroid, respectively. :
#
, :
#t
and :
/
are the cross sectional area of concrete slab,
transformed area of concrete above interface, cross sectional area of steel beam,
respectively.h
#
is the thickness of concrete slab and h
/
is the depth of steel beam.
#

is the effective modulus of elasticity for concrete slab due to lateral confinement of
slab and E
/
is the modulus of elasticity of steel. 8
#
is a factor found from
8
#
C
1
1
]
1

+
+

+

/ / # #
/
#/
/ / # #
. .
8
.
#
.
# n .
)2*
Bhere n is the number of connectors per row and p is the spacing of connectors along
the beam.
!ince
/
/
d(
y d

is the curvature , then the integration of this equation twice results

in

6
. w
y )6*
where is a factor depending on the boundary conditions )
256
%

for simply
supported beams under uniform load w per unit length*.
Thus
6
f
p
6
f
p
. w
. w
y
y

)w is the applied load* or

f
f

y
y

)%*
,y substituting Eq. )%* into Eq. )#*, then

( )
1
]
1

3 sinh 3 tanh 3 cosh #

3
#
/
#
3 %
8 /6
#
/
2
p
f
)E*
Fefining
( )
1
]
1

3 3 3
3 3
2
D sinh tanh cosh #
#
/
#
%
/6
/
2
#
and substituting this into Eq.
)E* ,then this equation can be written as
%

( )
#
# D
f

)1*
Point 4oad at Mid'san
9or the case of a point load at mid-span of a simply supported beam, the solution for
the ma(imum deflection is7

1
]
1

+ 3 tanh
3
#
#
3
8 2
#
y
y
/
2
f
p
)5*
where

/
2
f
65
. w
y
,y using the same procedure, the pertinent equation is
1
]
1

3 tanh
3
#
#
3
8 2
#
/
2
p
f
)$*
Asing the notation
1
]
1

3
3 3
2
D tanh
#
#
2
/
2
/
Eq. )$* reduces to
( )
/
# D
f

)#G*
Point 4oad at 5 6an
9or this loaded case the ma(imum deflection is
1
]
1

+
,
_

+
6
#
3 cosh
3 tanh
3 sinh
3
/ 3 sinh
3 ##
8 $E
#
y
y
/
2
f
p
)##*
Bhere

/
2
f
1E5
. w ##
y
Fefining
1
]
1

,
_

6
#
cosh
tanh
sinh / sinh
##
$E
/
2
2
3
3
3
3
3
3
2
D
, then
( )
2
# D
f

)#/*
Distri#uted 4oad of Trae-oidal 6hae
9or this case of loading the pertinent equation is
1
]
1

+
,
_

+
6
#
/
#
3 / sinh
3 sinh
3
#
3 %
8 65
#
y
y
/ /
2
f
p
)#2*
where
( )

+

/
6
/ #
f
. w w
1E5
%
y
E
Asing notation
1
]
1

,
_

6
#
/
#
/ sinh
sinh #
%
65
/ /
2
6
3
3
3 3
2
D

Eqs. )%* and )#2* are combined to give

( )
6
# D
f

)#6*
7oundary 2onditions
9urthermore, the effect of two types of boundary conditions on the prediction of
fle(ural rigidity of a composite beam is studied. They are a beam with fi(ed ends and
a cantilever. The effect of different boundary conditions can be considered by
changing the beam effective length. This effect should be included in Eq.)/* by
replacing the beam span ).*with the beam effective length ).e) . 9or the fi(ed ;
ended beam , the beam effective length is half its span, .eC G.% .. 9or the cantilever,
.e C /.. Thus Eq. )/* may be rewritten as7

/
. 8
3
e #

)#%*
.ffe!t of 4oad Pattern
The following three load patterns were studied7 )#* a concentrated load at the beam
centerH )/* a concentrated load at I spanH and )2* trapezoidal distributed load.
8omparisons were made between these types of load patterns with the uniformly
distributed load to find the fle(ural rigidity of composite beam with partial interaction
)E+
p
*. Jesults are presented for a representative composite beam 5.Em in span with
universal steel section A, 2G%K#/1K21 and concrete flange #%GGmm in width and
#%Gmm in depth. The Loung>s moduli of steel and concrete were taken as /G%GGG
-mm
/
and /%GGG -mm
/
, respectively. 8onnector stiffness k C #5GGGG -mm and
spacing = C %/G mm. Tab.)#* shows the ma(imum difference between the uniformly
distributed load case and other pattern load cases for E+
p
value. +n all cases, the
difference is less than #.2M, thus Eq. )1* may be used for all loading cases to obtain
the fle(ural rigidity of a composite beam with partial interaction. This means that for
each value of factor 8 the values of F
#
, F
/
, F
2
, and F
6
are almost equal for the
majority of 3
/
values. : discrepancy occasionally occurs in F
#
and it is about #M.
1
This leads to the conclusion that the same chart may be used for all types of loads
which in turn greatly simplifies the calculations needed in design
&%'
.
Thus, 9ig.)#* shows such a chart for various values of factor 8 and in terms of the
percentage increase in fle(ural rigidity of composite beam with partial shear
connection and the parameter 3
/
in this chart is for simply supported beams, 9igs )/*
and )2* are design charts to find F
#
for fi(-ended beam and cantilevers respectively.
Tab.)#*7 Na(imum difference in E+
p
between uniformly distributed load case and other load cases
.oad
arrangement
)a* !imply supported beam )b* ,eam with fi(ed ends
Aniform
load
8entral
point
load
=oint
load
at I
span
Trapezoidal
load
Aniform
load
8entral
point
load
=oint
load
at I
span
Trapezoidal
load
Na(imum
difference
between
fle(ural
rigidities
)M*
G *
reference
value )
#./G G.E/
G
G
)reference
value*
#.G/
G.%6 G
3.2 'orsional Rigidity of a (omposite Section
+t is hypothesized that the strength and the stiffness of composite sections under
torsion are to be considered as that of an open section consisting of two parts acting
independently, i.e., the upper part consisting of the reinforced concrete section with
the upper flange of the steel +-section firmly attached to it, and the lower part
consisting of the web and the lower flange of the steel +-section, as shown in
9ig.)6*. ,ased on this hypothesis the stiffness of a composite section is evaluated in
the pre ; cracked stage as follows
&5'
7
The upper part of the composite section is divided into three portions, two equal
concrete portions of dimensions )b
ce
Kh
1
* and a central composite portion of
dimensions )b
s
K )h
1
Ot
f
**, as shown in 9ig. )%*. The torsional stiffness of the upper part
may then be estimated from the following Eq. for the interior composite beam

( ) ( )
eq
2
f # s #
2
# ce
/
T= T=
4 t h b 4 h b /
#
0 4 + +

)#E*
5
and for the edge beam

( ) ( )
eq
2
f # s #
2
# ce
/
T= T=
4 t h b 4 h b
#
0 4 + +

)#1*
Bhere
( )
eq
eq
eq
# /
4
+

D
n
eq
7 equivalent =oisson>s ratio of central portion of the upper part, )
#% . G
eq

*
E
eq
7 equivalent modulus of elasticity of central portion of the upper part of composite
section,
f #
f / # #
eq
t h
t h
+
+

P
/
is a coefficient is a function of )b-a*
&$'
and b is the longer dimension of the
rectangular cross section and a is the shorter dimension of the rectangular cross
section. The torsional stiffness of the lower part may be estimated as follows
a. 9ree to warp7
( )
/
2
w
2
f s sd s
4 t h t b
2
#
0 4 +
)#5*
b. Barping prevented )or restrained*7 /
2
f s / s sd s
4 t b
2
#
4 0 0 4
)#$*
<ere
m /
s
4
.
0



D

,
_

/
.
tanh / .
8
#
#
2
# / w
m D
/
#
/ w
/ s
#
8
4 0

,
_

D
8
w
is the warping constant,
( )
/6
b t t h
8
2
s f
/
f
w
+

+n this work, the case of warping being prevented will be used, and the torsional
rigidity of a composite section can be calculated from the following equation
sd s T= T= =
0 4 0 4 40 +
)/G*
This hypothesis is giving an e(perimental to theoretical ratio of )G.$%*
&#G'
.
3.3 Shearing Rigidity
Fistortion by transverse shearing forces is one of the modes of deformation that can
occur in a composite structure when it is subjected to a general loading. The vertical
)or transverse* shearing force across a composite section causes the flanges and webs
to bend independently out of plane )as a result of shearing deformation*. +t is known
that the transverse shearing deformation is usually small compared with deformation
due to bending. ,ut in some cases, such as in short deep members subjected to high
$
shearing forces, it is necessary to consider the transverse shearing deformation in
order to obtain a more accurate description of the behavior of the beam. : shearing
rigidity )4:
V
* is assigned to the stiffness matri( of a grillage member to take into
account the effect of transverse shearing forces on the deformation of that member.
+n the grillage analogy, the ability of the composite structure to resist distortion can be
appro(imately achieved by providing the grillage members an equivalent shear area
):
V
*. The independent bending moments, which are developed in the webs and in the
flanges are caused by the shearing forces generated in these components. <owever, in
the present work, the transverse shearing rigidity for a composite member will be
computed by two methods as follows
#- !hearing rigidity for the steel component only by calculating the shear area for the
steel web, 9ig.)Ea*, and it can be stated as7
/ /
h t 8 8
" $

)/#*
/- !hearing rigidity for concrete and steel components together because the depth of
concrete may take into account the shear area especially when it is not small.
Jecognizing that the transformed section concept can be applied to the steel web as
shown in 9ig. )Eb*, thus this method can be stated as7

( ) ( )
/ # w / v
h h t m 4 4: +
)//*
Bhere m is the modular ratio C E
/
-E
#

#G
Fig. (1) Design chart for simply supported
beams.
/.%
/
#.%
#
G.%
"
a
l
u
e

o
f

F
#
8C2.%
)*.+
*
*.+
1
1.+
2
2.+
3
)3 )2 )1 * 1 2 3
8C2
8C/.
%
8C/
8C#.%
8C#./%
8C2.
%
.og
#G
3
/
Fig. (2) Design chart for fix- ended beams.
"
a
l
u
e

o
f

F
#
/.%
/
#.%
#
G.%
)3 )2 )1 * 1 2 3
8C2.%
8C2
8C/
.%
8C#.
%
8C#.
/%
8C
/
.og
#G
3
/
,. Applications
: composite slab-beam structure is selected from the available reference to assess the
accuracy of the grillage method. The theoretical results of 3ennedy model
&6'
were
derived by the finite element method using the orthotropic plate elementH also an
e(perimental study was made for this model. The composite slab-beam model
considered here is simply supported at two opposite edges and being free at the
longitudinal edges. This type of construction is used in bridge decks. The structure
dimensions are shown in 9ig.)1*, and material properties are as follows
Apper 8omponent )concrete slab*
Fepth of concrete h
#
C 65 mm.
8ompressive strength of concrete fQ
c
C 2% - mm
/
Nodulus of elasticity of concrete E
#
C /15GE - mm
/
)calculated from
/
c c
mm f 61GG *
=oisson?s ratio of concrete @
#
C G.#%
##
) b* Edge beam
h
#
t
f
b
s
b
ce
Fig. (5) !"aluation of pre # crac$ed stiffness for
upper part di"ision.
) a* +nterior beam
t
f
b
ce
b
s
b
ce
h
#
Fig. (%) trans"erse shearing rigidity .
) a* !teel area
h
/
h
#
t
w
) b* transformed area
mt
w
h
/
h
#
Fig. (&) Design chart for cantile"ers.
"
a
l
u
e

o
f

F
#
)2.+ )1.+ )*.+ *.+ 1.+ 2.+ 3.+
/.%
/
#.%
#
G.%
.og
#G
3
/
8C2.%
8C2
8C/.%
8C/
8C#.%
8C#./%
Fig. (') (hear stress flo) in composite sections .
) b* +ndependent action
t
f
h
#
) a* 8omposite action
t
f
20
!hear modulus of elasticity of concrete 4
#
C #/G$G - mm
/
)calculated from
4 CE-/)#O @**.
8onnector stiffness may be conservatively estimated as the secant stiffness at the
shear connector design strength with an equivalent slip of G.5 mm
&##'
, hence k C
%1GGG- G.5 C 1#/%G - mm.
Evaluating the elastic rigidities for each grillage member as given in section)2*
#- 9or longitudinal members7
a-edge beams7 )E+
p
C G.E E+
f
C /.$*#G
#/
.mm
/
* , )40C /.E *#G
##
.mm
/*.
b-interior beams7 )E+
p
C G.% E+
f
C 2.6*#G
#/
.mm
/
* , )40C 2.G*#G
##
.mm
/
*.
/- 9or transverse members in this model it is assumed that the fle(ural rigidity is the
average value between fully and zero interaction as follows, taking the effective of
the concrete slab in the longitudinal direction equal G.%b as shown in 9ig.)##*
&6'
7
E+
p
C G.%)E+
f
O E+
o
*
,ut if there are shear connectors between the concrete slab and the transverse steel
beam, the value of the fle(ural rigidity must be estimated by the same method
represented in section 2.%.#, thus7
a-for edge beams7 )E+
p
C G.%) E+
f
O E+
o
*C 6 *#G
#/
.mm
/
* ,
)40C 2.E *#G
##
.mm
/
*.
b-for interior beams7 )E+
p
C G.%) E+
f
O E+
o
*C 6 *#G
#/
.mm
/
* ,
)40C 2.% *#G
##
.mm
/
*.
The shearing rigidity is constant for all grid members and it can be calculated as
shown in section 2.%.2, thus
#/
.ower 8omponents ).ongitudinal and transverse steel !hear 8onnectors )stud shear connectors*
Fepth of steel beam h
2
C #%/./ mm .ength of shear connector C 25 mm
9lange width of steel beam b
s
C #%/./ mm Fiameter of shear connector C #/ mm
Thickness of flange of steel beam t
f
C E.E mm :ccording to )R<,F* code
Thickness of web of steel beam t
)
C %.56 mm umber of connectors per row n C/
8ross sectional area of steel beam +
2
C /5%5 mm
/
!pacing ,C#5G mm.
Noment of inertia of steel beam -
2
.#/##/226.6$ !trength of shear connector C %1GGG .
Nodulus of elasticity of steel beam !
2
C /GGGGG N=a
=oisson?s ratio of steel beam

/
2
C

G.2
!hear modulus of elasticity of steel beam 0
2
C 1E$/2 - mm
/
)calculated from 4 CE-/)#O@**.
4:
"
C #G#.E1 )for transformed shear area* ,or7 4:
"
C E5.21 )for steel
shear area*
Two different loading conditions are considered. =oint load of 5$ k is applied, the
position of this load is given in the following
#-: center load applied over the bridge )point no. #2, 9ig.)1**.This is the first
loading condition.
/-:n eccentric load applied over the edge of the bridge )point no. 2, 9ig.)1**.
This is the second loading condition.
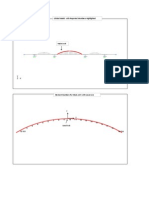
+n 9ig.)5*, the vertical deflections at the mid- span cross- section )section :-:* are
plotted for the first loading condition. The corresponding values of the deflections for
the second loading condition are plotted in 9ig. )$*.Tab. )/* shows the comparisons of
the ma(imum deflections in the composite structure as calculated by the suggested
method for the two loading conditions. +n the grillage analysis the ma(imum
deflections in both cases of loading are calculated for7
8ase )+*7 without transverse shear effect. , 8ase )++*7 with transformed shear
area. , 8ase )+++*7 with steel shear area only.
1ab. (2)2omparisons of maximum deflections (composite bridge model) (percentage differences
)ith respect to experimental results)
3ethod of analysis
1
st
loading 2
nd
loading
Na(.
Feflection
)mm*
=ercentage
Fifference
)M*
Na(.
Feflection
)mm*
=ercentage
Fifference
)M*
4rillage
analogy
8ase )+* 2.2G O#1.$G 1.5E O#G.G
8ase )++* 2.%1 O/1.%G 5./1 O#%.$
8ase )+++* 2.E$ O2#.5G 5.61 O#5.5
Rrthotropic plate method
&/G'
2.2G O#1.$G 1.%G O%./
E(perimental result
&6'
/.5G - 1.#2 -
9rom the above comparison, it is clear that when the effect of transverse shear area
):
v
* is ignored the deflections obtained by the grillage analogy are rather in acceptable
agreement with the e(perimental and finite element results )applied to the equivalent
orthotropic plate*. :lso this effect is shown in 9igures )5* and )$*, and it is well
known that an eccentric load on a bridge gives rise to twisting moments that are much
greater in magnitude than those caused by the same load applied at the center. Thus,
#2
the concrete deck slab, with its significant torsional resistance, is able to distribute
transversely the eccentric load quite effectively in composite bridges. 8omparisons
between the results are also given in Tabs. )2* and )6*.
8omparisons between the variations of center deflection with an applied central load
shown in 9ig. )#G*.
1ab. (&)Vertical deflections (in mm) at mid- span of bridge model under 1st. loading condition
(percentage differences )ith respect to experimental results)
ode
no.
E(per. Rrtho.
=erce.
Fi
ff.
)M*
4rill.
case +
=erce.
di
ff.
)M*
4rill.
case ++
=erce.
di
ff
.
4rill.
case +++
=erce.
dif
f.
)M*
/2 /.%6 #.$# -/6.5 /.2 -$.% /.25 -E.2 /.6# -%.#G
#5 /.E1 /./$ -#6./ /.$ O5.E 2.GE O#6.E 2.#/ O#E.5
#2 /.5 2.2G O#1.$ 2.2 O#1.$ 2.%1 O/1.% 2.E$ O2#.5
5 /.E1 /./$ -#6./ /.$ O5.E 2.GE O#6.E 2.#/ O#E.5
2 /.%6 #.$# -/6.5 /.2 -$.% /.25 -E.2 /.6# -%.#G
1ab. (')Vertical deflections (in mm) at mid- span of bridge model under 2nd. loading
condition (percentage differences )ith respect to experimental results)
ode
no.
E(per. Rrtho.
=erce.
Fi
ff.
)M*
4rill.
case +
=erce.
di
ff.
)M*
4rill.
case ++
=erce.
di
ff
.
)M*
4rill.
case +++
=erce.
dif
f.
)M*
/2 -#.1G -#.%G O##.5 -#./5 /6.1 -#.2/ //.6 -#.26 /#./
#5 -G.2G -G./$ -6.G G.2E /G.G G.21 /2.G G.25 /E.1
#2 /.#E /.2G OE.% /.2G E.% /.25 #G./ /.6# ##.E
5 6.22 6.E$ O5.2 6.5G #G.5 6.$5 #%.G %.G1 #1.G
2 1.#2 1.%G O%./ 1.5E #G.G 5./1 #%.$ 5.61 #5.5
+. Effect of -egree of Interaction
The degree of interaction between the concrete slab and the steel beams may be
increased by increasing the number of shear connectors or by increasing the connector
stiffness. This increase leads to increase in the )E+
p
- E+
f
* ratio. Thus, in this section
various values of this ratio are assumed to study its effect on the same bridge model,
without including the transverse shear effect.
#6
+n 9igures )##* and )#/*, the vertical deflections at the mid- span cross- section are
plotted for the first and second loading conditions respectively. +t is clear that the
values of the vertical deflection decreased when the degree of interaction increased.
This increase is obtained for longitudinal beams. 9rom this result, it is found that the
composite structure resistance is more efficient for applied load when the degree of
interaction is increased. :lso a comparison between the results is shown in Tabs. )%*
and )E*.
1ab. (5) -nfluence of degree of interaction on "ertical deflections (in mm) for 1st. loading
condition
ode no. E+C E+
o
E+
p
C G.1 E+
f
E+
p
C G.$ E+
f
E+C E+
f
/2 /.12 #.1G #./% #.G$
#5 2.25 /./E #.15 #.E#
#2 2.1E /.EG /.G$ #.$/
5 2.25 /./E #.15 #.E#
2 /.12 #.1G #./% #.G$
1ab. (%) -nfluence of degree of interaction on "ertical deflections (in mm) for 2nd.
loading condition
ode no. E+C E+
o
E+
p
C G.1 E+
f
E+
p
C G.$ E+
f
E+C E+
f
/2 -#.6% -#.22 -#.G$ -G.$$
#5 G.6$ G.G6 -G.GE -G.G52
#2 /.12 #.1G6 #./% #.G$
5 %.%1 2.$% 2.#G2 /.1$$
2 5.$$ E.5G %.%% %.G$
#%

Fig (4) Vertical deflections at mid-span section of bridge dec$ model under 1st.loading
condition
#E
:
Fig. (5) Details of composite bridge model.(a) ,lan "ie)6 (b) (ection (+-+)6 (c) (ection (7-7)
#
.
/
.
2
.
6
.
%
.
#G
.
$
.
5
.
1
.
E
.
#%
.
#6
.
#2
.
#/
.
##
.
/G
.
#$
.
#5
.
#1
.
#E
.
/%
.
/6
.
/2 //
. .
/#
.
(
y
)a*
2G%G mm
/
/
$
G

m
m
:
, ,
)b*
#%/./ mm
)c*
. %bC/E1.//%G
. %bC/E1.//%G
65 mm
6
5
#
%
/
.
/
/
%
6
.
#
1
b
C
%
2
6
.
6
%

Node number
Distance from left end (mm (
D e f
l e c
t i o
n
( m
m(
23
E!erimental
8 " 9
#rt$otro!ic !late
8 " 9
%rilla&e case '
%rilla&e case ''
%rilla&e case '''
()*
2
2)*
3
3)*
"
")*
3 + (3 (+
,-)( -(0)** (("* (-,.)"* 22(3).
Node number
Distance from left end (mm (
e D
e l f
i t c
n o
m (
m (
latnemire!E
'9 9
etal! ci!orto$tr#
'9 9
' esac e&allir%
'' esac e&allir%
''' esac e&allir%
0(
32 +( 3( + 3
*").,-( *"(( **)0(- ()-, .)3(22
/ "
/ 2
0
2
"
-
+
Fig. (:) Vertical deflections at mid-span section of bridge dec$ model under 2nd.loading
condition

Fig. (1;) <oad-deflection cur"e at center of =ennedy>s bridge dec$ model

Fig (11) -nfluence of degree of interaction on "ertical deflections for 1st.loading condition
#1
0
(0
20
30
"0
*0
-0
,0
+0
.0
(00
0 0)3 0)- 0). ()2 ()* ()+ 2)( 2)" 2), 3 3)3 3)- 3).
Deflection at center ( mm (
0 o a
d a t
c e n
t e r (
1 N (
Node number
0
(
2
3
"
*
-
,
+
3
+
(
3
(
+
2
3
Distance from left end (mm (
D e f
l e c
t i o
n
( m
m (EI
p
.*./ EI
f
E+CE+
o
EI
p
.*.0 EI
f
E+CE+
f
Grill. case I
E(perimental
&6'
1E.# E#G.%% ##6% #E1$.6%
//#2.$
EI.EI
o
EI
p
.*.0EI
f
EI
p
.*./EI
f
EI.EI
f
Grill. case I
E!erimental
2"3
Node number
/ "
/ 2
0
2
"
-
+
(0
Distance from left end (mm (
D e f
l e c t
i o n
( m
m(
1E.# E#G.%% ##6% #E1$.6%
//#2.$
/2 #5 #2 5
2
0
(0
20
30
"0
*0
-0
,0
+0
.0
(00
0 0)3 0)- 0). ()2 ()* ()+ 2)( 2)" 2), 3 3)3 3)- 3).
Deflection at center ( mm (
0 o a
d a t
c e n
t e r (
1 N (
E!erimental
%rill) case '
%rill) case ''
%rill) case '''
Fig (12) -nfluence of degree of interaction on "ertical deflections for 2nd.loading condition
1. (onclusions
The main concluding remarks that have been achieved in this study may be
summarized as follow
#. Fesign charts are constructed for estimating the percentage decrease in fle(ural
rigidity of each composite member with partial shear connection. The charts are in
terms of the parameter k
/
, and were given for various values of the factors 8.

it /
/
/
#
= 6
. 8 n 3
3

,
( )
it it
/
#/
it
#
8
# 8

+

/. The loss of interaction between the concrete slab and the steel beams leads to
considerable increase in deflection )as the sum of fle(ural rigidities of the two
separate components is considerably smaller than the value for the connected
components*. :lmost fully interacting components give stiffer structure.
2. To calculate the fle(ural rigidity of the equivalent grillage members the case of
uniformly distributed load can be used in place of any loading case because the
difference between the results from different load patterns is negligible )less than
#.2M*.
6. +n representing a composite structure by grillage members, the effective width of
each member should be used to calculate the fle(ural rigidity of that member. :lso
=oissons ratio effect is to be included in the calculation of the fle(ural rigidities of
the grillage members.
%. Effect of transverse shearing forces on deflection is found to be small and thus it
can be neglected )percentage differences is less than ##.5 M*.
References&
#. <eins,8.=. and 9an,<.N., SEffective 8omposite ,eam Bidth at Altimate
.oadS, 0ournal of the !tructural Fivision, =roc. of the :!8E, "ol.#G/, !T##,
pp. /#E2-/#1$, ov.#$1E.
#5
/. ewmark,.N.,!iess,8.=. and "iest,+.N., TTests and :nalysis of 8omposite
,eams with incomplete interactionS, =roc. !oc. E(perimental !tress :nalysis,
"ol.$, o.#, pp. 1%-$/ , #$%#.
2. 0ohnson,J.=., T8omposite !tructures of !teel and 8oncrete7 "ol.#S, 8rosby
.ockwood !taples, .ondon , /#Gpp. , #$1%.
6. 3ennedy,0.,.,4race,.9. and !oliman,N., TBelded- versus ,olted-!teel +-
Fiaphrams in 8omposite ,ridgesS, 0ournal of the !tructural Fivision, =roc. of
the :!8E, "ol.##%, !T/, pp. 6#1, 9eb.#$5$.
%. 0asim,.:., TThe Effect of =artial +nteraction on ,ehaviour of 8omposite
,eams T, Thesis presented for the degree of =h.F.,Fepartment of 8ivil
Engineering, 8ollege of Engineering, Aniversity of ,asrah, +raq,
#55pp.,Rct.#$$6.
E. <endry,:.B. and 0eager,..4., TThe :nalysis of 4rid 9ramework and Jelated
!tructuresS, 8hatto and Bindus , .ondon , #$%5.
1. 4ere,0.N.and Beaver,B.,S:nalysis of 9ramed !tructuresS,"an ostrand 8o.,
ew Lork,#$%5.
5. <assan,9.N. and 3adhum,F.:.J., T,ehaviour and :nalysis of 8omposite
!ections under =ure TorsionS, Engineering and Technology, "ol.1, o.#, pp.
E1-$1,#$5$.
$. Timoshenko, !., T!trength of Naterials 7=art ++S, "an ostrand 8o., ew Lork,
#$%5.
#G. 9rodin,0.4., Taylor, J. and !tark, 0.B.,S: 8omparison of Feflection in
8omposite ,eams <aving 9ull and =artial !hear 8onnectionS, =roc.of +nst.of
8ivil Engineers, =art /,"ol.6#,pp. 2G1-2//,0une#$15.
##. Bang,L.8., TFeflection of !teel-8oncrete 8omposite ,eams with =artial
!hear +nteractionS, 0ournal of !tructural Engineer,"ol.#/6,o.#G,pp. ##%$-
##E%,Rct.#$$5.
#$
456789: ;<=>?@ ABCD9: EF<G69 ;5HIJ>K9: LIB8M9:N ;=O=O79: ;BP>D9:
Q:OK8JI@ RF6JS 4T:O89: UVWX9:

!" # $% & ""' ()
* +, -. /012 3 &4 567 !*8
+, - !9 51 . !9 !:;) <0(
" 5 =8 ">
"* * ?* @AB, )
?'C . D'., * "> E
* /@FG H4 /@FI, ! 5 J& HJ&C
K .
L
H, M $& MN DO ?,A G
E PG !9 /@FI H4 Q 51
. A,, !:;) !9 R ! S% 4 & T6
UV S1@%, !9 WO /@FI H4 5 J&
. A,, !:% M0 P% UX Y. - $& . ?*
5.
L
A 4, Z,)" 11.8 % ", .S(%
/G