Академический Документы
Профессиональный Документы
Культура Документы
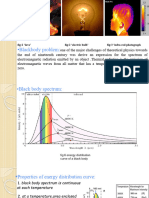
Blackbody radiation spectrum
Загружено:
kowletОригинальное название
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Blackbody radiation spectrum
Загружено:
kowletАвторское право:
Доступные форматы
Lecture 2 - Blackbody radiation
Absorption and emission of radiation
What is the blackbody spectrum?
Properties of the blackbody spectrum
Classical approach to the problem
Plancks suggestion - energy quantisation
Bose-Einstein statistics
Objectives
Learn how classical theories cannot account for the spectral distribution of
light from blackbody objects such as stars etc.
Show that by making the assumption that light consists of small packets
of energy (photons) we can develop an expression which perfectly fits the
experimental data.
Blackbody radiation
Heated bodies radiate energy, but what is the mechanism? On an atomic
scale, heat causes the molecules and atoms of a solid to vibrate. As atoms
consist of electrical charges in the form of electrons and protons, it is the
vibration of these charges which is responsible for the emission of
electromagnetic radiation. A very hot object will emit visible light as the
electrons vibrate.
How do bodies absorb radiation?
In order to radiate energy, an object must first absorb it.
Suppose we shine a light on an object.
If we shine it on glass Light passes through
If we shine it on a metal Light is reflected
If we shine it on carbon Light is absorbed
In glass the electrons are tightly bound to atoms and only oscillate at
certain frequencies outside the range of visible light. This makes glass
appear transparent as very little of the visible light is absorbed.
Blackbody radiation II
Metals conduct and have free electrons not bound to any particular atom.
These electrons oscillate in response to the light and then radiate light
themselves. This radiation is reflected light. Again, there is very little
absorption of light, most of it is reflected.
The electrons in carbon have a short mean free path, when they collide
their energy is transferred to the lattice. They are efficient absorbers of
the incident light, hence carbon appears black. Carbon and similar
materials are effective at converting incident light into heat.
In a reverse process, as the carbon atoms warm up and vibrate more
vigorously, more of the lattice energy is transferred to the free electrons,
thus carbon is also a good radiator of heat. It cools down much faster
than a metal as it is more efficient at converting the lattice energy into
radiation.
Measuring the distribution of emitted radiation
A simple spectroscope
If we pass white light through a prism we obtain a spectrum.
By measuring the intensity of each wavelength of light in the spectrum we
can plot the spectral distribution.
The blackbody spectrum
Consider a box with a small hole in the side. Radiation entering the hole is
scattered inside the box and only a small amount comes out again. If the
temperature of the box is in equilibrium the spectrum of light coming out
of the hole looks something like this.
0
0.5x10
-8
1.0x10
-8
1.5x10
-8
2.0x10
-8
0
0.5x10
15
1.0x10
15
1.5x10
15
2.0x10
15
T 3000K
T 6000K
Frequency (Hz)
U
(
I
)
(
a
r
b
.
u
n
i
t
s
)
U( f )
= Intensity of
radiation of frequency
f
.
We find similar spectral
distributions if we measure
the light from stars.
Typical blackbody spectra
From red hot to white hot
The colour of a hot object changes as the temperature increases
Properties of the blackbody spectrum
For small f, U is proportional to f
2
. But at some value of f there is a peak
before U falls to zero.
If we double the temperature the position of the peak doubles in
frequency (
f
peak
T
) (Wiens displacement law), however the height of
the peak is multiplied eight times.
Why? U f
2
so if the temperature is constant
U( 2 f )4U ( f )
, but we
doubled the temperature so in fact
U( 2T )8U (T )
.
The total energy radiated by the body, the area under the curve,
increases by a factor of 16, i.e 2
4
times more, when the temperature is
doubled.
Stefans law of radiation: UcT
4
,
c
= 5.6710
-8
W/m
2
/K
4
- Stefans
constant.
U
is the energy radiated from 1m
2
of black surface at
temperature
T
.
Wien's displacement law
f
peak
aT
or
\
peak
T b
, b =2.89810
-3
mK (Wiens displacement law).
For frequency
f
peak
2.82 k
B
T h
.
k
B
= Boltzmanns constant = 1.380710
-23
J/K. Note that
f
peak
\
peak
=c
.
Relationship between emitted radiation and radiation
inside the cavity
The energy (electromagnetic radiation) comes out of the hole at a speed
c. Some of the light comes out at an angle and the hole appears smaller.
Emitted radiation = R, radiation inside the cavity = P
Energy incident at an angle on a
hole of unit area.
R
|
0
2 n
|
0
n 2
cPcos
(
d D
4n
)
,
d Dsin d d
R
|
0
2 n
|
0
n 2
cPcos sin d d
|
0
2 n
cP
8n
d
cP
4
So
RcP 4
.
The energy emitted from the hole is representative of the energy inside
the cavity.
P
c
m
A = cos
Origins of the spectrum
The energy spectrum is formed by a continuous process of absorption and
re-emission of radiation by the atoms and molecules forming the walls of
the box. In this way the energy can shift from one mode to another. When
thermal equilibrium is reached the characteristic spectrum will be
established.
To form a theoretical description of the spectrum we need to determine
how many modes of oscillation have frequencies in a given energy range.
These oscillators are the electromagnetic waves inside the box, which can
be thought of as standing waves.
Modes in a box
The electric field at the cavity wall must be zero
Standing waves I
Pluck a string
n1
n2 n3
n4
n
(
\
2
)
L
The natural modes of vibration of the string are standing waves with
nodes at the ends. In the same way, electromagnetic waves inside the
box are also standing waves.
Standing waves II
-1.0
-0.5
0
0.5
1.0
0 0.2 0.4 0.6 0.8 1.0
n1
n2
n3
Position (x/a) (arb. units)
A
m
p
l
i
t
u
d
e
Standing waves inside a cavity of length a.
The standing waves have amplitude
vAsin( 2nx \) sin( 2n ft )
.
Let k2n\ , and
o2n f
then
vAsin( kx)sin(ot )
.
If the box has sides of length
a
then
an(\ 2)
for n 1,2,3.
The frequencies of these waves are
f c \n( c 2a)
.
So
knn a
and
ock
.
K space
We can represent the standing waves in 3D space by a set of k vectors
k( k
x
, k
v
, k
:
)
n
a
(l , m, n)
.
Each point can be associated with a cubic volume of space and represents
a frequency of ockc
.
k
x
2
+k
v
2
+k
:
2
, the volume of the associated space is
n
3
a
3
.
For a fixed frequency,
o
, we obtain a set of values for
k
x
,
k
v
and
k
:
which lie on a spherical surface:
o
2
c
2
k
x
2
+k
v
2
+k
:
2
with radius
ko c
.
To get the total number of vibrational modes in the frequency range zero
to o we count the number of cubes contained in the sphere with radius
ko c
.
N
cubes
Jolume between spheres/volume of cube.
K-space II
Each mode occupies a discrete volume of K-space.
Mode counting
The volume of the whole sphere is 4nk
3
3 , but we are limited to positive
values of k , i.e. one octant of the sphere, so the volume becomes
J
s
1
8
4nk
3
3
nk
3
6
.
Now
k
3
o
3
c
3
and o2n f so
k
3
8n
3
f
3
c
3
.
If J
cube
n
3
a
3
, the total number of cubes, N , is
J
s
J
cube
, so
N
8n f
3
a
3
6c
3
.
Putting, Ja
3
, differentiating with respect to f , and multiplying by two
because we can have two orthogonal transverse electromagnetic waves at
each frequency we get
N ( f )
df
8n f
2
J
c
3
.
Comparison with experiment
In the classical approach we assign each mode an energy
k
B
T
. The total
energy emitted at each frequency from a box of unit volume is given by
N ( f )k
B
TU
RJ
( f )
8n f
2
c
3
k
B
T
This is the Rayleigh-Jeans approximation (1900).
k
B
is Boltzmanns
constant = 1.38110
-23
J/K.
We find good agreement between the Rayleigh-Jeans equation and the
observed results for low values of f , i.e. where U( f ) f
2
. The higher the
temperature the bigger the frequency range over which the agreement is
good. Doubling the temperature doubles the energy output at low
frequencies, as expected from the proportionality to T .
However, at higher frequencies the experimental and theoretical results
diverge. We expect more energy to be output at higher frequencies, but in
experiments the energy distribution falls to zero. This failure of the
Reyleigh-Jeans model is sometimes called the "UV catastrophe.
Planck's suggestion
Planck suggested that energy could only be emitted in chunks that are
multiples of hf , where h is Plancks constant (6.62610
-34
Js).
Experimentally, we can see this reflected in the fact that
f
peak
T
. By
doubling the temperature the number of modes that can radiate freely is
also doubled.
From this explanation it is clear that if the average energy per mode is
k
B
T
and the value hf for a particular mode is, e.g.,
5k
B
T
, that mode will
be unlikely to radiate. As the frequency increases, the probability of
radiation decreases.
Replacing
Uk
B
T
with
Uhf
in the Rayleigh-Jeans equation gives
U
Planck
( f )
8n f
2
c
3
hf P
BE
( f ) , where
P
BE
( f )
is the Bose-Einstein factor for
the average number of photons per mode at frequency
f
.
hf P
BE
( f )
is the average energy,
E,
, of photons with frequency
f
.
The Bose-Einstein factor
We assume that the probability of occupying an energy level E is given by
P( E)oe
-E k
B
T
. This was proved by Planck.
Energy levels of a quantum oscillator
N
1
N
0
e
-hf k
B
T
N
2
N
0
e
-2hI k
B
T
N
n
N
0
e
-nhf k
B
T
Let
xhf k
B
T
, then N
1
N
0
e
-x
, N
2
N
0
e
-2x
, so N
Total
N
0
(1+e
-x
+e
-2x
+...) .
E
n
N
n
nhf ( N
0
e
-nx
)nhf N
0
hf (ne
-nx
) and E
Total
N
0
hf ( 0+e
-x
+2e
-2x
+...) .
N
3
N
1
N
2
N
0
E
0
= 0
E
1
= hf
E
2
= 2hf
E
3
= 3hf
P
0
= A
P
1
= Aexp(-hf/k
B
T)
P
2
= Aexp(-2hf/k
B
T)
P
3
= Aexp(-3hf/k
B
T)
The Bose-Einstein factor II
The average energy is given by
E,
E
Total
N
Total
N
0
hf
_
n
ne
-nx
N
0
_
n
e
-nx
hfP
BE
( f )
P
BE
( f )
_
n
ne
-nx
_
n
e
-nx
-
d
dx
log
_
n
e
-nx
-
d
dx
log
1
1-e
-x
1
e
x
-1
1
e
hf k
B
T
-1
So our final result is
U
Planck
( f )
8n f
2
c
3
hf
e
hf k
B
T
-1
.
Even though this is proportional to f
3
the Bose-Einstein term reduces the
energy to zero at high frequencies. At low frequencies the term on the
right approximates to 1, matching the Rayleigh-Jeans approximation.
As
f -0
or
T -
the average energy approaches
k
B
T
, the same as the
classical result.
Various blackbody spectra
Conclusions
Classical physics, in which electromagnetic radiation is assumed to be a
continuous wave, cannot account for the blackbody radiation spectrum.
The assumption that electromagnetic radiation is emitted in quanta with
energy Ehf allows us to develop an expression which accurately
describes the spectral distribution of radiation emitted from a blackbody.
Вам также может понравиться
- Black Body RadiationДокумент33 страницыBlack Body RadiationSafnas Kariapper100% (1)
- Lecture 2Документ10 страницLecture 2Ifra NoorОценок пока нет
- Blackbody Radiation PDFДокумент24 страницыBlackbody Radiation PDFAtul SinghОценок пока нет
- Notes on Quantum Physics and Planck's Explanation of Blackbody RadiationДокумент5 страницNotes on Quantum Physics and Planck's Explanation of Blackbody RadiationdfbgfbfgОценок пока нет
- Planck'smanual v1Документ12 страницPlanck'smanual v1spyzer.x.001Оценок пока нет
- PlanckДокумент15 страницPlanckPrincess ZoyaОценок пока нет
- Che 402 e Photochemistry NotesДокумент20 страницChe 402 e Photochemistry NotesKEVIN OMONDIОценок пока нет
- The Advent of Quantum PhysicsДокумент152 страницыThe Advent of Quantum PhysicsMary Grace Magpayo LanwangОценок пока нет
- FALLSEM2022-23 PHY1701 ETH VL2022230106333 Reference Material I 23-09-2022 1black Body RadiationДокумент11 страницFALLSEM2022-23 PHY1701 ETH VL2022230106333 Reference Material I 23-09-2022 1black Body RadiationTanishq AroraОценок пока нет
- Photometry PDFДокумент42 страницыPhotometry PDFDeepak SharmaОценок пока нет
- Chem. 266 Physical Chemistry III: Quantum MechanicsДокумент70 страницChem. 266 Physical Chemistry III: Quantum MechanicsJohn Edward ZapaterОценок пока нет
- Ch-03 Sunlight PDFДокумент9 страницCh-03 Sunlight PDFAntonio BartoloniОценок пока нет
- 4.1 Basics and Kirchoff's LawsДокумент38 страниц4.1 Basics and Kirchoff's LawsdkbradleyОценок пока нет
- 2021 PH107 Tutorial01Документ3 страницы2021 PH107 Tutorial01pahnhnykОценок пока нет
- Plancks Constant Version 2016-1Документ10 страницPlancks Constant Version 2016-1MR XОценок пока нет
- Ch1 Revision of EP203Документ31 страницаCh1 Revision of EP203mirckyОценок пока нет
- Radiation Emission and AbsorptionДокумент9 страницRadiation Emission and AbsorptionTitin Evania ManaluОценок пока нет
- Fisica Moderna PonceДокумент74 страницыFisica Moderna PonceWilmer MoncadaОценок пока нет
- Quantum Mechanics Notes-Part 1Документ15 страницQuantum Mechanics Notes-Part 1aman bhatiaОценок пока нет
- Temu 1Документ36 страницTemu 1Farida UtamiОценок пока нет
- Blackbody Radiation and Atomic Emission - Unit - 07Документ70 страницBlackbody Radiation and Atomic Emission - Unit - 07TEBATSOОценок пока нет
- Notes On PSO201A (Quantum Physics 2019-20-II) : 1 The Beginning of QMДокумент38 страницNotes On PSO201A (Quantum Physics 2019-20-II) : 1 The Beginning of QMKevalОценок пока нет
- PSO201A Quantum Physics Course NotesДокумент77 страницPSO201A Quantum Physics Course NotesAshray NarainОценок пока нет
- Assgn 1Документ4 страницыAssgn 1Spandana PrustyОценок пока нет
- Unit 11 Modern PhysicsДокумент90 страницUnit 11 Modern PhysicsPeril LousОценок пока нет
- Atomic StructureДокумент49 страницAtomic StructureFatimaОценок пока нет
- Particle and Wave Nature of RadiationДокумент12 страницParticle and Wave Nature of RadiationDaniyal HashmiОценок пока нет
- Development of Quantum Mechanics: Earning BjectivesДокумент83 страницыDevelopment of Quantum Mechanics: Earning Bjectivesshubham tejaniОценок пока нет
- Quantum Chemistry: An IntroductionДокумент71 страницаQuantum Chemistry: An Introductionbinseung skzОценок пока нет
- CH 2 The Particle Properties of WavesДокумент21 страницаCH 2 The Particle Properties of Wavesyohanse mehabawОценок пока нет
- Quantum PhysicsДокумент122 страницыQuantum PhysicsYang Xu100% (2)
- Chapter 6 Jan13Документ131 страницаChapter 6 Jan13kumutha100% (1)
- AP Physics Chapter 27 Quantum PhysicsДокумент78 страницAP Physics Chapter 27 Quantum PhysicsMythos EntertainmentОценок пока нет
- INTRODUCTIONДокумент6 страницINTRODUCTIONÃnkùr SultãnìyâОценок пока нет
- Electromagnetic Radiation Behaving As ParticlesДокумент48 страницElectromagnetic Radiation Behaving As ParticlesLeo YipОценок пока нет
- Chapter 12 Fundamentals of Thermal RadiationДокумент19 страницChapter 12 Fundamentals of Thermal RadiationMohsen Khandan BakavoliОценок пока нет
- Black Body RadiationДокумент9 страницBlack Body RadiationAnuradha Ramasundar100% (1)
- MODERN PHYSICS PRINCIPLESДокумент66 страницMODERN PHYSICS PRINCIPLESAk JaОценок пока нет
- 2.2 On The Nature of LightДокумент6 страниц2.2 On The Nature of LightAnonymous FYnBl0IzQZОценок пока нет
- Quantization of EnergyДокумент22 страницыQuantization of Energydavidolalere7Оценок пока нет
- Blackbody Radiation and Photon Gas PropertiesДокумент26 страницBlackbody Radiation and Photon Gas PropertiesIca LubisОценок пока нет
- CHEM-UA 127: Advanced General Chemistry I: I. The Classical View of The UniverseДокумент10 страницCHEM-UA 127: Advanced General Chemistry I: I. The Classical View of The Universehkalloli@gmail.comОценок пока нет
- High Level Summary On Blackbody RadiationДокумент7 страницHigh Level Summary On Blackbody RadiationMarcela ReynaОценок пока нет
- Lab 6 Stellar Temperatures and LuminosityДокумент9 страницLab 6 Stellar Temperatures and Luminositymei sya100% (1)
- 60 Surface Temperature & LuminosityДокумент2 страницы60 Surface Temperature & Luminosityvalsamis8334Оценок пока нет
- UofT Black BodyДокумент7 страницUofT Black BodyShayaan ZakaОценок пока нет
- Modern Physics and Quantum Mechanics Mod-2 PDFДокумент28 страницModern Physics and Quantum Mechanics Mod-2 PDFShreyas SeshadriОценок пока нет
- Quantum MechanicsДокумент46 страницQuantum MechanicsAbhilash Nair50% (2)
- CHM131 - CH 3 - The Electronic Structure of Atoms and Periodic Table PDFДокумент102 страницыCHM131 - CH 3 - The Electronic Structure of Atoms and Periodic Table PDFRabiatul AdawiyyahОценок пока нет
- 02 IntroQuantumPhysicsДокумент8 страниц02 IntroQuantumPhysicscychan410Оценок пока нет
- Quantum Mechanics PyEd 342Документ113 страницQuantum Mechanics PyEd 342mesfint100% (3)
- QM BasicsДокумент12 страницQM Basicsh.anurag248Оценок пока нет
- Electronic Structure of AtomsДокумент59 страницElectronic Structure of Atomstalktotiffanycheng100% (1)
- Black Body RadiationДокумент7 страницBlack Body RadiationIbifubara HumphreyОценок пока нет
- Bohr’s Model, Energy Bands, Electrons and HolesДокумент30 страницBohr’s Model, Energy Bands, Electrons and HolespurseyОценок пока нет
- Unit Iv: Quantum PhysicsДокумент27 страницUnit Iv: Quantum PhysicsEhsaas: Mere aur TumhareОценок пока нет
- Ch38 Young Freedman1Документ26 страницCh38 Young Freedman1Andrew MerrillОценок пока нет
- QuantumtheoryofradiationДокумент7 страницQuantumtheoryofradiationshweta khannaОценок пока нет
- Formally, Wien's displacement law states that the of black body radiation per unit wavelength, peaks at the wavelength λ given by: λ = b / TДокумент11 страницFormally, Wien's displacement law states that the of black body radiation per unit wavelength, peaks at the wavelength λ given by: λ = b / TYash TamakuwalaОценок пока нет
- GDP 2013Документ4 страницыGDP 2013kowletОценок пока нет
- 3LSMДокумент1 страница3LSMkowletОценок пока нет
- Gloria DeoДокумент5 страницGloria DeokowletОценок пока нет
- ASC Progress ReportДокумент1 страницаASC Progress ReportkowletОценок пока нет
- Amino ListДокумент8 страницAmino ListkowletОценок пока нет
- Data FileДокумент151 страницаData FilekowletОценок пока нет
- Revision SolnsДокумент13 страницRevision SolnskowletОценок пока нет
- Fap FappersonДокумент2 страницыFap FappersonkowletОценок пока нет
- Assignment 1Документ8 страницAssignment 1kowletОценок пока нет
- Assignment 2 Plot3Документ1 страницаAssignment 2 Plot3kowletОценок пока нет
- Emet2007 NotesДокумент6 страницEmet2007 NoteskowletОценок пока нет
- Assignment 5 AnalysisДокумент8 страницAssignment 5 AnalysiskowletОценок пока нет
- MATH2320 AssignmentДокумент4 страницыMATH2320 AssignmentkowletОценок пока нет
- Assignment 4 AnalysisДокумент5 страницAssignment 4 AnalysiskowletОценок пока нет
- Rexroth Rotary ActuatorsДокумент65 страницRexroth Rotary Actuatorsmoskys.07Оценок пока нет
- Physics DPP 4 (JP & JR) Advanced FCДокумент30 страницPhysics DPP 4 (JP & JR) Advanced FCAnudeex ShettyОценок пока нет
- Rotational Motion: Rotation in Two Dimensions: A Particle On A RingДокумент41 страницаRotational Motion: Rotation in Two Dimensions: A Particle On A RingAdelia Ayu WandiraОценок пока нет
- Dynamics of Machines-Unit 2 - NotesДокумент30 страницDynamics of Machines-Unit 2 - NotesSYLVIA ANITAОценок пока нет
- Floefd Validation Examples: Your Initials, Presentation Title, Month YearДокумент21 страницаFloefd Validation Examples: Your Initials, Presentation Title, Month YearVictor HuertaОценок пока нет
- Problem StatementДокумент5 страницProblem StatementShubhendra Nath SahaОценок пока нет
- AE302 FDDDSFДокумент3 страницыAE302 FDDDSFSasiKumarОценок пока нет
- Torsional Vibration 4.1 What Is Torsional Vibration?: M I K QДокумент7 страницTorsional Vibration 4.1 What Is Torsional Vibration?: M I K QMohammad Muhtasim Mashfy, 170011054Оценок пока нет
- Level II Questions - UtДокумент5 страницLevel II Questions - Utsenthil787878100% (4)
- Practice Test 01 - Physics - Arjuna JEE 2024Документ2 страницыPractice Test 01 - Physics - Arjuna JEE 2024kochharmadhav0Оценок пока нет
- Candidates Are Required To Give Their Answers in Their Own Words As Far As Practicable. The Figures in The Margin Indicate Full MarksДокумент4 страницыCandidates Are Required To Give Their Answers in Their Own Words As Far As Practicable. The Figures in The Margin Indicate Full MarksManish Shrestha100% (1)
- Classical MechanicsДокумент14 страницClassical MechanicswhatthemailОценок пока нет
- Flight DynamicsДокумент57 страницFlight Dynamicsmarker_inОценок пока нет
- Wave and Thermodynamic DCP PDFДокумент464 страницыWave and Thermodynamic DCP PDFAnik Mukherjee100% (1)
- For You To Read Wave Vocabulary: Activity 1 Making WavesДокумент2 страницыFor You To Read Wave Vocabulary: Activity 1 Making WavesReeja MathewОценок пока нет
- Term 1: Mechanics and Thermodynamics: Chapter 2: KinematicsДокумент7 страницTerm 1: Mechanics and Thermodynamics: Chapter 2: KinematicshanabeeОценок пока нет
- Kinematics - Problems With Vectors 1Документ24 страницыKinematics - Problems With Vectors 1Alexandre CabrelОценок пока нет
- CE Module 22 - Open Channel and Weirs (Principle)Документ3 страницыCE Module 22 - Open Channel and Weirs (Principle)Angelice Alliah De la CruzОценок пока нет
- Optimal Design of A Damped Dynamic Vibration AbsorberДокумент21 страницаOptimal Design of A Damped Dynamic Vibration AbsorberShrikant DholeОценок пока нет
- Dynamics Unit II AssignmentДокумент2 страницыDynamics Unit II Assignmentkannanviknesh086319Оценок пока нет
- Integrated Chassis Control System For Improving Vehicle StabilityДокумент5 страницIntegrated Chassis Control System For Improving Vehicle StabilityHaftayОценок пока нет
- Class 28: Outline: Hour 1: Displacement Current Maxwell's Equations Hour 2: Electromagnetic WavesДокумент33 страницыClass 28: Outline: Hour 1: Displacement Current Maxwell's Equations Hour 2: Electromagnetic Wavesakirank1Оценок пока нет
- A Projectile Is Projected From The Origin With A Velocity of 25Документ6 страницA Projectile Is Projected From The Origin With A Velocity of 25AloneОценок пока нет
- 3.13 - Vectors WorksheetДокумент2 страницы3.13 - Vectors Worksheetdilsharakavi100% (1)
- Grade 11 Physics Parachute Lab ReportДокумент16 страницGrade 11 Physics Parachute Lab ReportEric Zhang80% (5)
- ATPL POF - Principles of Flight Questions BankДокумент32 страницыATPL POF - Principles of Flight Questions Bankpilotmo100% (2)
- Short Note On LightДокумент3 страницыShort Note On LightRishu MannОценок пока нет
- Articulo - Estimacion Mejorada de La Resistencia A La Formación de OlasДокумент9 страницArticulo - Estimacion Mejorada de La Resistencia A La Formación de OlasAnthony MarineОценок пока нет
- SHM notes springs pendulumsДокумент6 страницSHM notes springs pendulumsLYENAОценок пока нет