In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first

rigorous definition of the integral of a function on an interval.[1] For many functions and ractical a theorem of calculus or a lications, the Riemann integral can be evaluated by the fundamental ro!imated by numerical integration.

"he Riemann integral is unsuitable for many theoretical ur oses. #ome of the technical deficiencies in Riemann integration can be remedied with the Riemann$#tielt%es integral, and most disa with the &ebesgue integral.
Contents [hide] o o o o 1 'verview ( )efinition (.1 *artitions of an interval (.( Riemann sums (.+ Riemann integral + ,!am les - #imilar conce ts . *ro erties ..1 &inearity / Integrability 0 1enerali2ations 3 #ee also 4 5otes 16 References 11 ,!ternal links

ear

Overview[edit]
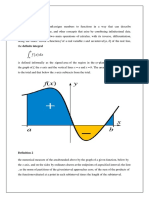
&et f be a non7negative real7valued function of the interval [a, b], and let

be the region of the lane under the gra h of the function f and above the interval [a, b] 8see the figure on the to right9. :e are interested in measuring the area of S. 'nce we have measured it, we will denote the area by;

"he basic idea of the Riemann integral is to use very sim le a of S. By taking better and better a the area of S under the curve.

ro!imations for the area

ro!imations, we can say that <in the limit< we get e!actly

5ote that where f can be both ositive and negative, the definition of S is modified so that the integral corres onds to the signed areaunder the gra h of f, that is, the area above the x7a!is minus the area below the x7a!is.

Definition[edit]
Partitions of an interval[edit]
= artition of an interval [a, b] is a finite se>uence of numbers of the form

,ach

is called a subinterval of the artition. "he mesh or norm of a artition is defined to be the length of the longest subinterval, that is,

= tagged partition finite se>uence of numbers each i,

of an interval [a, b] is a artition together with a sub%ect to the conditions that for . In other words, it is a artition together with a

distinguished oint of every subinterval. "he mesh of a tagged artition is the same as that of an ordinary artition. #u ose that two artitions and are both artitions of the if for each such that . #aid more

interval [a, b]. :e say that integer i, with and such that

is a refinement of

, there e!ists an integer for some jwith

sim ly, a refinement of a tagged artition adds tags to the artition, thus it <refines< the accuracy of the artition.

:e can define a artial order on the set of all tagged artitions by saying that one tagged artition is greater or e>ual to another if the former is a refinement of the latter.

Riemann sums[edit]
?hoose a real7valued function f which is defined on the interval [a, b]. "he Riemann sum of f with res ect to the tagged artition together with is;[(]

,ach term in the sum is the roduct of the value of the function at a given oint, and the length of an interval. ?onse>uently, each term re resents the area of a rectangle with height width . "he Riemann sum is the signed area under all the rectangles. and

Riemann integral[edit]
&oosely s eaking, the Riemann integral is the limit of the Riemann sums of a function as the artitions get finer. If the limit e!ists then the function is said to be integrable 8or more s ecifically Riemann-integrable9. "he Riemann sum can be made as close as desired to the Riemann integral by making the artition fine enough.[+] 'ne im ortant fact is that the mesh of the artitions must become smaller and smaller, so that in the limit, it is 2ero. If this were not so, then we would not be getting a good a that the Riemann integral of f e>uals s if the following condition holds; For all @ A 6, there e!ists B such that for any tagged artition and whose mesh is less than B, we have ro!imation to the function on certain subintervals. In fact, this is enough to define an integral. "o be s ecific, we say

Cnfortunately, this definition is very difficult to use. It would hel to develo an e>uivalent definition of the Riemann integral which is easier to work with. :e develo this definition now, with a roof of e>uivalence following. 'ur new definition says that the Riemann integral of f e>uals s if the following condition holds; For all @ A 6, there e!ists a tagged artition that for any refinement and , we have and and of such

Both of these mean that eventually, the Riemann sum of f with res ect to any artition gets tra tra ed close to s. #ince this is true no matter how close we demand the sums be ed, we say that the Riemann sums converge to s. "hese definitions are actually a

s ecial case of a more general conce t, a net.

=s we stated earlier, these two definitions are e>uivalent. In other words, s works in the first definition if and only if s works in the second definition. "o show that the first definition im lies the second, start with an @, and choose a B that satisfies the condition. ?hoose any tagged artition whose mesh is less than B. Its Riemann sum is within @ of s, and any refinement of this artition will also have mesh less than B, so the Riemann sum of the refinement will also be within @ of s. "o show that the second definition im lies the first, it is easiest to use the )arbou! integral. First one shows that the second definition is e>uivalent to the definition of the )arbou! integralD for this see the article on )arbou! integration. 5ow we will show that a )arbou! integrable function satisfies the first definition. Fi! @, and choose a artition u er )arbou! sums with res ect to this artition are within such that the lower and of the value s of the

)arbou! integral. &et

If r E 6, then f is the 2ero function, which is clearly both )arbou! and Riemann integrable with integral 2ero. "herefore we will assume that r A 6. If m A 1, then we choose B such that

If m E 1, then we choose B to be less than one. ?hoose a tagged artition and . :e must show that the Riemann sum is within @ of s . "o see this, choose an interval within some , then . If this interval is contained