THE SINE PRODUCT FORMULA AND THE GAMMA FUNCTION

ERICA CHAN DECEMBER 12, 2006

Abstract. The function sin x is very important in mathematics and has many applications. In addition to its series expansion, it can also be written as an innite product. The innite product of sin x can be used to prove certain values of (s), such as (2) and (4). The gamma function is related directly to the sin x function and can be used to prove the innite product expansion. Also used are Weierstrass product formula and Legendres relation.

1. Introduction There are a few special functions in mathematics that have particular signicance and many applications. The gamma function is one of those functions. The gamma function can be dened as (x) = et tx1 dt.
0

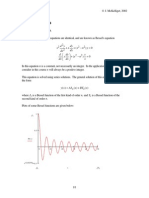
We can also get the formula (1) (x + 1) = x(x) by replacing x with x + 1 and integrating by parts. In addition, since (1) = 1, using Equation (1), by induction, we can relate the gamma function to the factorial formula (2) (n) = (n 1)!. The gamma function has the properties that it is log convex and monotonic, which will be used in a later proof. Another important function in mathematics is the sine function. The trigonometric function sin x can be written as an innite series x3 x5 x 7 sin x = x + + ... 3! 5! 7!
Date : December 12, 2006.
1

ERICA CHAN

The function sin x can also be written as an innite product expansion. The gamma function is directly related to the sine function. To derive the innite product expansion of the sine function, the Weierstrass product formula, Legendre relation, and the gamma function are all used. The sine product formula is important in mathematics because it has many applications, including the proofs of other problems. One such application is the calculation of the values of (2) and (4), where
1 1 1 1 (s) = = 1 + s + s + s + ... s n 2 3 4 n=1

is the Riemann zeta function. Section 2 derives Weierstrass product formula and Eulers constant. Section 3 introduces Stirlings formulas, Gauss multiplication formula, and the Legendre relation. In Section 4, the sine product formula is produced from the gamma function. Finally, Section 5 discuss the applications of the sine product formula, including the calculation of (2) and (4). 2. Weierstrass product formula Weierstrass derived a formula which, when applied to the gamma function, can be used to prove the sine product formula. To nd Weierstrass product formula, we rst begin with a theorem. Theorem 2.1. The function (x) is equal to the limit as n goes to innity of (3) (x) = lim nx n! . n x(x + 1) (x + n)

Proof. Begin with a dierence quotient expressed as the inequality log (1 + n) log (n) log (x + n) log (n) log (1 + n) log (n) . (1 + n) n (x + n) n (1 + n) n This inequality is true because of the gamma functions properties that it is monotonically increasing and log convex. Substitute for (n) using Equation (2) and simplify to get log(n 1) log (x + n) log(n 1)! log n. x

THE SINE PRODUCT FORMULA AND THE GAMMA FUNCTION

Rearrange the terms of the inequality and since the logarithm is a monotonically increasing function, we get (n 1)x (n 1)! (x + n) nx (n 1)!. Using Equation (1), we know that (x + n) = (x + n 1)(x + n 2) (x + 1)x(x). Substituting it into the inequality gives us (n 1)x (n 1)! nx n! x+n (x) . x(x + 1) (x + n 1) x(x + 1) (x + n) n If we replace n with n + 1 on the left hand side and then rearrange the inequality, we get n nx n! (x) (x). x+n x(x + 1) (x + n) Taking the limit as n gives us (x) = lim nx n! . n x(x + 1) (x + n) Equation (3) was derived by Gauss. From there, Weierstrass was able to derive another form of the same equation (x) = ex(log n1/11/2...1/n) The limit of 1 ex/1 ex/2 ex/n . x 1 + x/1 1 + x/2 1 + x/n

1 1 1 lim ( + + + log n) 1 2 n exists, is equal to C , and is often called Eulers constant. So we can rewrite Weierstrass product formula as ex/i Cx 1 (4) (x) = e . x i=1 1 + x/i
n

3. Multiplication Formula There are three formulas, (x) = 2xx1/2 ex+(x) , where 1 1 (x) = (x + n + ) log(1 + )1= , and 2 x + n 12 x n=0 n! = 2nn+1/2 en+/12n ,

ERICA CHAN

which are known as Stirlings formulas. Where is a number independent of other values and where 0 1. Stirlings formulas are approximations of (x) for large values of x and the accuracy increases as x increases. Gauss discovered a formula, which expresses (x) as a product of its factors. Gauss multiplication formula is (2 )(p1)/2 x x+1 x+p1 (x) = ( )( ) ( ), x 1 / 2 p p p p where p is a positive integer. (5) There is the special case discovered by Legendre, where p = 2, which is called Legendres relation. Legendres relation states x x+1 (6) ( )( ) = x1 (x). 2 2 2 The derivation and proof of these formulas can be found at [1]. They are based on nding an approximation for (x) in terms of an estimate for n!. 4. The Sine and and Gamma Functions To derive the sine product formula, we rst nd a relationship between the sine and gamma functions. We dene a function (x) and nd that (x + 1) = (x). Theorem 4.1. Dene the function (x), for nonintegral x, to be (7) (x) = (x)(1 x) sin x, then (x + 1) = (x). Proof. If we use Equation (1) and substitute x + 1 for x, then we get that (8) (x + 1) = x(x). (x + 1) = (x + 1)(x) sin( (x + 1)). Note that sin(x+ ) = sin x. Use Equation (1), rearrange Equation (8), and substitute them in to get (x + 1) = x(x) (x + 1) ( sin x) = (x)(x + 1) sin x. x Finding (x + 1), we get

This is equal to the original equation for (x), so (x +1) = (x).

THE SINE PRODUCT FORMULA AND THE GAMMA FUNCTION

The Legendre relation (Equation (6)) can be written as x x+1 ( )( ) = b2x (x), 2 2 where b = 2 is a constant. Replacing x with 1 x gives ( 1x x )(1 ) = b2x1 (1 x). 2 2

From there, we get that x x+1 x x x x + 1 1x x ( )( ) = ( )(1 ) sin ( )( ) cos . 2 2 2 2 2 2 2 2 Simplifying the above, we nd x x+1 b2 b2 ( )( ) = (x)(1 x) sin x = (x) = c(x) 2 2 4 4 where c =
b2 4

is a constant.

Using Equation (1) and the innite series expansion of sin x, we get that (1 + x) (x)3 (x)5 (x)7 (x) = (1 x) x + + ... x 3! 5! 7! 3 x2 5 x4 7 x6 = (1 + x)(1 x) + + ... . 5! 7! 3! The right hand side of the equation equals when x = 0. From there we see that (0) = . Let g (x) be a periodic function that is equal the second derivative of log (x). It is periodic because log (x) = log((x)(1 x) sin x) is periodic and so the second derivative will also be periodic. Since g (x) is periodic, then it satises the equation 1 x x+1 g (x) = (g ( ) + g ( )). 4 2 2 Since g (x) is continuous on the interval 0 x 1, it is bounded by a constant M , |g (x)| M . Because g (x) is periodic, it is bounded by M for all x. From Equation (9), we get that x+1 1 M x |g (x)| ) . g ( ) + g ( 4 2 2 2 (9) From this we see that g (x) can actually be bounded by M . We can 2 continue to repeat this process until the bound of g (x) goes to 0. Therefore g (x) = 0, which means that log (x) is a linear function, because g (x) = 0 is its second derivative. Since log (x) is periodic, this implies

ERICA CHAN

that it is a constant, which also implies that (x) is constant. We know that (0) = and therefore (x) must equal for all x. Rearranging Equation (7) and using the fact that (x) = , (x)(1 x) = . sin x Using (1), the above equation can be rewritten as sin x = . x(x)(x) The Weierstrass product formula allows us to replace the gamma function and rewrite sin x as an innite product expansion x2 (10) sin x = x 1 2 . i i=1 5. Applications of the Sine Product Formula Applications of the sine product formula include the calculation of certain values of the Riemann zeta function. The proof that (2) = 2 /6 is often called Eulers Theorem. Theorem 5.1. The sum of the reciprocal of the perfect squares is 2 /6: 1 2 = . 2 n 6 1 Proof. Consider the function sin x = 0, which has an innite number of roots , 2, 3, .... Using the innite series expansion of sin x and dividing sin x by x gives us the innite series x 2 x 4 x6 (11) 1 + + ... = 0. 5! 3! 7! Applying Equation (10) and dividing by x, we get the innite product expansion sin x x2 x2 x2 (12) = (1 2 )(1 2 )(1 2 )... x 4 9 When Equation (12) is expanded, the coecient of x2 will be 1 1 1 + 2 + 2 + ... 2 4 9 Using Equation (11), we get 1 1 1 1 + 2 + 2 + ... = . 2 4 9 3!

THE SINE PRODUCT FORMULA AND THE GAMMA FUNCTION

Multiplying both sides of the equation by 2 gives us 1 1 1 2 + + + ... = . 12 22 32 6 Using a similar method, we can also calculate (4), which is the sum of the reciprocals of numbers to the fourth power. Theorem 5.2. The value of (4) is 4 /90:
1 4 = . n4 90 1

Proof. From the calculation of (2), we know that

1 1 = . 22 i 6 i=1

(13)

If we square Equation (13), we get that 2 1 1 = 2. 2 2 i 6 i=1

(14)

Expanding the left hand side of Equation (14) we get 2 1 1 1 = + 2 . i2 2 i4 4 i2 j 2 4 i=1 i<j

(15)

If we use the sine innite product expansion, Equation (12), we get x that the coecient of x4 for sin is equal to the sum of the product of x 2 x . In other words, the coecient of x4 is i2 2
i<j

1 i2 j 2 4

From Equation (11), we also know that the coecient of x4 must be 1 , so 120

ERICA CHAN

(16)

i<j

1 1 = . i2 j 2 4 120

Therefore, substituting Equation (16) into Equation (15) gives us 2 1 1 1 1 = = +2 . i2 2 36 i4 4 120 i=0 1 To calculate (4), simply solve for and multiply both sides by i4 4 4 , to get
1 4 = . 4 i 90 i=1

References
[1] Artin, Emil. The Gamma Function. New York: Holt, Rinehart and Winston, 1964. [2] Simmons, George F. Calculus with Analaytic Geometry. New York: McGraw Hill, Second Edition, 1996. [3] Weisstein, Eric W. Gamma Function. From MathWorldA Wolfram Web Resource. http://mathworld.wolfram.com/GammaFunction.html [4] Young, Robert M. Excursions in Calculus: An Interplay of the Continuous and Discrete. United States of America: The Mathematical Association of America, 1992.