1

MJC 2011 H2 MATHS JC2 MID YEAR EXAMINATION PAPER 2

Qn Solution
1 System of Linear Equation

3
f (2) 7 4 2 7 a b c = + + = --------------- (1)
3
f ( 1) 2 2 2 a b = + = ----------------- (2)
At 3 x = , ( ) f (3) 2 3 10 16 = + =
3
f (3) 16 9 3 16 a b c = + + = --------------(3)
Using GC on the augmented matrix
4 2 1 7
2 1 0 2
9 3 116
| |
|

|
|
\ .
, the solution to this
system of equations is
3
1, 4, 5 a b c = = = .

Hence
3
4 1.59 b = = (3.sf).


Qn Solution
Q2 Binomial Expansion
(i)













( )( )
( ) ( ) ( )
( )
2
1
2
2
2
2
2
2 2
2
2
1
1 1
1
1 1
1
1 2 2
1 1 ...
2 2!
3
1 1 ...
2 8
3
1 1 ...
2 8
x
x bx
bx
x bx bx
bx b
x x
bx b
x
+
= +

( | || |

| |
(
\ .\ .
( = + + +
(
(

(
= + + + +
(

| |
= + + + +
|
\ .

2
2
2
7 3
coeff of 1
6 8
4
9
2
(Since is a positive constant)
3
b
x
b
b b
= = +
=
=

(ii)
(a)
2 3 3
1
3 2 2
x x < < <

3
or
2
x <

2
(b)
2
1 3
1 1
2 3
x
y x
| |
|
\ .
= + = +



(c) At 0, x =

2
2
d
7
d
2! 6
y
x
=

2
2
d 7
d 3
y
x
=




Qn Solution
Q3 Recurrence Relation
(i)
Let
n
x l as n . Then
1 n
x l
+
.
0.3e 0.03
l
l =
Using GC, 1.818 or 0.432 l = .
Thus, 0.432 and 1.818 = = .

(ii) Using GC,
For
1
0 x = , the sequence increases and converges to 0.432 (3 s.f.) (or ).
For
1
1 x = , the sequence decreases and converges to 0.432 (3 s.f.) (or ).
For
1
2 x = , the sequence increases and diverges.

(iii)
Sequence is increasing
1 n n
x x
+
> . Sequence is decreasing
1 n n
x x
+
<













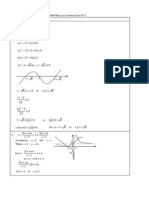
From the diagram,
(a)
1 n n
x x
+
> when 0.432 or 1.82
n n
x x < > .
(b)
1 n n
x x
+
< when 0.432 1.82
n
x < < .
n
x
1 n
x
+
n
x
y
x 0.432 1.818
O
y x =
0.3e 0.03
x
y =
n
x
n
x
1 n
x
+
n
x
1 n
x
+
n
x
3

Q4 Complex Number

Since coefficients of equation
4 3 2
2 6 2 5 0 z z z z + + + + = are real and 1 2i + is a
root, 1 2i is also a root.
( ) ( ) ( ) ( )
( ) ( ) ( ) ( )
( ) ( )
2 2
2
1 2i 1 2i
1 2i 1 2i
1 2i
2 5
z z
z z
z
z z
+
= + + +
= +
= + +


( )( )
4 3 2
2 2
2 6 2 5 0
2 5 1 0
z z z z
z z z
+ + + + =
+ + + =

The roots are i, i, 1 2i, 1 2i z = + .

(b)i)

( )
4
i
4 3
i 2
4 3
6
i
4 3
6
1
i
12
4
7 5 11
1 1 1 1
i i i i
12 12 12 12
4 4 4 4
1 3 i
2e
2e where 0, 1,2
2e
2 e
2 e ,2 e ,2 e ,2 e
k
k
k
z
z
z k
z
z

| |

|
\ .
| |
+
|
\ .
+ | |
|
\ .
+ | |
|
\ .
| | | | | | | |
| | | |
\ . \ . \ . \ .
=
=
= =
=
=
=


















Im
Re
O
5
12


7
1
i
12
4
1
2 e z
| |
|
\ .
=


1
i
12
4
2
2 e z
| |
|
\ .
=


5
1
i
12
4
3
2 e z
| |
|
\ .
=


11
1
i
12
4
4
2 e z
| |
|
\ .
=


1
4
2

2

4
Qn Solution
5 Differentiation of Parametric Equations
Application of Differentiation (Tangent and Normal)
Application of Integration (Area)
Vectors (Lines & Planes)

(i)










sin cos
d d
cos sin
d d
d sin
d cos
d
tan
d
x y
x y
y
x
y
x

= =
= =
=
=


(ii)













3 2 2 d 3
When , , , tan 1
4 2 2 d 4
y
x y
x

= = = = =
Equation of tangent at point A
2 2
2 2
2
y x
y x
| |
=
|
|
\ .
= +

d
When , 0, 1, 0
d
y
x y
x
= = = =
Equation of normal at point B
0 x =

(iii)








( )
( )
2 2
2 2
line curve
0 0
2 3
2
2 4
0
d d
2 d cos d
0.75 0.6427
0.107(3s.f.)
A y x y x
A x x
A
A

=
= +
=
=




(iv)





Vector equation of the normal at point B is
0 0
0 1 , .
0 0

| | | |
| |
= +
| |
| |
\ . \ .
r



5

(v)






o
0 1
1 1
0 1
sin
3
35.3 (1d.p.)

| | | |
| |
| |
| |
\ . \ .
=
=

or 0.615 radian(3 s.f.) =


Qn Solution
Q6 P&C
(i)
( ) ( )
2!
Number of ways 3! 3!
2
36
=
=

(ii)
( ) ( )
4!
Number of ways 2! 2!
4
24
| |
=
|
\ .
=

(iii)
6
3
3! 3!
Number of ways
2! 3 3
40
C
| | | |
=
| |
\ . \ .
=



Qn Solution
Q7 Probability
(i) P(exactly two of the cards are spades)
( )( )
( )
13 39
2 1
52
3
117
0.138
850
C C
C
= = = or
13 12 39 3! 117
0.138
52 51 50 2! 850
= = =

(ii)





P(more than one card is a diamond)

( )( )
( )
( )
( )
13 39 13
2 1 3
52 52
3 3
64
0.151
425
C C C
C C
= + = = or
13 12 39 3! 13 12 11 64
0.151
52 51 50 2! 52 51 50 425
= + = =
or
13 39 13 39
0 3 1 2
52
3
64
1 0.151
425
C C C C
C
+
= = =


6
(iii) P(all three cards are of different suits)
=
( )
4
3
C
( )
( )
3
13
1
52
3
C
C
=
169
425
=0.398 or
=
( )
4
3
C
13 13 13
3!
52 51 50
=
169
425
=0.398 or
=
425
169
50
26
51
39
52
52
= =0.398 or

= ( )
64
1 4
425
| |

|
\ .
=
169
425
=0.398



Qn Solution
Q8 Binomial Distribution + approximations
(i)




(ii)













(iii)
(1) Whether a child receives vaccination is independent of whether another
child receives vaccination.
(2) The probability that any child is vaccinated is the same throughout the
village.

( )
( )
,
39 (1)
39
1 (2)
40
Subst (1) into (2),
1
1
40
39
, 40
40
X B n p
np
np p
p
p n
=
=
=
= =

The maximum value that X can take is 40.


Let Y be the number of children out of 40 who have received vaccination and
are autistic.
39
40,0.08
40
Y B
| |

|
\ .

i.e. ( ) 40,0.078 Y B

Since n =40 is large and ( ) 40 0.078 3.12 5 np = = < ,
( )
o
P 3.12 Y approximately.

7


( )
there are more than 35 children who have
P
received vaccination and are not autistic
P 4
0.79471
0.795(3s.f.)
Y
| |
|
\ .
=
=
=



Qn Solution
Q9 Normal Distribution (Sum and Multiple of Normal R.V.)
(i) Let X be the time spent visiting a particular bookstore by Raphael.
( )
2
~N 35,2.2 X

Let Y be the time spent visiting a particular bookstore by Elizabeth.
( )
2
~N 30,1.1 Y
( )
( )
2
1 2 3
1 2 3
~N 3 35, 3 2.2
~N 105,14.52
X X X
X X X
+ +
+ +


( ) ( ) ( )
( )
2
1 2 3
1 2 3
2 ~N 105 2 30 ,14.52 4 1.1
2 ~N 45, 19.36
X X X Y
X X X Y
+ + +
+ +


( )
1 2 3
P 2 40 0.12790 0.128 (3s.f.) X X X Y + + = =

(ii)
( )
( )
2 2
~N 35 30,2.2 1.1
~N 5,6.05
X Y
X Y
+

( ) P 0 0.021037 X Y < =


( ) ( )
( )
( ) ( )
1
1
0.97896 0.021037 0.012
0.97896 0.57042
1 ln 0.97896 ln0.57042
1 26.400
27.400
n
n
n
n
n

<
<
<
>
>

Least 28 n = .



8
Qn Solution
10 Hypothesis Testing









( )
2
sample variance
1
n
s
n
=

( )
2 20
15
19
236.84
=
=


Let X be the glucose level of a child who has consumed bubble tea in mg/dl.
Let denote the population mean glucose level of a child.

Assume
( )
2
N , X ,
2
N , X
n

| |
|
\ .

H
0
: 83 =
H
1
: 83 >
Test Statistic:
1
~
n
X
T t
S
n

=
Level of significance: 1%
Reject H
0
if -value 0.01 p <

Under H
0
, using GC, -value 0.0109 p = .
Since -value 0.0109 0.01 p = > , we do not reject H
0
and conclude that there is
insufficient evidence, at 1% level, that the mean sugar level exceeds 83
mg/dl.














Unbiased estimate of is
4400
88
50
x
x
n
= = =

Unbiased estimate of
2
is
( )
2
2
1
1
s x x
n
(
=
(




| |
1
11020
49
224.89795 225 (3 s.f)
=
=


Since 50 n = is large, by Central Limit Theorem,
2
N , X
n

| |
|
\ .

approximately.
H
0
: 83 =
H
1
: 83
9
Test Statistic:
X
Z
S
n

=
Level of significance: 2%
Reject H
0
if -value 0.02 p <

Under H
0
, from the GC, -value 0.0184 p = .
Since -value 0.0184 0.02 p = < , we reject H
0
and conclude that there is
sufficient evidence, at 2% level, that the mean sugar level is not 83mg/dl.



Qn Solution
Q11 Correlation and Regression
(i)







(ii) r =0.964 (3 s.f.)
Since r =0.964 is close to 1, there is strong positive linear relation between
x and y and this is congruent with the behaviour seen in the scatter diagram
where the points lie close to a straight line with positive gradient.

(iii) Least squares line of y on x:
5.2665 1.1279 5.27 1.13 y x y x = + = + (3 s.f.)
Least squares line of x on y:
7.7756 0.82449 7.78 0.824 x y x y = + = + (3 s.f.)
(iv) When 70 y = ,
( ) 7.7756 0.82449 70 65.5 x x = + = (3 s.f.)
This value is a valid estimate because 70 y =

is within the data range of y.
Also the value of r indicates a strong positive linear correlation between x and
y.
x
29
71
33
80
y
10
(v) Essay score = 49 x =

Comprehension score = 50 y =
(vi) The product moment correlation coefficient remains unchanged because r is
independent of the scale of measurement.



Q12 Poisson Distribution +Approx +CLT


Let X be the no. of life insurance sold in a week.
X ~Po(1.3)
Required Probability P( 1)
1 P( 0)
0.727 (3s.f.)
X
X
=
= =
=




Let Y be the no. of life insurance sold in 10 weeks.
Y~Po(13)

Since 13 10 = > ,
~N(13,13) Y approximately

Required Probability P( 18)
P( 17.5) (after continuity correction)
0.894 (3s.f.)
Y
Y
= <
= <
=



Let S be the no. of life insurance sold in 2 weeks.
S ~Po(2.6)
Let R be the no. of accident insurance sold in 2 weeks.
R ~Po(1.4)
S +R ~Po(4)
( )
( ) ( )
Required Probability P 4 8
P 7 P 3
0.515 (3s.f.)
S R
S R S R
= + <
= + +
=


Assumption: The sale of the two types of insurances is independent.


( )
( )
( )
( ) ( )
( )
Required Probability P 2| 5
P 2 and 5
P 5
P 2 P 3
P 5
0.336 (3s.f.)
R S R
R S R
S R
R S
S R
= = + =
= + =
=
+ =
= =
=
+ =
=



As defined earlier, X ~Po(1.3)
E( ) X =1.3, Var( ) X =1.3
11

Since n =50 is large, by Central Limit Theorem,



P( 1.4) 0.268 (3sf) X > =


Alternative Method
Let W be the no. of life insurance sold in 50 weeks.
W ~Po(65)
( )
( )
Required Probability P 1.4
50
P 70
1 P 70
0.244 (3s.f.)
W
W
W
| |
= >
|
\ .
= >
=
=



1 2 50
...
1.3
N 1.3, approximately
50 50
X X X
X
+ + +
| |
=
|
\ .