Quadratic Functions

Roots of Quadratic Equations and the Quadratic Formula

In this section, we will learn how to find the root(s) of a quadratic equation. Roots are also
called x-intercepts or zeros. A quadratic function is graphically represented by a parabola
with vertex located at the origin, below the x-axis, or above the x-axis. Therefore, a
quadratic function may have one, two, or zero roots.
When we are asked to solve a quadratic equation, we are really being asked to find the
roots. We have already seen that completing the square is a useful method to solve
quadratic equations. This method can be used to derive the quadratic formula, which is
used to solve quadratic equations. In fact, the roots of the function,
f (x) =ax
2
+bx +c
are given by the quadratic formula. The roots of a function are the x-intercepts. By
definition, the y-coordinate of points lying on the x-axis is zero. Therefore, to find the roots
of a quadratic function, we set f (x) =0, and solve the equation,
ax
2
+bx +c =0.
We can do this by completing the square as,

Solving for x and simplifying we have,

Thus, the roots of a quadratic function are given by,

This formula is called the quadratic formula, and its derivation is included so that you
can see where it comes from. We call the term b
2
4ac the discriminant. The discriminant
is important because it tells you how many roots a quadratic function has. Specifically, if
1. b
2
4ac <0 There are no real roots.
2. b
2
4ac =0 There is one real root.
3. b
2
4ac >0 There are two real roots.
We will examine each case individually.
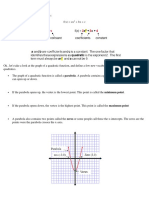
Case 1: No Real Roots
If the discriminant of a quadratic function is less than zero, that function has no real roots,
and the parabola it represents does not intersect the x-axis. Since the quadratic formula
requires taking the square root of the discriminant, a negative discriminant creates a
problem because the square root of a negative number is not defined over the real line. An
example of a quadratic function with no real roots is given by,
f(x) =x
2
3x +4.
Notice that the discriminant of f(x) is negative,
b
2
4ac =(3)
2
4 1 4 = 9 16 = 7.
This function is graphically represented by a parabola that opens upward whose vertex lies
above the x-axis. Thus, the graph can never intersect the x-axis and has no roots, as shown
below,

Case 2: One Real Root
If the discriminant of a quadratic function is equal to zero, that function has exactly one
real root and crosses the x-axis at a single point. To see this, we set b
2
4ac =0 in the
quadratic formula to get,

Notice that is the x-coordinate of the vertex of a parabola. Thus, a parabola has
exactly one real root when the vertex of the parabola lies right on the x-axis. The simplest
example of a quadratic function that has only one real root is,
y =x
2
,
where the real root is x =0.
Another example of a quadratic function with one real root is given by,
f(x) =4x
2
+12x 9.
Notice that the discriminant of f(x) is zero,
b
2
4ac =(12)
2
4 4 9 = 144 144 = 0.
This function is graphically represented by a parabola that opens downward and has vertex
(3/2, 0), lying on the x-axis. Thus, the graph intersects the x-axis at exactly one point (i.e.
has one root) as shown below,



Case 3: Two Real Roots
If the discriminant of a quadratic function is greater than zero, that function has two real
roots (x-intercepts). Taking the square root of a positive real number is well defined, and
the two roots are given by,

An example of a quadratic function with two real roots is given by,
f(x) =2x
2
11x +5.
Notice that the discriminant of f(x) is greater than zero,
b
2
4ac =(11)
2
4 2 5 = 121 40 = 81.
This function is graphically represented by a parabola that opens upward whose vertex lies
below the x-axis. Thus, the graph must intersect the x-axis in two places (i.e. has two roots)
as shown below,