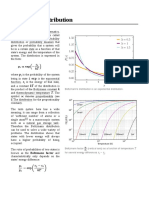
When a chemical system achieves equilibrium, it is through a process of energy transfer

between the components, with energetic parts constantly giving energy away. This means that
the probability distribution should favor situations where the energy is spread throughout the
system and disfavor situations where any system component has a great deal of energy. The
exact form of the probability distribution is an exponential function:

or

This equation means that the probability of finding a particle in state i or x (use i for discrete
distributions and x for continuous ones) is proportional to the exponential of -E (minus the
energy of the state) divided by the product of k
B
(Boltzmann's constant) and T (the
temperature in Kelvins). What is meant by a state? Each state corresponds to a set of possible
measured values. For an atom in an ideal gas, each state has particular values of the three
velocity components u
x
, u
y
, and u
z
. States of a molecule can be indexed by the same three
velocity components, plus vibrational and rotational energy levels. Since we know that any
probability distribution must be normalized, we can determine the constants C and C'
explicitly:
or
(The denominator in each case is called the "partition function".) This probability distribution
describes how energy is distributed at equilibrium for an amazingly wide variety of chemical
and physical systems. This probability distribution (in discrete and continuous forms) is the
Maxwell-Boltzmann distribution.

The Big Picture
The Maxwell-Boltzmann distribution as shown above gives the probability of finding the
system in any particular state. It applies to the ideal gas, among many other systems. For
the case of the ideal gas, we also want to know the probability of finding an atom with a
particular speed, regardless of direction. The Maxwell-Boltzmann speed distribution
provides this information.




)(((((((((((((((((((\








In physics, particularly statistical mechanics, the MaxwellBoltzmann
distribution or Maxwell distribution describes particle speeds in gases, where the
particles move freely without interacting with one another(except for very
brief elastic collisions in which they may exchange momentum and kinetic energy,
but do not change their respective states of intramolecular excitation, as a function of
the temperature of the system, the mass of the particle, and speed of the particle.)
It is a probability distribution for the speed of a particle constituting the gas -
the magnitude of its velocity vector( meaning that for a given temperature, the
particle will have a speed selected randomly from the distribution, but is more likely
to be within one range of some speeds than others)
The MaxwellBoltzmann distribution applies to ideal gases close to thermodynamic
equilibrium with negligible quantum effects and at non-relativistic speeds.
The distribution is named after James Clerk Maxwell and Ludwig Boltzmann. While
the distribution was first derived by Maxwell in 1860 on basic grounds,[4] Boltzmann
later carried out significant investigations into the physical origins of this distribution.
2 Distributions (various forms)
o 2.1 Distribution for the momentum vector
o 2.2 Distribution for the energy
o 2.3 Distribution for the velocity vector
o 2.4 Distribution for the speed
o 2.5 Distribution for relative speed
o 2.6 Typical speeds


BoseEinstein statistics
In quantum statistics, BoseEinstein statistics (BE statistics) is one of two possible
ways in which a collection of non-interacting indistinguishable particles may occupy a
set of available discrete energy states, at thermodynamic equilibrium.
The aggregation of particles in the same state, which is a characteristic of particles
obeying BoseEinstein statistics, accounts for the cohesive streaming of laser
light and the frictionless creeping of superfluid helium. The theory of this behaviour
was developed (192425) by Satyendra Nath Bose, who recognized that a collection
of identical and indistinguishable particles can be distributed in this way. The idea
was later adopted and extended by Albert Einstein in collaboration with Bose.
The BoseEinstein statistics apply only to those particles not limited to single
occupancy of the same statethat is, particles that do not obey the Pauli
exclusion principle restrictions. Such particles have integer values of spin and are
named bosons, after the statistics that correctly describe their behaviour. There must
also be no significant interaction between the particles.
Concept[edit]
At low temperatures, bosons behave differently from fermions (which obey the FermiDirac statistics)
in that an unlimited number of them can "condense" into the same energy state. This apparently
unusual property also gives rise to the special state of matter Bose Einstein Condensate. Fermi
Dirac and BoseEinstein statistics apply when quantum effects are important and the particles are
"indistinguishable". Quantum effects appear if the concentration of particles satisfies,

where N is the number of particles and V is the volume and n
q
is the quantum concentration, for
which the interparticle distance is equal to the thermal de Broglie wavelength, so that
the wavefunctions of the particles are barely overlapping. FermiDirac statistics apply to
fermions (particles that obey the Pauli exclusion principle), and BoseEinstein statistics
apply to bosons. As the quantum concentration depends on temperature, most systems at high
temperatures obey the classical (MaxwellBoltzmann) limit unless they have a very high density,
as for a white dwarf. Both FermiDirac and BoseEinstein become MaxwellBoltzmann
statistics at high temperature or at low concentration.
BE statistics was introduced for photons in 1924 by Bose and generalized to atoms
by Einstein in 192425.
The expected number of particles in an energy state i for BE statistics is

with
i
> and where n
i
is the number of particles in state i, g
i
is the degeneracy of state i,
i

is the energy of the ith state, is thechemical potential, k is the Boltzmann constant, and T is
absolute temperature. For comparison, the average number of fermions with energy given
by FermiDirac particle-energy distribution has a similar form,

BE statistics reduces to the RayleighJeans Law distribution for ,
namely .


*******************************************************************************************************************88


The partition function is the most important quantity in statistical thermodynamics.
, it indicates how particles in an assembly are partitioned among the
various energy levels of an atom or molecule. The partition function can also, of course,
be calculated by summing over energy states rather than energy levels, i.e.,