Libro Señales

Fundamentos de la Teora de
Seales y Sistemas
Alfredo Restrepo Palacios, Ph.D
Bogot, Agosto 2009
ndice general
0. Bases matemticas 4
0.1. INTRODUCCIN . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
0.2. Relaciones y Funciones . . . . . . . . . . . . . . . . . . . . . . . . 6
0.2.1. Par ordenado . . . . . . . . . . . . . . . . . . . . . . . . . 6
0.2.2. Producto cartesiano . . . . . . . . . . . . . . . . . . . . . 6
0.2.3. Relacin . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
0.2.4. Particin . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
0.2.5. Relaciones de orden . . . . . . . . . . . . . . . . . . . . . 12
0.2.6. Suprmum, Infmum . . . . . . . . . . . . . . . . . . . . . 12
0.2.7. Mximo y mnimo . . . . . . . . . . . . . . . . . . . . . . 13
0.3. Funciones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
0.3.1. Sobreyeccin . . . . . . . . . . . . . . . . . . . . . . . . . 15
0.3.2. Inyeccin. (funcin uno-a-uno) . . . . . . . . . . . . . . . 15
0.3.3. Biyeccin. (correspondencia uno-a-uno) . . . . . . . . . . 15
0.4. Relaciones Ternarias . . . . . . . . . . . . . . . . . . . . . . . . . 18
0.4.1. Propiedades de relaciones ternarias . . . . . . . . . . . . 18
0.5. Estructuras algebricas . . . . . . . . . . . . . . . . . . . . . . . . 20
0.5.1. Grupos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
0.5.2. Anillos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
ii
NDICE GENERAL iii
0.5.3. Espacio vectorial . . . . . . . . . . . . . . . . . . . . . . . 25
0.5.4. Matrices y Determinantes . . . . . . . . . . . . . . . . . . 26
0.5.5. Homomorsmos . . . . . . . . . . . . . . . . . . . . . . . 26
0.6. Los Nmeros Naturales . . . . . . . . . . . . . . . . . . . . . . . 27
0.6.1. Orden lineal para N . . . . . . . . . . . . . . . . . . . . . 28
0.6.2. Divisor y mltiplo . . . . . . . . . . . . . . . . . . . . . . 29
0.6.3. Nmeros Primos . . . . . . . . . . . . . . . . . . . . . . . 29
0.6.4. Factor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
0.6.5. Mximo comn divisor, mnimo comn mltiplo . . . . 30
0.6.6. Conjuntos contables y no contables . . . . . . . . . . . . 30
0.6.7. Conteos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
0.6.8. Cardinalidad . . . . . . . . . . . . . . . . . . . . . . . . . 31
0.7. Los Nmeros Enteros Z . . . . . . . . . . . . . . . . . . . . . . . 32
0.7.1. La relacin de orden lineal entre los nmeros enteros . . 33
0.7.2. Intervalos enteros . . . . . . . . . . . . . . . . . . . . . . . 33
0.7.3. Algoritmo de la divisin . . . . . . . . . . . . . . . . . . . 34
0.7.4. Congruencias mdulo N . . . . . . . . . . . . . . . . . . . 34
0.8. Los Nmeros Racionales Q . . . . . . . . . . . . . . . . . . . . . 35
0.8.1. Relacin de orden lineal para los nmeros racionales . . 38
0.8.2. Fallas geomtricas y algebricas de los racionales . . . . 39
0.8.3. Fallas topolgicas de los racionales . . . . . . . . . . . . . 40
0.8.4. Cortes de Dedekind . . . . . . . . . . . . . . . . . . . . . 42
0.9. Los Nmeros Reales R
1
. . . . . . . . . . . . . . . . . . . . . . . 43
0.9.1. Aproximacin de reales con racionales . . . . . . . . . . 45
0.9.2. Aproximacin de u con racionales . . . . . . . . . . . . . 45
0.9.3. Relacin de orden lineal . . . . . . . . . . . . . . . . . . . 45
0.9.4. Congruencia entre nmeros reales . . . . . . . . . . . . . 47
0.9.5. El conjunto de Cantor . . . . . . . . . . . . . . . . . . . . 48
0.9.6. Subconjuntos densos en ninguna parte . . . . . . . . . . 48
iv NDICE GENERAL
0.10. La circunferencia S
1
= T
1
. . . . . . . . . . . . . . . . . . . . . . . 49
0.10.1. Circularidad de S
1
. . . . . . . . . . . . . . . . . . . . . . 50
0.10.2. Deniciones Bsicas y Notacin . . . . . . . . . . . . . . 52
0.10.3. El promedio Circular . . . . . . . . . . . . . . . . . . . . . 52
0.10.4. Promedio y mediana en S
1
. . . . . . . . . . . . . . . . . 53
0.10.5. La lnea proyectiva P
1
. . . . . . . . . . . . . . . . . . . . 53
0.10.6. La esfera de dimensin n (S
n
) . . . . . . . . . . . . . . . . 54
0.10.7. El toro de dimensin n (T
n
) . . . . . . . . . . . . . . . . . 54
0.10.8. El espacio proyectivo de dimensin n (RP
n
) . . . . . . . 54
0.11. Los nmeros complejos C . . . . . . . . . . . . . . . . . . . . . . 54
0.11.1. Nomenclatura . . . . . . . . . . . . . . . . . . . . . . . . . 59
0.11.2. Equivalencias de ngulos . . . . . . . . . . . . . . . . . . 59
0.11.3. Estructura algebraica . . . . . . . . . . . . . . . . . . . . . 60
0.11.4. Equivalencia entre las representaciones rectangular ypo-
lar de un nmero complejo . . . . . . . . . . . . . . . . . 61
0.11.5. Interpretacin geomtrica del producto complejo . . . . 64
0.11.6. Inverso multiplicativo en coordenadas polares . . . . . . 64
0.11.7. Complejo conjugado . . . . . . . . . . . . . . . . . . . . . 66
0.11.8. La proyeccin estereogrca . . . . . . . . . . . . . . . . 67
0.11.9. Funciones lineales . . . . . . . . . . . . . . . . . . . . . . 68
0.11.10.Excepciones a la frmula (z
a
)
b
= z
ab
. . . . . . . . . . . . . 69
0.11.11.Transformaciones de Mbius . . . . . . . . . . . . . . . . 69
0.12. Los cuaternios (H) . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
0.12.1. Denicin . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
0.12.2. Suma y producto . . . . . . . . . . . . . . . . . . . . . . . 73
0.12.3. Partes escalar y vectorial . . . . . . . . . . . . . . . . . . . 74
0.12.4. Conjugado, magnitud e inverso . . . . . . . . . . . . . . 75
0.12.5. Nomenclatura para rotaciones en R
3
. . . . . . . . . . . . 76
0.12.6. H como una estructura de anillo para C C . . . . . . . 78
NDICE GENERAL v
0.13. Sucesiones . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
0.13.1. Subsucesiones . . . . . . . . . . . . . . . . . . . . . . . . . 81
0.14. Espacios mtricos . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
0.14.1. Bolas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
0.14.2. Mtrica para S
1
. . . . . . . . . . . . . . . . . . . . . . . . 83
0.14.3. Espacios normados . . . . . . . . . . . . . . . . . . . . . . 84
0.14.4. Espacio topolgicos . . . . . . . . . . . . . . . . . . . . . 84
0.14.5. Lmite de una sucesin de nmeros . . . . . . . . . . . . 85
0.14.6. Convergencia en sentido de Cauchy . . . . . . . . . . . . 85
0.14.7. Sucesiones y subsucesiones de nmeros reales . . . . . . 86
0.14.8. Espacios completos y completados . . . . . . . . . . . . . 88
0.15. Series . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
0.15.1. Re-ordenamiento de los trminos de una serie . . . . . . 92
0.15.2. Criterios de convergencia de series de nmeros reales y
de nmeros complejos . . . . . . . . . . . . . . . . . . . . 93
0.15.3. La serie geomtrica . . . . . . . . . . . . . . . . . . . . . . 95
0.15.4. La transformada zeta . . . . . . . . . . . . . . . . . . . . . 96
0.16. Puntos de R
n
y C
n
. . . . . . . . . . . . . . . . . . . . . . . . . . . 98
0.17. Intervalos de R
n
y de Z
n
. . . . . . . . . . . . . . . . . . . . . . . 99
0.18. Clculo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 100
0.18.1. Lmite de una sucesin de funciones . . . . . . . . . . . . 100
0.18.2. Convergencia uniforme . . . . . . . . . . . . . . . . . . . 101
0.18.3. Lmite de una funcin, dadas topologias con base para
el dominio y el rango . . . . . . . . . . . . . . . . . . . . . 102
0.18.4. Continuidad . . . . . . . . . . . . . . . . . . . . . . . . . . 103
0.18.5. Continuidad uniforme . . . . . . . . . . . . . . . . . . . . 103
0.18.6. Con respecto a la continuidad de funciones con rango S
1
104
0.18.7. Derivada . . . . . . . . . . . . . . . . . . . . . . . . . . . . 104
0.18.8. Interpretacin geomtrica de la derivada compleja . . . . 106
vi NDICE GENERAL
0.18.9. Aproximacin lineal . . . . . . . . . . . . . . . . . . . . . 107
0.18.10.Diferencial . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
0.18.11.Diferenciabilidad real y las ecuaciones de Cauchy- Rie-
mann . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
0.18.12.Extensin en series de potencias . . . . . . . . . . . . . . 110
0.18.13.Series de Laurent . . . . . . . . . . . . . . . . . . . . . . . 113
0.18.14.Integral de Riemann-Stieltjes . . . . . . . . . . . . . . . . 113
0.18.15.Particiones de intervalos . . . . . . . . . . . . . . . . . . . 113
0.18.16.Variacin de una seal continua . . . . . . . . . . . . . . 114
0.18.17.La integral de Riemann . . . . . . . . . . . . . . . . . . . 115
0.18.18.La integral de Riemann-Stieltjes . . . . . . . . . . . . . . 116
0.18.19.Integral de lnea . . . . . . . . . . . . . . . . . . . . . . . . 123
0.18.20.Transformada zeta inversa . . . . . . . . . . . . . . . . . . 123
0.18.21.Teorema de representacin de F. Riesz . . . . . . . . . . . 125
0.18.22.Transformadas . . . . . . . . . . . . . . . . . . . . . . . . 125
0.18.23.La distribucin de Dirac . . . . . . . . . . . . . . . . . . . 126
0.18.24.La distribucin constante . . . . . . . . . . . . . . . . . . 127
0.18.25.La distribucin con ncleo escaln . . . . . . . . . . . . . 127
0.18.26.La distribucin valor principal de 1/x y la transformada
de Hilbert . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
1. Seales y sistemas 144
1.0. INTRODUCCIN . . . . . . . . . . . . . . . . . . . . . . . . . . . 144
1.1. Clasicacin de las seales . . . . . . . . . . . . . . . . . . . . . . 149
1.2. Sistemas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 153
1.2.1. Espacio vectorial . . . . . . . . . . . . . . . . . . . . . . . 156
1.2.2. Transformacin lineal . . . . . . . . . . . . . . . . . . . . 157
1.2.3. Normas Elep . . . . . . . . . . . . . . . . . . . . . . . . . 157
1.3. La norma ele-innito . . . . . . . . . . . . . . . . . . . . . . . . . . 164
1.4. Variacin de seales discretas . . . . . . . . . . . . . . . . . . . . 166
NDICE GENERAL vii
1.5. Variacin de seales continuas . . . . . . . . . . . . . . . . . . . 166
1.6. Variacin promedio . . . . . . . . . . . . . . . . . . . . . . . . . . 166
1.7. Problemas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 166
2. Convolucin y sistemas de convolucin 170
2.0. INTRODUCCIN . . . . . . . . . . . . . . . . . . . . . . . . . . . 170
2.1. Convolucin (lineal) discreta . . . . . . . . . . . . . . . . . . . . 174
2.2. Convolucin (lineal) continua . . . . . . . . . . . . . . . . . . . . 177
2.2.1. Curvgrafos(Splines) . . . . . . . . . . . . . . . . . . . . 181
2.2.2. Convolucin de Stieltjes . . . . . . . . . . . . . . . . . . . 181
2.3. Sistemas de convolucin continuos . . . . . . . . . . . . . . . . . 183
2.3.1. Respuesta escaln . . . . . . . . . . . . . . . . . . . . . . 184
2.3.2. Funcin caracterstica (respuesta impulso) de sistemas
de convolucin continuos . . . . . . . . . . . . . . . . . . 186
2.3.3. Respuesta a una entrada constante . . . . . . . . . . . . . 187
2.3.4. Respuesta a la derivada de la entrada . . . . . . . . . . . 187
2.3.5. Identicacin de sistemas de convolucin . . . . . . . . . 188
2.3.6. Un aplicacin del teorema fundamental del clculo . . . 189
2.3.7. La carga (la integral o el rea) de la respuesta de un
sistema de convolucin . . . . . . . . . . . . . . . . . . . 192
2.4. La transformada de Hilbert . . . . . . . . . . . . . . . . . . . . . 194
2.5. Sistemas de convolucin discretos . . . . . . . . . . . . . . . . . 194
2.6. Impedancia y respuesta impulso . . . . . . . . . . . . . . . . . . 196
2.7. Correlacin determinstica . . . . . . . . . . . . . . . . . . . . . . 198
2.8. La convolucin de Stieltjes . . . . . . . . . . . . . . . . . . . . . . 199
2.9. Problemas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 200
3. Seales peridicas (Fourier) 205
3.0. Seales peridicas . . . . . . . . . . . . . . . . . . . . . . . . . . . 205
3.0.1. Deniciones . . . . . . . . . . . . . . . . . . . . . . . . . . 206
viii NDICE GENERAL
3.0.2. Frecuencia . . . . . . . . . . . . . . . . . . . . . . . . . . . 208
3.0.3. Unidades . . . . . . . . . . . . . . . . . . . . . . . . . . . 209
3.1. Sumas de seales peridicas . . . . . . . . . . . . . . . . . . . . . 209
3.1.1. Caso discreto . . . . . . . . . . . . . . . . . . . . . . . . . 210
3.1.2. Notacin . . . . . . . . . . . . . . . . . . . . . . . . . . . . 210
3.1.3. Caso continuo . . . . . . . . . . . . . . . . . . . . . . . . . 211
3.2. Seales semi peridicas . . . . . . . . . . . . . . . . . . . . . . . . 214
3.2.1. Caso continuo . . . . . . . . . . . . . . . . . . . . . . . . . 214
3.2.2. Caso discreto . . . . . . . . . . . . . . . . . . . . . . . . . 214
3.3. Exponenciales complejas y sinusoides . . . . . . . . . . . . . . . 215
3.3.1. Caso continuo . . . . . . . . . . . . . . . . . . . . . . . . . 215
3.3.2. Caso discreto . . . . . . . . . . . . . . . . . . . . . . . . . 215
3.4. Seales peridicas contnuas . . . . . . . . . . . . . . . . . . . . . 219
3.4.1. Series de Fourier . . . . . . . . . . . . . . . . . . . . . . . 219
3.4.2. Propiedades de simetra . . . . . . . . . . . . . . . . . . . 222
3.4.3. Frmula de Parseval . . . . . . . . . . . . . . . . . . . . . 222
3.4.4. Series de sinusoides . . . . . . . . . . . . . . . . . . . . . 224
3.4.5. Sumas parciales de una serie de Fourier . . . . . . . . . . 225
3.5. Convolucin circular continua . . . . . . . . . . . . . . . . . . . . 226
3.6. Series de Fourier de funciones discontinuas y fenmeno de Gibbs231
3.7. Seales peridicas discretas . . . . . . . . . . . . . . . . . . . . . 233
3.7.1. Sumas tipo I . . . . . . . . . . . . . . . . . . . . . . . . . . 235
3.7.2. Sumas tipo II . . . . . . . . . . . . . . . . . . . . . . . . . 236
3.7.3. Una biyeccin de C
N
a C
N
. . . . . . . . . . . . . . . . . . 237
3.8. Problemas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 239
4. Transf. de Fourier de seales continuas 246
4.0. Introduccin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 246
4.0.1. Motivacin . . . . . . . . . . . . . . . . . . . . . . . . . . 247
4.0.2. Objetivo . . . . . . . . . . . . . . . . . . . . . . . . . . . . 251
NDICE GENERAL ix
4.1. La transformada de Fourier L-1 . . . . . . . . . . . . . . . . . . . 252
4.2. Propiedades de la transformada de Fourier L-1 . . . . . . . . . . 256
4.3. Convolucin en frecuencia . . . . . . . . . . . . . . . . . . . . . . 270
4.4. Polos y ceros . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 276
4.5. Transformada de Fourier L-2 . . . . . . . . . . . . . . . . . . . . 279
4.5.1. Respuesta a sinusoides . . . . . . . . . . . . . . . . . . . . 281
4.5.2. Filtro pasa bajas RC de un polo . . . . . . . . . . . . . . . 283
4.5.3. Comportamiento transiente . . . . . . . . . . . . . . . . . 287
4.5.4. Anlisis del comportamiento asinttico . . . . . . . . . . 288
4.5.5. representacin de un sistema con respuesta escaln dis-
continua en trminos de una suma de sistemas identidad
(linea de retardo o ltro pasa todas) y un sistema con re-
spuesta escaln continua . . . . . . . . . . . . . . . . . . . 288
4.6. Distorsin de fase y distorsin de amplitud . . . . . . . . . . . . 291
4.6.1. Filtro ideal . . . . . . . . . . . . . . . . . . . . . . . . . . . 291
4.6.2. Distorsin . . . . . . . . . . . . . . . . . . . . . . . . . . . 291
4.6.3. Filtro pasa todas . . . . . . . . . . . . . . . . . . . . . . . 294
4.6.4. Dcadas y octavas . . . . . . . . . . . . . . . . . . . . . . 295
4.6.5. Frecuencias de corte y decibeles . . . . . . . . . . . . . . 296
4.7. La transformada de Fourier L-2 . . . . . . . . . . . . . . . . . . . 303
4.7.1. Denicin . . . . . . . . . . . . . . . . . . . . . . . . . . . 304
4.8. Distribuciones temperadas . . . . . . . . . . . . . . . . . . . . . . 304
4.8.1. Distribuciones . . . . . . . . . . . . . . . . . . . . . . . . . 305
4.9. Modulacin SSB y la transformada de Hilbert . . . . . . . . . . . 308
4.9.1. Pares de Hilbert . . . . . . . . . . . . . . . . . . . . . . . . 310
4.10. Apndice I . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 311
4.11. Apndice II: Anlisis en tiempo contra anlisis en frecuencia . . 313
4.11.1. Respuesta del circuito RC pasa bajas de primer orden a
una seal onda cuadrada . . . . . . . . . . . . . . . . . . 313
x NDICE GENERAL
4.11.2. Respuesta escaln . . . . . . . . . . . . . . . . . . . . . . 314
4.11.3. Respuesta de estado estable a una onda cuadrada . . . . 315
4.12. Problemas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 318
5. DFT y DTFT 337
5.0. Introduccin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 337
5.0.1. Transformada inversa . . . . . . . . . . . . . . . . . . . . 341
5.1. Propiedades de la DTFT . . . . . . . . . . . . . . . . . . . . . . . 341
5.2. Frecuencias grandes y pequeas . . . . . . . . . . . . . . . . . . 344
5.3. Filtros discretos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 347
5.4. Respuesta en frecuencia sistemas de convolucin . . . . . . . . . 348
5.5. Polos y ceros de H(z) y H() correspondiente . . . . . . . . . . . 353
5.6. Sistemas de convolucin . . . . . . . . . . . . . . . . . . . . . . . 355
5.6.1. Respuesta a exponenciales complejas discretas . . . . . . 355
5.7. Transformada Discreta de Fourier DFT . . . . . . . . . . . . . . . 356
5.7.1. Propiedades de corrimiento circular y modulacin de la
DFT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 358
5.7.2. Simetra circular par . . . . . . . . . . . . . . . . . . . . . 360
5.7.3. Convolucin circular discreta . . . . . . . . . . . . . . . . 360
5.7.4. Interpretacin de lo convolucin circular en trminos de
seales peridicas . . . . . . . . . . . . . . . . . . . . . . 362
5.7.5. Relacin de Parseval para la DFT . . . . . . . . . . . . . . 364
5.8. Propiedades de simetra . . . . . . . . . . . . . . . . . . . . . . . 364
5.8.1. Conjugada simtrica y conjugada antisimtrica . . . . . . 365
5.8.2. Implicaciones de las propiedades de simetra para trans-
formadas de seales discretas . . . . . . . . . . . . . . . . 367
5.9. Relacin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 370
5.10. Seal muestreada . . . . . . . . . . . . . . . . . . . . . . . . . . . 371
5.10.1. Muestreo de seales continuas . . . . . . . . . . . . . . . 372
NDICE GENERAL xi
5.10.2. Reconstruccinde la seal continua a partir de sus mues-
tras . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 375
5.10.3. Frmula para la interpolacin trigonomtrica de seales
contnuas a partir de muestras equiespaciadas . . . . . . 378
5.11. Resumen grco . . . . . . . . . . . . . . . . . . . . . . . . . . . . 380
5.12. Resumen de las transformadas . . . . . . . . . . . . . . . . . . . 382
5.13. Resumen para la propiedad de Parseval . . . . . . . . . . . . . . 384
5.14. Resumen convolucin . . . . . . . . . . . . . . . . . . . . . . . . 386
5.15. Problemas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 388
6. Propiedades de los sistemas 395
6.0. Clasicacin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 395
6.1. Sistemas lineales . . . . . . . . . . . . . . . . . . . . . . . . . . . . 397
6.2. Sistemas no lineales: los ltros L . . . . . . . . . . . . . . . . . . 399
6.2.1. Permutaciones . . . . . . . . . . . . . . . . . . . . . . . . 400
6.2.2. Muestra . . . . . . . . . . . . . . . . . . . . . . . . . . . . 401
6.2.3. Estadsticas . . . . . . . . . . . . . . . . . . . . . . . . . . 401
6.2.4. Estadsticas de orden . . . . . . . . . . . . . . . . . . . . . 402
6.2.5. Mediana, mnimo y mximo . . . . . . . . . . . . . . . . 402
6.2.6. Algunas estadsticas L . . . . . . . . . . . . . . . . . . . . 403
6.2.7. Notacin vectorial para las estadsticas L . . . . . . . . . 403
6.2.8. Estadsticas mviles o ltros de ventana mvil . . . . . . 404
6.2.9. Filtros L . . . . . . . . . . . . . . . . . . . . . . . . . . . . 404
6.2.10. Seales raz . . . . . . . . . . . . . . . . . . . . . . . . . . 405
6.3. Invarianza y Causalidad . . . . . . . . . . . . . . . . . . . . . . . 406
6.3.1. Invarianza . . . . . . . . . . . . . . . . . . . . . . . . . . . 407
6.3.2. Causalidad . . . . . . . . . . . . . . . . . . . . . . . . . . 408
6.4. Estabilidad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 410
6.5. Sistemas homogneos e invariantes . . . . . . . . . . . . . . . . . 412
6.5.1. Caso discreto . . . . . . . . . . . . . . . . . . . . . . . . . 412
xii NDICE GENERAL
6.5.2. Caso continuo . . . . . . . . . . . . . . . . . . . . . . . . . 412
6.6. Sistemas de convolucin . . . . . . . . . . . . . . . . . . . . . . . 413
6.6.1. Causalidad de un sistema de convolucin . . . . . . . . . 413
6.6.2. Estabilidad de un sistema de convolucin . . . . . . . . 415
6.7. Sistemas lineales e invariantes . . . . . . . . . . . . . . . . . . . . 418
6.7.1. Con dominio L
p
, p [1, ) . . . . . . . . . . . . . . . . . . 418
6.8. Representabilidad con convolucin . . . . . . . . . . . . . . . . . 418
6.8.1. Sistemas discretos . . . . . . . . . . . . . . . . . . . . . . 418
6.8.2. Sistemas contnuos . . . . . . . . . . . . . . . . . . . . . . 421
6.8.3. El teorema de representacin de Riesz y su relacin con
los sistemas contnuos . . . . . . . . . . . . . . . . . . . . 423
6.9. Sistemas de Volterra . . . . . . . . . . . . . . . . . . . . . . . . . 424
6.9.1. Sistemas de Volterra discretos . . . . . . . . . . . . . . . . 424
6.10. Problemas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 425
Notacin
A continuacin se da el signicado de parte de la terminologa matemtica
que se usa. Se asume que se tiene cierta familiaridad con lgica matemtica
as como con la teora de conjuntos: en particular, se asume que conoce el
signicado de la conjuncin , de la disyuncin , de la implicacin y de
la doble implicacin . Las letras son smbolos de elementos, conjuntos, etc.
x A : x pertenece a A (o, x es miembro de A).
P(x) : x cumple con la propiedad P.
x A : para algn (o existe un) elemento x en el conjunto A
x A : para cada (o para todo) elemento x del conjunto A
a = b : quiere decir que los smbolos a y b representan la misma cosa.
: tal que
B = x A : Q(x) : B es el conjunto de los elementos de A que cumplen con la
propiedad Q.
A B : el conjunto A contiene al conjunto B.
A B = x : x A x B.
A B = x : x A x B.
_
aA
B
a
= x : a A, x B
a
.
_
aA
B
a
= x : a A, x B
a
.
Conjunto vaco ; x, x A A = .
1
2 NDICE GENERAL
[a] : clase de equivalencia del elemento a.
[x]
N
: x mdulo N.
[a, b] : intervalos cerrados, elementos de R
2
.
[a, b, c, d] : elementos de R
N
.
x : P(x) : el conjunto de los elementos que cumplen con la propiedad P.
x
i
: sucesiones.
(a, b) : pares ordenados.
(a, b) : intervalos abiertos.
(a, b, c, d) : n-tuplas.
]a, b[: intervalos abiertos de R
N
.
Una operacin (clausurativa) entre los elementos de un conjunto A es una fun-
cin : A A A
:= : que se dene como.
=: : que se abrevia como.
EL ALFABETO GRIEGO
, A: alfa
, B: beta
, : gama
, : delta
, E : psilon
, Z : zeta
, H : eta
, , : teta
, I : yota
, K : kapa
, : lambda o labda
, M : my
, N : ny
NDICE GENERAL 3
, : ji
o, O : omicron
, , : pi
, P : ro
, , : sigma
, T : tau
, : upsilon
, , : phi
_
f i
_
, X : ji
, : psi
, : omega
Captulo 0
Bases matemticas
0.1. INTRODUCCIN
La mayora de los trminos que se usan con un sentido tcnico es este
libro se denen matemticamente. En este captulo se ven algunos conceptos
matemticos que son usados durante el resto del libro. La mayora le sern
probablemente conocidos, otros notanto. Parte de loque se pretende es acordar
la nomenclatura a ser usada. Otros objetivos son: adquirir familiaridad con las
congruencias mdulo ene, repasar los conceptos de dominio, rango y funcin
y, nalmente, ver las bases de la integral de Riemann-Stieltjes.
El lector iniciado, interesado en un tema particular en teora de seales,
puede saltar este captulo y referirse a l en caso necesario.
Ejercicio. Demuestre que A = B A B B A
Qu son conjuntos disyuntos?
Qu es el conjunto potencia de un conjunto?
Ejercicio. Demuestre que
4
0.1. INTRODUCCIN 5
i a, b = b, a
ii 1, 2, 2 = 1, 2
Tal vez laprimera persona que entiempos modernos relacionla lgica ylas
matemticas fue el lgico italiano Giuseppe Peano (1858-1932). Peano dio una
lista de propiedades que cumplen los nmeros naturales. La teora de conjuntos,
originada por Georg Cantor
1
, se usa como base para las matemticas hoy en
da. La idea de basar las matemticas en la teora de conjuntos y, a la larga en
lgica, tom as fuerza desde nales del siglo XIX. Los resultados de Gdel
(1906-1978) indicando la imposibilidad de obtener sistemas formales completos
en los cuales basar las matemticas, quizs le restaron algo de mpetu a esta
tendencia racionalista en las matemticas de comienzos de siglo. Poincar
sostuvo la importancia de la intuicin en las matemticas a comienzos del
siglo XX.
1
Georg Cantor (1845-1918) Destacado matemtico ruso, entre muchos avances matemticos se
destacan su inters por la idea del innito, su denicin del continuo y su teora de conjuntos.
6 CAPTULO 0. BASES MATEMTICAS
0.2. Relaciones y Funciones
De los varios conceptos que se denen en este captulo, el lector segu-
ramente tendr una idea intuitiva clara. Sin embargo, en aras de anclar la
intuicin con el mtodo axiomtico, los denimos en todo caso. As el caso de
par ordenado, que denimos de dos maneras dentro de la teora de conjuntos.
0.2.1. Par ordenado
Un par ordenado es una estructura de dos componentes en la cual hay una
asimetra que permite diferenciarlos. El origen del concepto tal vez se remonte
a los estudios de Fermat y Descartes en relacin con lo que hoy llamamos
geometra analtica. Dado que a, b = b, a, el conjunto a, b no dene el par
ordenado (a, b).
Denicin 1. (a, b) = a, b
Denicin 2. (a, b) = a, a, b
Ejercicio. Qu axiomas de la teora de conjuntos son necesarios para dar la
denicin 1? Para dar la denicin 2?
Similarmente, la n-tupla (x
1
, x
2
, . . . , x
n
), puede ser denida en la teora de
conjuntos.
0.2.2. Producto cartesiano
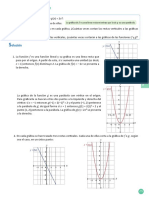
El producto cartesiano A B de los conjuntos A y B es el conjunto de
los pares ordenados cuya primera componente es un elemento de A y cuya
segunda componente es un elemento de B.
A B = (a, b) : a A, b B
0.2. RELACIONES Y FUNCIONES 7
Figura 1: El producto cartesiano de A y A
El producto cartesiano no es una operacin conmutativa: si A B entonces
A B B A, adems, el producto cartesiano tampoco es una operacin
asociativa ya que
A (B C) (A B) C
dado que (a, (b, c)) ((a, b), c), con cualquiera de las deniciones dadas de par
ordenado, es decir, por ejemplo con la denicin 2 de par ordenado, tenemos
que (a, (b, c)) = a, a, b, b, c mientras que ((a, b), c) = a, a, b, a, a, b, c
y as, a (a, (b, c)) pero a ((a, b), c) y entonces, (a, (b, c)) ((a, b), c).
Sin embargo, podemos denir tripla con (a, b, c) := (a, (b, c)), ((a, b), c) y
A B C como el conjunto de las triplas (a, b, c), con a A, b B, c C.
Ejercicio. D un ejemplo de un producto cartesiano que no conmute.
Podemos generalizar la nocin de tupla y denir las n-tuplas para cada entero
positivo n.
Ejercicio. Dena 4-tuplas.
0.2.3. Relacin
Una relacin entre los elementos de un conjunto es algn subconjunto
del producto cartesiano del conjunto con s mismo.
Ejemplo. A = 0, 1, 2
A A = (0, 0), (0, 1), (0, 2), (1, 0), (1, 1), (1, 2), (2, 0), (2, 1), (2, 2)
Sea R = (1, 0), (2, 1) decimos entonces que 1 R0 y 2 R1. (Se lee: 1
est relacionado con 0 y 2 est relacionado con 1, o R relaciona a uno con cero,
R relaciona a dos con uno; tambin, uno erre cero, dos erre uno y uno no
erre dos.)
Propiedades de relaciones
Sea R una relacin entre los elementos del conjunto A.
i) R es una relacin reexiva si
a A, (a, a) R
Figura 2: Para una relacin reexiva R, la diagonal de A A debe estar en R
ii) R es una relacin simtrica si
a, b A, (a, b) R (a, b) R
Figura 3: Una relacin simtrica
iii) R es una relacin transitiva si
a, b, c A, (a, b) R (b, c) R (a, c) R
Figura 4: Transitividad. Si est relacionada con y con entonces est relacionada con
Con respecto a la gura 4, note que (a, b) y (b, c) determinan dos vrtices
opuestos de un rectngulo y que uno de los vrtices restantes es (b, b)
que est sobre la diagonal, el vrtice restante, (a, c) es el requerido por
la propiedad de transitividad.
Ejemplo. es transitiva. A B, B C A C
Ejemplo. no es transitiva. A B, B C A C
iv) R es una relacin conectada si
a, b A, a b (a, b) R o (b, a) R
Figura 5: A la izquierda, relacin conectada. A la derecha, una de corrimiento circular: para
cada la y cada columna hay por lo menos un elemento de relacin
v) R es una relacin antireexiva si
a A, (a, a) R
vi) R es una relacin antisimtrica si
a, b A, (a, b) R (a, b) R a = b
vii) R es una relacin de corrimiento circular si
a A, ! b A a b, tal que: (a, b) R, o, (b, a) R
Ejercicio. Muestre o d un contraejemplo para la siguiente armacin: si una
relacin es simtrica y transitiva, entonces es reexiva.
Ejercicio. Muestre o d un contraejemplo para la siguiente armacin: si una
relacin es simtrica, transitiva y conectada, entonces es reexiva.
Ejercicio. Muestre que
n
m=0
(
n
m
) = 2
Ejercicio. Cuntas relaciones posibles hay entre los elementos de un conjunto
de n elementos?
Relaciones de equivalencia y clases de equivalencia
La relacin de equivalencia en muy til en matemticas. Decimos que una
relacin es una relacin de equivalencia si es reexiva, simtrica y tran-
sitiva. Sea E una relacin de equivalencia entre los elementos de un conjunto
A. Para cada elemento a de A denimos su clase de equivalencia como el
conjunto de los elementos de A que son equivalentes a a y se denota [a] :
[a] = x a : (x, a) E
Ejercicio. Muestre que b [a] si y slo si la [a] = [b].
Ejercicio. Muestre que, dados (a, b) A, [b] = [a], o, [a] [b] =
Ejercicio. Muestre que A =
_
aA
[a]
0.2.4. Particin
Una particin de un conjunto Aes una coleccin de subconjuntos disyun-
tos de A cuya unin es A.
Ejercicio. D una particin de 0, 1, 2
Ejercicio. Demuestre que, dado un conjunto A, la coleccin de equivalencias
determinadas por cada uno de los elementos de A es una particin de A.
Ejercicio. En cuntas clases de equivalencia particiona la relacin congruencia
mdulo 3 al conjunto de los nmeros naturales?
Ejercicio. Dada una particin de A, diga cmo denir una relacin de equiva-
lencia entre los elementos de A, tal que las clases de equivalencia resultantes
sean los elementos de la particin dada.
0.2.5. Relaciones de orden
R es un orden parcial si es una relacin transitiva, antisimtrica y reex-
iva. R es un orden lineal si es un orden parcial y es una relacin conectada.
El orden parcial tpico es el dado por ser subconjunto de entre el conjunto
de subconjuntos de un conjunto dado, por ejemplo en la gura 6 se muestra el
orden , para los subconjuntos de 0, 1, 2
Figura 6: Un orden parcial, no conectado
0.2.6. Suprmum, Infmum
Sea A un conjunto linealmente ordenado por la relacin . Sea B un sub-
conjunto de A y sea q un elemento de A. Si b B, se tiene b q, se dice que q
es una cota superior de B. q es una cota superior mnima (suprmum) de B si:
1. q es una cota superior de B.
2. Para cada cota superior r de B en A, q r.
Similarmente, sea A un conjunto linealmente ordenado por la relacin .
Sea B un subconjunto de A y sea q un elemento de A. Si b B, se tiene que q
0.3. FUNCIONES 13
es una cota inferior de B. q es una cota inferior mxima (infmum) de B si:
1. q es una cota inferior de B.
2. Para cada cota inferior r de B en A se tiene que r q.
Ejercicio. Demuestre que el suprmum de un subconjunto de un conjunto
linealmente ordenado, si existe, es nico.
0.2.7. Mximo y mnimo
Sea A un conjunto linealmente ordenado por la relacin . Sea B un sub-
conjunto de A. Si B tiene suprmum r que pertenece a B, decimos que r es el
mximo de B. Similarmente, si B tiene infmum t, y t pertenece a B, decimos
que t es el mnimo de B.
Ejemplo. En los reales, en el intervalo abierto (0, 1) no tiene ni mximo ni
mnimo, 0 es su cota inferior mxima o infmumy 1 es su cota superior mnima
o suprmum.
Ejemplo. En los racionales q Q : q
2
2 no tiene ni suprmum, ni infmum.
0.3. Funciones
Una funcin es una tripla ( f, A, B) donde f es un subconjunto del producto
AB, que no contiene dos pares ordenados con la misma primera componente
y que se conoce como la grca de la funcin; el conjunto A es el dominio de
la funcin y el conjunto B es el rango de la funcin. Ademas , cada elemento
del dominio es la primera componente de uno y solo un par de la grca. Tal
funcin tambin se denota como, f : A B. Note que dos funciones pueden
diferir solamente en el rango.
Normalmente (a, b) f , se denota como f (a) = b; y se dice que b es la imagen
de a. Otra forma de decir que no hay dos pares de f con la misma primera
componente es:
(a, b) f (a, c) f b = c
Como se dijo, todo elemento de Aes la primera componente de algnelemento
de f :
a A, x f : x = (a, b)
Sin embargo, no todos los elementos del rango son necesariamente segundas
componentes de pares de la grca. En caso de que lo sean, se dice que la
funcin es sobreyectiva.
Figura 7: Diagrama de una funcin con dominio A y rango B
Abusando la notacin descrita, si C es un subconjunto del dominio de
f , decimos que f (C) es el conjunto de las imgenes de los elementos de C,
o imagen de C. Tambin, si D es un subconjunto del rango de f , ponemos
f
1
(D) = a A : f (a) D.
Ejercicio. Si C y D son subconjuntos del dominio de ( f, A, B), demuestre o d
un contraejemplo para cada una de las armaciones siguientes:
i) f (C D) = f (C) f (D)
ii) f (C D) = f (C) f (D)
Ejercicio. Si C y D son subconjuntos del rango de ( f, A, B), demuestre o d un
contraejemplo:
0.3. FUNCIONES 15
i) f
1
(C D) = f
1
C) f
1
(D)
ii) f
1
(C D) = f
1
(C) f
1
(D)
0.3.1. Sobreyeccin
f : A B es una sobreyeccin si b Ba A (a, b) f , es decir,
una sobreyeccin es una funcin donde todo elemento del rango es la segunda
componente de algn par de la grca de la funcin.
Figura 8: f es una sobreyeccin de A en B, pero no una inyeccin
0.3.2. Inyeccin. (funcin uno-a-uno)
f : A B es una inyeccin si f no contiene dos pares con la misma
segunda componente. En smbolos, (a, b) f (c, d) f a = c.
0.3.3. Biyeccin. (correspondencia uno-a-uno)
Una biyeccin es una funcin que es uno-a-uno y tambin sobreyectiva.
Ejercicio. (Cantor) Muestre que no es posible establecer una biyeccin entre
ningn conjunto y su conjunto potencia. (El Conjunto potencia o partes de de un
conjunto dado, se dene como el conjunto de los subconjuntos del conjunto
dado.)
Figura 9: f es una inyeccin de A en B, pero no es sobreyectiva
Figura 10: Una biyeccin
0.3. FUNCIONES 17
Nota. Se puede argumentar que parte de la labor de un ingeniero consiste
en cuanticar las variables que modela y en disear con base en stas. As, el
uso de nmeros se convierte en una segunda naturaleza para el ingeniero. En
las secciones siguientes se dan deniciones de los nmeros naturales, enteros,
racionales, reales, complejos y de los cuaternios. Dado que en ingeniera las
magnitudes se cuantican se podra argumentar que es importante tener una
idea clara de cada uno de estos tipos de nmeros. Los naturales se denen con
base en nociones de la teora de conjuntos, los enteros con base en los naturales,
los racionales con base en los enteros, los reales con base en los racionales. En
cada uno de estos casos tenemos una relacin de orden lineal y las operaciones
de suma y producto. Luego, tenemos R
N
, en donde tenemos la operacin de
suma. En R
2
tenemos adems el producto complejo, y en R
4
el producto de
cuaternios.
Denicin 3. Una biyeccin p : A A de un conjunto nito a s mismo, se conoce
como una permutacin de ste.
Denicin 4. Una funcin t : A A de un conjunto nito A con al menos dos
elementos, a s mismo, se conoce como una transposicin si A tiene exactamente dos
elementos a
1
y a
2
para los que t(a
1
) = a
2
y t(a
2
) = a
1
y, para el resto de los elementos
de A, f () = .
Ejercicio. Muestre que si una permutacin se descompone como una composi-
cin de transposiciones en dos formas, el nmero de transposiciones es, en
ambos casos, par, o en ambos casos impar. (Dado el resultado positivo del
ejercicio anterior, clasicaremos las permutaciones en pares e impares).
Ejercicio. Escriba y clasique las permutaciones de los elementos del conjunto
A = 0, 1, 2 en pares e impares.
0.4. Relaciones Ternarias
Una relacin ternaria entre los elementos de un conjunto A es un sub-
conjunto del producto cartesiano A
3
.
Ejemplo. Para el conjunto A = 0, 1, 2, donde
A A A =
(0, 0, 0), (0, 0, 1), (0, 0, 2), (0, 1, 0),
(0, 1, 1), (0, 1, 2), (0, 2, 0), (0, 2, 1),
(0, 2, 2), (1, 0, 0), (1, 0, 1), (1, 0, 2),
(1, 1, 0), (1, 1, 1), (1, 1, 2), (2, 0, 0),
(2, 0, 1), (2, 0, 2), (2, 1, 0), (2, 1, 1),
(2, 1, 2), (2, 2, 0), (2, 2, 1), (2, 2, 2)
considere la relacin R = (0, 1, 2), (1, 2, 0), (2, 0, 1)
Figura 11: Un ordenamiento circular para 0, 1, 2
0.4.1. Propiedades de relaciones ternarias
Sea R una relacin ternaria entre los elementos del conjunto A.
0.4. RELACIONES TERNARIAS 19
i) R es una relacin ternaria dinmica si
(a, b, c) R, a b, b c, c a
ii) R es una relacin ternaria circulable si es cerrada con respecto a permuta-
ciones pares de sus elementos:
(a, b, c) R (b, c, a) R, (c, a, b) R
iii) R es una relacin ternaria de orientacin si no contiene ninguna per-
mutacin impar de ninguno de sus elementos:
(a, b, c) R (a, c, b) R, (b, a, c) R, (c, b, a) R
iv) R es una relacin ternaria total si:
a A(x, y, z) R a = x a = y a = z
v) R es una relacin ternaria transitiva si:
(a, b, c) R, (b, d, c) R (a, b, d) R, (d, c, a) R
vi) R es una relacin ternaria circular si cumplen.
Ejercicio. Muestre que dados dos puntos a y b, elementos de un conjunto A en
el que se ha denido una relacin circular R, resulta la particin
A = a, b x A : (a, x, b) R x A : (b, x, a) R
que podramos llamar el teorema de Jordan para conjuntos circularmente or-
denados.
Dado un conjunto circularmente ordenado, podemos denir los intervalos
(a, b) = x A : (a, x, b) R y (b, a) = x A : (b, x, a) R ahora podemos
denir una topologa con base dada por estos intervalos.
0.5. Estructuras algebricas
Las transformaciones lineales jueganunapapel importante eningeniera.Qu
es una transformacin lineal? Para responder a esta pregunta se hace necesario
el concepto de espacio vectorial; aunque el lector probablemente haya trabajado
en repetidas ocasiones con espacios vectoriales. Para una denicin formal,
necesitamos antes los conceptos ms bsicos de grupo y anillo.
Sean A un conjunto y o una operacin o: A A A entre los elementos de
A
Cuando el conjunto A es nito y pequeo, puede ser conveniente especicar
la operacin con una tabla.
a b c d
a a d b c
b c b a d
c d a c b
d b c a d
Tabla 1: La tabla de una opracin posible entre los elementos de {a, b, c, d}
As, decimos que un grupoide (A, o) est dado por un conjunto no vaco
A y una operacin entre los elementos o de ste. Note que no se requiere la
asociatividad de la operacin.
Ejemplo. Considere el conjunto {a, b, c, d} y la operacin en la Tabla 1
Un semigrupo (A, o) es un grupoide en el que la operacin es asociativa. La
propiedad asociativa de la operacin o se expresa as:
a, b, c A a (b c) = (a b) c
Ejemplo. (N, +) es un semigrupo.
0.5. ESTRUCTURAS ALGEBRICAS 21
Ejercicio. D un ejemplo de una operacin no asociativa.(Loas octoniones)
Ejercicio. Diga si la operacion del grupoide en la tabla 2 es asociativa.
Un monoide (o un mdulo) es un semigrupo en el cual hay un elemento
identidad. Es decir, debe existir un elemento e en el conjunto tal que: a
A a e = e a = a. Esta propiedad dene a e como elemento identidad del
monoide.
Ejemplo. (N, +) es un monoide, con identidad dada por 1.
Ejercicio. Diga si un monoide puede tener ms de un elemento identidad.
Ejercicio. D un ejemplo de un semigrupo que no sea un monoide.

Tabla 2: La tabla de una operacin entre los elementos del conjunto nito , , , ,
0.5.1. Grupos
Un grupo es un monoide (G, o) en el que cada elemento tiene un inverso
con respecto a la operacin denida el cual es un elemento que al multiplicarlo
por el elemento dado da el elemento identidad.As un inverso de g G es un
elemento h G tal que gh = e.
(G, o) es un grupo abeliano (o conmutativo) si: g, h G, g h = h g.
Ejercicio. Muestre que en un grupo, si gh = e entonces hg = e.
Ejercicio. Muestre que entonces en un grupo, cada elemento tiene uno y slo
un inverso.
La teora de grupos result impulsada inicialmente en forma importante
por los trabajos de Galois
2
, quien fue un matemtico francs que estudi la
posibilidad de resolver con races, sumas, restas, productos y cocientes, las
ecuaciones polinmicas de orden arbitrario. El matemtico Noruego Abel
3
,
contemporneo de Gauss y de Galois, trabaj enla imposibilidadde la solucin
general algebraica de la ecuacin de quinto grado.
4
Ejercicio. D un ejemplo de un grupo no abeliano.
Ejercicio. Sea G = e
j0
, e
j2/3
, e
j4/3
y como operacin o, la multiplicacin de
complejos. Muestre que (G, o) es un grupo abeliano. D la tabla de multipli-
cacin correspondiente:
e f = eg = f e = ge =
f g = ee = f f = gg =
Tabla 3: Complete la tabal mostrada e = e
j
20
3 , f = e
j
2
3 , g = e
j
4
3
(H, ) es un subgrupo del grupo (G, o), si H es un subconjunto de G y (H, o)
es un grupo. De ahora en adelante abreviaremos (G, ) como G.
2
variste Galois (1811-1933) fue un matemtico francs reconocido, junto con Abel, por su
estudio de las races de los polinomios y la idea de cuerpo (eld).
3
Niels Henrick Abel (1802-1829) matemtico Noruego, demostr que no existe una operacin
algebraica explcita con forma de races, productos, cocientes, sumas y restas, para encontrar las
races de un polinomio de orden 5.
4
Tanto Galois como Abel murieron bastante jvenes, Galois a causa de una herida recibida en
un duelo y Abel a causa de la tuberculosis.
El espacio cociente G/H. Dado un subgrupo H del grupo G, el conjunto de
los subconjuntos gH := gh : h H, g G de G se denota como G/H. El
espacio cociente es un grupo con respecto a la operacin g
1
H g
2
H = (g
1
g
2
)H
si y slo si H es normal, es decir, si Hg = gH para cada g en G (en donde
Hg := hg : h H, g G).
K es un conjunto de generadores del grupo G, si el subgrupo ms pe-
queo de G que contiene a K es G mismo.
Homorsmos de grupos
1 1 i i j j k k
1 1 1 i i j j k k
1 1 1 i i j j k k
i i i 1 1 k k j j
i i i 1 1 k k j j
j j j k k 1 1 i i
j j j k k 1 1 i i
k k k j j i i 1 1
k k k j j i i 1 1
Tabla 4: La tabla de los cuaterniones
0.5.2. Anillos
Un anillo (A, +, ) es un conjunto de elementos A junto con 2 operaciones
+ y en donde:
i) (A, +) es un grupo abeliano. (Denote el mdulo con 0).
ii) (A, ) es un semigrupo.
iii) la operacin distribuye con respecto a la operacin +, vale decir que,
a, b, c A : a (b + c) = (a b) + (a c) y (b + c) a = (c a) + (c a)
A es un anillo conmutativo si la operacin es conmutativa.
A es un anillo con unidad si (A, ) es un monoide, es decir, si existe un
elemento identidad (denote este elemento identidad con 1) para la operacin
; ste se conoce como mdulo multiplicativo. (0 es el mdulo aditivo.) r A Retocar anillos
es un divisor de cero, si r, s A, r 0, s 0, r s = 0
Ejercicio. Muestre que el anillo /0, N 1/ con respecto a las operaciones de
suma y producto mdulo-N, tiene divisores de cero si y slo si N no es primo.
Un dominio de enteros ( integer domain) es un anillo conmutativo, que no
tiene divisores de cero.
Ejemplo. El conjunto de los nmeros enteros con respecto a las operaciones
usuales de suma y producto, es un dominio de enteros.
Ejercicio. D un ejemplo de un dominio de enteros nito.
Un anillo de divisin es un anillo (A, +, ) donde (A 0, ) es un grupo.
Ejercicio. Es todo anillo de divisin nito conmutativo?
Un cuerpo (eld)es un anillo de divisin conmutativo.
Ejercicio. Todo dominio de enteros nito es un cuerpo
Un anillo de divisin no conmutativo se conoce como un cuerpo torcido
(skew eld).
Ejercicio. Demuestre que cada dominio de enteros nito es un cuerpo.
IDEALES
Cuando se tiene una relacin de equivalencia tipo mdulo-N entre los
elementos de un anillo A, denotamos la clase de equivalencia que contiene al
cero (mdulo aditivo) como la clase NA. Al escoger un elemento e cada una
de las clases de equivalencia obtenemos otro anillo, que denotamos A/NA.
Ideales y Cocientes de anillos
Sea (A, +, ) un anillo. Sea BCA tal que (B, +) es un grupo. y a A, b
B, ab Byba B. Decimos entonces que B es un ideal del anillo A, si en el
espacio cociente (A, +)/(B, +) = a + B : a A..... que la operacin (a
1
+ B)(a
2
+
B) := a
1
a
2
+ B resulta un anillo que llaman el cociente de anillos A/B.
Homorsmos de anillos
0.5.3. Espacio vectorial
Unespaciovectorial (V, , K, +, , ) locostituyenungrupoabeliano(V, )(de
vectores), con mdulo 0 y un cuerpo (K, +, ) (de escalares), con mdulo
aditivo 0, normalmente, el origen (0 o mdulo aditivo) de los espacios vecto-
riales lo representaremos con la letra griega teta: . Para R
5
, = [0, 0, 0, 0, 0], y
mdulo multiplicativo 1, en donde, para cada , Ky casa v, w V, se tiene
que:
i) Hay un elemento en V que se expresa v(
: K V)
ii) (v w) = ( v) ( w)
iii) ( + ) v = ( v) ( v)
iv) ( v) = ( ) v
vi) 1 v = v
Ejercicio. Demuestre que 0 v = 0
Ejercicio. Demuestre la base de un espacio vectorial, si la dimension de un
espacio es nita...
0.5.4. Matrices y Determinantes
0.5.5. Homomorsmos
Cuando se tiene una funcin, cuyo dominio y rango cuentan con alguna
estructura algebraica y sta es respetada por la funcin, se dice que se tiene un
homomorsmo si la funcin es una biyeccin, se dice que los espacios dominio
y rango, son algebraicamente equivalentes o que son isomorfos.
Por ejemplo, si (A, +) y (B, ) son semigrupos, W es una funcin de A en B
y a, b A W(a + b) = W(a) W(b), entonces A y B son homomrcos y W es
un homomorsmo.
Terminologa de vectores y de escalares se origin con Hamilton, cuan-
do hizo los estudios que culminaron con la denicin de los cuaternios. Si
recordamos la frmula del producto de cuaternios:
(a1 + bi + cj + dk)(1 + i + j + k) =
(abcd)1+(a+b+cd)i +(ab+c+d)j +(a+vc+d)k
tenemos que el producto (bi + cj + dk)(i + j + k) esta dado por
(b c d)1 + (c d)i + (b + d)j + (b c)k
y su parte escalar es (b c d), mientas que la parte vectorial es (c d)i +
(b + d)j + (b c)k, compare con: [b, c, d] = [, , ] y [b, c, d] [, , ].
0.6. LOS NMEROS NATURALES 27
0.6. Los Nmeros Naturales
Aunque todos tenemos una idea intuitiva de los nmeros naturales, ellos
se pueden denir axiomticamente, con base en la teora de conjuntos.
Los nmeros naturales se pueden denir en forma inductiva, as: Sea Nel
conjunto que:
i) contiene al conjunto vaco como elemento: N.
ii) si x N, entonces x x N.
Nota. x x se conoce como el sucesor de x y lo denotamos S(x).
iii) x NS(x) .
iv) El nico elemento de Nque no es el sucesor de algn elemento de Nes
.
v) x, y N n y S(x) S(y).
Ejercicio. Demuestre las propiedades iii y v a partir de los axiomas de la teora
de conjuntos.
Alos elementos de Nlos llamamos nmeros naturales. As, los siguientes
4 conjuntos son nmeros naturales: , , , , , , , y los deno-
tamos:
0 := =
1 := =
2 := 0, 1 = ,
3 := 0, 1, 2 = , , , note que S(n) = 0, 1, 2, . . . , n
Nota. El conjuntode los subconjuntos que acabamos de denir tiene lapropiedad
de que si un elemento es subconjunto de otro, tambin es elemento. Por esta
raznla relacinpara los elementos de Nnos da una relacintransitiva. Peano
5
fue el primero en dar una denicin axiomtica de los nmeros naturales.
Los axiomas de Peano se pueden expresar as:
1) 0 N
2) si n Nentonces S(n) N(Cada elemento tiene sucesor)
3) n N S(n) 0 (Cero no es sucesor de nadie)
4) n, m N n m implica S(n) S(m) (Elementos diferentes tienen
sucesores diferentes)
5) Si P es una propiedad del elemento 0 y el sucesor de cada elemento con
la propiedad tiene la propiedad, entonces cada elemento de N tiene la
propiedad. (Principio de induccin)
Ejercicio. m, n N m n = m o m n = n
[[conceptodevariable]]
[[conceptodex y]]
[[algoritmo]]
[[Operaciones!mveces; porcadalementodemcalculeS(n)m
1; m
= 0?; n

S(n
)]]
[[ n n; i m; n S( n)]]
0.6.1. Orden lineal para N
La relacin ser subconjunto de determina una relacin de orden lineal
entre los elementos de N. Por ejemplo, 7 5 y 1 0.
5
Giuseppe Peano (1858,1932), fue un matemtico italiano reconocido por sus aportes a la axiom-
atizacin de la matemticas, entre los que se destacan axiomas para el conjunto de los nmeros
enteros y sobre la estructura de un espacio vectorial, tambin la denicin del concepto de apli-
cacin lineal.
Adems, ponemos denir el elemento mximo y el mnimo de dos nmeros
as: m ax(m, n) = m n y mn(m, n) = m n.
Ejemplo. El mximo de 3, 7, y 10 es 3 7 10
0, 1, 2 0, 1, 2, 3, 4, 5, 6 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 = 10
Ejercicio. Muestre que Nno tiene cota superior.
Ejercicio. Muestre que cada subconjunto no vaco de Ntiene un mnimo.
Ejercicio. Es (N, +) un grupo?
Ejercicio. Es (N, ) un monoide?
0.6.2. Divisor y mltiplo
El nmero natural m es un divisor del nmero natural n si, para algn
nmero natural k, n = km. Escribimos m n. Decimos que n es un mltiplo de
m.
0.6.3. Nmeros Primos
El nmero natural natural p es un nmero primo si sus nicos divisores
son 1 y p.
0.6.4. Factor
El nmero natural f es un factor del nmero natural n si:
i. f n
ii. f es una potencia de un nmero primo: f = p
k
, con p prima y k entera.
iii. p
k+1
= p f no divide a n.
Factorizacin nica de los nmeros naturales Muestre que lafactorizacinennmeros
primos de cada nmero natural n, n = p
k
1
p
k
2
p
k
t
, p
1
< p
2
< < p
t
es nica.
(Gauss)
[[Elaborar]]
Ejercicio. Muestre que hay innitos nmeros primos.
0.6.5. Mximo comn divisor, mnimo comn mltiplo
Sean m y n nmeros naturales. Si el nmero natural d divide a m y a n y
ningn natural D con D > d, divide a m y a n, decimos que d es el mximo
comn divisor de m y n. Escribimos d = [m, n]. Tambin, si C es un mltiplo
de m y de n y ningn natural menor que C es mltiplo de m y de n, decimos
que C es el mnimo comn mltiplo de m y n. Escribimos C = (m, n)
Ejercicio. Muestre que mn = [m, n](m, n)
Como dijimos al comienzo del captulo, el uso de nmeros es fundamental
en la labor de ingeniera. Aunque un amplicador sea desde cierto punto de
vista simplemente una estructura slida en silicio, su diseo es impensable sin
el uso de nmeros.
Denicin 5. a y b son primos relativos si [a, b] = 1
0.6.6. Conjuntos contables y no contables
Se dice que un conjunto A es nito si hay una inyeccin de A a un nmero
natural N.
Se dice que unconjunto Aes contable (o enumerable) si existe una inyeccin
de A al conjunto Nde los nmeros naturales. note que segn esta denicin,
un conjunto nito es contable.
Figura 12: Una inyeccindel conjunto de los nmeros pares al conjunto de los nmeros naturales
Ejemplo. El conjunto de los nmeros naturales pares es contable.
Ejercicio. Muestre que todo subconjunto nito de Ntiene un mximo.
Ejercicio. Muestre que Nno es nito.
Ejercicio. Diga si el conjunto de los naturales es contable. Explique.
Ejercicio. Muestre que si A es un conjunto contable innito, entonces hay una
biyeccin de Na A.
0.6.7. Conteos
Una biyeccin de Na un conjunto A se conoce como un conteo de A.
0.6.8. Cardinalidad
Es una funcin de el conjunto de los conjuntos a N contable innito,
no contable
Figura 13: Clasicacin de conjuntos segn su cardinalidad
0.7. Los Nmeros Enteros Z
Probablemente la humanidad haya hecho uso de los nmeros enteros por
primera vez para llevar la contabilidad de los prstamos de dinero. Los antigu-
os prestamistas probablemente usaron colores diferentes para diferenciar los
nmeros positivos (negro?) de los negativos (rojo?). Se dice que en algunos
casos se usaba como tinta enel pergamino del prestamista la sangre del deudor.
El conjunto de los nmeros enteros se puede denir en la siguiente forma;
inicialmente consideramos el conjunto (x, y) : x 0, 1, y N0 = 0, 1
N 0, en donde tenemos dos copias de los nmeros naturales; una de los
enteros de la forma (0, n) que llamamos positivos, y la otra de enteros no
positivos (1, n); luego, identicamos los elementos (0, 0) y (1, 0), de tal forma
que slo haya un cero entero que, sin embargo, no tendr signo. Formalmente,
denimos el conjunto de los nmeros enteros as:
Z = (0, y) : y N (1, y) : y N
donde = (0, 0), (1, 0). Esta denicin y la notacin que comnmente usamos
para los nmeros enteros se relacionan as:
+n=n= (0, n), n > 0, (nmeros positivos)
n= (1, n), n < 0, (nmeros negativos)
0= .
0.7. LOS NMEROS ENTEROS Z 33
Por convencin, el nmero entero cero no es ni positivo, ni negativo.
Esta convencin la mantendremos para el cero racional y para el cero real.
Similarmente, en el caso de los nmeros complejos resulta contraproducente
denirle ngulo al origen del plano complejo, o cero complejo, y para usar
una sola convencin en todos los casos hemos decidido no denir signo para
el cero en ningn caso.(A diferencia de la convencin adoptada aqu, algunos matemticos
usan la convencin que el cero es negativo y positivo)
Ejercicio. Muestre que Z es contable.
0.7.1. La relacin de orden lineal entre los nmeros enteros
La relacin se menor o igual que entre los nmeros enteros x = (x
1
, x
2
) y
y = (y
1
, y
2
), est dada por el conjunto ((x
1
, x
2
)(y
1
, y
2
)) : x
1
= 1 y
1
= 0 o x
1
=
1 y
1
= 1 y
2
x
2
o x
1
= 0 y
1
= 0 x
2
y
2
Aunque los nmeros enteros se pueden contar, no se pueden contar man-

teniendo este orden lineal. (Por qu?)
Ejercicio. Muestre que aunque los enteros son contables, no se pueden contar
manteniendo el orden lineal denido. Es decir, para cada conteo b : N Z,
para algn natural n, b(n + 1) < b(n) y para algn natural m, b(m+ 1) > b(m).
0.7.2. Intervalos enteros
El intervalo entero /n, m/, sonde n y m son nmeros enteros, es el con-
junto de nmeros enteros mayores o iguales que n y menores o iguales que
m.
Ejemplo. /5, 9/ = 5, 6, 7, 8, 9
Ejemplo. /9, 5/ =
Ejercicio. Muestre que (Z, +, ) es un grupo.
Ejercicio. Es (Z, +, ) un anillo?.
0.7.3. Algoritmo de la divisin
El algoritmo de la divisin dice que, dado un nmero entero a y el
nmero natural positivo N, hay nmeros enteros nicos c (el cociente) y r (el
residuo), con 0 r < N, tales que:
a = cN + r. Escribimos r = a
N
y leemos a mdulo N.
Ejemplo. 5
3
= 2, 1
3
= 2
Ejercicio. Demuestre el algoritmo de la divisin.
[[algoritmo de Euclides]]
0.7.4. Congruencias mdulo N
K.F. Gauss
6
fue tal vez la persona que reconoci por primera vez la utilidad
y la generalidad de este tipo de relacin.
Considere el conjuntoZde los nmeros enteros; seanmynnmeros enteros
y sea N en estero positivo; se dice que los nmeros m y n son congruentes
mdulo N, si su diferencia es un mltiplo entero de N, es decir, si r Z m
n = rN.
Ejercicio. Muestre que la relacin de congruencia mdulos 3 es una relacin de
equivalencia. Cul es la clase de equivalencia [2], del nmero 2, con respecto
a la relacin de equivalencia congruencia mdulo 3?
Ejercicio. Sean m, n, c
1
, c
2
, r
1
, r
2
nmeros enteros tales que: m = 3c
1
+ r
1
, 0
r
1
< 3 y n = 3c
1
+ 2
1
, 0 r
2
< 3. Note que r
1
r
2
< 3 y muestre que: hay
una k entera tal que m n = 3k, si y solo si r
1
= r
2
6
Carl Friedrich Gauss (1777-1855) Matemtico alemn en su tesis doctoral demostr el teorema
fundamental del algebra e hizo grandes contribuciones en astronoma y fsica.
0.8. LOS NMEROS RACIONALES Q 35
Ejercicio. Muestre que los nmeros enteros m y n son congruentes mdulo N
si y slo si los residuos (segn el algoritmo de la divisin) al dividirlos por N
son iguales.
Ejercicio. Muestre que si m es congruente con n, mdulo N, y que si a es
congruente con b, mdulo N, entonces m+ a es congruente con n + b, mod
N
.
Ejercicio. Muestre que si m es congruente con n, mdulo N, y que si a es
congruente con b, mdulo N, entonces ma es congruente con nb, mod
N
.
0.8. Los Nmeros Racionales Q
El trmino razn tiene entre otros sentidos los de proporcin y de expli-
cacin as tambin los trminos griego oo y el latino ratio. La relacin entre
dos nmeros es un concepto al que los pitagricos dieron gran importancia y
lo que inicialmente tena como sentido razn de ser, pas a tener tambin en de
cociente. As, en nmero racional es una relacin entre dos enteros. El trmi-
no racional tiene pues los dos sentidos mencionados anteriormente desde el
nacimiento de la cultura occidental, y no es raro que la implicacin del teorema
de Pitgoras de la existencia de longitudes irracionales, o inconmensurables,
fuera causa de incomodidad.
El conjunto de los nmeros racionales es el tercer conjunto de nmeros
que denimos. Como veremos, tambin es un conjunto contable (lo cual po-
dra sorprendernos inicialmente). Desde ciertos puntos de vista, es similar al
conjunto de los nmeros reales que deniremos en la siguiente seccin; sin
embargo, los racionales con respecto a los reales adolecen de ciertas fallas ge-
omtrica, topolgica, algebraica y analtica. Sin embargo, en su denicin, son
ms intuitivos que los reales.
Ejercicio. Encuentre un conteo del conjunto Z Z
Considere el producto cartesiano Z(N0) del conjunto de los nmeros
enteros y el conjunto de los nmeros naturales con excepcin del cero. Con-
sidere all la relacin determinada por (x, y) (n, m) si y solo si xm = yn.
Ejercicio. Demuestre que la relacin , acabada de denir es efectivamente
una relacin de equivalencia entre los elementos del conjunto Z (N 0).
Con la notacin usual, el elemento (x, y) de Z (N 0) es la fraccin
x
y
. No queremos, sin embargo, denir el conjunto de los nmeros naturales
como Z (N 0) porque tendramos representaciones mltiples para un
mismo nmero racional (por ejemplo (1, 2) (2, 4)). Adoptamos la siguiente
denicin.
[[n + m =
n
i m= n S(n) S(S(n)) . . .
.,.
mveces
]]
Denicin 6. Con base en la relacin de equivalencia dada, el conjunto Q de los
nmeros racionales est dado por las clases de equivalencia resultantes de la relacin
en Z (N 0). En smbolos, Q = [(x, y)] : x Z y (N 0)
As, cada nmero racional es una clase de equivalencia, un subconjunto de
Z (N 0). Las lneas de la gura 14 indican estas clases de equivalencia.
Figura 14: Cada lnea representa un nmero racional
Ejemplo. El conjunto B =
p
q
Z :
p
q
2
< 2 es acotado superiormente pero no
tiene suprmum.
CASO 1. Si (
p
q
)
2
< 2 entonces existe un nmero entero tal que,
(
p
q
)
2
<
_
_
p + (
1
)
q
_
_
2
< 2
entonces x =
p1
q
>
p
q
y x B. Como,
_
_
p + (
1
)
q
_
_
2
=
_
p
q
_
2
+
2p
+
1
2
q
2
y queremos
(p +
1
)
q
2

p
2
q
2
< 2
p
2
q
2
por lo que necesitamos
2p
+
1
2
q
2
< 2
p
2
q
2
de donde
2p
+
1
2
< 2q
2
p
2
2p + 1 < (2q
2
p
2
)
2
la anterior tiene solucinpara unvalor de sucientemente grande, 14+1 <
2
(e.g.
p
q
=
7
5
y
1
=
1
15
)
CASO 2. Si (
p
q
)
2
> 2, decimos que existe un nmero entero tal que,
2 <
_
_
p + (
1
)
q
_
_
2
<
p
2
q
2
entonces x =
p1
q
es el infmum de B. Como,
_
_
p
1
q
_
_
2
=
p
2
q
2

2p
q
2
y queremos
p
2
q
2

_
_
p
1
q
_
_
2
<
p
2
q
2
2
por lo que necesitamos
2p
2
q
2
<
p
2
q
2
2
2p 1 <
2
(p
2
2q
2
)
la anterior tiene solucin para un valor de sucientemente grande, 2841 <
164
2
(e.g.
p
q
=
142
100
y
1
=
1
2
)
0.8.1. Relacin de orden lineal para los nmeros racionales
Decimos que el nmero racional [(x, y)] es menor o igual que el nmero
racional [(m, n)], o que [(x, y)] [(m, n)] si,
1. 0 myx 0
2. x 0, m 0, xn ym
3. x 0, m 0, ym xn
Note que este orden se puede interpretar con base en el dibujo de la gura
a14. Si una lnea q est despus que otra p movindose en sentido horario, el
nmero q es menor que el nmero p. Note que dadas dos lneas p y q, se puede
encontrar un punto de Z (N 0) entre las dos lneas (entre dos racionales
siempre hay otro racional) y por lo tanto, hay otra lnea que contiene el punto
mencionado y que est entre p y q segn el orden denido.
Ejercicio. Dados los nmeros racionales p y q, encuentre un nmero racional r
entre p y q tal que mn(p, q) < r < m ax(p, q).
Ejercicio. Muestre que hay conjuntos de racionales con cota superior pero sin
cota superior mnima.
Ejercicio. Es Z
2
contable? (sugerencia: considere un camino en espiral que
parte del origen)
Ejercicio. Es Z (N 0) contable?
Ejercicio. Es Q contable?
Como se puede mostrar, el conjunto de los nmeros racionales es contable;
sin embargo, no se puede contar manteniendo el orden lineal denido, por
qu? cmo se puede contar?
Ejercicio. Muestre que si c : N Q es una biyeccin, hay racionales p, q con
p q, tales que c(q) c(p).
Ejercicio. Muestre que (Q, +, ) es un cuerpo.
0.8.2. Fallas geomtricas y algebricas de los racionales
Como se descubri en la Grecia antigua, si la geometra Eucldea es vlida,
entonces el conjunto de los nmeros racionales es insuciente como modelo
para longitudes. Considere el triangulo mostrado en la 15 es cierto que los tres
lados son conmensurables? La pregunta la podemos expresar as: si dos de las
longitudes son nmeros racionales, es la tercera racional tambin? Hay una
unidad de longitud d, no importa que tan pequea, que nos permita expresar
las longitudes de los tres lados como mltiplos enteros de esta unidad? La pre-
gunta probablemente se la hicieron los griegos antiguos por primera vez, con
muchas otras, y para su sorpresa encontraron que en muchos casos, por ejem-
plo si el triangulo es rectngulo issceles, los lados no son conmensurables.
El hecho de que todo no sea proporcionable fue fuente de una sensacin
Figura 15: Un tringulo rectngulo: si x = y y l es una unidad de longitud tal que x = nl y y = nl
con m, n Z, para ninguna p Z se tiene que n = pl
de malestar inmensa entre algunos pitagricos quienes trataron de mantener
secreto este hecho.
Por lo tanto, si quisiramos mantener la hiptesis de la conmensurabilidad
tendramos que negar la existencia de ciertos tringulos rectngulos, en par-
ticular de tringulos rectngulos issceles. Esta es una falla geomtrica de los
racionales.
Ejemplo. Un falla algebraica es que x
2
= 2 no tiene solucin en los racionales.
Ejercicio. Demuestre que no existe ningn nmero racional q tal que qq = 2.
Tenemos entonces que no hay ningn nmero racional q tal que qq = 2.
sta es una falla algebraica de los racionales: no son cerrados con respecto a la
toma de races cuadradas (otra falla algebraica que heredan de los reales es la
no solucin de q
2
= 1).
0.8.3. Fallas topolgicas de los racionales
A continuacin mostramos que los racionales presentan tambin una falla
topolgica. Esta consiste en la existencia de colecciones contables de intervalos
de racionales, cerrados y encajonados, cuya interseccin es nula: decimos que
Q tiene huecos.
Un intervalo cerrado de racionales [a, b] est dado por el conjunto de los
nmeros racionales menores o iguales que el racional b y mayores o iguales
que el racional a. El intervalo de racionales [a, b] es no vaco si y slo si a b.
Considere el intervalo (de racionales) I
0
= [a
0
, b
0
] = [0, 1]; el conjunto de los
racionales es contable y por lo tanto tambin lo es el intervalo de racionales
[0, 1]. Sea r
n
un conteo de los racionales entre 0 y 1. Luego encontramos el
subintervalo [a
0
, b
1
] de I
0
, donde b
1
es la r
m
con mnima m tal que a
0
< r
m
< b
1
.
Luego encontramos el intervalo [a
1
, b
1
] donde a
1
es la r
m
con mnima m tal
que a
0
< r
m
< b
0
. Continuamos de la misma manera: a partir del intervalo
[a
n
, b
n
] encontramos el intervalo [a
n
, b
n+1
] con b
n+1
= r
m
con m mnima tal que
a
n
< r
m
< b
n
(entre dos racionales siempre hay otro racional)luego, [a
n+1
, b
n+1
]
donde a
n+1
= r
m
, m mnima tal que a
0
< r
m
< b
1
. As denimos una coleccin
contable I
k
: k N, decreciente I
k+1
I
k
, de intervalos de racionales no
vacos. La coleccin resultante tiene interseccin vaca, ya que si existiera una
q
_
k NI
k
, q = r
l
para alguna l N, pero por construccin r
l
I
l
y tenemos
una contradiccin.
Decimos entonces que el conjunto de los nmeros racionales tiene huecos
(es decir, hay subconjuntos acotados de Q que no tienen suprmum racional).
Note cmo la existencia de huecos es consecuencia de la contabilidad de Q.
Ms adelante veremos que los racionales tienen otra falla, esta vez analti-
ca: hay sucesiones de racionales que tienden a agruparse cada vez ms (estas
sucesiones se conocen como sucesiones de Cauchy) y sin embargo no conver-
gen. Es interesante que estas fallas, excepto una de las algebricas, quedan
resueltas en los reales, que Dedekind
7
deni usando ciertas particiones de
Q y Cauchy
8
deni usando ciertas clases de equivalencia de sucesiones de
racionales.
7
Willian Dedekind (1831-1916) Matemtico Alemn alumno de Gauss, es reconocido por desar-
rollar la idea de que los nmeros racionales y los irracionales forman un continuo: los nmero
reales. Cada nmero irracional divide el conjunto de los nmeros racionales de manera particular.
8
Auguste Louis Cauchy (1789-1857) Matemtica francs es reconocido por sutrabajo enel anlisis
y en teora de permutacin de grupos. Trabaj en convergencia y divergencia de series innitas,
ecuaciones diferenciales y fsica matemtica, entre otros.
Ejemplo. A = k Q : k = 1
1
n
, n Q es un conjunto acotado con suprmum.
0.8.4. Cortes de Dedekind
Habiendo denido los conjuntos de los nmeros naturales, los nmeros
enteros y los nmeros racionales, Cmo denir los nmeros reales? Cmo
darles carta de ciudadana a estos huecos de los racionales? Desde la poca de
Pitgoras, de alguna forma se usan, sin haber sido denidos, estos nmeros
que llamamos reales debido a que inicialmente a los nmero complejos se les
llam imaginarios porque no se les poda visualizar, y as el nombre result
por oposicin.
A mediados del siglo XIX se sinti una necesidad de rigor, por ejemplo al
hablar de lmite; hubo un renacimiento de la importancia de la lgica en las
matemticas, yse empezaxiomatizandoel conjuntode los nmeros naturales.
A partir de los Axiomas de Peano, de las ideas de Frege y Russell
9
y de la
teora de conjuntos, se dieron deniciones para los diferentes tipos de nmero.
Riemann
10
y Weierstrass
11
dieron deniciones de integral y de lmite. Quizs
la denicin ms difcil de dar fue la de los nmeros reales. As a nales del
siglo XIX la pregunta era muy pertinente pero la respuesta no era nada obvia.
Richard Dedekind, un matemtico alemn amigo de Riemann, dio la primera
denicin axiomtica de los nmero reales. El concepto bsico de su idea es
un corte.
Un corte de Dedekind es una particin Q = k l m del conjunto de los
nmeros racionales donde k y m no son vacos y l es un conjunto unitario o
vaco, tal que, para cada k k, l l, m m, se tiene que k < m y, si l no es vaco,
9
Bertrand Russell (1872-1970) Matemtico y lsofo ingls se le conoce como el fundador de la
lgica moderna.
10
Georg Riemann (1826-1866) Matemtico alemn conocido por sus desarrollos en geometra no
eucldea, teora analtica de nmeros y por sentar las bases para la topologa moderna.
11
Karl Weierstrass (1815-1897) Matemtico alemn tutor de Cantor y Engel entre otros. Aunque
no public ningn artculo, s escribi 3.
0.9. LOS NMEROS REALES R
1
43
k < l < m; adems, ni k tiene mximo (racional) ni m tiene mnimo (racional).
Un corte de Dedekind es una forma de partir el conjunto de los racionales (osea
expresar como una particin).
Ejemplo. q Q : q
2
< 2 q < 0 q Q : q
2
> 2 q > 0 es un corte de
Dedekind. Este corte se usa para denir el nmero real raz de dos, en la seccin
siguiente.
Ejemplo. q Q : q < 33q Q : q > 3. Tambin es un corte de Dedekind.
(Este corte se usa para denir el nmero real 3, en la seccin siguiente)
Algunos matemticos abrevian y dicen que un corte de Dedekind es slo
la componente k del corte formalmente denido anteriormente. La razn es
que la componente k determina unvocamente el corte y as es una cmoda
forma de abreviar. Adems el nfasis al hablar de corte pasa, de ser una forma
de partir los racionales, a ser un conjunto de racionales.
0.9. Los Nmeros Reales R
1
Podemos decir que tanto R como Q son modelos de longitudes bastante
aceptables. La relacin entre estos modelos y la realidad est dada por la in-
tuicin. Los racionales son un modelo que no nos permite tener tringulos
rectngulos issceles. Los reales, por otra parte, predicen longitudes y dura-
ciones que no podemos medir en el laboratorio. El modelar magnitudes fsicas
con los nmeros reales no cuadra entonces dentro del positivismo lgico, de-
fendido por Mach.
Tanto los ingenieros como los fsicos dicen que usan el conjunto de los
nmeros reales, o una intervalo de stos como modelo para ciertas magni-
tudes tales como el tiempo, el voltaje, la temperatura, etc. En realidad se trata
de un modelo intuitivo que slo en parte usa las propiedades matemticas
de los nmeros reales. Comnmente, tal modelo no es exactamente lo que
los matemticos entienden por nmeros reales; por ejemplo, tiene sentido
diferenciar una coordenada de tiempo, o un valor de voltaje, racional de uno
irracional? Es claro que ningn instrumento tiene tal precisin; adems, es
posible que no tenga sentido hablar de intervalos de tiempo, o de longitudes
arbitrariamente pequeos (ni arbitrariamente grandes). As, actualmente hay
una situacin de compromiso: la fsica usa un modelo que no tiene base exper-
imental, porque no hay nada mejor.
El teorema de Pitgoras nos permite argumentar que los nmeros racionales
no son sucientes para modelas longitudes, si es que los tringulos rectn-
gulos issceles van a existir. La fsica cuntica ha mostrado que los nmeros
reales probablemente tampoco sonadecuados (quizs los conjuntos difusos?).
Comnmente, ni el ingeniero ni el fsico se preocupan por tales considera-
ciones; ellos trabajan con un modelo, en parte intuitivo y en parte axiomtico,
de la lnea de los nmeros reales.
Veamos a continuacin el modelo axiomtico de los nmeros reales, que ya
esbozamos en la seccin anterior, desarrollado por R. Dedekind y G. Cantor.
Denicin 7. Cada corte de Dedekind kl mse denomina un nmero real. R
1
es
el conjunto de los nmeros reales. R
1
hereda a Q: para cada elemento r de Q, tenemos
el corte: q Q : q < r r q Q : q > r y el nmero real correspondiente
q Q : q < r. Los cortes para los que la componente l del corte es vaca, determinan
un nmero real que no tiene correspondiente racional. Por ejemplo, el nmero real raz
de dos corresponde al corte q Q : q
2
< 2 q < 0 q Q : q
2
> 2 q > 0
y est dado por el conjunto de racionales q Q : q 0, q
2
< 2
As un nmero real es un subconjunto propio (quizs subconjunto propi-
amente dicho sea una mejor traduccin de proper set) y no vaco de racionales,
con las propiedades de no tener mximo y de que, para cada elemento q del
subconjunto, cada racional menor que q tambin es elemento.
1
45
Teorema de Arqumedes
Si q Q, q > 0. Entonces n N, n > 0 : 0
1
n
< q
Demostracin:
q =
k
l
n = l
El teorema de Arqumedes:
x R : x > 0, n N: n > 0 0 <
1
n
< x
Ejercicio. Demuestre el teorema de Arqumedes.
Proposicin
Entre 2 reales s y r hay un racional q:
Por teorema de Arqumedes:
1
n
< s r(s > r) r <
1
n
+ r < s : q =
1
n
+ r =
rn + 1
n
0.9.1. Aproximacin de reales con racionales
0.9.2. Aproximacin de u con racionales
0.9.3. Relacin de orden lineal
La relacin ser subconjunto de sobre los reales as denidos como sub-
conjunto de racionales provee una relacin de orden lineal para los nmeros
reales.
Ejercicio. Muestre que la relacin ser subconjunto de, es un orden lineal para
R
Por ejemplo, note que q Q : q 0, , q
2
< 2 es subconjunto de q
Q : q < 3, correspondientemente decimos que el nmero real raz de dos es
menor o igual que el nmero real tres. Si se tiene un conjunto de nmeros
reales, la unin de los conjuntos racionales correspondientes es tambin un
nmero real, y corresponde al mximo; la interseccin al mnimo.
Ejercicio. Sea A un conjunto de nmeros reales. Muestre que su unin es un
nmero real, o Q. Similarmente muestre que su interseccin es o un nmero
real o vaca.
Podemos tambin denir un conjunto de reales extendido agregando al
conjunto de reales los subconjuntos Q y . Nuevamente tenemos un conjunto
linealmente ordenado por la relacin ser subconjunto de. En este contexto,
llamamos a Q innito y a menos innito; los denotamos y +, respecti-
vamente. Recuerde que ni +(osea Q) ni (osea vaco) son nmeros reales,
son nmeros reales extendidos. El conjunto de los nmeros reales junto con
las operaciones de suma y resta (R, +, ) es un cuerpo (ver seccin 0.5).
Ejercicio. Muestre que si Aes un conjunto de reales con cota superior, entonces
la unin de los cortes correspondientes es un nmero real, y es el suprmum
de A.
Ejercicio. Cmo dene la suma y el producto de reales, considerados como
subconjuntos de racionales? Asuma que ya se denieron la suma y la resta de
racionales.
Ejercicio. Es R
1
contable? Sugerencia: muestre primero que los reales no
tienen huecos y recuerde que la existencia de huecos en los racionales se
mostr basndonos en que son contables.
Ejercicio. Muestre que cada sucesin de intervalos cerrados encajonados de
reales tiene interseccin no vaca. (De hecho, que hay uno y slo un punto en
tal interseccin.)
1
47
0.9.4. Congruencia entre nmeros reales
El concepto de congruencias mdulo N se puede generalizar as: sean x, y, z
nmeros reales. Decimos que x y y son congruentes mdulo z, si su diferencia
es un mltiplo entero de z, osea: r Z xy = rz. La relacin de congruencia
normalmente se abrevia as: x y m od z. Es fcil mostrar que si x y m od z
y a b m od z entonces x +a y +b m od z; sin embargo, no siempre se tiene
que xa yb m od z.
Ejercicio. D un ejemplo donde x y m od z, a b m od z, y sin embargo,
xa yb m od z.
Ejercicio. Muestre que para cada real > 0 hay enteros my n tales que
m
n
<
.
Para terminar esta seccin, podramos decir que con los nmeros natu-
rales contamos, con los enteros llevamos contabilidades y con los racionales
medimos magnitudes fsicas que asumimos que se pueden subdividir en un
nmero arbitrariamente grande de partes iguales. El uso de nmeros reales es
antetodo terico ya que ninguna medida tiene precisin denitiva. Sin embar-
go, su utilidad es grande ya que al modelar magnitudes como nmeros reales
podemos usar tcnicas del clculo para maximizar, obtener transformadas, etc.
Una de las enseanzas del positivismo es que no es conveniente ser positivista
a ultranza: ni Kronecker acept el innito de los naturales ni Mach acept los
tomos; pero sin el innito y sin los tomos, la ciencia y la tcnica estaran
innecesariamente limitadas hoy en da.
Los reales por su parte tienen fallas algebricas: hay ecuaciones de la forma
p(x) = 0, con puna funcin polinmica que no tienen soluciones en R. Esta falla
la resuelven los complejos.
Denotemos con [xj el mximo entero menor o igual que x. As, x [xj es
la parte decimal de x.
0.9.5. El conjunto de Cantor
El conjunto de Cantor es de importancia en topologa y en sistemas dinmi-
cos; tambin en teora de la medida ya que es un conjunto no contable que
mide cero. Lo denimos a continuacin. Considere la representacin en base
3 de los nmeros reales en el intervalo cerrado [0, 1]. Cada nmero all est
representado por (al menos) una sucesin t
0
, t
1
, t
2
, donde cada t
i
0, 1, 2.
La idea es que cada nmero lo escribimos como 0.t
0
t
1
t
2
y que el nmero es
i=0
t
i
3
i
. El por qu todo nmero real tiene tal representacin lo explicamos ms
adelante. Dena ahora una sucesin de subconjuntos del intervalo [0, 1]. Sea
A
0
= [0, 1], sea A
1
el conjunto de los nmeros tales que t
0
1, A
2
el conjunto
de los nmeros tales que t
0
1 y t
1
1, etc. A
i
es el conjunto de los nmeros
con t
0
1, . . . , t
i1
1. Ahora dena C :=
_
iR
N
A
i
. Tenemos que:
i) C no es vaco: cualquier nmero en [0, 1] que en su expansin ternaria
no tenga unos est en el conjunto.
ii) De hecho, C es no contable ya que el conjunto de las sucesiones binarias
que representan nmeros diferentes es no contable.
iii) C mide cero ya que A
1
mide 1
1
3
, A
2
mide 1
1
3
2
9
, A
3
mide 1
1
3
2
9
4
27
y en el lmite, C mide 1
n=1
2
n1
3
n
= 0.
Ejercicio. Demuestre ii).
Ejercicio. Diga si el conjunto de cantor es contable. Demuestre.
Todo nmero real entre [0, 1] tiene una representacin ternaria.
0.9.6. Subconjuntos densos en ninguna parte
Decimos que un subconjunto de R es denso en ninguna parte si hay una
coleccin de intervalos disyuntos cada uno conteniendo exactamente uno de
0.10. LA CIRCUNFERENCIA S
1
= T
1
49
los puntos del conjunto.
Ejercicio. Muestre que un conjunto denso en ninguna parte es contable.
0.10. La circunferencia S
1
= T
1
En esta seccin denimos la esfera unidimensional S
1
, que para dimen-
sin 1 coincide con el toro unidimensional T
1
y con la lnea proyectiva RP
1
.
Considere las clases de equivalencia de R
1
que resultan cuando se con-
sidera la relacin congruencia mdulo 2. Dado un nmero real x, su clase de
equivalencia [x] est dada por el conjunto de los nmeros reales de la forma
x + 2n, donde n es un nmero entero. Note que la clase de equivalencia [x]
de cada nmero real x es contable. Vea la gura 16.
Figura 16: Los puntos indicados hacen parte de la clase de equivalencia de x
Las clases de equivalencia determinan una particin de R
1
. Adems, casa
clase de equivalencia [x] tiene un representante nico en el intervalo [0, 2) es
decir que [x] [0, 2) contiene exactamente (ni ms ni menos) un elemento.
As, a cada nmero real x le hacemos corresponder el nmero x := [x]
[0, 2), al que llamamos x mdulo-2. Es claro que [x] = [x]. Las clases de
equivalencia son los elementos de S
1
. S
1
= [x] : x R
1
.
Topologa de S
1
. El intervalo abierto con centro en [x] y radio , 0 < <
de S
1
es el subconjunto de S
1
[y] : [[ x y [< ] donde [x[ se muestra en la
gura 17.
Ahora denimos la suma en S
1
por medio de la frmula [x] + [y] = [x + y].
Ejercicio. Calcule [
3
2
] + [
5
4
].
Figura 17: [x[
Ejercicio. Diga si (S
1
, +) es un grupo. Diga si es un anillo.
Sobre el conjunto S
1
= [x] : e R
1
denimos ahora una relacin ternaria,
que demostraremos que es circular.
0.10.1. Circularidad de S
1
Considere la relacin ternaria T de puntos en S
1
denida a continuacin.
Sean[x], [y], [z] elementos de S
1
. Decimos que ([x], [y], [z]), ([y], [z], [x]), ([z], [x], [y])
T si y slo si:
i. x < y < z, o
ii. z < x < y, o
iii. y < z < x
en donde < es la relacin ser menor que entre nmeros reales.
Ejercicio. Muestre que la relacin denida es circular.
1
= T
1
51
Figura 18: El intervalo de S
1
de radio con centro en [x], corresponde a una coleccin innita
de intervalos de la lnea de los nmeros reales
Ejercicio. Muestre que para cada x, y, z R,
(mn(x, y, z), med(x, y, z), m ax(x, y, z)). (Donde med quiere de-
cir mediana) y sus permutaciones pares estn en T.
Una diferencia fundamental entre R
1
y S
1
es que, en S
1
, recorriendo el
conjunto hacia un lado, o el otro, regresamos al mismo punto. Es decir, dado
A, A + x = A x tiene solucin para x 0 en S
1
, pero no es R
1
.
Ejercicio. Demuestre que, para x, y [0, 2), mnx y, (mnx, y + 2
m axx, y) = [ x y ]
siempre que x y
Modelar la nocin de circularidad con una relacin es lo que podramos
llamar matematizar el concepto de circularidad. Matematizar es lo que hizo
Newton es sus estudios de la mecnica. Un investigador a veces encuentra
conveniente matematizar sus conceptos. El uso de las matemticas a su vez
requiere del rigor en las demostraciones.
0.10.2. Deniciones Bsicas y Notacin
Los tintes se denotan como nmeros complejos de magnitud 1; en particu-
lar, rojo = 1 + j0; anaranjado = (1 + j)/
2; amarillo = 0+ j; citrino= (1+j)/
2;
verde = -1 + j; cian = (1j)/
2; azul = 0 - j; violeta = (1j)/
2.
Es conveniente cuanticar las diferencias entre tintes; esto puede ser lleva-
do a cabo con una mtrica para el conjunto de nmeros complejos de magnitud
1. Adicionalmente a la mtrica d1(z
1
, z
2
) = z
1
z
2
resultante de la inmersin de
la circunferenca unitaria en el plano complejo, tambin se tienen las mtricas:
d2(z
1
, z
2
) = 1 cos(arg(z
1
) arg(z
2
)) = Re[z
1
z
1
2
]
d3(z
1
, z
2
) = T(arg(z
1
) arg(z
2
))
donde T es la funcin carpa peridica de periodo 2 dada por T(x)=x para
x [, ].
Una de las cuatro relaciones posibles opuesto, previo, posterior y simulta-
neo entre dos tientes z
1
y z
2
(posiblemente igual) resulta como sigue:
el tinte z
2
es opuesto a z
1
s z
2
= z
1
el tinte z
2
es simultaneo al tinte z
1
s z
2
= z
1
el tinte z
2
es previo(onegativo conrespecto) al tinte z
1
s sen((arg(z
1
)arg(z
2
)) =
Im[z
1
z
1
2
] < 0
el tinte z
2
es posterior (o positivo con respecto) al tinte z
1
s sen((arg(z
1
)
arg(z
2
)) = Im[z
1
z
1
2
] > 0
0.10.3. El promedio Circular
Direccin media o promedio circular
Sea z = [z
1
. . . z
N
] una coleccin de (posiblemente repetidos) Ndatos circulares;
asumiendo su suma diferente de 0 +0j, su direccin principal se dice que est
dada por:
1
= T
1
53
z =
N
1
z
i
N
1
z
i
0.10.4. Promedio y mediana en S

1
La media (o promedio) angular de una muestra de N datos
1
,
2
. . .
phi
N
viene dada por el argumento de la suma compleja de sus representaciones
complejas. Es decir la media es arg(Z), donde la suma compleja Z es
Z =
N
i=1
ej
i
Claramente la media no se encuetra denida para muestras cuya suma com-
pleja sea cero, tales como las muestras equiespaciadas.
Para una muestra de angular se aplica el proceso de reduccin de forma
reiterativa hasta llegar a una muestra irreducible. Si la muestra resultante es
trivialmente equiespaciada, diremos que es la mediana angular de la muestra.
En caso contrario, diremos que la muestra no tiene mediana.
0.10.5. La lnea proyectiva P
1
Considere la relacin de equivalencia entre los elementos de S
1
dada por:
x y si y slo si la distancia (como se deni para puntos en S
1
) entre x e y es
. As, cada clase de equivalencia contiene exactamente 2 puntos. Al conjunto
de estas clases de equivalencia lo denominamos P
1
. Tambin denimos una
distancia entre puntos en P
1
.
d
p
([x], [y]) = mnd
s
(a, b) : a x, b y =
_
_
[a b]
/2
, si a b /2,
2
, de lo contrario
Para n = 1, S
n
= P
n
, topolgicamente. Para dimensiones mayores, el espacio
proyectivo no es homeomorfo a la esfera.
0.10.6. La esfera de dimensin n (S
n
)
En R
n+1
, tenemos S
n
= n R
n+1
: x = 1.
0.10.7. El toro de dimensin n (T
n
)
Denimos T
n
=
n
k=1
S
1
, (producto cartesiano). Note que S
2
S
1
S
1
.
0.10.8. El espacio proyectivo de dimensin n (RP
n
)
Denimos RP
n
como el conjunto de las lneas que pasan por el origen
en R
n+1
; equivalentemente, RP
n
es la esfera de dimensin n S
n
, donde se
han identicado los puntos antpodas, es decir, el espacio topolgico cociente
correspondiente.
0.11. Los nmeros complejos C
Una vez que se detectaron fallas algebricas en los reales, result la con-
veniencia de inventar un nuevo tipo de nmero. La frmula para la solucin
cuadrtica era conocida en el ao 2000 A.C. Desde los griegos hasta el siglo
XVI, la solucin de estas ecuaciones fue considerada como la solucin de un
problema geomtrico; as, la ecuacin x
2
x 1 = 0 era la interseccin de la
parbola y = x
2
y la recta y = x + 1. Cuando la recta y la parbola no se inter-
secan, se deca que la solucin de la ecuacin era imaginaria (porque no se
poda visualizar). A los reales se les llam as, en oposicin. Ms tarde, el nom-
bre imaginario tom un sentido ms particular y a estos nmeros imaginarios
se les llama ahora nmeros complejos.
0.11. LOS NMEROS COMPLEJOS C 55
Basndose en resultados de del Ferro
12
y Tartaglia
13
, Cardano
14
public
en 1545 su Ars Margna, donde consider races de nmeros negativos por
primera vez en una publicacin, considerando las soluciones respectivas co-
mo intiles por carecer de interpretacin geomtrica. El Ars Margna tambin
inclua una solucin de la ecuacin cbica x
3
= 3px + 2q correspondiente
a la interseccin de una recta con la curva cbica y = x
3
. La solucin es
3
_
q +
_
q
2
+ p
3
+
3
_
q
_
q
2
+ p
3
.
Unos 30 aos despus, Bombelli
15
not que si la recta es tal que p
3
> q
2
resulta la raz de un nmero negativo an en casos en los que hay una solucin
geomtrica al problema. Por ejemplo, la recta y = 15x+4, que interseca la cbica
en x = 4, tiene este problema. Bombelli tuvo la (gran) idea de suponer que para
la ecuacin x
3
= 15x+4,
3
2 + 11i es de la forma 2+ni y

3
2 11i es de la forma
2 ni. Deniendo la multiplicacin y la adicin de nmeros complejos (como
la conocemos hoy en da) encontr que las cosas an cuadraban bien en la
frmula de Cardano.
Como los nmeros irracionales, los nmeros complejos encontraron un rec-
hazo inicial. An en 1702, Leibnitz consideraba estos nmeros como anbios
entre la existencia y la no existencia.En 1770 haba an una falta de claridad
tal que el mismo Euler dijo errneamente que

3
2 =
6.
Wessel, Argand y Gauss fueron las primeras personas en considerar los
12
Scipione del Ferro (1465-1526) Matemtico italiano su aporte a las matemticas en grande.
Aunque su nombre no es muy reconocido su trabajo en la resolucin de ecuaciones cuadrticas se
trata en muchos textos matemticos posteriores.
13
Niccol Fontana Tartaglia (1499-1557) Matemtico italiano plante la solucin de diversas
ecuaciones cbicas hasta establecer la solucin general de estas. Solucin que luego fue publicada
por Cardano como produccin propia.
14
Jrme Cardan Cardano (1501-1576) Matemtico italiano reconocido por la publicacin de
su Ars Magna, adems de otros libros sobre juegos y azar donde sienta una aproximacin a la
probabilidad.
15
Raaele Bombelli (1530-1572) Matemtico italiano. Entre sus publicaciones encontramos con-
tribuciones a la teora de nmeros y acercamientos a la geometra analtica.
Figura 19: La solucin grca de las races reales de una cbica
nmeros complejos como puntos del plano R
2
. Con la identidad de Euler,
los nmeros complejos se pueden ver como puntos de otro espacio tambin
(cilindro abierto ms punto).
Los aportes al anlisis complejo de Cauchy y Riemann, permitieron que
el tema de los nmeros complejos creciera durante los aos 1814 a 1815 en
una forma mucho mayor. El anlisis complejo ha dado aportes valiosos al
anlisis real, por ejemplo en la teora de funciones analticas, mostrando una
vez ms la utilidad de considerar casos ms generales para resolver problemas
en dominios particulares.
Los nmeros complejos son ahora de uso comn en la ingeniera elec-
trnica. En particular, son de uso comn la identidad de Euler, el teorema
de residuos de Cauchy y las funciones de Mbius
16
. El uso de los nmeros
complejos en ingeniera es debido entre otras cosas al concepto de impedancia,
el cual fue introducido por Charles P. Steinmetz
17
, un ingeniero que emigr de
16
August Ferdinand Mbius (1790-1886) Matemtico y astrnomo alemn, en su obra el baricn-
trico (1827) hace una introduccin a coordenadas proyectivas homogneas y correspondencias
poryectivas.
17
Charles Proteus Steinmetz (1865-1923) Matemtico e ingeniero elctrico nortamericano, es cono-
Alemania a Estados Unidos. El concepto de impedancia usado en el anlisis y
sntesis de circuitos, est relacionado con los de resistencia por una parte y con
los de la transformada de Laplace, la transformada de Fourier y la convolucin,
por la otra.
Paralos griegos, la geometra yaritmticaestabanntimamente relacionadas.
Aunque histricamente los nmeros complejos empezaron a ser aceptados al
considerar ecuaciones polinmicas de tercer orden, hoy en da es ms comn
denirlos axiomticamente. As, los modelos ms comunes para el conjunto
de los nmeros complejos estn basados en los siguientes conjuntos:
i) R
1
R
1
: para coordenadas rectangulares (plano)
ii) (0, ) S
1
: para coordenadas polares (cilindro compacticado por
un lado)
La representacin del nmero en coordenadas rectangulares es (0, 0). el
nmero entero cero se deni sin signo; similarmente, resulta inconveniente,
porque implica contradicciones, denirle coordenada polar (de fase o ngu-
lo) al nmero complejo , con coordenadas rectangulares (0, 0).
Para pasar del modelo del plano al modelo del cilindro, es conveniente un
paso intermedio pasando por un cono. Imagine que el plano complejo C es el
plano x y del espacio R
3
. Luego suponga que colocamos un cono con vrtice
en el origen del plano y con eje el eje z, como se muestra en la gura 22. Luego,
suponga que proyectamos hacia arriba, sobre el cono, los puntos del plano.
Si nos olvidamos del resto de R
3
y nos concentramos en el cono solamente,
resulta la imagen de C mostrada en la gura 23 en donde ya podemos indicar
las coordenadas polares y
Finalmente, imagine que quitamos el vrtice del cono y lo colocamos a un
lado y que hacemos que el resultante cono sin vrtice se deforme (como si
cido por su trabajo en el desarrollo de la corriente alterna; algunas de sus mayores contribuciones
son en el rea de hystresis, lo que permiti el avance del diseo de motores elctrico.
Figura 20: El modelo de coordenadas rectangulares: el producto R
1
R
1
Figura 21: El modelo de coordenadas polares:(0, ) S
1

Figura 22: El modelo geomtrico cono para las coordenadas polares
Figura 23: El modelo geomtrico cono para las coordenadas polares
fuera elstico) hasta convertirse en el cilindro de la gura 21, ensanchando el
cono para r pequea y angostando el mismo para r grande.
0.11.1. Nomenclatura
En coordenadas rectangulares, la primera componente de un nmero com-
plejo se denomina su parte real y la segunda su parte imaginaria. Las funciones
Re e Im estn denidas as:
Re(x, y) = x (parte real)
Im(x, y) = y (parte imaginaria)
Resulta conveniente denotar los nmeros con coordenadas rectangulares
(0, 0), (1, 0) y (0, 1) abreviadamente, as: := (0, 0), 1 := (1, 0) y j := (0, 1).
Por lo tanto, en coordenadas rectangulares, (a, b) = a(1, 0) +b(0, 1) = a1 +bj,
que escribimos simplemente como a + jb.
En coordenadas polares, la primera componente de un nmero complejo
se conoce como su magnitud mientras que la segunda se conoce como su fase:
(r, )
= r (magnitud)
(r, ) = (fase).
Como dijimos, al origen del plano no le denimos fase.
0.11.2. Equivalencias de ngulos
Sean , R
1
ngulos; se dice que y son ngulos equivalentes si son
congruentes mdulo 2, as, S
1
es el espacio natural para modelar ngulos.
Ejercicio. 2 6? 0 ? /2 3/2?
Aunque es cierto que y implica que + + , hay que
ser cuidadoso cuando se considera la posible congruencia de productos de
ngulos: y no implica que . Por ejemplo, 0 2 y
1/2 1/2 pero 0 .
Ejercicio.
_
e
j2
_
1/2
= e
j
?
0.11.3. Estructura algebraica
Lo que diferencia al conjunto de los nmeros complejos del plano de coor-
denadas rectangulares y del cilindro de coordenadas polares, es la estructura
algebraica dada por las operaciones (producto) y + (suma) se denen
como sigue:
+ (suma): (x, y) +(a, b) = (x +a, y +b) y es una funcin asociativa, conmu-
tativa, con mdulo aditivo y con inversos aditivos.
(producto): (x, y) (a, b) = (xa yb, xb + ya) y es una funcin asociativa,
conmutativa, con mdulo multiplicativo y con inversos. Con las deniciones
anteriores C tiene estructura de cuerpo.
Ejercicio. Muestre que las operaciones denidas son asociativas y conmutati-
vas.
Sea z = (x, y), si (x, y) + (a, b) = , entonces (a, b) = (x, y), por lo tanto el
inverso aditivo de z est dado por z = (x, y).
Cada nmero complejo z, con excepcin de , tiene un inverso multiplicativo
que denotamos z
1
. Para obtener una frmula en coordenadas cartesianas para
z
1
, procedemos como sigue.
Si (x, y) (a, b) = (1, 0) entonces, resolviendo para a y b encontramos los sigu-
ientes valores, siempre y cuando (x, y) , Completar
(x, y)
1
=: (a, b) =
_
x
x
2
+ y
2
,
y
x
2
+ y
2
_
Ejercicio. Deduzca la frmula del inverso multiplicativo.
0.11.4. Equivalencia entre las representaciones rectangular y
polar de un nmero complejo
Cada punto (x, y) de R
1
R
1
corresponde a un punto de (0, ) S
1

y viceversa. Si se tiene la representacin en coordenadas polares (r, ) de un
nmero complejo, sus partes real e imaginaria est dadas por: x = r cos y
y = r sen.
Figura 24: Equivalencia geomtrica de las representaciones polar y rectangular de los nmeros
complejos
Inversamente la magnitud r y la fase se obtienen a partir de las partes
real e imaginaria as: r =
_
x
2
+ y
2
=
_
_
arctan(y/x), si x > 0,
2
, si x = 0, y > 0
2
, si x = 0, y < 0
arctan(y/x) + , si x < 0
Note la adicin del trmino cuando la parte real es negativa, debida a
que la frmula arctan(y/x) sola es insuciente: le asigna el mismo valor a cada
nmero (x, y) que est sobre una lnea que pase por el origen. Vea por ejemplo
la gura 25, donde (aunque la fase de z es diferente de la de z), la frmula
= arctan(y/x) les asignara el mismo valor. Note tambin que si x = y = 0,
no se dene fase. Note tambin que re
j
= re
j+
(la exponencial compleja la
denimos ms adelante).
Figura 25: La fase de z es igual a la fase de z ms (o menos)
Dado que la funcin tangente no es inyectiva, la funcin arctan no se dene
siempre en la misma forma, aunque su imagen es siempre en intervalo abierto
de longitud . Tpicamente, por ejemplo en las calculadoras, se asume que el
rango es (/2, /2). (Vea la gura 26).
Suponga que z C; si Im(z) = 0, se dice que el nmero z es real, en este
caso, si a , su fase es 0 o , dependiendo del signo: 0 si la parte real es
positiva y si la parte real es negativa.
Si Re(z) = 0 e Im(z) 0, se dice que z es imaginaria y su fase es /2 o
/2 (Dependiendo de qu?).
Ejercicio. Muestre que zw = z w. (Lamagnitudde unproductoes el producto
de las magnitudes)
Ejercicio. Muestre que (zw) = z + w. (La fase de un producto es la suma de
las fases)
Ejercicio. Muestre que z + w z w. (La magnitud es subaditiva)
Ejercicio. Muestre que z w z w (Vea la gura 27)
Ejercicio. Sea g : R
1
C dada por g(t) = cos t. Graque la magnitud y la fase
de g(t) para t [0, 2).
Ejercicio. Sea h : R
1
C dada por h(t) = j sent. Graque la magnitud y la fase
de h(t) para t [0, 2).
Figura 26: Una forma de denir la funcin arctan: con rango (/2, /2)
Ejercicio. Muestre que:
e
j
1+e
j
=
1
2
+ j
1
2
sen()
1+cos()
. Tambin, graque la magnitud,
la fase, la parte real y la parte imaginaria contra , para [0, 2).
Figura 27: Ilustracin de la frmula z w z w
0.11.5. Interpretacin geomtrica del producto complejo
Suponga que w es un nmero complejo dado, y dena f : C C dada por,
f (z) = zw. Note que, geomtricamente, a cada punto z, f le hace corresponder
un punto a distancia z w del origen y ngulo con respecto al eje real z +w.
En particular, como f (1) = w podemos mostrar que los tringulos 1 z
y w zw, indicados en la gura 28 son semejantes: si multiplicamos los
vrtices zw y w de uno de los tringulos por e
jw
, obtenemos los vrtices del
tringulo similar a , 1, z; Dibjelo usted mismo!
0.11.6. Inverso multiplicativo en coordenadas polares
En coordenadas polares, el inverso multiplicativo de a = (r, ) est dado
por: (r, )
1
= (r
1
, ); recuerde que 2 .
Ejercicio. Cmo se denen las operaciones de suma y producto en coorde-
nadas polares?
Figura 28: Representacin geomtrica del producto complejo
Figura 29: Representacin geomtrica del inverso multiplicativo, el inverso aditivo y el conju-
gado
0.11.7. Complejo conjugado
Sea z = x + jy un nmero complejo. Su complejo conjugado se denota z
y est dado por: z
= x jy.
Ejercicio. Sea z = 2 + 3j; graque z, z
1
y z
en coordenadas rectangulares.
Ejercicio. Muestre que z
2
= Re[zz
].
2
=
z
2
.
= z, z
= z.
Ejercicio. Muestre que, si z 0, z
1
=
z
z
2
.
Ejercicio. Muestre que (z + w)
= z
+ w
.
Ejercicio. Muestre que (zw)
= z
.
Ejercicio. Muestre que Re(z) =
1
2
(z + z
).
Ejercicio. Muestre que Im(z) =
1
2
j(z z
)
Ejercicio. Usando la frmula tan(+) =
tan()+tan()
1tan() tan()
, muestre que zw = zw.
Ejercicio. Representando cada nmero complejo z con la matriz,
_
_
Re[z] Im[z]
Im[z] Re[z]
_
_
muestre que las operaciones de suma y producto de complejos coinciden con
las correspondientes de matrices.
Figura 30: La proyeccin estereogrca de x S
1
(/2] es p(x) R
1
0.11.8. La proyeccin estereogrca
Existe una funcin interesante p de S
1
/2 a R
1
, conocida como la
proyeccin estereogrca, y que puede generalizarse a esferas de dimensiones
mayores. En este contexto, S
1
es la compacticacin de un punto de R
1
.
Ejercicio. Encuentre una frmula para p(x) en trminos de x. (x es el ngulo
con respecto al radio horizontal de la circunferencia.)
Proyeccin estereogrca, plano complejo extendido
En muchos casos resulta til considerar el plano complejo extendido C
. Este se obtiene adicionando un punto abstracto, el punto , al plano
complejo. Al punto , como al origen , no se le dene fase; su magnitud
se asume mayor que la magnitud de cualquier nmero complejo. Sus partes
real e imaginaria no se especican. (Topolgicamente, el espacio localmente
compacto R
2
, mediante su compacticacin de un punto es la esfera S
2
)
El plano complejo extendido es topolgicamente equivalente a la supercie
2
de la esfera bidimensional. La proyeccin estereogrca es un homeomor-
smo (es decir un a equivalencia topolgica: una biyeccin bicontinua) de S
2
al plano complejo extendido. Esta proyeccin le asigna el polo sur de la esfera
al origen del plano, el polo norte a , puntos diferentes del polo norte a la
interseccin de un lnea que pasa por el polo norte y el punto en cuestin, con
el plano, cuando ste se imagina como tangente a la esfera en el polo sur.
As es posible decir por ejemplo, que una funcin tenga un polo en innito
y que las funciones de Mbius son biyecciones del plano complejo extendido
a s mismo.
Una utilidad de visualizar as el plano junto con el innito, es que el innito
es ms intuitivo u no algo que no se puede ver porque est muy lejos.
Figura 31: La proyeccin estereogrca
Para efectos algebraicos, se asume que:
z + =
si z , z = z =
=
z/ = , si z
z/ = , si z
0.11.9. Funciones lineales
Las funciones lineales f : C C, dependiendo de si se considera como
conjunto de escalares (el cuerpo de los escalares) a R o a C, son de la forma
f (z) = wz, con z C constante, en el segundo caso, y de la forma f (z) = az, con
a R constante, en el primero. Note que si f es lineal con cuerpo C, tambin
es lineal con cuerpo R, pero no viceversa. Por ejemplo, f (z) = z
es lineal con
campo R pero no con cuerpo C.
0.11.10. Excepciones a la frmula (z
a
)
b
= z
ab
Sea z = 1 = e
j
, Cunto vale (z
2
)
1/2
? La respuesta, que podramos llamar
La raz cuadrada de 1, es 1
1/2
= 1 y tenemos una expresin con valor nico. Sin
embargo, qu hay incorrecto al escribir (z
2
)
1/2
= z
1
= 1? Lo que no se est
teniendo en cuenta es lo siguiente: (e
j2
)
1/2
= e
j
; el producto (1/2)(2) est
dado por (1/2) 0 = 0 = 2 y no por . Cuando se usan complejos y se tienen
exponentes fraccionarios, hay que ser cuidadoso al usar la frmula (z
2
)
1/2
!
Por otra parte, el conjunto de nmeros que elevados al cuadrado son 1, lo
podramos llamar el conjunto de las races cuadradas de 1. As, las races de 1
son 1 y -1 pero la raz de 1 es 1. Las races cbicas de 1 son 1, e
j2/3
y e
j2/3
.
Ejercicio. Diga si la funcin f : C C, dada por f (z) = z
2
es inyectiva o
sobreyectiva. tambin, dibuje las imgenes con respecto a f de los ejes real e
imaginario, de las lineas Re[z] = Im[z], Re[z] = Im[z], de las lineas Re[z] = 1,
Re[z] = 1, Im[z] = 1, Im[z] = 1 y de las curvas z = 1, z = 0,5, z = 2.
Ejercicio. Diga si la funcin f : C C, dada por f (z) = e
z
es inyectiva o
sobreyectiva. tambin, dibuje las imgenes con respecto a f de los ejes real e
imaginario, de las lineas Re[z] = Im[z], Re[z] = Im[z], de las lineas Re[z] = 1,
Re[z] = 1, Im[z] = 1, Im[z] = 1 y de las curvas z = 1, z = 0,5, z = 2.
Ejercicio. Diga si la funcin f : C C, dada por f (z) = e
z
tiene inversa
0.11.11. Transformaciones de Mbius
Suponga que , , , son nmeros complejos tales que 0 y
considere m :

, donde

= C , dada por m(z) =
z+
z+
, m() =
[QUEVAACA] y m
_
/
_
= .
La funcin de Mbius f (z) = 1/z, que pertenece a esta familia , tiene
una interpretacin geomtrica en trminos de la proyeccin estereogrca,
que explicamos a continuacin. Primero, usando la proyeccin estereogrca,
proyectamos los puntos de

en S
2
; tomando el radio de la esfera como 1/2. A
continuacin, rotamos la esfera S
2
media vuelta de tal forma que el polo sur y
el polo norte intercambien posiciones, manteniendo la circunferencia imagen
del eje imaginario invariante; nalmente volvemos a proyectar sobre el plano
: m = p
1
r p :

S
2
S
2

.
Veamos primero que, como el radio es 0.5, el procedimiento indicado deja
invariante (pasando por el ecuador de la esfera) la circunferencia de radio 1
con centro en el origen.
Figura 32: Transformaciones de Mbius 1 (COMO LE PONEMOS A ESTA GRFICA)
Veamos tambin que las partes positivas y negativa del eje real permanecen
invariantes, y que las partes positiva y negativa del eje imaginario se intercam-
bian. Finalmente, veamos que, con el procedimiento indicado, la magnitud de
cada punto resulta invertida.
Si mostramos que los ngulos y son iguales, el resultado buscado se
sigue, ya que entonces los tringulos 0NB y CNA son similares por tener 2
ngulos iguales, entonces
N0
0B
=
NC
CA
, entonces
1
0B
=
NC
1
osea 0B =
1
0A
.
Para mostrar que = , note que los arcos de circunferencia subtendidos
por y son iguales ya que los tringulos FDGy FEGson iguales, por lo tanto,
= . Ahora, ms general, note que
z+
z+
= +

z+
, donde =

y = .
Ejercicio. Diga qu rotacin r : S
2
S
2
es necesaria, para implementar la
funcin de Mbius f (z) =
1z
1+z
en la forma ya indicada.
Figura 33: Transformaciones de Mbius 2 (COMO LE PONEMOS A ESTA GRFICA)
Ejercicio. Encuentre una funcin de Mbius que no se pueda implementar en
la forma indicada.
Ejercicio. Muestre que la suma de dos funciones de Mbius es una funcin de
Mbius.
Ejercicio. Muestre que la composicin de dos funciones de Mbius es una
funcin de Mbius.
Ejercicio. Muestre que cada transformacin de Mbius transforma rectas y
circunferencias de C en rectas o circunferencias de C. Muestre que cada trans-
formacin de Mbius transforma circunferencias de

en circunferencias de
.
Ejercicio. Encuentre la imagen de los ejes de C y de los semiplanos de parte
real positiva y negativa, con respecto a la transformacin f (z) =
1z
1+z
.
Ejercicio. Encuentre la imagen de la circunferencia de radio 1 con centro en
de C y el crculo de radio 1 con centro en , con respecto a la transformacin
f (z) =
1z
1+z
.
0.12. Los cuaternios (H)
Los cuaternios fueron inventados por W. R. Hamilton hacia 1860, despus
de haber tratado en vano durante aos de denir un producto con inversos en
R
3
. en R
2
tenemos el producto correspondiente al producto de complejos,
en coordenadas rectangulares. No es posible sin embargo, dotar al grupo
(R
3
, +) con estructura de anillo de divisin, sin divisores de cero; es decir,
no hay producto tal como al que estamos acostumbrados para R
3
. en R
4
s es
posible aunque el producto resultante no es conmutativo. Estos resultados se
los debemos a Hamilton.
Hoy sabemos que, de los R
n
, solo en R
1
, R
2
, R
3
y R
4
es posible denir
un producto que, junto con la suma por coordenadas en R
n
(osea, la ley del
paralelogramo), resulte en un anillo de divisin, sin divisores de cero. Por
ejemplo, el producto vectorial que se ve en el curso de clculo vectorial (del
cual tendremos algo que decir ms adelante en esta seccin) tiene divisores
de cero. La terminologa de producto vectorial y producto escalar se originaron
igualmente con Hamilton.
Los cuaternios tienen varias aplicaciones en ingeniera. recientemente se
ha explorado el uso de una transformada de Fourier denida con base en
los cuaternios, en vez de en los complejos. Los cuaternios permiten el uso de
frmulas cortas para expresar transformaciones de perspectiva y de proyec-
ciones; en grcas y en robtica, se usan para codicar rotaciones en el espacio.
Tambin, el uso de cuaternios para el tratamiento de imgenes a color es un
tema de actualidad. En geometra, son especialmente tiles para trabajar con
estructuras basadas en la esfera tridimensional S
3
.
0.12.1. Denicin
Si x es un punto en R
4
= R
1
R
3
(como explicamos abajo, resulta conve-
niente pensar que las ltimas 3 componentes de un cuaternio son las coorde-
0.12. LOS CUATERNIOS (H) 73
nadas de un punto en R
3
), con coordenadas cartesianas (a, b, c, d), poniendo
1 = (1, 0, 0, 0), i = (0, 1, 0, 0), j = (0, 0, 1, 0) y k = (0, 0, 0, 1), tenemos el cuaternio
x = a1 + bi + cj + dk, abreviadamente x = (a + ib + jc + kd).
0.12.2. Suma y producto
La operacin suma se dene en forma estndar, con la ley del paralelo-
gramos, como (a1+bi +cj +dk) +(1+i +j +k) = (a+)1+(b+)i +(c+)j +
(d + )k, mientras que el producto queda determinado por la ley distributiva
y los productos elementales:
11 = 1
ii = jj = kk = 1
jj = ji = i
ki = ik = j
jk = kj = k
Figura 34: Orden para productos elementales positivos
Note que el producto resultante no es conmutativo. El resultado del pro-
ducto se puede recordar con la ayuda de la gura 34; el producto de i, j, o k
con s misma, es -1. El producto de elemento i, j, o k con otro diferente, es la
que no se usa, con signo positivo cuando seguimos el orden indicado en la
gura 34, negativo en caso contrario. As,
(x
0
1 + x
1
i + x
2
j + x
3
k)(y
0
1 + y
1
i + y
2
j + y
3
k) =
((x
0
y
0
x
1
y
1
x
2
y
2
x
3
y
3
)1 + (x
0
y
1
+ x
1
y
0
+ x
2
y
3
x
3
y
2
)i+
(x
0
y
2
+ x
2
y
0
x
1
y
3
+ x
3
y
1
)j + (x
0
y
3
+ x
3
y
0
+ x
1
y
2
x
2
y
1
)k)
Ejercicio. Mostrar que los cuaternios son un anillo. (Anillo de enteros?)
0.12.3. Partes escalar y vectorial
con x = [x
0
, x
1
, x
2
, x
3
], como punto de R
4
, o x = x
0
+ x
1
i + x
2
j + x
3
k, como
cuaternio, tenemos:
Parte escalar: S(x) = S(x
0
+x
1
i+x
2
j+x
3
k) = x
0
1 = [x
0
, 0, 0, 0] que comnmente
se confunde intencionalmente con el nmero real x
0
.
Parte vectorial: V(x) = V(x
0
+x
1
i +x
2
j +x
3
k) = x
1
i +x
2
j +x
3
k = [0, x
1
, x
2
, x
3
]
que comnmente se confunde intencionalmente con el punto [0, x
1
, x
2
, x
3
] de
R
3
.
As, escribimos la frmula del producto de cuaternionico como: xy = x
0
y
0
V(x) V(y) + x
0
V(y) + y
0
V(x) + V(x) V(y) donde los productos y son los
productos escalar y vectorial de R
3
, respectivamente. Vemos que el producto
cuaternionico no es conmutativo. Esta nomenclatura de producto escalar
y producto vectorial, tal como la conocemos hoy, se origin con Hamilton.
Vale la pena memorizar esta frmula.
Si S(x) = 0, decimos que x es un cuaternio puro. As, un cuaternio puro q
es de la forma [0, x
1
, x
2
, x
3
], cumple q = V(q) y como acabamos de decir, comn-
mente lo identicamos con el punto [0, x
1
, x
2
, x
3
] de R
3
. Si V(x) = [0, 0, 0], deci-
mos que x es un escalar puro. As, un escalar puro es de la forma [x
0
, 0, 0, 0]
y como dijimos, comnmente lo identicamos con el punto x
0
de R
1
.
Llamaremos a los cuaternios puros vectores y los denotaremos con letras
con diresis. Llamaremos a los escalares puros escalares y los denotaremos con
variables con subndice 0. Osea, a = a
0
+ a.
0.12.4. Conjugado, magnitud e inverso
Denimos el conjugado del cuaternio x = (x
0
1 + x
1
i + x
2
j + x
3
k) como
x
= x
0
1 (x
1
i + x
2
j + x
3
k).
Entonces, xx
= x
2
0
+x
2
1
+x
2
2
+x
2
3
es unescalar de la magnitud del cuaternio:
x
2
:= xx
(que tambin se conoce como la norma regular N(x) de x)

Ejercicio. Muestre que si x = [0, 0, 0, 0], su inverso multiplicativo est dado
por: x
1
= x
2
x
.
Ejercicio. Muestre que (xy)
= y
.
Ejercicio. Muestre que (xy)
1
= y
1
x
1
.
Ejercicio. Muestre que q + q
= 2q
0
.
Ejercicio. Encuentre
1
1+i+j+k
.
Ejercicio. Diga por qu, el producto en R
3
dado por [x, y, z][a, b, c] = [yc
zb, xc az, xb ay] junto con la operacin normal suma, no permite tener un
anillo de divisin sin divisores de cero.
Un cuaternio es unitario si su magnitud vale 1. Por lo tanto, el anillo de los
cuaternios unitarios es la esfera tridimensional S
3
(el conjunto de los puntos
de R
4
a distancia unitaria del origen). En forma anloga a como los nmeros
complejos de magnitud 1 viven en la esfera unidimensional, los cuaternios de
magnitud 1 viven en la esfera tridimensional.
Si u es un cuaternio puro, u
2
= [0, u
1
, u
2
, u
3
][0, u
1
, u
2
, u
3
] = [u
1
u
2
2

u
2
3
, 0, 0, 0] osea, su cuadrado es un escalar (de valor la norma). En general, el
producto de dos cuaternios puros est dado por u e = u e u e. El cuadrado
de un cuaternio unitario puro es -1. Esto nos permite escribir, usando las series
de Taylor de seno y coseno e
ut
= cos t + usent, siempre que u sea un cuaternio
unitario puro.
Los cuaternios puros unitarios viven en una esfera bidimensional, en forma
anloga a como los nmeros imaginarios puros (j) viven en una esfera de
dimensin 0 (un conjunto de puntos).
Ejercicio. Muestre que un cuaternio puro tiene como cuadrado el escalar -1.
Ejercicio. Muestre que el inverso de un cuaternio unitario es unitario.
Ejercicio. Muestre que el producto de dos cuaternios unitarios es unitario.
Sea q un cuaternio unitario. Sea u =
1
V(q)
V(q) el vector unitario en la
direccin de V(q). As, q = q
0
+
V(q)
u. Note que tanto
q
0
como
V(q)
son
menores o iguales a 1 ya que q
2
0
V(q)
2
= 1. De hecho, como dijimos, podemos
escribir q = cos + usen, donde es la fase del nmero complejo con parte
real q
0
y parte imaginaria
V(q)
. Por lo tanto [0, ] (ya que el nmero

complejo en cuestin tiene parte imaginaria no negativa).
0.12.5. Nomenclatura para rotaciones en R
3
Suponga que q es un cuaternio unitario (por lo tanto q
1
= q
), y e un
cuaternio puro (de hecho, el punto de R
3
que queremos rotar). Entonces, q eq
es tambin un cuaternio puro ya que:
q eq =
_
cos + usen
_
e
_
cos usen
_
=
_
sen( u e) + cos e + sen( u e)
_ _
cos usen
_
= sencos ( u e) + cos ( u e) sen + V(q eq
)
= 0 + V(q eq
)
Por otra parte,
q eq
= e ya que
q eq
q eq
1
q
1
= e.Osea que
q eq
est a la misma distancia del origenque e. Adems, comose puede vericar,

para cada q unitaria, la funcin L
q
: R
3
R
3
dada por L
q
( e) = q eq
es lineal.
Por lo tanto, L es representable como producto por una matriz L( e) = eM, con
la propiedad que ( eM) ( eM)
T
= e e
T
, por lo tanto, e
_
MM
T
_
e
T
= e e
T
por lo tanto
MM
T
es la matriz identidad, por lo tanto M es una matriz ortogonal especial;
as, decimos que L
q
es una rotacin o una reexin, dependiendo de si el
determinante de M es 1 o -1. Mostraremos que el determinante es 1 y que por
lo tanto se trata de un rotacin. Sea : S
3
R
3
R
3
; dada por (q, e) = L
q
( e);
as, es una funcin continua de dos variables. Por lo tanto, det M depende
continuamente de q y, como para q = 1, det M = det I = 1, y como det M slo
puede tomar valores 1 y -1, concluimos que det M = 1.
Ejercicio. Muestre que L
q
es lineal.
Ejercicio. Encuentre las las de M en trminos de q y concluya que el determi-
nante vale 1.
Alternativamente, considere el caso especial en que q = cos +i sen. con
e = e
1
i + e
2
j + e
3
k,
L
q
( e) = q
_
e
1
i + e
2
j + e
3
k
_
q
= qq
ie
1
+ qjq
e
2
+ qkq
e
3
= ie
1
+ q
2
je
2
+ q
2
e
3
= ie
1
+ (cos 2 i sen2)(e
2
+ e
3
i) j
y tenemos que el eje x (el subespacio generado por i) permanece invariante
mientras que el plano yz (el subespacio generado por j, k) se rota en un
ngulo de valor 2. (Lo cual es interesante ya que entonces [0, ], como en
el caso de la recta proyectiva).
en el caso general, q = cos + e sen, descomponemos a e en una compo-
nente normal a u, y otra paralela. Usando e = e
[
+e
, donde con = e u, e
[
=
u
u
(la componente paralela a u), y e
= e
u
u
(la componente perpendicular a u),
queda:
q eq
= (cos + usen)(e
[
+ e
)(cos usen)
= e
[
cos
2
+ e
cos
2
e
[
ucos sen e
ucos sen
+ ue
[
sencos + ue
sencos ue
[
usen
2
ue
usen
2
= e
[
cos
2
+e
[
sen
2
+ 0 + (e
cos
2
e
sen
2
+ 2e
usencos )
= e
[
+ (e
cos
2
+ 2e
usencos )
donde vemos que el sumando paralelo permanece invariante mientras que el
sumando ortogonal re rota un ngulo 2.
0.12.6. H como una estructura de anillo para C C
Nota: En esta seccin, la unidad imaginaria se denota con i.
En esta seccin usamos la convencin que los cuaternios son pares orde-
nados de nmeros complejos. Considere las siguientes operaciones de suma y
producto denidas para pares de nmeros complejos:
a + b = (a, ) + (b, ) = (a + b, + )
ab =(a, )(b, ) = (ab
, + b)
donde el asterisco indica nmero complejo conjugado. Note que el par (1,0)=(1
+ 0i, 0 + i) se comporta como mdulo para este producto. Denotamos en
forma abreviada los pares de la forma (a, 0) como a; a C. Note que (0, ) =
(, 0)(0, 1) = (0, 1).
Denotamos de forma abreviada el par (0, 1) con j. Note que j
2
= 1 y que
ja = a
j, a C.
El conjugado a del cuaternio a = a + j esta dado por:
a = a
j
Note que con a = a + j, a a = aa = aa
0
Como se puede vercar, cada cuaternio a = a +j diferente de 0 +0j, tiene
0.13. SUCESIONES 79
un inverso multiplicativo a
1
dado por:
a
1
=
a
j
aa
de lo que se concluye que se tiene un anillo de divisin.

Propiedades
i. Un cuaternio a = a +j conmuta con cada cuaternio si y solo si es real, es
decir, a Re y = 0
ii. ab = a
b
Resulta a un espacio vectorial de dimensin 4, con base 1, i, j, i j. El espacio
se forma con la norma eucldea dada por:
a = (a a)
1/2
En el espacio se dene el porducto interno dado por:
< a, b >=
1
2
((a + b)( a +

b) a a b
b)
=
1
2
(a
b b a)
La norma satisface xy = xy. La base 1, i, j, i j es ortonormal. El orde-
namiento da una orientacin para H.
0.13. Sucesiones
Una sucesin unilateral de elementos de A es una funcin con dominio
el conjunto de los naturales, s : N A.
Una sucesin bilateral de elementos de A es una funcin con dominio
el conjunto de los enteros, r : Z A.
Si A es el conjunto de los nmeros reales, se dice que la sucesin es real; si
A es el conjunto de los nmeros complejos, se dice que la sucesin es compleja,
etc. La notacin comnmente usada es r = r
n
, la cual tiene el inconveniente
de ser muy similar a la usada para denotar conjuntos. Las sucesiones bilat-
erales complejas son el modelo del tipo de seal que denominaremos seal
discreta de longitud infinita.
Ejemplo. s : N R, s = s
n
donde s(n) = s
n
= 2n + 3; ms explcitamente,
pero incompletamente, podramos escribir tambin, s = 3, 5, 7, 9, donde
es importante recordar que se est representando una sucesin (sequence)
y no un conjunto.
Figura 35: s es una sucesin unilateral
Ejemplo. r = r
n
, donde r(n) = r
n
= n; r = 0, , 2, 3, .
Ejemplo. a = a
n
, donde a(n) = a
n
= (1)
n
; a = 0, , 0, , , A continuacin
se muestra una grca de a:
Ejercicio. Considere el conjunto S = 0, 1
N
de las sucesiones unilaterales bina-
rias. Es decir, S = ss : N 0, 1. D ejemplos de elementos de S. Es nito?
Es S contable?
0.13. SUCESIONES 81
Figura 36: La sucesin a
Ejercicio. Diga qu es la diagonal de Cantor.
Ejercicio. Graque la magnitud y la fase de a
n
= j cos(n) como funciones de
la variable n.
Como explicaremos en la seccin siguiente, el conjunto de las sucesiones
bilaterales complejas se denota C
Z
0.13.1. Subsucesiones
Sea s : N N una sucesin unilateral de nmeros naturales creciente, es
decir, s
i
< s
j
siempre que i < j. Si r : N A es una sucesin, decimos que
t : N A, con t
i
:= r
s
i
es una subsucesin de r.
_
n=0
_
k=n
A
k
_
n=0
_
k=n
A
k
0.14. Espacios mtricos, convergencia
y espacios completos
Un espacio mtrico (X, d) consiste en un conjunto X y una funcin d :
X X [0, ), que se conoce como mtrica, tal que:
i. x
inX, d(x, x) = 0
ii. x, y X, si d(x, y) = 0, entonces x = y (denitivamente positiva)
iii. x, y X, d(x, y) = d(y, x), (simetra)
iv. x, y, z X, d(x, y) + d(y, z) d(x, z) (desigualdad del tringulo)
En un espacio mtrico, la bola con centro c X y radio r (0, ) est dada
por el conjunto x X : d(x, c) < r, que denotamos B
c
(r).
Ejercicio. Muestre que la funcin d : R
2
R
2
[0, ), dada por d(x, y) =
_
(x + y)
2
+ (x y)
2
para cada x, y R
2
, con x = (x
1
, x
2
), y = (y
1
, y
2
), determina
una mtrica para R
2
. Esta mtrica se conoce como la mtrica eucldea para R
2
.
Ejercicio. Para la mtrica del ejemplo anterior, dibuje la bola con centro en el
origen y con radio l.
Ejercicio. En R
2
, para cada x, y R
2
, con x = (x
1
, x
2
), y = (y
1
, y
2
), considere la
mtrica dada por d(x, y) = x
1
y
1
+ x
2
y
2
. Esta mtrica se conoce como la
mtrica del taxista.
Ejercicio. En R
2
, para cada x, y R
2
, con x = (x
1
, x
2
), y = (y
1
, y
2
), considere la
mtrica dada por d(x, y) = m axx
1
y
1
, x
2
y
2
. Esta mtrica se conoce como
la mtrica del producto.
0.14. ESPACIOS MTRICOS 83
0.14.1. Bolas
En un espacio mtrico, denimos la bola de centro y y radio r B
r
(x)
como el subconjunto dado por xd(y, x) < r.
Ejercicio. Para las mtricas eucldea, del producto y del taxista, dibuje las bolas
con centro el origen y radio 1.
0.14.2. Mtrica para S
1
Denimos una mtrica para s
1
con base en la funcin T(x) mostrada en la
gura 37. La idea es que dos puntos en la circunferencia parten esta en 2 arcos
y que la distancia entre los puntos es la longitud del arco ms corto. As, si x, y
son ngulos en [0, 2], su distancia est dada por d(x, y) := T(x y).
Figura 37: Funcin para denir una mtrica en S
1
Damos a continuacin una denicin equivalente de distancia entre puntos
sobre la circunferencia. dados puntos [x], [y] en la circunferencia, denimos su
distancia como sigue:
d
s
([x], [y]) = mnx y, mnx, y + 2 m axx, y
=
_
_
x y]
, si x y ,
, de lo contrario
as, estamos tomando la longitud mnima de los recorridos entre x y y.
0.14.3. Espacios normados
Un espacio normado (X, ) consiste en un espacio vectorial X con vector
cero , y una funcin : X [0, ), que se conoce como la norma, tal que:
i. x X, x 0 (es no negativa)
ii. x X, six = 0, entonces x = (denitivamente positiva)
iii. x, y, z X, x y + y z x z (desigualdad del tringulo)
0.14.4. Espacio topolgicos
Un espacio topolgico (X, 1) consiste de un conjunto X, y una familia
1 de subconjuntos de X, que denominaremos subconjuntos abiertos de X, tal
que:
i. , X 1(tanto el espacio completo como el conjunto vaco sonconjuntos
abiertos)
ii. Las uniones de elementos de 1 estn en 1 (Las uniones arbitrarias de
conjuntos abiertos son conjuntos abiertos).
iii. Las intersecciones nitas de elementos de 1 estn en 1 (Las intersec-
ciones nitas de conjuntos abiertos son abiertas).
Un subconjunto de un espacio topolgico se dice cerrado si su comple-
mento es abierto.
Estas deniciones son debidas esencialmente a Hausdor.
Un elemento p del espacio es un punto de acumulacin (limit point) de
un subconjunto A si cada conjunto abierto que contiene a p, contiene al menos
un elemento de A diferente de p.
Ejercicio. Muestre que un subconjunto es cerrado si y slo si contiene sus
puntos de acumulacin.
Equivalentemente, dado un subconjunto A de un espacio mtrico X, dec-
imos que el punto x X es un punto de acumulacin de A, si cada bola que
contenga a x, contiene un punto de A diferente de x.
A partir de una norma se puede denir una mtrica d(x, y) = xy pero no
viceversa: se necesita un espacio vectorial y la propiedad de la homogeneidad
positiva. Similarmente, con una mtrica se puede denir una topologa, pero
no viceversa: la desigualdad del tringulo no es una propiedad topolgica.
0.14.5. Lmite de una sucesin de nmeros
Sea s : N X una sucesin unilateral con valores en un espacio mtrico X.
Se dice que l es el lmite de s
n
si, para cada bola que contenga a l, para cada
n a partir de cierta N, s
n
est en la bola. Si la imagen s(N) es nita, claramente
la sucesin converge.
Equivalentemente, en un espacio normado, l es el lmite de la sucesin si,
para cada nmero real , hay un nmero natural N tal que, para cada n mayor
que N, s
n
l < . Esto se denota s
n
l. En tal caso, se dice que la sucesin
convergente.
Ejercicio. Muestre que ninguna sucesin puede converger a dos lmites.
Cauchy supo de la idea de Dedekind para denir los nmeros reales pero
de alguna manera, no le satisfaca. Cauchy dio otra denicin de los reales,
basada en sucesiones de racionales en vez de subconjuntos de racionales. La
desventaja es que un nmero real, con la denicin de Cauchy, es una clase de
equivalencia de sucesiones (algo ms complejo que un corte de Dedekind). La
ventaja es que la idea se generaliza y se aplica a espacios mtricos en general.
0.14.6. Convergencia en sentido de Cauchy
Se dice que una sucesin s
n
en un espacio mtrico es una sucesin de
Cauchy si d(s
n
, s
m
)tiende a cero cuando n y m tienden a innito. Es decir, si
para cada positiva hay un nmero natural N tal que, siempre que n y m sean
mayores que N, d(s
n
, s
m
) < Esto lo denotamos como d(s
n
, s
m
) 0. Si una
sucesin es convergente, claramente es una sucesin de Cauchy: esto se sigue
de la desigualdad del tringulo: d(s
n
, s
m
) d(s
n
, l) + d(l, s
m
).
Ejercicio. Diga si R
2
es un espacio mtrico completo. Diga si (0,1) lo es. Diga si
es necesario aclarar qu mtrica se usa en cada caso.
0.14.7. Sucesiones y subsucesiones de nmeros reales
Sea a
n
una sucesin real.
Lema 1. Si a
n
es no decreciente y acotada superiormente, entonces converge.
Demostracin 1. Como la imagen de a tiene cota superior, tiene cota superior
mnima, digamos . Con > 0, no es cota superior, entonces para alguna N,
< a
n
, y se cumple la denicin de convergencia de una sucesin.
Lema 2. Toda sucesin contiene una subsucesin que es o no creciente o no decreciente.
Demostracin 2. Denimos inicialmente lo que es un pico y un valle: a
k
es un
pico de una sucesin a
n
si, para cada n > k se tiene a
n
< a
k
. Similarmente, a
k
es un
valle de la sucesin a
n
si para cada a > k se tiene a
n
> a
k
. hay dos posibilidades, o
la sucesin tiene innitos picos, o no. en el primer caso, los picos dan una subsucesin
no creciente. En el segundo caso, o hay innitos valles, o no. Si no, la sucesin es
eventualmente constante y esto nos da una subsucesin montona; si s, los valles
determinan una subsucesin no decreciente.
Corolario 1. (Bolzano-Wierstrass) Toda sucesin acotada tiene una subsucesin con-
vergente.
Teorema 1. Una sucesin (real o compleja) converge si y slo si es una sucesin de
Cauchy.
Como resultado del ejercicio anterior, tenemos que R es completo.
Ejercicio. Diga si la sucesin a
n
converge, cuando a
n
est dada por:
a. a
n
= (1)
n
b. a
n
= (0,9)
n
c. a
n
= ( j)
n
d. a
n
= (
2
n
)
e. a
n
= (
n
n+1
)
f. a
n
= sen(
1
n+1
)
g. a
n
= (n)
n
h. a
n
= sen
1
n
PRUEBA M de Weierstrass.
Sea f
n
una sucesin de funciones denidas en A, y sea m
n
una sucesin de
nmeros tales que x A, f
n
(x) m
n
. Suponga que
n=1
m
n
converge. Entonces
x A
n=1
f
n
(x) converge en valor absoluto y

f
n
(x) converge uniformemente
a
n=1
f
n
(x).
Teorema 2. Si a
n
es no decreciente y est acotada superiormente, entonces a
n
converge.
Demostracin. Sea la cota superior mnima. Dado > 0, no es cota
superior, entonces hayuna a
n
tal que < a
n
. Comoa
n
es nodecreciente,
de algn N en adelante, las a
n
son < a
n
.
Lema 3. Cualquier sucesin a
n
contiene una subsucesin que es o bien no decreciente
o bien no creciente.
Demostracin. Denimos un punto cumbre a el nmero n tal que a
m
< a
n
m <
n. Un punto valle se dene de manera anloga.
CASO 1. La sucesin tiene innitos puntos cumbre. Entonces estos conforman
una sucesin no creciente.
CASO 2. La sucesin tiene un nmero nito de puntos cumbre. Encuentre el
ltimo de los puntos cumbre, el siguiente punto no es punto cumbre, tome ste.
Como no es cumbre, hay puntos a nivel o ms abajo, tome uno de estos puntos
y repita el procedimiento. Lo anterior resulta en una sucesin no creciente.
Para la sucesin no decreciente usamos los puntos valle.
Corolario 2. Toda sucesin acotada tiene una subsucesin convergente.
Teorema 3. Una sucesin a
n
converge si y slo si es un sucesin de Cauchy.
Demostracin. n, m > N a
n
a
m
< n > N a
n
a
N
<
0.14.8. Espacios completos y completados
Se dice que un espacio mtrico es completo si cada sucesin de Cauchy es
una sucesin convergente.
Ejercicio. Muestre que tanto el conjunto de los nmeros reales como el de los
nmeros complejos, son completos, con respecto a la mtrica d(x, y) = x y.
Ejercicio. Muestre que el conjunto de los nmeros racionales no es completo,
con respecto a la mtrica d(x, y) = x y.
Ejercicio. D un ejemplo de un espacio mtrico no completo.
ahora proseguimos con la idea de Cauchy para denir los nmeros reales.
suponga que inicialmente tenemos solamente los nmeros racionales (y los
enteros y los naturales). Note que Q es un espacio mtrico con la mtrica
racional : Q Q dada por d(p, q) = p q. Se puede tener una sucesin
de Cauchy s
n
de racionales, (es decir (s
n
, s
m
) 0) pero que no converja a
ningn racional, indicando que los racionales son completos.
Ejercicio. D un ejemplo de una sucesin de Cauchy de racionales que no
converja (a ningn racional).
La idea de Cauchy tiene la ventaja, sobre la de Dedekind, que general-
iza a espacios mtricos en general. Cauchy deni cierta relacin de equiv-
alencia en cierto conjunto de sucesiones de racionales. Considere el conjun-
to de las sucesiones racionales de Cauchy. Dos sucesiones tales s
n
, t
n
se
dicen equivalentes si (s
n
, t
m
) 0. Veamos que efectivamente se tiene una
relacin de equivalencia. Es reexiva ya que si s es una sucesin de Cauchy,
(s
n
, s
m
) 0. La relacin es simtrica ya que (s
n
, t
m
) = (t
n
, s
m
). Finalmente, si
(s
n
, t
m
) y (t
i
, r
j
) tienden a cero, por la desigualdad del tringulo de la mtrica,
(s
n
, r
m
) (s
n
, t
m
) + (t
n
, r
m
) tambin tiende a cero y tenemos que la relacin
es transitiva.
Ahora denimos los nmeros reales como las clases de equivalencia resul-
tantes. Para denir una mtrica en el conjunto resultante de los reales, den-
imos antes la operacin de suma de reales. Si y son dos nmeros reales,
denimos + como: [t
n
+ s
n
] = [t
n
+ s
n
], donde t
n
y s
n
. Note
que esta denicin tiene sentido ya que el resultado es el mismo si tomamos
otros representantes T
n
y S
n
, es decir, si tanto s
n
y S
n
como t
n
y T
n
,
estn en las mismas clases de equivalencia, respectivamente, entonces T
n
+S
n
y t
n
+s
n
estn en la misma clase de equivalencia. Deniendo como [t
n
],
podemos denir la mtrica d(, ) = .
Enel conjuntoresultante Rtenemos elementos representantes de los nmeros
racionales: las clases de equivalencia de sucesiones convergentes (a nmeros
racionales). Tambin, hay elementos de Rque no son representantes de ningn
nmero racional, que son las clases de equivalencia de sucesiones de Cauchy
no convergentes.
Finalmente debemos mostrar que el espacio mtrico as denido es com-
pleto. Es decir, que sus sucesiones de Cauchy convergen. Si
k
= [t
k
n
] es una
sucesin de Cauchy de nmeros reales, la clase de equivalencia de la sucesin
racional diagonal (t
i
i
) es el lmite de
k
(por qu?).
Podemos decir que la incompletitud de Q es una falla analtica de los
racionales.
Ejemplo. Considere la sucesin q
n
=
x
n
y
n
de racionales resultantes de la
ecuacinde recurrencia,
_
_
x
n+1
y
n+1
_
_
=
_
_
x
n
+ 2y
n
x
n
+ y
n
_
_
con,
_
_
x
0
y
0
_
_
=
_
_
7
5
_
_
los primeros valores
son 7/5 = 1,4, 17/12 = 1,416 . . . , 41/29 = 1,413 . . . , . . . .
Ejercicio. Encuentre una expresin para los componentes de la matriz en el
ejemplo anterior.
Ejercicio. Muestre que la sucesin q
n
del ejemplo anterior es de Cauchy.
muestre que q
2
n
converge a 2 y que q
n
converge a raz de 2.
Ejercicio. Muestre que los reales de Dedekind y los de Cauchy son equiva-
lentes.
Ejercicio. Diga si Q es completo.
Ejercicio. Diga si el intervalo de reales (0, 1) es completo.
a) Con respecto a la mtrica d(x, y)0x y
Con respecto a la mtrica (x, y) = atan(x) atan(y)
0.15. SERIES 91
0.15. Series
Denicin 8. El trmino serie (series en ingls) quiere decir aqu el lmite de una
sucesin de sumas parciales. En otros contextos, por ejemplo una serie de tiempos
(time series) es una sucesin de datos tomados a medida que avanza el tiempo. En
cierto sentido, lo que un profesional de la estadstica llama una serie de tiempos es lo
que un ingeniero llama una seal discreta.
Suponga que tenemos la sucesina
n
contrminos: a
0
= 1; a
1
= 1+1/2 = 1,5
a
1
= 1 + 1/2 + 1/4 = 1,75 a
1
= 1 + 1/2 + 1/4 + 1/8 = 1,895, etc. En donde el
trmino genrico a
n
est dado por a
n
= 1 +
n1
i=1
(1/2)
i
. Ahora, queremos saber
si la sucesin a
n
converge y, el tal caso, lmite. Tal lmite lo denotamos as:
1 +
n1
i=1
(1/2)
i
y lo llamamos el valor de la serie. Si ha ledo sobre la paradoja de
Zenn, y sabe el resultado de la serie, quizs vea aqu una solucin matemtica
a la paradoja, es decir, tenemos que el resultado de una suma innita es nito:
1 +
n1
i=1
(1/2)
i
= 2.
En esta seccin consideramos el problema de averiguar cundo tiene una
sucesin a
n
en donde los trminos son sumas parciales de la forma a
n
=
n
i=0
b
i
,
en donde asumimos que sabemos el valor de b
i
para cada i, y en caso de
convergencia, saber cunto vale el lmite, que denotamos
n
i=0
b
i
.
Ejercicio. Muestre que la serie
n
i=0
1
i+1
=
n=1
1
n
diverge hacia innito, comparn-
dola con las reas indicadas en la gura 38, sabiendo que la integral de
1
x
sobre
[0, ) es innita.
0.15.1. Re-ordenamiento de los trminos de una serie
A partir de una serie dada
i=0
b
i
podemos obtener otra redondeando los tr-
minos:
i=0
b
g(i)
, es decir en donde asumimos que g es una biyeccin g : N N.
Es posible que
i=0
b
i
converja pero que
i=0
b
g(i)
no. Si converge para toda biyec-
cin g, decimos que la serie converge incondicionalmente. Es decir que para
cualquier re-ordenamiento de sus trminos la serie resultante converge al mis-
mo valor.
Por ejemplo, resulta que la serie
n=1
(1)
n+1
n
converge a ln2, lo que podramos
escribir como: 1
1
2
+
1
3

1
4
+
1
5

1
6
+ = ln2, pero si sumamos en el siguiente
orden [13],
1
1
2

1
4
+
1
3

1
6

1
8
+
1
5

1
10

1
12
+
= (1
1
2
)
1
4
+ (
1
3

1
6
)
1
8
+ (
1
5

1
10
)
1
12
+
=
1
2

1
4
+
1
6

1
8
+
1
10

1
12
+
=
1
2
(1
1
2
+
1
3

1
4
+
1
5

1
6
+ )
=
1
2
ln2
y, como vemos, el resultado cambia! En este caso, la permutacin g est dada
por: g(0) = 0, g(1) = 1, g(2) = 3, g(3) = 2, g(4) = 5, g(5) = 7, g(6) = 4,
Decimos que la serie
i=0
z
i
converge en magnitud, si la serie
i=0
z
i
con-
verge.
Ejercicio. Encuentre una frmula para g(n).
Ejercicio. D un ejemplo de una serie que no converja incondicionalmente.
0.15. SERIES 93
Figura 38: No tiene epgrafe
Ejercicio. Muestre que si una serie converge en magnitud, entonces converge
incondicionalmente.
0.15.2. Criterios de convergencia de series de nmeros reales
y de nmeros complejos
La prueba de la integral es usada a veces para mostrar convergencia y a
veces para mostrar divergencia. En ambos casos la idea es hacer corresponder
los trminos de la serie con las reas de ciertos rectngulos, por encima o
por debajo de la curva de la funcin que se integra. Por ejemplo, considere la
funcin f (x) =
1
x
, para x > 0, y la serie con trmino genrico s
n
=
1
n
. Notando
que
N
n=1
1
n
>
N+1
_
1
1
x
dx = , (vea la gura 39) concluimos que la serie
n=1
1
n
diverge.
Similarmente, con g(x) = x
2
, x > 0, tenemos que la serie
n=1
1
n
2
converge ya que
N
n=1
1
n
2
< 1 +
N
_
1
1
x
2
dx < 1 + 1 = 2.
Ejercicio. Encuentre el valor de
n=1
1
n
2
, usando series de Fourier.
Si una serie de nmeros reales (de complejos) converge cuando se toma
el valor absoluto (la magnitud) de sus trminos, entonces la serie converge
incondicionalmente.
Encontrar el lmite de una serie normalmente es ms difcil que mostrar
que converge. El saber que ciertas series convergen, o divergen, sirve para
deducir la convergencia o divergencia de otras.
Figura 39: El criterio de la integral para mostrar divergencia
Figura 40: El criterio de la integral para mostrar convergencia
Ejercicio. En qu consiste el criterio de convergencia de la raz?
0.15. SERIES 95
0.15.3. La serie geomtrica
Como veremos ms adelante, la frmula para la serie geomtrica 1 +
n=1
z
n
,
que en forma abreviada escribimos como
n=0
z
n
, es til para evaluar la trans-
formada de Fourier y la transformada zeta de ciertas seales discretas.
La versin nita de esta serie, que llamaremos la suma geomtrica,
N
n=0
z
n
tambin es til y tambin tiene una frmula sencilla, que deducimos a contin-
uacin, y que,
1z
m
1z
+z
m
=
1z
m+1
1z
. Esto permite demostrar la frmula de la suma
de potencias de z. Para evaluar
N
n=0
z
n
procedemos inductivamente. el truco a
recordar es que, para z 1, 1 + z =
1z
2
1z
,
N
n=0
z
n
=
1z
N
+1
1z
, si z 1, y, claro est,
N
n=0
z
n
= N + 1, si z = 1.
Alternativamente, podemos deducir la suma geomtrica de la frmula
telescpica: (1 z)(1 +z +z
2
+z
3
+ +z
N
) = 1 z
N+1
, siempre y cuando z 1.
La frmula de la suma geomtrica nos permite ahora deducir la frmula de
la serie geomtrica. Si z = 1, el valor de
N
n=0
z
n
= N+1 y la serie
N
n=0
z
N
diverge. En
otro caso, el valor de la serie
N
n=0
z
N
queda determinado por el comportamiento
de z
N
a medida que N crece. Considerando la representacin en coordenadas
polares de z dada por z = ze
j
, se tiene que z
N
= z
N
e
jN
. Si z < 1, z
N
tiene a
cero y
n=0
z
n
es
1
1z
; si z 1, z
N
= z
N
e
jN
diverge. Por lo tanto, la frmula para
la serie geomtrica est dada por,
n=0
z
n
=
1
1z
si y slo si z < 1.
Ejercicio. Calcule
n=0
2
n
.
Ejercicio. Calcule
n=1
2
n
.
0.15.4. La transformada zeta
Sea w
n
una sucesin bilateral de complejos; denimos su transformada
zeta como la funcin W : D Cdada por la serie de Laurent W(z) =
w
n
z
n
,
con dominio los valores de z en el anillo de la regin de convergencia de la
serie. Es comn que la suma de la serie sea una funcin racional de la variable
z, u otra funcin conocida. Es claro que es tan importante dar la dependencia
funcional de W de z como su dominio, ya que dos sucesiones diferentes w
n
,
v
n
pueden tener transformada con la misma dependencia funcional W(z) y
diferentes dominios D.
Ejemplo. La transformada de u
n
est dada por
n=0
z
n
=
1
1z
, con regin de
convergencia dada por z < 1.
0.15. SERIES 97
Ejemplo. La transformada de u
n
est dada por:
1
2 z
=
1/2
1 z/2
=
1
2
n=0
(
z
2
)
n
=
1
2
n=0
(
z
2
)
n
=
1
2
n=0
2
n
(z)
n
con z es la transformada de la seal x
n
= 2
n
u
n
.
Ejemplo.
W(z) =
1
(1 z)(2 z)
=
1
1 z

1
2 z
=
1
z(1 z
1
)

1
2 z
=
1
z(1 z
1
)
+
1
2z(1/2 z
1
)
Corresponde a diferentes sucesiones en cada una de las regiones z < 1, 1 <
z < 2 y 2 < z.
Ejercicio. Encuentre las sucesiones correspondientes al ejemplo anterior.
0.16. Interpretacin funcional de los puntos de R
n
y C
n
y notacin para conjuntos de funciones
Un elemento de R
n
se denota con la n-tupla x = [x
0
, x
1
, . . . , x
n1
]. Con base
en la n-tupla x, podemos denir la funcin x : 0, 1, . . . , n 1 R en la forma
obvia con x(0) = x
0
, x(1) = x
1
, . . . , x(n 1) = x
n1
; en este sentido, R
4
es el
conjunto de las funciones de 0, 1, 2, 3 a R.
Por ejemplo, el punto x = [2, 1, 3, 0] corresponde a la funcin con grca
como se muestra:
Figura 43: Grca de la funcin x
El conjunto de las funciones con dominio n = 0, 1, . . . , n 1 y rango
C, lo podemos representar como C
n
.Por ejemplo, considere la funcin f :
0, 1, 2, 3 C, dada por f (0) = 1, f (1) = j, f (2) = j, f (3) = 1; podemos decir
que el punto [1, j, j, 1] de C
4
especica completamente la funcin f : 4 C.
0.17. INTERVALOS DE R
N
Y DE Z
N
99
Extendiendo esta idea, decimos que el conjunto de las funciones de Z a C es
C
Z
y que, en general, el conjunto de las funciones con dominio D y rango R,
es R
D
.
Algunos conjuntos que podemos denotar en forma similar son:
C
Z
: El conjunto de la sucesiones bilaterales complejas.
C
N
: El conjunto de la sucesiones unilaterales complejas.
R
Z
: El conjunto de la sucesiones bilaterales reales.
R
N
: El conjunto de la sucesiones unilaterales reales.
C
R
: El conjunto de las funciones complejas con dominio real.
C
C
: El conjunto las funciones complejas con dominio complejo.
0.17. Intervalos de R
n
y de Z
n
Sean a = [a
1
, a
2
, . . . , a
n
] y b = [b
a
, b
2
, . . . , b
n
] elementos de R
n
. El intervalo
cerrado [a, b] es el conjunto de puntos x = [x
1
, x
2
, . . . , x
n
] de R
n
tales que par
cada i en /1, n/, a
i
x
i
b
i
. El intervalo abierto ]a, b[ es el conjunto de
puntos x = [x
1
, x
2
, . . . , x
n
] de R
n
tales que par cada i en /1, n/, a
i
< x
i
< b
i
.
Ejemplo. Sean a = [3, 2] y b = [4, 3], puntos de R
2
, el intervalo ]a, b[ se muestra
en la gura (44
Sean r = [r
1
, r
2
, . . . , r
N
] y s = [s
a
, s
2
, . . . , s
N
] elementos de Z
N
. El intervalo
entero, de dimensin N, /r, s/ es el conjunto de elementos k = [k
1
, k
2
, . . . , k
N
]
tales que, para cada i en /1, N/, r
j
k
i
s
i
,
Las uniones de intervalos son los dominios naturales de las seales. Los in-
tervalos multidimensionales son los dominios de las seales multidimension-
ales; por ejemplo, las imgenes tienen como dominio intervalos de dimensin
dos y se consideran seales de dimensin dos.
Por otra parte, los intervalos proveen bases para la topologa estndar de
R
n
. Estos intervalos se conocen como las bolas con respecto a la mtrica del
producto.
Figura 44: El intervalo ](3, 4), (2, 3)[ de R
2
Tambin, decimos que un subconjunto de R
n
es abierto si es una unin
de intervalos abiertos de R
n
.
0.18. Clculo
0.18.1. Lmite de una sucesin de funciones
Suponga que para cada nmero natural n, f
n
: X C, donde X es un
subconjunto de R
1
, es una funcin. Si r es un nmero en X, entonces f
n
(r)
es una sucesin de nmeros. Si para cada x X, la sucesin f
n
(x) converge,
podemos denir la funcin f : X C, dad por f (x) = lm
n
f
n
(x) y decimos
que la sucesin de funciones f
n
converge a la funcin f . En smbolos, f es el
lmite de f
n
si, x X > 0 Nn > N, f
n
(x) f (x) < , (donde es real y
n y N son naturales). Este tipo de convergencia se conoce como convergencia
punto a punto o convergencia puntual.
Ejemplo. La sucesin de funciones f
n
, donde cada f
n
: [0, 1] C est dada
por f
n
(x) = x
n
, converge a la funcin c(x) dada por c(0) = 0 y c(x) = 1 si x (0, 1].
0.18. CLCULO 101
Observe la gura siguiente. note que las f
n
son continuas y que el lmite c no
lo es.
Figura 45: Las funciones x
n
para n = 1, 2, 4, 6 y la funcin lmite
0.18.2. Convergencia uniforme
Se dice que la sucesin de funciones f
n
(x) converge a la funcin c(x)
uniformemente si la N en la denicin no depende de x, es decir, la funcin f
es el lmite uniforme de la sucesin de funciones f
n
(x) si, > 0 N Nx
X f
n
(x) f (x) < .
Ejemplo. La sucesin de funciones indicada en la gura 45 no converge uni-
formemente. (Por qu?)
Ejercicio. Diga en qu cosiste el criterio conocido como prueba de la M de
Wierstrass.
0.18.3. Lmite de una funcin, dadas topologias con base para
el dominio y el rango
Sea f : D W una funcin cuyo dominio D y rango W son espacios
topolgicos cuyas topologias tienen bases; informalmente hablando, eso ocurre
cuando tenemos intervalos abiertos, como por ejemplo en el caso de los nmeros
reales. Decimos que b es el lmite de f (x) cuando x tiende a a si para cada
intervalo abierto I, en W, que contenga a b existe un intervalo abierto J, en
D, que contenga a a tal que x J a, f (x) I es decir , f (J a) es un
subconjunto de I.
Esto se denota: lm
xa
f (x) = b.
Figura 46: En la denicin de lmite, los puntos del intervalo J, con la posible excepcin de a,
tienen imgenes dentro del intervalo I; en el caso de la denicin de continuidad, la imagen de J
es un subconjunto de I
Se puede comprobar que, cuando el rango yel dominio sonespacios mtricos,
con mtricas d y D, la denicin anterior es equivalente a: > 0, > 0
0 < x a < d( f (x), b) < .
Cuando el rango y el dominio son R o C, tenemos la denicin usual:
> 0, > 0 0 < x a < f (x), b < .
0.18. CLCULO 103
0.18.4. Continuidad
Sea f : R
1
R
1
una funcin de los reales a los reales. Sea R
1
un
nmero real. Se dice que f es continua en si para cada intervalo abierto I
que contenga a f () existe un intervalo abierto J que contiene a y es tal que
f (J) es un subconjunto de I.
Para la lnea de los nmeros reales, tenemos la denicin usual: f es con-
tinua en si: > 0 > 0 x < f (x f ()) < .
Ejercicio. D un ejemplo de una funcin f : R
1
R
1
que sea continua ni-
camente en cero. Sugerencia: f (x) = x si x es racional, y f (x) = x si x es
irracional.
0.18.5. Continuidad uniforme
Se dice que la funcin f es continua en el intervalo I si I, > 0 >
0 x < f (x) f () < .
Se dice que la funcin f es uniformemente continua en un intervalo I si
en la denicin anterior no depende de x. En smbolos > 0 > 0
I, x < f (x) f () < .
Ejercicio. Muestre que la funcin f (x) = 1/x es continua pero que no es uni-
formemente continua en el intervalo (0,1).
Ejercicio. Muestre que la funcin f (x) = x
2
es uniformemente continua en el
intervalo (0,1).
Ejercicio. Muestre que la funcin sent es uniformemente continua.
0.18.6. Con respecto a la continuidad de funciones con rango
S
1
Suponga que se tiene una funcin f : R
1
S
1
. La fase de una funcin
compleja puede ser una de tales funciones y dos fases cuya diferencia sea un
mltiplo entero de 2 determinan la misma clase de equivalencia en S
1
. As,
una funcin de fase continua puede tener saltos de magnitud 2 pero no saltos
de magnitud . Si d mide la distancia entre puntos en s
1
y D la distancia entre
puntos de R, tenemos que f es continua en a si > 0, > 0 d(x, a) <
D( f (x), b) < .
Ejercicio. Diga cul de las siguientes funciones es continua y cul discontinua:
f : R
1
S
1
dada por f () = e
j
.
f : R
1
S
1
dada por f () = (e
j
1).
0.18.7. Derivada
La derivada, de funciones tanto reales como complejas, con dominio real o
complejo, est dada por el siguiente lmite, siempre y cuando ste exista:
f
(x) = lm
h0
f (x + h) f (x)
h
donde f puede ser una funcin f : R
1
R
1
, R
1
C, C R
1
, C C. En cada
caso, la suma y el cociente se calculan apropiadamente.
En el ltimo caso, para funciones complejas con dominio complejo, la
derivada est basada en el hecho de que hay un cociente bien denido entre
nmeros complejos. Esto hace que el clculo complejo sea una teora riqusi-
ma en conceptos: estn los derivados del clculo vectorial y los derivados de
las operaciones complejas. As, por ejemplo, hay dos productos; el escalar y
el complejo. Se dice que una funcin f : C C que sea derivable en z
0
, es
holomrfica en z
0
.
0.18. CLCULO 105
Ejercicio. D ejemplos de funciones derivables y no derivables en cada uno de
los siguientes casos:
f : R
1
R
1
f : R
1
C
f : C R
1
f : C C
Ejercicio. Cules son las ecuaciones de Cauchy-Riemann?
Ejercicio. D un ejemplo de una funcin g : R
1
R
1
que slo sea derivable en
0. (Sugerencia: g(x) = x f (x) donde f (x) = x para x racional, y f (x) = x para x
irracional.)
Para funciones de R a R, la derivada tiene 3 interpretaciones: el lmite de
un cociente, que tiene sabor algebraico y analtico; la tangente a una curva,
que es una contribucin de Fermat y es probablemente la idea germinal del
clculo; y una aproximacin lineal que es la idea con mayores posibilidades
de generalizacin. Las dos primeras seguramente le son ms conocidas. La
tercera resulta de considerar:
f (x + h) f (x + h f
(x)) y, por lo tanto, con t = x + h, x = t

0
, resulta:
f (t) f (t
0
) + (t t
0
) f
(t
0
), para t cerca a t
0
(es decir h pequea),
= f (t
0
) +(t), donde la funcin : R Rdada por (t) = (t t
0
) f
(t
0
) es lineal.
La derivada de funciones de C a C tiene las interpretaciones de derivada
de lmite de un cociente y de aproximacin lineal. La derivada de funciones de
R
N
a R
M
tiene las interpretaciones de hiperplano tangente y de aproximacin
lineal local.
Figura 47: La ecuacin de la tangente est basada en la funcin lineal (x) = f
(x)(t x)
0.18.8. Interpretacin geomtrica de la derivada compleja
Si f : C C es derivable en z
0
, entonces, para z en las cercanas de z
0
, f
est dada aproximadamente por f (z) f (z
0
) + (z z
0
) = f (z
0
) + w(z z
0
),
donde : C C es lineal, con cuerpo C, y donde w := f
(z
0
) es el nmero
complejo conocido como la derivada compleja de f en z
0
.
Ahora, si z
1
y z
2
son puntos cercanos a z
0
, el ngulo z
1
z
0
z
2
, est dado por
la fase del cociente
[z
2
z
0
]
[z
1
z
0
]
. Por otra parte, considerando los puntos resultantes
f (z
1
), f (z
0
) y f (z
2
), al aplicar f , tenemos que el ngulo f (z
1
) f (z
0
) f (z
2
) est
dado por la fase de
[ f (z
2
)f (z
0
)]
[ f (z
1
)f (z
0
)]
. Entonces
[ f (z
2
) f (z
0
)]
[ f (z
1
) f (z
0
)]
=
[w(z
2
z
0
)]
[w(z
1
z
0
)]
=
[z
2
z
0
]
[z
1
z
0
]
y, por lo tanto las fases son iguales. As, a menos que w = 0, tenemos que si f
es derivable en z
0
, con derivada no nula, f preserva los ngulos con vrtice en
z
0
. Esta propiedad es de fundamental importancia en el clculo complejo.
0.18. CLCULO 107
Figura 48: El ngulo con vrtice z
0
y el ngulo con vrtice f (z
0
) son iguales
Ejercicio. Es posible denir un cociente para los elementos diferentes del
origen, de R
3
? Cul sera el producto correspondiente?
Ejercicio. Para la funcin f : C C dada por f (z) = z
2
, aproxime f (1,1 + 0,9j)
usando f
(1 + j).
Si f tiene derivada compleja en cada uno de los puntos de una regin
abierta, se dice que f es holomorfa en la regin.
0.18.9. Aproximacin lineal
Para funciones f : R
N
R
M
, el concepto de derivada se basa en el de
aproximacin lineal local. As decimos que f es diferenciable en x
0
R
N
si en
las cercanas de x
0
, f se comporta aproximadamente como, f (x) x
0
+(xx
0
),
en donde : R
N
R
M
es una funcin lineal. ahora, recordemos que una
funcin de R
N
a R
M
es lineal si y slo si tienen representacin (x) = xL,
donde L es una matriz de M N. As, tenemos que en cierto sentido la matriz
L es la derivada de f en x
0
. como recordar esta matriz es precisamente la
matriz Jacobiana de f evaluada en x
0
: L = J(x
0
) donde:
J(x) =
_
_
f
1
(x)
x
1

f
1
(x)
x
N

f
M
(x)
x
1

f
M
(x)
x
N
_
_
0.18.10. Diferencial
Equivalentemente, tenemos la siguiente nocin de derivada. Sea f : R
N
R
M
una funcin con N y Mnaturales positivos. Se dice que f es diferenciable
(en sentido real) en el punto c R si existe una funcin lineal (con cuerpo los
reales) T : R
N
R
M
tal que, lm
h0
f (c+h)f (c)T(h)
h
= 0, donde son las normas
para R
N
y R
M
.
Se puede mostrar que T es nica y se conoce como el diferencial Tf (c), y
tambin como la funcin tangente a f en c. Tf (c) es la matriz Jacobiana
M N de f .
Ejercicio. Sea f : R
2
R
1
dada por f (x, y) = x
2
+ y
2
. Encuentre la ecuacin del
plano tangente a la supercie de f en el punto (x, y) = (3, 5).
Ejercicio. Diga si f : C Cdada por f (z) = zz
es diferenciable o no. Explique.

0.18.11. Diferenciabilidad real y las ecuaciones de Cauchy-
Riemann
si L : C C es una funcin lineal con cuerpo C, entonces es de la forma
L(z) = wz con z C. En R
2
, con z = (x, y) y w = (a, b), tenemos la siguiente
representacin matricial de L:
L
_
_
x
y
_
_
=
_
_
a b
b a
_
_
_
_
x
y
_
_
0.18. CLCULO 109
Por otra parte, dada f : C C como funcin R
2
R
2
f est dada por:
f
_
_
x
y
_
_
=
_
_
u(x, y)
v(x, y)
_
_
y si es diferenciable su Jacobiano est dado por:
J =
_
x
u
y
u
x
v
y
v
_
_
resultando la funcin lineal
LL
_
_
x
y
_
_
= J
_
_
x
y
_
_
y si f tiene derivada compleja w,
_
x
u
y
u
x
v
y
v
_
_
=
_
_
a b
b a
_
_
y tenemos que las ecuaciones de Cauchy-Riemann se siguen:
x
u =
y
v y
x
v =
y
u. Las ecuaciones de Cauchy-Riemann son una condicin necesaria
para diferenciabilidad, pero no suciente. A menos que la f sea diferenciable
en un conjunto abierto
Ejercicio. Sea f : T T la funcin del conjunto de los cuaternios al conjunto
de los cuaternios, dada por f (z) = wz, donde w = [w 1, w
2
, w
3
, w
4
]. Exprese f
en forma matricial.
Ejercicio. Muestre que la siguiente funcin no es diferenciable en el origen
aunque cumple con las ecuaciones de Cauchy-Riemann all. f (x + jy) =
x
4
y
4
x
3
+y
3
+
j
x
4
+y
4
x
3
+y
3
, f () =
0.18.12. Extensin en series de potencias
Las series de potencias determinan funciones con dominio dado por la
regin de convergencia de la serie. Si la serie no incluye potencias negativas de
la variable, sta se denomina una serie de Taylor mientras que si las incluye,
se denomina una serie de Laurent. Las series mostradas a continuacin
indican series de Taylor:
1. f (x) = a
0
+
n=1
a
n
x
n
, que escribimos abreviadamente como
n=0
a
n
x
n
.
2. g(z) = b
0
+
n=1
b
n
(z z
0
)
n
, que escribimos abreviadamente como
n=1
b
n
(z
z
0
)
n
.
Mientras que la siguiente es una serie de Laurent:
n=1
b
n
(z z
0
)
n
+h(z) = b
0
+
n=1
b
n
(z z
0
)
n
, que escribimos abreviadamente
como
n=
b
n
(z z
0
)
n
.
La funcin determinada por una serie de Taylor se conoce como funcin
analtica. Tales funciones poseen derivadas de orden arbitrario: f
(x) =
n=1
na
n
x
n1
(Por qu?) y, por lo tanto f
(0) = (2)(1)a
2
, en general, procedi-
endo inductivamente, se tiene que, f
(n)
= n!a
n
, de donde resulta la frmula de
los coecientes: a
n
=
f
(n)
(0)
n!
.
Por ejemplo, las funciones seno y coseno son funciones analticas mientras
que la funcin x no lo es. Las series de Taylor son usadas en los programas
de computadores y calculadoras que usan aproximaciones a funciones tales
como la raz cuadrada y las trigonomtricas.
Una diferencia importante entre funciones de la variable real y funciones
de la variable compleja, es que en el caso complejo, tener derivada compleja es
0.18. CLCULO 111
condicin suciente para que una funcin de variable compleja tenga derivada
(continua) de cualquier orden.
Ejercicio. Que dice el teorema de Morera?
Note que el conocimiento de una funcin analtica en un intervalo, por
pequeo que sea, determina completamente la funcin. Por lo tanto, dos fun-
ciones analticas (diferentes) no pueden coincidir en ningn intervalo. Por
ejemplo, ninguna funcin analtica que no sea la funcin constante, es con-
stante en ningn intervalo. en este sentido, la informacin de la totalidad de la
grca de cualquier funcin analtica est incluida en la grca de cualquier
intervalo no vaco, no importa que tan pequeo sea.
Ejercicio. Cul es la extensin en series de Taylor de la funcin seno alrededor
de cero?
Ejercicio. Cul es la de la funcin coseno?
Ejercicio. Si una serie converge en valor absoluto o en magnitud, se puede
alterar el orden de los trminos de la serie sin que su valor se altere?
Ejemplo. Sea f : R
1
R
1
la funcin dada por f (x) =
n=0
x
n
n!
que converge para
cada nmero real (Por qu?). deniendo e =
n=0
1
n!
y dado que f (x + y) =
f (x) f (y), es decir,
n=0
(x)
n
n!
=
n=0
(y)
n
n!
n=0
(x+y)
n
n!
(Por qu?) y que f es continua y
est denida para los reales, podemos concluir que f (x) = e
x
.
n=0
(x+y)
n
n!
=
n=0
(x)
n
n!
n=0
(y)
n
n!
para cualesquier nmeros
reales x y y.
Sugerencias:
1. Use la frmula del binomio de Newton.
2. El conjunto (n, k) NN; k n se puede barrer como se muestra en
la gura 49, variando n y m = n k de 0 en adelante en vez de n de 0 en
adelante y k de 0 hasta n.
Figura 49: El conjunto (n, k) N N; k n
A veces (en particular cuando hay convergencia en valor absoluto) una
funcin analtica f con dominio R
1
se puede extender a la funcin g : C
C (con dominio C) utilizando la misma serie de Taylor: g(z) =
n=0
c
n
z
n
por
ejemplo, si c
n
=
1
n!
, resulta la serie de la exponencial compleja.
Ejercicio. Muestre que, para R
1
, g( j) = cos + j sen.
Ejercicio. Muestre que, para u, v C, g(u + v) = g(u)g(v).
Usando los resultados de los ejercicios anteriores escribamos g(z) = e
z
.
Ejercicio. Muestre que, pera x, R
1
, g(x + j) = e
x
(cos + j sen)
Por lotanto, si se tiene el nmerocomplejoz conrepresentacinencoordenadas
polares z = (r, ), entonces z = re
j
.
Ejercicio. muestre que,
e
j
1+e
j
=
1
2
+ j
sen
2(1+cos )
0.18. CLCULO 113
0.18.13. Series de Laurent
Sea s = s
i
una sucesin bilateral, por denicin, la serie
i=
s
i
es la suma
de dos series:
i=
s
i
=
i=0
s
i
+
i=1
s
i
. una serie de Laurent es una serie de
potencias de la forma g(z) =
n=
c
n
(z z
0
)
n
.
El residuo de una funcin con expansin en series de Laurent es el coe-
ciente del trmino que incluye a z
1
.
Teorema 4. si se sabe que la serie
n=
c
n
(z)
n
converge para z = z
0
, entonces se puede
concluir que la serie converge para cada z con z < z
0
.
Ejercicio. Demuestre el teorema anterior.
As, la reginde convergencia de una serie de Laurent es una corona circular
abierta junto con quizs algunos puntos de su frontera (la frontera est dada
por las circunferencias que acotan la corona). si la funcin g que se representa
con la serie es una funcin racional, en cada componente conectado de la frontera
de la regin de convergencia hay por lo menos un polo de g(z) (Por qu?).
0.18.14. Integral de Riemann-Stieltjes
A continuacin, consideramos particiones de intervalos en intervalos y
denimos la variacin de una funcin con el objeto de denir posteriormente
la integral de Riemann-Stieltjes.
0.18.15. Particiones de intervalos
Es comn particionar un intervalo en una coleccin de intervalos. Sea J un
intervalo de nmeros reales, una particin de J es un conjunto de intervalos
cuya unin es J.
Ejemplo. [0, 1) [1, 3) [3, 5) es una particin en subintervalos de [0, 5).
Note que la particin de un intervalo [a, b) = [a
0
, a
1
) [a
1
, a
2
) [a
n1
, a
n
)
queda determinada por el conjunto de puntos a
0
, a
1
, a
2
, . . . , a
n1
, a
n
que de-
limitan los subintervalos, donde asumimos que a = a
0
< a
1
< a
2
< . . . < a
n1
<
a
n
= b. As, muchas veces se habla de la particin a
0
, a
1
, a
2
, . . . , a
n1
, a
n
de [a, b).
Con esta representacin de particiones con conjuntos, se dice que la par-
ticin Q es un refinamiento de la particin P, si Q es un subconjunto de
P.
Ejercicio. Muestre que si una funcin es montona (es decir, es o no creciente, o
no decreciente) entonces, el subconjunto de su dominio donde es discontinua
es contable o vaco.
0.18.16. Variacin de una seal continua
Dada una funcin real f , denida en el intervalo [a, b] y siendo
P = x
0
, x
1
, x
2
, . . . , x
n1
, x
n
una particinde [a, b), decimos que variacin de f
en [a, b] con respecto a P est dada por Var( f, [a, b], P) =
n
i=1
f (x
i
) f (x
i1
).
Si ahora consideramos el conjunto de las posibles particiones de [a, b] (un
conjuntobastante grande) yel conjuntode los nmeros reales correspondientes
a las variaciones de f con respecto a cada particin; decimos que el suprmum
de tal conjunto (recuerde que todo conjunto acotado de reales tiene suprmum)
es la variacin total de f en [a, b]. Si la variacin total de f es un nmero
real (es decir, si es nita) se dice que f es de variacin acotada.
Ejercicio. Calcule la variacin total de senx en [0, 2].
Ejercicio. Muestre que si f es una funcin montona entonces la variacin total
de f en [a, b] est dada por f (b) f (a).
0.18. CLCULO 115
Ejercicio. (Aditividad con respecto al intervalo.) Muestre que si [a, b] = [a, c]
[c, b], entonces la variacin total de f en [a, b] es igual a la variacin total de f
en [a, c] ms la variacin total de f en [c, b].
Ejercicio. (Opcional.) Muestre que f es de variacin acotada si y slo si f es la
suma de dos funciones montonas.
0.18.17. La integral de Riemann
Sea f una funcin real denida en [a, b], sea p = x
i
N
i=0
x
i
, x
i+1
N1
i=0
una
particin de [a, b] con x
0
= a y x
N
= b. Sea = m axx
i+1
x
i
: i /0, N 1/ el
dimetro de la particin.
La integral superior de Riemann de f , en [a, b], con respecto a la parti-
cin p est dada por
_
b
a p
f (x)dx :=
N1
i=0
sup f (x) : x (x
i
, x
i+1
)[x
i+1
x
i
]
mientras que la integral inferior de Riemann de f en [a, b], con respecto a
la particin p est dada por
_
b
a
p
f (x)dx :=
N1
i=0
nf f (x) : x (x
i
, x
i+1
)[x
i+1
x
i
]
La integral superior de Riemann sobre [a, b] est dada por
_
b
a
f (x)dx = lm
0
_
b
a p
y a la integral inferior sobre [a, b], por
_
b
a
f (x)dx = lm
0
_
b
a
p
si se cumple la igualdad
_
b
a
f (x)dx =
_
b
a
f (x)dx
decimos que f tiene integral de Riemann y que esta est dada por este valor
comn
_
b
a
f (x)dx =
_
b
a
f (x)dx =
_
b
a
f (x)dx
Ejercicio. Sea f (x) =
_
_
1 x Q
0 x R Q
diga si tiene integral de Riemann en [0, 1].
0.18.18. La integral de Riemann-Stieltjes
La integral de Riemann es la que normalmente se estudia en un curso de
Clculo I. La integral de Riemann-Stieltjes es una poderos herramienta que
no necesita para su denicin basas matemticas sosticadas y que permite
unicar ciertos resultados en teora de seales, de sistemas y en probabilidad.
La integral de Riemann-Stieltjes nos permite obviar el uso de impulsos en
sistemas de convolucin continuos. La integral de Riemann-Stieltjes no tiene
una interpretacin geomtrica intuitiva y sencilla como la tiene la integral de
Riemann,en trminos de reas. Como la integral de Riemann, la integral de
Riemann-Stieltjes se dene con un proceso de lmite.
Una diferencia importante con respecto a la integral de Riemann es que una
integral de Riemann-Stieltjes involucra dos funciones, el integrando y el inte-
grador. Para las aplicaciones que usaremos en teora de seales ser suciente
recordar una frmula que permite calcular muchas integrales de Riemann-
Stieltjes en trminos de integrales de Riemann. La integral de Riemann es un
caso particular de la integral de Riemann-Stieltjes.
0.18. CLCULO 117
Nomenclatura
Una integral de Riemann-Stieltjes se expresa as:
_
b
a
f d o
_
b
a
f (x)d(x)
donde [a,b] es el intervalo de integracin, f es la funcin integrando y es la funcin
integrador. Dos restricciones que asumiremos vlidas son que el integrando no
son discontinuas simultneamente y que son de variacin acotada.
Ejemplo. Para dar una idea de lo que puede suceder al evaluar integrales de
Riemann-Stieltjes mostramos a continuacin el resultado de una integral de
Riemann, sin deducir el resultado. Suponga que es una funcin escaln
desplazada, como la mostrada en la gura 50, (x) = 0 si x < 1, y (x) = 1
si x > 1 y que el intervalo (a,b) contiene el nmero 1. Entonces, si f es una
funcin continua en 1, se tiene que,
_
b
a
f d = f (1).
Sean f y funciones denidas en [a, b] y sea P = t
o
, t
1
, . . . , t
n
una parti-
cin de [a, b); la suma de Riemann-Stieltjes de f en [a, b], con respecto a la
particin P y a la funcin est dada por: S(P, f, ) =
n
i=1
f (t
i
)[(t
i
) (t
i1
)].
Por denicin, la integral de Riemann-Stieltjes de f con respecto a
existe si hay un nmero real A tal que para cada positiva existe una particin
P de [a, b] tal que para cada particin Q que sea un renamiento de P, se tiene
que S(Q, f, ) A < . En tal caso, escribimos
_
b
a
f d = A.
Ejercicio. Sea la funcin mostrada en la gura 50. Calcule
_
2
0
cos x d(x).
Integracin por partes
Para la integral de Riemann, la frmula de integracin por partes se puede
recordar a partir de la derivada de un producto: d(uv) = udv+vdu. En trminos
Figura 50: Una funcin escaln desplazada
de la integral de Riemann-Stieltjes, asumiendo que f y son continuas en a y
b, la frmula de integracin por partes est dada por:
_
b
a
f (x)d(x) +
_
b
a
(x)df (x) = f (b)(b) f (a)(a)
Ejercicio. Sean f (x) = senx y (x) = u(x /2).
Calcule
_
3
0
f (x)d(x) +
_
3
0
(x)d f (x).
Caso particular I: La integral de Riemann
Si es la funcin identidad, dada por (x) = x, tenemos que
_
b
a
f (x)d(x) =
_
b
a
f (x)dx donde la integral a la derecha es un integral de Riemann. B. Riemann
fue la primera persona en dar una denicin axiomtica de la integral. Ar-
qumedes fue tal vez la primera persona en considerar el rea bajo una curva
arbitraria.
Caso particular II: La integral de Riemann-Stieltjes cuando el integrador es
derivable
En general, si (x) tiene derivada
(x) en [a, b], entonces,

_
b
a
f (x)d(x) =
_
b
a
f (x)
(x) en donde la integral a la derecha es una integral de Riemann.

0.18. CLCULO 119
Caso particular III: La integral de Riemann-Stieltjes cuando el integrador es
derivable a trozos
Si (x) es derivable excepto en un conjunto denso en ninguna parte (ver
seccin 0.9.6) de puntos t
i
, y f es una funcin que tiene integral de Riemann
y es continua en los puntos de no-diferenciabilidad de (x), se tiene que:
_
b
a
f (x)d(x) =
_
t
1
a
f (x)
(x)dx +
i
_
t
i
t
i1
f (x)
(x)dx
+
_
b
t
n
f (x)
(x)dx +
i
f (t
i
)[(t
+
i
) (t
i
)]
Caso particular IV: La integral de Riemann-Stieltjes cuando el integrador es
continuo y estrictamente creciente
_
b
a
f (x)d(x) =
_
(b)
(a)
f (
1
(x))dx
Teorema fundamental del clculo
Como se ver ms adelante, la siguiente versin del Teorema fundamental
del clculo es particularmente til para relacionar la respuesta escaln con la
funcin caracterstica de un sistema de convolucin.
Sea f una funcin continua en t, y sea G(t) =
_
t
a
f (x)dx entonces , para a < t,
d
dt
_
t
a
f (x)dx =
dG(t)
dt
= f (t)
Ejercicio. Demuestre que si f es continua en t, el lmite cuando h tiene a cero
de
1
h
_
t+h
t
f (x)dx es f (t).
Figura 51: Teorema fundamental del clculo
Ejercicio. En qu puntos es derivable la funcin de la gura 51?
Ejercicio. Demuestre el teorema fundamental del clculo.
Integrales de lnea complejas
Si f : C C y : [a, b] C con := g[a, b], con la expresin
_
f (z)d
queremos decir:
_
b
a
Re[ f ()(t))]dRe[)(t)]
_
b
a
Im[ f ()(t))]dIm[)(t)]
+ j
__
b
a
Re[ f ()(t))]dIm[)(t)]
_
b
a
Im[ f ()(t))]dRe[)(t)]
_
Ejercicio. Sea g : [0, 2] C, dada por (t) = e
jt
. = ([0, 2]). Sea f : C C
dada por f (z) = z
n
. Calcule
_
f (z)d, para diferentes valores enteros de n.

0.18. CLCULO 121
La formula con integral de Cauchy es:
f (z)
wz
dw = f (z)
1
wz
dw, donde
es una curva cerrada tipo estrella y z es un punto en la regin acotada por .
El teorema del residuo dice: Sea una curva tipo estrella, sea f una funcin
compleja analtica en la regin abierta acotada por , excepto posiblemente en
un conjunto nito de puntos z
1
, z
2
, . . . , z
n
. Entonces,
f (z)dz = 2j
n
k=1
Res
z=z
k
f (z).
Uso de la integral de Riemann-Stieltjes en probabilidad
Un uso interesante de la integral de Riemann-Stieltjes ocurre en probabil-
idad. Como sabemos, toda variable aleatoria tiene funcin de distribucin,
aunque quizs no tenga funcin de densidad (por ejemplo, si es discreta) o no
tenga funcin de masa. La integral de Riemann-Stieltjes nos permite dar una
expresin nica para la esperanza de la variable (en caso de que esta exista,
claro). Si X es la variable aleatoria con primer momento y F es su distribucin,
la esperanza de X est dada por: E[X] =
xdF(x).
La integral de una sucesin uniformemente convergente de funciones con-
tinuas
Suponga que f
n
es una sucesin uniformemente convergente en el in-
tervalo [a, b] de funciones continuas. Dena una nueva sucesin g
n
de fun-
ciones con dominio [a, b] a partir de la ecuacin g
n
(x) =
x
_
a
f
n
(t)dt. Entonces
se puede demostrar (vea el libro de Clculo de Apstol, por ejemplo) que
si la sucesin f
n
converge uniformemente a la funcin f , entonces la suce-
sin g
n
converge uniformemente a la funcin
x
_
a
f (t)dt, en otras palabras,
lm
x
_
a
f
n
(t)dt =
x
_
a
lm f
n
(t)dt.
Este resultado permite concluir que si la serie de funciones continuas
n=0
f
n
(t) converge uniformemente a la funcin f (t) en el intervalo [a, b], en-
tonces
lm
m
m
n=0
_
x
a
f
n
(t)dt =
_
x
a
lm
m
m
n=0
f
n
(t)dt
para x [a, b]. Es decir, el orden de la integral y la serie se puede cambiar.
Promedio de una funcin en un intervalo
Sea f : R R decimos que el promedio de f en [a, b] est dado por
f
[a,b]
=
1
b a
_
b
a
f (t)dt
Note que

f es la altura del rectngulo con base [a, b] y la misma rea que la
Figura 52: Promedio de una funcin
que hay bajo la grca de f .
0.18. CLCULO 123
0.18.19. Integral de lnea
Una integral de lnea es una integral de Riemann-Stieltjes
_
f d donde
: I C es una funcin denida sobre un intervalo I R, f : D C C (D
es e dominio de f ) y := (I) D. Ms especcamente,
_
f d =
_
b
a
f ((t))d(t)
si es derivable, tenemos
_
b
a
f ((t))
(t)dt
Ejemplo. Sea f (z) = z
n
, a = 0, b = 2 y (t) = e
jt
entonces,
_
S
1
z
n
d =
_
2
0
e
jnt
( je
jt
)dt
= j
_
2
0
e
j(n+1)t
dt
=
_
_
2j si n = 1
0 si n Z 1
Ejercicio. Qu dice el teorema del residuo?
0.18.20. Transformada zeta inversa
Suponga que X(z) con regin de convergencia R es la transformada zeta de
x
n
, entonces X(z) =
n=
x
n
z
n
.
Ejemplo. Considere ahora una circunferencia de radio r. (t) = re
jt
entonces
_
z
n
d =
_
2
0
r
n
e
jnt
( jre
jt
)dt
= jr
n+1
_
2
0
e
j(n+1)t
dt
=
_
_
jr
0
2 n = 1
0 n 1
=
_
_
2j n = 1
0 n 1
(El resultado no cambia.)
Ejercicio. Muestre que el resultado no cambia tampoco si es una curva simple
cerrada que encierra el origen en sentido antihorario.
Si integramos sobre una curva simple cerrada en la regin de convergencia,
_
X(z)d =
_
n=
x
n
z
n
d
=
_
2
0
n=
x
n
z
n
d
Qu radio de convergencia debe tener? Si se puede intercambiar el orden de
la serie y la integral,
_
X(z)d =
n=
_
2
0
x
n
z
n
d
= 2jx
1
Ejercicio. D la frmula para x
n
en general.
0.18. CLCULO 125
0.18.21. Teorema de representacin de F. Riesz
Hacia el nal del curso estaremos interesados en responder la pregunta
de cmo representar un sistema lineal e invariante. El siguiente resultado
es valioso: el funcional : C[a, b] R, donde C[a, b] es el conjunto de las
funciones continuas con dominio [a, b], es lineal si y slo si es de la forma
(g) =
_
b
a
g(x)d(x), donde es la variacin acotada en [a, b].
El funcional Dirac
El funcional : C
R
Cdado por (g) = g(0), tiene representacin de Riesz
de la forma (g) =
_
1
1
g(x)du(x), donde u es la funcin escaln.
0.18.22. Transformadas
Finalmente, en esta seccin, denimos las transformadas de Fourier del
escaln y de las seales constantes, en un sentido muy especial, que afortu-
nadamente tiene muchos puntos de empate con las transformadas L1 y L2.
Inicialmente, denimos la clase de Schwartz y las distribuciones temperadas.
Decimos que una funcin f : R R est en la clase de Schwartz, [, si
es indenidamente derivable y ella y sus derivadas decrecen rpidamente en
innito, en el sentido que , N supx
f (x) : x R <
Las funciones innitamente derivables de soporte compacto y otras como
e
x
2
que no tienen soporte compacto, estn en [. p
a,b
( f ) := supx
f (x) : x
R, determina una familia contable de seminormas para [con la que se dene
su topologa: f
n
converge a 0 si y slo si el lmite cuando n tiende a innito
de p
a,b
( f ) es cero, para cada y cada naturales.
El espacio de funcionales continuos sobre [, que se denota [
se llama
espacio de distribuciones temperadas.
Teorema 5. La transformada de Fourier es una aplicacin continua de [ en [ tal
que:
1.
_

g(x)H(x)dx =
_

h(x)G(x)dx donde H es la transformada de h y G la de g.

2. g(t) =
1
2
_

G()e
jt
d (frmula de inversin)
Denicin 9. La transformada de Fourier de [
es la distribucin temperada
[
dada por g [(g) = (G)

Teorema 6. La transformada de Fourier es una biyeccin lineal continua.
Denicin 10.
Llamamos a g el ncleo del funcional dado por ( f ) =
_

g(t) f (t)dt.
Llamamos a g la semilla del funcional dado por ( f ) =
_

f (t)dg(t).
Es interesante observar lo que le sucede, cuando tienen ncleo o semilla, a
los ncleos o semillas de las distribuciones y en la denicin 9.
0.18.23. La distribucin de Dirac
Considere la distribucin dada por ( f ) = f (0), que no tiene ncleo pero
s semilla: el escaln u(t). Por denicin, su transformada es la distribucin
dada por ( f ) = (F) = F(0), donde F es la transformada de f . As, D s tiene
ncleo, ya que ( f ) = F(0) =
f (t)e
j0t
dt =
f (t)1dt y vemos que el ncleo

de D es la funcin constante 1.
0.18. CLCULO 127
0.18.24. La distribucin constante
Sea dada por ( f ) =
_

f (t)dt, que, como vemos, tiene ncleo la funcin

constante 1. Por denicin, su transformada est dada por,
K( f ) = (F)
=
_

F()d
=
_

f (t)e
jt
dtd
?
=
_

f (t)
_

e
jt
ddt
que sinembargonotiene sentido, ya que
_

e
jt
dnoconverge. As, tenemos
que K no tiene ncleo.
0.18.25. La distribucin con ncleo escaln
Considere la distribucin con ncleo u(t): ( f ) =
_

u(t) f (t)dt =
_

0
f (t)dt.
por denicin, la transformada de m est dada por,
M( f ) = (F)
=
_

0
F()d
=
_

0
_

f (t)e
jt
dtd
?
=
_

f (t)
_

0
e
jt
ddt
que tampoco tiene sentido, ya que
_

0
e
jt
d no converge. As, tenemos que
M no tiene ncleo.
0.18.26. La distribucin valor principal de 1/x y la transforma-
da de Hilbert
Considere la distribucin temperada dada por ( f ) = lm
0
_
>0
f (t)
t
dt. Por
denicin, la transformada de f est dada por,
( f ) = (F)
= lm
0
_
>0
F()
d
= lm
0
_
>0
1
f (t)e
jt
dtd
?
=
_

f (t) lm
0
_
>0
e
jt
ddt
resultando un distribucin con ncleo
_
>0
e
jt
d = jsgnt, donde sgn es la

funcin sgnum. (sgn vale 1 para argumento positivo, -1 para argumento neg-
ativo y 0 para argumento nulo). Sugerencia: evale
_
0
e
jt
dt usando clculo de
residuos.
As, en cierto sentido, 1/x y jsgn(x) son un par de Fourier.
Variacin de seales discretas
Sea X : Z C. La variacin total de la seal se dene como
i=
x
i

x
i1
.
Variacin promedio
La variacin promedio se dene como lm
N
1
2N+1
N
i=N
x
i
x
i1
.
Ejercicio. Si X es una exponencial compleja peridica con periodo N, muestre
que su variacin promedio est dada por
1
N
i=
x
i
x
i1
0.18. CLCULO 129

Ejercicio. Muestre que la variacin promedio de e
j
0
n
est dada por 1 e
j
0
Problemas
1. Muestre o d un contraejemplo en relacin con la armacin: Si una
relacin es simtrica y transitiva, entonces es reexiva.
2. C y D son dos subconjuntos del rango de f . Demuestre o d un contrae-
jemplo:
a) f
1
(C D) = f
1
(C) f
1
(D)
b) f
1
(C D) = f
1
(C) f
1
(D)
3. C y D son dos subconjuntos del dominio de f . Demuestre o d un con-
traejemplo:
a) f (C D) = f (C) f (D)
b) f (C D) = f (C) f (D)
4. Muestre o d un contraejemplo: Para ningn conjunto hay una biyeccin de
ste a su conjunto potencia.
5. D ejemplos de conjunto nito, contable innito y no contable.
6. Muestre que hay innitas ternas pitagricas. (Nmeros naturales a, b, c
tales que a
2
+ b
2
= c
2
)
7. Muestre que si se tiene una inyeccin de un conjunto A al conjunto Nde
los nmeros naturales, y que si Ano es nito, entonces hay una biyeccin
de A a N.
8. a) D un ejemplo de un subconjunto acotado de Qque no tenga supr-
mum (racional).
b) Es cierto que todo subconjunto acotado de R tiene suprmum
(real)?
9. a) Diga si el siguiente conjunto tiene suprmum racional: A = q Q :
q
2
< 9.
b) Diga si el siguiente conjunto tiene suprmum racional: B = q Q :
q
2
< 8.
10. D una sucesin de intervalos cerrados encajonados de racionales, con
interseccin vaca.
11. Sea f : R
1
(/2, /2) dada por f (x) = arctan(x). Diga si f es una
biyeccin, o no.
12. D las fases de 1 + j y de 1 j.
13. Sea N un nmero entero positivo y sea r un nmero entero. Sea z = e
j
2
N
r
,
muestre que z
N
= 1.
14. Muestre que e
jn
= e
jn
= cos(n) = cos(n) = (1)
n
.
15. D un ejemplo de una serie

n=0
q
n
de racionales q
n
que converja a un
irracional pero que, en valor absoluto

n=0
q
n
, converja a un irracional.
16. Muestre que e
jt
+ 1 = 2e
jt/2
cos(t/2).
17. Graque en el plano complejo 1 e
j
, [0, 2].
0.18. CLCULO 131
18. Para [, ], graque la fase de e
j
e
2j
.
19. Graque la magnitud y la fase de f (t) = e
jt
+ 1 para t [, ].
20. Sea f : R C dada por f () =
j
1+j
. Graque magnitud y fase.
21. Ses H : R C dada por H() =
1
1+j
.
a) Graque magnitud y fase.
b) Sea F() = H(+ 2) + H( 2). Graque magnitud y fase.
22. a) Graque en el plano complejo la imagen de la funcin f : R C
dada por f (t) =
e
jt
1+e
jt
b) Graque aproximadamente las partes real e imaginaria, contra t.
c) Graque aproximadamente la magnitud y la fase contra t.
23. Sea f : R C dada por f () = e
j2
. Graque la magnitud y la fase de
f (), para [0, 2].
24. Calcule
2024
n=0
e
j2/7
.
25. Sea p : R Cdada por p(t) = (tz)(tz
), donde z = e
j
, R. Muestre
que p es real y no negativa.
26. Se tiene f : C C dada por f (z) = z
. Calcule el lmite cuando a R

tiende a cero de
f (z+h)f (z)
h
, si:
a) h = a(1 + j)
b) h = a(1 j)
27. Muestre que p(z) = z
N
1 tiene una raz real (z = 1) y N 1 races
complejas, dada por las races de q(z) = z
N1
+ z
N2
+ + z + 1.
28. Deduzca las ecuaciones de Cauchy-Riemann.
29. Sea f : Z C dada por f (n) = e
j(2/5)n
, indique en el plano complejo los
puntos f (n) para n / 10, 10/.
30. Graque la magnitud y la fase de f contra n, para n /0, 10/, donde f es
la funcin denida en el problema anterior.
31. Encuentre k //0, 4 tal que e
j(2/5)1024
= e
j(2/5)k
.
32. Sea z = e
j2(1/)(12/15)
. D el mnimo valor entero de n, positivo, tal que
z
n
= 1.
33. Encuentre un polinomio equivalente a a(1 z
9
)/(1 z), para z 1.
34. Sea f : C C dada por f (z) = (1 + 2j)z. Sea T el tringulo mostrado.
dibuje la imagen f (T) de T.
35. Graque la imagen del tringulo rectngulo con vrtices , 1 y 1 + j con
respecto a la funcin f : C C dada por f (z) = (1 + 2j)z
2
.
36. Sea f : C 1 C dada por f (z) = (1 z)/(1 + z).
0.18. CLCULO 133
a) Graque en el plano complejo las imgenes con respecto a f de los
ejes real e imaginario de C.
b) Diga si f es una biyeccin, o no. Cul es la preimagen de -1?
37. Sea f : C C dada por f (z) = e
z
. Graque las imgenes de los ejes del
plano complejo, y de las lneas que salen del origen con ngulos de n/4.
diga si es sobreyectiva.
38. Graque en el plano complejo la imagen de la funcin f : R C dada
por f (t) = cos
3
(t) + j sen
3
(t), para t [0, 2]. Diga si f est parametrizada
por longitud de arco.
39. Sea f : R Cuna funcin continua parametrizada por longitud de arco.
Es posible que la imagen de f en el plano tenga un vrtice? (un vrtice
es un punto con dos tangentes) Es f diferenciable?
40. Sea p : R R dada por p(x) = (x z
1
)(x z
2
), donde z
1
= e
j
, R,
z
2
= z
1
y muestre que p es una funcin no negativa.
41. Graque en el plano complejo la imagen de F : R C dada por F() =
e
j
1+e
j
. Tambin, graque la magnitud y la fase de F para [0, 2].
42. D la magnitud y la fase de
8
n=0
(1 + j)
n
.
43. Se tiene g : C C dada por g(z) = e
z
. Dibuje la imagen de las lineas,
a) 1 + jt, con t [0, ).
b) 1 jt, con t [0, ).
c) t(1 + j), con t [0, ).
d) t(1 j), con t [0, ).
44. Sea f : C C dada por f (z) = z
2
. Diga si f respeta ngulos entre lneas que
se intersecten en los puntos z = , z = 1 y z = 1 + j. Explique.
45. Se sabe que f : R
3
R
1
es lineal y que f (0, 1, 1) = 1, f (1, 0, 1) = 2 y que
f (0, 1, 0) = 3. Encuentre A tal que f (x) = Ax.
46. Encuentre x en trminos de y si:
a)
b)
47. Encuentre la extensin en series de Taylor de ln(1+x) alrededor de x = 0.
48. Encuentre la extensin en series de Taylor de
1
1+x
alrededor de x = 0.
49. Encuentre la extensin en series de Taylor de la funcin ln(1 + 2z
1
).
Cul es la regin de convergencia?
50. Diga si las siguientes series convergen. Si s, d el valor de convergencia.
a)
n=1
1
n
0.18. CLCULO 135
b)
n=1
1
n
2
51. Exprese
9
n=0
z
n
como una funcin racional de z, para z 1.
52. D los primeros cinco coecientes de la extensin en series de Taylor de
la funcin f : R R dada por f (x) = 2
x
, alrededor de cero.
53. Graque la magnitud y la fase de
n=1
(
j
2
)
n
. Indique los nmeros
2
n=1
(
j
2
)
n
y
5
n=1
(
j
2
)
n
en el plano complejo.
54. Sea g : (1, 1] R dada por g(x) = ln(1 + x). Encuentre los coecientes
de la serie de Taylor a
0
+
n=1
a
n
x
n
de g al rededor de cero. Diga si la serie
encontrada converge tambin para x = 1. Encuentre f
(1
) (la derivada
por la izquierda en 1). Diga si f
(1
) =
n=1
na
n
x
n1
con x = 1.
55. Encuentre la transformada zeta U(z) con su respectiva regin de conver-
gencia (RC) del escaln discreto u
n
(u
n
= 1, si n 0, u
n
= 0, si n < 0). A
continuacin, encuentre otra seal discreta con transformada zeta U(z)
pero con diferente regin de convergencia.
56. Demuestre que si
n=0
a
n
converge, entonces
n=0
a
n
tambin.
57. Muestre que
10
n=10
z
n
= z
10 1z
2
1
1z
.
58. Graque las seales sen(5t) y sen
2
(5t).
59. Diga si la seal sen(5t) es derivable o no.
60. Diga si la seal sen
2
(5t). es derivable o no.
61. Encuentre el lmite, cuando t tiende a cero, de
sent
t
, t R
1
.
62. Encuentre el lmite, cuando h tiende a cero, de
1
h
_
h
0
cos xdx.
63. Sea f : C C dada por f (z) = z
. Encuentre, si existe, f
(z).
64. Sea f : C 1 C dada por f (z) =
z1
z+1
. Diga si f respeta ngulos en
z = , j, 1. Explique.
65. Calcule
_
1
1
f (t)d(t) donde f (t) = t
2
y (t) = 0 para t < 0 y (t) = 1 t
para t 0.
66. Evale
_

e
t
2
e
jt
dt, R.
67. Evale
_

1
1+t
2
e
jt
dt, R.
68. Evale
_

d
(1,25cos )
2
.
69. Encuentre la variacin total de f (x) = x(x1)(x2) en el intervalo [1, 3].
70. Encuentre la variacin total de la funcin sent en el intervalo [0, 4].
71. Sean f, : R R dadas por (x) =
n=0
u(x n 0,5) y, g(x) = x
2
, para
x 0 y g(0) = 0. Calcule
_

g(x)d(x).
72. Sea (t) = u(t 0,25) u(t 0,75). Calcule
_

0
sen(t)d(t),
_

0
sen
2
(t)d(t)
y
_

0
cos(2t)d(t).
73. Calcule la integral de lnea
_
e
z
2
d donde es el camino dado por
(t) = 1 + jt, t[0, 1], (t) = j + 1 t, t[1, 2].
74. Calcule
_

e
t
2
e
jt
dt.
75. Calcule
_
1
1
u(t)d cos(t) usando la frmula de integracin por partes.
0.18. CLCULO 137
76. Calcule
_
2
0
f ((t))d(t), donde f : C C est dada por f (z) = z
2
y
: R C est dada por (t) = e
j(t+u(t1))
(u(t) es el escaln).
77. Sea f : [0, ) R
1
dada por f (x) = 0 si x = 0 y f (x) = sen(1/x) si x > 0.
Diga si f es de variacin acotada en [0, 1]. Explique.
78. a) Dibuje la grca y la imagen de la funcin g : [0, 8] C dada por
g(t) = te
jt
. Tambin graque la magnitud y la fase de la funcin.
b) Graque la magnitud y la fase de f : C C dada por f (z) = sen(z).
Tambin, graque las parte real e imaginaria de la funcin.
c) Graque la magnitud y la fase de f : C C dada por f (z) = e
z
.
Tambin, graque las parte real e imaginaria de la funcin.
79. Demuestre que la funcin f : C 0 C dada por f (z) =
1
z
puede ser
implementada en la siguiente forma:
Coloque el polo sur de una esfera de radio
1
2
sobre el origen del plano.
Suba los puntos del plano a la esfera, usando proyeccin estereogrca.
Rote la esfera manteniendola tangente al plano, y manteniendo invari-
antes las imgenes del eje real, de tal forma que al nal, con proyeccin
estereogrca inversa, la imagen del punto que parti del punto j del
plano inicialmente, aterrice ahora sobre el punto j.
80. Demuestre o d un contraejemplo: para cada nmero complejo z 0,
para todos nmeros complejos w
1
, w
2
y w
3
, no colineales en el plano, los
tringulos w
1
w
2
w
3
y zw
1
zw
2
zw
3
son similares.
81. Represente los productos de complejos y de cuaternios con matrices; es
decir, diga cmo obtener una matriz a partir de cada complejo (o cuater-
nio) de tal forma que al multiplicar las matrices correspondientes, resulte
la matriz correspondiente al producto de los complejos (o cuaternios).
82. Graque la imagen del conjunto z C : t R, z = e
jt
con respecto a
la funcin f : C1 C dada por f (z) =
z1
z+1
. Graque la magnitud y la
fase con respecto a t.
83. Demuestre que si h es un cuaternio unitario y q un cuaternio puro, en-
tonces hqh
es tambin un cuaternio puro.

84. D frmulas para el ngulo y el cuaternio puro q que permitan expresar
el cuaternio a + bi + cj + dk en la forma cos() + q sen().
85. Encuentre los puntos de acumulacin del conjunto z C : n N,
1
n
+
j
n
.
86. Encuentre el valor de la serie

n=1
1
n
2
.
87. Encuentre el lmite cuando z tiende a 0 de e
1
z
.
88. Demuestre que las sucesiones reales de Cauchy convergen (a reales).
89. Encuentre la matriz Jacobiana de f : R
2
R
2
, dada por f (x, y) =
(
x
4
y
4
x
3
+y
3
,
x
4
+y
4
x
3
+y
3
), si (x, y) (0, 0) y, f (0, 0) = (0, 0).
90. Diga si g : C C dada por g(x + jy) =
x
4
y
4
x
3
+y
3
+ j
x
4
+y
4
x
3
+y
3
derivable.
91. Encuentre tres seales discretas con transformada zeta X(z) =
1+z
z
3
+2z
2
+5
6
,
indique las regiones de convergencia correspondientes.
92. Encuentre la serie de Taylor alrededor de 0 de g : [1, ) R; usando
10 trminos, aproxime raz de 2.
93. Encuentre la transformada zeta U(z), z RC del escaln discreto u,
(u
n
= 1 si n 0 y u
n
= 0 si n < 0). A continuacin, encuentre otra seal
discreta con transformada U(z) pero diferente regin de convergencia.
0.18. CLCULO 139
94. Sea f : C 1 C dada por f (z) =
z1
z+1
. Diga si f preserva ngulos en
z = , z = j y z = 1. Explique.
95. Diga si la siguiente funcin tiene derivada compleja en el origen. Tam-
bin, evale las ecuaciones de Cauchy-Riemann all.
f (x + jy) =
x
4
y
4
x
3
+ y
3
+ j
x
4
+ y
4
x
3
+ y
3
96. D una sucesin de intervalos cerrados encajonados de racionales con
interseccin vaca.
97. Encuentre las componentes del inverso del cuaterio a + bi + cj + dk.
98. Calcule la integral
_
2
0
f ((t))d(t), donde f : C C est dada por
f (z) = z
2
y : R C est dada por e
j(t+u(t))
. Donde u es el escaln.
99. D el periodo de la seal s : Z C dada por s
n
= e
j(6/27)n
.
100. Exprese la seal s : Z C dada por s
n
= [n]
3
, como una suma de
exponenciales complejas.
101. Muestre que

10
n=10
z
n
= z
10 1z
21
1z
.
102. Sea A un conjunto de reales, considerados como cortes de Dedekind.
Recuerde que el orden lineal para R est dado entonces por x y si y
slo si x y. suponga que :=
_
A
Q. Demuestre entonces que es la
una cota superior mnima de A; osea, que es un corte de Dedekind, que
es una cota superior de A y que no hay cotas superiores de A menores
que .
103. Cada sucesin de reales no decreciente y acotada superiormente, con-
verge.
104. Cada sucesin real acotada tiene una subsucesion convergente.
105. Una sucesin de reales converge si y slo si es una sucesin de Cauchy.
106. Si p y q son cuaterinios, demuestre o d un contraejemplo para, (pq)
=
p
.
107. Encuentre una sucesin de racionales que converja a un irracional pero
que en valor absoluto converja a un racional.
Referencias
[1] Mathematical Analysis. Tom M. Apostol. Adyson-Wesley,
Reading MA, 1974. (Integral de Riemann-Stieltjes)
[2] EssayonTheoryof Numbers. RichardDedekind. Dover, N.Y.,
1963.
[3] Science and Hypothesis. Henri Poincar. Dover, N.Y., 1963.
[4] Contributions to the Founding of the Theory of Transnite
Numbers. Georg Cantor. Dover, N.Y., 1955.
[5] Geometry of Complex Numbers. Hans Schwerdteger. Dover,
N.Y.,1979.
[6] Elementary Theory of Analytic Functions on One or Several
Complex Variables. Henri Cartan. Dover, N.Y., 1995.
[7] Principles of Mathematics. Bertrand Russell. Norton, N.Y.,
1902. (Relaciones)
[8] The Large, the small and the Human Mind. Roger Penrose.
[9] Theory of Complex Functions. Reinhold Remmert. Springer,
N.Y.,1991.
141
142 REFERENCIAS
[10] The Real Line and Calculus. William Eaton. Class notes for
665A. The University of Texas at Austin, 1985. (Huecos de Q)
[11] Visual Complex Analysis. Tristan Needham. Clarendon, Ox-
ford, 1997. (Visualizaci del producto de complejos)
[12] Quaternion-Fourier Transforms for Analysis of Two Dimen-
sional Linear Time-Invariant Partial Diferential Systems. Proc.
32nd Conf. Decision Contr., Dec. 1993, pp. 1830-1841.
[13] Calculus. Clculo Innitesimal. Michael Spivak. Revert,
Mxico, 1992. (Sucesiones, denicin de reales)
[14] Georg Cantor, His Mathematics and Philosophy of the In-
nite. J.W. Dauben. Princeton University Press, Princeton, 1979.
[15] Hypercomplex Fourier Tansformof Color Images. IEEEInter-
national Conference on Image Procesing (ICIP 2001). S.J. Sang-
wine. Thessaloniki, Grece, Oct. 2001, vol. I, pp. 137-140.
[16] Quaternions and Rotation Sequences. J.B. Kuipers. Princeton
University Press, Princeton, 1999.
[17] Computational Conformal Mapping. P.K. Kythe. Birkhuser,
Boston, 1998. (ecs- Cauchy-Riemann y diferenciabilidad)
[18] OnQuaternions andOctonions. J.H. ConwayandD.A. Smith.
AK Peters, Natick, 2003.
[19] Elementary Geometry in Hyperbolic Space. Werner Frenchel
- de Gruyter, Berln, 1989.
[20] Circular Processing of the hue variable: a Particular Trait
of Colour Image Procesing. A. Restrepo, C.Rodriguez and
REFERENCIAS 143
C.Vejarano. VISSAP-Second International Conference on Com-
puter Vision Theory and Applications. Barcelona, Spain, March
2007
[21] Colour spaces.A. Restrepo, C.Rodriguez and C.Vejarano.
VISSAP-First International Conference on Computer Vision
Theory and Applications. Setubal, Portugal, 2006.
[22] Directional Statistics. K.V. Mardia and P.E. Jupp. Wiley,
Chichester, 2000.
[23] Color Appearance Models. Mark D. Fairchild. Wiley, 2005.
Captulo 1
Seales y sistemas
1.0. INTRODUCCIN
Imagnese en una noche despejada al capitn de un barco comunicndose
con el de otro por medio de seales luminosas. Imagine que en el cerebro de
una persona se origina un impulso nervioso que al cabo de algn tiempo hace
que la persona mueva su mano izquierda. Imagine que por el cable de una
impresora viaja una seal que har que se imprima la frase Hello World.
Un modelo sencillo de un sistema de comunicacin incluye un emisor, un
canal de transmisin y un receptor; pero hay adems otras cosas involucradas.
Por una parte est el vocabulario y la sintaxis del lenguaje de comunicacin.
Por otra parte est la semntica de los mensajes que se pueden transmitir. Por
otra estn las caractersticas de la implementacin fsica del sistema.
En este curso, el sentido tcnico de la palabra seal est dado por el aspecto
matemtico de lo que se transmite en un proceso de comunicacin. Aunque este sea
un aspecto del proceso de comunicacin, su estudio resulta provechoso y bsi-
co para el entendimiento y potencial avance de los sistemas de comunicacin
144
1.0. INTRODUCCIN 145
electrnicos y de otros tipos.
Como decimos, una seal es desde cierto punto de vista, una funcin. As,
una seal es una abstraccin de lo que se transmite en un proceso de comu-
nicacin. Se supone que una seal contiene informacin y que es producida
por un proceso fsico: es la variacin de una magnitud fsica en trminos de
algn parmetro (tpicamente el parmetro tiempo) y no cualquier funcin
que pueda denir un matemtico.
Como ejemplo de seal, tenemos la funcin de voltaje (en la variable tiem-
po) resultante al convertir la intensidad de la onda de presin de aire corre-
spondiente a algn sonido por medio de un micrfono, como se ilustra en la
gura 1.1. O tambin, la funcin de transmitancia luminosa (en la variable
posicin) de una pelcula fotogrca despus de haber sido expuesta. Ms
Figura 1.1: Obtencin de una seal
especcamente, usaremos la siguiente denicin de seal.
Denicin 11. Una seal continua es una funcin cuyo intervalo de R
N
, con la
posible excepcin de un subconjunto denso en ninguna parte de puntos.
146 CAPTULO 1. SEALES Y SISTEMAS
Denicin 12. Una seal discreta es una funcin cuyo dominio es un intervalo
de Z
N
. El rango de una seal discreta es un conjunto de nmeros; por ejemplo, el
conjunto de los nmeros complejos, o el intervalo /0, 255/.
Denicin 13. Un subconjunto W de R
N
es denso en ninguna parte si para
cada punto de W hay in intervalo de R
N
que contiene al punto y a ningn otro
elemento de W.
Denicin 14. Una seal continua en sentido laxo es una seal continua que se ha
dejado sin denir en un subconjunto denso en ninguna parte de su dominio.
La ingeniera es a veces el arte de asignar nmeros a magnitudes fsicas con
el objeto de optimizar diferentes aspectos en un diseo. As como los fsicos,
los ingenieros cuantican las variables con que trabajan, lo que les permite usar
herramientas matemticas y poder hablar objetivamente de los resultados
esperados de un diseo.
Ejemplo. En la gura 1.1 indicamos la funcin de voltaje v denida en el
intervalo (t
1
, t
2
), los valores del voltaje son nmeros reales: v : (t
1
, t
2
) R
1
Seguramente, no cualquier funcin es una seal que provenga de algn
fenmeno fsico, pero la funcin matemtica es un poderoso modelo de seal.
Muchas de las herramientas usadas en ingeniera para el anlisis de seales,
estn basadas en el clculo y en otras disciplinas matemticas.
En un principio, en ingeniera de comunicaciones, las seales consideradas
eran generalmente continuas: seales de voltaje o corriente, en el dominio del
tiempo. La idea de poder transmitir palabras a distancia era muy atractiva. As
como el estudio de la electricidad se impulso con los experimentos de Volta
con patas de ranas, probablemente la idea de usar un cable coaxial para la
transmisin de informacin a distancia se inspir en los axones largos y mieli-
nados del sistema nervioso de los mamferos. El problema con un cable coaxial
(o de bra ptica) es la atenuacin que sufre la seal con la distancia. As, re-
sultaba muy importante poder amplicar una seal. La tecnologa de tubos
de vaco con electrodos conectados a terminales externos permiti efectuar tal
amplicacin. esta misma tecnologa permiti el desarrollo del tubo de rayos
catdicos, que es con lo que se construyen las pantallas de TV comnmente.
A nales de la dcada de los 40 se desarroll un dispositivo amplicador
semiconductor que era pequeo, conable y permita integracin (es decir, la
fabricacin de un circuito electrnico muy denso: (muy denso: miles de com-
ponentes en un milmetro cuadrado, as como la posibilidad de producirlos en
gran cantidad): este dispositivo es el transistor de silicio. Probablemente en un
futuro se usen las seales luminosas tanto como las electrnicas.
La tecnologa de las comunicaciones y del control para los vuelos Apolo
fue anloga en gran medida (aunque usaron computadores rudimentarios al
nal). En los sesentas, el anlisis de seales discretas o series de tiempo era
ms del dominio de los estadsticos que de los ingenieros.
A partir de los setentas, la tecnologa digital entr en auge; se desarrollaron
varias familias de circuitos integrados que implementaban funciones lgi-
cas, se invent el microprocesador, aparecieron las calculadoras electrnicas
de bolsillo (de 4 operaciones), las memorias bajaron de precio y aumentaron
en capacidad, etc. (la industria electrnica japonesa que hasta el momento
era de calidad regular lleg a sobrepasar el desempeo de la industria esta-
dounidense en algunos aspectos). Paralelamente, la teora matemtica bsica
que sera usada para el anlisis y el tratamiento lineal de seales digitales, se
sostic en algn grado interpretando algunos resultados aplicables y desar-
rollando otros como por ejemplo la transformada rpida de Fourier. Hoy en
da, para tasas de muestreo por debajo de, aproximadamente, 10
6
Hz, la tec-
nologa digital supera en muchos aspectos a la tecnologa anloga; en el caso
ms patente es el tratamiento de seales de audio donde el uso de tcnicas
digitales permite una gran versatilidad en la implementacin de sistemas para
el tratamiento de seales. Desde los ochentas, compaas como Texas Instru-
ments producen procesadores (DSP o digital signal processor) con arquitectura
orientada al tratamiento de seales.Desde la dcada de los noventas ha habido
un boom de las comunicaciones, que ha sido posible en parte por la tecnologa
para el tratamiento digital de seales.
Por razones de espacio no hemos dado la denicin de la integral de
Lebesgue. Sinembargo, ella junto con la teora de la medida de Lebesgue, son
necesarias para denir rigurosamente los espacios L
p
, p [1, ].
1.1. CLASIFICACIN DE LAS SEALES 149
1.1. Clasicacin de las seales
Inicialmente clasicamos las seales dependiendo de la cardinalidad de los
conjuntos dominio y rango de la funcin correspondiente. Si el dominio de la
seal es un conjunto contable, se dice que la seal es discreta.
Figura 1.2: Una seal discreta de longitud nita
Ejemplo.
Como dijimos, un ingeniero normalmente cuantica las variables que usa,
es decir, las modela con conjuntos de nmeros. En relacin con el ejemplo
anterior, podemos denir la seal s : /1, 5/ /0, 1/ donde el conjunto /1, 5/
representa los das y el conjunto /0, 1/ las posibilidades llovi y no llovi:
s(1) = 0, s(2) = 1, etc. Dado que en este curso el anlisis de Fourier tiene en
papel importante, asumiremos que el rango de una seal es un subconjunto
de los nmeros complejos C.
Asumiremos tambin que el rango es realista en el sentido que est dado
por el conjunto de valores que la seal en efecto podra tomar. Si el rango de una
seal es nito, se dice que la seal es digital. este punto es algo sutil ya que
dos funciones pueden tener el mismo grco y distinto rango; como acabamos
de decir, se asume que el rango es el conjunto de valores que la seal puede
tomar, fsicamente. por ejemplo, la seal almacenada en un disco compacto
es digital ya que cada componente est codicado con 16 bits. La seal del
ejemplo anterior es una seal digital, as como la del ejemplo siguiente:
Ejemplo. f : 1, 2, 3, 4, 5 /0, 15/, dada por f (1) = 10, f (2) = 0, f (3) = 1,
f (4) = 9, f (5) = 15.
Cuando una seal se procesa o se almacena en un dispositivo electrnico
de tecnologa digital, por ejemplo un computador, la seal es normalmente
discreta y digital. es discreta ya que slo una cantidad nita de valores de la
seal pueden ser almacenados y es digital ya que los valores se representan
en algn cdigo de bits y por lo tanto slo hay un nmero nito de valores
posibles que la seal puede tomar.
Una seal continua es una seal cuyo dominio es R
1
o, en general, un
intervalo de R
N
, con la posible excepcin de un conjunto nito de puntos.
Es importante resaltar que las deniciones de continuidad de un funcin y de
continuidad de una seal son diferentes. La continuidad de una funcin es la se
ve en un curso de clculo y se repas en el captulo anterior. La continuidad
de una seal, como se acaba se denir aqu, depende slo de su dominio, f
puede ser una seal continua y no ser una funcin continua.
Seales escaln
La seal escaln continua u : R C est dada por
u(t) =
_
_
1 si t 0
0 si t < 0
1.1. CLASIFICACIN DE LAS SEALES 151
La seal escaln discreta u : Z C est dada por
u
n
=
_
_
1 si n 0
0 si n < 0
Tambin, la seal impulso discreta, : Z C est dada por
n
=
_
_
1 si n = 0
0 si n 0
Por razones que explicaremos, en este curso no deniremos la seal impulso
continua.
Ejercicio. Puede ser digital una seal continua?
Ejemplo. Sea v : R
1
Ndonde v(x) = parte entera(x)
Figura 1.3: Una seal continua. (La funcin correspondiente no es continua)
Tamao
Denimos el tamao de un conjunto a continuacin. Si el conjunto es con-
table, sutamao est dado por sucardinalidad. Si el conjunto es unsubconjunto
de R
N
, su tamao est dado por la correspondiente medida (de Lebesgue) de
longitud, rea, volumen, etc. del subconjunto.
Ejemplo. El tamao del intervalo /4, 9/ es 6.
El tamao de Z es innito.
El tamao del producto cartesiano /0, 1023/ /0, 1023/ es 1.048.576 (o un
mega en la jerga de los programadores).
El tamao del intervalo (0, 10) es 10, as como tambin lo es el del intervalo
[0, 10].
El tamao de R
1
es innito.
El tamao del producto cartesiano [2, 5] [0, 2] es 4.
Soporte
El soporte de una funcin es el subconjunto del dominio donde la funcin
toma valores diferentes de cero.
Ejemplo. El soporte de la seal escaln continua u : R C, es el intervalo
[0, ).
El soporte de la seal seno sen : R
1
C, es R
1
Z.
El soporte de la seal escaln discreta, u : Z C, es el conjunto de los nmeros
naturales.
El soporte de la seal pulso discreta p : Z C, p
n
= u
n
u
n10
es /0, 9/.
Longitud y duracin
La longitud de una seal est dada por el tamao de su dominio. La
duracin de una seal est dada por el tamao del intervalo ms pequeo
que contenga su soporte.
Ejemplo. A continuacin se muestra una seal digital de longitud nita. Sea
s : /0, 3/ 0, 2 dada por s = [0, 2, 0, 2], s(0) = 0, s(1) = 2, s(0) = 0, s(1) = 2.
1.2. SISTEMAS 153
Figura 1.4: Una funcin del conjunto 4 al conjunto de los nmeros reales
Ejemplo. La seal s : NC dada por s(n) = 2
n
es de longitud innita.
Ejemplo. La seal continua g(t) = u(t) u(t 1), donde u es la seal escaln
continua, es de longitud innita pare de duracin nita.
Ejemplo. La duracin de la seal discreta s
n
=
n
+
n5
es 6. (Por qu?)
Ejercicio. Graque la seal g(t) del ejemplo anterior para t (1, 2).
Despus de toda esta taxonoma, concluimos esta seccin diciendo que en
este curso, en general, las seales continuas sern funciones de R
1
C las
seales discretas de longitud innita sern funciones de Z C y las seales
discretas de longitud nita, funciones de N C, donde N = /0, 1, . . . , N
1/ es algn nmero natural, por ejemplo, N = 4 = 0, 1, 2, 3. Casi siempre
trabajaremos con seales de uno de estos tres tipos.
1.2. Sistemas
El concepto de sistema es tan bsico como el de seal pero si denicin
matemtica es ligeramente ms compleja. La idea es que los sistemas trans-
forman las seales. Un sistema es una funcin cuyos dominio y rango son
Figura 1.5: Una seal discreta con rango complejo
conjuntos de seales. Los sistemas son modelos del tipo caja negra en cuan-
to que no necesariamente conocemos su implementacin fsica. Sabemos qu
entra y qu sale pero solamente se tiene una abstraccin de lo que ay dentro
de la caja: aveces interesa ms saber qu hace el sistema que cmo lo hace.
Con frecuencia, en teora de seales los sistemas se denominan filtros.
En matemticas, una funcin cuyo dominio sea un conjunto de funciones se
conoce como un funcional (si el rango es un conjunto de nmeros), o como
una transformacin (si el rango es un conjunto de funciones). As, un sistema
puede ser una familia indexada de funciones.
En teora de seales, de control y de sistemas, se acostumbra representar un
sistema como una caja negra; sin embargo, un ingeniero seguramente deber
tener en mente otras caractersticas del dispositivo que se modela, ya que todo
modelo tarde o temprano deja de ser vlido, por una u otra razn.
Si tanto el dominio como el rango contienen seales discretas nicamente,
se dice que se tiene un sistema discreto. Si tanto el dominio como el rango
contienen seales continuas nicamente, se tiene un sistema continuo. En
otro caso, se tiene un sistema mixto.
Si tanto el dominio como el rango son espacios vectoriales sobre el mismo
1.2. SISTEMAS 155
Figura 1.6: Un sistema es una funcin entre conjuntos de seales
Figura 1.7: Representacin de un sistema como una caja negra
cuerpo y el sistema es una transformacin lineal, se dice que el sistema es
lineal. En caso contrario, se dice que el sistema es no lineal.
Notacin
Suponga que se tiene un sistema continuo S y que cuando la seal de
entrada es la seal x, la seal de salida es, y = S(x). Si se quiere indicar el valor
que las seales toman en t, se escribe x(t) y y(t). Tambin, y(t) = [S(x)](t).
1.2.1. Espacio vectorial
Quizs sea este el momento conveniente para repasar la denicin de
espacio vectorial. decimos que la quntupla (V, +, K, +, , ), donde (V, +) es un
grupo abeliano (de vectores) con mdulo aditivo , y (K, +, ) es un anillo
(de escalares) con mdulo aditivo 0, y mdulo multiplicativo 1 y hay una
operacin de producto de escalares por vectores que es quizs la razn del
nombre escalar: escalar un vector. Las deniciones precisas de grupo y anillo
se dan en el captulo 4. Por ahora, decimos que, para cada , K y cada
v, w V, se tiene que:
1) Hay un elemento en V que se expresa v (v escalado por ).
2) (v + w) = ( v) + ( w)
3) ( + ) v = ( v) + ( v)
4) ( v) = ( ) v
5) 1 v = v
Ejercicio. 0 v = .
1.2. SISTEMAS 157
1.2.2. Transformacin lineal
Sean (V, +, K, +, , ) y (W, , K, +, , ,) espacios vectoriales sobre el mismo
campo. La funcin T : V W es una transformacin lineal si para cada
, K y cada x, y V se tiene que: T( x + y) = , T(x) , T(y). As
una transformacin lineal es una transformacin que preserva la estructura de
espacio vectorial. De manera anloga, T es lineal si cumple con las propiedades
de homogeneidad: K u V, T( u) = ,T(u), y de superposicin:
u, v V, T(u + v) = T(u) + T(v).
Ejercicio. Demuestre que si T es una transformacin lineal entre los espacios
(V, +, K, +, , ) y (W, , K, +, , ,) y si 0 es el mdulo del grupo (V, +) y es el
mdulo del grupo (W, ), entonces T(0) = .
Para cada sistema lineal, continuo o discreto, se tiene por lo tanto que la respuesta
a la seal cero es la seal cero.
Ejemplo. Considere el espaciovectorial Vde las funciones continuas h : [0, 1]
C, con las operaciones de suma de funciones, sobre el cuerpo de los complejos.
Considere el conjunto de los funcionales lineales, denido sobre este espacio.
Como se enuncia en el teorema de Riesz, para cada funcional lineal : V C,
de este tipo, hay una funcin g : R C, de variacin acotada, tal que se
puede representar como una integral de Riemann-Stieltjes:
(h) =
_
1
0
h(t)dg(t)
Ejercicio. En relacin con el ejemplo anterior, si (h) = h(0), para cada h, Cmo
est dada la funcin g?
1.2.3. Normas Elep
Dado unespacio vectorial, podemos proceder a denir una funcindel con-
junto de los vectores al conjunto de los nmeros reales no negativos, llamada
norma.
Ms precisamente, una norma (que se denota similarmente a un valor
absoluto: [ [, donde el punto indica el argumento) es un funcional real (es
decir una funcin de un conjunto de funciones a los reales) denido sobre el
conjunto de vectores de un espacio vectorial, que cumple con las propiedades
de ser positivo homogneo, denitivamente positivo y subaditivo:
i) [a f [ = a[ f [ para cada funcin f del espacio y cada escalar a. (Homo-
geneidad positiva)
ii) [ f [ = 0 si y slo si f es la funcin cero. (Denitivamente positivo)
iii) [ f + g[ [ f [ + [g[. (subaditividad)
Ocasionalmente se dice que la norma de una funcin de el tamao de la
funcin o qu tan lejos est del origen (el vector cero) del espacio vectorial.
Nosotros asumiremos que los vectores son seales.
Inicialmente consideramos algunas normas de seales discretas; usare-
mos eles minsculas para denotar las normas. Posteriormente consideraremos
seales continuas cuyas normas denotaremos con eles maysculas.
Algunas normas para subconjuntos de C
Z
(eles minsculas)
Sea s : Z C una seal discreta. Se dice que s es sumable en magnitud si
cada una de las series
1
n=
s
n
y
n=0
s
n
convergen (a nmeros reales). Sea l
1
el
conjunto de las seales discretas sumables en magnitud. Es claro que l
1
es un
espacio vectorial con la adicin r = s + t dada por r
n
= s
n
+ t
n
. en este espacio
1.2. SISTEMAS 159
denimos la norma l-1 dada por:
[s[ =
1
n=
s
n
+
n=0
s
n
n=1
s
n
+
n=0
s
n
Ejercicio. Muestre que efectivamente se tiene una norma.

Ejemplo. Suponga que para cada n, s
n
= s
n
, entonces, [s[
1
=
1
n=
2
n
+
n=0
2
n
=
1 + 2 = 3.
La norma l-2 de s est dada por:
[s[
2
=
_
1
n=
s
2
n
+
n=0
s
2
n
El conjunto de las seales discretas con normal l-2 nita se denota l

2
.
Ejercicio. Muestre que efectivamente se tiene una norma.
Ejercicio. Diga si las siguientes series convergen. en caso de convergencia, d
el valor del lmite.
n=1
1
n
n=1
1
n
2
n=1
(1)
n+1
n
Ms generalmente, denimos
[s[
p
:=
_
n=
s
p
_
_
1
p
Eles maysculas
Para seales continuas, tambin se dene la norma Ele-uno y se denota con
ele mayscula. Sea h : R
1
C una seal continua. La norma L-1 de h est
dada por:
[h[
1
=
_

h(t)dt
Se dice que s es integrable en magnitud si su norma L-1 es nita. El
conjunto de las seales continuas que son integrables en magnitud se denota
L
1
.
La norma L-2 de h est dada por:
[h[
2
=
_
_

h(t)
2
dt
El conjunto de las seales continuas con norma L-2 nita se denota L
2
. En
general para p > 1
[h[
p
=
__

h(t)
2
dt
_1
p
Originalmente en ingeniera elctrica, las seales consideradas eran fun-
ciones de voltaje o de corriente casi siempre. Dado que la potencia instantnea
que disipa una resistencia es proporcional al cuadrado del voltaje entre sus
terminales, y al cuadrado de la corriente que pasa por ella, resulta intuitivo
darle a la integral (y a la suma en el caso discreto) del cuadrado de seales el
nombre de energa. En teora de seales es comn hablar de la energa de una
seal h la cual est por el cuadrado de su norma L
2
: E(h) = ([h[
2
)
2
.
Para seales peridicas, dividimos la energa correspondiente a un pe-
riodo entre el valor del periodo T y la denominamos potencia promedio:
p =
1
T
_
T
0
h
2
(t)dt.
Ejercicio. Sea f : R
1
C dada por, f (t) =
1
t
para t 0 y f (0) = 0; encuentre
[ f [
1
y [ f [
2
. Diga si f L
1
y/o f L
2
.
1.2. SISTEMAS 161
Figura 1.8: La seal de voltaje h se aplica a una resistencia de un ohmio
Ejercicio. Sea f la funcin dada por
f (t) =
_
_
1
t
, si t (, 1) (1, )
0, si t [1, 1]
Encuentre [ f [
1
y [ f [
2
. Diga si f L
1
y/o f L
1
.
Ejercicio. Sea f la funcin dada por
f (t) =
_
_
1, si t = 0
sent
t
, si t 0
Encuentre [ f [
1
y [ f [
2
. Diga si f L
1
y/o f L
1
.
Ejercicio. Compruebe la tabla de la gura siguiente:
_
1
0

_

0

1
t

1
t
2
1
t
2
1
Tabla 1.1: Integrales
Figura 1.9: Grca
1
t
,
1
t
,
1
t
2
Ejercicio. Sea s : R
1
R
1
dada por s(t) = cos 5t. Diga si s(t) es una seal
integrable en valor absoluto. Diga si s
2
es una seal integrable.
L
p
[0, 2)
Para seales continuas denidas en un intervalo solamente, por ejemplo
el intervalo [0, 2), tambin se denen las normas ele-p, las cuales se denotan
como L
p
[a, b). Sea h : [0, 2) C una seal continua de longitud nita o,
equivalentemente, una seal peridica h : R
1
C con tiempo de repeticin
2 o, tambin equivalentemente, una seal h : S
1
C. La norma L-1 de h est
dada por:
[h[
1
=
_

h(t)dt
Se dice que s es integrable en magnitud si su norma L-1 es nita. El
conjunto de las seales continuas que son integrables en magnitud se denota
L
1
.
1.2. SISTEMAS 163
Figura 1.10: La seal cos 5t para t [0,1, 0,6]
Figura 1.11: La seal de la gura anterior, en valor absoluto
Figura 1.12: La seal dela gura anterior, al cuadrado
La norma L-2 de h est dada por:
[h[
1
=
_
_

h
2
(t)dt
El conjunto de las seales integrables con norma L-2 nita se denota L
2
.
1.3. La norma ele-innito
El conjunto de las seales continuas acotadas se denota L
y el de las
seales discretas acotadas se denota l
. La norma L- de una seal continua

s est dada por:
[s[
= sups(t) : t R
1
Similarmente, si r es una seal discreta, su norma l-est dada por:

[r[
= supr
n
: n Z
1.3. LA NORMA ELE-INFINITO 165
Por lo tanto, una seal es acotada si y slo si su norma ele-innito es nita. Por
ejemplo, la norma de la seal continua cos t es 1, mientras que la seal discreta
2
n
no es acotada.
Ejercicio. Encuentre la norma L
de la seal g(t) = 1 2
t
.
Ejercicio. Sea F : R C dada por F() = e
j
+ a + j. Encuentre [F[
.
Adndum 1. La acotabilidadde las seales es usada para denir la estabilidad
de un sistema, como lo haremos en el captulo 5. El espacio ele-dos es un
espacio de Hilbert con propiedades interesantes, tales como la ortogonalidad y
el teorema de la proyeccin. Los espacios ele-uno y ele-innito son duales en
cierto sentido que tiene que ver con el conjunto de funcionales lineales que se
pueden denir sobre el espacio (en este mismo sentido el espacio ele-dos es el
dual de s mismo). Los espacios ele-uno y ele-innito tambin estn relacionados
en la teora de estabilidad de sistemas de convolucin.
Las seales enel espacioL
1
tienentransformada de Fourier, comose deni;
esta transformada la llamaremos transformada L
1
. Para las seales en L
2
es
posible denir una transformada de Fourier L
2
, la cual daremos enunapndice
al nal del captulo 5. Es claro que ms simple sea la teora que subyace al uso
de una herramienta es mejor. El hecho de que la seal senc no est en L
1
y
no tenga transformada de Fourier L
1
es una de las razones principales (otra
siendo la bsqueda de una homogeneidad en el rigor del curso) por la que
damos la denicin de la transformada de Fourier L
2
.
Adndum 2. Una deduccin de por qu voltios por amperios da vatios.
Suponga que del ctodo salen n electrones por segundo, y que la carga del
electrn es q. As, del ctodo sale una carga de nq culombs por segundo. El
trabajo que realiza la fuente de voltaje al acelerar un electrn cuando viaja del
ctodo a la pantalla es qV.
Figura 1.13: Tubo de rayos catdicos
Ejercicio. Calcule la energa cintica que adquiere el electrn, asumiendo que
la velocidad inicial es aproximadamente cero y que viaja horizontalmente, y
que el campo elctrico es aproximadamente uniforme de valo V/q donde d es
la distancia del ctodo al nodo (pantalla). Compruebe que es qV.
1.4. Variacin de seales discretas
FALTA
1.5. Variacin de seales continuas
FALTA
1.6. Variacin promedio
FALTA
1.7. Problemas
1. Muestre que las normas L
1
, L
2
yL
cumplenla desigualdaddel tringulo:

[ f + g[ [ f [ + [g[.
2. Calcule la energa de la seal [u(t) u(t )] sen(t).
1.7. PROBLEMAS 167
3. Muestre que
_
0
(
sen(t)
t
)
2
dt = /2.
4. Muestre que
_
0
(
sen(t)
t
)dt = /2.
5. Muestre que
_
0
sen(t)
t
dt = . Sugerencia: considere una seal tringulo
como la mostrada en la gura 1.14, la cual es no negativa y acotada por
sen(t)
t
. Cunto vale la integral de F(t)/t para t (0, )?
Figura 1.14: La seal sen(t) y una onda tringulo F(t)
6. Sea f (t) = (
sen(t)
t
)
2
, para t 0 y f (0) = 1. Encuentre [ f [
1
y [ f [
2
. Diga si
f L
1
y si f L
2
.
7. Encuentre el valor de lm
0
_
>
e
jt
d.
8. A una resistencia de 1Kse le aplica la seal de voltaje sen(5000t). Diga
cunta energa disipa la resistencia en un segundo. Diga cunta energa
disipa durante un periodo de la seal aplicada. Resuelva el problema
para el caso de la seal sen(5000t).
9. Si r : Z C est dada por r
n
= 2
n
[u
n
u
n100
], calcule [r[
1
y [r[
2
.
10. Encuentre las normas L-1, L-2 y L-de la seal r(t) =
1
1+t
2
.
11. D un ejemplo de una seal con norma L
1
nita, pero con norma L
2
innita.
12. D un ejemplo de una seal con norma L
2
nita, pero con norma L
1
innita.
13. Calcule la norma L
de s(t) = arctan(x) .
14. Con ejemplos, muestre que ni L
1
es subconjunto de L
2
, ni L
2
de L
1
.
15. Demuestre que L
2
[0, 2) L
1
[0, 2).
16. Demuestre que l
1
l
2
.
17. Encuentre una seal continua que est el L
1
pero no en L
2
, y viceversa.
18. Muestre que cada seal discreta s : Z C sumable en magnitud, es
sumable en magnitud al cuadrado.
Referencias
[1] Geometry of Complex Numbers. Hans Schwerdteger. Dover,
N.Y.,1979.
[2] Elementary Theory of Analytic Functions on One or Several
Complex Variables. Henri Cartan. Dover, N.Y., 1995.
[3] Mathematical Analysis. Tom M. Apostol. Adyson-Wesley,
Reading MA, 1974.
[4] Signals and Systems. A. V. Oppenheim, A. S. Willsky y I. T.
Young. Prentice Hall, Londres, 1983.
[5] Fourier and Wavelet Analysis. Bachman, Narici and Becken-
stein. Springer, N.Y., 2000.
[6] Functional Analysis. F. riesz y B. Sz-Nagy. dover, N.Y., 1990.
[7] Fuctional Analysis. G. Bachman y L. Narici. Academic Press,
N.Y., 1966.
169
Captulo 2
Convolucin y sistemas de
convolucin
2.0. INTRODUCCIN
La convolucin se puede ver como una operacin que, dadas dos funciones
produce otra funcin. La convolucin es usada en probabilidad, anlisis de
sistemas, anlisis de Fourier y otras reas. La solucin de muchas ecuaciones
diferenciales (y de diferencia) lineales, no homogneas y con coecientes con-
stantes, en funcin del trmino no homogneo
1
, es una convolucin continua
o discreta, respectivamente.
Por stas y otras razones, tales como la fcil representabilidadenel dominio
de la frecuencia de Fourier de los sistemas de convolucin, la convolucin es
una herramienta muy til y popular en tratamiento de seales.
1
Los sistemas que se modelan con ecuaciones homogneas se conocen como los sistemas
autnomos.
170
Las funciones de corriente y voltaje en los circuitos con resistencias, in-
ductancias y capacitancias lineales son soluciones de ecuaciones integro -
diferenciales lineales con coecientes constantes, en las que el trmino no
homogneo es funcin de los generadores y las fuentes en el circuito, adems
de las condiciones iniciales. En realidad, en este curso asumiremos condi-
ciones iniciales. Tambin vale la pena resaltar que si derivamos una ecuacin
integro-diferencial al querer convertirla en una ecuacin diferencial, perde-
mos informacin; adems, es posible que el trmino no homogneo no tenga
derivadas del orden requerido. En el contexto de los circuitos mencionados,
asumimos que la corriente por una inductancia es una integral y que por lo
tanto adems de continua, cuenta con derivadas izquierda y derecha en cada
punto; similarmente, el voltaje entre los terminales de una capacitancia es una
integral y es derivable por la izquierda y por la derecha en cada t.
Por ejemplo, considere el circuito RL mostrado en la gura 2.1, el cual
se excita con una seal de voltaje e(t), que conocemos en su totalidad, desde
t , y con respuesta la seal de corriente s(t), la cual queremos conocer
tambin para cada t real. La ecuacin 2.1 describe el sistema correspondiente.
e(t) = Ls
(t) + Rs(t) (2.1)

Figura 2.1: Circuito RL serie
172 CAPTULO 2. CONVOLUCIN Y SISTEMAS DE CONVOLUCIN
Como mostraremos ms adelante, la solucin general de la ecuacin 2.1,
en trminos de e, est dada por:
s(t) =
_

e(t )dg() (2.2)

donde g(t) =
1
R
(1e
Rt/L
)u(t) que comomostramos a continuacines la respuesta
escaln del sistema, es decir, la solucin de la ecuacin cuando e = u. Vea
la gura 2.2. La nica suposicin adicional que haremos para encontrar la
respuesta escaln g, es que sta es acotada, es decir, g L
. A la integral en la
ecuacin 2.2 la llamaremos la convolucin de Stieltjes de la seal e con la seal
g.
Figura 2.2: Respuesta escaln del circuito de la gura 2.1
Para encontrar la respuesta escaln, consideramos primero el caso t < 0,
luego el hecho que s es continua y nalmente el caso t > 0. Para t < 0, la
ecuacin 2.1 se reduce a:
0 = Ls
(t) + Rs(t)
0 = s
(t) + [R/L]s(t) (2.3)

mientras que para t > 0 la ecuacin es:
1 = Ls
(t) + Rs(t)
1/L = s
(t) + [R/L]s(t) (2.4)

en el primer caso, la solucin est dada por s(t) = ke
Rt/L
y como requerimos
que la solucin sea acotada, necesitamos k = 0. As, tenemos s(0) = 0. En el
segundo caso, la solucin es s(t) = 1/R + ke
Rt/L
y como requerimos que la
corriente sea una funcin continua, con s(0
+
) = 0, resulta que el voltaje sobre
la resistencia en 0
+
es 0 y que por lo tanto el voltaje sobre la inductancia en 0
+
es 1 y como ste est dado por Ls(0
+
) = kR, tenemos que k = L/R. Por lo
tanto, podemos escribir,
g(t) = [a/R][1 e[Rt/L]u(t)
Ejercicio. Usando la frmula 2.2, encuentre la respuesta del circuito cuando
s(t) = 1 + cos t.
Note que para un circuito RL, el valor de R juega un papel inverso en la
constante de tiempo L/R al que juega la resistencia en la constante de tiempo
RC en un circuito RC. Un circuito RC con resistencia grande es lento, mientras
que un circuito RL con resistencia grande es rpido.
Ejercicio. Es vlido asumir que la seal mostrada en la gura 2.2 ha llegado a
un estado estable para t = 5, donde = L/R?
Ejercicio. Cul es la respuesta escaln del circuito RC pasa bajas? De un RC
pasa altas?
Por otra parte, la convolucin discreta es la solucin de las ecuaciones
de diferencia lineales y con coecientes constantes. As por ejemplo, para
la ecuacin de diferencia, s
n
= 0,5s
n1
+ e
n
, donde nuevamente asumimos
que e es la entrada a algn sistema discreto gobernado por esta ecuacin
y que s es la salida correspondiente; resulta que, asumiendo causalidad, la
salida s para una entrada e arbitraria est dada por,
k=
e
nk
h
k
. Donde h es
la solucin de la ecuacin cuando la entrada es una seal impulso discreta, o
delta de Kronecker,
n
. A la sumatoria de la ecuacin anterior la llamaremos
la convolucin discreta de las seales e y h.
2.1. Convolucin (lineal) discreta
Dado que a veces una serie es ms intuitiva que una integral, quizs la
convolucin discreta sea ms fcil de visualizar que la continua; por esto
comenzamos con ella. Sean f y gseales discretas con dominio Z; la convolu-
cin de f y g se denota f g y es tambin una seal discreta. Sea h = f g; para
cada n, h
n
est dada por, h
n
=
k=
f
k
g
nk
.
Dado un valor especco N de n, para calcular h
N
calculamos el valor de
la serie h
n
=
k=
f
k
g
Nk
resulta conveniente gracar g
Nk
, contra k, lo cual
corresponde a trasladar la grca de g
k
hasta que g
0
quede en N y luego
reejar al rededor de k = N. Esto resulta de reemplazar el argumento n, en la
denicin de g
n
, por N k.
Ejemplo. Sean f, g : Z C dadas por:
f
n
=
_
_
n, n / 10, 10/
0, n / 10, 10/
g
n
=
_
_
0, n /1, 4/
1, n /1, 4/
Ejercicio. Usando la informacin dada en la gura 2.4, calcule h
2
si f y g son
como en el ejemplo anterior y h = f g.
2.1. CONVOLUCIN (LINEAL) DISCRETA 175
Figura 2.3: Las seales discretas f y g a ser convolucionadas
k -2 -1 0 1 2 3 4 5
2 k 4 3 2 1 0 -1 -2 -3
g
2k
1 1 1 1 0 0 0 0
f
k
-2 -1 0 1 2 3 4 5
Tabla 2.1: La seal g
2k
Figura 2.4: g
2k
Ejemplo. Sea x una seal discreta cualquiera y sea y = h x, donde h est dada
por,
h
n
=
_
_
1/3, n 1, 0, 1
0, n 1, 0, 1
si x = u, donde u es la seal escaln discreta (u
n
= 0 para n < 0, u
n
= 1 para
n 0), tenemos que,
y
0
= (1/3
0) + (1/3
1) + (1/3
1) = 2/3
y
1
= (1/3 x
2
) + (1/3 x
1
) + (1/3 x
0
) = 1
y
2
= 1
y
2
= 0
. . .
y por lo tanto,
y
n
=
_
_
0, n 2
1/3, n = 1
2/3, n = 0
1, n 1
Ejercicio. Para el ejemplo anterior, demuestre que, engeneral, para una entrada
x, y
n
= 1/3(x
n1
+ x
n
+ x
n+1
)
Ejemplo. Queremos encontrar unaformula paralasolucin y
n
= x
n
+0,5y
n1
, en
trminos de x, asumiendo que y
n
tiende a 0 cuando n tiende a . Procediendo
2.2. CONVOLUCIN (LINEAL) CONTINUA 177
directamente, tenemos que, usando y
n1
= x
n1
+ 0,5y
n2
,
y
n
= x
n
+ 0,5x
n1
+ 0,25y
n2
= x
n
+ 0,5x
n1
+ 0,25x
n2
+ 0,125y
n3
= x
n
+ 0,5x
n1
+ 0,25x
n2
+ 0,125x
n3
+ (1/16)y
n4
= x
n
+ 0,5x
n1
+ 0,25x
n2
+ 0,125x
n3
+ (1/16)x
n4
+ (1/32)y
n5
= . . .
=
n=0
2
k
x
nk
= x h
con h
n
= 2
n
u
n
2.2. Convolucin (lineal) continua
Bajo este ttulo deniremos dos tipos de convolucin, que no siempre son
equivalentes. Una es la convolucin de Stieltjes y la otra es la convolucin
estndar. Suponga que s, e, g, h : R1 Ccontnuas. La convolucinde Stieltjes
s de e con g, se denota f dg y para cada t, est dada por, s(t) = [e dg](t) =
_

e(t )dg(); mientras que la convolucin estndar s, de e y h, est dada

por, s(t) = [e h](t) =
_

e(t )h()d().
Ejercicio. Muestre que si s y h estn en L
1
, entonces e h tambin.
Inicialmente damos un ejemplo de convolucin continua estndar.
Ejemplo. Sean h y e las funciones mostradas en la gura 2.5. La funcin e es
una seal escaln. sea s = e h. Las guras 2.6 y 2.7 ilustran el clculo de s(1).
La funcin e(1 ), en el eje , es una versin reejada y desplazada de e(),
como se muestra en la gura 2.6. La integral de h()e(1 ), con respecto a ,
es el rea sombreada en la gura 2.7, la cual vale 2/3; por lo tanto, s(1) = 2/3.
Figura 2.5: Las seales e y h a ser convolucionadas
Figura 2.6: Para calcular s(1) es necesario multiplicar h() y e(1 )
Ejemplo. Sean h(t) = u(t + 1) u(t 1) y e(t) = u(t + 2) u(t 2). Si s = s h
Figura 2.7: El valor de s(1) es el rea sombreada
entonces s est dada por,
s(t) =
_
_
0, t 3
t + 3, 3 t 1
2, 1 t 1
3 t, 1 t 3
0, t 3
(vea la gura 2.8) Compruebe. as decimos que la convolucin de dos pulsos
es un trapecio. Similarmente, la convolucin de un pulso con sigo mismo, es
un triangulo.
Ejercicio. Calcule y graque h h, para la h denida en el ejemplo anterior.
Ejercicio. Calcule f g si f (x) = x
3
y g = esta dada por, g(x) = 1/2, x [1, 1] y
g(x) = 0, x [1, 1].
En general, no hay garanta de que convolucin de dos seales exista. como
se indicacin en un ejercicio anterior, en el caso particular en que las seales
tengan normas ele 1 nitas, la convolucin existe. Tambin, se puede mostrar
Figura 2.8: g = f h
que cuando f tiene norma ele 1 nita, si g es acotada entonces f g tambin
es acotada.
Ejercicio. (La operacin de convolucin es conmutativa.) Demuestre, para el
caso discreto y para el caso continuo, que si f g existe, entonces f g = g f .
Ejercicio. (La operacin de convolucin distribuye con respecto a la suma.)
Demuestre que si f h y g h existen, entonces ( f + g) h = f h + g h.
Ejercicio. (La operacin de convolucin es homognea) Demuestre que si es
una constante y f h existe, entonces (f ) h = ( f h).
2.2.1. Curvgrafos(Splines)
Denimos el curvgrafos de orden creo, como s
0
(t) = u(t +0,5) u(t 0,5),
El spline de orden 1 como s
1
(t) = [s
0
s
0
](t) y en general, en forma inductiva,
s
n
(t) = [s
n1
s
0
](t).
Ejercicio. Graque s
0
(t), s
1
(t), s
2
(t) y s
3
(t).
Ejercicio. Muestre que el lmite de s
n
(t), cuando n tiende a innito, es una
gaussiana, ke
t
2
/
. Encuentre k y .
2.2.2. Convolucin de Stieltjes
La convolucin (lineal, continua) de Stieltjes de la seal e con la
seal g la denotamos e dg. Si s = e dg, para casa t, s(t) est dada por,
s(t) =
e(t )dg()
si g(t) es derivable, con derivada g
= h, la convolucin de Stieltjes se puede

expresar en trminos de una convolucin continua estndar:
s(t) =
e(t )dg() =
e(t )h()d
La convolucin de Stieltjes es til para caracterizar los sistemas de con-
volucin que tengan respuesta escaln discontinua (con saltos), ya que evita
el uso de herramientas de anlisis funcional tales como los impulsos de Dirac.
Figura 2.9: Una seal con salto en t = 0
Ejemplo. Sea g(t) la seal mostrada en la gura 2.9 y suponga que quere-
mos evaluar la convolucin de Stieltjes [sendg](t). Segn la denicin que
2.3. SISTEMAS DE CONVOLUCIN CONTINUOS 183
acabamos de dar, sta est dada por:
_

sen(t )dg() =
_
0
sen(t )g
()d + sen(t 0)[g(0

+
) g(0
)]
+
_
1
0
sen(t )g
()d + sen(t 1)[g(1

+
) g(1
)]
+
_

0
sen(t )g
()d
= 0 + sen(t) +
_
1
0
sen(t )g
()d + 0 + 0
= sen(t) [cos(t 1) cos(t)]
=
2 cos(t /4) cos(t 1)

= z cos(t + z)
donde z =
2e
j/4
e
j
.
Ejercicio. Muestre que, para constantes y , y seales x, w, h : (x +w) dg =
(x dg) + (w dg)
2.3. Sistemas de convolucin continuos
En esta seccin continuamos el tema expuesto en la introduccin de ste
captulo. Dado que es comn que la respuesta escaln de un sistema lineal
e invariante tenga saltos, como por ejemplo un RC pasa-altas, denimos los
sistemas de convolucincontinuos entrminos de una convolucinde Stieltjes.
As, un sistema de convolucin continuo es un sistema que, para cada
entrada e, produce la salida
s = e dg (2.5)
donde g se conoce como la respuesta escaln del sistema.
Figura 2.10: Un sistema de convolucin
Asumiremos que las seales involucradas (e, g, s) pueden estar indenidas
en un subconjunto denso en ninguna parte de S. Esta denicin de sistema de
convolucin nos permite obviar el uso de impulsos.
2.3.1. Respuesta escaln
A continuacin con las suposiciones hechas con respecto de la respuesta
escaln, as como la frmula de la integracin por partes de la integral de
Riemann-Stieltjes, mostramos que la g en la ecuacin 2.5 es efectivamente la
respuesta escaln del sistema.
_

u(t )dg() +
_

g()du(t ) = u()g() u()g()

= 0g() 1g()
= g()
por lo tanto,
_

u(t )dg() =
_

g()du(t ) g()
= g(t) g()
Y slo en caso que g() = 0 (que sinembargo es lo que asumiremos de ahora
en adelante) se tiene que g es la respuesta escaln del sistema.
El resultado obtenido muestra que g es la respuesta escaln de un sistema
que tenga relacin entrada/salida dada por la ecuacin 2.5. Tambin, dadas las
propiedades de superposicin y homogeneidad de la operacin de convolu-
cin indicadas en los ejercicios nales de la seccin 2.2, podemos concluir que
los sistemas de convolucin son lineales.
Muchos sistemas de inters en ingeniera electrnica son sistemas de con-
volucin; por ejemplo, los circuitos re resistencias, inductancias y capacitancias
lineales, ya que stos se modelan con ecuaciones diferenciales lineales con coe-
cientes constantes y, como mostraremos en la seccin 2.8, la solucin de estas
ecuaciones es una convolucin de Stieltjes.
Ejemplo. El circuito de la gura 2.11 es un sistema de convolucin con respues-
ta escaln g(t) = [1 e
t/RC
]u(t).
Ejercicio. Para el sistema del ejemplo anterior, encuentre la respuesta corre-
spondiente a la entrada e(t) = cos 10t.
Figura 2.11: Circuito RC pasa bajas de primer orden
2.3.2. Funcin caracterstica (respuesta impulso) de sistemas
de convolucin continuos
Como dijimos, un sistema es un sistema de convolucin continuo, si para
cada seal de entrada e(t), la salida s(t) est dada por s = e dg, donde g(t) es
la respuesta escaln del sistema:
s(t) =
_

e(t )dg()
Si g cumple con la condicin de ser esencialmente derivable, como denimos
ms abajo, decimos que el sistema tiene funcin caracterstica, esta fun-
cin tendr como dominio R
1
con la posible excepcin del conjunto nito de
puntos donde g no sea derivable. Las condiciones que la respuesta escaln
g debe cumplir para que esto suceda son: que g sea continua.
que g sea derivable excepto, posiblemente, en un conjunto nito
de puntos.
De una funcin que cumpla con las condiciones anteriores, decimos que
es esencialmente derivable. As, si g es esencialmente derivable, no tiene
saltos (es decir, lm por derecha es igual al lm por izquierda en todas partes)
y es derivable, con derivada g
, con la posible excepcin de un conjunto nito

de puntos. En tal caso, denotamos con h a la derivada g
de g y la lla-
mamos la funcin caracterstica del sistema, que se conoce tambin como
respuesta impulso del sistema. Si la respuesta escaln no es esencialmente
derivable, diremos que el sistema no tiene respuesta impulso. Cuando el sis-
tema tenga respuesta impulso escribiremos la salida como:
s(t) =
_

h()e(t )d =
_

h(t )e()d
2.3.3. Respuesta a una entrada constante
Un caso interesante ocurre cuando la seal de entrada a un sistema de
convolucin es constante. Suponga que se tiene un sistema de convolucin
continuo con respuesta escaln g y que la integral
_

dg() (corresponde a la
salida cuando la entrada es la seal constante 1) en nita y vale H.
As, si la seal de entrada es constante, con e(t) = A, la seal de salida
tambin es constante de valor AH.
s(t) =
_

e(t )dg() = A
_

dg() = AH
Como se ver en el captulo 5, la respuesta de un sistema de convolucin
a una sinusoide es, o una sinusoide de la misma frecuencia, o la seal cero. El
resultado que acabamos de ver es uncaso particular ya que una seal constante
es una sinusoide con frecuencia cero.
2.3.4. Respuesta a la derivada de la entrada
En ciertos casos, se conoce la respuesta de un sistema de convolucin a una
entrada dada e(t) y se quiere saber la respuesta correspondiente a la derivada
e
(t). Con gran generalidad, si la salida correspondiente a la entrada e es s,

entonces la salida cuando la entrada es la derivada e
de e, es la derivada s
de
s, ya que:
s
(t) =
d
dt
_

e(t )dg()
?
=
_

d
dt
e(t )dg()
=
_

(t )dg()
Ejercicio. Diga cundo es vlido el segundo paso en la deduccin anterior.
As, la derivada de la salida se obtiene derivando la entrada. Tambin, dado
que, usando integracin por partes,
s(t) =
_

e(t )dg()
= g()e() g()e()
_

g()de(t ), cambio de variable

= g()e() g()e()
_

g(t )de(), como g() = e() = 0

=
_

g(t )de()
entonces, si la respuesta escaln es derivable,
s
(t) =
d
dt
[
_

g(t )de()]
?
=
_

d
dt
g(t )de()
y usando integracin por partes y g() = e() = 0
s
(t) =
_

e(t )dg
()
Ejercicio. Hay casos como s(t) = cos t, para los cuales e() 0, qu pasa en
estos casos?
2.3.5. Identicacin de sistemas de convolucin
Suponga que se tiene un sistema de convolucin continuo que se desea
identicar. Es decir, cmo podemos encontrar su funcin caracterstica si slo
tenemos acceso a la entrada y la salida del sistema? Como veremos a contin-
uacin, el primer paso es aplicar una seal escaln. Como es posible que la
respuesta escaln tenga saltos, y por lo tanto no tengo funcin de transferen-
cia caracterstica, a menudo debemos contentarnos con representar el sistema
como una convolucin de Stieltjes.
2.3.6. Un aplicacin del teorema fundamental del clculo
Como dijimos, la respuesta escaln de un sistema se dene como la seal
que se obtiene a la salida de ste cuando la entrada es una seal escaln u(t).
A continuacin, usando el teorema fundamental del clculo, veremos cmo
estn relacionadas la funcin caracterstica h de un sistema de convolucin
continuo y su respuesta escaln g.
Si se tiene un sistema de convolucin continuo con funcin caracterstica
h, su respuesta escaln est dada por,
g(t) = u h(t) =
_

u()h(t )d
como u(t) = 0 para < 0 y u(t) = 1 para 0
g(t) =
_

0
u()h(t )d
con t ja, sea x = t y dx = d, entonces,
g(t) =
_

t
h(x)(dx) =
_
t
h(x)(dx)
y, de acuerdo con el teorema fundamental del clculo, si h es continua en t,
entonces, g
(t) = h(t). As, otra vez, cuando la funcin caracterstica existe, sta
se obtiene derivando la respuesta escaln del sistema.
Ejemplo. El circuito RC pasa bajas de primer orden mostrado en la gura 2.11,
tiene funcin de caracterstica h(t) = [1/RC]e
t/RC
u(t), que es la derivada de su
respuesta escaln, g(t) = [1 e
t/RC
]u(t), para t 0.
Ejercicio. Graque la respuesta escaln del circuito de la gura 2.12.
En muchos textos de teora de seales, se dene la seal impulso (t)
como la derivada de la seal escaln u(t), o como el lmite el una sucesin
Figura 2.12: Circuito RC pasa altas
de funciones d
n
(t): por ejemplo,
d
n
(t) =
_
_
n, si t [
1
2n
,
1
2n
]
0, si t R
1
[
1
2n
,
1
2n
]
esta sucesin de funciones tiende a la funcin : R
1
R
1
, dada
por,
(t) =
_
_
0, t 0
, t = 0
Para cada n,
_
d
n
= 1 y, por lo tanto, lm
_
d
n
= 1; sin embargo. la funcin
(t) tiene integral (de Riemann o de Lebesque) nula, es decir,
_

(t)d(t) = 0
Como se ve, lm
_
d
n
(t)dt
_
lmd
n
(t)dt. La razn por la cual es comn
el uso de la notacin para integrales para denotar funcionales lineales es que
la integral es lineal, pero aparte de esta propiedad de linealidad, el funcional
lineal D
t
con dominio el conjunto de funciones contnuas f : R
1
R
1
, y rango
el conjunto de los reales, dado por D
t
( f ) = f (t) es en realidad diferente de la
integral
_

f ()(t )d.
Aunque mnemotcnicamente sea conveniente el uso de distribuciones de
Dirac connotacin de integral, es probable que no sean convenientes en un
estudio inicial de los sistemas de convolucin continuos por parte de un futuro
investigador, que no conozca la teora de las distribuciones pero que s conoce
el clculo elemental. El funcional D
t
s se puede expresar en trminos de una
integral de Riemann-Stieltjes:
D
t
( f ) =
_

f ()d
t
() = f (t)
donde
t
() = u( t) y u es la seal escaln.
Dado que hemos denido la seal como una funcin de un conjunto de
nmeros a otro conjunto de nmeros, no hablaremos de seal impulso con-
tinua; sin embargo s hablaremos de (seal) respuesta impulso. Tambin
hablaremos de seal impulso discreta, o delta de Kronecker.
Ejemplo. La seal g(t) = [1e
t
]u(t) es continua (aunque no tenga derivada en
t = 0). La convolucin de Stieltjes est dada por,
_
0
e(t )g
()d + 0 +
_

0
e(t )g
()d = 0 + 0 +
_

0
e(t )e
(
)d
Note que aunque, eh = he, se tiene que, siempre ycuando g() = e() = 0,
_

e(t )dg() =
_

e()dg(t )
donde la variable de integracin es .
Ejemplo. Considere el circuito RC pasa altas mostrado en la gura 2.12. Como
sabemos, la respuesta escaln de este circuito est dada por g(t) = e
t/RC
u(t),
la cual tiene un salto en t = 0. Si queremos obtener la salida de este circuito
cuando la entrada es e(t) = sent, debemos evaluar la siguiente integral:
s(t) =
_

sen(t )dg()
Ejercicio. Calcule la integral indicada en el ejemplo anterior.
Ejercicio. Sean e(t) = 1 + cos t y g(t) = e
t
u(t). Calcule
_

e(t )dg().
Ejercicio. Se tiene un sistema de convolucin continuo cuya respuesta escaln
es como se muestra en la gura 2.13. Calcule la respuesta del sistema a la
entrada e(t) = 1+cos t. Recuerde que esta respuesta escaln ya la consideramos
en la gura 2.9.
Figura 2.13: La respuesta escaln de un sistema de convolucin. Note que as como un RC pasa
altas, la respuesta escaln de este sistema no es diferenciable.
2.3.7. La carga (la integral o el rea) de la respuesta de un
sistema de convolucin
As como al cuadrado de una seal lo llamamos la potencia instantnea
de la seal, a la integral de una seal, asumiendo que es una seal de corriente,
la podemos llamar la carga
2
de la seal. La carga, o rea, de una seal, cuando
existe, es uno de los parmetros que la caracteriza. Sea s = e dg la convolucin
de Stieltjes de la seal e con la seal g. Se puede demostrar que la carga de s es
el producto de la carga de e y
_

dg(), es decir,
_

s(t)dt =
__

e(t)dt
_ __

dg(t)
_
o, si el sistema tiene funcin caracterstica h, como el producto de las cargas de
e y de h:
_

s(t)dt =
__

e(t)dt
_ __

h(t)dt
_
para demostrar esto, procedemos directamente:
_

s(t)dt =
_

e(t )dg()dt
cambiando el orden de integracin y con el cambio de variable u = t ,
_

s(t)dt =
_

f (t )h()dtd
tenemos
_

s(t)dt =
_

f (u)du
_

dg
y el sistema tiene funcin caracterstica,
_

s(t)dt =
_

f (u)du
_

h()d
Note que la misma constante de proporcionalidad H que relaciona el nivel
de la seal constante de salida, con el de la entrada, cuando la entrada es
2
La convolucin de dos funciones de densidad de probabilidad tiene rea unitaria ya que cada
una de ellas tiene rea igual a uno. Este resultado se puede inferir del hecho que la funcin de
densidad de probabilidad de la suma de dos variables aleatorias independientes es la convolucin
de las densidades de las variables que se suman.
una constante, es el que relaciona las reas (cuando existen) de las seales de
entrada y salida.
Ejemplo. Suponga que se aplica la seal u(t) u(t 2) a un sistema de con-
volucin con respuesta impulso e
t
u(t); la integral de la seal de salida vale
2.
Ejercicio. Compruebe el resultado del ejemplo anterior.
Ejercicio. Muestre que si a un sistema de convolucin se aplica un pulso de la
forma u(t + 1/2) u(t 1/2), la salida tiene una integral igual a la integral de
la respuesta impulso del sistema.
2.4. La transformada de Hilbert
La transformada de Hilbert de una seal s es la convolucin s h con
h(t) =
_
_
1
t
, t 0
0, t = 0
Por lo tanto, es la respuesta de unsistema de convolucinconrespuesta escaln
h(t) y con funcin caracterstica
1
t
.
2.5. Sistemas de convolucin discretos
Los sistemas discretos cuya relacin entrada/salida est gobernada por
una ecuacin de diferencia lineal con coecientes constantes, son sistemas de
convolucin discretos.
Un sistema discreto que produzca para cada entrada e, una respuesta r
igual a la convolucin discreta de la entrada y cierta funcin caracterstica h
2.5. SISTEMAS DE CONVOLUCIN DISCRETOS 195
del sistema, se denomina un sistema de convolucin discreto:
r
n
=
k=
e
k
h
nk
La seal impulso discreta
n
se indica a continuacin:
n
=
_
_
0, si n 0,
1, si n = 0
Figura 2.14: La seal impulso discreta
La respuesta impulso de un sistema es la respuesta del sistema cuan-
do la seal que se aplica a la entrada es una seal impulso. A continuacin
se mostrar que la respuesta impulso de un sistema de convolucin discre-
to es precisamente su funcin caracterstica h. Si la entrada al sistema es la
seal impulso , entonces la salida evaluada en la instancia n est dada por,
k=
k
h
nk
=
k=
nk
h
k
= h
n
ya que
nk
= 1 cuando k = n, y 0 en caso
contrario.
Ejercicio. Se tiene un sistema promedio mvil, el cual para cada entrada e y
produce la salida r dada por: r
n
= (1/3)(e
n1
+e
n
+e
n+1
). Encuentre la respuesta
impulso del sistema. Diga si el sistema es de convolucin, es decir diga si existe
una seal h que permita representar la salida en trminos de la entrada como
una convolucin: r
n
=
k=
e
k
h
nk
Ejercicio. Se tiene un sistema discreto con entrada x y salida y gobernado por
la ecuacin de diferencia y
n
= x
n
+ 0,5y
n1
.
1. Encuentre la respuesta impulso h, si se sabe que h
1
= 0.
2. Encuentre h si h
1
= 0.
2.6. El uso de impedancias para hallar la respuesta
impulso de sistemas de convolucin
Las impedancias son una de las herramientas ms usadas por la ingeniera
elctrica. El uso de impedancias se debe en gran medida a los trabajos de
Charles P. Stienmetz.
Como se vio, una forma de hallar la respuesta impulso de un sistema de
convolucincontinuo consiste enplantear la ecuacindiferencial que relaciona
la entrada con la salida, resolverla cuando la entrada es una seal escaln y
derivar la respuesta escaln as hallada.
Otra forma, particularmente apropiada cuando se tiene prctica con el
anlisis de circuitos resistivos, es resolver el circuito en trminos de impedan-
cias, por ejemplo en el plano de la variable compleja s. La relacin entra las
transformadas de Laplace del voltaje y la corriente en una resistencia, un con-
densador o una inductancia (asumiendo que los elementos reactivos no tienen
energa almacenada en t = 0) es una funcin que slo depende de la variable s.
As, la impedancia de una resistencia de R ohmios es R, la de una capacitancia
de C faradios es 1/(sC) y la de una inductancia de L henrios es sL. Adems,
como se sabe, la transformada de Laplace de una convolucin es un producto,
es decir, L(e h) = L(e)L(h); para condensador lineal, V(s) =
1
sC
I(s), para una
inductancia lineal, V(s) = LsI(s) y para una resistencia lineal, V(s) = RI(s).
El procedimiento a seguir, es el siguiente: si se quiere encontrar la respuesta
impulso de un circuito con entrada a y salida b, primero se pasa el circuito al
2.6. IMPEDANCIA Y RESPUESTA IMPULSO 197
plano s, escribiendo A(s) en lugar de a(t), B(s) en lugar de b(t) y trabajando
el circuito como un circuito de impedancias. Luego se despeja la relacin
B(s)/A(s), la cual llamaremos H(s); nalmente, se calcula la respuesta impulso
como h = L
1
(H). Tambin se puede calcular la respuesta escaln dada por
g = L
1
[
1
s
H(s)].
Ejemplo. Para encontrar la respuesta impulso de un RC pasa bajas de primer
orden, encontramos la relacin B(s)/A(s) con base en el circuito mostrado en la
gura 2.15, as:
H(s) =
B(s)
A(s)
=
1/(sC)
r + 1/(sC)
=
1
rsC + 1
h(t) = L
1
1
rsC + 1
= (1 e
t/rC
)u(t)
Figura 2.15: Circuito RC pasa bajas e primer orden en el plano s
Ejercicio. Encuentre H(s) para el circuito RC pasa altas.
Ejercicio. Si decimos que el sistema identidad (el que tiene entrada = salida)
tiene funcin de transferencia H(s) = 1, muestre que pasa altas = identidad -
pasa bajas.
Ejercicio. Encuentre la funcin de transferencia (la relacin [volt. salida]/[volt.
entrada]) para uncircuitosimilar al de la gura 2.15, enel dominio j. Graque
la magnitud y la fase. considere los siguientes casos:
Inductancia, capacitancia.
Resistencia, paralelo (capacitancia, inductancia).
Paralelo (capacitancia, inductancia), resistencia.
Serie (capacitancia, inductancia), resistencia.
Resistencia, serie (capacitancia, inductancia).
2.7. Correlacin determinstica
La correlacin determinstica
3
de dos seales se puede denir en tr-
minos de una convolucin. La correlacin determinstica de las seales
contnuas g y h se denota corrdet(g, h) entonces, para cada t,
f (t) =
_

g()h
( t)d
note que f (t) = g(t) h(t).
Similarmente, para seales discretas s y t, si r = corrdet(s, t), se tiene que
para cada n,
r
n
=
k=
s
k
t
kn
por lo tanto, r
n
= s
n
t
n
.
Ejercicio. Es cierto que corrdet(g, h) = corrdet(h, g)? Demuestre o d un con-
traejemplo.
3
En contraste con la correlacin estocstica est dada por la esperanza E[XY] de dos variables
aleatorias o de dos procesos estocsticos.
2.8. LA CONVOLUCIN DE STIELTJES 199
La correlacin determinstica es un estimador usado en estimacin espec-
tral. La densidad espectral de potencia de un proceso aleatorio estacionario est
dada por la transformada de Fourier de su funcin de autocorrelacin. Norbert
Wiener del MIT, con una amplia gama de intereses, hizo aportes importantes
en esta rea de a caracterizacin espectral de procesos aleatorios y, en general,
en anlisis de Fourier.
2.8. La convolucin de Stieltjes es la solucin de las
ecuaciones diferenciales
Suponga que se tiene la siguiente ecuacin diferencial:
y
(n)
+ a
n1
y
(n1)
+ + a
1
y + a
1
_
t
y = x (2.6)
donde podramos pensar que y es la salida de un sistema cuando la entrada
es x.
Si g es la respuesta escaln, es decir la solucin cuando x = u, es decir si g
es tal que,
g
(n)
+ a
n1
g
(n1)
+ + a
1
g + a
1
_
t
g = u
asumiendo g con derivadas hasta de orden n, veamos qu sucede si reem-
plazamos la funcin g = x dg en el lado izquierdo de la ecuacin 2.6:
(x dg)
(n)
+ a
n1
(x dg)
(n1)
+ + a
1
(x dg) + a
1
_
t
(x dg)
= (x dg
(n)
) + a
n1
(x dg
(n1)
) + + a
1
(x dg) + a
1
x
_
t
dg
= x [dg
(n)
+ a
n1
dg
(n1)
+ + a
1
dg + a
1
_
t
dg]
= x du
= x
por lo tanto, g es solucin de la ecuacin 2.6.
La diferenciabilidad o integrabilidad de g las garantizamos en este caso
por ser estas derivadas e integrales variables fsicas.
2.9. Problemas
1. Muestre que si f, g L
1
entonces f g L
1
.
2. Sean g(t) y f (t) seales continuas con soportes (1, 1) y (2, 7) respectiva-
mente. Encuentre el intervalo ms pequeo que con seguridad contenga
el soporte de g f .
3. Sea f (t) = u(t) u(t 1). Calcule y graque [ f f ](t). Calcule y graque
[ f f f ](t).
4. Se tiene un sistema discreto promedio mvil, el cual para cada entrada e
produce la salida r dada por r
n
=
1
4
(e
n1
+2e
n
+e
n+1
). Encuentre la respuesta
impulso del sistema. Diga si el sistema es de convolucin, es decir, diga
si se puede representar con la ecuacin de la forma, r
n
=
k=
e
k
h
nk
.
2.9. PROBLEMAS 201
5. Encuentre la respuesta escaln de un circuito LR pasa altas. Exprese
la salida en trminos de la entrada usando una convolucin con una
integral de Riemann-Stieltjes. Evale la integral cuando la entrada es la
seal:
a) 1 + sen(t)
b) e
t
cos(t)
6. Encuentre la respuesta impulso de un sistema discreto con ecuacin de
diferencia r
n
= e
n
+(1/2)r
n
1
donde r es la salida, e es la entrada y adems
se sabe que r
n
= 0, para n < 0. Sugerencia: Haga una tabla con columnas
n, e
n
y r
n
.
7. Se tiene un sistemas de convolucin continuo con funcin caracterstica
h(t) = e
t
u(t).
a) Encuentre la respuesta r(t) del sistema si la entrada x(t) est dada
por:
1) x(t) = 5
2) x(t) = cos(2t)
b) Si x(t) = u(t) u(t 1), calcule
_

r(t)dt.
8. Se tienen dos sistemas de convolucin, uno con funcin caracterstica h
1
y el otro h
2
. Si la salida del primer sistema se conecta con la entrada del
segundo (es decir se colocan en cascada) como se muestra en la gura
2.16, resulta un nuevo sistema. Es de convolucin? Si s, Cul es su
funcin caracterstica
9. Par el siguiente circuito, usando impedancias,
a) Encuentre su funcin de transferencia H(s).
b) A partir de H(s), encuentre la funcin caracterstica h(t).
Figura 2.16: Dos sistemas de convolucin en cascada
Figura 2.17: Un circuito RLC pasa banda de segundo orden
10. Calcule f dg si f (t) = sen(t) y g(t) = e
t
u(t).
11. Se tiene unsistemas de convolucincontinuoconrespuesta escalncomo
se muestra g(t) = 0 para t [0, 5].
a) Encuentre la respuesta del sistema a la seal cos(t). Expresela en la
forma Acos(t + ).
b) Si la entrada es el pulso unitario. Encuentre la carga de la salida.
12. Se tiene un sistema de convolucin continuo con respuesta escaln dada
por g(t) = u(t)e
t
, al cual se aplica una entrada x(t) produciendo la salida
y(t). Si se sabe que
_

x(t)dt = 2, encuentre
_

y(t)dt.
13. Se tiene un sistema de convolucin discreto con funcin caracterstica
dada por h
n
= 2
n
. Encuentre la respuesta a la seal e
n
= u
n
u
n2
.
2.9. PROBLEMAS 203
Figura 2.18: Respuesta escaln
Referencias
[1] Mathematical Analysis. Tom M. Apostol. Addison-Wesley,
Reading MA, 1974.
[3] Ecuaciones Diferenciales. D. L. Kreider, R. G. Kuller y D. R.
Ostberg. Fondo Educativo Interamericano, Bogot , 1973.
204
Captulo 3
Representacin de seales
peridicas en el dominio de la
frecuencia (de Fourier)
3.0. Seales peridicas
Algunas de las seales que se originan en procesos fsicos son aproximada-
mente peridicas durante algn intervalo de tiempo. Por ejemplo la seal de
voltaje tomada por un micrfono e un violn tocando un La. A los sonidos
graves les corresponden frecuencias ms bajas que a los sonidos ms agudos.
Parece ser que el sistema auditivo humano reconoce patrones que son aprox-
imadamente peridicos durante periodos cortos de tiempo. Por otra parte,
las funciones peridicas (principalmente sinusoidales) han jugado un papel
importante en fsica y en matemticas, y su teora est bastante desarrollada.
Por estas y otras razones es de utilidad el estudio de las seales peridicas en
205
206 CAPTULO 3. SEALES PERIDICAS (FOURIER)
ingeniera.
Tambin, es importante diferenciar entre la frecuencia con que un proceso
peridico se repite y las frecuencias que un anlisis de Fourier produce. As,
deniremos frecuencia de Fourier como la frecuencia de una sinusoide o
una exponencial compleja. como veremos en el captulo 4, las exponenciales
complejas son las eigenfunciones, o funciones propias de los sistemas de convolu-
cin. Aunque la frecuencia de Fourier ha jugado un papel fundamental en la
teora de sistemas lineales y en el anlisis de seales , nuevas tcnicas como
las onditas (ondelettes, wavelets), permiten la consideracin de otros conjuntos
de seales bsicas.
Figura 3.1: Obtencin de una seal
3.0.1. Deniciones
Inicialmente, damos unas deniciones que permitenhablar sinambigedad
sobre los conceptos de seal peridica y de periodo, tanto en el caso discreto como
en el continuo.
3.0. SEALES PERIDICAS 207
Sea s : R
1
C una seal continua. El nmero real a es un tiempo de
repeticin de la seal s si tR
1
s(t a) = s(t), es decir, a es un tiempo de
repeticin si al correr la seal a unidades, resulta la misma seal.
Note que el nmero cero es un tiempo de repeticin de cualquier seal.
Sea S el conjunto de os tiempos de repeticin de s mayores que cero; si S no es
vaco, se dice que la seal s es peridica; en caso contrario, se dice que s es no
peridica. Si s es peridica, su periodo es el infmum de S.
Para una seal constante, casa nmero real es un tiempo de repeticin; por
lo tanto , las seales continuas constantes son peridicas y tienen perodo cero.
Similarmente, si r : Z C es una seal discreta, se dice que k Z es
un tiempo de repeticin de la seal si n Z r
n
= r
n+k
; cero es siempre un
tiempo de repeticin, y si el conjunto de los tiempos de repeticin positivos
(en este caso aquellos mayores o iguales a 1) de r, no es vaco, se dice que r es
peridica y, en tal caso, su periodo est dado por el mnimo de este conjunto
de tiempo de repeticin positivos. Note que el periodo de una seal discreta
constante es 1.
Ejemplo. Sea r la seal peridica dada por r
n
= [n]
3
, o
r
n
=
_
_
1, si n es mltiplo de 3
0, si n no es mltiplo de 3
Figura 3.2: Una seal discreta con periodo 3.
Ejercicio. Diga si la seal s
n
= e
jn/2
es peridica, o no. En caso armativo,
encuentre el periodo.
Ejercicio. Diga si la seal s
n
= e
jn
es peridica, o no. En caso armativo, en-
cuentre el periodo.
3.0.2. Frecuencia
Si se tiene una seal peridica, continua con periodo T, o discreta con peri-
odo N, mayor que cero, su frecuencia est dada por
1
T
o
1
N
, respectivamente.
La frecuencia de una seal continua est en [0, ], mientras que la frecuencia
de una seal discreta es un nmero en el intervalo [0, 1]. Por cierta razn que
explicamos a continuacin, para seales discretas, la frecuencia 0 es equiv-
alente a la frecuencia 1, mientras que para frecuencias de seales contnuas
asumiremos que 0 es equivalente a .
1
Por convencin, decimos que la frecuencia de una seal constante (disc-
reta o continua) es cero. As, las seales discretas con periodo 1 (las discretas
constantes) tienen 2 frecuencias: uno y cero. Las seales constantes (y otras)
contnuas tambin tienen 2 frecuencias: 0 y .
Ejercicio. D un ejemplo de una seal continua peridica no constante, con
periodo cero.
Como se dene ms adelante, para exponenciales complejas y para sinu-
soides, la frecuencia angular de una sinusoide o de una exponencial compleja
con frecuencia f , es = 2f .
Ejercicio. Sea s una seal discreta con periodo N, con N > 1. Sea r un nmero
natural dado. Es la seal t dada por t
n
= s
m
peridica? si s, cul es su
periodo?
Las sinusoides discretas y las exponenciales complejas discretas no siempre
son peridicas; dado que su periodo es un nmero natural, son peridicas slo
1
Recuerde que no es un nmero real. Ms bien, es un smbolo conveniente.
3.1. SUMAS DE SEALES PERIDICAS 209
si su frecuencia f es el inverso de un natural; Sin embargo, la frecuencia
angular de una exponencial compleja discreta o de una sinusoide discreta no
est determinada en forma nica por su frecuencia: dado un entero N > 0
todas las exponenciales complejas con frecuencia angular de la forma 2M/N,
con N y M primos relativos, tienen periodo N y frecuencia 1/N.
3.0.3. Unidades
Frecuencia de una sinusoide o exponencial compleja: Hz (herzios).
Frecuencia de una seal que no se sinusoide o exponencial compleja: cps
(ciclos por segundo).
3.1. Sumas de seales peridicas
Tanto en la prctica como en la teora, es frecuente encontrara sumas de
seales peridicas. Las series de Fourier permiten representar seales con-
tnuas peridicas como lmites de simas de exponenciales complejas armni-
camente relacionadas. Las seales discretas peridicas se puede escribir como
simas de exponenciales complejas discretas. Las sinusoides son las funciones
propias
2
de los sistemas lineales e invariantes y, para estudiar el efecto que un
sistema lineal tiene sobre una seal peridica, es til saber el efecto producido
sobre la sinusoide. Tambin es interesante saber cundo la suma de dos seales
es peridica y, en caso que lo sea, tener una idea de cul puede ser el periodo
de la suma.
2
Recuerde que x es un auto vector de la matriz Asi Ax = x, para algn escalar . Similarmente,
e es una eigenseal del sistema S si para algn nmero complejo w, S(e) = we.
3.1.1. Caso discreto
Sean x, y : Z C, seales discretas peridicas. Es x + y peridica? Es
posible que la suma sea una seal constante, y por lo tanto peridica; por
ejemplo y si x = y. Es posible que sea no- peridica?
Ejercicio. Sean x y y seales discretas peridicas con periodos positivos M y N
respectivamente. Demuestre que el producto MN es un tiempo de repeticin
de la seal suma y que por lo tanto, la seal suma de las seales es peridica.
Ejercicio. Sean x y y seales discretas peridicas con periodos positivos M y
N respectivamente. Demuestre que el mnimo comn mltiplo de M y N es
tambin un tiempo de repeticin de la seal suma.
3.1.2. Notacin
MCM denota el mnimo comn mltiplo. MCD denota al mximo comn
divisor.
Ejercicio. Muestre que, m, n Z, mn = MCM(m, n)MCD(m, n).
Ejercicio. Sean x = x
n
y y = y
n
las seales discretas dadas por:
x
n
=
_
_
1, n 3Z
0, de lo contrario
y
n
=
_
_
1, n 4Z
0, de lo contrario
donde 3Z es el conjunto de los nmeros enteros mltiplos de 3 y 4Z es el
conjunto de los nmeros enteros mltiplos de 4. Cul es el periodo de x? el
de y? el de x + y?
Ejercicio. Sean x y y seales peridicas con periodos 6 y 3 dadas por x =
. . . 0, 1, 2, 1, 0, 3, 0, 1, 2, 1, 0, 3, 0, . . . , y = . . . 0, 0, 2, 0, 0, 2, 0, 0, 2 . . . Cul
es el periodo de x + y?
Figura 3.3: Una seal con periodo 3, otra con periodo 4 y su suma
Ejercicio. Caracterizacin del periodo de la suma de seales peridicas. Sean x
y y seales discretas peridicas con periodos M y N respectivamente. Sea z =
x + y peridica, y sea K el periodo de z. Muestre que, entonces, MCM(M, N) =
MCM(M, K) = MCM(N, K).
Ejercicio. Sean x y y seales discretas peridicas con periodos M y N respec-
tivamente. Muestre que si no se cumple que MCM(M, N) = MCM(M, K) =
MCM(N, K) entonces x + y z.
3.1.3. Caso continuo
Cuando se suman dos seales peridicas contnuas, la situacin es ms
sutil: la suma no necesariamente es peridica.
Sean s : R
1
C y r : R
1
C seales contnuas y peridicas con periodos
V y W respectivamente. Es s + r peridica? Puede ser constante?
Ejercicio. Calcule el periodo de f (t) = sent + 1/2 sen2t. Figura 3.4.
Figura 3.4: Las seales sent, 1/2 sen2t y su suma
Figura 3.5: La seal g(t) = sent + sent
Ejercicio. Diga si la seal g(t) = sent + sent es peridica. Figura 3.5.
Se puede mostrar que la seal del ejercicio anterior no es peridica; por
lo tanto, la suma de dos seales peridicas contnuas no necesariamente es
peridica. La suma de dos seales contnuas peridicas, resulta ser semi
peridica. Segn la denicin de H. Bohr, las seales peridicas son semi
peridicas pero no todas las seales semi peridicas son peridicas. Si el co-
ciente de los periodos V y W de dos seales contnuas es un nmero racional
entonces existen nmeros enteros M y N tales que MV = NW, entonces MV es
un tiempo de repeticin positivo de la sima y sta es peridica.
Ejercicio. tiene periodo cero toda sima de dos seales contnuas con periodo
cero?
Conjetura 1. La suma de dos seales peridicas contnuas es peridica si y solo si el
cociente de sus perodos es un nmero racional.
Aunque la propiedad de semi periodicidad de una seal ha sido denida
rigurosamente y es intuitiva, no ha sido explotada en ingeniera. Es posible
observar diagramas de tiempo correspondientes a sonidos naturales tales
como una nota musical siendo tocada por un violn o cantada por una persona
y se observa que la seal se repite pero slo aproximadamente. En teora de caos
se estudian sistemas dinmicos no lineales de orden tercero o mayor y se ha
observado que algunos de ellos producen seales que se repiten aproximada-
mente. Por otra parte, cuando se audica una seal (estrictamente) peridica,
el sonido no es agradable, suena como un pito.
El estudio de los sistemas dinmicos ha recibido un impulso reciente da-
do el inters en la teora del caos. All, las seales semi peridicas son ms
comunes.
Ejercicio. Demuestre que la suma de dos sinusoides es peridica si y slo si el
cociente de los periodos es racional.
3.2. Seales semi peridicas
Quizs la denicin ms conocida sea la de Harald Bohr (hermano de
Niels). Inicialmente, denimos tiempo de repeticin con error .
Sea s : R
1
C una seal, y sea un real. Decimos que un nmero real t
es un tiempo de repeticin de s, con error , si para cada nmero real
t, se tiene que s(t) s(t ) < . Si para casa positiva, no importa qu tan
pequea, hay una longitud L, tal que cada intervalo de reales de longitud L
contiene al menos un tiempo de repeticin positivo de s con error , decimos
que s es semi peridica, o semi peridica.
Ejercicio. Muestre que si s es peridica, entonces es semi peridica.
Ejercicio. Muestre que sen

2t +sent es semi peridica y que no es peridica.
Sea s : Z C una seal, y sea un real. Decimos que un nmero entero k
es un tiempo de semirepeticin de s, con error , si, para cada nmero
entero n, se tiene que s
n
s
n+k
< . Si, para cada positivo, no importa qu
tan pequea, s tiene tiempo de repeticin con error , decimos que s es semi
peridica.
Ejercicio. Muestre que cos(n) es una seal semi peridica, y no peridica.
Sugerencias: 1. Muestre que cos es uniformemente contnua. 2. Muestre que
> 0 m, n tal que 2n m <
3.3. EXPONENCIALES COMPLEJAS Y SINUSOIDES 215
3.3. Exponenciales complejas y sinusoides
Una clase importante de seales peridicas est dada por las sinusoides
y las exponenciales complejas. Estas son las funciones propias de los sistemas
lineales e invariantes.
Una sinusoide es de una seal s : R
1
C de la forma, s(t) = b cos(t +
), R
1
, R
1
, donde b es la amplitud, es la frecuencia angular y
es la fase de la seal sinusoidal.
Una exponencial compleja es una seal s : R
1
C de la forma, s(t) =
be
jt
, R
1
, b C donde b es la amplitud de la exponencial compleja y
es su frecuencia angular. Tanto la parte real como la parte imaginaria de
una exponencial compleja son sinusoides: s(t) = be
jt
= b cos t + jb sent.
Tanto las exponenciales complejas contnuas como las sinusoides contnuas
son funciones peridicas. Si la frecuencia angular es diferente de cero, el
periodo de la seal es 2/ y la frecuencia es /2. Si = 0, la seal es
constante y, por denicin, su periodo es cero.
Para seales discretas, las deniciones son similares. Una exponencial
compleja discreta es una seal s : Z C dada por, s
n
= be
jn
R
1
, C,
donde b es la amplitud de la exponencial compleja y es su frecuencia
angular. Tanto la parte real como la parte imaginaria de una exponencial
compleja discreta son sinusoides discretas: s
n
= be
jt
= b cos n + jb senn.
Las exponenciales complejas discretas y las sinusoides discretas no siempre
son peridicas; lo son slo si la frecuencia angular es un mltiplo racional
de 2.
Si la frecuencia angular es un mltiplo racional q, de 2, diferente de
cero, donde q = M/N es la forma irreducible de q, el periodo de la seal est
dado por N (Por qu?).
Si = 0, la seal es constante y, por denicin, su periodo, su periodo
es 1. Las frecuencias angulares de las seales discretas se pueden considerar
como ngulos y, como tales son equivalentes bajo la relacin de congruencia
mdulo 2. Por lo tanto, una exponencial discreta constante tiene periodo uno,
frecuencia angular 0 = 2 y frecuencias 1 y 0.
Ejercicio. Muestre que la seal s : Z C dada por s
n
= cos(3n), no peridica.
Ejercicio. Encuentre el periodo de la seal s : Z C dada por s
n
= e
j2(4/124)n
.
Con el anlisis de Fourier, las exponenciales complejas y las sinusoides
juegan un papel importante en la teora de seales porque permiten la repre-
sentacin de seales peridicas en trminos de simas o series de exponenciales
complejas as como la representacin de seales no peridicas como integrales
de exponenciales complejas.
La frecuencia de un exponencial compleja o la de una sinusoide se de-
nomina frecuencia de Fourier. La frecuencia angular de una exponencial
Figura 3.6: La seal sent
compleja, o de una sinusoide constante continua, es cero.
3.3. EXPONENCIALES COMPLEJAS Y SINUSOIDES 217
Figura 3.7: La seal cos t
Deduccin de ciertas frmulas tiles utilizando nmeros complejos
1.
cos(a + b) = Re(e
j(a+b)
)
= Re(e
j(a)
e
j(b)
)
= cos a cos b sena senb
2.
sen(a + b) = Im(e
j(a+b)
)
= Im(e
j(a)
e
j(b)
)
= cos a senb + sena cos b
Dado que la funcin coseno es par, y la seno es impar, de las frmulas
anteriores se deduce que:
3. cos a cos b =
1
2
[cos(a + b) + cos(a b)]
4. sena senb =
1
2
[cos(a b) cos(a + b)]
5. cos a senb =
1
2
[sen(a + b) + sen(b a)]
6. Sea ce
j
= a jb. Entonces,
c cos( + ) = (c/2)e
j
e
j
+ (c/2)e
j
e
j
= (1/2)(a jb)e
j
+ (c/2)(a + jb)e
j
= (a/2)(e
j
+ e
j
) + (b/2j)(e
j
e
j
)
= a cos b sen
Similarmente, si a cos +b sen = c cos( +), entonces
a
2
(e
j
+e
j
) +
b
2j
(e
j
e
j
) = c cos( + ), por lo tanto ce
j
= a jb. En conclusin, tenemos que ,
asumiendo c > 0, a cos + b sen = c cos( + ), si y slo si, ce
j
= a jb. Es
decir, a cos + b sen = c cos( + ), si y slo si c = a jb y = (a jb).
Esta identidad permite representar la suma de dos sinusoides (de la misma
frecuencia) en cuadratura, como una seal coseno desfasada.
Ejercicio. Muestre que cos a = cos(a + ).
Ejemplo. La seal sent +cos t se puede escribir como

2 cos(t /4) y tambin
como
2 cos(t 3/4)
Ejercicio. Muestre que a cos( + ) + b sen( + ) = z cos( + z) donde z =
ae
j
be
j
.
Ejercicio. Exprese cos a + cos b como un coseno.
Ejercicio. Exprese sena + senb como un coseno.
Ejercicio. Exprese cos a + senb como un coseno.
Ejercicio. Muestre que: z cos( + z) = 0,5ze
j
+ 0,5z
e
j
.
3.4. SEALES PERIDICAS CONTNUAS 219
3.4. Representacin en el dominio de la frecuencia
de seales peridicas contnuas
A mediados del siglo XVIII Daniel Bernoulli consider la posibilidad de
representar una funcin como una serie de sinusoides. En 1777, Euler public
la frmula de los coecientes de dicha serie. Las series de Fourier fueron in-
troducidas por el fsico-matemtico J. B. J. Fourier, a comienzos del siglo XIX
como un mtodo de solucin de ecuaciones con derivadas parciales. Inicial-
mente, sus ideas no fueron bien recibidas por los miembros de la Academia
de ciencias francesa. Durante el tiempo transcurrido desde la publicacin de
sus ideas hasta ahora, se ha dedicado un gran esfuerzo para hacer su formu-
lacin ms precisa. El estudio de las series de Fourier ha propiciado directa o
indirectamente el desarrollo de otras reas en matemticas.
Las series Fourier, que son series de sinusoides o de exponenciales com-
plejas armnicamente relacionadas, permiten representar muchas seales per-
idicas en el dominio de la frecuencia.
Haciendo una analoga con los experimentos de Newton con prismas,
relacionandofrecuencias concolores, al anlisis de Fourier se le conoce tambin
como anlisis espectral.
3.4.1. Series de Fourier
Sea s : R
1
C na funcin peridica con periodo 2 y suponga que:
2
0
f (t)
2
dt R
1
, (es decir, que la integral existe y es nita), entonces, f
se puede representar con una serie de Fourier: f (t) =
n=
c
n
e
jnt
donde los
coecientes estn dados por:
c
n
=
1
2
_
2
0
f (t)e
jnt
dt
Si f es continua en t
0
, entonces,
c
n
e
jnt
0
= 0,5[ f (t
+
0
) + f (t
0
)].
En general, si f es peridica con periodo T y
_
T
0
f (t)
2
dt R
1
(es decir,
la integral de la magnitud al cuadrado sobre un periodo existe y es nita)
entonces:
f (t) =
n=
c
n
e
jn
0
t
donde
c
n
=
1
T
_
T
0
f (t)e
j
0
nt
dt
0
se conoce como la frecuencia angular fundamental de f y est dada
por:
0
= 2/T (la frecuencia fundamental es 1/T). Los mltiplos de la frecuen-
cia fundamental se conocen como frecuencias armnicas. La fundamental
es la primera armnica. Cuando un conjunto de frecuencias tienen mnimo
comn mltiplo, se dice que estn armnicamente relacionadas. El valor del
coeciente c
0
, el cual est dado por el promedio de la seal sobre un periodo,
se conoce tambin como el nivel DC o nivel promedio de la seal.
La representacin en series de Fourier de una seal peridica permite su
representacin en el dominio de la frecuencia de Fourier.
Ejemplo. Sea f (t) = sent + cos 2t. Su representacin en el dominio de la fre-
cuencia es el seal discreta mostrada en la gura siguiente, correspondiente
a los coecientes c
n
de las exponenciales complejas en la serie (suma nita en
este caso) de Fourier
n=
c
n
e
jn
0
t
.
Ejercicio. Sea s(t) una onda cuadrada, como se muestra en la gura 3.9. En-
cuentre los coecientes c
n
de su expansin en series de Fourier para 6 < n < 6.
Ejercicio. Encuentre la serie de Fourier de la seal de periodo 2 dada por e
t
pera t (, ). Con base en la frmula de los coecientes, encuentre el valor
de la serie

n=1
1
n
2
.
Figura 3.8: Representacin de sent + cos 2t en el dominio de la frecuencia de Fourier
Figura 3.9: Una onda cuadrada con periodo 2 y nivel DC cero
Ejercicio. Suponga que se tiene una seal cuadrada de voltaje, positiva, con
frecuencia 60. Cunto vale su periodo? Cunto cale su frecuencia angular
fundamental? Si su amplitud es de 12 voltios, Cunto vale su nivel DC?
Calcule la magnitud de la fundamental, y de la segunda y tercera armnicas.
Ver gura 3.10.
Figura 3.10: Onda cuadrada con periodo 1/60 y nivel DC de 6V
Ejercicio. Demuestre que la serie de Fourier de una funcin continua converge
uniformemente.
3.4.2. Propiedades de simetra
Ejercicio. Muestre que si f es peridica y par, y su serie de Fourier tiene coe-
cientes c
n
, entonces c
n
es una sucesin par.
Ejercicio. Muestre que si f es peridica y real, con serie de Fourier con coe-
cientes c
n
, entonces Im[c
n
] es una sucesin impar y Re[c
n
] es una sucesin
par.
Ejercicio. Muestre que si f es peridica y real y par, su serie de Fourier tiene
sucesin de coecientes real y par.
3.4.3. Frmula de Parseval
La siguiente identidad, conocida como frmula de Parseval, permite rela-
cionar la potencia promedio de una seal peridica con la norma l 2 de sus
coecientes de Fourier:
n=
c
n
2
=
1
T
_
T
0
f (t)
2
dt
La frmula de Parseval se puede considerar como una generalizacin
del teorema de Pitgoras, donde los catetos son los coecientes c
n
y la
hipotenusa es la energa promedio de la seal, denida como el promedio
del cuadrado de la seal, tomado sobre un periodo.
Ejercicio. Para la onda tringulo mostrada en la gura 3.11, calcule su poten-
cia promedio E. Calcule tambin la potencia promedio E
5
de sus primeras 5
armnicas:
E
5
=
5
n=5
c
n
2
nalmente, calcule E
5
/E.
Figura 3.11: Onda tringulo de frecuencia 60, con nivel DC de 6 voltios
Ejercicio. Use la frmula de Parseval para encontrar la potencia promedio de
la seal sent/3 + sent/5.
Ejemplo. Se pide calcular [
1
1+t
2
[
2
.
_

1
1 + t
2
dt =
1
2
_

_
1 t
2
(1 + t
2
)
2
+
1
1 + t
2
_
dt
_

1
(1 + t
2
)
2
dt = arctant
=
_

t
2
(1 + t
2
)
2
dt =
_
/2
/2
tan
2
u
(1 + tan
2
u)
2
sec
2
udu =

2
de donde tenemos que
[
1
1 + t
2
[
2
=
_
2
3.4.4. Series de sinusoides
resulta conveniente, para seales peridicas reales, representarlas con una
serie de sinusoides. Sea f una seal continua peridica real, con periodo 2.
Suponga que
f (t) =
n=
c
n
e
jnt
donde
c
n
=
1
2
_

f (t)e
jnt
dt
Entonces, tambin podemos expresar a f as:
f (t) =
n=0
a
n
cos nt +
n=1
b
n
sennt
donde
a
0
= c
0
=
1
2
_

f (t)dt y a
n
=
1
f (t) cos(nt)dt y b
n
=
1
f (t) sen(nt)dt,
n 1. Tambin como, f (t) =
n=0
e
n
cos(nt + ).
Ejercicio. Muestre que: c
n
= 0,5(a
n
+ b
n
), c
n
= (a
n
+ jb
n
), n > 0. c
0
= a
0
Ejercicio. Muestre que: a
n
= c
n
+ c
n
, b
n
= j(c
n
c
n
).
Ejercicio. Muestre que si f es real, Re(c
n
) es una sucesin par e Im(c
n
) es una
sucesin impar.
3.4.5. Sumas parciales de una serie de Fourier
Suponga que f es una onda cuadrada impar. La fundamental y las sigu-
ientes 3 armnicas de f son entonces sent, 1/3 sen3t, 1/5 sen5t, 1/7 sen7t,
recuerde que una onda cuadrada no tiene armnicas pares. Las armnicas se
muestran en la gura 3.13 y las sumas parciales a continuacin en las guras
3.14 y 3.15.
Sea f una seal continua peridica, con periodo 2. Suponga que f (t) =
n=
c
n
e
jnt
donde, c
n
=
1
2
_

f (t)e
jnt
dt. Para cada nmero natural positivo
m, dena f
m
as: f
m
=
m
n=m
c
n
e
jnt
, entonces,
f
m
(t) =
m
n=m
c
n
e
jnt
=
1
2
m
n=m
_

f ()e
jn
de
jnt
=
1
2
_

f ()
m
n=m
e
jn
e
jnt
d
=
1
2
_

f ()
m
n=m
e
jn(t)
d
=
1
2
_

f ()SE
m
(t )d
donde SE
m
es la funcin senc enmascarada de orden m, tambin conocida
como ncleo de Dirichlet, y est dada por:
SE
m
(x) =
e
jmx
(1 e
j(2m+1)x
)
a e
jx
=
sen[(m+ a/2)x]
sen[x/2]
Si x no es mltiplo de 2 y
SE
m
= 2m+ 1
Si x es un mltiplo de 2.
A continuacin se graca la funcin senc enmascarada de orden 4; note
que es peridica con periodo 2.
Figura 3.12: La seal senc enmascarada, SE
4
(x), de orden 4

m
n=m
z
n
=
z
m
(1z
2m+1
)
1z
Ejercicio. Graque SE
5
(x).
Acontinuacinse muestranlas primeras sumas parciales, correspondientes
a la serie de una onda cuadrada. Note cmo se va cuadrando la seal y cmo
va apareciendo el fenmeno de Gibbs.
3.5. Convolucin circular continua
Suponga que tanto f como g son funciones peridicas con periodo T y con
expansiones en series de Fourier dada por:
f (t) =
n=
c
n
e
jn
0
t
g(t) =
n=
d
n
e
jn
0
t
3.5. CONVOLUCIN CIRCULAR CONTINUA 227
Figura 3.13: Las seales sent, 1/3 sen3t, 1/5 sen5t, 1/7 sen7t
Figura 3.14: La suma parcial seales sent + 0
Figura 3.15: La suma parcial seales sent + 1/3 sen3t
Figura 3.16: La suma parcial seales sent + 1/3 sen3t + 1/5 sen5t
Figura 3.17: La suma parcial seales sent + 1/3 sen3t + 1/5 sen5t + 1/7 sen7t
3.5. CONVOLUCIN CIRCULAR CONTINUA 229
donde
c
n
=
1
T
_
T
0
f (t)e
jn
0
t
dt d
n
=
1
T
_
T
0
g(t)e
jn
0
t
dt
Suponga que uno est interesado en saber qu funcin h(t) tiene serie de
Fourier con coecientes c
n
d
n
, es decir,
h(t) =
n=
c
n
d
n
e
jn
0
t
=
1
T
n=
_
T
0
f (s)e
jn
0
s
d
n
e
jn
0
t
ds
=
1
T
_
T
0
n=
d
n
e
jn
0
(ts)
f (s)ds
=
1
T
_
T
0
g(t s) f (s)ds
Esta ltima frmula la denominamos la convolucin circular continua de
g y f .
Ejercicio. Calcule y graque la convolucin circular continua de una onda
cuadrada de periodo 1, ciclo til de 50 %, nivel mnimo 0V y mximo 1V y una
onda tringulo de periodo 1, nivel mnimo 0V y mximo 1V. Asuma cualquier
tra condicin necesaria no estipulada.
Ejercicio. Se tienen dos seales contnuas peridicas, con periodo 2 como se
muestra en la gura 3.18:
f (t) =
n=
c
n
e
jnt
g(t) =
n=
d
n
e
jnt
si h(t) =
n=
c
n
d
n
e
jnt
, graque h contra t.
Figura 3.18: Dos seales peridicas con periodo 2
si r(t) =
n=
d
n
e
j2nt
, graque r.
Ejercicio. Calcule la convolucin circular continua de SE
5
() y T(), donde T
es como se muestra en la gura 3.19
Figura 3.19: La onda tringulo par de periodo 2
3.6. SERIESDEFOURIERDEFUNCIONESDISCONTINUASYFENMENODEGIBBS231
3.6. Series de Fourier de funciones discontinuas y
fenmeno de Gibbs
Considere la onda tipo sierra mostrada en la gura 3.20. As, s(t) =
Figura 3.20: Onda sierra
n=
c
n
e
jnt
con c
n
=
(1)
n+1
jn
si n 0 y c
0
= 0.
Sea S
m
(s, t) =
m
n=m
c
n
e
jnt
la versin truncada a 2m + 1 trminos de su serie
de Fourier.
S
m
(s, t) =
m
n=1
(1)
n+1
jn
_
e
jnt
e
jnt
_
=
m
n=1
(1)
n+1
2
n
sen(nt)
por lo tanto S
m
(s, t)
m
0.
Lema 4. Si f tiene integral de Riemann, sus coecientes decrecen proporcionalmente
como
1
n
o ms rpido, cuando n y f (t) tiene lmites f (
) y f (
+
) cuanto
t
y t
+
, respectivamente, entonces las sumas parciales de la serie de
Fourier S
m
(t) =
m
n=m
c
n
e
jnt
tienden a
f (t
+
)+f (t
)
2
.
Demostracin. Considere el caso t = y ponga
g(t) = f (t) +
1
2
_
f (
+
) f (
)
_
s(t)
si t donde s es la sierra y g() =
f (
+
)+f (
)
2
.
As,
lm
t
g(t) = f (
) +
f (
+
) + f (
)
2
= g()
y
lm
t
+
g(t) = f (
+
) +
f (
+
) + f (
)
2
() = g()
y tenemos que g es continua en . Los coecientes de Fourier g
n
de g estn
relacionados conlos coecientes de

f
n
yde s, ( s
n
) as: g =

f
f (
+
)f (
)
2
s
n
ypor un
resultado previo, como g
n
tambindecrece por lo menos proporcional a
1
n
y g es
continua, S
m
( f, ) g(). Por lo tanto, S
m
( f, )
f (
+
)f (
)
2
S
m
(s, )
f (
+
)f (
)
2
y como S
m
(s, ) = 0, S
m
( f, )
f (
+
)f (
)
2
.
Teorema 7. Si f : S
1
C es continua con derivada continua y acotada excepto en
un conjunto nito, entonces lm
tx
f (t) y lm
tx
+
f (t) existen para cada x S
1
y
S
m
( f, x)
f (x
+
) f (x
)
2
en particular, si f es continua en x, S
m
( f, x) = f (x).
Lord Kelvin dise mquinas para el clculo de funciones peridicas a
partir de sus coecientes de Fourier y viceversa. Michelson construy una
de estas mquinas y la prob con la sierra denida anteriormente, con los
primeros 80 coecientes. Sorpresivamente encontr que la mquina no dibu-
jaba un serrucho sino que le aada 2 pequeas oscilaciones a cada lado de la
discontinuidad.
Luego de comprobar que la mquina estaba funcionando correctamente,
not que al aumentar el nmero de coecientes las oscilaciones se corran hacia
la discontinuidad y se mantenan con una amplitud de aproximadamente 17 %
con respecto al valor absoluto correcto. Esto parece contradecir el teorema 16.4
de [8]. Gibbs, en 2 cartas a Nature, claric y resolvi el problema. A pesar de
3.7. SEALES PERIDICAS DISCRETAS 233
que S
n
(h, t) h(t) punto a punto, las grcas de s
n
no se aproximan a la grca
de h necesariamente, en el caso en que la convergencia es uniforme las grcas
s se hacen similares. En general el exceso a cada lado de una discontinuidad
es de aproximadamente 9 % del valor de la discontinuidad.
Para el caso de la sierra, esto lo demostramos as:
s(
+
) = lm
n
n
r=1
2
r
sen
r
n
2
_
x
0
d
(ver [8], captulo 17.)
3.7. Expresin de seales discretas peridicas como
sumas de exponenciales complejas
El objetivo de esta seccin es doble: por una parte, obtener la representacin
de seales discretas peridicas como sumas de exponenciales complejas (disc-
retas) y por otra, hacer una introduccin a la transformada discreta de Fouri-
er(DFT). La expansin de seales peridicas discretas como sumas de expo-
nenciales complejas permite la representacin en el dominio de la frecuencia
Figura 3.21: hjkhl
de Fourier de tales seales; estas sumas se conocen tambin como seres discretas
de Fourier.
Las seales discretas peridicas se pueden representar como sumas nitas
de exponenciales complejas, a diferencia de las seales peridicas contnuas
las cuales se representan como series de exponenciales complejas. De hecho, si
el periodo de la seal discreta en cuestin es N, no ms de N trminos en la
suma son necesarios.
Como se ver en el captulo 5, tal expansin permite tambin la repre-
sentacin en el dominio de la frecuencia de seales discretas de longitud ni-
ta, conocida como DFT. La representacin en el dominio de la frecuencia de
seales discretas de longitud innita se trata en la seccin siguiente; la repre-
sentacin en el dominio de la frecuencia de estas seales se obtiene por medio
de la Transformada de Fourier de tiempo discreto.
El camino para obtener la expansin de las seales peridicas discretas en
sumas de exponenciales discretas tomado aqu, es algo indirecto; inicialmente,
la idea es obtener cierta biyeccin lineal de C
N
a C
N
. Empezamos por mostrar
que el resultado de ciertas sumas de exponenciales complejas es cero.
3.7.1. Sumas tipo I
Las sumas tipo I son de la forma
N1
k=0
e
j
2
N
k
. Sea W
N
= e
j
2
N
y considere la
suma
N1
k=0
W
k
N
, donde N > 1.
Ejercicio. Demuestre que para N = 3,
N1
k=0
W
k
N
= 0 (Vea la gura 3.22.)
A continuacin se demuestra que, en general, para N > 1,
N1
k=0
W
k
N
= 0.
Geomtricamente se puede argumentar como sigue. Los nmeros W
k
N
, k
/0, N1/, estn uniformemente distribuidos sobre la circunferencia de radio 1
Figura 3.22: La suma de los tres nmeros complejos mostrados es cero
con centro en el origen del plano complejo C. Si la suma no fuera cero, al rotar
el plano 2/N radianes, los sumandos seguirn siendo los mismos mientras
que el resultado sera diferente, y esto es una contradiccin.
Algebraicamente, argumentamos como sigue. Suponga que
N1
k=0
W
k
N
= x
y que x 0. A continuacin, multiplique por W
N
obteniendo, W
N
N1
k=0
W
k
N
=
W
N
x entonces
N1
k=0
W
k+1
N
= W
N
x, dado que W
N
N
= W
0
N
, se tiene que
N1
k=0
W
k+1
N
=
N1
k=0
W
k
N
+W
0
N
=
N1
k=0
W
k
N
; por lo tanto
N1
k=0
W
k
N
= W
N
x y x = xW
N
, entonces, x = 0,
lo cual es una contradiccin ya que se asumi que x 0.
Ejercicio. Muestre el resultadoanterior usandola frmula de la suma geomtri-
ca.
3.7.2. Sumas tipo II
Ahora, suponga que r es un nmero natural y considere la suma
N1
k=0
W
rk
N
.
Hay dos casos importantes por considerar, dependiendo de si r es un mltiplo
entero de N, o no.
Ejercicio. Demuestre que si r es un mltiplo de N (es decir, si r es congruente
con 0, mdulo N, y r
N
0), entonces,
N1
k=0
W
rk
N
= N
Ejercicio. Demuestre que si Nno es unmltiplo de r, (es decir , si r no es congru-
ente con 0, mdulo N, y r
N
0), entonces,
N1
k=0
W
rk
N
=
N1
k=0
W
k
N
= 0 (Sugerencia:
si r y N son primos relativos, W
0
N
, W
r
N
, . . . , W
r(N1)
N
= W
0
N
, W
1
N
, . . . , W
(N1)
N
. En
caso contrario, si m es el mximo comn divisor de r y N, s = r/m y M = N/m,
se tiene que:
W
0
N
, W
r
N
, . . . , W
r(N1)
N
= W
0
N
, W
r
N
, . . . , W
r(M1)
N
, W
0
N
, W
r
N
,
. . . , W
r(M1)
N
, . . . , W
0
N
, W
r
N
, . . . , W
r(M1)
N

donde la lista W
0
N
, W
r
N
, . . . , W
r(M1)
N
se repite m veces.)
Como conclusin, tenemos que las sumas de la forma
N1
k=0
W
rk
N
valen N, cuando
r
N
= 0, y 0, cuando r
N
0
Ejercicio. Muestre el resultadoanterior usandola frmula de la suma geomtri-
ca.
3.7.3. Una biyeccin de C
N
a C
N
Toda matriz cuadrada Ade N por N nmeros complejos dene la funcin
lineal L : C
N
C
N
dada por L(x) = xA. Similarmente, toda funcin lineal de
C
N
a C
N
se puede representar como el producto por una matriz cuadrada de
N por N. si la matriz es invertible, se tiene una biyeccin: adems, los vectores
la y los vectores columna de la matriz sern linealmente independientes y
bases para C
N
. A continuacin presentaremos una de tales matrices.
Lema 5. La matriz A = A
rk
= W
(r1)(k1)
N
, donde cada componente A
rk
de la
matriz est dado por A
rk
= W
(r1)(k1)
N
es invertible.
Prueba. La matriz es invertible ya que tiene inversa. La matriz
1
N
, donde
B = B
rk
con B
rk
= W
(r1)(k1)
N
, es la matriz inversa, como se muestra a contin-
uacin. Sea C = AB, con componentes C
i j
, entonces,
C
i j
=
N
k=1
W
(k1)(i1)
N
W
( j1)(k1)
N
=
N
k=1
W
0
N
= N
Adems, para i j
C
i j
=
N
k=1
W
(k1)(i1)
N
W
( j1)(k1)
N
=
N
k=1
W
(k1)(ij)
N
= 0
ya que [i j]
N
0, por lo tanto, C es una matriz diagonal con componentes en
la diagonal de valor N y
1
N
C es la matriz identidad.
Corolario 3. Los N vectores de la forma [W
0k
N
, W
1k
N
, . . . , W
(N1)k
N
], con k /0, N1/,
forman una base para C
N
.
Prueba. Dado un elemento x = [x
0
, x
1
, . . . , x
N1
] de C
N
, sea X = xA, X =
[X
0
, X
1
, . . . , X
N1
] es tambin un elemento de C
N
. Como Aes invertible, pode-
mos escribir x = XA
1
. As, estamos expresando a x como una combinacin
lineal de los vectores columna de A
1
. Como esto es vlido para cualquier
3.8. PROBLEMAS 239
vector x en C
N
, concluimos que los vectores columna de
1
N
Bson una base para
C
N
.
Corolario 4. Dada una seal x = [x
0
, x
1
, . . . , x
N1
] de duracin nita, sus compo-
nentes se pueden expresar as:
x
n
=
N1
k=0
X
k
e
j
2
N
nk
donde los coecientes X
k
estn dados por:
X
k
=
1
N
N1
n=0
x
n
e
j
2
N
nk
Prueba. La prueba consiste en expresar a x como x = XA
1
= (xA)A
1
.
Lema 6. Si en la expresin x
n
=
N1
k=0
X
k
e
j
2
N
nk
se permite que n tome cualquier valor
entero, resulta una seal discreta, de longitud innita, peridica.
Prueba. Se sigue del hecho que los trminos W
nk
N
tienen tiempo de repeticin
N.
3.8. Problemas
1. Exprese la seal a
n
= Im(j
n
) como una suma de exponenciales complejas
discretas. Muestre que x
n
es una seal impar y exprsela tambin como
una suma de senos discretos.
2. Exprese la seal mostrada en la gura 3.23 como una suma de exponen-
ciales complejas discretas.
3. Encuentre el periodo de las siguientes seales contnuas:
Figura 3.23: Una seal peridica discreta
a) sen
2
(t)
b) sen(9t) + sen(15t)
c) sen(2t/7) + sen(2t/5)
d) sencos(t)
e) sen
2
(t) + cos
2
(t)
f ) sen(
_
(2)t)
g) tan(t)
h) sen(2t)
i) e
jt
4. Diga si la seal discreta x
n
= e
j5n
es peridica, o no. Explique.
5. D el periodo de la seal discreta x
n
= [n]
4
.
6. Sea w = e
j2/16
. Calcule w
1073741823
. Sugerencia: w
n
es peridica (Cul es
el periodo?). Calcule log
2
1073741823.
7. Sea f (t) = sen(2t/3) + sen(2t/4) + sen(2t/5). Encuentre un nmero
real T 0 tal que f (t + T) = f (t).
3.8. PROBLEMAS 241
8. Encuentre la representacin en series de Fourier (de exponenciales com-
plejas) de la seal f (t) = sen(2t) + cos(3t) 0,5 sen(3t) + sen(5t).
9. a) Encuentre la frecuencia fundamental de la seal g(t) = sen(2t/5) +
7 cos(2t/7).
b) Usando la frmula de Parseval correspondiente, encuentre la en-
erga promedio de la seal.
10. Encuentre w
1073741825
si w = e
j2/16
. Sugerencia: encuentre log
2
1073741825
11. Diga si la seal cos(t) + cos(t) es peridica, o no. Si s, encuentre el
periodo.
12. Encuentre el periodo de la seal continua sen
2
(t).
13. Encuentre el periodo de sen(2t/4) + cos(2t/3), t R.
14. Encuentre el periodo de e
j2n/5
+ e
j2n/3
, n Z.
15. Exprese la seal discreta peridica s = . . . 1, 1/2, 0, 1/2, 1, 1/2, 0, . . . , de
periodo 4, como una suma de exponenciales complejas discretas. Asuma
que s
0
= 0 y que, por lo tanto, la seal es par.
16. Una serie de Fourier se puede expresar en trminos de exponenciales
complejas o de senos y cosenos:
n=
c
n
e
jn
0
t
=
n=0
a
n
cos(n
0
t) +
n=1
b
n
sen(n
0
t)
exprese las c
n
s en trminos de las a
n
s y b
n
s, y viceversa.
17. Graque 1/2 + 1/2(1)
n
contra n.
18. Exprese s
n
= 1/2 +1/2(1)
n
como una suma de exponenciales complejas
discretas. Tambin, la seal (j)
n
.
19. Encuentre el periodo de la seal rZ Cdada por r
n
= e
j2n(256/1023)
. nota:
1023 es nmero primo y por lo tanto, la fraccin 256/1023 es irreducible.
20. Diga si la seal s : Z C dada por s
n
= e
j8n/34
es peridica, o no. En
caso armativo, d el periodo.
21. Muestre que para cada nmero real x 0, para cada > 0, hay un
nmero natural N tal que x 2N
N
< .
22. Muestre que para cada funcin continua peridica con periodo 2, f ,
para casa > 0, hay una suma de exponenciales complejas
N
k=0
c
k
e
jtk
tal
que f (t)
N
k=0
c
k
e
jtk
< .
23. Se tiene la seal f (t) = sen(9t) + sen(15t).
a) Diga si es peridica. Si s, d el periodo.
b) Diga si hay coecientes c
n
tales que f (t) =
n=
c
n
e
jn
0
t
. Si s, d
los valores para
0
y c
n
.
24. Muestre que la convolucin (lineal continua) de dos seales peridicas
con norma L1 no nula, no existe.
25. Encuentre una seal r : Z Cde periodo 15 y una r : Z Cde periodo
10, tales que su suma tenga periodo 6.
26. Usando la frmula de Parseval, encuentre la potencia promedio de
cos(t) + cos(t).
27. Se tiene una seal peridica g : R C con periodo 2 y dada por g(t) =
u(t) u(t 1) para t [0, 2). Calcule y graque la convolucin circular de
g consigo misma.
28. Exprese Asen(a) + Bsen(b) como Ccos(c + ).
3.8. PROBLEMAS 243
29. Muestre que
e
jmx
(1e
j(2m+1)x
)
1e
jx
=
sen[(m+1/2)x]
sen(x/2)
, para x 0. Encuentre el lmite
cuando x tiene a cero. Graque para m = 10.
30. Encuentre el periodo de r : Z C dada por r
n
= e
j3n/7
.
31. Demuestre que cos(2t) + cos(2t/
2) no es peridica. O, en caso con-

trario, d el periodo.
32. Muestre que, para cada natural n,
_

0
sen((0+0,5)t)
sen(0,5t)
dt = .
33. Se tiene una onda cuadrada de 60 ciclos por segundo, de nivel prome-
dio 0.5 y amplitud pico a pico de 1. Encuentre la potencia promedio
de la seal as como la potencia promedio asociada con las primeras 5
armnicas.
34. D seales discretas de periodos M y N tales que
a) El periodo de la suma sea mcm(M, N) MN.
b) El periodo de la suma sea menor que mcm(M, N).
35. Muestre que la seal s : Z C dada por s
n
= e
jn
es casi peridica pero
no peridica.
36. Se tiene una onda peridica de periodo 2, nievl promedio 0.5 yamplitud
pico a pico de 1, como se muestra en la gura 36. Si su serie de Fourier
es

c
n
e
jnt
, encuentre la potencia promedio de la versin truncada de
su serie de Fourier dada por

6
6
c
n
e
jnt
.
37. Usando la propiedad de Parseval de la DTFT, calcule

n=
s
2
n
, donde
s
n
= 2
n
.
Referencias
[1] Digital Signal Processing. A. V. Oppenheim y R.W. Shafer.
Prentice Hall, Englewood Clis, 1975.
[2] Mathematical Analysis. T.M. Apostol. 2nd Ed. Addison-
Wesley, Reading, 1974.
[3] Fourier Series. G.P. Tolstov. Dover, N.Y., 1962.
[4] Almost Periodic Functions. H. Bohr. chelsea, N.Y., 1947.
[5] Sobre la periodicidad de sumas de seales discretas peridi-
cas. A. Restrepo y L. Chacn. Memorias del simposio de
Tratamiento de Seales, Imgenes y Visin Articial, Universi-
dad de los Andes, Bogot, 1995.
[6] On the period of sums of discrete periodic signals. A. Restre-
po y L. Chacn. IEEE Signal Processing Letter, vol. 5, No. 7, pp.
164-166, 1998.
[7] Anlisis de Fourier. J. Duoandikoetxea. Addison- Wesley,
Wilmington, 1995.
[8] Fourier Analysis. T.W. Krner. Cambridge University Press,
Cambridge, 1998.
245
Captulo 4
La Transformada de Fourier
de Seales continuas
4.0. Introduccin
La invarianza, tanto de las exponenciales complejas como de las sinusoides,
con respecto a la diferenciacin, nos dice que la respuesta de un sistema lin-
eal descrito por una ecuacin diferencial lineal con coecientes constantes, a
una sinusoide o una exponencial compleja, es una sinusoide o una exponen-
cial compleja de la misma frecuencia. La idea de representar seales peridicas
con series de sinusoides o de exponenciales complejas resulta as doblemente
poderosa: con gran generalidad, para sistemas lineales e invariantes, la re-
spuesta a una exponencial compleja de frecuencia arbitraria, es todo lo que
necesitamos para encontrar la respuesta a seales peridicas.
El anlisis de Fourier es til en audiologa, en lingistica, en teora de sis-
temas, en ptica, en mecnica cuntica y en otras reas. En el caso de ingeniera
246
electrnica, sus principales aplicaciones estn en las reas de comunicaciones,
voz y audio, bioingeniera y control.
4.0.1. Motivacin
Inicialmente, indicamos una forma plausible de obtener la transformada
de Fourier de ciertas seales, usando una serie de Fourier. Considere una seal
peridica s(t), como la mostrada en la gura 4.3.a. Suponga que 2 es un
tiempo de repeticin de la seal y que tiene serie de Fourier con coecientes
c
n
, como se muestra en la gura 4.3.b. Ahora suponga que queremos aislar el
segmento de s en el intervalo [, ] agregando segmentos de valor cero, antes
y despus de cada intervalo de la forma [(2k 1), (2k + 1)], k Z, dando
lugar a la seal f (t) con tiempo de repeticin T y concordante con s en [, ],
como se muestra en la gura 4.3.c. Y, nalmente, que alargando la longitud de
los intervalos nulos se obtiene en el lmite la seal g(t) que se muestra en la
gura 4.3.d, concordante con s en [, ], y nula por fuera de [, ].
As, la seal s(t), tiene una serie de Fourier de la forma, s(t) =
n=
c
n
e
jnt
,
con coecientes dados por, c
n
=
1
2
_

s(t)e
jnt
dt.
Suponga que la serie de Fourier de f (t) tiene coecientes d
n
, es decir,
f (t) =
n=
d
n
e
j
2
T
nt
(4.1)
con
d
n
=
1
T
_
T/2
T/2
f (t)e
j
2
T
nt
dt (4.2)
Deniendo = 2/T,
n
= n y F(
n
) = Td
n
, aumentamos T y obtenemos
ecuaciones correspondientes a las ecuaciones 4.1 y 4.2, cuando T tiende a .
248 CAPTULO 4. TRANSF. DE FOURIER DE SEALES CONTINUAS
Figura 4.1: a. Una seal peridica
Figura 4.2: b. El resultado de agregar intervalos nulos entre periodos
Figura 4.3: c. el resultado en el lmite.
Sea
g(t) = lm
T
f (t)
= lm
T
n=
d
n
e
j
2
T
nt
= lm
T
n=
1
T
F(
n
)e
j
n
t
= lm
T
n=
1
2
F(
n
)e
j
n
t
que podemos ver como el lmite de una suma de Riemann,

g(t) =
1
2
_

G()e
jt
d
con G() = lm
T
F(
n
) = lm
T
_
T/2
T/2
f (t)e
j
n
t
dt. As, G() se puede ver como una
de interpolacin de F(
n
). Vea la gura 4.3.d.
Ejemplo. Queremos calcular la serie de Fourier de la seal que se muestra en
la gura 4.4.
d
n
=
1
T
_
T/2
T/2
f (t)e
jn
0
t
dt
=
1
T
_
1
1
e
jn
0
t
=
1
T
_
1
1
e
jn
2
T
t
=
_
_
2
T
, n = 0
1
T
T
j2n
_
e
j
2n
T
e
j
2n
T
_
, n 0
=
_
_
2
T
, n = 0
2
T
sen(
2n
T
)
2n
T
, n 0
=
2
T
senc (
2n
T
)
=
2
T
senc (n)
Figura 4.4: Pulsos
4.0.2. Objetivo
Quizs tenga sentido decir que en la prctica las seales tienen duracin
nita; sin embargo, no es conveniente restringirnos a conjuntos de seales de
duracin nita, la generalidad tiene sus ventajas. En todo caso, muchas seales
continuas, de longitud innita, de duracin innita y no peridicas, se pueden
expresar como las integral de una funcin de la forma S()e
jt
:
s(t) =
1
2
_

S()e
jt
d (4.3)
En estos casos, la funcin S() provee la caracterizacin en el dominio de la
frecuencia de Fourier de la seal s(t). S() se conoce como la transformada de
Fourier de s(t).
Para seales s en L
1
, su transformada S() se calcula as:
S() =
_

s(t)e
jt
dt (4.4)
Note la similitud entre la frmula 4.4 de la transformada y la de la trans-
formada inversa 4.3. El factor
1
2
y el signo del exponente de la exponencial
compleja e
jt
son la nicas diferencias; algunos autores cambian estas conven-
ciones.
En ingeniera, tradicionalmente, t es la variable en el dominio natural de la
seal y la del dominio de la frecuencia. El par que acabamos de denir se conoce
como la transformada de Fourier L-1, la razn es que para que la transformada
exista para cada valor real del argumento , es suciente que la seal sea
integrable en magnitud. Muchas seales no son integrables en magnitud, en
particular, la seal senc no lo es. La seal senc s es integrable en magnitud al
cuadrado.
Las transformadas de seales enLa2 yla de distribuciones las consideramos
ms adelante, brevemente, en este captulo. Es una lstima que el tratamiento
riguroso de la transformada de Fourier de seales bastante arbitrarias tenga
que ser en alguna medida lento: hay que empezar por seales en L 1, luego
en L 2, luego L p, luego distribuciones funcionales.
Para seales en L
2
se dene una transformada de Fourier L 2 que es un
lmite en norma de funciones en L
1
L
2
- La transformada de una distribucin
est dada por la distribucin aplicada a la transformada de la funcin.
4.1. La transformada de Fourier L-1
As como convergencia de una serie en magnitud implica convergencia
incondicional, la existencia de una integral, cuando el integrando est en mag-
nitud, implica la existencia de la integral con el integrando sin magnitud.
Ejercicio. Muestre que si una funcin es integrable en magnitud, entonces es
integrable.
Si g : R
1
C es una seal integrable en magnitud, la siguiente frmula
determina un nmero complejo G() para cada R
1
:
G() =
_

g(t)e
jt
dt
ya que, la integrabilidad en magnitud de g(t) implica la integrabilidad en
magnitud de g(t)e
jT
ya que
_

g(t)e
jt
dt =
_

g(t)dt
Note que G() se dene como la suma de los siguientes lmites, cuando T
tiende a innito, de
_
0
T
g(t)e
jt
dt +
_
T
0
g(t)e
jt
dt (4.5)
4.1. LA TRANSFORMADA DE FOURIER L-1 253
y no como el lmite cuando T tiende a innito de,
_
T
T
g(t)e
jt
dt (4.6)
La expresin de la ecuacin 4.6 se conoce como el valor principal de Cauchy
de g(t)e
jt
. Esta diferencia es importante ya que, en ciertos casos, el lmite en
la ecuacin 4.6 puede ser cero mientras que los lmites en la la ecuacin 4.5
pueden ser + y , y su suma no est denida. Por ejemplo,
_
T
T
sentdt es
cero para toda T, sin embargo,
_
T
0
sentdt no tiende a ningn valor particular a
medida que T crece.
Ejemplo. Calcule la transformada de Fourier dela seal s(t) dada por:
s(t) =
_
_
1, t [, ]
0, t [, ]
Note que la seal es integrable en magnitud. Por denicin, la transforma-
Figura 4.5: Una seal pulso
da S(), que tambin escribimos [F(s)]() (la transformada de Fourier de s
evaluada en ), est dada por,
_

s(t)e
jt
dt =
_

e
jt
dt
=
1
j
e
jt
, siempre que 0
=
e
jt
e
jt
j
=
2 sen
si = 0
_

e
jt
dt = 2
resumiendo,
S() =
_
_
2, = 0
2 sen
, 0
= 2senc
Esta funcin aparece con relativa frecuencia en teora de seales; la funcin
senc x est denida como senc =
senx
x
, para x 0, y senc (0) = 1. Como se
puede comprobar, la funcin senc es continua. La funcin senc tambin es
conocida como el ncleo de Fourier continuo.
Ejercicio. Calcule la transformada de la seal continua f dada por f (t) = e
t
.
(La campana de Laplace).
Ejercicio. Diga si la seal campana de Cauchy dada por
1
1+t
2
est en L
1
.
Ejercicio. Diga si la seal e
t
2
est en L
1
.
Ejercicio. Calcule la transformada de Fourier de la seal e
t
2
. Es cierto que la
transformada de Fourier de una campana de Gauss es otra campana de Gauss?
Figura 4.6: La funcin senc x
Ejercicio. Calcule la transformada de Fourier de la seal
1
1+t
2
.
Ejercicio. Muestre que e
x
2
=
2
_

0
e
t
2
cos(2tx)dt
Nota. La representacin en el dominio de la frecuencia de Fourier de seales
peridicas tales como las sinusoides y las exponenciales complejas la obten-
emos por medio de su representacin como series (o sumas) de Fourier, es
decir, con el conjunto de coecientes c
n
de la serie, gracado contra = n
0
(donde
0
= 2/T y T es un tiempo de repeticin) mejor que contra n. Las
sinusoides no nulas no son seales en L
1
ni en L
2
. Estas seales no tienen trans-
formada (segn la denimos aqu); la integral correspondiente no converge
para ninguna frecuencia .
Ejercicio. Para qu valores de existe el lmite de
_
T
0
cos te
jt
dt cuando T
tiende a innito?
De aqu enadelante, hasta la seccin4.5, solose considerar la transformada
de Fourier de seales integrables en magnitud. En esta forma, se tendr la
seguridad de que la transformada es tambin una seal cuyo dominio es la
lnea de los nmeros reales. Lamentablemente, como vimos en el ejemplo
anterior, la transformada de una seal en L
1
no necesariamente est en L
1
.
Nota. El lector familiarizado con las teoras de Fourier, de sistemas o de proba-
bilidad, puede preguntarse en este punto las razones por las cuales la funcin
impulso no se utiliza en la denicin de transformada de Fourier de las seales
sinusoidales; algunas de stas son:
i El autor no considera conveniente su uso en un curso introductorio tal
como Teora de Seales.
i El impulso, en matemticas, no es ninguna funcin con dominio un
conjunto de nmeros; es una entidad cticia que tal vez sera el ncleo del
funcional de Dirac, el funcional de Dirac est dado por el funcional que
asigna a cada funcin en un espacio vectorial de funciones con dominio
R, el valor de la funcin cero.
iii La teora matemtica en la cual se denen los impulsos es la teora de las
distribuciones. Esta teora es ms sosticada que el clculo y cubrirla es
innecesario ya que:
a La funcin escaln, junto con la integral de Riemann-Stieltjes y las
series de Fourier, son sucientes para desarrollar la teora de seales
y sistemas en el contexto del clculo.
b Las series de Fourier permiten una representacin adecuada de
seales peridicas continuas en el dominio de la frecuencia.
4.2. Propiedades de la transformada de Fourier L-1
La transformada de Fourier es ampliamente usada por varias razones; tal
vez las ms importantes tengan que ver con las propiedades de modulacin,
4.2. PROPIEDADES DE LA TRANSFORMADA DE FOURIER L-1 257
de convolucin y la transformada inversa. La propiedad de modulacin (lin-
eal) de la transformada de Fourier se aprovecha para compartir un canal por
multiplexacin en frecuencia; por ejemplo, ste es el sistema usado par la trans-
misin de radio AM comercial. La propiedad de convolucin junto con la de
la transformada inversa, permiten el modelaje y el diseo de sistemas lineales
invariantes (e.g. ltros) en el dominio de la frecuencia.
Una tercera razn para la popularidad de la frecuencia de Fourier se en-
cuentra en el campo del procesamiento de audio y de voz: hay una correspon-
dencia entre la frecuencia percibida de un sonido y las frecuencias de Fourier
de sus componentes, especialmente de la fundamental; de hecho, hay quienes
aseguran que los nicos tonos puros son los de tipo sinusoidal. Sin embar-
go, el odo humano no es muy sensitivo a fase de Fourier: si se escuchan dos
seales peridicas y luego se escuchan nuevamente, esta vez retardando una
con respecto a la otra, es difcil escuchar una diferencia.
Otra razn es que las exponenciales complejas (en general, las exponen-
ciales) son funciones propias de los sistemas lineales invariantes: la respuesta
de un sistema lineal e invariante a una exponencial compleja es una expo-
nencial compleja de la misma frecuencia, multiplicada por una constante (el
valor propio que resulta estar dado por la transformada de Fourier de la
funcin caracterstica del sistema evaluada en la frecuencia de la exponencial
compleja). Cuando un sistema lineal e invariante con funcin caracterstica
real se excita con una sinusoide, la salida es tambin una sinusoide (real) de la
misma frecuencia, posiblemente desfasada y con amplitud diferente (o la seal
cero). En modelos dispersivos de medios de propagacin de ondas, las nicas
seales que no se distorsionan, en cuando a forma de onda, son la sinusoides.
A continuacin se listan algunas de las propiedades de la transformada de
Fourier. Se asume que la seal s en su dominio natural (en contraste con la
seal s en el dominio de la frecuencia) es una funcin integrable en magnitud
(i.e. s L
1
). Estrictamente hablando, se asume que la integral de Fourier se
dene con una integral de Lebesgue, en vez de con una de Riemann; tambin
, que dos funciones son equivalentes si el subconjunto de su dominio donde
dieren (es decir, el soporte de su diferencia) tiene medida cero.
i) (Teorema de Riemann-Lebesgue.) Si la seals : R
1
Ces integrable en mag-
nitud, su transformada de Fourier S() tiende a cero a medida que
crece: lm
S() = lm
S() = 0. G() =
g(t)e
jt
dt, despus
se toma G() (G()) = 2G() y entonces
G() = 0,5
_
g(t)e
jt
dt +
g(t)e
jt
e
j
dt
_
_
= 0,5
_
g(t)e
jt
dt +
g(t)e
j(t
)
dt
_
_
haciendo t
= t

2
G() = 0,5
_
g(t) g(t

)
_
e
jt
dt
As, no es posible, posible, por ejemplo, que la transformada de una seal
integrable en magnitud sea la seal escaln: u().
Ejercicio. Demuestre el teorema de Riemann-Lebesgue.
Sugerencia: Muestre que si g est en L
1
, lm
0
_

g(t + ) g(t)dt = 0
luego, con
G() =
_

g(t)e
jt
dt
y
G() =
_

g(t)e
jt
dt
=
_

g(t /)e
jt
dt
y
2G() =
_

g(t)e
jt
dt +
_

g(t /)e
jt
dt
=
_

_
g(t) + g(t /)
_
e
jt
dt
resulta
G() 0,5
_

_
g(t) + g(t /)
_
e
jt
dt
ii) (Si s es integrable en magnitud), su transformada de Fourier S() es
acotada:
S() =
_

s(t)e
jt
dt
_

s(t)e
jt
dt =
_

s(te
jt
dt
dado que e
j
= 1, se puede concluir que, para cada ,
S()
_

s(tdt
por lo tanto, [S[
[s[
1
y por lo tanto, S L
. As, la transformada de
Fourier F es una transformacin de L
1
a L
. En la seccin 4.7, extendere-

mos el dominio de la transformada a L
1
L
2
.
F : L
1
L
, F(h) = H,
H() =
_

h(t)e
jt
dt
Figura 4.7: La transformada de Fourier
iii) La transformada de S() de una seal en L
1
es una funcin uniformemente
continua.
Demostracin.
S(+ h) S() =
_

s(t)e
j(+h)t
dt
_

s(t)e
jt
dt
=
_

s(t)e
jt
[e
jht
1]dt
por lo tanto,
S(+ h) S()
_

s(t)e
jht
1dt
como el lado derecho no depende de , si el lmite cuando h tiende a
0 es 0, tendremos continuidad uniforme. Como s(t)e
jht
1 2s(t),
que es integrable; si tenemos una sucesin h
n
0 entonces s(t)[e
jht
1] 0 usando el teorema de la convergencia dominada de Lebesgue, e

intercambiando las operaciones de lmite e integral, tenemos
lm
nto
_

s(t)e
jt
[e
jht
1]dt =
_

lm
nto
s(t)e
jt
[e
jht
1]dt
= 0
y, como h
n
es cualquier sucesin que converja a cero, tenemos que S es
continua. *Caso particular. Considere el caso particular enque g L
1
L
2
.
Para mostrar que S es continua en =
0
, considere S() S(
0
).
S() S(
0
) =
_

s(t)e
jt
dt
_

s(t)e
j
0
t
dt
=
_

s(t)[e
jt
e
j
0
t
]dt
as,
S() S(
0
)
_

s(t)[e
jt
e
j
0
t
]dt
y, con la desigualdad de Cauchy-Schwartz.
S() S(
0
) [s[
2
[e
jt
e
j
0
t
]dt
que tiende a cero cuando tiende a
0
. As no es posible, por ejemplo,
que la transformada de una seal integrable en magnitud sea 1/.
iv) (Propiedad de convolucin.) La transformada de Fourier de la convolucinde
dos seales integrables en magnitud, es el producto de las transformadas
correspondientes. Si s, r L
1
entonces,
F[s r] = F[s] F[r] :
[F(s r)]() =
_

e
jt
_

s()r(t )d dt
=
_

s()
_

e
jt
r(t )dt d Teorema de Fubini
=
_

s()e
j
_

e
j
e
jt
r(t )dt d
=
_

s()e
j
d
_

e
ju
r(u)du con u = t
= [F(s)]()[F(r)]()
Nota. Una de las diferencias entre las transformadas de Laplace bilateral
R(s) y de Fourier R() de una seal r(t) es que la transformada de Laplace
tiene como dominio un subconjunto del plano complejo C mientras que
la de Fourier tiene como dominio un subconjunto de la lnea R
1
:
R() = [F(r)]() =
_

r(t)e
jt
dt, A R
1
R(s) = [L(r)](s) =
_

r(t)e
st
dt, s B C
Ejercicio. Cmo est dada la regin de convergencia B de la transfor-
mada de Laplace de una seal de orden exponencial?
v) (Frmula de inversin.) Si tanto s como S son integrables en magnitud,
acotadas y uniformemente continuas,
s(t) =
1
2
_

S()e
jt
d
es decir, podemos recuperar la seal s a partir de su transformada S con
una frmula muy similar a la de la transformada.
La demostracin no es directa, como tal vez uno podra esperar, ya que
la integral
_

e
j(t)
d no converge. La demostracin se basa en los
siguiente resultados:
lm
r
1
2
_
r
r
_
1

r
_
e
jt
S()d = s(t) y lm
r
1
2
[ f K
r
](t) = f (t)
donde
K
r
(t) = r
_
sen(
t
2
)
t
2
_2
Figura 4.8: La funcin 1

r
para varios valores de r
_
r
r
_
1

r
_
e
j
d = r
_
sen(r/2)
r/2
_
. Sugerencia: Un
tringulo es la convolucin de un pulso con sigo mismo.
_
r
r
_
1

r
_
e
jt
S()d = s K
r
,
donde K
r
= r
_
sen(t/2)
t/2
_
2
Ejercicio. Muestre que lm
r
1
2
[s K
r
](t) = s(t).
Para el caso de la transformada L
2
veremos que tiene derivada izquierda
y derecha en cada punto y, para cada numero real t.
s(t) =
lm
rt
+ s(x) + lm
rt
s(x)
2
(es decir, en los puntos donde s es discontinua, s toma un valor igual al
promedio de los lmites izquierdo y derecho) y si su transformada S()
es integrable en valor absoluto, entonces. Creo que ac hace falta al-
go!!!
Ejercicio. Demuestre (indirectamente) que la funcin senc x no es un ele-
mento de L
1
. (Sugerencia: si la seal senc fuera integrable en magnitud,
su transformada sera uniformemente continua.)
Tambin aplicando 4 veces la transformada de Fourier a s, tenemos,
(4)
2
s. Excepto por un factor de escala aplicar 4 veces la transformada
de Fourier es la identidad, en cierto subespacio de L
1
.
Ejercicio. Calcule la transformada de Fourier, iterativamente, cuatro ve-
ces.
vi) (Transformada del complejo conjugado.) Si la transformada de s es S, la
transformada del complejo conjugado s
de s est dada por,

[F(s
)] = S
()
Para ver esto, dado que para todo nmero complejo z, (z
, que (
_
z)
=
_
z
, y que (e
j
)
= e
j
, se tiene que,
_

(t)e
jt
dt =
_

[s(t)e
jt
]
dt
=
__

s(t)e
jt
dt
_
= [S()]
vii) (Modulacin.) Si la transformada de s(t) es S(), entonces la transformada

de e
j
0
t
s(t) es S(
0
):
F[e
j
0
t
s(t)]() =
_

e
j
0
t
s(t)e
jt
dt
=
_

s(t)e
j(
0
)t
dt
= S(
0
)
Esta propiedad es base para el anlisis de sistemas de modulacin vesti-
gial (para TV). DSB y SSB (radio no comercial), AM y otros.
Ejemplo. Calcular la transformada de Fourier de s(t) = cos(10t)e
t
Sabiendo que la transformada de Fourier de e
t
es
2
1+
2
, podemos utilizar
la propiedad de modulacin y obtener (usando linealidad tambin):
S() =
_
1
1 + (10 )
2
+
1
1 + (10 + )
2
_
Figura 4.9: Sistema bsico de modulacin y demodulacin DSB. (No se incluyen ltros ni
amplicadores.)
viii) (Desplazamiento en tiempo.) Si la transformada de s(t) es S(), entonces la
transformada de s(t ) es e
j
S():
F[s(t )]() =
_

s(t )e
jt
dt x = t
=
_

s(x)e
j(x+)
dx
=e
j
S()
Note que esta propiedadse puede considerar comoladual de lapropiedad
de modulacin.
Ejercicio. Calcule y graque: Re[S()], Im[S()], S() y S(), si s(t) =
[u(t 2/5) u(t 8/5)] sen5t, donde u(t) es la funcin escaln.
ix) (Linealidad.) La linealidad de la transformada de Fourier se muestra uti-
lizando la linealidad de la integral:
[F(f + g)]() =
_

(f (t) + g(t))e
jt
dt
=
_

f (t))e
jt
dt +
_

g(t))e
jt
dt
= [F( f )]() + [F(g)]()
Ejemplo. Sea r : R
1
C una seal con trasformada R() y sea, s(t) =
r(t+h)r(t)
h
con h 0. Entonces, la transformada de s est dada por S() =
1
h
[e
jh
1]R(). Esto se deduce fcilmente de las propiedades de lineal-
idad y desplazamiento
S() = [F(s)]()
=
_

r(t + h) r(t)
h
e
jt
dt
=
_

r(t + h)
h
e
jt
dt
_

r(t)
h
e
jt
dt
=
1
h
[e
jh
1]R()
Ejercicio. Calcular el lmite cuando h tiende a cero de
1
h
[e
jh
1] (R/ j).
x) (Transformada de la derivada.) Si s es derivable (e integrable en magnitud)
con transformada de Fourier S() entonces, si la derivada r = s
es
tambin integrable en magnitud, la transformada de Fourier R de r est
dada por:
R() = [F(s
)]() = jS()
Ejercicio. Sea g(t) = e
t
2
. Graque g
(t) y g
(t). Encuentre y graque las

transformadas de Fourier de g(t), g
(t) y g
(t).
Ejercicio. Demuestre la propiedad de la derivada de la transformada de
Fourier. sugerencia: vea las propiedades ix, x y xi.
Ejercicio. Muestre que si f (t) y jt f (t) son integrables en magnitud y que si
la transformada de f es F() entonces la transformada de jt f (t) es F
().
xi) (Parseval.) (Mark Antoine Parseval, Circa 1776 - 1836) La energa de una
seal multiplicada por 2 es igual a la energa de su transformada:
2
_

s
2
(t)dt =
_

S
2
()d
Aunque la frmula es ms general, aqu trabajaremos en L
1
L
2
.
La frmula se puede deducir as: sean e y r seales y asuma que S = F[s]
y R = F[r]. Como F[s r] = SR, se tiene que s r = F
1
[SR], es decir,
_

s()r(t )d =
1
2
_

S()R()e
jt
d
tomando t = 0 resulta,
_

s()r()d =
1
2
_

S()R()d
ahora, asuma que s(t) = r
(t), entonces s(t) tiene transformada S() =

R
() o, equivalentemente, s
(t) = r(t) y R() = S
(), y se tiene que,

_

s()s
()d =
1
2
_

S()S
()d
La frmula deseada.
La frmula de Parseval nos dice que la energa de una seal es pro-
porcional a la energa de su transformada. Esto nos permite llamar a
S()
2
el espectro de energa de la seal s(t). Por esta razn tambin,
muchas tcnicas conducentes al clculo de la transformada de Fourier de
una seal se conocen como tcnicas de estimacin espectral. De hecho, una
parte de la terminologa del anlisis de Fourier y de ltros est basada en
la correspondiente a la luz. Si en la gura siguiente, el rayo izquierdo es
incidente y blanco, e interrumpimos el paso de una gama de rayos en la
regin entre los prismas, la luz al otro lado sale coloreada. si interrumpi-
mos el paso de las luces de longitud de frecuencia baja (rojos), de qu
color es la luz resultante?
Como dijimos, es necesario asumir que la seal tiene energa nita, es
decir, que est en L
2
, para que la demostracin dada tenga sentido.
Ejercicio. Muestre que,
_

s()r
()d =
1
2
_

S()R
()d
Ejercicio. Muestre que toda seal integrable acotada y de duracin nita,
es integrable en magnitud.
Ejercicio. Encuentre una relacin entre la correlacin de dos seales
_

s()r
( t)d y la correlacin de sus transformadas

_

S()R
(
)d
Ejercicio. Muestre que si S() es la transformada de s(t), entonces la
transformada de s(t) es S().
xii) (Propiedades de simetra.)
a) Si s(t) es una seal real, es decir si su parte imaginaria es cero
para cada t, entonces las partes real e imaginaria son par e impar,
respectivamente. Consecuentemente, la magnitud S() es par y la
fase impar.
Demostracin. Por denicin,
S() =
_

s(t)e
jt
dt
=
_

s(t) cos(t)dt
_

s(t) sen(t)dt
Por lo tanto, si s es real,
Re[S()] =
_

s(t) cos(t)dt
Que es una funcin par de la variable ; tambin,
Im[S()] =
_

s(t) sen(t)dt
es una funcin impar de la variable .
Entonces, dado que
S() =
_
Re[S()]
2
+ Im[S()]
2
yque tantoRe[S()]
2
comoIm[S()]
2
sonfunciones pares, podemos
concluir que S() es par.
Ejercicio. Muestre que si s es real, la fase de S es impar.
b) Si s(t) es una seal par, es decir s(t) = s(t), entonces sutransformada
S() es par tambin. Por denicin
S() =
_

s(t)e
jt
dt u = t
=
_

s(u)e
ju
du
=
_

s(u)e
ju
= S()
Ejercicio. Muestre que si s es una seal real par, su transformada S
tambin es real y par.
Ejercicio. Muestre que la transformada de una seal impar es impar.
4.3. Respuesta en frecuencia de sistemas de con-
volucin continuos
Suponga que se tiene un sistema de convolucin continuo, con respuesta
escaln g, como se muestra en la gura 4.10.
Figura 4.10: Un sistema de convolucin
Inicialmente, mostramos el siguiente resultado: la respuesta de un sistema
de convolucin a una exponencial compleja es una exponencial compleja de la
misma frecuencia, o la seal . Suponga que la entrada al sistema es la seal
e
j
0
t
. Por denicin, la respuesta del sistema est dada por,
r(t) =
_

e
j
0
(t)
dg()
=
_

e
j
0
t
e
j
0
dg()
= e
j
0
t
_

e
j
0
dg()
4.3. CONVOLUCIN EN FRECUENCIA 271
dado que
_

e
j
0
dg() es un nmero complejo, que depende de

0
, vemos
que, a menos que tal nmero sea cero, r(t) es una exponencial compleja de
frecuencia
0
. A este factor de amplicacin para exponenciales complejas,
en funcin de la frecuencia, lo llamamos la funcin de transferencia del
sistema, que denotamos H():
H() =
_

e
j
dg()
Ahora suponga que la entrada s(t), es una seal en L
1
, con transformada
S(). Por denicin, la salida estar dada por,
r(t) =
_

s(t )dg()
la transformada de r estar dada por
R() =
_

e
jt
_

s(t )dg() dt
=
_

e
jt
s(t )dg() dt
si podemos cambiar el orden de integracin, y con el cambio de variable
u = t
R() =
_

e
j(+u)
s(u)du dg()
=
_

e
j
_

e
ju
s(u)du dg()
=
_

e
j
dg()
_

e
ju
s(u)du
= H()S()
donde H es la funcin de transferencia del sistema, y S la transformada de
Fourier de la entrada s(t).
Alternativamente, suponga que, tanto la respuesta impulso del sistema h
como la respuesta escaln g y la seal de entrada s, son seales en L
1
. Sea
H() la transformada de Fourier de h(t), G() la de g(t) y S() la se s(t). Sea
y(t) la respuesta del sistema. Usando las propiedades de convolucin y de
la derivada de la transformada de Fourier, la transformada de Y de y est
dada por la relacin siguiente entre la funcin de transferencia del sistema y
la transformada de su respuesta escaln: H() = jH().
Y() = jG()S() = H()S()
Figura 4.11: Representacin en tiempo y en frecuencia de un sistema de convolucin
Los sistemas de convolucin tambin se conocen en ingeniera elctrica
como ltros (lineales e invariantes). Dado que los sistemas de convolucin son
modelos bastante comunes de sistemas fsicos y que es ms fcil de visualizar
el producto de dos funciones que su convolucin, tenemos que la transforma-
da de Fourier es una herramienta til para el anlisis de sistemas lineales e
invariantes.
Suponga que se hace pasar una haz de luz solar (blanca) por un prisma y
que a continuacin se coloca una placa con una rendija muy delgada, entonces,
obtendremos una luz coloreada bastante monocromtica despus de la rendija.
En cierto sentido, habremos ltrado una luz con muchas componentes de
frecuencia para obtener luz de cierto color, con un contenido de frecuencias
diferente. este sera un ejemplo de un ltro pasa banda ya que en la salida,
en frecuencia, slo se tiene un pequeo intervalo (banda) de frecuencias.
Figura 4.12: Descomposicin espectral de un rayo de luz
La transformada de Fourier H de la funcin caracterstica h de un sistema
de convolucin se conoce como la funcin de transferencia del sistema.
Por la propiedadde la derivada de la transformada de Fourier, la transformada
G de la respuesta escaln est relacionada con la funcin de transferencia as:
H() = jG() 0
H(0) =
_

h(t)dt
= lm
t
g(t) lm
t
g(t)
= lm
t
g(t)
Suponga ahora que por medio de un micrfono convertimos la seal de
intensidad de presin de aire producida por una contralto que canta, en una
seal de voltaje la cual pasamos por un sistema de convolucin cuya funcin
de transferencia es par y, para frecuencias positivas, cero para frecuencias
por encima de 2KHz y uno entre 0 y 2 KHz. Si por medio de un parlante
reconvertimos la seal elctrica en una seal audible, escucharemos una seal
ms grave, probablemente sin valor artstico, que la original.
Ejercicio. Se tiene un ltro con funcin de transferencia como la mostrada en
la gura 4.13, si la seal mostrada en la gura 4.14 tiene como transformada de
Fourier la mostrada en la gura 4.15, graque aproximadamente el espectro
(i.e. la magnitud de la transformada de Fourier) de la seal de salida.
Figura 4.13: La funcin de transferencia de un pasa bajas ideal
Figura 4.14: Esta seal se aplica al ltro pasa bajas ideal
Las transformadas involucradas en los dos ejercicios siguientes tienen sen-
tidoenla teora de la transformada de Fourier L
2
, que cubriremos ms adelante.
Las incluimos debido a su popularidad en el rea de tratamiento de seales.
Figura 4.15: Transformada de Fourier de la seal en la gura anterior
Ejercicio. Calcule F
1
(H) donde H es,
H() =
_
_
1, (, )
1/2, ,
0, [, ]
Ejercicio. Sea
e(t) =
_
_
1, t = 0
senc t
t
, t 0
Suponga que esta seal se aplica a unltro conla funcinde transferencia H()
dada en el ejercicio anterior. Graque aproximadamente el espectro Y()
2
de
la seal de salida.
Ejercicio. Encuentre la funcin de transferencia de un pasa bajas RC de primer
orden y la de un pasa altas RC de primer orden.Asuma R=C=1. Graque las
magnitudes y las fases de las funciones de transferencia.
Ejercicio. Un inversor sinusoidal de voltaje se obtiene a menudo ltrando la
fundamental de una onda cuadrada. Suponga que se tiene una onda cuadrada
de 60 ciclos por segundo, y que se ltra con un RC pasa bajas de primer
orden.Encuentre la frecuencia de corte para maximizar el cociente:
Potencia promedio de la fundamental
Potencia promedio de la tercera armnica
Recuerde que una onda cuadrada no tiene armnicas pares.
Figura 4.16: Falta epgrafe
4.4. Comportamiento en frecuencia en trminos de
los polos y ceros de H(s)
Sea H(s) = s
1
G(s) la transformada de Laplace de la funcin caracterstica
de un sistema de convolucin con respuesta escaln con respuesta escaln g,
donde G es la transformada de Laplace de g. Asumiremos que s es la variable
compleja s = + j C; con , R.
As asumiendo que el sistema es causal y que por lo tanto h(t) = g(t) = 0
para t < 0, tenemos que las transformadas de Fourier de h y de g estn dadas
4.4. POLOS Y CEROS 277
por
H() = H(0 + j)
G() = G(0 + j)
Es decir, la transformada de Fourier corresponde a la transformada de Laplace
evaluada sobre el eje imaginario del plano complejo s.
Asumiendo que la funcin de transferencia H(s) es una funcin racional de
la variable s (lo cual ocurre siempre que el sistema tenga una ecuacin difer-
encial correspondiente), por el teorema fundamental del lgebra, tenemos que
tanto el numerador como el denominador se pueden factorizar. As, podemos
escribir
H(s) =
a(s z
1
)(s z
2
) (s z
n
)
(s p
1
)(s p
2
) . . . (s p
m
)
para una funcin de transferencia con n ceros y m polos. Al restringirse al
dominio de la frecuencia de Fourier, tenemos:
H() =
a( j z
1
)( j z
2
) ( j z
n
)
( j p
1
)( j p
2
) . . . ( j p
m
)
Concentrndonos en la magnitud de H y obviando la fase, ya que para decir el
tipo de ltro (pasa bajas, pasa altas, banda rechazada, etc.) que H representa,
slo se usa la magnitud, tenemos
H() =
a( j z
1
)( j z
2
) ( j z
n
)
( j p
1
)( j p
2
) . . . ( j p
m
)
Queremos visualizar la relacin entre la ubicacin de los polos y ceros de G
(que son los de Hcon la posible excepcin en s = ). Interpretando cada factor
como la distancia de j a cada polo y cero, tenemos que la magnitud de H en
la frecuencia , es proporcional al producto de las distancias a los ceros de j
dividido por el producto de las distancias a los polos de j. En particular, si
hay algn polo de la forma j
0
, la funcin de transferencia H() se anula en
=
0
y si hay un polo en las cercanas de j
1
, la funcin de transferencia
crece en las cercanas de =
1
. Vea la gura 4.17.
Figura 4.17: NO TIENE EPGRAFE
Ejercicio. Para el diagrama de polos y ceros de H(s), mostrado en la gura
anterior, graque aproximadamente H().
Ejercicio. Para cada una de las funciones de transferencia listadas a contin-
uacin, haga un diagrama de polos y ceros y diga de qu tipo de ltro se
trata.
H(s) =
1
s
2
+s+1
H(s) =
s
s
2
+4s+1
H(s) =
s
2
+1
s
2
+4s+s
H(s) =
s
2
s
2
+4s+1
4.5. TRANSFORMADA DE FOURIER L-2 279
4.5. Transformada de Fourier L-2
Como se vio en la seccin anterior, si la seal de entrada s a un sistema de
convolucin continuo con funcin de transferencia H(), tiene transformada
S() entonces la transformada de la seal de salida es el producto S()H().
Si la seal de entrada s es peridica y no tiene norma L1 nula, entonces no
tiene transformada. A continuacin se obtiene una caracterizacin en frecuen-
cia de sistemas de convolucin continuos, para seales peridicas. suponga
que la seal de entrada (t) es peridica, con frecuencia angular fundamental
0
y con representacin en series de Fourier dada por
(t) =
n=
c
n
e
j
0
nt
suponga adems que la transformada de la respuesta impulso h(t) del sistema
es H(). Por denicin, la respuesta del sistema (t) es la convolucin de y
h:
(t) = (t) h(t)
=
_

h()(t )d
=
_

h()
n=
c
n
e
j
0
n(t)
d
=
n=
_

h()c
n
e
j
0
n(t)
d
=
n=
c
n
e
j
0
nt
_

h()c
n
e
j
0
n
d
=
n=
c
n
e
j
0
nt
H(n
0
)
=
n=
H(n
0
)c
n
e
j
0
nt
por lo tanto, la salida tiene representacin como serie de Fourier dada por:
(t) =
n=
d
n
e
j
0
nt
donde los coecientes d
n
estn dados por:
d
n
= c
n
H(n
0
)
Las dos ltimas frmulas caracterizan la seal de salida en el dominio de
la frecuencia de Fourier. Ahora podemos concluir que el periodo de la seal
de entrada es un tiempo de repeticin de la seal de salida. Por qu?
Si la entrada es una suma de exponenciales complejas no necesariamente
armnicamente relacionadas (es decir, que las frecuencias no sean mltiplos
enteros de una cierta frecuencia fundamental), la suma es una seal casiper-
idica, y se tiene el mismo resultado: los coecientes de las exponenciales de
la seal de salida estn dados por el producto del coeciente de cada exponen-
cial de entrada por la funcin de transferencia evaluada en la frecuencia de la
exponencial. en general, si la entrada est dada por,
(t) =
n=
c
n
e
j
0
nt
la salida ser,
(t) =
n=
d
n
e
j
0
nt
donde d
n
= c
n
H(n
0
).
4.5.1. Respuesta a sinusoides
Suponga que la respuesta impulso h(t) de un sistema de convolucin con-
tinuo es real. Entonces, la magnitud de la funcin de transferencia H() del
sistema es par, y la fase es impar. Si a este sistema se le aplica la seal cos(
0
t),
la respuesta r del sistema, por linealidad, estar dada por:
r(t) = 0,5H(
0
)e
jH(
0
)
e
j
0
t
+ 0,5H(
0
)e
jH(
0
)
e
j
0
t
= 0,5H(
0
)e
jH(
0
)+j
0
t
+ 0,5H(
0
)e
jH(
0
)j
0
t
(Por qu?)
= H(
0
) cos( j
0
t + H(
0
))
As la respuesta de un sistema de convolucin con respuesta escaln real
es tambin una sinusoide y de la misma frecuencia, a menos que la funcin de
transferencia valga cero para esa frecuencia.
Ejercicio. Se tiene una seal cuadrada con frecuencia de 60 Hz; esta seal se
aplica a un ltro pasa bajas ideal con frecuencia de corte en 100Hz. cul es la
seal de salida del ltro? (Expresela como una serie de sinusoides).
Figura 4.18: La respuesta de un sistema de convolucin a una sinusoide, es una sinusoide de
la misma frecuencia, o la seal cero si H(
0
) = 0
Ejercicio. Una onda tringulo de frecuencia 1cps (ciclo por segundo) es pasada
por un recticador de media onda, obteniendo la seal s(t) mostrada en la
gura 4.19. Graque la salida cuando s(t) es ltrada con un ltro pasa bajas
ideal con frecuencia de corte 0.2Hz y 1.5Hz.
Figura 4.19: Onda tringulo con recticacin de media onda
Ejemplo. Suponga que se tiene una seal cuadrada g(t), como se muestra en
la gura siguiente. Es fcil mostrar que su expansin en series de Fourier
contiene armnicas impares nicamente y que est dada por,
g(t) = a
0
+
n=0
b
n
sen(nt)
donde a
0
= 1/2, b
n
= 2/(n) con n impar y b
n
= 0 con n par. Suponga que g(t)
Figura 4.20: Una onda cuadrada y su espectro
se pasa por un ltro pasa bajas ideal, con frecuencia angular de corte igual a
5, como se muestra en la gura 4.21. A la salida del ltro se tiene la suma del
nivel DC, y de la primera y tercera armnicas. En la gura 4.23 se muestra la
Figura 4.21: Funcin de transferencia de un pasa bajas ideal
suma de las seales 0,5 sen(t) y 1/3 sen(3t).
4.5.2. Filtro pasa bajas RC de un polo
Ejercicio. Calcule la respuesta escaln g(t) del ltro RC mostrado
Figura 4.22: Espectro de la suma de dos seales coseno y un nivel DC
Figura 4.23: La seal 0,5 sen(t) + 1/3 sen(3t)
Figura 4.24: Filtro RC pasa bajas de primer orden
Ejercicio. Calcule la derivada h(t) de la respuesta escaln del ejercicio anterior
(es decir, la respuesta impulso).
Ejercicio. Calcule la transformada de Fourier de la seal h(t) = e
t
si t 0 y
h(t) = 0 si t < 0. Las partes real e imaginaria de la funcin H() =
1
1+j
se
gracan a continuacin.
Figura 4.25: La parte real de la funcin de transferencia del pasa bajos RC con RC=1
Ejercicio. D expresiones para la magnitud, la fase, la parte real, y la parte
imaginaria de la funcin de transferencia H() =
1
1+j
. A continuacin se
muestran grcas de la magnitud y la fase de la funcin de transferencia
H() =
1
1+j
.
Ejercicio. Repita el anlisis anterior para un RC pasa altas de un polo. La
respuesta escaln en este caso es g(t) = u(t)e
t
. Por lo tanto, la funcin de
transferencia est dada por H() =
j
1+j
(Compruebe). Graque g as como la
magnitud y la fase de H.
Figura 4.26: La parte imaginaria de la funcin de transferencia del pasa bajos RC con RC=1
Figura 4.27: La magnitud de H() =
1
1+j
Figura 4.28: La fase de H() =
1
1+j
4.5.3. Comportamiento transiente
El que la respuesta de una sistema de convolucin a una sinusoide sea una
sinusoide de la misma frecuencia, o la seal cero, es algo que vale la pena
recordar. El anlisis de Fourier asume que se conocen las seales para toda
t, desde t . (Esto no sucede cuando se estudian modelos de sistemas
usando la transformada de Laplace unilateral.) En el anlisis de Fourier no
consideramos condiciones iniciales y asumimos que la seal se aplica desde
menos innito.
Si asumimos que la entrada al sistema es una sinusoide multiplicada por
la seal escaln: u(t)Acos(
0
t). Para sistemas estables, la respuesta a este tipo
de sinusoides truncadas tiende asintticamente a la respuesta de la seal no
truncada Acos(
0
t), a medida que t tiende a innito. Larespuesta ala sinusoide
la denominamos respuesta en estado estable sinusoidal. La respuesta a
la sinusoide truncada la denominamos respuesta total. La diferencia entre la
total y la de estado estable la denominamos respuesta transiente.
Un caso particular se tiene cuando la frecuencia de la sinusoide es cero. En
este caso, la respuesta escaln tiende asintticamente ala respuesta a la seal
constante de valor 1; esta respuesta, como vimos en es captulo 2, es una seal
constante de valor
_

dg(t), donde g es la respuesta escaln del sistema.

Ejercicio. Se tiene un sistema de convolucin con respuesta escaln g(t) =
(1 e
t
)u(t). Encuentre la respuesta a la seal cos t y a la seal u(t) cos t.
4.5.4. Anlisis del comportamiento asinttico
Considere la respuesta
_
cos(
0
[t ])dg() a una sinusoide aplicada desde
menos innito y la respuesta
_
cos(
0
[t ])u(t )dg() a una sinusoide
aplicada en cero:
_

cos(
0
[t])dg()
_

cos(
0
[t])u(t)dg() =
_

t
cos(
0
[t])dg()
As, tendremos comportamientoasintticosi lm
t
_

t
cos(
0
[t])dg() =
0.
Ejercicio. diga qu condiciones debe cumplir g para tener comportamiento
asinttico.
4.5.5. representacin de un sistema con respuesta escaln dis-
continua entrminos de una suma de sistemas identidad
(linea de retardo o ltro pasa todas) y un sistema con re-
spuesta escaln continua
Suponga que se tiene un sistema identidad. Es decir, un sistema cuya
salida es siempre igual a la entrada. Para este sistema la respuesta escaln es la
seal escaln: g(t) = u(t) y la funcin de transferencia es la funcin constante
H() = 1.
Suponga ahora que se tiene una linea de retardo: para cada entrada e(t), la
salida del sistema es la entrada retardada unidades: s(t) = e(t ). en este
caso, la respuesta escaln est dada por g(t) = u(t ). (Dado que este sistema
es claramente lineal e invariante, y dada la propiedad de desplazamiento en
tiempo de la transformada de Fourier, es ese sentido, diremos que la funcin
de transferencia de la linea de retardo, tambin conocida como un ltro pasa
todas, est dada por: H() = e = j.)
Suponga que se tiene un sistema de convolucin con respuesta escaln
g(t) con derivadas excepto en un conjunto nito de puntos, con una posible
cantidad nita de saltos, y acotada. Note que podemos expresar una respuesta
escaln as como la suma de: una seal derivable en sentido relajado, es decir
continua y con derivada excepto en un conjunto nito de puntos, por una
parte y una seal escalonada, es decir, una suma de seales escaln desplazadas
yescaladas, por la otra. La seal escalonada corresponder a la suma (es decir el
paralelo) de sistemas identidad y la seal sin saltos a un sistema de convolucin
con funcin caracterstica.
Ejemplo. La respuesta escaln de un RC pasa altas es g(t) = e
t
u(t) = u(t)
(1 e
t
)u(t). As, decimos que un pasa altas es un pasa todas menos un pasa
bajas. Vea las guras 4.29, 4.30 y 4.31.
Figura 4.29: Un pasa altas es la identidad menos un pasa bajas
Figura 4.30: respuesta escaln del pasa altas de primer orden
Figura 4.31: La respuesta en la gura anterior es equivalente a la suma de un escaln y el
negativo de la respuesta escaln de un pasa bajas de primer orden, que no salta
4.6. DISTORSIN DE FASE Y DISTORSIN DE AMPLITUD 291
4.6. Distorsin de fase y distorsin de amplitud
4.6.1. Filtro ideal
Un filtro ideal es un ltro cuya funcin de transferencia H() tiene una
magnitud H() que es o uno, o cero (constante a trozos), y cuya fase H()
es lineal: H() = m, donde m es una constante (recuerde quedos ngulos se
consideran equivalentes si su diferencia es un mltiplo entero de 2).
Considere el caso en el que la entrada es una seal peridica representable
como una serie de Fourier. Una fase lineal asegura que cada componente,
sinusoidal o exponencial, sufra el mismo retardo temporal y una magnitud
binaria y constante a trozos asegura que cada componente en la banda de paso
reciba la misma atenuacin.
Ejemplo. Suponga que se tiene un ltro con funcin de transferencia H() =
e
j5
, cuya magnitud es constante e igual a uno y con fase lineal dada por
H() = 5. Si la entrada al ltro es e(t) = cos(at) + cos(bt), la salida est dada
por,
cos(at + H(a)) + cos(bt + H(b))
= cos(at + 5a) + cos(bt + 5b)
= e(t + 5)
Por lo tanto, el nico efecto de este ltro es adelantar la seal que se ltra.
4.6.2. Distorsin
Cuando la magnitud de la funcin de transferencia no es contante a trozos
con valores cero, en la banda de rechazo, y uno, en la banda de paso, se dice que
se tiene distorsin de amplitud. Cuando la fase no es lineal, se dice que se
tiene distorsin de fase.
Para ilustrar los efectos de estas distorsiones, comparemos un ltro ideal
pasa bajas con un ltro pasa bajas RC. Sean H
I
() y H
R
C(), respectivamente,
las funciones de transferencia de los ltros, dadas por
H
I
() =
_
_
1, 1
0, > 1
H
R
C() =
1
1 + j
suponga que la seal e(t) = cos(0,1t) + cos(0,5t) + cos(2t) mostrada en la gura
4.32.a, se ltra con cada uno de estos ltros. La idea es dejar pasar las seales
con frecuencias angulares 0.1 y 0.5 y rechazar la seal de frecuencia 2. La
respuesta del ltro ideal est dada por:
r
I
(t) = cos(0,1t) + cos(0,5t)
mientras que la del RC est dada por:
r
RC
(t) = 0,995 cos(0,1t 0,099) + 0,894 cos(0,5t 0,463) + 0,447 cos(2t 1,107)
En la medida que 0.995 es diferente de 1, 0.894 es diferente de 1 y 0.447 es
diferente de 0, tenemos distorsin de amplitud; el la medida en que 0.099/0.1
es diferente de 0.463/0.5, se tiene distorsin de fase. Note que en realidad no
hay mucha distorsin de fase; esto se debe a que la fase de la funcin de
transferencia de H
RC
() es aproximadamente lineal para omegas pequeas,
ya que es una arcotangente. El que H
RC
() atene la seal cos(2t) slo a
0,447 cos(2t . . . ) s es bastante problemtico y se debe a que la magnitud
de H
RC
() decrece lentamente alrededor de = 1.
Ejercicio. Utilizando Matlab, graque las respuestas r
I
(t) y r
RC
(t), mencionadas
arriba, para t [0, 200]; compare las diferencias.
Figura 4.32: a. Seal de entrada b. Seal de salida del ltro ideal c. Seal de salida del ltro RC
La distorsin de fase que sufre una seal que se ltra con un ltro de fase
no lineal, es similar a lo que le sucede a una onda que viaja a travs de un
medio dispersivo.
4.6.3. Filtro pasa todas
Un filtro pasa todas ideal nos permite ver lo que sucede en la banda
de paso de un ltro que no distorsiona. Un ltro pasa todas es un ltro con
respuesta escaln de la forma: g(t) = u(t ), es decir, une escaln atrasado o
adelantado, dependiendo del signo de . Por lo tanto, la funcin de transfer-
encia de un pasa todas est dada por:
H() =
_

e
j
0
t
dg(t)
que incluye el caso H() = 1, correspondiente al sistema identidad.
Ms generalmente, un pasa todas es cualquier ltro con funcin de trans-
ferencia con magnitud unitaria, es decir de la forma,
H() = e
j()
, : R
1
S
1
donde () es la funcin fase de la funcin de transferencia. La respuesta a
una exponencial compleja estar dada entonces por,
s(t) = e
j(
0
)
e
j
0
t
= e
j(
0
)+j
0
t
= e
j
0
((
0
)/
0
+t)
tenindose que, si la entrada es una exponencial compleja, la salida s es una
versin desplazada de la entrada e; el retardo, dado por (
0
)/
0
, depende
de la frecuencia
0
de la exponencial compleja.
Si la funcin de fase lineal, (
0
) = m, como asumimos inicialmente,
entonces la salida correspondiente a una entrada igual a una suma de expo-
nenciales complejas es una versin retardada de la entrada y el retardo est
dado por m, independientemente de las frecuencias involucradas. De hecho, si
la fase es lineal, la funcin de transferencia del ltro est dada por H() = e
jm
y la seal de entrada e(t) tiene transformada de Fourier E(), la transformada
de la seal de salida s(t) es
S() = E()H() = E()e
jm
y, por las propiedades de desplazamiento en t y de transformada inversa, la
salida est dada por, s(t) = e(t +m), por esta razn, un pasa todas ideal tambin
se conoce como una lnea de retardo ideal. El ltro identidad que produce a la
salida la misma seal de entrada, en un pasa todas con fase cero.
Ejercicio. Suponga que se desea un ltro pasa todas, que introduce un retardo
de valor 10 a la seal de entrada; es decir, s(t) = e(t 10) donde s y e son la
salida y la entrada respectivamente. Cul es la funcin de transferencia H()
del ltro?
Ejercicio. Suponga que se desea un ltro pasa todas, como el diseado en el
ejercicio anterior. Si la entrada es la seal e(t) = cos(5t). Cul es la salida?
Exprese la salida en cuadratura: a cos(5t) + b sen(5t)
Note que, en el ejercicio anterior, puede ser equivalente usar el pasa todas
o un pasa bajas ideal con banda de paso que incluya las frecuencias de la seal,
por qu?.
4.6.4. Dcadas y octavas
Las dcadas y las octavas se usan para medir relaciones (es decir cocientes)
en forma logartmica. As, se dice que 20.000 est 3 dcadas por encima de 20 y
que 1000 est 3 octavas por debajo de 8000. Las frmulas para medir la relacin
entre f
1
y f
2
en dcadas y en octavas, respectivamente, estn dadas por,
D = log
10
(
f
1
f
2
)
O = log
2
(
f
1
f
2
)
Ejercicio. Cuntas octavas tiene un piano estndar?
Ejercicio. Cuntas octavas hay de un do al siguiente fa?
Ejercicio. Cuantas dcadas hay en 3 octavas?
Figura 4.33: Do=C(261.626Hz), Re=D(293.665Hz), Mi=E(329.628Hz), Fa=F (349.228Hz), Sol=G
(391.995Hz), La=A (440.0Hz), Si=B (493.883Hz)
4.6.5. Frecuencias de corte y decibeles
En la practica, muchos ltros se implementan con elementos tales como
bobinas, resistencias y condensadores (o elementos anlogos para variable no
x1/x2 300/30 880/440 25/50 Relacin natural
log(x1/x2) 1 0.301 -3.01 en dcadas
log
2
(x1/x2) 3.322 1 -1 en octavas
10 log(x1/x2) 10 3.01 -3.01 dB de potencia
20 log(x1/x2) 20 6.02 -6.02 dB de voltaje
Tabla 4.1: Relacin natural
elctricas), y la funcin de transferencia resultante es una funcin racional
(es decir, el cociente de dos polinomios) en la variable . Un ltro ideal, en
general un ltro con una funcin de transferencia que tenga magnitud discon-
tinua, no tiene una funcin de transferencia racional y por lo tanto no puede
ser implementado as. Las funciones de transferencia racionales tienen tran-
siciones suaves entre las bandas de paso (donde la magnitud de la funcin
de transferencia es relativamente grande) y las bandas de rechazo (donde la
magnitud es relativamente pequea) graduales, sin discontinuidades.
Normalmente, se considera que las frecuencias de corte de los ltros
ocurren donde la magnitud de la funcin de transferencia es
1
2
veces la
magnitud mxima en la banda pasante. eso se debe a que la variable fsica que
la seal representa normalmente, por ejemplo voltaje, es proporcional a la raz
cuadrada de la potencia correspondiente y as, en las frecuencias de corte, la
relacin de potencias entre las seales de salida y de entrada es la mitad de la
correspondiente relacin en la banda de paso.
Una relacin entre potencias
P
s
P
e
se expresa en dBs (decibeles) dando el
valor 10 log
10
P
s
P
e
. Una relacin entre voltajes
V
s
V
e
o corrientes se expresa en dBs
dando el valor 20 log
10
V
s
V
e
. La utilidad del uso de dBs est en poder sumar y
restar ganancias en vez de multiplicarlas dividirlas.
Una ganancia de voltaje de 0.707 equivalente a una de potencia de 1/2,
corresponde a: 10 log
10
0,5 3dB; por esto, en ingeniera electrnica, fre-
cuencias
c
para las que la magnitud de la ganancia se reduce a
1
2
, donde
H(
c
)
2
= 1/2, se les llama frecuencias de corte de 3dB.
Ejemplo. Suponga que se tiene un pasa bajas RC de primer orden.Para encon-
trar su frecuencia de corte procedemos as,
H() =
1
1 + jRC
H()
2
=
1
1 + jRC
2
=
1
1 + (RC)
2
El valor mximo de la magnitud es H
max
= 1, y ocurre cuando = 0. Si
H
max
=
1
2
, entonces =
c
=
1
RC
.
El ancho de banda (Band Width=BW) se mide normalmente sobre el
semieje positivo e frecuencias, de tal forma que, para un pasa bajas, el ancho
de banda es igual a su frecuencia de corte.
Resulta conveniente gracar la magnitud en decibeles de la funcin de
transferencia de un ltro, contra la frecuencia, en dcadas. Para un pasa bajas
de primer orden, resulta la siguiente ecuacin,
20 log(
1
1 + jRC
) = 20 log([
1
1 + (RC)
2
]
1/2
)
= 10 log(1 + (RC)
2
)
= 20 log(/
c
)
donde
c
= 1/RC.
Ejercicio. Para la funcin de transferencia H del ejercicio anterior, con
c
= 10,
graque 20 log
10
H() contra log
10
. Si la grca es aproximadamente lineal,
encuentre la pendiente.
Ejercicio. Si la entrada al circuito RC pasa bajas es una seal escaln, y el
voltaje inicial del condensador es cero, el tiempo de subida t
r
se dene como
Figura 4.34: Representacin en decibeles de la funcin de transferencia
el tiempo que toma a ala seal de salida en ir de 0.1 a 0.9. Cmo se relaciona
el tiempo de subida con la frecuencia de corte en un pasa bajas RC de primer
orden?
Ejercicio. Para el circuito RC pasa bajas, si R=1Ky la frecuencia (no angular)
de corte es 10KHz, Cunto vale C? Cunto vale el tiempo de subida?
Ejercicio. Se tiene un bombillo de 110V y potencia de 60W. Cul debe ser
el voltaje para que disipe una potencia de 30W? (Asuma que el cambio de
temperatura no afecta signicativamente la resistencia del bombillo, lo cual es
falso.)
Ejercicio. Se tiene una resistencia de 1K, si se aplica un voltaje V=10V, Qu
potencia disipa? Sea x el voltaje que se debe aplicar a la resistencia para que
disipe 5W, Cunto vale la relacin r = x/10 Cunto vale 20 log(r)?
Ejercicio. Se tiene un pasa bajas RC con frecuencia (angular) de corte de 10 r/s.
Cul es la salida si la entrada es e(t) = sent + sen10t + sen10
2
t?
Ejercicio. Encuentre la funcin de transferencia al colocar en cascada un RC
pasa bajas de primer orden y un RC pasa altas de primer orden. a) Si las dos
etapas se aslan con un seguidor. b) Si la salida de una se conecta directamente
a la entrada del otro.
Ejercicio. Suponga que tiene un ltro pasa todas con funcin de transferencia
dada por H() = e
j
(la magnitud y la fase de H se muestran en la gura
4.35); si la entrada es e(t) = sint +sin2t, Cul es la salida s(t)? Cunto vale la
pendiente de la fase de H?
Figura 4.35: La magnitud y la fase de un pasa todo con fase lineal
Ejercicio. Suponga que se tiene un ltro pasa todo con funcin de transferencia
tal como se indica en la gura 4.36; si la entrada es e(t) = sent + sen2t, Cul
es la salida s(t)? Graque e(t) y s(t) para t [0, 2].
Ejemplo. Si la seal cos t 0,2 cos 3t se ltra con el pasa todas de la gura 4.36,
resulta la seal cos t 0,2 cos(3t ). Observe la distorsin en la forma de onda
en las guras siguientes.
Figura 4.36: Un pasa todo con fase no lineal
Note que el ltropasa bajas RCde primer orden, para frecuencias pequeas,
tiene una magnitud aproximadamente plana (es decir constante) y una fase
bastante lineal. Por lo tanto, el ltro no distorsiona mucho las componentes de
baja frecuencia de la seal (las que se supone que interesan y deben aparecer a
la salida del ltro). Para frecuencias cercanas a la frecuencia de corte del ltro
las distorsiones de amplitud y de fase introducidas son apreciables.
Ejercicio. Comente sobre la distorsin introducida por el ltro RC pasa bajas
de primer orden a la frecuencia de corte, y para frecuencias mucho mayores
que la frecuencia de corte
Ejercicio. 1. Disee un ltro pasa bajas RC con frecuencia de corte 60Hz.
2. Calcule los coecientes de Fourier c
n
para una onda tringulo con peri-
odo 1/60 seg., amplitud de dos voltios pico a pico, nivel DC de un voltio,
como se muestra en la gura siguiente.
Figura 4.37: a) La seal de entrada. b) La seal de salida (alteracin de la forma de onda)
3. Si la onda tringulo se ltra con el pasa bajas, calcule los coecientes de
Fourier de la seal de salida.
4. Utilizando Matlab, calcule y graque aproximadamente dos periodos de
la seal de salida. (Utilice las 10 primeras armnicas.)
Figura 4.38: Onda tringulo
4.7. La transformada de Fourier L-2
Desafortunadamente, tres de las seales no peridicas ms comunes en
teora de sistemas y seales no son integrables en magnitud: la seal constante
1, la seal escaln y la seal senc . De stas, solo la seal senc est en L
2
.
Para sta ltima podemos denir una transformada de Fourier, que es como
esperbamos, un pulso en frecuencia. Note de paso que la transformada L 2
no necesariamente produce funciones uniformemente continuas.
Un hecho bsico es que L
1
L
2
es denso en L
2
. As, es posible aproximar
cada funcin de L
2
con seales en L
1
L
2
, que en particular estn en L
1
y
tienen transformada tal como la acabamos de denir. La aproximacin es en
el sentido de la norma L
2
y no necesariamente es lineal. Es decir, decimos que
una sucesin de funciones f
n
en L
1
L
2
aproxima a la funcin en L
2
si [ f
n
f [
2
tiende a cero.
4.7.1. Denicin
Sea s(t) una seal con magnitud al cuadrado integrable, es decir, una seal
en L
2
. Sea N un nmero natural y considere las versiones truncadas de s dadas
por: s(t)[u(t + N) u(t N)]. Note que cada s
n
es integrable en magnitud, y en
magnitud al cuadrado, es decir est en L
1
L
2
. Por lo tanto, cada s
N
(t) tiene una
transformada de Fourier L 1 que denotaremos S
N
(). Se puede mostrar que
S
N
es una sucesin de Cauchy en L
2
y, dado que L
2
es un espacio completo,
existe una funcin S() tal que [S S
n
[
2
tiene a cero a medida que N crece. A
sa S la llamamos tambin el lmite en norma L 2 de S
N
. Este lmite nos da la
transformada de Fourier L 2 de la seal s.
Ejercicio. Calcule el lmite, a medida que N crece, de
_
N
N
senc (t)e
jt
dt.
Ejercicio. Encuentre la transformada de Fourier L 2 de la seal senc .
4.8. La transformada de Fourier de distribuciones
temperadas
Finalmente, en esta seccin, deniremos las transformadas de Fourier del
escaln y de las seales constantes, en un sentido muy especial, que afortu-
nadamente tiene muchos puntos de empate con las trasformadas L 1 y L 2.
Inicialmente, denimos la clase de Schwartz y las distribuciones temperadas.
Decimos que una funcin f : R R est en la clase de Schwartz, [, si
es indenidamente derivable y ella y sus derivadas decrecen rpidamente en
innito, en el sentido que:
, N supx
f (x) : x R <
Las funciones innitamente derivables de soporte compacto y otras como
e
x
2
que no tienen soporte compacto, estn en [. p
,
( f ) := supx
f (x) : x
4.8. DISTRIBUCIONES TEMPERADAS 305
R, determina una familia contable de seminormas para [con la que se dene
su topologa: f
n
converge a 0 si y slo si el lmite cuando n tiende a innito
de p
,
( f ) es cero, para cada y cada naturales.
El espacio de funcionales continuos sobre [, que se denota [
se llama
espacio de distribuciones temperadas.
Teorema 8. La transformada de Fourier es una aplicacin continua de [en [tal que
1.
_

g(x)H(x)dx =
_

h(x)G(x)dx donde H es la transformada de h, y G la de

g.
2. g(t) =
1
2
_

G()e
jt
d (frmula de inversin)
Denicin 15. La transformada de Fourier de [
es la distribucin temperada
[
dada por
g [ (g) = (G) (4.7)
Teorema 9. La transformada de Fourier es una biyeccin lineal continua.
4.8.1. Distribuciones
Llamamos a g el ncleo del funcional dado por
( f ) =
_

g(t) f (t)dt
mientras que g es la semilla del funcional dado por
( f ) =
_

f (t)dg(t)
Es interesante observar lo que le sucede, cuando tienen ncleo o semilla, a
los ncleos o semillas de las distribuciones y en la ecuacin 4.7.
La distribucin de Dirac
considere la distribucin dada por ( f ) = f (0), que no tiene ncleo pero
s semilla: el escaln u(t). Por denicin, su transformada es la distribucin
dada por
( f ) = (F)
= F(0)
donde F es la transformada de f . As, s tiene ncleo, ya que
( f ) = F(0)
=
_

f (t)e
j0t
dt
=
_

f (t)1dt
y vemos que el ncleo de es la funcin constante 1.
La distribucin constante
Sea dada por ( f ) =
_

f (t)dt, que como vemos, tiene ncleo la funcin

constante 1. Por denicin, su transformada est dada por,
K( f ) = (F)
=
_

F()d
=
_

f (t)e
jt
dtd
?
=
_

f (t)
_

e
jt
ddt
que sin embargo no tiene sentido, ya que
_

e
jt
dno converge. As, tenemos
que K no tiene ncleo.
4.8. DISTRIBUCIONES TEMPERADAS 307
La distribucin con ncleo escaln
Considere la distribucin con ncleo u(t):
( f ) =
_

u(t) f (t)dt
=
_

0
f (t)dt
por denicin, la transformada de m est dada por,
M( f ) = (F)
=
_

0
F()d
=
_

0
_

f (t)e
jt
dtd
?
=
_

f (t)
_

0
e
jt
ddt
que tampoco tiene sentido, ya que
_

0
e
jt
dno converge. Tenemos que M no
tiene ncleo.
La distribucin valor principal de 1/x y la transformada de Hilbert
Considere la distribucin temperada dada por ( f ) = lm
0
_
>0
f (t)
t
dt. Por
denicin la transformada de f est dada por
( f ) = (F)
= lm
0
_
>0
F()
d
= lm
0
_
>0
1
f (t)e
jt
dt d
?
=
_

f (t) lm
0
_
>0
e
jt
ddt
resultando una distribucin con ncleo lm
0
_
>0
e
jt
d.
Ejercicio. Muestre que lm
0
_
>0
e
jt
d = jsgn(t), donde sgn es la funcin

sgnum. (sgn vale 1 para argumento positivo, -1 para argumento negativo y
cero para argumento nulo). Sugerencia: evale
_

0
sen(t)
dusando clculo de
residuos.
As, en cierto sentido, 1/x y jsgn(t) son un par de Fourier.
4.9. Modulacin SSB y la transformada de Hilbert
Con relacin al sistema de modulacin en la gura 4.39 note que el espectro
de h es sgn()S() y que b(t) es una modulacin de banda lateral inferior de
s(t). Observe tambin la gura 4.43.
Figura 4.39: Espectro de la seal s(t)
Ejercicio. Implemente la modulacin de banda lateral inferior.
4.9. MODULACIN SSB Y LA TRANSFORMADA DE HILBERT 309
Figura 4.40: Espectro de la seal modulada f (t)
Figura 4.41: Espectro de la seal h(t)
Figura 4.42: Espectro de la seal resultante b(t)
Figura 4.43: Modulacin SSB usando la transformada de Hilbert
4.9.1. Pares de Hilbert
z(t) tiene Z() = 0 para < 0 entonces Re(z) y Im(z) son pares de Hilbert.
Demostracin
Suponga f (t) := Rez(t) y g(t) := 0z(t) pare de Hilbert. Entonces:
G() =
1
j
sgn()F()
Entonces
Z() = F() + jG()
= F() + sgn()F()
Entonces
Z() =
_
_
0, < 0
2F(), > 0
4.10. APNDICE I 311
Suponga que no existe Z() = 0 para cada > 0 desde que F y G sean reales,
Z() = F() + jG() = F
() + jG
() = [F() + jG()]
entonces para > 0, F() = jG(), y por hiptesis tambin para < 0,
F() = jG(), tenemos:
F() = jsgn()G()
G() =
1
j
sgn()F()
Nota. X() = X
() TX() par y 0X() impar.

Nota. g(t) = f (t)
1
t
f (t) = g(t)
1
t
= ( f (t)
1
t
)
1
t
. La convolucin es
asociativa?? si:
_ _
a(s)b(s)s g(t) =
_
a(s)
_
b(s)g(t)s =
_
a(s)b g(t)s
4.10. Apndice I
Considere el circuito mostrado en la gura 4.44:
Deseamos hallar la ganancia G() = S()/E() y el ancho de banda (BW)
de tres decibeles del circuito realimentado y mostrar que el producto es aprox-
imadamente constante, independientemente de la cantidad de realimentacin,
dada por la relacin entre R1 y R2. Como sabemos, para un pasa bajas RC de
un polo, V2()/V1() = a/(a + j/
0
), donde
0
= 1/RC.
Note que V2(0)/V1(0) es decir la ganancia del RC en frecuencia cero, es 1
y por lo tanto, S(0) = A(E(0) KS(0)), donde K = R1/(R1 + R2); despejando
obtenemos: S(0) = E(0)A/(1 +AK) y tenemos que, en DC, la ganancia es A/(1 +
AK) = 1/A
1
+ K; que para A sucientemente grande, es aproximadamente
1/K. Llamaremos a esta ganancia G
0
.
Figura 4.44: Modelo de un polo de un amplicador operacional realimentado
En general, para una frecuencia ,
S() = A[E() KS()][1/(1 + j/
0
)]
despejando,
S()
E()
=
A
1 + AK + j/
0
=
1
1/A + K + j/A
0
asumiendo que 1/A tiene un valor despreciablemente pequeo,
G() =
1
1/A + K + j/A
0
=
K
1
1 + j/AK
0
Note que esta es la funcin de transferencia de un ltro pasa bajas de
primer orden con ganancia en frecuencia cero de G(0) = K
1
y BW = AK
0
,
por lo tanto, el producto ganancia por ancho de banda es A
0
, independiente
de la cantidad de realimentacin K. Las aproximaciones dejan de ser vlidas
en la medida en que K
1
se aproxime a A. Por ejemplo, para el operacional
monoltico uA741, A vale un milln y
0
vale 2 (1Hz).
4.11. APNDICEII: ANLISISENTIEMPOCONTRAANLISISENFRECUENCIA313
Laboratorio. usando un 741, monte un amplicador de ganancia 20 y mida
el ancho de banda.
4.11. Apndice II: Anlisis en tiempo contra anli-
sis en frecuencia
4.11.1. Respuesta del circuito RC pasa bajas de primer orden
a una seal onda cuadrada
Este ejemplo ilustra el hecho de que el anlisis en frecuencia puede ser
insuciente y que el dominio del tiempo no se puede ignorar. suponga que a
un circuito pasa altas RC de primer orden, como se muestra en la gura 4.45,
se aplica una onda cuadrada c(t), con periodo T, como se muestra en la gura
4.46.
Figura 4.45: Circuito RC pasa bajas
Un anlisis en frecuencia de la respuesta r(t) de este sistema de convolucin
a esta entrada peridica nos da los coecientes de Fourier de la seal de salida,
Figura 4.46: Una onda cuadrada
dados los coecientes de Fourier de la onda cuadrada de entrada c(t):
c(t) =
1
2
(E + F) + (E F)
2
n=1
1
n
sen
n
2
cos
2nt
T
(4.8)
r(t) =
1
2
(E+F) +(EF)
2
n=1
RC
n
_
1 + (n
0
RC)
2
sen
n
2
cos(n
0
t +atan(n
0
RC))
(4.9)
donde
0
= 2/T. Note que las seales tienen armnicas pares nulas. La
seal r(t) es tambin la respuesta en estado estable del circuito; es decir, es la
respuesta a la entrada e(t) = c(t)u(t) para t >> 5RC.
Aunque la frmula 4.9 nos da una descripcin analtica de la seal de
salida, la cual en principio contiene toda la informacin sobre sta, hay ciertos
detalles que no aparecen explcitamente y que de hecho son bastante difciles
de obtener a partir de la frmula. por ejemplo, la funcin de transferencia del
ltro nos da el nivel promedio de la salida en trminos del nivel promedio
de la entrada; sin embargo, el voltaje pico a pico de la seal de salida no es
tan fcil de obtener. Para encontrar este voltaje podemos hacer un anlisis en
tiempo.
4.11. APNDICEII: ANLISISENTIEMPOCONTRAANLISISENFRECUENCIA315
4.11.2. Respuesta escaln
Suponga que en el circuito de la gura 4.44, el voltaje inicial del conden-
sador, v
c
(0
) es B y que a la entrada se aplica la seal i(t) = B + (A B)u(t); as,

para t < 0, v
i
(t) = B y para t > 0, v
i
(t) = A. Resolviendo la ecuacin diferencial
correspondiente con la condicin inicial dada encontramos que,
v
c
(t) = A[a e
t
RC
] + Be
t
RC
(4.10)
4.11.3. Respuesta de estado estable a una onda cuadrada
Suponga que la entrada al circuito es una onda cuadrada (ciclo til de 50 %)
con techo (nivel alto) E voltios, piso (nivel bajo) F voltios y perido T,
como se muestra en la gura 4.46; note que el nivel promedio de esta seal
es
1
2
(E + F) y que su voltaje pico a pico es E F. La respuesta del circuito es
como se muestra en la gura 4.47 donde se observa la respuesta transiente y
la transicin a la respuesta estable.
Figura 4.47: Respuesta del circuito RC a una onda cuadrada
Para hallar los valores pico C y D de la seal de salida en estado estable,
utilizamos la frmula 4.10, denimos = RC y resolvemos el siguiente par de
ecuaciones:
C = E(1 e
T
2
) + De
T
2
D = F(1 e
T
2
) + Ce
T
2
de las que podemos deducir
C = (E + Fe
T
2
)
1 e
T
2
1 e
= (E + Fe
T
2
)
1
1 e
T
2
D = (F + Ee
T
2
)
1 e
T
2
1 e
= (F + Ee
T
2
)
1
1 e
T
2
ya que (1 e
) = (1 e
T
2
)(1 e
T
2
); as tenemos que C + D = E + F y,
consecuentemente con el hecho de que el circuito es un pasa bajos con ganancia
1 para frecuencia cero, los niveles DC de entrada y salida son iguales: (C +
D/2) = (E + F)/2; adems, el voltaje pico a pico de la seal de salida est dado
por
C D = (E F)
1 e
T
2
1 + e
T
2
= (E F)tanh(
T
4
)
Ejercicio. Demuestre que
1e
T
2
1+e
T
2
= tanh(
T
4
).
En la gura 4.48 se graca tanh(
T
4
) contra
T
2
. En las guras 4.49 y 4.50 se
muestra la salida en estado estable para dos valores extremos de T, en un caso
para T << y en el otro para T >> .
4.12. Problemas
1. Calcule la transformada de Fourier F(), si f (t) =
4.12. PROBLEMAS 317
Figura 4.48: Grca de la relacin de los voltajes pico a pico de entrada y salida del circuito RC
Figura 4.49: Respuesta estable para T <<
Figura 4.50: Respuesta estable para T >>
a) e
t
b)
1
1+t
2
c) cos(10t)e
t
d) e
t
2
e) u(t) u(t 1)
f ) e
5t
2
cos(20t)
2. Diga si la seal senc (t) es integrable en magnitud, o no. Si s, d el valor
de la integral, si no, demuestre.
3. La respuesta impulso de un sistema de convolucin continuo es h(t) =
u(t)e
t
. Encuentre la respuesta r(t) cuando la entrada al sistema es e(t)
a) cos(t) + cos(2t)
b) u(t) u(t 1). (Encuentre la transformada de Fourier de la salida.)
4. Se tiene un ltro pasa bajas ideal con frecuencia de corte en 70Hz. En-
cuentre la salida si la entrada es la seal mostrada en la gura 4.51.
Figura 4.51: Seal peridica
5. Encuentre la transformada de Fourier, G(), de la seal e
t
sen(100t).
Graque la magnitud y la fase de G. Sea cuidadoso con la fase.
4.12. PROBLEMAS 319
6. Considere el circuitomostradoenla gura4.52, el cual modelalaimpedan-
cia de una punto de oscilodcopio X10 (atenuado por 10) y la impedancia
de entrada del amplicador del osciloscopio. Se dice que la punto est
compensada si C=9pF.
a) Encuentre la respuesta escaln para C=9pF, 5pF y 12 pF. (Ha visto
estas formas de onda en la pantalla de un osciloscopio?)
b) Encuentre la funcin de transferencia del circuito para C=9pF, 5pF
y 12pF.
Figura 4.52: Circuito
7. La magnitud y la fase de la transformada de la seal x(t) se muestran
a continuacin. Graque la magnitud y la fase de la transformada de
x(t) sen(10t). Sea cuidadoso con la fase.
8. Calcule la transformada de Fourier de la seal u(t +1) u(t 1). Con base
en sta, calcule la transformada de:
a) u(t) u(t 2)
b) u(t) u(t 1)
c) u(t) 2u(t 1) + u(t 2)
Figura 4.53: Magnitud y fase
d) r(t) 2r(t 1) + r(t 2), donde r es la funcin rampa, la integral del
escaln.
9. Calcule y graque la transformada de f (t) = e
t
2
2
as como la de f
(t) =
te
t
2
2
.
10. Se tiene un sistema de convolucin cuya respuesta impulso est dada
por
h(t) =
_
_
1/2, t 1
0, t > 1
encuentre la respuesta del sistema a la entrada e(t) = sen(t) + sen(10t).
11. Se tiene un ltro con funcin de transferencia H() =
1
1+j
. Si la entrada
est dad por e(t) = sen(t) +sen(2t), sea s(t) la salida. Encuentre
_

e
2
(t)dt
y
_

s
2
(t)dt. Sugerencia: utilice la frmula de Parseval para series de
Fourier (captulo 3).
12. Se tiene un ltro con funcin de transferencia dada por H() =
j
1+j
.
a) Graque H() y H().
b) Encuentre las frecuencias de corte
c
de 3 dB.
c) D los valores de H(
c
) y H(
c
). 4.12c est bien?
4.12. PROBLEMAS 321
d) Encuentre la respuesta escaln del sistema.
13. Sabiendo que la transformada del pulso p(t) = u(t + 1) u(t 1) es una
senc : P() = 2senc (), muestre que la transformada del tringulo
r(t) = [p p](t) es R() = 4senc
2
(). Graque r(t) y R().
14. Haciendo un anlisis de 10 armnicas, graque la salida del sistema (no
lineal) mostrado en la gura siguiente.
Figura 4.54: Rectivador de media onda y pasabajas RC
15. a) Encuentre la transformada G() de la seal g(t) = u(t + 1) u(t
1). Graque g y G. Utilizando propiedades de la transformada de
Fourier,
b) Encuentre la transformada H() de la seal h(t) = g(t 1). Graque
h y H.
c) Encuentre la transformada R() de la seal r(t) = g(t)h(t). Graque
r y R.
d) Encuentre la transformada S() de la seal s(t) si se sabe que r(t) =
s
(t).
16. Encuentre la transformada de Fourier de la seal mostrada (Figura 4.56).
Sugerencia:
Figura 4.55: Pasabajs RC con frecuencia de corte 1Hz y entrada con nivel DC
Figura 4.56: Seal triangular
Figura 4.57: La convolucin de dos pulsos es un tringulo
4.12. PROBLEMAS 323
17. Suponga que PB es un sistema de convolucin con respuesta escaln
g(t) = (1 e
t
)u(t) y funcin coracterstica correspondiente h(t) = e
t
u(t).
Figura 4.58: Pasa-altas = identidad - pasabajas
a) Encuentre la respuesta escaln del sistema compuesto: PA=I-PB,
donde I es el sistema identidad.
b) Calcule la funcin de transferencia H() del subsistema PB.
c) Encuentre la funcin de transferencia del sistema compuesto.
18. Se tiene un sistema con funcin de transferencia H() =
j
1+j
.
a) GRaque H() y H(). Diga qu tipo de ltro es.
b) Encuentre la frecuencia de corte de 3dB.
c) Encuentre la respuesta escaln del sistema.
19. Encuentre la potencia promedio de la seal de entrada as como la po-
tencia promedio de la fundamental y de las dos primeras armnicas de
la salida (gura 4.59). Asuma estado estable (i.e. la seal se aplica desde
siempre).
20. ) Se tiene un sistema de convolucin continuo con respuesta escaln
g(t) = e
t
u(t), donde u es la seal escaln. Diga qu tipo de ltro es
(pasabajas, pasabanda, etc.) y d la transformada S() de la salida s(t) si
la entrada es la seal mostrada: e(t) = 0 para t < 0, t para 0 < t.
Figura 4.59: Problema 20
Figura 4.60: La seal mostrada se ltra con el sistema de convolucin
21. Sea el funcional valor principal
1
x
, dado por
( f ) = lm
0
_
>0
f (t)
t
dt
encuentre g(t) para que el funcional ( f ) dado por ( f ) = f (F), donde F
es la transformada de Fourier L
1
de f , se puede expresar como:
( f ) =
_

f (t)g(t)dt
22. Sea el funcional delta de Dirac, dado por ( f ) = f (0), encuentre g(t) para
que el funcional ( f ) dado por ( f ) = (F), donde F es la transformada
de Fourier L
1
( f ) =
_

f (t)g(t)dt
4.12. PROBLEMAS 325
23. Sea el funcional con distribucin g dada por
( f ) =
_

f (t)g(t)dt
muestre que el funcional ( f ) dado por ( f ) = (F), donde F es la trans-
formada de Fourier L
1
( f ) =
_

f (t)G(t)dt
donde G es la transformada de Fourier L
1
de g.
24. Calcule la transformada de Fourier G() de la seal g(t) =
1
1+t
2
, diga si G
es par o impar, real o imaginaria, o ninguna de las anteriores.
25. La seal cos(t) + u(u) u(t 2) se aplica a un sistema de convolucin
continuo con respuesta escaln u(t) u(t 1). Encuentre la salida.
26. A un sistema de convolucin continuo con funcin de transferencia
H() =
1
1+j
se aplica una onda cuadrada de frecuencia 5 ciclos por
segundo, nivel promedio 1V y amplitud pico a pico de 2 V. Encuentre:
a) La potencia promedio de la entrada.
b) La potencia promedio de salida.
c) La potencia promedio de las 2 primeras armnicas de la entrada.
d) La potencia promedio de las 2 primeras armnicas de la salida.
27. Se tiene un sistema de convolucin continuo con respuesta escaln g(t) =
e
t
u(t). Al sistema se aplica la seal e(t) = 1 + cos(t) + cos(5t).
a) Encuentre la salida.
b) Encuentre la potencia promedio de la entrada.
c) Usando Parseval, encuentre la potencia promedio de la salida.
28. Se tiene unsistema de convolucincontinuoconrespuesta escaln g
1
(t) =
e
t
2
. Sea g
2
(t) = g
1
(t).
a) GRaque g
1
(t) y g
2
(t).
b) Si g
1
(t) y g
2
(t) son respuestas escaln de sistemas de convolucin,
graque las funciones caractersticas correspondientes.
c) Encuentre los anchos de banda de 3dB de los dos sistemas.
29. Se tiene un sistema de convolucin con respuesta escaln u(t 1) + (1
e
t
2
)u(t), donde u es la seal escaln.
a) Con una convolucin de Stieltjes, encuentre la respuesta r(t) del
sistema, cuando la entrada es una exponencial compleja de la forma
e
j
0
t
.
b) Encuentre y graque
r(t)
e
j
0
t
.
30. Encuentre la respuesta del siguiente sistema a la seal 1+cos(t) +cos(2t).
Expresela como una suma de cosenos desfasados.
31. Con un ltro con funcin de transferencia H() =
1
1+j
se ltra la seal
cos(5t), encuentre la potencia promedio de las primeras 3 armnicas de
la seal de salida.
32. Las seales s(t) = e
t
yw(t) = u(t+1)u(t1) se aplicanal sistema mostra-
do en la gura 4.61. Describa con una frmula cada una de las seales
a(t), b(t), c(t), e(t), d(t), f (t), g(t) en el dominio del tiempo, y graque
aproximadamente sis espectros: A(t)
2
, B(t)
2
, C(t)
2
, E(t)
2
, D(t)
2
, F(t)
2
,
G(t)
2
.
33. Se tiene un sistema con funcin de transferencia H() = u( + 450)
u(450). Si se aplica a la entrada una onda cuadrada de periodo 16.6ms,
como se muestra en la gura 4.62.
4.12. PROBLEMAS 327
Figura 4.61: Sistema
Figura 4.62: Onda cuadrada
a) Encuentre la potencia promedio de la entrada y de la salida.
b) Encuentre y graque la salida.
por g(t) = (1 e
t
)u(t). Si la entrada es e(t) = 1 + cos(t) + cos(3t), exprese
la salida como suma de cosenos desfasados.
e
t
u(t). Al sistema se aplica la seal e(t) = 1 + cos(t) + cos(5t). Usando
Parseval, encuentre la potencia promedio de la entrada y de la salida.
36. Muestre que si f y g estn en L
1
, f g tambin.
37. Evale el lmite cuando tiende a cero de
_
>
e
jt
dsea cuidadoso con

el signo de t.
4.12. PROBLEMAS 329
38. Encuentre una funcin de fase no nula, que sea par e impar. (Sugerencia:
= .)
39. Muestre que, si g es integrable en magnitud, entonces lm
0
_

g(t +
) g(t)dt = 0.
40. El circuito mostrado est en estado estable sinusoidal. Encuentre la fre-
cuencia de oscilacin y graque las seales a(t), b(t) y c(t). Cules son las seales a(t),
b(t) y c(t) en la grca?
41. A un RC pasa bajas de primer orden con frecuencia de corte de 3dB de
1, se aplica la seal e(t) = arctan(t). Encuentre la energa de la seal de
salida.
42. Se tiene un sistema de convolucin continuo con funcin caracterstica
dada por cos(10t)e
t
. Diga qu tipo de ltro es (pasa bajas, pasa altas,
etc.) y d las frecuencias de corte de 3dB.
43. Se tiene la seal x(t) con transformada X() = [u(+11)u(+9)+u(
9) u( 11)]e
j
. Graque la transformada de la seal x(t) cos(10t).
44. Encuentre la respuesta del siguiente sistema a la seal 1+cos(t) +cos(2t). Cul es el siguiente sis-
tema? Exprsela como una suma de cosenos desfasados.
45. Con un ltro con funcin de transferencia H() =
1
1+j
se ltra la seal
cos(5t), encuentre la potencia promedio de las primeras 3 armnicas de
la seal de salida.
46. Utilizando las propiedades de la transformada de Fourier, sabiendo que
la transformada de f (t) = u(t +1) u(t 1) es F() = 2senc (), encuentre
la transformada de g
(t), si g(t) = e
j10t
[u(t) 2u(t 1) + u(t 2)].
47. Utilizando las propiedades de la transformada de Fourier , sabiendo que
la transformada de Fourier de f (t) = e
(at)
2
es F() =
a
e
(

2a
)
2
, encuentre
el ancho de banda de un ltro con respuesta impulso h(t) = f
(t).
e
2t
u(t).
a) Encuentre la transformada de Fourier G() de g(t).
b) Graque la magnitud y la fase de la funcin de transferencia H().
c) Si la entrada es 3 + cos(t) + sen(3t), encuentre la salida.
49. Se tiene un sistema de convolucin con funcin de transferencia H( =
1
1+2j
),
a) Encuentre el nivel promedio de la salida cuando la entrada est
dada por e(t) = sen(t).
b) Graque aproximadamente la magnitud de la transformada de la
salida cuando la entrada est dada por e(t) =
cos(t)
1+t
2
.
50. Encuentre la potencia promedio de sen(t).
51. Usando impedancias, encuentre la funcin de transferencia del circuito
mostrado. Luego, encuentre la respuesta a la seal 1 + cos(t) + cos(10t).
Figura 4.63: Circuito impedancias
e
2t
u(t). Diga qu tipo de ltro es. D la transformada S() de la salida
s(t), si la entrada es la seal tringulo que se muestra en la gura 4.64.
4.12. PROBLEMAS 331
Figura 4.64: Seal de entrada
53. a) Encuentre la funcin de transferencia H(), del sistema (gura 4.65)
b) Encuentre H(0), BW de 3dB y el producto H(0)BW.
Figura 4.65: Sistema
54. A un RC pasa bajas de primer orden, con frecuencia de corte de un
radian por segundo, se aplica una onda cuadrada de amplitud pico a
pico 1, nivel promedio
1
2
y periodo 2. Encuentre las series de Fourier de
la entrada y de la salida. Repita para el caso de un pasa altas.
55. A un RC pasa bajas de primer orden, con frecuencia de corte de un
1
2
y periodo 2. Encuentre las potencias promedio
de la entrada y de la salida.
56. A un RC pasa altas de primer orden, con frecuencia de corte de un
1
2
y periodo 2. Encuentre las potencias promedio
de la entrada y de la salida.
57. A un pasa banda con factor de calidad 5 y frecuencia de resonancia 10 se
aplica una onda cuadrada de amplitud pico a pico 1, nivel promedio
1
2
y
periodo /5. Encuentre las series de Fourier de la entrada y de la salida.
58. Usando propiedades de la transformada de Fourier, a partir de la trans-
formada del pulso p(t) = u(t +1) u(t 1), encuentre la transformada de
la seal tringulo d(t) = (t + 1)u(t + 1) 2tu(t) + (t 1)u(t 1). Graque
p, d y sus transformadas.
59. Encuentre la funcin de transferencia del sistema con respuesta escaln
g(t) = e
t
u(t).
60. Diga a cuntas dcadas por octava equivalen -20dB por dcada.
61. A un RC pasa bajas de primer orden con frecuencia de corte de 3dB de
1, se aplica la seal e(t) = arctan(t). Encuentre la energa de la seal de
salida.
62. Se tiene un sistema de convolucin continuo con funcin caracterstica
dada por cos(10t)e
t
. Diga qu tipo de ltro es (pasa bajas, pasa altas,
. . . ) y d las frecuencias de corte de 3dB.
63. Encuentre la transformada de la seal s(t) = e
t
cos(10t). Expresela de tal
forma que se vea que es real y par. Graquela.
g(t) = e
t
u(t).
4.12. PROBLEMAS 333
por g(t) = e
t
u(t). Encuentre y graque (magnitud y fase) la funcin de
transferencia del sistema, la cual est dada por: H() =
_

e
jt
dg(t).
66. Demuestre que
2
_

s(t)
2
dt =
_

S()
2
d
donde S es la transformada de Fourier (CTFT) de s.
67. Encuentre la transformada de la seal s(t) = e
t
cos(10t). Expresela de tal
forma que se vea que es real y par. Graquela.
68. Graque la magnitud y la fase de la transformada de la derivada de la
campana de Gauss e
t
2
69. Aunsistema de convolucincontinuoconrespuesta escaln g(t) = e
t
u(t)
se aplica una seal e(t) = sen(t)[u(t) u(t 3)]. Encuentre la integral de
la seal de salida.
70. Se tiene un sistema de convolucin discreto con respuesta impulso dada
por h
n
= u
n
2
n
. Si la entrada es la seal peridica s = . . . 1, 1, 0, 1, 1, 0, . . .
de periodo 3, exprese la salida como una suma de exponenciales com-
plejas discretas.
g(t) = (1 e
t
)u(t). Exprese la salida como una suma de sinusoidales si la
entrada es cos
2
(t).
Referencias
[4] Fourier Transforms. S. Bochner y K. Chandrasekhanran.
Princeton University Press, Princeton, 1949.
Wilmington, 1995.
[6] Sistemas Digitales y Analgicos, Transformadas de Fouri-
er, Estimacin Espectral. A. Papoulis. Marcombo, Barcelona,
1986.
[7] Special Functions and their Applications. N.N. Lebedev.
Dover, N.Y. 1972.
[8] Exercices Rsolus de Mathmatiques. M. Carbon, P. Marry,
N. Point y D. Vial. Dunod, Paris, 1986.
334
REFERENCIAS 335
[9] Fourier andWavelet Analysis. G. Bachman, L.Narici, E. Beck-
enstein. Springer, N.Y., 2000.
Captulo 5
DTFT, DFT y Relaciones entre
transformadas
5.0. Introduccin
En este captulo consideramos el anlisis de Fourier de las seales discretas
de longitud innita, peridicas y el l
2
; respectivamente, la DFT, la DTFT. Las
seales discretas de longitud nita se analizan en forma similar a las discretas
peridicas con la DFT (Discrete Fourier Transform) la consideramos con
otro nombre cuando representamos seales discretas peridicas como sumas
de exponenciales complejas discretas, en el captulo 3 podemos decir que la DFT
es la transformada de Fourier para seales discretas de longitud nita; ms
exactamente, de seales con dominio nito y circular, retomaremos ese tema
en la seccin 5.7.
Por otra parte, la DTFT (Discrete Time Fourier Transform) es la trans-
formada de Fourier para seales discretas de longitud innita; la DTFT de la
336
seal s : Z C, sumable en magnitud, est dada por:
S() =
n=
s
n
e
jn
Como asumimos que s es sumable en magnitud, entonces su transformada
de Fourier S() existe, por convergir en magnitud, para toda real, y es una
funcin acotada ya que,
n=
s
n
e
jn
n=
s
n
e
jn
n=
s
n
e
jn
n=
s
n
= [s[
1
Ejercicio. Muestre que cada seal discreta s : Z C en l
2
, est en l
1
.
Note que la transformada S() de una seal discreta es una funcin per-
idica, para la que 2 es un tiempo de repeticin: S(+ 2) = S(), ya que 2
es un tiempo de repeticin de cada trmino s
n
e
jn
.
Tambin note que S() tiene serie de Fourier con coecientes s
n
. Esta
propiedadnos permitir dar una frmula para la transformada inversa DTFT
1
basada en los resultados sobre series de Fourier, vistos en el captulo 3. Antes,
veamos un ejemplo.
Ejemplo. Sea s : Z C la seal dada por
s
n
=
_
_
1, n 1, 0, 1
0, n 1, 0, 1
338 CAPTULO 5. DFT Y DTFT
entonces
S() =
n=
s
n
e
jn
=
1
n=1
s
n
e
jn
= e
j
+ 1 + e
j
= 1 + 2 cos
Tanto S como su magnitud y fase, se gracan a continuacin.
Figura 5.1: La funcin 1 + cos
Ejercicio. Graque la magnitud y la fase de H() = (1 + cos 2)e
j
Como vimos, 2 es un tiempo de repeticin de S(). Si s
1
0 o s
1
0, el
periodo de S() es 2. Si s
1
= 0 y s
1
= 0, y s
2
0 o s
2
0, entonces es el
tiempo de repeticin de S() ya que, ahora
S() = + s
2
e
j2
+ s
0
+ s
2
e
j2
+ . . .
Figura 5.2: La magnitud de la funcin 1 + cos
Figura 5.3: La fase de la funcin 1 + cos 2. Como = , la funcin tambin es impar
y, cada exponencial compleja s
k
e
jk
tiene periodo 2/k. en general, el perio-
do de S es el mnimo comn mltiplo de los periodos de las exponenciales
complejas no nulas en la serie, ya que stas son funciones linealmente inde-
pendientes.
5.0.1. Transformada inversa
Para obtener la frmula de la trasformada inversa, para recuperar s
n
a
partir de S(), utilizamos el hecho de que S() tiene expansin en series de
Fourier con coecientes s
n
. Por lo tanto, la frmula de los coecientes de
Fourier, vista en el captulo 3, nos da la transformada inversa:
s
n
=
1
2
_
2
0
S()e
jn
d
y, por lo tanto, la frmula de la transformada inversa es,
s
n
=
1
2
_
2
0
S()e
jn
d
Tambin, tenemos la siguiente frmula de Parseval:
n=
s
n
2
=
1
2
_
2
0
S()
2
d
que relacione la norma l
2
de la seal s con la potencia promedio de la seal S,
en forma similar al caso correspondiente a las series de Fourier.
5.1. Propiedades de la transformada de Fourier en
tiempo discreto, DTFT
La transformada de Fourier en tiempo discreto es lineal: la transformada
de una combinacin lineal de seales es la combinacin respectiva de las trans-
5.1. PROPIEDADES DE LA DTFT 341
formadas individuales. Las propiedades de desplazamiento y modulacin son
similares a las del caso continuo.
i) Linealidad. Sean s = s
n
y r = r
n
seales en l
1
y sean y constantes
complejas. Entonces, F[s + r] = F[s] + F[r], ya que
nZ
[s + r]e
jn
=
nZ
se
jn
+
nZ
re
jn
ii) Desplazamiento. Sea S() la transformada de Fourier Fs
n
() de la seal
s
n
, entones, la transformada de la seal desplazada s
nk
est dada por,
Fs
nk
() =
nZ
s
nk
e
jn
m = n k
=
mZ
s
m
e
j(m+k)
= e
j(k)
mZ
s
m
e
j(m)
= e
j(k)
S()
Ejercicio. Como se puede mostrar, la transformada S() de la seal s(t)
mostrada en la gura 5.4 est dada por S() =
1
3
(1 +2 cos()); encuentre
y graque la transformada de la versin desplazada s
n1
, mostrada en la
gura 5.5.
Figura 5.4: La respuesta impulso de un promedio mvil
Figura 5.5: La respuesta impulso de un promedio mvil causal
iii) Modulacin. Desplazar en tiempo corresponde a multiplicar con una
exponencial compleja en frecuencia. Si la transformada se desplaza en
frecuencia, qu ocurre con s, en tiempo? Si S() = [F(s)](), cunto vale
F
1
[S(
0
)]? por denicin:
F
1
[S(
0
)] =
1
2
_
2
0
S(
0
)e
jn
d
=
0
=
1
2
_
2
0
0
S()e
j(+
0
)n
d
=
e
j
0
n
2
_
2
0
0
S()e
jn
d
=
=
e
j
0
n
2
_
2
0
S()e
jn
d
= e
j
0
n
s
n
dado que
1
2
_
2
0
S()e
jn
d y que la integral es independiente de dnde
empiece y dnde termine, siempre y cuando se integre sobre un periodo.
Por lo tanto, un desplazamiento en frecuencia del espectro de la seal,
corresponde a la multiplicacin de la seal por una exponencial compleja
discreta en tiempo, es decir, a una modulacin de la seal.
5.2. FRECUENCIAS GRANDES Y PEQUEAS 343
As, si s
n
es una seal discreta, al multiplicar por la seal discreta cos(
0
n)
resulta que, utilizando las propiedades de linealidad y de modulacin,
si la transformada de s
n
es S(), la transformada de s
n
cos(
0
n) est
dada por:
1
2
[S( +
0
) + S(
0
)].
Ejercicio. Demuestre que si f es peridica, con periodo T, entonces, para
cualquier nmero real , (Observe la gura 5.6.)
_
T
0
f (t)dt =
_
T+
f (t)dt
Figura 5.6: En los dos casos se ha sombreado el rea sobre un periodo
5.2. Frecuencias (de Fourier) grandes y pequeas de
seales discretas
La mejor forma de visualizar la frecuencia angular de una exponencial
compleja discreta e
jn
es con el punto de una circunferencia, que subtiende el
ngulo de valor . As, estar cerca a 2 es lo mismo que estar cerca a 0. Las
frecuencias cercanas a cero son frecuencias bajas mientras que las lejanas de
cero, son frecuencias altas.
Figura 5.7: La circunferencia de Fourier para seales discretas
Por lo tanto, la mayor frecuencia es y la exponencial compleja de magni-
tud unitaria con mayor frecuencia es e
jn
:
Re (e
jn
) = cos(n) = (1)
n
Im(e
jn
) = sen(n) = 0
Figura 5.8: Una seal con periodo 2
El periodo mnimo que una seal discreta peridica no constante puede
tener es 2 y correspondiente al caso de frecuencia angular .
La frecuencia angular menor es 0 = 2 y la exponencial compleja discreta
correspondiente es e
j0n
que es constante: Re (e
j0n
) = 1, Im(e
j0n
= 0).
5.2. FRECUENCIAS GRANDES Y PEQUEAS 345
Figura 5.9: Una seal discreta, con frecuencia 0 y periodo 1
Nota. Como se dijo, para que una exponencial compleja discreta de la forma
s
n
= e
jn
sea peridica, es necesario (y suciente) que la frecuencia angular
sea un mltiplo racional de 2: = 2q, q Q. En otro caso, la seal no es
peridica sino casi peridica. (Como dijimos en el captulo 0: sea x un nmero
real; denimos x mdulo 2, que denotamos [x]
2
, como el nico nmero
en el intervalo [0, 2) que es congruente con x, mdulo 2. Es decir, y = [x]
2
si
y slo si, y [0, 2) y para algn nmero entero m, x = 2m+ y. Por ejemplo,
[31]
2
= 5,86722 . . . mientras que [32]
2
= 0,58407 . . . )
Considere la seal s
n
= e
jn
. El grafo de s es un subespacio denso de S
1
; s no
es peridica: s
0
= 1 y para ningn valor de n diferente de 0 se tiene que s
n
= 1;
sin embargo, a medida que n crece, n toma valores arbitrariamente cercanos
a mltiplos de 2 y [n]
2
toma valores arbitrariamente cercanos a cero; por
ejemplo, [31416]
2
= 0,07346 . . . .
Ejercicio. Demuestre que e
jn
: n Z es denso en S
1
.
Ejercicio. Demuestre que e
jn
es una seal discreta casi peridica.
Dos exponenciales complejas discretas del mismo periodo pueden tener
diferente variacin promedio.
Ejemplo. Las seales e
j
2
7
n
y e
j
3
7
2n
son ambas de periodo 7 pero la primera
tiene variacin promedio 1 e
j
2
7
n
y la segunda 1 e
j
3
7
2n
. Como podemos
ver, la variacin promedio de una exponencial compleja e
j
0
n
es proporcional
a su frecuencia de Fourier, mdulo 2.
Figura 5.10: Las distancias correspondientes a las variaciones promedio de las
exponenciales complejas e
j
o
n
y e
j
o
n
5.3. Filtros discretos
Dado que la respuesta a la exponencial compleja e
j
o
n
de un ltro con
funcin de transferencia H() es H(
o
)e
j
o
n
, diremos que el ltro es pasa bajas
si para < y 2 < .
Figura 5.11: Pasa bajas
5.4. RESPUESTA EN FRECUENCIA SISTEMAS DE CONVOLUCIN 347
Figura 5.12: Pasa altas
Figura 5.13: Pasa bandas
5.4. Respuesta en frecuencia de sistemas de con-
volucin discretos
Las exponenciales complejas, en general, las seales peridicas no nulas,
no tienen transformada de Fourier; stas se representan en el dominio de
la frecuencia como sumas de exponenciales complejas. Las seales que son
sumables en valor absoluto tienen transformada de Fourier para toda .
Como enel caso continuo, trataremos por separado la respuesta de sistemas
de convolucin; primero la respuesta a seales que tienen transformada y
despus la respuesta a seales peridicas.
Suponga que se tiene un sistema de convolucin discreto, con entrada x,
salida y y respuesta impulso h, tal como se muestra en la gura 5.14.
Figura 5.14: Un sistema de convolucin con respuesta impulso h
Por denicin, la transformada Y de la salida est dada por
Y() =
n=
y
n
e
jn
y es la convolucin de x y h, por lo tanto.
Y() =
n=
_
i=
x
i
h
ni
_
_
e
jn
=
n=
i=
x
i
h
ni
e
jn
y, asumiendo que el oren de la suma se puede alterar,
Y() =
i=
n=
x
i
h
ni
e
jn
con el cambio de variable k = n i
n=
x
i
h
ni
e
jn
=
k=
x
i
h
k
e
j(k+i)
entonces
Y() =
i=
k=
x
i
h
k
e
j(k+i)
=
i=
x
i
e
j(i)
k=
h
k
e
j(k)
= X()H()
por lo tanto, se tienen dos representaciones del sistema: una en tiempo y la
otra en frecuencia, como se muestra en la gura 5.15.
Figura 5.15: Las representaciones en tiempo y frecuencia de un sistema de convolucin
Ejemplo. Se tiene un promedio mvil con ancho de ventana igual a tres, donde
la salida y
i
est dada por el promedio
1
3
(x
i1
+x
i
+x
i+1
) de los tres componentes
de la seal de entrada en una ventana centrada en i.
Ejercicio. Demuestre que el sistema promedio mvil es un sistema de convolu-
cin y que su respuesta impulso est dada por la gura 5.16.
Ejercicio. Muestre que la funcin de transferencia del promedio mvil est
dada por
H() =
1
3
(e
j
+ e
j0
+ e
j
) =
1
3
(1 + 2 cos )
Figura 5.16: La respuesta impulso de un promedio mvil con ancho de ventana igual a tres
Figura 5.17: Magnitud
Figura 5.18: Fase
Ejemplo. Suponga que se tiene un sistema discreto de convolucin cuya re-
spuesta impulso est dada por
h
n
=
_
_
1/2, n 1, 1
1, n = 0
0, n Z 1, 0, 1
por lo tanto, su funcin de transferencia est dada por,
H() = 1 + cos()
Ejercicio. Graque la magnitud y la fase e a + cos()
Ejercicio. Suponga que el ltro del ejemplo anterior se coloca en cascada con
el promedio mvil de ancho de ventana 3. Calcule la respuesta impulso del
ltro resultante as como su funcin de transferencia. Graque la magnitud y
la fase de la funcin de transferencia.
Ejercicio. Encuentre la funcin de transferencia de un promedio mvil con
ancho de ventana igual a cinco.
Ejercicio. Graque la magnitud y la fase de
Y() =
1
3
(1 2 cos )(1 + cos ) =
1
3
(cos + cos(2))
5.5. Polos y ceros de H(z) y H() correspondiente
Suponga que H(z) es una funcin racional de la variable z, es decir que es
un cociente de polinomios
H(z) =
a
0
+ a
1
z + + a
n
z
n
b
o
+ b
1
z + + b
n
z
m
por el teorema fundamental del lgebra, tanto el numerador como el denomi-
nador pueden ser factorizados.
H(z) =
n
i=1
(z c
i
)
m
i=1
(z p
i
)
a las constantes c
i
se les llama los ceros de H(z) y las p
i
los polos de H(z).
Ahora, dado que H() = H(e
i
) tenmos que
H(z) =
n
i=1
(e
i
c
i
)
m
i=1
(e
i
p
i
)
que interpretamos geomtricamente para cada como el producto de las
distancias de e
j
a los ceros, partido por el producto de las distancias a los
polos. Note que dado el diagrama de polos y ceros, partido por el producto de
la gura 5.19, podemos gracar aproximadamente H() (gura 5.20).
5.5. POLOS Y CEROS DE H(Z) Y H() CORRESPONDIENTE 353
Figura 5.19: Diagrama de polos y ceros
Figura 5.20: Magnitud de H()
5.6. Respuesta de sistemas de convolucindiscretos
a seales peridicas
5.6.1. Respuesta a exponenciales complejas discretas
Como se vio en el captulo 3, las seales peridicas discretas se pueden
representar como sumas nitas de exponenciales complejas discretas. Si x =
x
n
es una seal peridica con periodo N, sta se puede representar como,
x
n
=
N1
k=0
X
k
e
j
2
N
nk
Como los sistemas de convolucin son lineales, para conocer la respuesta
a x, basta con conocer la respuesta del sistema a cada exponencial compleja
e
j
2
N
nk
.
Si la respuesta impulso del sistema es h = h
n
y la entrada es la exponencial
compleja, r
n
= e
j
0
n
la salida y = y
n
est dada por la convolucin,
y
n
=
k=
h
k
e
j
0
(nk)
= e
j
0
n
k=
h
k
e
j
0
k
= e
j
0
n
H(
0
)
donde H(
0
) es la funcin de transferencia del sistema evaluada en =
0
.
Por lo tanto, la respuesta u a la seal de entrada x, expresada como
x
n
=
N1
k=0
X
k
e
j
2
N
nk
5.7. TRANSFORMADA DISCRETA DE FOURIER DFT 355
est dada por
u
n
=
N1
k=0
X
k
H(
2
N
k)e
j
2
N
k
Ejercicio. Calcule la respuesta del sistema promedio mvil a las siguientes
seales utilizando la frmula anterior:
1. x
n
= cos(n)
2. x
n
= cos(0n)
3. x
n
= cos([2/3]n)
Ejercicio. Exprese como una sima de sinusoides la respuesta del sistema causal
con ecuacin de diferencia y
n
= x
n
+0,5y
n1
(x la entrada, y la salida) a la seal
(1)
n
.
5.7. Transformada Discreta de Fourier DFT
Acontinuacinconsideramos la representacinenel dominio de la frecuen-
cia de Fourier de las seales discretas de longitud nita. Las seales discretas de
longitud nita son seales cuyo dominio es un conjunto nito , normalmente
un intervalo entero, y su rango es el conjunto de los nmeros complejos.
nosotros asumiremos normalmente que el dominio de las seales discretas de
longitud nita es un intervalo de la forma /0, N 1/.
Las seales digitales discretas de longitud nita son las seales que mejor
se pueden representar en un computador digital: son arreglos (arrays) uni-
dimensionales; su representacin en el dominio de la frecuencia resulta ser
tambin una seal de longitud nita y por lo tanto, tambin un array. Por esta
y otras razones, la transformada correspondiente, conocida como la Transfor-
mada Discreta de Fourier (Discrete Fourier Transform, DFT) es una se las
herramientas ms usadas hoy en da en el campo del tratamiento de seales
digitales. Estrictamente hablando, es una familia de algoritmos conocida co-
mo FFT (Fast Fourier Transform) para el clculo rpido de la DFT cuando la
longitud de la seal es una potencia de dos, la que es ampliamente usada. (Si
est interesado en estudiar los algoritmos de la FFT, puede consultar [1], por
ejemplo.)
Como se mencion en el captulo 1, la seal s : /0, N1/ Ctiene longitud
N, y se puede modelar como un punto en C
N
. La representacin de las seales
de longitud nita en el dominio de la frecuencia, es similar a la representacin
de las seales discretas peridicas de longitud innita, vista en el captulo 3, lo
cual tienen sentido si se piensa que en periodo es suciente para especicar
completamente tales seales.
Sea x = [x
0
, x
1
, . . . , x
N1
] C
N
una seal discreta de longitud N. Se dene
su transformada discreta de Fourier DFT(x) como la seal X C
N
donde
cada componente est dado por
X
k
=
1
N
N1
n=0
x
n
e
j
2
N
nk
=
1
N
N1
n=0
x
n
W
nk
N
Con base en los resultados del captulo 3, decimos que la DFT es una biyec-
cinlineal (unhomomorsmo) de C
N
C
N
. enparticular, la DFTes invertible:
a partir de X podemos recuperar x como DFT
1
(X); sta transformada inversa
est dada por: x = [x
0
, x
1
, . . . , x
N1
] = DFT
1
(X).
Ejercicio. Para la seal mostrada en la gura 5.21, calcule su transformada
discreta de Fourier.
Ejemplo. Sea x la seal de longitud 3 dada por x = [1, 2, 3]. su transformada
Figura 5.21: Una seal de longitud nita N = 3
discreta de Fourier X = DFT(x) est dada por,
X
k
=
1
3
(1 + 2e
j2k/3
+ 3e
j4k/3
)
por lo tanto,
X
0
=
1
3
(1 + 2e
j20/3
+ 3e
j40/3
) = 3
X
1
=
1
3
(1 + 2e
j2/3
+ 3e
j4/3
)
X
2
=
1
3
(1 + 2e
j4/3
+ 3e
j8/3
)
X = [X
0
, X
1
, X
2
]
Ejercicio. Calcule la transformada inversa DFT
1
(X) de la seal X del ejemplo
anterior. compruebe su respuesta.
5.7.1. Propiedades de corrimiento circular y modulacin de la
DFT
Sea x = [x
0
, x
1
, . . . , x
N1
] una seal de longitud N con transformada X =
[X
0
, X
1
, . . . , X
N1
]. Considere la seal y = [y
0
, y
1
, . . . , y
N1
] = [x
[n+m]
N
: n
N] = [x
m
, x
m+1
, . . . , x
N1
, x
0
, . . . , x
m1
] obtenida a partir de x por medio de un
corrimiento circular de magnitud m. Sea Y = DFT(y); entonces,
Y
k
=
1
N
N1
n=0
x
[n+m]
N
e
j
2
N
nk
=
1
N
(x
m
e
j
2
N
0k
+ x
m+1
e
j
2
N
k
+ + x
N1
e
j
2
N
(N1m)k
+ x
0
e
j
2
N
(Nm)k
+ + x
m1
e
j
2
N
(N1)k
)
=
1
N
(x
m
e
j
2
N
mk
e
j
2
N
mk
+ x
m+1
e
j
2
N
mk
e
j
2
N
(m+1)k
+ + x
N1
e
j
2
N
(N1)k
e
j
2
N
mk
+ x
0
e
j
2
N
mk
+ + x
m1
e
j
2
N
mk
e
j
2
N
(N1+m)k
)
=
1
N
e
j
2
N
mk
(x
m
e
j
2
N
mk
+ x
m+1
e
j
2
N
(m+1)k
+ + x
N1
e
j
2
N
(N1)k
+ x
0
+ + x
m1
e
j
2
N
(N1+m)k
)
= e
j
2
N
mk
1
N
(x
0
+ + x
m1
e
j
2
N
(N1+m)k
+ x
m
e
j
2
N
mk
+ x
m+1
e
j
2
N
(m+1)k
+ + x
N1
e
j
2
N
(N1)k
)
= e
j
2
N
mk
X
k
As, hacer un corrimiento circular en el dominio natural de la seal, equivale
a multiplicar por una exponencial compleja en el dominio de la frecuencia:
DFT([x
[n+m]
N
: n N]) = e
j
2
N
mk
DFT([x
n
: n N]).
Similarmente, la DFT de [e
j
2
N
nm
x
n
: n N] est dada por [X
[km]
N
: k N];
es decir, la multiplicacin en el dominio natural por una exponencial compleja
(lo que podramos llamar la modulacin de la seal), equivale a un corrimiento
circular en el dominio de la frecuencia.
5.7.2. Simetra circular par
Decimos que la seal x = [x
n
: x N] = [x
0
, x
1
, . . . , x
n1
] tiene simetra
circular par si, para cada n N= /0, N 1/,
x
n
= x
n
N
Ejercicio. Muestre que si x tienen simetra circular par, entonces DFT(x) tam-
bin tiene simetra circular par.
Ejercicio. Muestre que si x es real y tiene simetra circular par, entonces DFT(x)
tambin es real y tiene simetra circular par.
5.7.3. Convolucin circular discreta
Suponga que r = [r
0
, r
1
, . . . , r
N1
] y s = [s
0
, s
1
, . . . , s
N1
] son seales discretas
de longitud N. Suponga que R = [R
0
, R
1
, . . . , R
N1
] y S = [S
0
, S
1
, . . . , S
N1
] son
las correspondientes DFTs de r y s. Qu seal es la transformada inversa
u = [u
0
, u
1
, . . . , u
N1
] = DFT
1
(RS) del producto RS? Es una convolucin?
Por denicin, RS est dada por
R
k
S
k
=
1
N
N1
m=0
r
m
W
mk
N

1
N
N1
n=0
s
n
W
nk
N
=
1
N
2
N1
m=0
N1
n=0
r
m
W
mk
N
s
n
W
nk
N
=
1
N
2
N1
m=0
N1
n=0
r
m
s
n
W
(m+n)k
N
y, dado que,
u
i
= [DFT
1
(RS)]
i
=
N1
k=0
R
k
S
k
W
ik
N
se tiene que,
u
i
=
N1
k=0
R
k
S
k
W
ik
N
=
N1
k=0
1
N
2
N1
m=0
N1
n=0
r
m
s
n
W
(m+n)k
N
W
ik
N
=
1
N
2
N1
m=0
r
m
N1
n=0
s
n
N1
k=0
W
(imn)k
N
note que cuando n es congruente (mdulo N) con i m, es decir, cuando
(i m) n es un mltiplo de N, se tiene que
N1
k=0
W
(imn)k
N
= N
y que en caso contrario,
N1
k=0
W
(imn)k
N
= 0
por lo tanto
u
i
=
1
N
N1
m=0
r
m
s
im
N
donde i m
N
es un nico nmero en /0, N1/ que es congruente mdulo-N
con i m. note que para cada i, a medida que m toma valores consecutivos en
/0, N 1/, i m
N
tambin lo hace, aunque comenzando en i en vez de en
cero y teniendo en cuenta que a continuacin de N1 sigue 0. La razn por la
cual u se denomina la convolucin circular de r y s se hace ahora aparente;
observe la gura siguiente.
Figura 5.22: Los trminos r
m
s
im
a ser sumados, para computar u
i
. Note el eje m
5.7.4. Interpretacin de lo convolucin circular en trminos de
seales peridicas
Si consideramos extensiones de r y s (las cuales tienen como dominio el
conjunto /0, N 1/) a seales s y r que tengan como dominio el conjunto Z
de los nmeros enteros, haciendo que s y r sean peridicas con periodo N,
podemos escribir,
u
i
=
1
N
N1
m=0
s
m
r
im
donde,
r
n
=
N1
k=0
R
k
W
nk
N
, n Z
s
n
=
N1
k=0
S
k
W
nk
N
, n Z
Enla gura 5.23 se muestra unejemplo especco de la convolucincircular
de dos seales de longitud 8, para el clculo de u
2
.
Ejercicio. Calcule u
2
si u es la convolucin circular de [1, 2, 3, 3, 3, 3, 2, 1, 0] y
[3, 3, 3, 3, 3, 3, 2, 1, 0].
Figura 5.23: Las seales r
n
ys
n
, ylas correspondientes extensiones peridicas r
k
y s
2k
, necesarias
para el clculo de u
2
5.8. PROPIEDADES DE SIMETRA 363
5.7.5. Relacin de Parseval para la DFT
Sean x = [x
0
, x
1
, . . . , x
n1
] y r = [r
0
, r
1
, . . . , r
n1
] seales de longitud N; y sean
X = [X
0
, X
1
, . . . , X
n1
] y R = [R
0
, R
1
, . . . , R
n1
] sus respectivas DFTs. Dado que
la DFT de una convolucin circular es el producto de las DFTs, es decir que,
xr = DFT
1
(XR)
1
N
N1
k=0
x
k
r
[nk]
N
=
N1
k=0
X
k
R
k
W
nk
N
n = 0
1
N
N1
k=0
x
k
r
[k]
N
=
N1
k=0
X
k
R
k
r
k
= x
[k]
N
, R
k
= X
k
1
N
N1
k=0
x
k
x
[k]
N
=
N1
k=0
X
k
X
k
1
N
N1
k=0
x
k
2
=
N1
k=0
X
k
2
que es la frmula buscada.
Ejercicio. Muestre que si r
n
= x
[n]
N
entonces s
n
= r
[k]
N
.
5.8. Propiedades de simetra de la transformada de
Fourier DTFT
Las propiedades que se mencionan aqu son aplicables a las transformadas
de Fourier de seales continuas y de seales discretas.
inicialmente recordemos que la transformada de una seal par es par.
tambin, que las partes real e imaginaria, as como la magnitud y la fase, de
la transformada de una seal real (es decir de una seal compleja con parte
imaginaria cero) son par e impar, respectivamente.
Las componentes de la transformada de una seal dada como la suma de
una seal par y una seal impar. Dada una seal discreta s, Cmo se expresa
s como la suma s = p + i de una seal par p y una impar i? Hay ms de una
expresin del tipo deseado?
Ejercicio. Muestre que las seales p e i denidas a continuacinsonpar e impar,
respectivamente, y que su suma es s. p
n
= 1/2(s
n
+ s
n
), i
n
= 1/2(s
n
s
n
).
Ejercicio. Descomponga la seal escaln discreta como la suma de una seal
par y una impar.
Si f (t) es una seal continua, entonces f (t) = p(t)+i(t), donde p(t) = 0,5[ f (t)+
f (t)] e i(t) = 0,5[ f (t) f (t)], provee la descomposicin deseada.
Ejercicio. Encuentre la descomposicin en suma de seal par e impar de la
seal p(t) = 1 si t [0, 1), y 0 si t [0, 1)
5.8.1. Conjugada simtrica y conjugada antisimtrica
Si s es una seal discreta compleja, se dice que s es conjugada simtrica
si s
n
= s
n
; s es una seal conjugada antisimtrica si s
n
= s
n
. Si la parte
imaginaria de la seal es cero, las deniciones de conjugada simtrica y de
conjugada antisimtrica coinciden con las de seal par y seal impar, respecti-
vamente. Similarmente, si f (t) es una seal continua compleja, f es conjugada
simtrica si f (t) = f
(t) y es conjugada antisimtrica si f (t) = f
(t).
Ejercicio. Dada una seal compleja, encuentre su descomposicin como una
suma de una seal conjugada simtrica y una conjugada antisimtrica.
Ejercicio. Encuentre una seal que sea conjugada simtrica y conjugada anti-
simtrica, simultneamente.
Figura 5.24: La suma de una seal par y una impar
La transformada de Fourier de una seal real es conjugada simtrica, por
lo tanto, la magnitud de la transformada es par, mientras que la fase es una
impar. La transformada de Fourier de una seal real par, tiene componente
imaginaria nula. Note que esto no implica que la fase sea cero. La transformada
de una seal imaginaria (i.e. con parte real nula) es conjugada antisimtrica;
as, la parte real de la transformada es impar y la parte imaginaria es par.
Ejercicio. Muestre que, si g es una seal continua con transformada de Fourier
G.
G
() = [F(g)]
() = [F(g
)]()
Similarmente, si s es una seal discreta con transformada de Fourier S.
S
() = [F(s)]
() = [F(s
)]()
Si g es una seal conjugada simtrica, su parte real es par y su parte
imaginaria es impar. Si g es conjugada antisimtrica, su parte real es impar y
su parte imaginaria es impar.
Ejercicio. Si H es una seal conjugada simtrica, Qu propiedades de simetra
tienen su magnitud y su fase? Si es conjugada antisimtrica?
5.8.2. Implicaciones de las propiedades de simetra para trans-
formadas de seales discretas
Las propiedades de simetra mencionadas anteriormente son vlidas tanto
para la transformada de Fourier de seales continuas como para la trans-
formada de seales discretas. Para seales discretas, la periodicidad de la
transformada tiene implicaciones ulteriores que consideramos a continuacin.
Dado que la transformada de Fourier S() de una seal discreta s = s
n
es
peridica, con tiempo de repeticin 2, y que si la seal es real, la magnitud
S() de su transformada es par y la fase S() impar, es posible conocer S()
para toda R
1
dados sus valores para

omega [0, ] solamente. Como S
es par, S() = S() y, como es peridica, S() = S( + 2), por lo tanto,
S( + ) = S( ); vea la gura 5.25. Por otra parte S() = S() y
S() = S( + 2) implican S( + ) = S( ); adems, el hecho de que
la fase sea impar y que tome el mismo valor en y en implica que la fase
en estas frecuencias es o cero o : S() = S() = 0 o S() = S() = .
Ejercicio. Muestre que las soluciones del siguiente sistema de ecuaciones estn
dadas por los ngulos equivalentes a cero y los ngulos equivalentes a .
a
2
b a
2
b
similarmente, asumiendo que la parte imaginaria de s es cero, conociendo
la fase de S() entre 0 y , es posible averiguarla para cualquier valor de
Figura 5.25: La restriccin de una seal discreta a [0, ]. a. es suciente para reconstruir
la transformada en [, ]. b. ya que sta es par y, para cada real. c. ya que es peridica con
periodo 2
R
1
.
Im(s
n
) = 0 y S() =
n=
s
n
e
jn
implican,
Re [S()] =
n=
s
n
cos(n) funcin par
Im[S()] =
n=
s
n
sen(n) funcin impar
La magnitud de S() es una funcin par: S() =
_
Im[S()]
2
+ Re [S()]
2
Ejercicio. Comente sobre las propiedades de simetra de la transformada de
Fourier de la seal p
n
= 1 si n / 1, 1/, y p
n
= 0 si n / 1, 1/.
Ejemplo. Muestre que la transformada de s
n
= e
n
es real y par.
S() =
n=0
2
n
e
jn
+
n=0
2
n
e
jn
1
=
1
1
e
j
2
+
1
1
e
j
2
1
=
2 cos()
1,25 cos()
1
Ejercicio. Graque la magnitud y la fase de la transformada de 2
n
.
Nota. Hemos visto 4 transformadas de Fourier: series de Fourier, trasformada
de seales continuas, transformada de seales discretas y DFT (que tambin la
podramos llamar sumas de Fourier). Adems de otras propiedades, encada uno
de os cuatro casos tenemos una propiedadde Parseval y una de convolucin. la
relacin de Parseval nos permite considerar la transformada como un espectro
de energa. La propiedadde convolucin nos permite visualizar convoluciones
como productos en el dominio de la frecuencia.
5.9. RELACIN 369
5.9. Relacin entre la transformada de Fourier de
seales de duracin nita (y longitud innita)
y la transformada discreta de Fourier de la seal
de longitud nita correspondiente
Suponga que se tiene una seal discreta de longitud innita, s : Z C.
Adems, suponga que s es de duracin nita N; en particular, suponga que el
soporte de s est contenido en el intervalo /0, N 1/. Sea x : N C la seal
de longitud nita x = [s
0
, s
1
, . . . , s
n1
], que coincide con s donde est denida.
La transformada de Fourier de s est dada por:
s() =
n=
s
n
e
jn
=
N1
n=0
s
n
e
jn
mientras que la transformada discreta de Fourier de x est dada por
X
k
=
1
N
N1
n=0
s
n
e
j
2
N
nk
por lo tanto, podemos concluir que,
X
k
=
1
N
S(
2
N
k)
y por lo tanto, las X
k
son muestras a escala de S().
En otras palabras, la DFT de la versin truncada x de s, da N muestras a
escala de la transformada de Fourier S de s, en el intervalo [0, 2); una cada
2
pi/N radianes, comenzando en cero y terminando en2(N1/N). Enla gura

5.26 se ilustra un ejemplo.
Figura 5.26: Las X
k
s son muestras a escala de S()
5.10. Relacin entre las transformadas de Fourier
de una seal continua y la de la seal discreta
muestreada correspondiente
Una seal continua se puede procesar con un sistema continuo. Sin em-
bargo, la versatilidad y resistencia al ruido de los sistemas digitales hacen
prctica otra alternativa para seales que no incluyen frecuencias por encima
de aproximadamente 300kHz ; por ejemplo, seales ssmicas, de audio, poten-
ciales nerviosos, etc. As, la seal continua se convierte en una seal digital, se
procesa digitalmente y se reconvierte en seal anloga con un conversor D/A.
El primer paso consiste en muestrear y cuanticar (en nmero de bits dados, e.g.
16) la seal continua; esto se logra con un S/H (Sampler and Holder), y un
conversor A/D (anlogo/digital) y un ltro pasa bajas que suaviza la salida del
D/A. Esta es la tecnologa usada para el tratamiento digital de audio y la que
seguramente ser usada en TV comercial en el futuro.
5.10. SEAL MUESTREADA 371
Para que una seal continua pueda ser ltrada pueda ser ltrada efecti-
vamente as, es necesario que no se pierda informacin al pasar de la seal
continua a la seal discreta, es decir, que la seal continua sea recuperable a
partir de sus muestras. Una condicin que garantiza este requisito, es que la
seal continua tenga transformada con soporte acotado y que las muestras se
tomen a una tasa lo sucientemente alta. Esto se explica a continuacin.
Es importante advertir que los efectos del proceso de cuanticacin no se
consideran aqu. La cuanticacin tiene dos efectos: introducir un ruido con
densidad uniforme en la seal que se muestrea y hacer los sistemas discretos
efectivamente no lineales. La no linealidad de los ltros puede hacer que se
produzcan oscilaciones inesperadas (limit cycles, por ejemplo) o incluso
seales caticas. Una referencia clsica para este tema es [1].
5.10.1. Muestreo de seales continuas
Suponga que tiene una seal continua g(t) la cual se muestrea a una tasa
de
1
T
muestras por unidad del parmetro t, obteniendo la seal discreta x dada
por x
m
= g(nT), donde T es un nmero real positivo y n Z. Asuma que tanto
x como g y G son seales en ele uno. Sean G() y X() las transformadas,
respectivamente, de las seales g(t) y x
n
. Por lo tanto,
X() =
n=
x
n
e
jn
(5.1)
x
n
=
1
2
X()e
jn
d (5.2)
G() =
_

g(t)e
jt
dt (5.3)
g(t) =
_

G()e
jt
d (5.4)
Usando la ecuacin 5.4 tenemos,
x
n
= g(nT) =
1
2
_

G()e
jnT
d
=
1
2
r=
_
(2r+1)/T
(2r1)/T
G()e
jnT
d
donde el intervalo de integracin se ha particionando usando intervalos de
la forma . . . , (3/T, /T], (/T, /T], (/T, 3/T], . . . etc. con el cambio de
variable u = 2r/T se obtiene,
x
n
=
1
2
r=
_
/T
/T
G(u +
2r
T
)e
j(u+
2r
T
)nT
du
usando en vez de u, nuevamente,
x
n
=
1
2
r=
_
/T
/T
G(+
2r
T
)e
j(+
2r
T
)nT
d
note que e
j2rn
= 1 para cada n; intercambiando el orden de la serie y la integral,
x
n
=
1
2
_
/T
/T
r=
G(/T +
2r
T
)e
jnT
d
con el cambio de variable = T,
x
n
=
1
2
_

_
1
T
r=
G(
T
+
2r
T
)
_
_
e
jn
d
comparando con 5.2 tenemos que,
X() =
1
T
r=
G(
T
+
2r
T
)
Por lo tanto, X es una seal suma de versiones desplazadas y escalizadas
de G. Por ejemplo, para r = 0, se tiene el trmino G(
T
), para r = 1, el trmino
Figura 5.27: La transformada de una seal continua
Figura 5.28: La transformada de la seal muestreada correspondiente
G(
T
+
2
T
), etc. En las guras siguientes se ilustra la posible relacin entre X y
G para una seal g pasa bajas. BW (Band width) se reere al ancho de banda
total de la seal, incluyendo frecuencias negativas.
Como se ver ms adelante, es importante que los componentes del espec-
tro de X estn separados, como ocurre en la gura. Esto ocurrir siempre que
T
0
< , es decir,
1
T
>
2
0
2
, por lo tanto, la tasa de muestreo debe ser mayor
que dos veces la componente de frecuencia (en Hertz) mxima de g. Esta tasa
se conoce como tasa de Nyquist.
En caso contrario, si T
0
, los componentes se sobrelapan y se dir que
hay enmascaramiento (aliasing) de frecuencias. Note que como toda transfor-
mada de seal discreta, X tiene tiempo de repeticin 2; as, normalmente slo
es de inters el intervalo [, ] o el intervalo [0, 2]. Las frecuencias
cercanas a 0 son frecuencias bajas, frecuencias cercanas a son frecuencias
altas; cuando hay un enmascaramiento leve, la informacin de frecuencias
altas se distorsiona. Si el enmascaramiento es fuerte, todas las componentes
de frecuencias se distorsionan. Por esta razn, antes de muestrear una seal
continua, sta se debe ltrar con un pasa bajas anlogo (continuo) para evitar que
una contaminacin fortuita de la seal continua, a altas frecuencias, termine in-
uyendo de manera indeseada en frecuencias ms bajas al hacer la conversin
D/A; por ejemplo, un murcilago cerca al micrfono de una cantante podra
hacer el truco. Este ltro se conoce como filtro antialiasing.
5.10.2. Reconstruccin de la seal continua a partir de sus
muestras
Suponga que la seal continua g(t) se ha muestreado por lo menos a la tasa
de Nyquist
1
T
tal que:
0
<

T
, donde
0
es la mximacomponente de frecuencia
de g. Expresandoa g comola transformada inversa de sutransformada se tiene,
g(t) =
1
2
_

G()e
jt
d
como g(t) est limitada en frecuencia,
g(t) =
1
2
_

0
0
G()e
jt
d
como
0
< /T,
g(t) =
1
2
_
/T
/T
G()e
jt
d
dado que g se muestreo por lo menos a la tasa de Nyquist, usando un resultado
que se deriv anteriormente, para [, ], se tiene que G() = TX(T),
por lo tanto,
g(t) =
1
2
_
/T
/T
TX(T)e
jt
d
dado que X() =
n=
x
n
e
jn
, tenemos que,
g(t) =
1
2
_
/T
/T
T
n=
x
n
e
jTn
e
jt
d
=
T
2
_
/T
/T
n=
g(nT)e
jTn
e
jt
d
intercambiando el orden de la serie y la integral,
g(t) =
n=
g(nT)
_
T
2
_
/T
/T
e
j(tTn)
d
_
=
n=
g(nT)
sen[
T
(t nT)]
T
(t nT)
n=
g(nT)senc (
T
(t nT)) (5.5)
esta ltima frmula expresa la seal g(t) en trminos de sus muestras g(nT).
Desde ciertopuntode vista esta es una formula de interpolacin; la interpolacin
se hace usando funciones senc .
Este resultado nos dice que no hay prdida de informacin al pasar de una
seal limitada en frecuencia a la sucesin de sus muestras, si stas se toman
con una rapidez de al menos la tasa de Nyquist.
Esta frmula es vlida tambin para seales g L
2
. El lector interesado
puede consultar el artculo siguiente:
A.J. Jerry. The Shannon Sampling Theorem, its Various Extensions . . . Proc.
IEEE vol. 65, pp. 1565-1596, Nov. 77.
La frmula 5.5 se puede interpretar as: sobre la lnea de los nmeros
reales, marque las posiciones t = nT, coloque una seal sen(
T
(t nT) centrada
en t = nT, para cada marca; luego, sume todas las seales. Note que cada
senc se anula en las posiciones t = NT excepto en la que est centrada.
Ejemplo. Como una ilustracin de la frmula 5.5, considere la seal de du-
racin 3, g
n
= . . . , , 0, 1, 0,8, 0,6, 0, . . . , como se muestra en la gura 5.29. En
Figura 5.29: Una seal discreta de duracin nita
la gura 5.30 se muestran las seales g
0
senc (t), g
1
senc (t 1) y g
2
senc (t 2). En
Figura 5.30: Las seales g
0
senc (t), g
1
senc (t 1) y g
2
senc (t 2)
la gura 5.31 se muestran la seal f (t) = g
0
senc (t)+g
1
senc (t1)+g
2
senc (t2).
Note que efectivamente, f (0) = g
0
, f (1) = g
1
y f (2) = g
2
.
Figura 5.31: La seal f (t) = g
0
senc (t) + g
1
senc (t 1) + g
2
senc (t 2)
5.10.3. Frmula para la interpolacintrigonomtricadeseales
contnuas a partir de muestras equiespaciadas
Suponga que nos dan N muestras s
0
, s
1
, . . . , s
N1
de la seal continua g(t),
g : [0, T] C, espaciadas regularmente en el intervalo [0, T]:
s
n
= g(nT/[N 1]), N 0, 1, . . . , N 1
Es posible entonces encontrar una seal continua que es una suma de
exponenciales complejas y que concuerda con las muestras dadas de g. Esta
seal est dada por,
g =
N1
k=0
X
k
e
j
2
A
kt
donde
X
k
=
1
N
N1
k=0
s
n
e
j
2
N
nk
Ejercicio. Explique por qu la frmula dada cumple con las especicaciones
indicadas.
Ejercicio. Interpole las muestras 0, 1, 0,8, 0,6, 0usandolafrmuladada. Graque
y compare con la gura 5.30.
5.11. RESUMEN GRFICO 379
5.11. Resumen grco
Figura 5.32: Serie de Fourier
Figura 5.33: Transformada de Fourier
Figura 5.34: DTFT
Figura 5.35: Suma de Fourier
Figura 5.36: DFT
5.12. RESUMEN DE LAS TRANSFORMADAS 381
5.12. Resumen de las transformadas
Serie de Fourier:
c
n
=
1
T
_
T
0
f (t)e
jn
0
t
dt f (t) =
n=
c
n
e
jn
0
t
t R
1
periodo T = 2/
0
Suma de Fourier:
X
k
=
1
T
N1
n=0
f (t)e
jn
2
N
nk
dt x
n
=
N1
k=0
X
k
e
jn
2
N
nk
n Z, periodo N
Transformada de Fourier (de seales discretas de longitud innita en l
1
) [DTFT]:
S() =
n=
s
n
e
jnn
dt s
n
=
1
2
_
2
0
S()e
jnn
d n Z, R
1
, Speridica
Transformada Discreta de Fourier (de seales discretas de longitud innita) [DFT]:
X
k
=
1
T
N1
n=0
f (t)e
jn
2
N
nk
dt x
n
=
N1
k=0
X
k
e
jn
2
N
nk
n N, k NN = /0, N 1/
Transformada de Fourier (de seales continuas en L
1
):
F() =
_

f (t)e
jt
dt f (t) =
1
2
_

F()e
jt
d t R
1
, R
1
5.13. RESUMEN PARA LA PROPIEDAD DE PARSEVAL 383
5.13. Resumen para la propiedad de Parseval
Se mantienen los smbolos de la pgina anterior. Serie de Fourier:
n=
c
n
2
=
1
T
_
T
0
f (t)
2
dt
Suma de Fourier:
1
N
N1
n=0
x
n
2
=
N1
n=0
X
k
2
1
) [DTFT]:
n=
s
n
2
=
1
2
_
2
0
S()
2
d
1
N
N1
n=0
x
n
2
=
N1
n=0
X
k
2
1
):
_

f (t)
2
dt =
1
2
_

F()
2
d
5.14. RESUMEN CONVOLUCIN 385
5.14. Resumen convolucin
Se mantienen los smbolos de la pgina anterior. Serie de Fourier:
k=
c
n
d
n
e
jn
0
t
=
1
T
_
T
0
f (t )g()d
donde c
n
y d
n
son los coecientes de Fourier de f y g.
Suma de Fourier:
N1
k=0
R
k
S
k
W
nk
N
=
1
N
N1
m=0
s
m
r
nm
1
) [DTFT]:
1
2
_
2
0
S()R()d =
k=
s
k
r
nk
1
N
N1
k=0
r
k
s
k
W
nk
N
=
N1
m=0
S
m
R
km
1
):
1
2
_

F()G()e
jt
d =
_

f ()g(t )d
_

f (t)g(t)e
jt
d =
1
2
_

F(W)G(t W)dW
5.15. PROBLEMAS 387
5.15. Problemas
1. Las seales x, y : 6 C, discretas de longitud nita, se muestran en la
gura 5.37. Encuentre DFT
1
[DFT(x)DFT(y)]. Sugerencia: Qu relacin
hay entre la DFT y la convolucin circular?
Figura 5.37: Dos seales discretas de longitud nita
2. Sea r : Z C, la seal discreta pulso discreto de longitud innita (y
duracin nita) dada por
r
n
=
_
_
1, si n 0, 1, . . . , L 1
0, si n 0, 1, . . . , L 1
a) Graque r
n
contra n.
b) Muestre que la transformada de Fourier R() de r, est dada por
R() = e
j
L1
2
sen(
L
2
)
sen

2
si 0 y R(0) = L. (Una seal senc enmascarada).
c) Utilizando Mathematica, graque R() contra para L = 10,
[, ).
3. Sea s : Z C, la seal dada por s
n
= 2
n
cos(3n). Calcule su transfor-
mada de Fourier.
4. Se tiene un sistema de convolucin discreto con funcin de transferencia
H() = (1/3)(1+2 cos()). Calcule la respuesta del sistema (en el dominio
n) a la seal x
n
= (1/5) cos(
2
3
n).
5. a) Calcule la convolucin circular de las seales [1, 2, 3] y [0, 1, 0].
b) Calcule la convolucin circular de [0, 1, 0, 1, 0] y [2, 2, 3, 4, 5].
H() = cos(). Calcule la respuesta del sistema (en el dominio n) a la
seal x
n
= sen(n
2
) +cos(n). Para n / 10, 10/ graque la entrada y la
salida.
7. La respuesta impulso de un sistema de convolucin discreto est dada
por:
h
n
=
_
_
0, n < 0
3
n
n 0
Si la entrada al sistema es la seal x
n
= cos(n/2) +cos(n), exprese la salida
y
n
como una suma de cosenos (desfasados).
H() = cos(). Encuentre la respuesta impulso del sistema.
9. a) Encuentre la transformada G() de la seal continua g(t) = e
t
,
t R
1
.
b) Encuentre la transformada S() de la seal discreta s
n
= g(n/10),
n Z.
c) Usando Matlab, graque S() y 10
5
r=5
G(10 + 210r). Compare
y Explique.
10. Si la funcin de transferencia de un sistema est dada por H() =
2j sen()
5.15. PROBLEMAS 389
a) Graque la magnitud y la fase de H.
b) Encuentre la respuesta impulso del sistema.
c) D la ecuacin de diferencia entrada/salida del sistema.
d) Encuentre la salida si la entrada est dada por e
n
= cos(n).
e) Encuentre la salida si la entrada est dada por e
n
= 1 +cos(2n/3) +
cos(n).
11. Se tiene un sistema e convolucin discreto que produce a la salida una
versin retardada de la seal de entrada: y
n
= x
n2
, como se muestra en
la gura 5.38.
a) Encuentre la funcin de transferencia H(), del sistema.
b) Encuentre la respuesta impulso del sistema.
Figura 5.38: Un ltro de retardo
12. Suponga que se tiene un sistema de convolucin discreto con funcin de
transferencia H() = e
j/2
. Encuentre la respuesta impulso del sistema.
13. Suponga que se tiene un sistema de convolucin discreto con funcin de
transferencia H() = e
j3
. Encuentre la respuesta impulso del sistema.
14. Si x = [1, 0, 0], z = [1, 1, 1] y se sabe que z es la convolucin circular de x
y cierta seal y, encuentre y.
15. Se tiene un sistema discreto con entrada x, y salida y, que cumple con las
siguiente condiciones:
y
n
= x
n
+ 0,5y
n1
.
La relacin se puede iterar hacia atrs, y es vlida en el lmite,
cuando n :
y
n
= x
n
+ 0,5x
n1
+ 0,25y
n2
= x
n
+ 0,5x
n1
+ 0,25x
n2
+ 0,125y
n3
=
Siempre que la entrada tienda a 0 cuandon , la salida tambin.
a) Diga si el sistema es de convolucin. Explique.
b) Exprese la salida como una suma de exponenciales complejas, si la
entrada est dada po n
3
.
16. La seal g(t) tiene transformada G(), con G() = 0 para > 210000.
Muestreando g, se obtiene la seal discreta x : Z C dada por x
n
=
g(nT), T = 10
5
. La seal x es ltrada con el sistema discreto con ecuacin
de diferencia y
n
= x
n
x
n1
, produciendo la seal discreta y = y
n
.
Finalmente, a partir de la seal y se obtiene la seal continua s(t), con la
siguiente frmula de interpolacin:
s(t) =
n=
y
n
senc [
t nT
T
]
a) Encuentre la funcin de transferencia D() = Y()/X() del sistema
discreto.
b) Encuentre la respuesta impulso del sistema discreto.
c) Si S() es la transformada de la seal de salida, encuentre la fun-
cin de transferencia S() = S()/G() correspondiente al sistema
completo.
5.15. PROBLEMAS 391
Note que sta es una forma verstil de implementar ltros anlogos con
base en ltros digitales. Diga cules inconvenientes tiene.
17. Diga qu tipo de ltro es el promedio mvil ponderado que para cada
seal de entrada x produce a la salida la seal y dada por y
n
= 0,25(x
n1
+
2x
n
+ x
n+1
). es decir,
a) Encuentre la respuesta impulso.
b) Compruebe que es de convolucin.
c) Encuentre la funcin de transferencia. Ahora, de qu tipo es?
d) Tambin, diga i el sistema es lineal, invariante, estable y causal. En
cada caso, explique.
18. Calcule la DFT de la seal [1,1,0,0,1]. Expresela como un vector real.
19. Se tiene un sistema de convolucin discreto con respuesta impulso dada
por h
n
= u
n
2
n
,
a) Encuentre la funcin de transferencia H() y muestre que es real u
par.
b) Si la entrada es la seal s
n
= e
j(20/45)n
, exprese la seal de salida
como una suma de exponenciales complejas.
c) La seal g(t) tiene transformada G() con G() = 0 para >
210000. Se obtiene luego la seal discreta x usando x
n
= g(nT)
con n Z, T = 10
5
. Luego, la seal discreta es ltrada con un
sistema de convolucindiscretoconecuacinde diferencia dada por
y
n
= 0,5(x
n
x
n1
). Finalmente, se reconstruye una seal continua
s(t) =
0
y
n
senc (/T[t nT]).
1) Encuentre la funcin de transferencia del sistema discreto. Diga
qu tipo de ltro es.
2) Encuentre la respuesta impulso del sistema discreto.
3) Si S() es la transformada de la seal de salida, encuentre la
funcin de transferencia H() =
S()
G()
del sistema completo.
Referencias
[2] Computer BasedExercises for Signal Processing. C-S. Burrus,
et.al., Prentice Hall, Englewood Clis, 1994.
[3] Dicrete-Time Signal Processing. A. V. Oppenheim y R.W.
Shafer. Prentice Hall, Englewood Clis, 1989.
[4] Digital Signal Processing. J.G Proakis y D.G. Manolakis. Pen-
tice Hall, Upper Saddle River, 1996.
[5] Chaos in Digital Filters. L.O. Chua y T. Lin. IEEE trans. on
Circuits and Systems, vol. 35, no. 6, pp. 648-658,1988.
393
Captulo 6
Propiedades de los sistemas y
su correspondiente
clasicacin
6.0. Clasicacin
Los sistemas de clasican de acuerdo a sus propiedades. Una de ellas, que
ya mencionamos en el captulo 2 al hablar de sistemas de convolucin, es la
linealidad. La propiedad de linealidad se frasea en trminos del concepto de
espacio vectorial de seales, y del cuerpo de los complejos. Otras propiedades
que unsistema puede tener yque consideramos eneste captuloson: invarianza,
causalidad y estabilidad.
Los sistemas de convolucin son lineales e invariantes pero hay sistemas
lineales y sistemas invariantes que no son de convolucin. Con gran general-
idad, un sistema lineal e invariante es un sistema de convolucin. Como era
394
6.0. CLASIFICACIN 395
de esperar, la causalidad y la invarianza de un sistema de convolucin estn
determinados por la respuesta escaln del sistema, o por la respuesta impulso,
cuando existe.
Sea S : A B un sistema lineal de un espacio vectorial de seales A a un
espacio vectorial de seales B, ambos con el mismo cuerpo. Si a medida que
consideramos diferentes seales de entrada x, evaluamos la seal de salida
y(t) = [S(x)](t) del sistema en un tiempo dado t = t
0
, resulta el funcional lineal
: A C (C es el conjunto de los complejos) dado por (x) = [S(x)](t
0
). Esta
observacin, junto con un resultado conocido como el Teorema de representacin
de Riesz nos permite expresar la salida de un sistema lineal (no necesariamente
invariante) como una integral de Riemann-Stieltjes, similar en forma a la con-
volucin de Stieltjes vista en el captulo 2 para sistemas lineales e invariantes,
cuando el espacio de las seales de entrada A es el conjunto de las seales
contnuas con soporte contenido dentro de un intervalo dado.
Otro espacio de seales que es importante en teora de sistemas, es el
espacio de las seales de variacinacotada. Si una seal es de variacinacotada
y es derivable, entonces su derivada est en L
1
(Por qu?).
Los sistemas contnuos lineales, pero no necesariamente invariantes, se
modelan con,
y(t) =
_

e()dg
t
()
y, menos generalmente pero a menudo equivalentemente, con,
y(t) =
_

h(t, )e()d
La teora de los sistemas lineales est bastante sosticada. No existe una
teora que cubra los sistemas en general (lineales y no lineales) que tenga un
nivel de desarrollo similar. Apartir de la dcada de los setentas se comenzaron
a estudiar los ltros L, o los ltros basados en estadsticas de orden. El ltro
ms conocido de esta familia es el ltro mediana, introducido por Tukey como
la media mvil, para el estudio de series de tiempo en estadstica.
396 CAPTULO 6. PROPIEDADES DE LOS SISTEMAS
Los sistemas no lineales se hanestudiado conlas llamadas series de Volterra
(en honor a Vito Volterra, matemtico italiano, quien public varios resulta-
dos relacionados a nales de siglo pasado). Sin embargo, esta teora no es
sucientemente general, en particular, no modela el ltro mediana.
As, hay dos reas grandes en las que se clasican los sistemas no lineales:
en el caso continuo, los sistemas pueden ser lisos, y si son de forma y
=
f (y) + x, donde x es la entrada y y es la salida, cuando f tiene Jacobiano, y
los sistemas arrugados (osea no lisos) pero lineales a trozos (o PL: picewise
linear), comoenel caso del circuito de Chua. Los sistemas discretos no lineales
que se estudian normalmente son de la forma y
n
= f (y
n1
) + x
n
, donde f tiene
Jacobiano o es lineal a trozos. la seccin6.1 pasal captulo
cero, revisar la introduccin.
6.1. Sistemas lineales
Sean (V, , K, +, ) y (W, , K, +, ) espacios vectoriales sobre el mismo cuer-
po. La funcin T : V W es una transformacin lineal si para cada
, K y cada x, y V se tiene que T( x y) = T(x) T(y). As, una
transformacin lineal es un homomorsmo entre espacios vectoriales.
Enotras palabras, Tes lineal si cumple conlas propiedades de homogeneidad:
para cada K y cada u V, T(u) = T(u), y de superposicin: para cada
u, v V, T(u + v) = T(u) + T(v).
Ejercicio. Demuestre que si T es una transformacin lineal entre los espacios
(V, , K, +, ) y (W, , K, +, ) , que 0 es el mdulo del grupo (V, ) y es el
mdulo del grupo (W, ), entonces, T(0) = .
6.1. SISTEMAS LINEALES 397
Ejemplo. Considere el espacio vectorial V de las funciones contnuas con do-
minio [0, 1] y rango complejo, con la operacin de suma de funciones, so-
bre el cuerpo de los complejos. Considere el conjunto de funcionales lineales
denidos sobre este espacio. Como se puede mostrar, para cada funcional lin-
eal f : V C, de este tipo hay una funcin g de variacin acotada tal que f se
puede representar como una integral de Riemann-Stieltjes:
f (h) =
_
1
0
h(t)dg(t)
Ejemplo. Considere el espacio vectorial V de las funciones contnuas con do-
minio [0, 1] y rango complejo, con la operacin de suma de funciones, sobre el
cuerpo de los complejos. Considere el espacio vectorial W = C
2
sobre el cuerpo
de los complejos C. Sea T : V W dada por
T(h) =
__
1
0
h(t)e
j2t
dt,
_
1
0
h(t)e
j2t
dt
_
Ejercicio. Diga si la funcinT del ejemploanterior es una transformacinlineal.
Ejercicio. Diga si el promedio mvil es una transformacin lineal y, en caso
armativo, Entre qu espacios vectoriales?
Ejercicio. Diga si la DFT es un homomorsmo entre C
N
y C
N
, o no y Por qu?
Teorema 10. Riesz. La integral de Riemann-Stieltjes
_
b
a
s()d() donde es una
funcin dada de variacin acotada, dene un funcional lineal sobre el espacio de las fun-
ciones contnuas. Conversamente, cada funcional lineal denido sobre el espacio de las
funciones contnuas con soporte incluido en el intervalo [a, b], puede ser representado
en esta forma.
Suponga que se tiene un sistema lineal S y que las posibles seales de
entrada e son las seales contnuas con soporte acotado por el intervalo [a, b].
Entonces, para un valor t
1
jo, el valor de la seal de salida [S(e)](t
1
) es un
funcional lineal sobre el espacio de seales de entrada. Por el teorema anterior,
tenemos que
[S(e)](1) =
_
b
a
s()d
1
()
y similarmente para otro valores de t, por lo tanto, en general tenemos que,
[S(e)](t) =
_
b
a
s()d
t
()
o, abusando un tanto de la notacin,
[S(e)](t) =
_
b
a
s()d()
o, si es derivable con derivada h,
[S(e)](t) =
_
b
a
s()h(t, )d
Para seales de entrada con soporte lo sucientemente centrado y localiza-
do en el intervalo [a, b], con respecto a un posible corrimiento, tenemos que si
t
() = ( t) entonces el sistema es invariante con respecto al corrimiento.
6.2. Sistemas no lineales: los ltros L
Es comn en ingeniera el pasar una seal por un sistema con el objeto de
quitarle una caracterstica indeseable, o de resaltar una deseable. Por ejemplo,
considere el ecualizador de un equipo de sonido.
Con frecuencia, una seal resulta contaminada con ruido al ser trans-
mitida; por ejemplo, la seal de un satlite. Es decir, la seal que se recibe es
diferente de la seal que se transmite y no hay mucho que se pueda hacer para
evitarlo. Este problema se alivia en parte usando sistemas digitales ya que para
6.2. SISTEMAS NO LINEALES: LOS FILTROS L 399
que un 1 se convierta en un 0 o viceversa, se necesita un nivel de ruido
alto.
Otra forma de aliviar el problema consiste en estimar la seal original en el
punto de recepcin, dado cierto conocimiento de las seales que se transmiten
y del ruido. Por ejemplo, si se sabe que la seal no tiene componentes de
frecuencia por encima de 5KHz, cualquier cosa a frecuencias ms altas es
ruido y se puede considerar el uso de un ltro pasa bajas.
Si la seal y el ruido tienen espectros que se traslapen apreciablemente,
el uso de un sistema de convolucin no permitir separar la seal del ruido.
Por ejemplo, considere una imagen, donde los bordes tienen componentes
de frecuencia altas y contienen parte importante de la informacin que se
transmite, la cual result contaminada conruido aditivo de alta frecuencia. este
problema se resuelve en forma relativamente satisfactoria usando un sistema
no lineal: ltro mediana.
Otra razn por la que es importante estudiar los sistemas no lineales es que
los sistemas lineales son slo modelos aproximados de sistemas reales. As, no
siempre es conveniente ni realista asumir que cierto sistema es lineal. Por ejem-
plo, cuando se quiere estudiar la distorsin introducida por un amplicador
con transistores.
A continuacin repasamos algunos conceptos tiles en la denicin de los
ltros L, tambin conocidos como estadsticas L mviles.
6.2.1. Permutaciones
Una permutacin es una biyeccin de un conjunto nito a s mismo. Para
funciones de un conjunto nito a s mismo, los conceptos de induccin, so-
breyeccin y biyeccin coinciden; as una permutacin de los elementos del
conjunto N = 0, 1, . . . , N 1 es una biyeccin de N a N. Como sabemos, a un
conjunto de n elementos le corresponden n! permutaciones posibles.
Ejemplo. La funcin p : 0, 1, 2, 3 0, 1, 2, 3, dada por p(0) = 2, p(1) = 1,
p(2) = 3, p(3) = 0 es una permutacin del conjunto 4 = 0, 1, 2, 3. Tambin,
usando vectores, escribimos: [0, 1, 2, 3] [2, 1, 3, 0].
6.2.2. Muestra
En la prctica, una muestra (Sample) es el resultado de una encuesta
o experimento. Tcnicamente, una muestra [x
0
, x
1
, . . . , x
N1
] es un punto en
R
N
, es decir, un vector de N componentes. La razn por la cual modelamos
una muestra como un vector y no como un conjunto es que en una muestra
podemos tener elementos repetidos mientras que en un conjunto n
0
: 2, 2 =
2.
Nota. Un vector sin embargo, tiene ms estructuras que la necesaria ya que
normalmente el orden de las componentes de una muestra no es relevante (a
diferencia de una serie de tiempo). As, una denicin apropiada podra ser la
clase de vectores dada por las permutaciones de sus componentes.
6.2.3. Estadsticas
En la prctica, una estadstica extrae cierta informacin de la muestra y la
condensa en un solo nmero. Tcnicamente, una estadstica es una funcin de
R
N
R
1
.
As por ejemplo, el promedio es una estadstica. es la funcin promedio:
R
N
R
1
dada por, promedio[x
0
, x
1
, . . . , x
N1
] =
1
N
N1
n=0
x
n
.
El grafo de la funcin promedio es un plano que pasa por el origen de R
N+1
,
sta es una forma de ver que el promedio es una estadstica lineal. El promedio
es el estimador de mxima verosimilitud de la media de una distribucin
gausiana.
6.2.4. Estadsticas de orden
El vector de las estadsticas de orden (order statistics) de la muestra x =
[x
0
, x
1
, . . . , x
N1
] se denota como x = [x
(
0), x
(
1), . . . , x
(N1)
]; los componentes
de este vector, conocidos como las estadsticas de orden, corresponden a un
ordenamiento de la muestra: x
(
0) x
(
1) x
(N1)
Ejemplo. Las estadsticas de orden de x = [5, 3, 3, 8, 0, 2, 5] son:
x = [x
(
0), x
(
1), . . . , x
(N1)
] = [2, 0, 3, 3, 5, 5, 8]
La notacin x
(i)
corresponde al hecho siguiente: sea p una permutacin de
N = 0, 1, . . . , N 1 tal que, x
p(0)
x
p(1)
x
p(N1)
: omitiendo la pe
en x
p(i)
nos resulta la notacin mostrada. Las estadsticas de orden son una
herramienta muy til y antigua en la estadstica. Por ejemplo, la mediana es el
estimador de mxima verosimilitudde la media de una distribucinlaplaciana.
Para calcular la mediana no es necesario hacer sumas ni divisiones, esto haca
su uso muy atractivo cuando no haba calculadoras ni computadoras. Algunas
personas enInglaterra no las considerabandignas yse referana suuso como
quick and dirty. Hoy en da la situacin se ha invertido en cierto sentido ya
que las instrucciones de sumas y divisiones se llevan a cabo muy rpidamente
en un computador, mientras que las de ordenar datos toman ms tiempo.
6.2.5. Mediana, mnimo y mximo
Si el tamao N de la muestra x = [x
0
, x
1
, . . . , x
N1
] es impar, con N = 2k + 1,
y por lo tanto k =
[N1]
2
, su mediana est dada por,
med(x) = x
(k)
Similarmente, su mnimo y su mximo estn dados por,
mn(x) = x
(0)
m ax(x) = x
N1
6.2.6. Algunas estadsticas L
Las estadsticas L son combinaciones lineales de las estadsticas de orden de
una muestra. As, por ejemplo, el rango (range) y el midrango (midrange)
de la muestra x, denidos a continuacin, son estadsticas L:
rango(x) := x
(N1)
x
(0)
midrango(x) := 0,5(x
(N1)
+ x
(0)
)
Los cuasirangos (quasiranges) se denen as:
Q
r::N
(x) := x
(Nr1)
x
(r)
6.2.7. Notacin vectorial para las estadsticas L
Resulta conveniente expresar las estadsticas L en notacin matricial, co-
mo el producto, x
T
donde el vector = [
0
,
1
, . . . ,
N1
] es un vector de
coecientes, y T indica vector transpuesto. As, para N = 5, los vectores de
coecientes para la mediana, el mnimo, el mximo, el rango y el midrango
estn dados por,
estadstica vector de coecientes
mediana [0, 0, 1, 0, 0]
mnimo [1, 0, 0, 0, 0]
mximo [0, 0, 0, 0, 1]
rango [1, 0, 0, 0, 1]
midrango [0,5, 0, 0, 0, 0,5]
promedio [0,2, 0,2, 0,2, 0,2, 0,2]
6.2.8. Estadsticas mviles o ltros de ventana mvil
Cuando se tiene una seal discreta (serie de tiempo en la jerga estadstica) y
a partir de sta se obtiene otra desplazando una ventana sobre la seal original
y escribiendo como valor de la seal de salida correspondiente a la coordenada
en la que la ventana est centrada el valor correspondiente a alguna estadstica
aplicada a la muestra de los datos en la ventana, decimos que tenemos un
filtro de ventana mvil o una estadstica mvil. Si m : R
2k+1
R
1
es
la estadstica en cuestin, x : R C la entrada y y : R C la salida, tenemos
que, para cada i entera, y
i
= m[x
ik
, . . . , x
i
, . . . , x
i+k
].
6.2.9. Filtros L
Cuando se tiene un ltro de ventana mvil y la estadstica en cuestin es un
estadstica L, decimos que tenemos un filtro L, o filtro de estadsticas
de orden. Quizs el ltro L ms conocido sea el ltro mediana que, como
el promedio mvil, se usa para buscar tendencias subyacentes en series de
tiempo en estadstica.
El filtro mediana Con ventana de ancho 2k + 1 se puede implementar
como se muestra en la gura 6.1.
Ejercicio. Muestre que el ltro mediana cumple con la propiedad de homo-
geneidad.
Ejercicio. D un contraejemplo que ilustre el hecho que el ltro mediana no
cumple con la propiedad de superposicin.
Ejercicio. Diga si el ltro mediana es un sistema lineal.
Ejercicio. Filtre la seal peridica . . . , 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 0 . . . de periodo
6, con un ltro mediana de ancho de ventana tres, con uno de ancho de ventana
igual a cinco, y con uno de ancho de ventana igual a siete.
Figura 6.1: Un ltro mediana tiene tres bloques principales: uno que toma segmentos de la
seal de entrada, otro que ordena los datos en los segmentos y otro que toma el valor ordenado
intermedio, o mediana
6.2.10. Seales raz
Los ltros no lineales son ms difciles de analizar, debido a que hay que
hacerlo caso por caso y no se tiene un volumen de conocimiento para ninguno
en particular, similar al que se ha acumulado para los ltros no lineales. La
caracterizacin de las seales que pasan sin sufrir alteracin por un ltro, o
seales raz del ltro, constituye una caracterizacin terica importante de
un ltro no lineal. (En el caso de un ltro de convolucin, las exponenciales
complejas con frecuencias para las que la funcin de transferencia del ltro
vale 1 + j0).
Tyan, Brandt y Longbotham han caracterizado las seales raz del ltro
mediana. Como dijimos, una seal x = x
n
es una seal raz (o seal invariante,
o seal idempotente) del ltro mediana si al ltrarla obtenemos nuevamente la
misma seal.
Las seales raz del ltro mediana se pueden clasicar en dos conjuntos.
Uno contiene seales localmente montonas congradode monotonicidadlocal
igual al ancho de la ventana del ltro en cuestin. Por ejemplo, las seales
6.3. INVARIANZA Y CAUSALIDAD 405
lomo-3 son seales raz del ltro mediana con ventana de ancho 3. el otro
conjunto, contiene seales binarias y peridicas, no necesariamente localmente
montonas. Tyan anot en 1981 que las seales localmente montonas eran
invariantes, posteriormente, Brandt y Longbotham, independientemente en
1987, indicaron la relevancia de los conjuntos de seales peridicas binarias. A
continuacin damos ejemplos de seales peridicas binarias. Por simplicidad,
las seales tienen rango 0, 1 en todos los casos.
Ejemplo. La seal . . . , 0, 1, 2, 2, 1, 0, 0, 1, 2, 2, 1, 0, 0, . . . es localmente montona
de grado 3 y es seal raz del ltro mediana de ventana de ancho 3.
Ejemplo. La seal . . . , 0, 1, 0, 1, 0, . . . es una seal raz del ltro mediana con
ancho de ventana 5. Note que no lo es del de ventana de ancho 3.
Ejemplo. La seal . . . , 1, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, . . . de periodo 8, es seal raz
del ltro mediana con ventana de ancho 7.
Ejemplo. La seal . . . , 1, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, . . . de periodo 7, es seal raz
del ltro mediana con ventana de ancho 9.
6.3. Invarianza y Causalidad
Los nombres de invarianza y de causalidad resultan de considerar la evolu-
cin de las seales en la variable tiempo. Hoy en da el dominio de una seal
no necesariamente se reere a tiempo si no, por ejemplo a desplazamiento;
sin embargo, se sigue utilizando la misma terminologa. Antes de denir las
propiedades, considere el uso de cierta notacin para seales desplazadas.
Sea f : R
1
C una seal continua. Sea t un nmero real y sea g : R
1
C
la seal continua tal que, t R
1
g(t) = f (t ), decimos que la seal g es
una versin desplazada de la seal f y a denotamos como

f . Usando esta
convencin,
0
f = f y t R
1
g(t) = f (t )
Figura 6.2: La seal s y una versin desplazada

s de sta
Similarmente, para seales discretas, si r : Z C, entonces .
v
r es la versin
de la seal r desplazada v unidades hacia la derecha, es decir, n Z.
v
r
n
= r
nv
.
6.3.1. Invarianza
Se dice que el sistema continuo S es invariante si, x C
R
, y R,
S(
x) =
(S[x]), es decir
t R
1
[S(
x)](t) = [S(x)](t )
Esta propiedad se ilustra en la gura 6.3.
Similarmente, para sistemas discretos, se dice que el sistema discreto S es
invariante si, x C
Z
, y v Z, S(
v
x) =
v
(S[x]), es decir
n Z [S(
v
x)]
n
= [S(x)]
nv
Ejercicio. Diga si el ltro RC pasa bajas de primer orden es invariante.
Ejercicio. Diga si el ltro promedio mvil es invariante.
Ejercicio. Muestre que el ltro mediana es invariante.
6.3. INVARIANZA Y CAUSALIDAD 407
Figura 6.3: Si la seal de entrada a un sistema invariante se desplaza, la salida se desplaza en
la misma forma.
6.3.2. Causalidad
Aunque la causalidad es un concepto bastante intuitivo, una denicin
axiomtica en teora de sistemas quizs no sea obvia. El tema de la causalidad
ha sido considerado con frecuencia en losofa, por ejemplo por Hume y por
Russell, y en la losofa de la fsica cuntica.
Decimos pues, que el sistemas continua S es un sistema causal si el valor
de la salida y(t) = [S(x)](t), en t no depende de la entrada x() para valores
de mayores que t. (Osea, el presente de la seal de salida depende solamente
del presente y el pasado de la seal de entrada y no del futuro de la seal de
entrada.) En smbolos, S es causal si:
x, u C
R
, R t < x(t) = u(t) t < [S(u)](t) = [S(x)](t)
en palabras: el sistema S es causal si siempre que dos seales concuerden hasta
un cierto punto , las salidas correspondientes tambin concordarn hasta .
Figura 6.4: Las tres seales mostradas x, y, z para t < , coinciden
Es claro que cualquier sistema clsico que evolucione en el tiempo, por
ejemplo un ltro RC ser causal. En mecnica cuntica no es claro que todo
sistema sea causal. Tambin, si el dominio de las seales no es el tiempo, no
hay razn para asumir a priori que el sistema sea causal.
Similarmente, el sistema discreto S es un sistema causal si siempre que 2
seales concuerden hasta n = v, las salidas correspondientes tambin concuer-
dan hasta n = v:
x, u C
Z
, v Z n v x
n
= u
n
n v[S(u)]
n
= [S(x)]
n
la salida y
n
= [S(x)]
n
, evaluada en n no depende de la entrada x
v
, para valores
de v mayores que n.
Ejercicio. Diga si el ltro RC pasa bajas de primer orden es causal.
Ejercicio. Diga si el ltro promedio mvil es causal.
Ejercicio. D un ejemplo de un promedio mvil causal.
Ejercicio. Diga si el ltro continuo pasa bajas ideal es causal.
Ms adelante en este captulo daremos caracterizaciones alternas para la
causalidad de los sistemas de convolucin.
6.4. ESTABILIDAD 409
6.4. Estabilidad
Intuitivamente, un sistema es estable si siempre que la entrada no sea
demasiado grande, la salida tampoco lo es. Como se vio en el captulo anterior,
el tamao de las seales se mide utilizando las normas elep: L
p
y l
p
. Aqu nos
restringiremos al caso p = .
El Estado de un sistema es un vector de seales correspondientes a varias
variables de un sistema (por ejemplo la corriente y el voltaje en el condensador
de un circuito RC serie), es decir, un estado es un elemento del producto
cartesiano de las magnitudes de inters de un sistema. cuando se estudian los
sistemas usando el concepto de estado, es til denir la estabilidad del sistema
en trminos de sensitividad a condiciones iniciales diciendo que dos estados
son lo sucientemente similares entonces la evolucin del sistema a partir de
cada uno de estos tambin ser similar. Esta idea tiene que ver con la llamada
estabilidad en el sentido de Liapunov y con la posible caoticidad de un sistema.
Otro tipo de estabilidad tiene que ver con el hecho de que un sistema pue-
da oscilar, es decir, producir una seal de salida peridica con entrada cero.
Normalmente esto es indeseable, cuando hay realimentaciones espurias. Para
sistemas de convolucin, es posible predecir si esto suceder conociendo la
posicin de los polos de la funcin de transferencia en el plano complejo, us-
ando la transformada de Laplace o la transformada zeta, respectivamente, para
sistemas contnuos y discretos. Un sistemas dinmico sin entrada (por ejemplo
un oscilador) se caracteriza con una ecuacin de diferencia homognea; en este
caso, con sistema estable, se quiere decir que las soluciones sean acotadas.
El tipo de estabilidad en el que estamos interesados aqu se conoce como
estabilidad EASA. Decimos que un sistemas es estable en el sentido entrada
acotada - salida acotada, o EASA (BIBO: bounded input, bounded output),
si para cada seal de entrada con norma ele-innito, nita, la salida tiene
norma ele-innito nita. Es decir, para cualquier seal de entrada acotada, la
salida es una seal acotada.
Quizs sea conveniente anotar que aunque normalmente un sistema in-
estable es indeseable, no siempre es as. Por ejemplo, la maniobrabilidad de un
avin puede incrementar notablemente bajo condiciones de inestabilidad. Lo
importante es poder predecir el resultado y que el sistema produzca la salida
deseada.
Ejercicio. Diga si el promedio mvil es estable en sentido EASA, o no.
Ejercicio. D un ejemplo de un sistema no estable.
Ejercicio. Se tiene un sistema discreto T el cual, para cada seal de entrada x,
produce la seal de salida T(x), x = x
n
y T(x) = [T(x)
n
]. Si T est denida
como se indica en cada caso abajo, diga si T es:
Lineal
Causal
Invariante
Estable
1. [T(x)
n
] = g
n
x
n
Cmo dependen sus respuestas de g?
2. [T(x)
n
] =
n
k=n
0
x
k
3. [T(x)
n
] =
n+n
0
k=nn
0
x
k
4. [T(x)
n
] = x
nn
0
5. [T(x)
n
] = e
x
n
6. [T(x)
n
] = a x
n
+ b
6.5. SISTEMAS HOMOGNEOS E INVARIANTES 411
6.5. Sistemas homogneos e invariantes
Es interesante considerar esta clase de sistemas, que incluye la clase de los
sistemas de convolucin, debido a la interesante propiedad de que la respuesta
a una exponencial es un exponencial. As, las exponenciales son las seales
propias de los sistemas homogneos e invariantes.
Sea x
n
la entrada a un sistema discreto homogneo e invariante, aunque no
necesariamente lineal (es posible que no cumpla con la propiedad de super-
posicin). Suponga que la entrada es exponencial, de la forma x
n
= a
n
. Sea y
n
la respuesta correspondiente del sistema. Por ser invariante el sistemas, si se
aplica la entrada x
n+1
= aa
n
, la salida correspondiente ser ahora y
n+1
y como
el sistema es homogneo, y
n+1
= ay
n
, por lo tanto,
y
n
= y
0
a
n
mostrando que la salida tambin es exponencial.
Sea x(t) = a
t
la entrada a un sistema discreto homogneo e invariante,
aunque no necesariamente lineal (es posible que no cumpla con la propiedad
de superposicin). Sea y(t) la respuesta correspondiente del sistema. Por ser
invariante el sistema, si se aplica la entrada x(t + ) = a
a
t
, por lo tanto,
y(t) = y
0
a
t
mostrando que la salida tambin es exponencial.
6.6. Sistemas de convolucin
En esta seccin se estudian los sistemas de convolucin con cierto detalle,
a la luz de las propiedades denidas. La funcin caracterstica del sistema
permite decir en forma inmediata si el sistema es causal y evaluando una
integral o una serie, si es estable en sentido EASA. Es fcil probar que los
sistemas de convolucin son lineales e invariantes.
Es prctica comn asumir que si un sistema es lineal e invariante, entonces
es representable con una convolucin. Los casos de sistemas lineales e invari-
antes no representables con convolucin se presentan cuando el sistema es
discontinuo en el sentido que el orden de ciertos lmites no se puede cambiar.
Ejercicio. Demuestre que un sistema de convolucin continuo es lineal.
Ejercicio. Demuestre que un sistema de convolucin discreto es lineal.
Ejercicio. Demuestre que un sistema de convolucin es continuo invariante.
Ejercicio. Demuestre que un sistema de convolucin es discreto invariante.
Un sistemas de convolucin queda completamente especicado cuando se
conocen su respuesta impulso o su respuesta escaln. Por lo tanto, debe ser
posible decir si el sistema es causal o no, si es estable o no, conociendo su
respuesta impulso o su respuesta escaln.
6.6.1. Causalidad de un sistema de convolucin
Cmo es la respuesta impulso de un sistema de convolucin causal?
suponga que el sistema de convolucin continuo S es causal. como S es lineal,
la respuesta a la seal cero, es la misma seal cero. Como asumimos que el
sistema es causal, la respuesta a una seal que sea cero con anterioridad a
tiempo cero; es tambin cero con anterioridad a tiempo cero. La seal escaln
6.6. SISTEMAS DE CONVOLUCIN 413
es cero para tiempos menores que cero; como conclusin tenemos que la re-
spuesta escaln de un sistema de convolucin causal tiene que ser cero para
tiempos menores a cero. Por lo tanto la respuesta impulso, si existe, es cero
para tiempos menores que cero (la derivada de una constante es cero).
Para sistemas discretos, la situacin es similar y el resultado es el mismo:
suponga que S es un sistema de convolucin discreto; como S es lineal, la
respuesta a la seal cero es la seal cero, como la seal impulso discreta es cero
para instancias menores que cero y el sistema es causal, la respuesta impulso
es cero para instancias menores que cero.
Por lo tanto, si un sistema de convolucin es causal, entonces su respuesta
escaln y su respuesta impulso son cero en la parte negativa de su dominio.
Si h(t) es la respuesta impulso de un sistema continuo de convolucin causal,
entonces para t < 0, h(t) = 0. Si h
n
es la respuesta impulso de un sistema
discreto de convolucin causal, para n < 0, h
n
= 0.
Conversamente, suponga que se tiene un sistema de convolucin continuo
y que su respuesta escaln se anula en la parte negativa de su dominio. Sea e
una seal de entrada; la salida est dada entonces por,
r(t) =
_

e(t )dg()
=
_
=
=
e()dg(t )
como la respuesta escaln g(t) es cero para t < 0, se tiene que,
r(t) =
_
=t
=
e()dg(t )
y, dados los lmites de la integral, concluimos que la salida r para cada entrada
e, para cada tiempo t, solo depende de los valores que e tome con anterioridad
a t. Es decir, r slo depende de la restriccin de e al intervalo(, t) de su
dominio. Por lo tanto, el sistema es causal.
Similarmente, si se tiene un sistema discreto de convolucin cuya respuesta
impulso h se anula en la parte negativa de su dominio, para cada entrada x se
tiene la salida y est dada por
y
n
=
n
k=
h
nk
x
k
de donde concluimos que la salida y para una instancia n, depende solamente
de la restriccin de la entrada al intervalo / , n/; por lo tanto, el sistema es
causal.
Resumimos diciendo que unsistema de convolucinconrespuesta impulso
h es causal si y slo si si funcin caracterstica h (o en su defecto, la respuesta
escaln g) se anula en la parte negativa de su dominio.
6.6.2. Estabilidad de un sistema de convolucin
Suponga que se tiene un sistema de convolucin continuo cuya respuesta
impulso h es integrable en magnitud, es decir, h L
1
. Suponga que la seal de
entrada x es acotada y que su norma L
est dada por [x[
(y es nita). La
6.6. SISTEMAS DE CONVOLUCIN 415
norma L
de la seal de salida y est dada por,

[y[
= supy(t) : t R
1
= sup
_

h()x(t )d : t R
1
sup
_

h()x(t )d : t R
1
= sup
_

h()x(t )d : t R
1
sup
_

h()[x[
d : t R
1
= sup[x[
h()d : t R
1
= [x[
sup
_

h()d : t R
1
= [x[
[h[
1
<
Enforma similar se puede mostrar que si se tiene unsistema de convolucin
discreto, [y[
< [x[
[h[
1
, por lo tanto, si la respuesta impulso h
n
es sumable
en magnitud (i.e. si est en l
1
) y si la entrada es acotada (i.e. si est en l
)
entonces la salida est acotada y sunorma ele-innito es menor que el producto
de las normas ele-uno de h y ele-innito de x.
Concluimos que, si la respuesta impulso de un sistema de convolucin
tiene norma ele-uno nita, entonces el sistema es estable en sentido EASA.
Viceversa, suponga que se tiene un sistema de convolucin continuo cuya
respuesta impulso no est en L
1
, es decir, su norma ele-uno es innita. Quere-
mos mostrar que entonces podemos encontrar una seal de entrada acotada a
la que le corresponda una seal de salida no acotada.
Suponga primero que la integral de la respuesta impulso es innita. En este
caso, la respuesta escaln no es acotada y por lo tanto el sistema es inestable.
Por otra parte, si la integral de la respuesta impulso es nita, como el caso
de una funcin h(t) = u(t)senc (t) tenemos que la respuesta escaln acotada.
Similarmente, si la respuesta impulso tiene integral divergente (como en
el caso de una funcin seno), y la integral en magnitud innita, queremos
encontrar una seal que tienda a innito cuando t tiende a innito.
No nos interesa una seal que tome el valor innito ya que esta no sera
una funcin de los reales a los complejos. Una seal puede estar indenida
en un conjunto nito de puntos, segn dijimos en el captulo 1. As, lo que
necesitamos es una seal que diverja hacia innito en un punto.
Por ejemplo, si la seal de entrada es la seal
x(t) =
_
_
1, h(t) 0
1, h(t) < 0
entonces, la seal de salida y est dada por
y(t) =
_

h()x(t )d
y(0) =
_

h()x()d
=
_

h()d
= [h[
1
=
Conjetura 2. Un sistema de convolucin con respuesta impulso no integrable en
magnitud no es estable EASA.
Ejercicio. Diga si es cierto que un sistema de convolucin continuo es estable
EASA si y slo si la la transformada unilateral de Laplace de su respuesta
escaln no tiene polos en el semiplano abierto derecho. Explique.
6.7. SISTEMAS LINEALES E INVARIANTES 417
Ejercicio. Diga si es cierto que un sistema de convolucin discreto es estable
EASA si y slo si la transformada zeta de su funcin caracterstica no tiene
polos en el crculo de radio 1 con centro en el origen. Explique.
6.7. Sistemas lineales e invariantes
6.7.1. Con dominio L
p
, p [1, )
6.8. Representabilidad con convolucin
Como se vio en la seccin anterior, un sistema de convolucin es lineal e
invariante. Inversamente, suponga que se tiene un sistema continuo S, lineal e
invariante. Es S necesariamente representable con una convolucin? Es decir,
si h es la derivada de la respuesta escaln del sistema, o funcin caracterstica,
se tiene que para cada seal de entrada x, S(x) = x h?
6.8.1. Sistemas discretos
Considere inicialmente un sistema discreto lineal e invariante. Sea la seal
impulso discreta y sea h la correspondiente respuesta impulso, es decir,
h = S()
h
n
= [S()]
n
sea x = x
n
una seal de entrada arbitraria.
Sea .
m
la seal impulso desplazada m unidades y sea una constante; as,
para cada n, [(
m
)]
n
=
nm
.
Note que toda la seal discreta se puede expresar como una serie de seales
Figura 6.5: La seal impulso discreta (o delta de Kronecker)
impulso desplazadas y pesadas:
x =
i=
x
i
.
i
x
n
=
i=
x
i
[
i
]
n
Ejemplo. Suponga que x es la seal mostrada en la gura 6.6.
Figura 6.6: Una seal discreta
La seal de la gura anterior se puede descomponer comouna suma innita
de seales impulso desplazadas y pesadas:
Suponga que el sistema es lineal en sentido amplio es decir que cumple con la
propiedad de convolucin no slo para sumas nitas de seales sino tambin
con respecto a series de seales, entonces, denotando y como la respuesta a la
6.8. REPRESENTABILIDAD CON CONVOLUCIN 419
Figura 6.7: La descomposicin de la seal en la gura 6.6 como una suma de seales impulso
pesadas y desplazadas.
seal x.
y = S(x) = S(
i=
x
i
.
i
)
=
i=
x
i
S(
i
)
y si S es invariante,
y = S(x) =
i=
x
i
.
i
h
entonces, para cada nmero entero n,
y = S(x) =
i=
x
i
h
ni
= x h
Lo anterior muestra que si un sistema discreto es invariante y lineal en
sentido amplio, entonces es representable por una convolucin.
Ejercicio. Para un sistema de convolucin con respuesta impulso como la
mostrada en la gura 6.8.
Figura 6.8: La respuesta impulso de un promedio mvil
h
n
=
_
_
1/3, n 1, 0, 1
0 n 1, 0, 1
muestre que la salida r, para una entrada s, est dada por r
n
= (1/3)(s
n1
+s
n
+
s
n+1
).
6.8.2. Sistemas contnuos
para sistemas contnuos lineales e invariantes la situacin es ms compleja
pero la conclusin es similar: con gran generalidad, los sistemas contnuos
lineales e invariantes, son representables con una convolucin.
Suponga que se tiene un sistema continuo S, lineal e invariante, con re-
spuesta escaln g(t). Sea u(t) la seal escaln, as, g(t) = [S(u)](t). Suponga que
se tiene una entrada que es una suma nita de seales escaln desplazadas:
e(t) =
N
k=N
e
k
[u(t t
k
) u(t t
k+1
)]
como se muestra en la gura 6.9. a este tipo de seales las llamaremos seales
simples. como el sistema es lineal e invariante, la respuesta correspondiente
6.8. REPRESENTABILIDAD CON CONVOLUCIN 421
Figura 6.9: Una seal simple
r = S(e) est dada por,
r(t) =
N
k=N
e
k
[u(t t
k
) u(t t
k+1
)]
y se puede observar que para seales de entrada simples, dada la linealidad
e invarianza del sistema se concluye que es de convolucin ya que la suma
anterior es equivalente a una convolucin de Stieltjes:
r(t) =
_
N
N
e(t )dg()
Ejercicio. Demuestre la frmula anterior.
qu sucede para seales de entrada ms complejas? ES suciente saber
que S es lineal e invariante y conocer su respuesta escaln g para encontrar la
respuesta r?
Suponga que e es una funcin continua y de variacin acotada que se anula
por fuera de [T, T]: suponga tambin que g es de variacin acotada. Dado un
nmero natural N 2, decimos que la funcin
e
N
(t) =
N1
k=N
e(
kT
N
)
_
u(t kT
N
) u(t
(k + 1)T
N
)
_
es una funcin simple de orden N que aproxima a e(t). El lmite de e
N
(t) cuando
N tiende a innito es e(t) (Por qu?). Por lo tanto, la respuesta del sistema a
e(t) est dada por
r(t) = S
_
lm
N
e
N
(t)
_
si el sistema es continuo en el sentido de poder conmutar la operacin lmite
con S,
r(t) = lm
N
S[e
N
(t)]
= lm
N
N1
k=N
e(
kT
N
)
_
u(t kT
N
) u(t
(k + 1)T
N
)
_
ya que S es lineal e invariante. Nuevamente tenemos que
r(t) =
_
=T
=T
e(dg())
r(t) =
_
=
=
e(t )dg()
que es una convolucin.
Ejercicio. Sea el espacio de las seales que son lmites de seales simples.
Es L
1
un subconjunto de ?
6.8.3. El teorema de representacin de Riesz y su relacin con
los sistemas contnuos
El teorema en cuestin dice que un funcional f : R
C[a,b]
R es lineal si y
slo si es representable en la forma
f (g) =
_
b
a
g()d()
6.9. SISTEMAS DE VOLTERRA 423
donde es una funcin de variacin acotada y g : [a, b] R es continua.
Entonces, para seales de entrada contnuas de duracin nita y con du-
racin contenida en el intervalo [a, b], tenemos que un sistema es lineal si y
slo si es representable as:
[ f (g)](t) =
_
b
a
g()d(, t)
donde la restriccin de : [a, b] R R a (, t), para cada t, es de variacin
acotada.
Conjetura 3. El resultado anterior es vlido si las seales de entrada no son de
duracin nita.
6.9. Sistemas de Volterra
Los sistemas de Volterra
1
son sistemas invariantes no-lineales. No todo
sistema invariante no-lineal es un sistema de Volterra, en particular, el ltro
mediana es un sistema invariantes o-lineal que no es un sistema de Volterra.
Para que un sistema sea un sistemas de Volterra se necesita que cumpla ciertas
condiciones de diferenciabilidad.
6.9.1. Sistemas de Volterra discretos
Suponga que g es una funcin de R
L+1
a R
1
la cual tiene extensin en series
de Taylor alrededor del origen [0, 0, . . . , 0] de R
L+1
. Si y = S(x), y para cada n,
y
n
est dada por y
n
= g(x
n
, x
n1
, . . . , x
nL
) entonces
y
n
= h
0
+
L
i=0
h
1
i
x
ni
+
L
i=0
L
j=0
h
2
i j
x
ni
x
nj
+
L
i=0
L
j=0
L
k=0
h
3
i jk
x
ni
x
nj
x
nk
+
1
Vito Volterra fue un matemtico italiano de comienzos del siglo 20 que hizo aportes impor-
tantes a la teora del anlisis funcional
Esta representacin se conoce como una serie de Volterra. Los coecientes
h
0
, h
1
i
, h
2
i j
, etc. son los coecientes de Volterra del sistema.
Ejercicio. Suponga que se tiene un sistema de convolucin T con respuesta
impulso dada por h
0
= 1, h
1
= 2, h
2
= 1 y h
n
= 0 para n /0, 2/. Suponga que
la salida de este sistema se pasa por un sistema U que eleva al cuadrado, es
decir, si z = U(y), entonces, para cada n, z
n
= (y
n
)
2
. Sea z = S(x) = U(T(x)).
Encuentre los coecientes de Volterra del sistema S = UT.
6.10. Problemas
1. Se tiene un sistema discreto causal que cumple con la ecuacin de difer-
encia y
n
= (1/2)y
n1
+ x
n
, donde x es la entrada y y la salida. Encuentre
la funcin de transferencia del sistema.
2. Se tiene un sistema continuo el cual, para cada seal de entrada e(t)
produce la seal de salida s(t) =
_
t
e()d. Diga si el sistema es estable.

Si s, demuestre, si no, d un contraejemplo.
3. Se tiene un sistema discreto rango mvil con ventana de ancho tres.
La relacin entrada-salida est dada por, y
n
= rangox
n1
, x
n
, x
n+1
=
m axx
n1
, x
n
, x
n+1
mnx
n1
, x
n
, x
n+1
. Diga si el sistema es estable y si
es invariante. en cada caso, si s, demuestre, si no, d un contraejemplo.
4. Se tiene un sistema continuo que produce a la salida la seal s(t) dada
por s(t) =
_

e
t2
r()d cuando la entrada es la seal r(t).
a) Encuentre la salida correspondiente a la entrada u(t).
b) Encuentre la salida correspondiente a la entrada u(t 10).
c) Diga si el sistema es estable. (Demuestre o d un contraejemplo.)
d) Diga si la seal es lineal. (Demuestre o d un contraejemplo.)
6.10. PROBLEMAS 425
e) Diga si el sistema es estable. (Demuestre o d un contraejemplo.)
f ) Diga si el sistema es de convolucin.
5. Se tiene un sistema de convolucin continuo con respuesta impulso dada
por h(t) = (1 e
t
)u(t). Diga si el sistema es causal y si es estable. En cada
caso, argumente o d contraejemplo.
6. Se tiene un sistema continuo con entrada e(t) y salida s(t), relacionadas
por,
s(t) =
_

1
1 + (t 2)
2
e()d
a) Diga si el sistema es lineal.
b) Diga si es invariante.
c) Diga si es de convolucin.
d) Diga si es causal.
e) Diga si es estable EASA.
7. Se tiene un sistema continuo con entrada e(t) y salida s(t), relacionadas
por, s(t) =
_

h(t, )e()d donde h es una funcin de R

2
C.
a) Muestre que el sistema es lineal
b) D condiciones que deba cumplir h para que el sistema sea:
1) Estable en sentido EASA.
2) Causal.
3) Invariante.
4) De convolucin.
tu(t).
a) Diga si es estable (muestre o d contraejemplo).
b) Diga si es causal (muestre o d contraejemplo).
9. Se tiene un sistema causal discreto donde la salida y
n
y la entrada x
n
estn relacionadas as: y

n
= m axx
n1
, x
n
, x
n+1
mnx
n1
, x
n
, x
n+1
a) Diga si el sistema es lineal.

b) Diga si es invariante.
c) Encuentre la respuesta impulso del sistema.
10. Se tiene un sistema continuo con relacin entrada/salida dada por, s(t) =
_

e()h(t, )d si h(t, ) = e
t5
.
a) Graque h(t, ) contra para t = 1 y t = 10.
b) Diga si es causal (muestre o d contraejemplo).
c) Diga si es invariante (muestre o d contraejemplo).
d) Diga si es lineal (muestre o d contraejemplo).
e) Diga si es estable EASA (muestre o d contraejemplo).
11. Se tiene un sistema que, para cada entrada s(t), produce la seal de salida
r(t) =
_

h(t, )s()d donde h(t, ) = th

1
() +(1t)h2(t) y h
1
() = (1e
)
y h
1
() = (1 e
2
).
12. D la denicin de sistema causal. muestre que si un sistema de con-
volucin continuo tiene respuesta escaln g(t) nula para t < 0, el sistema
es causal.
Referencias
[3] Fourier Series. G.P. Tolstov. Dover, N.Y., 1962.
[4] Almost Periodic Functions. H. Bohr. Chelsea, N.Y., 1947.
[5] Sobre la periodicidad de sumas de seales discretas peridi-
cas. A. Restrepo y L. Chacn. Memorias del simposio de
Tratamiento de Seales, Imgenes y Visin Articial, Universi-
dad de los Andes, Bogot, 1995.
[6] On the period of sums of discrete periodic signals. A. Restre-
po y L. Chacn. IEEE Signal Processing Letter, vol. 5, No. 7, pp.
164-166, 1998.
Wilmington, 1995.
[8] Fourier Analysis. T.W. Krner. Cambridge University Press,
Cambridge, 1998.
427
428 REFERENCIAS
Nuevo
en cap V
FILTROS DISCRETOS
FUNDAMENTOS DE LA TEORA DE SEALES Y
SISTEMAS
Por: Alfredo Restrepo Palacios, Ph. D.
Este libropuede ser usadocomotextopara el cursobsicode unsemestre en
Teora de Seales, que se ve en las carreras de Ingeniera Elctrica y Electrnica.
El enfoque es axiomtico, por lo que tambin es un buen libro de referencia.
Es bastante autocontenido: se repasan varios conceptos de clculo, la in-
tegral de Riemann-Stiletjes, las normas L
p
. Aunque el libro comienza con los
fundamentos necesarios, es recomendable cierta madurez; as, es recomend-
able haber visto clculo diferencial e integral y variable compleja.
El libro est diseado para estudiantes de pregrado de ingeniera o fsica
que estn interesados en adquirir los conceptos bsicos para la representacin
y tratamiento de las seales en el dominio de la frecuencia de Fourier. Es
posible tambin que un estudiante de matemticas quiera ver aplicaciones
que le permitan generar intuicin para varias deniciones.
El tema que ms se desarrolla es el anlisis de Fourier. Se consideran cuatro
casos: series de Fouries para seales continuas peridicas, transformada de Fourier
para seales continuas integrables en magnitud, transformada de Fourier en
tiempo discreto para seales discretas sumables en magnitud, sumas de Fourier o
DFT tanto para seales discretas de longitud nita como para seales discretas
peridicas.
El siguiente tema en extensin es el de los sistemas de convolucin, que
son los sistemas ms importantes en el enfoque clsico para este curso. Se hace
nfasis en que las exponenciales complejas son eigenfunciones o funciones
propias de los sistemas de convolucin.
Tambin se consideran sistemas no lineales donde el anlisis de Fourier
es poco til. Se dan deniciones de invarianza y causalidad de sistemas, en
general, sin restringirlas a sistemas de convolucin inicialmente.
El enfoque tomado es matemtico, lo cual redunda en precisin y en gen-
eralidad. Se dan ejemplos resueltos as como ejercicios y problemas al nal de
cada captulo. Un aspecto en el que este curso se diferencia de la mayora de
los cursos introductorios de seales es que se ha evitado el uso de funciones
delta de Dirac, para el caso continuo. Para esto, se usa la respuesta escaln de
los sistemas de convolucin continuos, la integral de Riemann-Stieltjes y las
series de Fourier.
El profesor Restrepo es Ingeniero Electrnico de la Ponticia Universidad
Javeriana, MSc. y Ph.D. de la Universidadde Texas en Austin y, actualmente, es
profesor investigador en el departamento de Ingeniera Elctrica y Electrnica
de la Universidad de los Andes, en Bogot. Sus reas de investigacin incluyen
el tratamiento no lineal y estadstico de seales.
ndice de guras
1. El producto cartesiano de A y A . . . . . . . . . . . . . . . . . . . . . . 7
2. Para una relacin reexiva R, la diagonal de A A debe estar en R . . . . . . 8
3. Una relacin simtrica . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
4. Transitividad. Si est relacionada con y con entonces est relacionada
con . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
5. A la izquierda, relacin conectada. A la derecha, una de corrimiento circular:
para cada la y cada columna hay por lo menos un elemento de relacin . . . 10
6. Un orden parcial, no conectado . . . . . . . . . . . . . . . . . . . . . . . 12
7. Diagrama de una funcin con dominio A y rango B . . . . . . . . . . . . . 14
8. f es una sobreyeccin de A en B, pero no una inyeccin . . . . . . . . . . . 15
9. f es una inyeccin de A en B, pero no es sobreyectiva . . . . . . . . . . . . 16
10. Una biyeccin . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 16
11. Un ordenamiento circular para 0, 1, 2 . . . . . . . . . . . . . . . . . . . 18
12. Una inyeccin del conjunto de los nmeros pares al conjunto de los nmeros
naturales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
13. Clasicacin de conjuntos segn su cardinalidad . . . . . . . . . . . . . . 32
14. Cada lnea representa un nmero racional . . . . . . . . . . . . . . . . . . 36
15. Un tringulo rectngulo: si x = y y l es una unidad de longitud tal que x = nl y
y = nl con m, n Z, para ninguna p Z se tiene que n = pl . . . . . . . . . . 40
16. Los puntos indicados hacen parte de la clase de equivalencia de x . . . . . . . 49
431
17. [x[ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 50
18. El intervalo de S
1
de radio con centro en [x], corresponde a una coleccin
innita de intervalos de la lnea de los nmeros reales . . . . . . . . . . . . 51
19. La solucin grca de las races reales de una cbica . . . . . . . . . . . . . 56
20. El modelo de coordenadas rectangulares: el producto R
1
R
1
. . . . . . . . 58
21. El modelo de coordenadas polares:(0, ) S
1
. . . . . . . . . . . . . . 58
22. El modelo geomtrico cono para las coordenadas polares . . . . . . . . . . . 58
23. El modelo geomtrico cono para las coordenadas polares . . . . . . . . . . . 59
24. Equivalencia geomtrica de las representaciones polar y rectangular de los
nmeros complejos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 61
25. La fase de z es igual a la fase de z ms (o menos) . . . . . . . . . . . . . 62
26. Una forma de denir la funcin arctan: con rango (/2, /2) . . . . . . . . . 63
27. Ilustracin de la frmula z w z w . . . . . . . . . . . . . . . . . . 64
28. Representacin geomtrica del producto complejo . . . . . . . . . . . . . . 65
29. Representacin geomtrica del inverso multiplicativo, el inverso aditivo y el
conjugado . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 65
30. La proyeccin estereogrca de x S
1
(/2] es p(x) R
1
. . . . . . . . . . 67
31. La proyeccin estereogrca . . . . . . . . . . . . . . . . . . . . . . . . 68
32. Transformaciones de Mbius 1 (COMO LE PONEMOS A ESTA GRFICA) . . 70
33. Transformaciones de Mbius 2 (COMO LE PONEMOS A ESTA GRFICA) . . 71
34. Orden para productos elementales positivos . . . . . . . . . . . . . . . . . 73
35. s es una sucesin unilateral . . . . . . . . . . . . . . . . . . . . . . . . . 80
36. La sucesin a . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
37. Funcin para denir una mtrica en S
1
. . . . . . . . . . . . . . . . . . . 83
38. No tiene epgrafe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
39. El criterio de la integral para mostrar divergencia . . . . . . . . . . . . . . 94
40. El criterio de la integral para mostrar convergencia . . . . . . . . . . . . . . 94
41. No tiene epgrafe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 96
42. No tiene epgrafe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
43. Grca de la funcin x . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
44. El intervalo ](3, 4), (2, 3)[ de R
2
. . . . . . . . . . . . . . . . . . . . . . . 100
45. Las funciones x
n
para n = 1, 2, 4, 6 y la funcin lmite . . . . . . . . . . . . . 101
46. En la denicin de lmite, los puntos del intervalo J, con la posible excepcin
de a, tienen imgenes dentro del intervalo I; en el caso de la denicin de
continuidad, la imagen de J es un subconjunto de I . . . . . . . . . . . . . 102
47. La ecuacin de la tangente est basada en la funcin lineal (x) = f
(x)(t x) . . 106
48. El ngulo con vrtice z
0
y el ngulo con vrtice f (z
0
) son iguales . . . . . . . 107
49. El conjunto (n, k) N N; k n . . . . . . . . . . . . . . . . . . . . . . 112
50. Una funcin escaln desplazada . . . . . . . . . . . . . . . . . . . . . . 118
51. Teorema fundamental del clculo . . . . . . . . . . . . . . . . . . . . . . 120
52. Promedio de una funcin . . . . . . . . . . . . . . . . . . . . . . 122
1.1. Obtencin de una seal . . . . . . . . . . . . . . . . . . . . . . . . . . 145
1.2. Una seal discreta de longitud nita . . . . . . . . . . . . . . . . . . . . 149
1.3. Una seal continua. (La funcin correspondiente no es continua) . . . . . . . 151
1.4. Una funcin del conjunto 4 al conjunto de los nmeros reales . . . . . . . . . 153
1.5. Una seal discreta con rango complejo . . . . . . . . . . . . . . . . . . . 154
1.6. Un sistema es una funcin entre conjuntos de seales . . . . . . . . . . . . 155
1.7. Representacin de un sistema como una caja negra . . . . . . . . . . . . 155
1.8. La seal de voltaje h se aplica a una resistencia de un ohmio . . . . . . . . . 161
1.9. Grca
1
t
,
1
t
,
1
t
2
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 162
1.10. La seal cos 5t para t [0,1, 0,6] . . . . . . . . . . . . . . . . . . . . . 163
1.11. La seal de la gura anterior, en valor absoluto . . . . . . . . . . . . . . . 163
1.12. La seal dela gura anterior, al cuadrado . . . . . . . . . . . . . . . . . . 164
1.13. Tubo de rayos catdicos . . . . . . . . . . . . . . . . . . . . . . . . . . 166
1.14. La seal sen(t) y una onda tringulo F(t) . . . . . . . . . . . . . . . . . . 167
2.1. Circuito RL serie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 171
2.2. Respuesta escaln del circuito de la gura 2.1 . . . . . . . . . . . . . . . . 172
2.3. Las seales discretas f y g a ser convolucionadas . . . . . . . . . . . . . . 174
2.4. g
2k
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175
2.5. Las seales e y h a ser convolucionadas . . . . . . . . . . . . . . . . . . . 178
2.6. Para calcular s(1) es necesario multiplicar h() y e(1 ) . . . . . . . . . . . 178
2.7. El valor de s(1) es el rea sombreada . . . . . . . . . . . . . . . . . . . . 179
2.8. g = f h . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 180
2.9. Una seal con salto en t = 0 . . . . . . . . . . . . . . . . . . . . . . . . 182
2.10. Un sistema de convolucin . . . . . . . . . . . . . . . . . . . . . . . . . 184
2.11. Circuito RC pasa bajas de primer orden . . . . . . . . . . . . . . . . . . . 185
2.12. Circuito RC pasa altas . . . . . . . . . . . . . . . . . . . . . . . . . . . 190
2.13. La respuesta escaln de un sistema de convolucin. Note que as como un RC
pasa altas, la respuesta escaln de este sistema no es diferenciable. . . . . . . 192
2.14. La seal impulso discreta . . . . . . . . . . . . . . . . . . . . . . . . . 195
2.15. Circuito RC pasa bajas e primer orden en el plano s . . . . . . . . . . . . . 197
2.16. Dos sistemas de convolucin en cascada . . . . . . . . . . . . . . . . . . 202
2.17. Un circuito RLC pasa banda de segundo orden . . . . . . . . . . . . . . . 202
2.18. Respuesta escaln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 203
3.1. Obtencin de una seal . . . . . . . . . . . . . . . . . . . . . . . . . . 206
3.2. Una seal discreta con periodo 3. . . . . . . . . . . . . . . . . . . . . . . 207
3.3. Una seal con periodo 3, otra con periodo 4 y su suma . . . . . . . . . . . . 211
3.4. Las seales sent, 1/2 sen2t y su suma . . . . . . . . . . . . . . . . . . . . 212
3.5. La seal g(t) = sent + sent . . . . . . . . . . . . . . . . . . . . . . . . 212
3.6. La seal sent . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 216
3.7. La seal cos t . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 217
3.8. Representacin de sent + cos 2t en el dominio de la frecuencia de Fourier . . . 221
3.9. Una onda cuadrada con periodo 2 y nivel DC cero . . . . . . . . . . . . . 221
3.10. Onda cuadrada con periodo 1/60 y nivel DC de 6V . . . . . . . . . . . . . . 222
3.11. Onda tringulo de frecuencia 60, con nivel DC de 6 voltios . . . . . . . . . . 223
3.12. La seal senc enmascarada, SE
4
(x), de orden 4 . . . . . . . . . . . . . . . . 226
3.13. Las seales sent, 1/3 sen3t, 1/5 sen5t, 1/7 sen7t . . . . . . . . . . . . . . . 227
3.14. La suma parcial seales sent + 0 . . . . . . . . . . . . . . . . . . . . . . 227
3.15. La suma parcial seales sent + 1/3 sen3t . . . . . . . . . . . . . . . . . . 227
3.16. La suma parcial seales sent + 1/3 sen3t + 1/5 sen5t . . . . . . . . . . . . . 228
3.17. La suma parcial seales sent + 1/3 sen3t + 1/5 sen5t + 1/7 sen7t . . . . . . . 228
3.18. Dos seales peridicas con periodo 2 . . . . . . . . . . . . . . . . . . . 230
3.19. La onda tringulo par de periodo 2 . . . . . . . . . . . . . . . . . . . . 230
3.20. Onda sierra . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 231
3.21. hjkhl . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 234
3.22. La suma de los tres nmeros complejos mostrados es cero . . . . . . . . . . 236
3.23. Una seal peridica discreta . . . . . . . . . . . . . . . . . . . . . . . . 240
4.1. a. Una seal peridica . . . . . . . . . . . . . . . . . . . . . . . . . . . 248
4.2. b. El resultado de agregar intervalos nulos entre periodos . . . . . . . . . . 248
4.3. c. el resultado en el lmite. . . . . . . . . . . . . . . . . . . . . . . . . . 248
4.4. Pulsos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 250
4.5. Una seal pulso . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 253
4.6. La funcin senc x . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 255
4.7. La transformada de Fourier . . . . . . . . . . . . . . . . . . . . . . . . 260
4.8. La funcin 1

r
para varios valores de r . . . . . . . . . . . . . . . . . . 263
4.9. Sistema bsico de modulacin y demodulacin DSB. (No se incluyen ltros ni
amplicadores.) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 265
4.10. Un sistema de convolucin . . . . . . . . . . . . . . . . . . . . . . . . . 270
4.11. Representacin en tiempo y en frecuencia de un sistema de convolucin . . . . 272
4.12. Descomposicin espectral de un rayo de luz . . . . . . . . . . . . . . . . . 273
4.13. La funcin de transferencia de un pasa bajas ideal . . . . . . . . . . . . . . 274
4.14. Esta seal se aplica al ltro pasa bajas ideal . . . . . . . . . . . . . . . . . 274
4.15. Transformada de Fourier de la seal en la gura anterior . . . . . . . . . . . 275
4.16. Falta epgrafe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 276
4.17. NO TIENE EPGRAFE . . . . . . . . . . . . . . . . . . . . . . . . . . . 278
4.18. La respuesta de un sistema de convolucin a una sinusoide, es una sinusoide
de la misma frecuencia, o la seal cero si H(
0
) = 0 . . . . . . . . . . . . . 282
4.19. Onda tringulo con recticacin de media onda . . . . . . . . . . . . . . . 282
4.20. Una onda cuadrada y su espectro . . . . . . . . . . . . . . . . . . . . . . 283
4.21. Funcin de transferencia de un pasa bajas ideal . . . . . . . . . . . . . . . 283
4.22. Espectro de la suma de dos seales coseno y un nivel DC . . . . . . . . . . . 284
4.23. La seal 0,5 sen(t) + 1/3 sen(3t) . . . . . . . . . . . . . . . . . . . . . . . 284
4.24. Filtro RC pasa bajas de primer orden . . . . . . . . . . . . . . . . . . . . 284
4.25. La parte real de la funcin de transferencia del pasa bajos RC con RC=1 . . . . 285
4.26. La parte imaginaria de la funcin de transferencia del pasa bajos RC con RC=1 286
4.27. La magnitud de H() =
1
1+j
. . . . . . . . . . . . . . . . . . . . . . . . 286
4.28. La fase de H() =
1
1+j
. . . . . . . . . . . . . . . . . . . . . . . . . . 287
4.29. Un pasa altas es la identidad menos un pasa bajas . . . . . . . . . . . . . . 289
4.30. respuesta escaln del pasa altas de primer orden . . . . . . . . . . . . . . . 290
4.31. La respuesta en la gura anterior es equivalente a la suma de un escaln y el
negativo de la respuesta escaln de un pasa bajas de primer orden, que no salta 290
4.32. a. Seal de entrada b. Seal de salida del ltro ideal c. Seal de salida del ltro RC293
4.33. Do=C (261.626Hz), Re=D (293.665Hz), Mi=E(329.628Hz), Fa=F (349.228Hz),
Sol=G (391.995Hz), La=A (440.0Hz), Si=B (493.883Hz) . . . . . . . . . . . . 296
4.34. Representacin en decibeles de la funcin de transferencia . . . . . . . . . . 299
4.35. La magnitud y la fase de un pasa todo con fase lineal . . . . . . . . . . . . . 300
4.36. Un pasa todo con fase no lineal . . . . . . . . . . . . . . . . . . . . . . . 301
4.37. a) La seal de entrada. b) La seal de salida (alteracin de la forma de onda) . 302
4.38. Onda tringulo . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 303
4.39. Espectro de la seal s(t) . . . . . . . . . . . . . . . . . . . . . . . 308
4.40. Espectro de la seal modulada f (t) . . . . . . . . . . . . . . . . . 309
4.41. Espectro de la seal h(t) . . . . . . . . . . . . . . . . . . . . . . . 309
4.42. Espectro de la seal resultante b(t) . . . . . . . . . . . . . . . . . 309
4.43. Modulacin SSB usando la transformada de Hilbert . . . . . . . 310
4.44. Modelo de un polo de un amplicador operacional realimentado . . . . . . . 312
4.45. Circuito RC pasa bajas . . . . . . . . . . . . . . . . . . . . . . . . . . . 313
4.46. Una onda cuadrada . . . . . . . . . . . . . . . . . . . . . . . . . . . . 314
4.47. Respuesta del circuito RC a una onda cuadrada . . . . . . . . . . . . . . . 315
4.48. Grca de la relacin de los voltajes pico a pico de entrada y salida del circuito RC316
4.49. Respuesta estable para T << . . . . . . . . . . . . . . . . . . . . . . . 317
4.50. Respuesta estable para T >> . . . . . . . . . . . . . . . . . . . . . . . 317
4.51. Seal peridica . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 318
4.52. Circuito . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 319
4.53. Magnitud y fase . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 320
4.54. Rectivador de media onda y pasabajas RC . . . . . . . . . . . . . . . . . 321
4.55. Pasabajs RC con frecuencia de corte 1Hz y entrada con nivel DC . . . . . . . 322
4.56. Seal triangular . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 322
4.57. La convolucin de dos pulsos es un tringulo . . . . . . . . . . . . . . . . 323
4.58. Pasa-altas = identidad - pasabajas . . . . . . . . . . . . . . . . . . . . . 323
4.59. Problema 20 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 323
4.60. La seal mostrada se ltra con el sistema de convolucin . . . . . . . . . . . 324
4.61. Sistema . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 327
4.62. Onda cuadrada . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 328
4.63. Circuito impedancias . . . . . . . . . . . . . . . . . . . . . . . . . . . 330
4.64. Seal de entrada . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 331
4.65. Sistema . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 331
5.1. La funcin 1 + cos . . . . . . . . . . . . . . . . . . . . . . . . . . . . 339
5.2. La magnitud de la funcin 1 + cos . . . . . . . . . . . . . . . . . . . . 340
5.3. La fase de la funcin 1 + cos 2. Como = , la funcin tambin es impar . . 340
5.4. La respuesta impulso de un promedio mvil . . . . . . . . . . . . . . . . 342
5.5. La respuesta impulso de un promedio mvil causal . . . . . . . . . . . . . 343
5.6. En los dos casos se ha sombreado el rea sobre un periodo . . . . . . . . . . 344
5.7. La circunferencia de Fourier para seales discretas . . . . . . . . . . . . . . 345
5.8. Una seal con periodo 2 . . . . . . . . . . . . . . . . . . . . . . . . . . 345
5.9. Una seal discreta, con frecuencia 0 y periodo 1 . . . . . . . . . . . . . . . 346
5.10. Las distancias correspondientes a las variaciones promedio de
las exponenciales complejas e
j
o
n
y e
j
o
n
. . . . . . . . . . . . . . 347
5.11. Pasa bajas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 347
5.12. Pasa altas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 348
5.13. Pasa bandas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 348
5.14. Un sistema de convolucin con respuesta impulso h . . . . . . . . . . . . . 349
5.15. Las representaciones en tiempo y frecuencia de un sistema de convolucin . . 350
5.16. La respuesta impulso de un promedio mvil con ancho de ventana igual a tres . 351
5.17. Magnitud . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 351
5.18. Fase . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 352
5.19. Diagrama de polos y ceros . . . . . . . . . . . . . . . . . . . . . . 354
5.20. Magnitud de H() . . . . . . . . . . . . . . . . . . . . . . . . . . . 354
5.21. Una seal de longitud nita N = 3 . . . . . . . . . . . . . . . . . . . . . 358
5.22. Los trminos r
m
s
im
a ser sumados, para computar u
i
. Note el eje m . . . . . . 362
5.23. Las seales r
n
y s
n
, y las correspondientes extensiones peridicas r
k
y s
2k
,
necesarias para el clculo de u
2
. . . . . . . . . . . . . . . . . . . . . . . 363
5.24. La suma de una seal par y una impar . . . . . . . . . . . . . . . . . . . 366
5.25. La restriccin de una seal discreta a [0, ]. a. es suciente para reconstruir
la transformada en [, ]. b. ya que sta es par y, para cada real. c. ya que es
peridica con periodo 2 . . . . . . . . . . . . . . . . . . . . . . . . . . 368
5.26. Las X
k
s son muestras a escala de S() . . . . . . . . . . . . . . . . . . . 371
5.27. La transformada de una seal continua . . . . . . . . . . . . . . . . . . . 374
5.28. La transformada de la seal muestreada correspondiente . . . . . . . . . . . 374
5.29. Una seal discreta de duracin nita . . . . . . . . . . . . . . . . . . . . 377
5.30. Las seales g
0
senc (t), g
1
senc (t 1) y g
2
senc (t 2) . . . . . . . . . . . . . . 377
5.31. La seal f (t) = g
0
senc (t) + g
1
senc (t 1) + g
2
senc (t 2) . . . . . . . . . . . 378
5.32. Serie de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 380
5.33. Transformada de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . 380
5.34. DTFT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 381
5.35. Suma de Fourier . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 381
5.36. DFT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 381
5.37. Dos seales discretas de longitud nita . . . . . . . . . . . . . . . . . . . 388
5.38. Un ltro de retardo . . . . . . . . . . . . . . . . . . . . . . . . . . . . 390
6.1. Un ltro mediana tiene tres bloques principales: uno que toma segmentos de la
seal de entrada, otro que ordena los datos en los segmentos y otro que toma el
valor ordenado intermedio, o mediana . . . . . . . . . . . . . . . . . . . 405
6.2. La seal s y una versin desplazada

s de sta . . . . . . . . . . . . . . . . 407
6.3. Si la seal de entrada a un sistema invariante se desplaza, la salida se desplaza
en la misma forma. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 408
6.4. Las tres seales mostradas x, y, z para t < , coinciden . . . . . . . . . . . . 409
6.5. La seal impulso discreta (o delta de Kronecker) . . . . . . . . . . . . . . . 419
6.6. Una seal discreta . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 419
6.7. La descomposicinde la seal enla gura 6.6 comouna suma de seales impulso
pesadas y desplazadas. . . . . . . . . . . . . . . . . . . . . . . . . . . 420
6.8. La respuesta impulso de un promedio mvil . . . . . . . . . . . . . . . . 421
6.9. Una seal simple . . . . . . . . . . . . . . . . . . . . . . . . . . . . 422
ndice de cuadros
1. La tabla de una opracin posible entre los elementos de {a, b, c, d} . . . . . . . 20
2. La tabla de una operacin entre los elementos del conjunto nito , , , , . . 21
3. Complete la tabal mostrada e = e
j
20
3 , f = e
j
2
3 , g = e
j
4
3 . . . . . . . . . . . . 22
4. La tabla de los cuaterniones . . . . . . . . . . . . . . . . . . . . . . . . 23
1.1. Integrales . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 161
2.1. La seal g
2k
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 175
4.1. Relacin natural . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 297
440

Libro Señales

Загружено:

Сведения о документе

Авторское право

Доступные форматы

Поделиться этим документом

Поделиться или встроить документ

Параметры публикации

Этот документ был вам полезен?

Это неприемлемый материал?

Авторское право:

Доступные форматы

Libro Señales

Загружено:

Авторское право:

Доступные форматы

Fundamentos de la Teora de

Aunque los nmeros enteros se pueden contar, no se pueden contar man-

2; amarillo = 0+ j; citrino= (1+j)/

2; azul = 0 - j; violeta = (1j)/

0.10.4. Promedio y mediana en S

2 + 11i es de la forma 2+ni y

y est dado por: z

(que tambin se conoce como la norma regular N(x) de x)

u. Note que tanto

. Por lo tanto [0, ] (ya que el nmero

est a la misma distancia del origenque e. Adems, comose puede vericar,

de lo que se concluye que se tiene un anillo de divisin.

(x)) y, por lo tanto, con t = x + h, x = t

es diferenciable o no. Explique.

(x) en [a, b], entonces,

(x) en donde la integral a la derecha es una integral de Riemann.

f (z)d, para diferentes valores enteros de n.

h(x)G(x)dx donde H es la transformada de h y G la de g.

dada por g [(g) = (G)

f (t)1dt y vemos que el ncleo

f (t)dt, que, como vemos, tiene ncleo la funcin

d = jsgnt, donde sgn es la

0.18. CLCULO 129

. Calcule el lmite cuando a R

es tambin un cuaternio puro.

Ejercicio. Muestre que efectivamente se tiene una norma.

El conjunto de las seales discretas con normal l-2 nita se denota l

. La norma L- de una seal continua

Similarmente, si r es una seal discreta, su norma l-est dada por:

cumplenla desigualdaddel tringulo:

(t) + Rs(t) (2.1)

e(t )dg() (2.2)

(t) + [R/L]s(t) (2.3)

(t) + [R/L]s(t) (2.4)

e(t )dg(); mientras que la convolucin estndar s, de e y h, est dada

= h, la convolucin de Stieltjes se puede

()d + sen(t 0)[g(0

()d + sen(t 1)[g(1

2 cos(t /4) cos(t 1)

g()du(t ) = u()g() u()g()

, con la posible excepcin de un conjunto nito

(t). Con gran generalidad, si la salida correspondiente a la entrada e es s,

g()de(t ), cambio de variable

g(t )de(), como g() = e() = 0

2) no es peridica. O, en caso con-

que podemos ver como el lmite de una suma de Riemann,

. En la seccin 4.7, extendere-

1] 0 usando el teorema de la convergencia dominada de Lebesgue, e

de s est dada por,

vii) (Modulacin.) Si la transformada de s(t) es S(), entonces la transformada

(t). Encuentre y graque las

(t), entonces s(t) tiene transformada S() =

(t) = r(t) y R() = S

(), y se tiene que,

( t)d y la correlacin de sus transformadas

dg() es un nmero complejo, que depende de

dg(t), donde g es la respuesta escaln del sistema.

h(x)G(x)dx donde H es la transformada de h, y G la de

f (t)dt, que como vemos, tiene ncleo la funcin

d = jsgn(t), donde sgn es la funcin

() TX() par y 0X() impar.

) es B y que a la entrada se aplica la seal i(t) = B + (A B)u(t); as,

dsea cuidadoso con

(t) y es conjugada antisimtrica si f (t) = f