Music and mathematics

Music theorists sometimes use mathematics to understand music. Mathematics is "the basis of
sound" and sound itself "in its musical aspects... exhibits a remarkable array of number
properties", simply because nature itself "is amazingly mathematical".
[1]
Though ancient hinese,
!gyptians and Mesopotamians are kno"n to ha#e studied the mathematical principles of sound,
[$]
the %ythagoreans of ancient &reece are the first researchers kno"n to ha#e in#estigated the
expression of musical scales in terms of numerical ratios,
[']
particularly the ratios of small
integers. Their central doctrine "as that "all nature consists of harmony arising out of numbers".
[(]
)rom the time of %lato, harmony "as considered a fundamental branch of physics, no" kno"n
as musical acoustics. !arly *ndian and hinese theorists sho" similar approaches+ all sought to
sho" that the mathematical la"s of harmonics and rhythms "ere fundamental not only to our
understanding of the "orld but to human "ell,being.
[-]
onfucius, like %ythagoras, regarded the
small numbers 1,$,',( as the source of all perfection.
[.]
To this day mathematics has more to do "ith acoustics than "ith composition, and the use of
mathematics in composition is historically limited to the simplest operations of counting and
measuring.
[citation needed]
The attempt to structure and communicate ne" "ays of composing and
hearing music has led to musical applications of set theory, abstract algebra and number theory.
/ome composers ha#e incorporated the golden ratio and )ibonacci numbers into their "ork.
[0][1]
Time, rhythm and meter
2ithout the boundaries of rhythmic structure 3 a fundamental e4ual and regular arrangement of
pulse repetiti#ity, accent, phrase and duration 3 music "ould be impossible.
[5]
*n 6ld !nglish the
"ord "rhyme", deri#ed from "rhythm", became associated and confused "ith rim 3 "number"
[17]

3 and modern musical use of terms like meter and measure also reflects the historical importance
of music, along "ith astronomy, in the de#elopment of counting, arithmetic and the exact
measurement of time and periodicity that is fundamental to physics.
Musical form
Musical form is the plan by "hich a short piece of music is extended. The term "plan" is also
used in architecture, to "hich musical form is often compared. 8ike the architect, the composer
must take into account the function for "hich the "ork is intended and the means a#ailable,
practicing economy and making use of repetition and order.
[11]
The common types of form kno"n
as binary and ternary 9"t"ofold" and "threefold": once again demonstrate the importance of
small integral #alues to the intelligibility and appeal of music.
Frequency and harmony
; musical scale is a discrete set of pitches used in making or describing music. The most
important scale in the 2estern tradition is the diatonic scale but many others ha#e been used and
proposed in #arious historical eras and parts of the "orld. !ach pitch corresponds to a particular
fre4uency, expressed in hertz 9<z:, sometimes referred to as cycles per second 9c.p.s.:. ; scale
has an inter#al of repetition, normally the octa#e. The octa#e of any pitch refers to a fre4uency
exactly t"ice that of the gi#en pitch. /ucceeding superocta#es are pitches found at fre4uencies
four, eight, sixteen times, and so on, of the fundamental fre4uency. %itches at fre4uencies of half,
a 4uarter, an eighth and so on of the fundamental are called subocta#es. There is no case in
musical harmony "here, if a gi#en pitch be considered accordant, that its octa#es are considered
other"ise. Therefore any note and its octa#es "ill generally be found similarly named in musical
systems 9e.g. all "ill be called doh or A or Sa, as the case may be:. 2hen expressed as a
fre4uency band"idth an octa#e A2A3 spans from 117 <z to $$7 <z 9span=117 <z:. The next
octa#e "ill span from $$7 <z to ((7 <z 9span=$$7 <z:. The third octa#e spans from ((7 <z to
117 <z 9span=((7 <z: and so on. !ach successi#e octa#e spans t"ice the fre4uency range of the
pre#ious octa#e.
>ecause "e are often interested in the relations or ratios bet"een the pitches 9kno"n as inter#als:
rather than the precise pitches themsel#es in describing a scale, it is usual to refer to all the scale
pitches in terms of their ratio from a particular pitch, "hich is gi#en the #alue of one 9often
"ritten 1/1:, generally a note "hich functions as the tonic of the scale. )or inter#al size
comparison cents are often used.
Tuning systems
-,limit tuning, the most common form of ?ust intonation, is a system of tuning using tones that
are regular number harmonics of a single fundamental fre4uency. This "as one of the scales
@ohannes Aepler presented in his <armonice Mundi 91.15: in connection "ith planetary motion.
The same scale "as gi#en in transposed form by ;lexander Malcolm in 10$1 and by theorist
@ose 2uerschmidt in the $7th century. ; form of it is used in the music of northern *ndia.
;merican composer Terry Biley also made use of the in#erted form of it in his "<arp of Ce"
;lbion". @ust intonation gi#es superior results "hen there is little or no chord progression+ #oices
and other instruments gra#itate to ?ust intonation "hene#er possible. <o"e#er, as it gi#es t"o
different "hole tone inter#als 95+1 and 17+5: a keyboard instrument so tuned cannot change key.
[1$]
To calculate the fre4uency of a note in a scale gi#en in terms of ratios, the fre4uency ratio is
multiplied by the tonic fre4uency. )or instance, "ith a tonic of ;( 9; natural abo#e middle :,
the fre4uency is ((7 <z, and a ?ustly tuned fifth abo#e it 9!-: is simply ((7D9'+$: = ..7 <z.
%ythagorean tuning is tuning based only on the perfect consonances, the 9perfect: octa#e, perfect
fifth, and perfect fourth. Thus the ma?or third is considered not a third but a ditone, literally "t"o
tones", and is 95+1:
$
= 11+.(, rather than the independent and harmonic ?ust -+( = 17+.( directly
belo". ; "hole tone is a secondary inter#al, being deri#ed from t"o perfect fifths, 9'+$:
$
= 5+1.
The ?ust ma?or third, -+( and minor third, .+-, are a syntonic comma, 11+17, apart from their
%ythagorean e4ui#alents 11+.( and '$+$0 respecti#ely. ;ccording to arl Eahlhaus 91557,
p. 110:, "the dependent third conforms to the %ythagorean, the independent third to the harmonic
tuning of inter#als."
2estern common practice music usually cannot be played in ?ust intonation but re4uires a
systematically tempered scale. The tempering can in#ol#e either the irregularities of "ell
temperament or be constructed as a regular temperament, either some form of e4ual temperament
or some other regular meantone, but in all cases "ill in#ol#e the fundamental features of
meantone temperament. )or example, the root of chord ii, if tuned to a fifth abo#e the dominant,
"ould be a ma?or "hole tone 95+1: abo#e the tonic. *f tuned a ?ust minor third 9.+-: belo" a ?ust
subdominant degree of (+', ho"e#er, the inter#al from the tonic "ould e4ual a minor "hole tone
917+5:. Meantone temperament reduces the difference bet"een 5+1 and 17+5. Their ratio, 95+1:F
917+5: = 11+17, is treated as a unison. The inter#al 11+17, called the syntonic comma or comma
of Eidymus, is the key comma of meantone temperament.
*n e4ual temperament, the octa#e is di#ided into t"el#e e4ual parts, each semitone 9half,step: is
an inter#al of the t"elfth root of t"o so that t"el#e of these e4ual half steps add up to exactly an
octa#e. 2ith fretted instruments it is #ery useful to use e4ual temperament so that the frets align
e#enly across the strings. *n the !uropean music tradition, e4ual temperament "as used for lute
and guitar music far earlier than for other instruments, such as musical keyboards. >ecause of
this historical force, t"el#e,tone e4ual temperament is no" the dominant intonation system in
the 2estern, and much of the non,2estern, "orld.
!4ually,tempered scales ha#e been used and instruments built using #arious other numbers of
e4ual inter#als. The 15 e4ual temperament, first proposed and used by &uillaume osteley in the
1.th century, uses 15 e4ually spaced tones, offering better ma?or thirds and far better minor
thirds than normal 1$,semitone e4ual temperament at the cost of a flatter fifth. The o#erall effect
is one of greater consonance. $( e4ual temperament, "ith $( e4ually spaced tones, is "idespread
in the pedagogy and notation of ;rabic music. <o"e#er, in theory and practice, the intonation of
;rabic music conforms to rational ratios, as opposed to the irrational ratios of e4ually,tempered
systems. 2hile any analog to the e4ually,tempered 4uarter tone is entirely absent from ;rabic
intonation systems, analogs to a three,4uarter tone, or neutral second, fre4uently occur. These
neutral seconds, ho"e#er, #ary slightly in their ratios dependent on ma4am, as "ell as
geography. *ndeed, ;rabic music historian <abib <assan Touma has "ritten that "the breadth of
de#iation of this musical step is a crucial ingredient in the peculiar fla#or of ;rabian music. To
temper the scale by di#iding the octa#e into t"enty,four 4uarter,tones of e4ual size "ould be to
surrender one of the most characteristic elements of this musical culture."
[1']
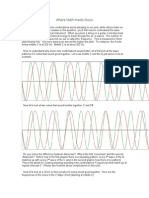
The follo"ing graph re#eals ho" accurately #arious e4ual,tempered scales approximate three
important harmonic identities+ the ma?or third 9-th harmonic:, the perfect fifth 9'rd harmonic:,
and the "harmonic se#enth" 90th harmonic:. [Cote+ the numbers abo#e the bars designate the
e4ual,tempered scale 9i.e., "1$" designates the 1$,tone e4ual,tempered scale, etc.:]
>elo" are 6gg Gorbis files demonstrating the difference bet"een ?ust intonation and e4ual
temperament. Hou may need to play the samples se#eral times before you can pick the
difference.
T"o sine "a#es played consecuti#ely 3 this sample has half,step at --7 <z 9 in
the ?ust intonation scale:, follo"ed by a half,step at --(.'0 <z 9 in the e4ual temperament
scale:.
/ame t"o notes, set against an ;((7 pedal 3 this sample consists of a "dyad". The
lo"er note is a constant ; 9((7 <z in either scale:, the upper note is a in the e4ual,tempered
scale for the first 1", and a in the ?ust intonation scale for the last 1". %hase differences make
it easier to pick the transition than in the pre#ious sample.
Connections to set theory
Main article+ /et theory 9music:
Musical set theory uses some of the concepts from mathematical set theory to organize musical
ob?ects and describe their relationships. To analyze the structure of a piece of 9typically atonal:
music using musical set theory, one usually starts "ith a set of tones, "hich could form moti#es
or chords. >y applying simple operations such as transposition and in#ersion, one can disco#er
deep structures in the music. 6perations such as transposition and in#ersion are called isometries
because they preser#e the inter#als bet"een tones in a set.
Connections to abstract algebra
Main article+ ;bstract algebra
!xpanding on the methods of musical set theory, some theorists ha#e used abstract algebra to
analyze music. )or example, the notes in an e4ual temperament octa#e form an abelian group
"ith 1$ elements. *t is possible to describe ?ust intonation in terms of a free abelian group.
[1(]
Transformational theory is a branch of music theory de#eloped by Ea#id 8e"in. The theory
allo"s for great generality because it emphasizes transformations bet"een musical ob?ects, rather
than the musical ob?ects themsel#es.
Theorists ha#e also proposed musical applications of more sophisticated algebraic concepts.
Mathematician &uerino Mazzola has applied topos theory to music,
[citation needed]
though the result
has been contro#ersial.
[citation needed]
The chromatic scale has a free and transiti#e action of the cyclic group , "ith the action
being defined #ia transposition of notes. /o the chromatic scale can be thought of as a torsor for
the group .
The golden ratio and Fibonacci numbers
@ames Tenney reconcei#ed his piece ")or ;nn 9Bising:", "hich consists of up to t"el#e
computer,generated tones that glissando up"ards 9see /hepard tone:, as ha#ing each tone start so
each is the golden ratio 9in bet"een an e4ual,tempered minor and ma?or sixth: belo" the
pre#ious tone, so that the combination tones produced by all consecuti#e tones are a lo"er or
higher pitch already, or soon to be, produced.
[citation needed]
!rnI 8end#aJ analyzes >Kla >artLkMs "orks as being based on t"o opposing systems+ those of
the golden ratio and the acoustic scale. *n >artokMs Music for Strings, Percussion, and Celesta,
the xylophone progression at the beginning of the 'rd mo#ement occurs at the inter#als
1+$+'+-+1+-+'+$+1. )rench composer !rik /atie used the golden ratio in se#eral of his pieces,
including Sonneries de la Rose Croix.
[citation needed]
The golden ratio is also apparent in the organization of the sections in the music of EebussyMs
Image, "Reflections in Water", in "hich the se4uence of keys is marked out by the inter#als '(,
$1, 1', and 1 9a descending )ibonacci se4uence:, and the main climax sits at the N position.
"%relude to the ;fternoon of a )aun" also reaches a climax point, marked by the entrance of the
anti4ue cymbal, at the N position.
[citation needed]
Many of the important musical e#ents in Arzysztof %endereckiMs "Threnody for the Gictims of
<iroshima" occur at N positions.
[citation needed]
>oards of anada ha#e discussed using the golden ratio and )ibonacci numbers in their "ork.
[1-]

/ong titles such as "Music is Math", and numerous songs featuring samples of people counting
or discussing numbers, also illustrate the influence of mathematics on their music.
[citation needed]