Chat. I.

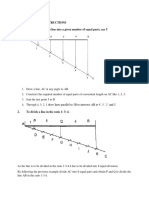
CONIC SECTIONS.
315
1099. Theorem TV. Tlie radius vector is equal to the sum
of
the distajices betwcsn the focux
and the vertex, and between the ordinate and the vertex. {Fig. 44G.)
That is,
For
Therefore
Eut, hy Cor. Theor. II.,
Therefore, by addition,
FM = AP+ AF.
FP = AP-AF;
FP'i=AP--:^APx AF+ AF^.
PM-= P X AP= 4AF X AP.
FPi + PM'^ ^ AP- + 2 A F X AP
+ AV
-'.
But bv the right-angled tringles, FP- + PM2 = FM'^
;
And therefore FM^ = A
Pa
+ 2 A F x A P + A F-.
Hence, extracting the roots, FM = A P + AF =2 AF + FP
;
Or by making A G = A F, FM =
G
P.
Coroll. 1. If through the point G
{fg.
447.) the line GQ be drawn perpendicular la
the axis, it is called the directrix of the parabola.
By the property shown in this theorem, it ajjpears that if any line QM be drawn parallel
to the axis, and if FM be joined, the straight line FM is equal to QM
;
for QM is eipial
to GP.
Coroll. 2. Hence, also, the curve is easily described by points. Take AG ecpial to A F,
{fig.
447.), and draw a number of lines M, INI perpendicular to tlie axis AP
;
then with the
distances GP, GP, &c. as radii, and from F
as a centre, describe arcs on each side of A P,
cutting the lines MiM, WM, &.c. at MIM,&c.
;
then through all the points jM, M, jM, &c.
draw a curve, which will be a parabola.
1 100. Theohem V.
//"
a tangent be drawn
from the vertex
of
an ordinate to meet the axis
jiroduced, the subtangent PT
(_^^.
448.) will
lie equal to twice the distance
of
the ordinate
Fid. 4i7. FiK. 418.
from tlie vertex.
If JIT be a tangent at I\I, the extremity of the ordinate PM
;
then the sub-tangent PI
is e(jual to twice A P. For draw MK parallel to All,
KM : KI::GK::P;
KM : KI::PT : PM.
P : PM::GK : PT;
P : PM::PM : AP.
AP : PT::PM : GK.
Then, by Theor. II.,
And as MKI, TPIM are similar.
Therefore, by equality.
And by Cor. Theor. 1.,
Therefore, by equality,
But when the ordinates HI and PM coincide, MT will become a tangent, and GK 'vill
become ecjual to twice PM.
Therefore AP : PT::PM : 2PM, or
PT=2AP.
From this property is obtained an easy and accurate method of drawing a tangent ;o any
point of the curve of a parabola. Thus, let it be re-
.^
r
((uired to draw a tangent to any point M in the curve. A
Produce PA to T
{fg.
449.), and draw MP perpendi- /
cular to PT, meeting AP in the point P. Make AT
/ |
ecpial to AP, and join MT, which will be the tangent
re(]uired.
1101. Theorem VI. The radius vector is equal to
the distance between the focus and the intersection
of
a
tangent at the vertex
of
an ordinate and the axis pro-
duced.
FiK.410. Fig. l.',0.
Produce PA to T
{fig.
450.), and let MT be a tangent at M ; then will FT= FM.
For FT=AF+AT;
But, by last theorem, A P= AT
;
Therefore FT= A F + A P.
But, by Theorem III., FM = AF+ AP;
Therefore, by equality,' FIM = FT.
Coroll. 1. If MN be drawn perpendicular to MT to meet the axis in N, then will
FN=FM= FT. For draw FH perpendicular to M T, and it also bisects MT, because
F.AI=FT; and since HF and MN are parallel, and MTis bisected in II, the line TN will
also be bisected in F. It therefore follows that FN= FM= FT.
Coroll. 2. The subnormal PN is a constant quantity, and it is ecjual to half the para-
meter, or to 2AF. For since TMN is a right angle,
Therefore 2AP or TP : P]\I
: : PM
; PN.
But, by the dclinition oF parameter, AP : PM::PM ; I';
Therefore PN = iP