Академический Документы
Профессиональный Документы
Культура Документы
MCAT Prep Physics Equation Sheet
Загружено:
Chris_Barber09Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
MCAT Prep Physics Equation Sheet
Загружено:
Chris_Barber09Авторское право:
Доступные форматы
MCAT Physics Equation Sheet
Weve helped over 50,000 students get better grades since 1999!
!"#$%&'() &( +'%&'(
Average speed
t
d
v =
d = distance, t = time
Average velocity
t
x
v
A
A
=
x = displacement, t = elapsed time
Average acceleration
t
v
a
A
A
=
v = change in velocity, t = elapsed
time
Linear motion kinematics 1-D
(constant acceleration a)
) 0 ( 2
) ( 2
0
2
0
2
2
2
1
0 0
0
velocity from fall Free gh v
x x a v v
at t v x x
at v v
=
+ =
+ + =
+ =
To apply in two dimensions, the easiest
way is to choose an x-y coordinate
system so that the direction of the
acceleration is entirely along either the x
or the y direction. This greatly simplifies
things as the acceleration in the other
coordinate direction will have a
component of 0 and the motion in that
other direction will have constant
velocity. The components of motion in
the x and y directions are analyzed
separately.
Vector components
u cos v v
x
=
,
2 2
y x
v v v + =
u sin v v
y
=
,
x
y
v
v
= u tan
For a vector of magnitude v making an
angle u with the x-axis
Centripetal acceleration
R
v
a
R
2
=
Centripetal acceleration a
R
is toward the
center of the circle of radius r for an
object traveling with constant speed v
,'-.!) $(/ %'-"#!
Newtons first law of
motion (Equilibrium)
ckwise counterclo clockwise
F
t t =
= 0
At equilibrium, every body continues in its state
of rest or of uniform speed as long as no net
force and no net torque act on it.
Newtons second law of
motion (Dynamics)
ma F =
The acceleration a of an object is directly
proportional to the net force acting on it and is
inversely proportional to its mass. The direction
of the acceleration is in the direction of the net
force action the object.
Newtons third law of
motion
Whenever one object exerts a force on a
second object, the second exerts an equal and
opposite force on the first.
Force of static friction
N s fr
F F s
Opposes any impending relative motion
between two surfaces, where the magnitude
can assume any value up to a maximum of
s
F
N
where
s
is the coefficient of static friction and
F
N
is the magnitude of the normal force.
Force of kinetic friction
N k fr
F F =
Force between two surfaces sliding against one
another that opposes the relative motion of the
two surfaces, where
k
is the coefficient of
kinetic friction.
Force of gravity between
any two objects
The force F
G
between two objects of masses m
1
and m
2
and separated by a distance r. The
value of the universal gravitation constant is:
2
2 1
r
m m
G F
G
=
G = 6.67!10
-11
Nm
2
/kg
2
Inclined Planes
u
u
cos
sin
mg F
mg F
normal
incline
=
=
u is the angle between the inclined plane and
the horizontal surface
Hookes Law
x k F A =
The further a spring is stretched, the more force
it pulls back with.
Torque
Fl = t
Torque, which can be roughly thought of as a
twisting force, is proportional to the force
applied and the lever arm length.
0'-1 $(/ !(!-23
Work done by a constant
force
u cos Fd W =
Work W done by a constant force of
magnitude F on an object as it is displaced by
a distance d. The angle between the directions
of F and d is u .
Work is positive if the object is displaced in the
direction of the force and negative if it is
displaced against the force. The work is zero if
the displacement is perpendicular to the
direction of the force.
Kinetic energy
2
2
1
mv K =
Kinetic energy K for a mass m traveling at a
speed v.
Gravitational potential
energy
) (
) (
general
r
GMm
U
local mgh U
=
=
Potential energy U is the energy that an object
of mass m has by virtue of its position relative
to the surface of the earth. That position is
measured by the height h of the object relative
to an arbitrary zero level.
Conservative forces
- Gravitational force
- Elastic spring
force
- Electric force
Non-conservative forces
- Frictional forces
- Air resistance
- Tension
- Normal force
- Propulsion of a
motor
A force is conservative if either:
- The work done by the force on an
object moving from one point to
another depends only on the initial
and final positions and is
independent of the particular path
taken.
- The net work done by the force on
an object moving around any
closed path is zero
Conservation of
Mechanical Energy (Only
holds true if non-conservative
forces are ignored)
1 2
E E =
1 1 2 2
U K U K + = +
The total mechanical energy of a system,
remains constant as the object moves,
provided that the net work done by external
non-conservative forces (such as friction and
air resistance) is zero.
Work-energy Theorem
i nc
E U K W A + A + A =
The work due to non-conservative forces W
nc
is equal to the change in kinetic energy AK
plus the change in gravitational potential
energy AU plus any changes in internal energy
due to friction.
Rest Mass Energy
2
mc E =
The energy inherent to a particle by nature of it
having a mass.
www.prep101.com
Need help for exams?
Check out our classroom prep sessions - customized to your exact course - at www.prep101.com
Our Course Booklets - free at prep sessions - are the Perfect Study Guides.
Power
Fv
t
W
P = =
Power P is defined as the rate at which work is
done. It can also be expressed in terms of the
force F being applied to the object traveling at
a speed v. It is more correct to express this
version of the relationship as
u cos Fv P =
where u is the angle between F and v.
+'+!(%#+
Linear momentum:
mv p =
v m p
=
Linear momentum p is the product of an
objects mass m and velocity v. Linear
momentum is a vector that points in the
same direction of the velocity.
Principle of conservation of
linear momentum:
1 2
P P
=
The total linear momentum of an isolated
system remains constant.
Impulse-momentum theorem:
t F p = A
t F p p
net
A =
1 2
An impulse produces a change in an
objects momentum. Impulse is given by
the product of average force F
(F) and
the time interval t (t) over which the force
is applied. Impulse is a vector that points
in the same direction as the average force.
Elastic collisions:
- Bodies do not stick
together
- Kinetic energy is
conserved
- Momentum is
conserved
Inelastic collisions:
- Bodies stick together if
completely inelastic
- Kinetic energy is not
conserved
- Momentum is
conserved
A completely inelastic collision is one in
which the bodies stick together completely
after the collision.
In inelastic collisions, kinetic energy is not
conserved as some of the initial kinetic
energy is converted into other forms of
energy such as thermal and sound energy.
Center of Mass (CM or CofM)
total
i i
n
i
cm
M
x m
x
1 =
=
For two bodies:
2 1
2 2 1 1
m m
x m x m
x
cm
+
+
=
The center of mass is a point that
represents the average location for the
total mass of the system.
In a collision, the velocity of the center of
mass of all the colliding objects remains
constant.
,4#&/) $(/ )'4&/)
Density
V
m
=
Density of a liquid at rest. Density can also be
measured relative to water, which is termed
specific gravity. A specific gravity > 1 means the
liquid is more dense than water, A specific gravity
< 1 means the liquid is less dense than water
Pressure
) ( definition general
A
F
P =
Hydrostatic pressure at
a fixed depth
The hydrostatic pressure on a fluid volume is
dependent on its depth, and is equal in all
directions.
gy P =
Buoyant Force
Vg F
buoyant
=
The buoyant force on an object in fluid is upward
and equal to the weight of the fluid that the object
displaces.
Continuity Equation
Av Q =
The volume flow rate of a fluid is proportional to
the cross-sectional area of the pipe and the
velocity of the fluid. Q
in
must be equal to Q
out
.
Bernoullis Equation
constan
2
1
2
= + + v gy p
One way to remember the Bernoulli equation is to
think of it as an energy conservation equation.
The three terms roughly correspond to pressure
energy, potential energy, and kinetic energy,
respectively.
Elastic modulus of a
solid
Strain
Stress
Modulus =
A high modulus material is hard and rigid.
Examples are metal and ceramic. A low modulus
material is elastic, like rubber.
0$5!) $(/ 6!-&'/&. +'%&'(
Wave Velocity
f v =
The velocity of a wave is the product of its
frequency and wavelength.
Wave Period
f
T
1
=
Sound decibels
o
I
I
log 10 = |
A difference of 10 in decibels corresponds to
sound intensity levels that differ by a factor of 10.
For example, 90dB is 10 times as loud as 80dB.
Standing Waves
Both ends fixed or free
,...) 3 , 2 , 1 (
2
= = n
n
L
n
One end fixed one end
free
,...) 5 , 3 , 1 (
4
= = n
n
L
n
When a standing wave is formed on a piece of
string, the string length is some fractional multiple
of the standing wave wavelength. Depending on
how the string is fixed, each end can be a node
or an anti-node.
Beat frequency
2 1
f f f
beat
=
When two waves of constant amplitude but
different frequencies interfere with each other,
the resulting waves amplitude is confined to an
envelope with some periodicity. The frequency of
the envelope is the beat frequency and can be
heard as distinct beats because of the amplitude
variation with time.
Doppler effect
c
v
f
f
s
=
A
c
v
s
=
A
The apparent frequency of the source is
increased as the source approaches the
observer, and is decreased as the sources
leaves the observer.
!4!.%-')%$%&.) $(/ +$2(!%&)+
Bolztmanns constant k and has a value of: k = 9.0!10
9
Nm/C
2
Coulombs law (electric
force)
2
2 1
r
Q Q
k F =
The magnitude of the force F between two
charges (Q
1
and Q
2
) in terms of the distance r
between the two charges. The direction of the
force is directed along the line between the two
forces. This force is repulsive if the two charges
are both positive or both negative, and attractive
www.prep101.com
Need help for exams?
Check out our classroom prep sessions - customized to your exact course - at www.prep101.com
Our Course Booklets - free at prep sessions - are the Perfect Study Guides.
if the one charge is positive and the other
negative.
Electric field due to a
point charge q at a
distance r
2
r
Q
k E =
E is a vector and points away from a positive
charge and toward a negative charge.
Electric potential energy
r
Q Q
k U
2 1
=
The potential energy stored between the
interaction between two point charges.
Electric potential
r
Q
k V =
The electric potential V due to a point charge q
at a distance r away from the charge.
In constant electric fields
E q F
= qEd U =
Ed V = Vq U =
Note that the force F is in the same direction as
the electric field E if the charge q is positive and
in the opposite direction if the charge is
negative.
The energy gained by some charge in a field is
simply force times the distance traveled.
Potential is the energy per unit charge.
Force on a charge moving
in a magnetic field
B v q F
=
u sin qvB F =
A charge q moving in a magnetic field B
with
a velocity v
experiences a force F
. The
magnitude of this force can also be expressed
in terms of the angle u between v
and B
.
!4!.%-'(&. .&-.#&%)
Ohms law
IR V =
The potential difference V across a device
is given by its resistance R and the current I
that flows through it
Resistance of a wire
A
L
R =
The resistance R of a length L of wire with a
cross-sectional area A and resistivity .
Resistivity has units Om.
Electric power
R
V
R I IV P
2
2
= = =
With help from Ohms law, electric power P
can be calculated using any combination of
two of the following quantities: resistance R,
voltage V or current I
RMS voltage and current (AC
circuits)
2
2
0
0
I
I
V
V
rms
rms
=
=
The root-mean-square values can be
calculated from the peak values (V
0
and I
0
)
and are used to calculate the average
power P in AC circuits:
R
V
R I P
rms
rms
2
2
= =
Resistances in series
2 1
R R R
eq
+ =
For more than two resistances in series:
...
4 3 2 1
+ + + + = R R R R R
eq
Resistances in parallel
2 1
1 1 1
R R R
eq
+ =
For more than two resistances in parallel:
...
1 1 1 1 1
4 3 2 1
+ + + + =
R R R R R
eq
Capacitance
V
Q
C =
A higher capacitance capacitor can store
more charge at the same voltage.
Capacitors in series C
S
and
parallel C
P
2 1
1 1 1
C C C
S
+ =
2 1
C C C
P
+ =
For more than two capacitors:
...
1 1 1 1 1
4 3 2 1
+ + + + =
C C C C C
S
...
4 3 2 1
+ + + + = C C C C C
P
Electric energy stored by a
capacitor
C
Q
QV CV U
E
2
2
1
2
1
2
2
1
= = =
Amount of electric energy stored in a
capacitor is given in terms of the
capacitance C and the potential difference
between the conductors V.
4&27% $(/ 2!'+!%-&.$4 '6%&.)
Snells law
2 2 1 1
sin sin u u n n =
The angle of incidence u
1
is with respect to
the perpendicular of the surface between the
two media (with indices of refraction n
1
and
n
2
). The angle of refraction u
2
is also with
respect to the perpendicular.
Total internal reflection
1
2
sin
n
n
c
= u
The critical angle u
c
is the angle of incidence
beyond which total internal reflection occurs.
The index of refraction for the medium in
which the incident ray is traveling is n
1
Energy of one photon
hf E =
The energy of light is dependent on its
frequency. H is the planck constant
6.626068 ! 10
-34
m
2
kg / s
Index of refraction
v
c
n =
The higher the index of refraction is for a
medium, the slower is the speed of light in
that medium.
The lens equation
f d d
i o
1 1 1
= +
The focal length of the lens f is:
- Positive for a converging lens
- Negative for a diverging lens
The object distance d
o
is:
- Positive if it is on the side of the
lens from which the light is coming
- Negative if on the opposite side
The image distance d
i
is:
- Positive if it is on the opposite side
of the lens from which the light is
coming
- Negative if on the same side
Lateral magnification
o
i
o
i
d
d
h
h
m = =
For an upright image, the magnification m is
positive and for an inverted image m is
negative.
Power of a lens
f
P
1
=
Focal length of a spherical
mirror
r f
2
1
=
For a spherical mirror, the focal length is half
of the radius of curvature.
Вам также может понравиться
- MCAT Physics Formula SheetДокумент3 страницыMCAT Physics Formula Sheetemma_reese100% (2)
- MCAT Formula Sheet Cheat SheetДокумент2 страницыMCAT Formula Sheet Cheat Sheetdjanisz2100% (3)
- MCAT Math PortionMCATДокумент22 страницыMCAT Math PortionMCATwbowen92888100% (1)
- MCAT ShortcutsДокумент12 страницMCAT ShortcutsShafqat Shakeel100% (2)
- MCAT Biology Complete OutlinesДокумент34 страницыMCAT Biology Complete OutlinesJacob Mikhail90% (10)
- Testing Solutions Section Bank Notes V1.8Документ85 страницTesting Solutions Section Bank Notes V1.8megОценок пока нет
- MCAT CoverageДокумент10 страницMCAT Coveragecapt_zoe100% (1)
- Practice MCAT Test 1Документ42 страницыPractice MCAT Test 1Rowena Concepcion Penafiel64% (11)
- MCAT Exam Strategy EbookДокумент32 страницыMCAT Exam Strategy EbookMary PОценок пока нет
- 500 Review Questions For The MCAT Behavioral SciencesДокумент177 страниц500 Review Questions For The MCAT Behavioral Sciencesimperiouxx100% (5)
- MCAT Organic Summary SheetДокумент6 страницMCAT Organic Summary SheetSpencer Thomas100% (2)
- 16 - MCAT G-Chem Formula SheetДокумент2 страницы16 - MCAT G-Chem Formula SheetNathan Korean Kim100% (7)
- MCAT - BiologyДокумент15 страницMCAT - BiologyEmily Teo100% (1)
- MCAT Review Biology Notes (Full 1)Документ30 страницMCAT Review Biology Notes (Full 1)Chris_Barber09100% (2)
- MCAT Crash CourseДокумент15 страницMCAT Crash CourseDe ShepОценок пока нет
- Mnemonics For The MCATДокумент11 страницMnemonics For The MCATsujsam100% (2)
- Examkrackers 1001 Questions in MCAT ChemistryДокумент2 страницыExamkrackers 1001 Questions in MCAT Chemistrysahil Jairamani0% (2)
- Khan Academy Notes - Psych and Sociology For MCATДокумент238 страницKhan Academy Notes - Psych and Sociology For MCATJuan100% (1)
- SB Notes Master Version 2.0Документ156 страницSB Notes Master Version 2.0anamargarita1962388Оценок пока нет
- MCAT Physics Reference NotesДокумент16 страницMCAT Physics Reference NotesChris_Barber09100% (1)
- Next-Step MCAT OutlineДокумент24 страницыNext-Step MCAT OutlineSage NorrieОценок пока нет
- Jack Westin MCAT Content BiochemistryДокумент52 страницыJack Westin MCAT Content BiochemistryLora100% (2)
- 1 MCAT Leah4scimcatcheatsheetcollection2017Документ50 страниц1 MCAT Leah4scimcatcheatsheetcollection2017JD Ampaya100% (2)
- MCAT MnemonicsДокумент14 страницMCAT Mnemonicskmulqs100% (1)
- Formulas For The MCAT: General ChemistryДокумент1 страницаFormulas For The MCAT: General Chemistrymissee728Оценок пока нет
- Atoms Molecules Quantum MechanicsДокумент20 страницAtoms Molecules Quantum Mechanicsrvar839100% (3)
- MCAT Prep Organic Equation SheetДокумент6 страницMCAT Prep Organic Equation SheetChris_Barber09Оценок пока нет
- Berkeley Review MCAT Prep ChemistryДокумент356 страницBerkeley Review MCAT Prep Chemistrydavidbvides50% (2)
- How To Destroy The MCAT With Minimal Study TimeДокумент11 страницHow To Destroy The MCAT With Minimal Study TimeKristin SmithОценок пока нет
- MCAT Physics Review: Key Concepts and Paradigms for Solving ProblemsДокумент46 страницMCAT Physics Review: Key Concepts and Paradigms for Solving Problemsdana milstein100% (1)
- Menus SaludablesДокумент364 страницыMenus SaludablesEnerolisa Paredes89% (9)
- MCAT Physics Equations SheetДокумент4 страницыMCAT Physics Equations SheetAshley ShanaéОценок пока нет
- Aamc 8Документ58 страницAamc 8TravanL.Hurst100% (1)
- (The Berkeley Review) The Berkeley Review MCAT GenДокумент324 страницы(The Berkeley Review) The Berkeley Review MCAT GenSara El100% (3)
- General Chemistry MCAT - 1Документ63 страницыGeneral Chemistry MCAT - 1pparik10100% (2)
- FREE MCAT ResourcesДокумент16 страницFREE MCAT ResourcesDivjot KaranОценок пока нет
- TBR Bio1 OptДокумент333 страницыTBR Bio1 OptChris Daniels90% (10)
- Princeton WB ChemДокумент762 страницыPrinceton WB Chemrajatgoyal20Оценок пока нет
- 100 MCAT TipsДокумент23 страницы100 MCAT TipsJhilianne Batino100% (1)
- Explanations For Every Single Question For Every Userful Resource For The MCATДокумент643 страницыExplanations For Every Single Question For Every Userful Resource For The MCATBaoz Ping0% (10)
- MCAT Sample Questions Template 1Документ42 страницыMCAT Sample Questions Template 1gendut_novri0% (1)
- MCAT Physics Formulas Study GuideДокумент6 страницMCAT Physics Formulas Study Guidejetone472100% (2)
- Selective Attention and Problem Solving TechniquesДокумент28 страницSelective Attention and Problem Solving TechniquesMahdeeHaqueSyed100% (2)
- MCAT Review SheetsДокумент92 страницыMCAT Review SheetsShafia Batool100% (1)
- MCAT Full Length 1Документ77 страницMCAT Full Length 1GIlgamesh417100% (2)
- Sterling Test Prep MCAT Organic Chemistry & Biochemistry Practice Questions: High Yield MCAT Practice Questions with Detailed ExplanationsОт EverandSterling Test Prep MCAT Organic Chemistry & Biochemistry Practice Questions: High Yield MCAT Practice Questions with Detailed ExplanationsОценок пока нет
- Don's Tactical-Nuclear MCAT Test-Taking Tips and TechniquesОт EverandDon's Tactical-Nuclear MCAT Test-Taking Tips and TechniquesРейтинг: 4 из 5 звезд4/5 (2)
- MCAT Test Prep Inorganic Chemistry Review--Exambusters Flash Cards--Workbook 2 of 3: MCAT Exam Study GuideОт EverandMCAT Test Prep Inorganic Chemistry Review--Exambusters Flash Cards--Workbook 2 of 3: MCAT Exam Study GuideОценок пока нет
- Sterling Test Prep OAT General Chemistry Practice Questions: High Yield OAT General Chemistry Practice QuestionsОт EverandSterling Test Prep OAT General Chemistry Practice Questions: High Yield OAT General Chemistry Practice QuestionsОценок пока нет
- MCAT Biology & Biochemistry Practice Questions: High Yield MCAT QuestionsОт EverandMCAT Biology & Biochemistry Practice Questions: High Yield MCAT QuestionsОценок пока нет
- MCAT Test Prep Biology Review--Exambusters Flash Cards--Workbook 1 of 3: MCAT Exam Study GuideОт EverandMCAT Test Prep Biology Review--Exambusters Flash Cards--Workbook 1 of 3: MCAT Exam Study GuideРейтинг: 2 из 5 звезд2/5 (3)
- MCAT Test Prep Physics Review--Exambusters Flash Cards--Workbook 3 of 3: MCAT Exam Study GuideОт EverandMCAT Test Prep Physics Review--Exambusters Flash Cards--Workbook 3 of 3: MCAT Exam Study GuideОценок пока нет
- MCAT General Chemistry Practice Questions: High Yield MCAT QuestionsОт EverandMCAT General Chemistry Practice Questions: High Yield MCAT QuestionsОценок пока нет
- 101 Ways to Score Higher on Your MCAT: What You Need to Know About the Medical College Admission Test Explained SimplyОт Everand101 Ways to Score Higher on Your MCAT: What You Need to Know About the Medical College Admission Test Explained SimplyОценок пока нет
- Sterling Test Prep College Organic Chemistry Practice Questions: Practice Questions with Detailed ExplanationsОт EverandSterling Test Prep College Organic Chemistry Practice Questions: Practice Questions with Detailed ExplanationsОценок пока нет
- Reproductive System NotesДокумент3 страницыReproductive System NotesChris_Barber09Оценок пока нет
- Protein Synthesis Notes PDFДокумент3 страницыProtein Synthesis Notes PDFChris_Barber09Оценок пока нет
- BSC 2010: Explore Macromolecules and Their FunctionsДокумент11 страницBSC 2010: Explore Macromolecules and Their FunctionsChris_Barber09Оценок пока нет
- Notes RNA and DNAДокумент23 страницыNotes RNA and DNAChris_Barber09Оценок пока нет
- MCAT O-Chem NotesДокумент1 страницаMCAT O-Chem NotesChris_Barber09Оценок пока нет
- Heart Notes PDFДокумент2 страницыHeart Notes PDFChris_Barber09Оценок пока нет
- Nucleic Acids and Their Structure: Information?Документ4 страницыNucleic Acids and Their Structure: Information?Chris_Barber09Оценок пока нет
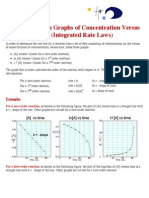
- Rate Law GraphsДокумент2 страницыRate Law GraphsChris_Barber09Оценок пока нет
- Digestive System PDFДокумент3 страницыDigestive System PDFChris_Barber09Оценок пока нет
- Cardiovasculary System PDFДокумент5 страницCardiovasculary System PDFChris_Barber09Оценок пока нет
- Bacteria: Type of Food Depends On Organism)Документ5 страницBacteria: Type of Food Depends On Organism)Chris_Barber09Оценок пока нет
- Notes CarbohydratesДокумент21 страницаNotes CarbohydratesChris_Barber09100% (1)
- Amino Acid NotesДокумент15 страницAmino Acid NotesChris_Barber09Оценок пока нет
- Extra Chirality ProblemsДокумент21 страницаExtra Chirality ProblemsChris_Barber09Оценок пока нет
- Notes CarbohydratesДокумент3 страницыNotes CarbohydratesChris_Barber09Оценок пока нет
- AP Physics 1 Review: Essential Equations and ConceptsДокумент9 страницAP Physics 1 Review: Essential Equations and ConceptsChris_Barber09Оценок пока нет
- Leaving GroupsДокумент1 страницаLeaving GroupsChris_Barber09Оценок пока нет
- Carbs: Nature's Most Abundant MoleculesДокумент24 страницыCarbs: Nature's Most Abundant MoleculesGulus CfОценок пока нет
- Physics Rules 1Документ2 страницыPhysics Rules 1Chris_Barber09Оценок пока нет
- Chapter 16:substituent Effects in Aromatic SubstitutionДокумент2 страницыChapter 16:substituent Effects in Aromatic SubstitutionChris_Barber09Оценок пока нет
- Physics Rules 5Документ10 страницPhysics Rules 5Chris_Barber09100% (6)
- Aromatic Notes 2 PDFДокумент6 страницAromatic Notes 2 PDFChris_Barber09100% (1)
- Physics Rules 4Документ6 страницPhysics Rules 4Chris_Barber09Оценок пока нет
- Physics Equation SheetДокумент2 страницыPhysics Equation SheetChris_Barber09Оценок пока нет
- Regents Physics Exam Prep: 101 Facts You Should Know: MechanicsДокумент3 страницыRegents Physics Exam Prep: 101 Facts You Should Know: MechanicsChris_Barber09Оценок пока нет
- 107 Rules in PhysicsДокумент2 страницы107 Rules in PhysicsChris_Barber09Оценок пока нет
- Physics Rules 2Документ4 страницыPhysics Rules 2Chris_Barber09Оценок пока нет
- AAMC 11 Essay 2Документ5 страницAAMC 11 Essay 2Chris_Barber09Оценок пока нет
- MCAT Physics Equation SheetДокумент6 страницMCAT Physics Equation SheetChris_Barber09Оценок пока нет
- AAMC 11 Essay 1Документ6 страницAAMC 11 Essay 1Chris_Barber09Оценок пока нет
- CP S HW CH 6 DetailedДокумент7 страницCP S HW CH 6 Detailedanon_156453388100% (1)
- Mechanics Practice Problem SetДокумент38 страницMechanics Practice Problem SetflexflexОценок пока нет
- Classical and Relativistic MechanicsДокумент7 страницClassical and Relativistic MechanicsJosé Fernando Pérez PérezОценок пока нет
- Physics NotesДокумент183 страницыPhysics NotesPrashant ShuklaОценок пока нет
- Harald Fritzsch - Quantum Field TheoryДокумент167 страницHarald Fritzsch - Quantum Field TheoryAlex Santiago100% (1)
- 02 Newtonian Mechanics AdvancedДокумент37 страниц02 Newtonian Mechanics AdvancedRithish BarathОценок пока нет
- Radiation PressureДокумент19 страницRadiation PressurebhishanОценок пока нет
- AP Physics 1 and 2 Diagnostic Test SectionsДокумент9 страницAP Physics 1 and 2 Diagnostic Test SectionsJohn BoswellОценок пока нет
- Paper 2 Form 4 2020Документ28 страницPaper 2 Form 4 2020Yusfalina Mohd YusoffОценок пока нет
- LESSON 2.5 Momentum: M U + M U M V + M VДокумент11 страницLESSON 2.5 Momentum: M U + M U M V + M VKriyaashini VijeyanОценок пока нет
- Module 4-Mechanics: CollisionsДокумент32 страницыModule 4-Mechanics: CollisionsHead LightОценок пока нет
- Monthly Chart (Curve Chart)Документ15 страницMonthly Chart (Curve Chart)AhmedSiragОценок пока нет
- Notes on the Fogal TransistorДокумент29 страницNotes on the Fogal TransistorUn Chubacca YetiОценок пока нет
- Fundamentals of Accelerator Physics and Technology (Presentation Slides) (2006) WWДокумент452 страницыFundamentals of Accelerator Physics and Technology (Presentation Slides) (2006) WWKostas LiapisОценок пока нет
- 31bbd483 E8d3 4376 Abcc Cde0e74e950a o Level Quick Physics QN BankДокумент138 страниц31bbd483 E8d3 4376 Abcc Cde0e74e950a o Level Quick Physics QN BankMaama PhionaОценок пока нет
- Belcher-Feynman Cylinder ParadoxДокумент9 страницBelcher-Feynman Cylinder ParadoxH LОценок пока нет
- Two 5 KG Bodies Approach Each Other, Both Having Speed of 2 M S - What Is The Total Momentum?Документ20 страницTwo 5 KG Bodies Approach Each Other, Both Having Speed of 2 M S - What Is The Total Momentum?Sam JordanОценок пока нет
- Momentum Physics Form 4Документ5 страницMomentum Physics Form 4Kosyalan Sivasundram KøĉħâОценок пока нет
- Laws of Motion (Irodov)Документ70 страницLaws of Motion (Irodov)akhileshvv123Оценок пока нет
- 01 Edem FluentДокумент15 страниц01 Edem Fluentbresler_lin100% (4)
- Newton Law of Motion-Practice ProblemДокумент13 страницNewton Law of Motion-Practice ProblemANURAG TYAGI100% (2)
- Edexcel GCSE Additonal Science P2 Topic 4 Test 13 - 14 With Marks SchemeДокумент15 страницEdexcel GCSE Additonal Science P2 Topic 4 Test 13 - 14 With Marks SchemePaul BurgessОценок пока нет
- Electricidad y MagnetismoДокумент53 страницыElectricidad y MagnetismoroalramiОценок пока нет
- Classical Mechanics - Marion, ThorntonДокумент252 страницыClassical Mechanics - Marion, ThorntonFRANCISCO C.N. SANTOS100% (4)
- E 1952 A GuptaДокумент13 страницE 1952 A GuptaNgô Lưu Duy TháiОценок пока нет
- Paramahamsa Tewari - On Planetary Motion Caused by Solar Space VortexДокумент9 страницParamahamsa Tewari - On Planetary Motion Caused by Solar Space VortexKluff5878Оценок пока нет
- AQA A Level Physics Equation SheetДокумент5 страницAQA A Level Physics Equation SheetCamila Lorenzoni100% (2)
- Chap 10 Transport PhenomenaДокумент6 страницChap 10 Transport PhenomenaElsa JovankaОценок пока нет
- Atomic Structure QB 1Документ2 страницыAtomic Structure QB 1vengateshwaran kОценок пока нет
- lATTICE BOLTZMANN METHODДокумент15 страницlATTICE BOLTZMANN METHODKrunal GangawaneОценок пока нет