2D - 1

9/28/2013 University of Colorado at Boulder

Motion in 2D

Velocity and acceleration are vectors. They can have any direction. When we are considering
motion in the xy plane, these vectors can point anywhere in the plane. A common example of
motion in 2D is...

Projectile motion
Consider a projectile fired from a cannon, with an initial velocity
0
v with a direction of u above
the horizontal.



0x 0
0y 0
v v cos
v v sin
= u
= u




Acceleration is a vector, and can have any direction. But in the special case of acceleration due
solely to gravity, the acceleration is always straight down.


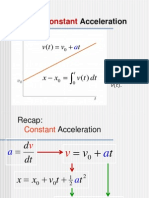
Review of 1D motion:
d v d x
a , v
d t d t
= = ,

From these two equations, we can derive, for the special case a = constant,
(a)
o
v v a t
(b)
2
o o
x x v t (1/ 2) a t
(c)
2 2
o o
v v 2a (x x )
(d)
o
v v
v
2

x
o
, v
o
= initial position, initial velocity x, v = position, velocity at time t


y
x
a
x
= 0
a
y
= g
a

y
v
o
x
v
x
u
v
y
2D - 2
9/28/2013 University of Colorado at Boulder
Suppose that a = 0 . In this case v = constant, and
0
x
v v v constant
t
A
= = = =
A


0
0 0 0 0 0
x x
v , v t x x , x x v t
t

= = = +

If a 0 then
2
1
0 0 2
position if a = 0 how much more (a > 0)
or less (a < 0) distance you
go if a 0
x x v t a t
=
= + +

End of 1D motion review.

Now, 2D Motion

y
x
x y
d v
d v d v
a a , a
d t d t d t
= = =

and
x y
d r d x d y
v v , v
d t d t d t
= = =

Special case:
x y
a constant a constant, a constant = = =

This is exactly like the 1D motion case, except now we have separate equations for x-motion and
y-motion. We can treat the x-motion and y-motion separately, because the x-eqns do not involve
the y-coordinate, and the y-eqns do not involve the x-coordinate.


These are the x- and y-components of the vector
equations
2
1
o o 2
r r v t a t
o
v v a t


Comment about 1D vectors: When we were restricting ourselves to 1D motion, there were only
2 possible directions, so we could represent direction with (+) or () sign. We said that, in 1D,
the velocity v could be represented by a signed number. For example, v = 2 m/s means a
velocity with a speed of 2 m/s, in the negative direction. But technically, we should not
represent a vector with a number (even a signed number). Suppose we are describing 1D
motion, and we choose to call our 1D line the x-axis. Then what we were calling the velocity
v in 1D, is really x-component of the velocity vector, v
x
. The velocity vector in this case is
x

v v i . Vectors are not numbers, but in 1D there is a one-to-one correspondence between

the vectors v and the components v
x
, so we can use the terms interchangeably, although this is
technically incorrect.

2
1
o ox x 2
x ox x
2
1
o oy y 2
y oy y
x x v t a t
X
v v a t
y y v t a t
Y
v v a t
2D - 3
9/28/2013 University of Colorado at Boulder
Example: Horizontal Rifle. A rifle bullet is fired horizontally with v
o
= 100 m/s from an initial
height of y
0
= 2.0 m above the ground level (y = 0). Assume no air resistance. How long is the
bullet in flight? How far does the bullet go before it hits the ground?

Key idea in all projectile motion problems: treat x- and y-motions separately!
The motion along the y-direction (vertical motion) is completely independent of the motion
along the x-direction (horizontal motion).

0
ox
x
X: x 0
v 100m/ s
a 0
=
=
=

0
oy
2
y
Y: y 2m
v 0
a g 9.8 m/ s
=
=
= =


The time to hit the ground is entirely controlled by the y-motion. Why is this? Because hitting
the ground means y = 0, so it is the y-motion that controls when the ground is hit.

2 2 2
1 1 1
o oy 0 0 2 2 2
0
0
2 2 0 0
0
y y v t g t 0 y g t , y g t
2y 2y 2(2)
2y g t , t , t 0.64s
g g 9.8


Now we look at the x-equations to see how far along the x-direction the bullet traveled in 0.64 s.

x x ox
2
1
o ox x ox 2
0 0
a 0 v constant = v 100 m/ s
x x v t a t v t 100(0.64) 64m


Why v
x
= constant ? The force of gravity is straight down. So there is no sideways force to
change v
x
(assuming no air resistance). No sideways force to speed up or slow down the bullet,
so, in the x-direction, the bullet just coasts, like a glider on an airtrack.

- Another question: What is the speed of the bullet as it falls?
x ox o
y oy y
0 g
v constant v v
v v a t g t

= = =
= + =

As the bullet travels, its v
x
remains constant, while |v
y
| grows larger and larger.
y
x
v
ox
= 100 m/s

2 m

2D - 4
9/28/2013 University of Colorado at Boulder


speed = magnitude of velocity = ( )
2
2 2 2
x y ox
v v v v g t = + = +

The speed is a minimum at t = 0 when v
y
= 0 (the moment when the bullet leaves the gun). The
speed is maximum when v
y
is maximum, just before the bullet reaches the ground. Dont forget
that we are assuming no air resistance. For a real rifle fired in real air, the bullets speed is
usually maximum when leaving the barrel, and then air resistance slows the bullet down as it
travels.

Example: A projectile is fired on an airless world with initial speed v
o
at an angle u above the
horizontal. What is the minimum speed of the projectile? Answer: v
ox
= v
o
cos u .

Proof:
x x ox o
y y oy
a 0 v constant = v v cos
a g v v g t
= = = u
= =



Review of acceleration:
1D:
d v
a
d t
= 2D:
2 1
v v d v v
a
d t t t
A
= ~ =
A A


2 1
v v v A = means
2 1
v v v = + A

v A is the vector you add to
1
v to get
2
v .

The direction of a is the same as the direction of v A
y
x
v
y

( v
y
= 0 )
v
oy

v
ox

v
ox

v
ox

Here, the speed is minimum at the top of the trajectory, where v
y
= 0.
u
y
x
v
ox
= v
o

v
x

v
y

v
v
x

|v
y
|
v
v
1

Av
v
2

2D - 5
9/28/2013 University of Colorado at Boulder
(since a v positive number (1/ t ) = A A


"Shoot the Monkey" Experiment:

A hunter aims a rifle at a monkey hanging in a tree. The rifle fires at the same instant that the
monkey lets go and drops. Does the bullet hit the poor monkey? Answer: Yes!

First, consider the situation with no gravity :
If there is no gravity, then the bullet goes
in a straight line, and the monkey does not
fall. So the monkey is hit.

The height of the bullet (with a
y
= 0) is

0 0y 0
0
y y v t v sin t = + = u




Now, turn on gravity. The height of the bullet is now:
2
1
0 0y 2
y y v t g t = + .



With gravity on, the bullet falls below the straight-line path by a distance (1/2)g t
2
, which is
exactly the same distance that the monkey falls. So the monkey falls into the path of the bullet.
Poor monkey!
x
AV V
2
V
1
The direction of the acceleration of gravity is the direction of AV: straight down!
V
1
V
2
y
x
(1/2)g t
2
y
x
u
2D - 6
9/28/2013 University of Colorado at Boulder
Circular Motion and Acceleration

Circular motion: consider an object moving in a circle of radius r, with
constant speed v.

T = period = time for 1 complete revolution, 1 cycle

2 r
distance
speed v v
time T
t
= = =

An object moving in a circle is accelerating, because its velocity is changing -- changing
direction. Recall the definition of acceleration:

2 1
d v
v v v
a
d t t t
A
~ =
A A
, velocity v can change is two ways:

Magnitude can change or
direction can change:



For circular motion with constant speed, we will show that
1) the magnitude of the acceleration is
2
v
a a
r
=

2) the direction of the acceleration is always towards the center of
motion. This is centripetal acceleration. "centripetal" = "toward center"
Notice that the direction of acceleration vector is always changing,
therefore this is not a case of constant acceleration (so we cannot use
the "constant acceleration formulas")

Is claim (1) sensible?
Check units:
( )
| |
2
2
2 2
2
m
m
s v m
s
a
r m m s
| |
|
(
\ .
= = = =
(

Yep.

Think: to get a big a, we must have a rapidly changing velocity. Here, we need to rapidly change
the direction of vector v need to get around circle quickly need either large speed v or a
small radius r. a = v
2
/ r makes sense. (Proof is given below.)

Is claim (2) sensible? Observe that vector
Av is toward center of circle.

r
v
v
1
v
2
Av

v
2
v
1
Av

r
v
v
a
a
v
2
v
1
Av

v
1
v
2
2D - 7
9/28/2013 University of Colorado at Boulder
Direction of a = direction toward which velocity is changing


Example: acceleration on a merry-go-round. Radius r = 5 m , period T = 3 s

( )
2
2
2
2
2 r 2 5
v 10 5 m/s
T 3
1g
10 5 v
a = 22 m/s 2 3 g's !
r 5 9 8m s
t t
= = =
= = =
( )
.
.
.
. /



A human can withstand an acceleration of about 5 g's for a few minutes or ~10 g's for a few
seconds without losing consciousness.

Proof of a = v
2
/ r

for circular motion with constant speed

The proof involves geometry (similar triangles). It is
mathematically simple, but subtle.

Consider the motion of a particle on a circle of radius r with
constant speed v. And consider the position of the particle at two
times separately by a short time interval At. (In the end we will
take the limit as At 0.) We can draw a vector diagrams
representing
1 2
r r r + A = and
1 2
v v v + A = :

Notice that these are similar triangles (same angles, same length ratios). Also, note that
1 2
r r r = = and
1 2
v v v = = .

Because the triangles are similar, we can write
v t
v r
v r r
A
A A
= = . A little algebra gives
v v
v
t r

A
=
A
. Finally, we take the limit At 0 and get acceleration
2
v
a
r
= .

r
1
r
2
Ar = v At

v
1
v
2
Av

r
v
a
r
2
v
1
r
1
v
2