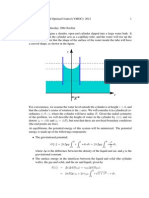
Theorem

There are three possibilities as displayed in the figures below.

1. The two lines are secants of the circle and intersect inside the circle (figure on the left). In
this case, we have

2. One of the lines is tangent to the circle while the other is a secant (middle figure). In this
case, we have

3. Both lines are secants of the circle and intersect outside of it (figure on the right). In this
case, we have

Proof
Draw extra lines to create similar triangles! (Hint: Draw

on all three figures. Draw

another line as well.)

Alternate Formulation
This alternate formulation is much more compact, convenient, and general.
Consider a circle
line through

and a point

in the plane where

that intersects the circle in two places. The power of a point theorem says

that the product of the length from

from

is not on the circle. Now draw a

to the first point of intersection and the length

to the second point of intersection is constant for any choice of a line through

that intersects the circle. This constant is called the power of point
the figure below

. For example, in

Notice how this definition still works if

Consider also when

and

coincide (as is the case with

).

is inside the circle. The definition still holds in this case.

Additional Notes
One important result of this theorem is that both tangents from a point

outside of a

circle to that circle are equal in length.

The theorem generalizes to higher dimensions, as follows.
Let

be a point, and let

intersect

be an

at

-sphere. Let two arbitrary lines passing through

, respectively. Then

Proof. We have already proven the theorem for a -sphere (i.e., a circle), so it only
remains to prove the theorem for more dimensions. Consider the plane
of the lines passing through
consider the lines and

. The intersection of

and

containing both

must be a circle. If we

with respect simply to that circle, then we have reduced our

claim to the case of two dimensions, in which we know the theorem holds.

Problems
The problems are divided into three categories: introductory, intermediate, and
olympiad.

Introductory
Problem 1
Find the value of

in the following diagram:

Solution

Problem 2
Find the value of

in the following diagram:

Solution

Problem 3
(ARML) In a circle, chords
and

and

intersect at

, find the ratio

. If

Solution

Problem 4
(ARML) Chords

and

of a given circle are perpendicular to each other and

intersect at a right angle. Given that

Solution

Intermediate
Problem 1

, and

, find

Two tangents from an external point

A third tangent meets the circle at
respectively. Find the perimeter of

are drawn to a circle and intersect it at

, and the tangents

and

at points

and
and

.
,

Problem 2
Square
of

of side length

has a circle inscribed in it. Let

Find the length of that portion of the segment

be the midpoint

that lies outside of the circle.