ECON1203 Statistics

Chapter 16 Simple Linear

Regression & Correlation
Contents
1.
2.
3.
4.
5.
6.

Model
Estimating the Coefficients
Error Variable: Required Conditions
Assessing the Model
Using the Regression Equation
Regression Diagnostics (Part 1)

Introduction

Regression analysis predicts one variable based on other variables.

The dependant variable is to be forecast ( Y ).

The statistics practitioner believes that it is related to independent

variables ( X 1 , X 2 , , X k ).

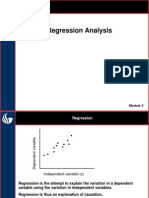
Correlation analysis determines whether a relationship exists:

o Scatter diagram
o Coefficient of correlation
o Covariance

16.1 Model

Deterministic models determine the dependent variable from the

independent variables. They are unrealistic because there may be other
influencing variables.
Probabilistic models include the randomness of real life (e.g. an error
variable).

The error variable ( ) is the difference between the estimated and

actual dependent variable.

The first-order linear model (or simple linear regression model) is a
straight-line model with one independent variable:
o

y= 0 + 1 x +

y=

dependant variable

x=

independent variable

0=

y-intercept

1=

slope of the line

error variable

16.2 Estimating the coefficients

The least squares line ( ^y =b 0+ b1 x ) uses the least squares method

n

to minimise the sum of squared deviations (

i=1

).

The sum of squares for error (SSE) is the minimised sum of squared
deviations.
Residuals are the deviations between the actual data points and the line:
o

( y i ^y i )2

e i= y i ^y i

Least squares line coefficients:

s xy

b1 =

b0 = y b 1 x

s2x

( x ix )( y i y )

s xy = i=1

n1

( x i x )2

s 2x = i=1

n1

xi

x = i=1
n
n

y = i=1
n

Shortcuts:
o

yi

s xy =

1
n1

1
s =
n1
2
x

xi yi

i=1

x i y i i=1

x
i=1

( )
xi

n
2
i

i=1

i=1

Excel:
o Have two columns of data: one for the dependent variable; the
other for the independent variable.
o Click Data, Data Analysis, and Regression.
o

Specify the Input

Range and the Input

Range.

Assumptions of Classical Linear Regression Model

1. The least squares line coefficients ( 0

1 ) are linear.

and

2. The observed variables ( x i , y i ) are randomly sampled.

x i ; they are not all equal.

3. There is sample variation in

4. The mean of

a. Therefore,
5. The variance of

x :

is 0, regardless of

and

E ( i|x i )=0 .

are uncorrelated.

is a constant:

Var ( i ) = 2 .
i

a. But in reality, not necessarily true (e.g. higher income may increase
variance in expenditure because they have a greater range of
choices)
6. The error variables are uncorrelated:

Cov ( i , j )=0 .

7. The error variables are normally distributed:

i N ( 0, 2 ) .

16.4 Assessing the Model

There are three ways of assess how well the linear model fits the data:
1. The standard error of estimate
2. The

t -test of the slope

3. The coefficient of determination

Sum of Squares for Error (SSE)

n

SSE= ( y i ^y i ) =( n1 ) s
i=1

2
y

s2xy
s2x

Standard Error of Estimate ( s )

SSE
( s = n2
) isusually compared with y

Testing the Slope

We can use hypothesis testing to infer the population slope ( 1 ) from

the sample slope ( b1 ).

If

1=0 , there is no linear relationship (but there may be a quadratic

relationship).

The sample slope ( b1 ) is an unbiased estimator of the population

slope ( 1 ) ( E ( b1 )= 1 ) because the estimated standard error of

b1

s
s
=
b
(
( n1 ) s 2x ) decreases as
1

Test statistic for

1=t=

increases.

b1 1
[ where =n2 ]
sb
1

Confidence interval estimator of

1=b1 t 2 s b [ where =n2 ]

1

Coefficient of Determination

Coefficient of Determination:

R 2=

s2xy
2

=1
2

sx s y

( y i y ) SSE = Explained variation

SSE
=
2
Variation y
( y i y )
( yi y )2

( y i y ) =( y i y ) + ^y i^y i

( y i y ) =Unexplained residual ( y i ^y i ) + Explained variation ( ^y y )

( y i y )2= ( yi ^y i )2+ ( ^y i y )2

Variation y=SSE+ SSR

Coefficient of Correlation

We can use hypothesis testing to infer the population coefficient of

correlation ( ) from the sample coefficient of correlation ( r ).

Sample coefficient of correlation:

Test statistic for

t=r

r=

s xy
sx sy

n2
1r 2 [where

=n2 and variables are

bivariate normally distributed]

16.5 Using the Regression Equation

^y i=b 0+b1 x i

is a point estimator.

There are two interval estimators:

1. Prediction interval:

1 ( x gx )
^y t 2,n2 s 1+ +
n ( n1 ) s 2x

2. Confidence interval estimator of the expected value of

y : ^y t 2,n2 s

2
1 ( x gx )
+
n ( n1 ) s 2x

The farther the given value of

x , the greater the estimated error:

is from

( x gx )

( n1 ) s 2x

16.6 Regression Diagnostics (Part 1)

Residual analysis

Standard deviation of the ith residual : s =s 1h i

i

2
1 ( x ix )
Where hi= +
n ( n1 ) s 2x

Normality

The residuals should be normally distributed.

Homoscedasticity

The variance of the error variable should be constant.

Independence of the error variable

The error variable should be independent.

Outliers
Outliers may be:
1. Recording errors
2. Points that should not have been included in the sample
3. Valid and should belong to the sample

Influential observations

Some points are influence in determining a least squares line. Without it,
there would be no least squares line.

Procedure
1. Develop a model that has a theoretical basis; find an independent variable
that you believe is linearly related to the dependent variable.
2. Gather data for the two variables from (preferably) a controlled
experiment, or observational data.
3. Draw a scatter diagram. Determine whether a linear model is appropriate.
Identify outliers and influential observations.
4. Determine the regression equation.
5. Calculate the residuals and check the required conditions:
a. Is the error variable normal?
b. Is the variance constant?
c. Are the errors independent?

6. Assess the models fit:

a. Compute the standard error of estimate.
b. Test
c.
7. If the
a.
b.

1 or

to determine whether there is a linear

relationship.
Compute the coefficient of determination.
model fits the data, use the regression equation to:
Predict a particular value of the dependant variable
Estimate its mean