Chapter 4 / Maxima and Minima in Several Variables ‘The abstract setting forthe situation discussed in Example 1 is to find m ima or minima of a function f(x,x2,...%,) subject 10 the constraint th (1.23, ---5%,) = € for some function g and constant c. (In Example 1, th function f is A(e, y, 2), and the constraint is xyz = 4.) One method for finn cconstrainod critical points is used implicitly in Example 1: Use the const ‘equation g(x) = c to solve for one of the variables in terms ofthe others. Th substitute for this variable in the expression for f(x), thereby creating a ne function of one fewer variables. This new function can then be maximize! wf ‘minimized, using the techniques of §4.2. In theory, this is an entirely appropris ‘way to approach such problems, but in practice there is one major drawback: | may be impossible to solve explicitly for any one of the variables in terms oft others. For example, you might wish to maximize fey oar t3y tye subject to eo -sy'c+c0s(Z) a2 ¥%. ‘There is no means of isolating any of x, y, or z on one side of the constrain equation, and so itis impossible for us to proceed any further along the fines u Example 1 The Lagrange Multiplier ‘The previous discussion points to the desirability of having another metho ti solving constrained optimization problems, The key to such an alternative mettu is the following theorem: Let § = [x ¢ X | g(x) = c) denote the level set of g at height ¢, if fs (the restriction of f to $) has an extremum at a point x9 € such th ‘Vet%o) #0, there must be some scalar such that VF (Ho) = AV (0). ‘The conclusion of Theorem 3.1 implies that to find possible sites for extren of f subject to the constraint that g(x) = ¢, we can proceed in the followlu manner: 1, Form the vector equation V f(x) = AVg(X). 2. Solve the system e HAV gO) Fe) for x and A. When expanded, this is actually a system of + 1 equations | nt Lunknowns x1, %2,.-.» Xa, 2, namely, Fay B10, 0025 Hn) = Ae ty A262) Lay Hae +s Xn) = Ag Od RD + in) Fan 19 825 +2 Xn) = ABag 1. X25 +++ Xn) BO Mase he) =Section 4.3 / Lagrange Multipliers an ‘The solutions for (1,95. %q)p along with any other points satisfying a(x) =c and Ve(x) are the candidates for extrema for the problem, 3. Determine the nature of f (as maximum, minimum, or neither) at the critical points found in Step 2. ‘The scalar 2 appearing in Theorem 3.1 is called a Lagrange multiplier, after the French mathematician Joseph Louis Lagrange (1736-1813) who first devel- ‘oped this method for solving constrained optimization problems. In practice, ‘Step 2 can involve some algebra, so it is important to keep your work organized. (Alternatively, you can use a computer to solve the system.) Infact, since the La- grange muliplier 2 is usually not of primary interest, you can avoid solving for itexplicitly, thereby reducing the algebra and arithmetic somewhat. Determining the nature of a constrained ertical point (Step 3) can be a tricky business, We'll have more to say about that issue in the examples and discussions that follow. EXAMPLE 2 Let us use the method of Lagrange multipliers to identify the crit ical point found in Example 1. Thus, we wish fo find the minimum of AG, y, 2) = 2xy + 2y2- baz subject to the constraint Ve,y.2) xy a4. ‘Theorem 3.1 suggests that we form the equation VAG, y,2) = AVVO, y, 2). This relation of gradients coupled with the constraint equation gives rise to the system, a+ nz Since 2. is not essential for our final solution, we can eliminate it by means of any of the first three equations. Hence, y+ 2 ye Simplifying, this implies that 2 = or ‘Substituting these relations into the constraint equation xyz = 4 yields 2NGI@y) =4, so that we find that the only solution is y = 1, 2, which agrees with our work in Example 1. 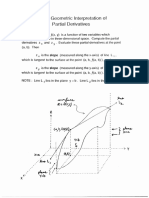(Note that VY = @ only along the coordinate axes, and such points do not satisfy the constraint V(x, y, 2) = 4.) e272 Chapter 4/ Maxima and Minima in Several Variables Figure 4.26: The level sets of the function f(x, ») = 27/44 »* efine a family of ellipses. The extrema af f subject t the constraint that x? +3? = 1G, that fie on the unit cirele) occur st points where an ellipse ofthe family is tangent tothe unit circle Figure 4.27: The gradient ‘Vag(s) is perpendicular to (& | g(x) =] hence to the tangent vector atx {0 any ceurve x(t) Iying in $ and passing through xo. If f has an extremum at X then the resttition of to the curve also Jhas an extresmum at x “Aminteresting consequence of Theorem 3.1 is this: By Theorem 6.4 0° Chip ter2, we know thatthe gradient Vg, when nonzero is perpendicular othe [vel wis of. Thus, the equation V f= AV g gives the condition for the norm WE, forte a evel set of / to be parallel to that ofa level sct of g. Hence, fora pl seta be the site of an extremum of f on the Tevel et S = {x | g(3) = ch while” Vetaq) 0, we rust have that the level set of f that contains xo is tangent Sat xo. EXAMPLE 3 Consider the problem of finding the extrema of f(s) 7 entre abject tothe condition that x? + y? = 1, Welet g(t 9) = 2b | 2A ate Lagrange multiplier equation VG, ») = A¥g(x. yD along with ht ‘constraint equation, yields the system 3 There axe no points simultaneously satisfying gy) {0,0),) The first equation of this system implics that either » 0, then the second two equations, taken together, imply that y FT Ira = dy thon the socond two equations imply y = 0 and x “Therefore, there are four constrained critical points: (0, £1), comesponding (13 d= Land CE, 0), comesponding to 2 = 4 Wc wan understand the nature of these critical points by using geometry al te preceding remarks. The collection of level sets of the function ate tht femly of ellipses 12/4 + 9? = k whose major and minor axes Te along the 1 tnd janes, respectively. In fact, the value f(x,y) = 32/4 + 9 Square of the length of the semiminor axis ofthe ellipse 21/4 + y ‘optimization problem then isto find those points on the wnt circle ery that when considered as points in the family of ellipses, inimize and maxivvi the length of the minor axis. When we view the problem in thi way, We 0 that such points must oocur where the crcl is tangent fo one of the elipss the family, A sketch shows tbat constrained minima of f oceur at CEL, 0) a a eteined maxima at (0,1. In this ease, the Lagrange multiplier 2 represc wi the square ofthe length ofthe semiminor axis, (See Figure 426.) 7 sketch of a proof of Theorem 3.1 We present the key ideas of the pro seer geometric in nature. Try to visualize the sitution forthe case 7 = weet the constraint equation g(X, y,2) = ¢ defines a surface S in R. (Sel Figure 427) In general, if Sis defined as (x| g(x) = ¢} with Va(ao) 7 0. al {at leas locally near xo) 5 is a hypersurface in R°, Tho proof that tis ise cd ‘erolves the implicit function theorem (Theorem 6.5 in §2.6), and this is why proof here is justa sketch. ‘Thus, suppose that xp is an extremum of f restricted to S. We consider farther reaticton of f—t0 2 cutve lying in S and passing through Xo, This wil aable us to use results from one-variable calculus, The notation and analy particulars areas follows: Let x: 1 ¢ R—> $C R® bea C* path lying in § will eit) 2 xo for some fy € 7. Then the restriction of f tox is given by the Functnl F, where FO) = fe).Section 43/Lagrange Multipliers 273 Because Xo is an extremum of / on S, it must also be an extremum on x. Conse- quently, we must have F’(jp) = 0, and the chain rule implies that 0= F@) LHe VL (RCt0)) +X’ (00) = V F(a) +x’ (o). ', Vf (x9) is perpendicular to any curve in S passing through xp; that is, Vf (%o) is normal to S at xo. We've seen previously in §2.6 that the gradient V2(Xo) is also normal to S at xo. Since the normal direction to the level set is uniquely determined and Vg(xo) # 0, we must conclude that V f(x) and Va (xo) are parallel vectors. Therefore, for some scalar A € R, as desired, 2 ‘The Case of More than One Constraint {tis natural fo generalize the situation of finding extrema of a function f subject to a single constraint equation to that of finding extrema subject to several con- strsinis. In other words, we may wish to maximize or minimize f subject to k simultaneous conditions of the form eC) = oy The result that generalizes Theorem 3.1 is as follows: eee EERE Theorem 3.2 Let X be open in R" and let igi... mu? X OR” > Rbe CC? functions, where k = -2. Hence, Vi iil ‘Vo are linearly independent at all points that satisfy the two constraints, “he fore, by Theorem 3.2, we know that any constrained critical points (xo, stg) oust satisty VF ox Jou 20) = 21 V816%o, You 20) + 22 V 800%» Yo. Zoe as well as the two constraint equations. Thus, we must solve the system De = Max tar Dy = My +2 2g = Dede wy xtye Eliminating 22 from the first two equations yields Ja = 2x — Bax = 2y— Bay, which implies that 2x ~ y= 21) = 0.Figure 4.29: The point ay is the point on the hyperbola closest to the origin, The point 2; is the point on the lower branch of the hyperbola closest to the origin Section 43/Lagrange Multipliers 275 ‘Therefore, either x=y or yy ‘The condition 21 = 1 implies immediately 22 = 0, and the third equation of the system becomes 2z = ~2z, so z must equal 0, Ifz = 0, then x and y must be zero by the fourth equation, However, (0, 0,00) is aot a point on the plane <= x+y+2, Thus, the condition 4; = 1 leads to no critical point. On the other hhand, if x = , then the constraint equations (the last two in the original system. of five) become Substituting z = 2x +2 yields 2x? — Qx +27 <0, equivalent to + 8rt4=0, Whose solutions are x = ~2 + V3. Therefore, there are two constrained critical points a and ® We can check that fla) =24—16V2, f(a) = 24+ 16/2, so itscems that a; must be the point on C lying nearest the origin, and ay must be the point that lies farthest. However, we don’t know a prior’ if there is a farthest Point. Ifthe conic section C is a hyperbola or a parabola, then there is no point that is farthest from the origin, To understand what kind of curve C is, note that a has positive z-coordinate and ay has negative z-coordinaie, Therefore, the Plane z = x + y +2 interscets both nappes of the cone z? >, The only Conic section that intersects both nappes of a cone is a hyperbola. Hence, C is a hyperbola, and we see that the point a is indesd the point nearest the origin, but the point az i not the farthest point, Instead, as isthe point nearest the origin on the branch of the hyperbola not containing a). That is, local constrained minima ‘occur at both ay and ay, but only ay isthe site of the global minimum. (See Figure 429.) «Chapter 4/ Maxima and Minima in Several Variables A Hessian Criterion for Constrained Extrema (optional) point (constr Jem at hand, Sometimes this is not dificult to do in practice and can provite useful insight into the problem. Nonetheless, occasionally itis advantageus (8 have a more automatic means of discerning the nature of a constrained criti point. We therefore present a Hessian criterion for constrained critical joints, Like the one in the unconstrained cae, this criterion only determines the fw if nature ofa critical point It does not provide information about global consti extrema? In general, the context for the Hessian criterion is this: We seek exteeii vif a function f: X CR" + R subject tothe k constraints Bi, 2 gale. BAUR Xe We assume that f, 1, ..-, ge are all of class C2, and assume, for simplicity, di f and the g's ali have the same domain X. Finally, we assume that Vg +...) are linearly independent at the constrained critical point a. ‘Then, by Thee 3.2, any constrained extremum a must satisfy V f(a) = A,Vgi(a) + Aa Van(a) +--+ ia Vee(a) for some scalars 21, ..., 2. We can consider a constrained critical point to bt pair of vectors Osa) satisfying the aforementioned equation. In fact, we can check that (; unconstrained critical point ofthe so-called Lagrangian function Z defined) ods My 0nd = Fy ote) — Dg "The Hessian criterion comes from considering the Hessian of Z atthe ei point (A; a), 5iie invite the rear to consult D. Spring, Ammer Math Monthly, 92 (1988), No.9, 631-641 fi more complete discussion, 3Section 43/Lagrange Multipliers 277 Second derivative test for constrained local extrema. Given a con- strained critical point a of f subject to the conditions g(x) = cy, x(x C1y +14 848) = 4, consider the matrix hy = Ios (Note that HG: a) isan (n-+£) x (nF) mateix.) As in the unconstrained case, let Hj be the upper letmnost j x j submatrix of HL, a), For j 1,2,...,4+ 1, let dj = dot Hj, and calculate the following sequence of n= k numbers (are CD Maa ss (Deen oO Note that, if > 1, the sequence in (1) is nor the complete sequence of principal minors of HL(Q.,a). Assume diy, = det HLQ,a) # 0. The umerical test is as follows 1, If the sequence in (1) consists entirely of positive numbers, then f has @ local minimum at a subject to the constraints Bi) =Cr, BK) rs BeCR) =e 2. If the sequence in (1) begins with @ negative number and thereafter alternates in sign, then 7 has a iocal maximum at a subject to the constraints, gis) BOS. gO) =e 3. Ifncither case 1 nor case 2 holds, then f has a constrained saddle point ata, Jn the event that det H L(A, a) = 0, the constrained critical point ais de- enerate, and we must use another method to determine whether or not it is the site of an extremum.Chapter 4/ Maxima and Minima in Several Variables lly, in the case of no constraint equations gy(x) = oy (ue b=) He: preceding criterion becomes the usual Hessian test fora function fof vii EXAMPLE 5 In Example 1, we found the minimum of the area function Alt, y.2) = ey +2y2 + xz of an open rectangular box subject to the condition Vouy.2) (21,2), The value of the multiplier 4 corresponding to this point is 2, tw the Hessian criterion to check that (2, 1, 2) really does yield a local mini ‘we construct the Lagrangian function LO; x, ¥,2) = Ale, y, 2) — VG, y.2)— 4) = Day + 2ye- +2 — Maye 4). yz 0 xe 2x sry I-ly 2k HL x, 9,2) = At the constrained critical point (2; 2, 1,2), we have 0-2 -4 2 0 ~2 4200 -2 -1 -2 HLQ;2,1,) ‘The sequence of determinants to consider is 0 (1)! det Aaa y1 = — det [2 nce these numbers are both positive, we see that (2, 1, 2) indeed minimize tii area ofthe box subject to the constant volume constraint. EXAMPLE 6 In Example 4, we found points on the conie section C de equations gilt, 2) = + y= that are (constrained) critical points of the “distance” function £92) Pa yaa?Section 4.3 / Lagrange Multipliers 279 ‘To apply the Hessian criterion in this case, we construct the Lagrangian function LQ mix, y.2) = 4 422-168 +P 2)— me +y —2 +9. ‘The critical points of L, found by setting DL(I, m;.x, y, z) equal to 0, are Qusan) = (-3 + 2v2, ~24 4 16V2; -2 + V3, +2,-2+2V3) and (ai te) = (-3 — 2V2, -24 — 16V2; ~2— V2, -2- V2, -2-W). ‘The Hessian of L is 0 0 -2 — ~2y % 0 0 -1 1 1 ke -1 2-0 00 0 ty -1 0 2-2 0 2% 1 «0 0 2421 Alter we evaluate this matrix at each of the critical points, we need to compute (FIP det Hayy = det Hs. We leave it to you to check that for (Ay3,a)) this determinant is 128 — 64/3 = 37.49, and for (22; a2) it is 128 + 64V2 * 218.51. Since both numbers are positive, the points (~2 + V2, -2 + V2, —2 + 2V3) are both sites of local minima. By comparing the values of f at these two points, we see that (-24 /2, 2+ V2, ~2-+ 22) must be the global minimum, ° 41. In this problem, find the point on the plane 2x — 3y — origin in two ways: 4 that is closest w the (8) by using the methods in §4.2 (that is, by finding the minimum value of an appro- priate function of wo variables): (b) by using a Lagrange multiplies, In Exercises 2-8, use Lagrange multipliers to identify the critical points of f subject to the given constrains, 2 fay=y, Wayta4 3. /G.y)=Se42y, Se? 429 = 4 FO," =xy, 2e—3y=6 3. fy Dany, Iet3y te 6 6 feydettyed, ety 7 fluyd=muty~ B fy dartyte Poel rt2=1 9. (@) Find the critical points of f(x, y) =a? + y subject to x? 4 29? (©) Use the Hessian criterion to determine the nature ofthe eritical point.