International Journal of Science and Advanced Technology (ISSN 2221-8386)

http://www.ijsat.com

Volume 1 No 3 May 2011

Energy function approach for transient stability

analysis of power system using advanced controlled
STATCOM-SMES
Anil Kumar Dahiya

Ratna Dahiya

Electrical Engineering Department

National Institute of Technology
Kurukshetra-136 119, India
E-mail: anildau@yahoo.co.in

Electrical Engineering Department

National Institute of Technology
Kurukshetra-136 119, India
E-mail: ratna_dahiya@yahoo.co.in

D.P. Kothari
Director general
Vindhya Institute of Technology & Science
Indore (M.P.), India
E-mail: dpk0710@yahoo.com

Abstract The rate of active power exchanged by SMES plays a

vital role in improving the dynamic performance of power system
during transient conditions. Single Machine Infinite Bus (SMIB)
system is considered along with Static Synchronous
Compensator-Supercounducting Magnetic Energy Storage
(STATCOM-SMES). In the present work, PI controller has been
replaced with fuzzy logic controller (FLC) and Artificial Neural
Network controller (ANN). The dynamic performance of the
proposed work is evaluated through digital simulation by using
SimPower of SIMULINK/MATLAB and through the energy
function to analyze damping and stability of SMIB system.
Keywords: SMES; STATCOM; Energy function; fuzzy logic;
ANN; Transient Stability; Directs methods;

I.

INTRODUCTION

The Direct Method of Energy Function approach in the area

of stability analysis has proven its effectiveness in recent years
[1-2]. In the present paper Lyapunov Function has been
developed to study the transient stability [3] of SMIB system
connected with STATCOM-SMES. The Superconducting
Magnetic Energy Storage (SMES) has been recognized as most
viable energy storing device as well as prominent Flexible AC
transmission System (FACTS) due to its high efficiency and
fast response [4]. The integration of the SMES with a
STATCOM controller has been developed. The fast response
and the capability to follow nonlinear changes are the key
aspect of a controller to compensate the real and reactive
powers effectively during transients in power system [5].

damp out the system oscillation and improving transient

stability of power system after being subjected to some
disturbances [6-7].
II.

STATCOM-SMES AND CONTROLLERS

The major components of SYAYCOM-SMES are

STATCOM, SMES, dc-dc chopper and controller as explained
in the next subsection.
A. STATCOM-SMES
A 48-pulse, three levels, neutral point clamped (NPC), gate
turn off thyristors (GTO) voltage source inverter (VSI) is the
basic component of STATCOM used. The major advantages of
using 48-pulse three-level, NPC topologies for VSI are
reduction of Total Harmonic Distortion (THD), voltage stress
of each thyristor and additional flexibility of a level in the
output voltage [8]. An SMES coil has been attached to the DC
bus of STATCOM through a dc-dc chopper. A two quadrant,
three level dc-dc chopper is used as an interfacing between
STATCOM and SMES to control the rate of charge/discharge
of SMES coil without affecting the dc bus voltage of
STATCOM [9].

The various controllers such as PI, Fuzzy Logic and

Artificial Neural Network (ANN) controller have been
developed in MATLAB environment and implemented in
STATCOM-SMES to enhance the transient stability. The
integrated STATCOM-SMES can also be used as stabilizer to

41

International Journal of Science and Advanced Technology (ISSN 2221-8386)

http://www.ijsat.com

Volume 1 No 3 May 2011

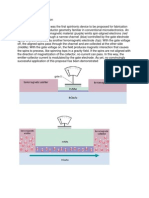
respectively. The rule base which is used for the proposed

controller is shown in Table 1. The logic of rule definition is

Figure 2. Input membership function of

Figure 1. Block representation of STATCOM-SMES

The SMES coil has been modeled by a lumped inductor of

2.0 H and a resistance of 0.01 . The maximum operating
voltage VL of SMES is restricted by insulation of the
superconducting coil, while the maximum SMES current is
limited by the maximum rate of change under constant
voltage. The current and voltage of the superconducting inductor are related as given by the following equation:

iL

1
V dt I L0
L t L

Figure 3. Input membership function of d /dt

(1)
Figure 4. Output membership function

where L is the equivalent full inductance of the SMES coil

and IL0 is the initial current of the inductor.
The the rated power (P in Watt) and inductively stored
energy (E in Joule) of SMES can be expressed as follows:
P = VLIL

(2)

E = 1/2L(IL)2

(3)

that when frequency is high and it is rising fast, the SMES

should absorb active power from the power system. Similarly,
when the frequency is low and decreasing, it should supply
active power to the power system and during the steady state
condition of power system it remains in standby mode.
TABLE 1. Rule base of fuzzy controller

d /dt
nnb
nb
z
pb
ppb

A general expression for the chopper average output

voltage Vsm at SMES terminal to the VSI average dc bus
voltage Vd as follow:
Vsm=mVd

(4)

nnb

nb

pb

ppb

nb
nb
n
p
p

nb
nb
n
p
p

n
n
z
p
p

n
n
p
pb
pb

n
n
p
pb
pb

m = (D1+ D2) chopper buck mode.

m = - (1-D1- D2) chopper boost mode.
where m is modulation index, D1 and D2 are the duty cycles
for buck and boost mode respectively.
B. Fuzzy logic controller
The Mamdanis fuzzy controller, which uses if-then rules
for inference engine has been used in the present work [10].
The deviation of frequency and derivative of frequency are
used as input variables and fuzzified by proper membership
functions. Crisp output is calculated by Center of Area (COA)
method.
The input and output membership functions assigned to
each input variable are shown in Fig. 2, Fig. 3 and Fig. 4

The membership functions are defined as:

Z=zero, p=positive small, pb=positive big,
ppb=positive very big, n=negative small,
nb=negative big and nnb=negative very big.
Based on two input variables ( and d /dt), the output
and hence the rate of charging/discharging of SMES coil is
determined.
C.

Artificial neural network controller

The back propagation algorithm has been used for the training
of feed-forward neural networks as it updates the network weights
and biases in the direction so that the performance function,
usually the sum of square errors, decreases most rapidly [11-12].
The Neural Network is trained for two input variables, i.e.
deviation of frequency and derivative of frequency, and

This work was supported in part by National Institute of Technology

Kurukshetra, India.

42

International Journal of Science and Advanced Technology (ISSN 2221-8386)

http://www.ijsat.com
required signals at its output. The output signal of controller is fed
to the GTOs firing circuit of dc-chopper and voltage phase angle
controller. The 2 layers and 10 neurons network controller is
trained with the help of nntool box of MATLAB using the
TRAINLIM Transfer function, and LERNGDM Adaptation
learning function.
III.

POWER SYSTEM MODEL

The single machine infinite bus system operates at 400 kV, 50

Hz. The model system consists of a synchronous generator feeding
an infinite bus having a short circuit rating of 10000 MVA, through
a transformer and single circuit line shown in Fig. 5. The 500 MVA,
11kV, 50 Hz synchronous generator is powered by tandem
compound steam turbine prime mover including speed governor
system. The three phases to ground (3-LG) fault is applied near the
infinite bus. at time t = 5.2 s and cleared at t=5.3 s, with automatic
breaker re-closing. The integrated STATCOM-SMES controller is
placed near the sending end of transmission line.The major test
system data related to transformer, synchronous machine, line and
STATCOM-SMES are summarized in Appendix.
11kV

Synchronous
Generator

Volume 1 No 3 May 2011

E =

Internal voltage behind

E fd =

Excitation voltage

Pm , Pe = Mechanical and electrical power

D=

Damping coefficient

X 'd
Xd

Direct axis transient reactance

Direct axis reactance

Xl =
Xt =

Line reactance
Transformer reactance
Inertia constant of machine
direct axis current

M =

id =

Incorporating the effect of active power Psm exchanged by

SMES coil of STATCOM-SMES, (6) can be represented as :

1
[ Pm Pe Psm D ]
M

PCC
Fault

(10)

Where SMES output power is given as

Psm I smVsm

(11)

Psm increases the demping effect as shown

The SMES power

400kV

X 'd

in (10) is of the SMES to increased the damping of power

swing. Thus the change in SMES power Psm is proportional

Infinite
Bus

to the change in angular speed of machine and can be

expressed as :

STATCOM
SMES

Psm K D

(12)

Further from (11)

Psm I sm0 Vsm Vsm0 I sm

Figure 5. Single line diagram of SMIB power system

The synchronous machine used in SMIB power system

shown in Fig.5 may be model as d-q axis as follows:

=
1
=
M

E

(5)
(

Pm Pe D ) ]

(6)

1
[ E ( X d X ' d )id E fd ] (7)
T 'd 0

EV
Pe
sin
X 'd X t X l
E V cos
id
X 'd X t X l

(8)

where as

(13)

Vsmo 0

Hence

Psm I sm0 Vssm

(14)

Dc voltage is controlled by changing the firing angle alpha of

the converter. The firing angle controlled is proportional to
speed deviation.

Vsm
Where

KS

1 pTS

(15)

K S and TS the loop gain and time constant of SMES

respectively. Substituting (15) in (14)

Psm
(9)

I sm0 K S

1 pTs

(16)

Assuming Ts=0 The instantaneous action of SMES

where

=
=

Machine stator angle in radian

Angle velocity rad/s

KD

Psm
I sm0 K S

at

(17)

43

International Journal of Science and Advanced Technology (ISSN 2221-8386)

http://www.ijsat.com

Volume 1 No 3 May 2011

x A ( x) F ( x)
Similarly the deviation of Pe and id may be given [2]. Since the
parameter is defined the above equation may enter as
followed.
(18)
Pe f ( , e)

LF is proposed [5] with the form

V ( x)

i n j n

(19)

Vt K e e K f f ( , e)

(20)

ke

vq0
Xe
;
X e X 'd VT0

V
kf 0 0
E B cos 0

(D K D )

M
0

0
0

0

2 g ( )
0

0

Pij are the entries of propose matrix [2] P = pij

V ( x) P T ( x) ( x)
n

i Pkl
k 1 l 1
l i

(28)

k ( )
l :
xi
0

Xl

i=1,2,3,4, . N.
Where

(29)

( x) [ 1 ( x) 2 ( x) 3 ( x)......... n ( x)]

0
0

2
4

and the Lyapunoves matrix equation is given as

Q ( AT P T PA)

(30)

But the time darivitive of Lyapunove function is given by

V ( x) X T QX
For the validity of Lyapunove function V(x) there are several
ways to assure the sign-definiteness of the derivative of V(x),
here To assure the sign-definiteness of V (x) for validity of
V(x) as a Lyapunov function the one condition is
If one can state

(24)

F ( x) AP T 1 ( x) 0

X d X 'd
T 'd 0

K
1
1
; 4
; 5 R K e ;
TR
T 'd 0
TR
K
6 R K f ;
TR

IV.

(26)

(27)

Where
;

( )d i

VT is the deviation of the terminal voltage.

Xe Xd
X e X 'd

The gradient of the V-function is given by

(23)

where

ij

1
V ( x) [ P T 1V ( x)]T Q[ P T 1V ( x)] V T ( x)[ F ( x) AP T 1 ( x)]
2

Xq
v q0
v0
X 'd
cos 0 d0
sin 0 0

X e X 'd
VT
VT
X e X q
(22)

j 1

The time derivative of (24) is given as

(21)

1
[ K R VT ]
TR

f ( , e)

+
e

Where

Xi

P
i 1

id B 0 e g ( )

(25)

LYAPUNOV FUNCTION

A Lyapunov function is constructed for a so-called

generalized Persidskii system as given by

(31)
For all x, if Q is positive definite or positive semi-definite
then function V(x) has negative definite derivative or negative
semi-definite derivative then the origin of (25) is a stable
equilibrium point.
The Q matrix is then given as
P1
1
D

P2 6 P14
5 P14
4 P14 P41
2 P1 ( D K D ) M
M
M
P
P
1 P2 6 P14
0
0
P4 6 41
Q M
M
5 P14
0
21 P3
5 P4 3 P3

(D K D )
P41
6 P4 2 P3 5 P4
2 4 P4
4 P14 P41
M
M

(32)

Thus the Lyapunove Function for system (24) is given as:

44

International Journal of Science and Advanced Technology (ISSN 2221-8386)

http://www.ijsat.com

2
e2 2
1
V ( x) (1 M 3 6 1 )M 2 f ( , e)d 1 1 3
2
25
2 2 2 25
0
V.

(33)

ENERGY FUNCTION WITHOUT THE FIELD DECAY EFFECT

AND AVR ACTION

1
M

0 f ( )

(34)

The related matrix is

2D 0
Q

0 0

will be some term in the Lyapunove Function such that to

increase the value of the term represents the potential energy
of the system and further enhancement of the stability of the
system.
VI.

To observe the electromechanical system dynamic

performance of system (24) without SMES the factor K D ,
action of field decay and AVR is neglected from equation
(24). Then the system is represented as

D
M
1

Volume 1 No 3 May 2011

(35)

RESULTS

The analysis of stability of SMIB has been carried out using

Lyapunove Function concedering the effect of SMES of
STATCOM-SMIB system. The Matrix Q is semi-definite
positive, hence the system is stable.
The performance of controllers in STATCOM-SMES has
been analyzed through the simulation results. The simulation
results for 3-LG fault in Fig. 6-9. The rotor seed and angle of
machine have been compared in Fig. 6 and 7 respectively. The
active power output and terminal voltage of machine have
been compared in Fig. 8 and 9 respectively. These results
clearly revels that the SMIB system is stable and the dynamic
responses of machine are improved more effectively with
neural network controller as compared with fuzzy logic and PI
controller.

To observe the effect of SMES on the dynamic performance

of the system the factor K D is considered and the system is
represented as

(D K D )
M
1

1
M f ( )

(36)

And the Lyapunove Function is given as

V ( , )

1
M 2 f ( )d
2
0

Where the first term

Figure 6. Comparison of speed deviation

(37)

1
M 2 represent the transient kinetic
2

energy and the last term represent the potential energy of the
system. The function V ( , ) is the sum of kinetic and
potential energies and remains constant once the fault is
cleared since the system is conservative. This energy must be
absorbed by the system once the fault is cleared if the system
to be stabile.
The related Q matrix is

2( D K D ) 0
Q
0
0

(38)

Figure 7. Comparison of load angle

Matrix Q is semi-definite positive; hence the system is stable

because the effect of SMES is to increase the damping of the
system. If the time constant of the system is considered there

45

International Journal of Science and Advanced Technology (ISSN 2221-8386)

http://www.ijsat.com

Volume 1 No 3 May 2011

controller. Further, the performance of ANN controller has

been found best among all the controllers used. The overall
dynamic response of power system has been improved
significantly with STATCOM-SMES using intelligent
controllers.
REFERENCES
G.M. Dhole and. M.K. Khedkar Antigen Energy Function: A New
Energy Function for Transient Stability Assessment, Electric Power
System Research 74, pp 315-322, 2005.
[2] L.D.Colvara, S.C.B.Araujo and E.B.Festraits Stability Analysis of
Power System Including FACTS(TCSC) effect by Direct Method
Approach, IJEPES, vol. 27,Issue 4, pp 264-274,May 2005.
[3] A. Ghosh and D. Chatterjee, Transient Stability Assessment of Power
System Containing Series and Shunt Compensators, IEEE Trans. on
Power System, vol. 22, Issue 3, pp. 210-220, 2007.
[4] ] M.H. Ali, Wu Bin and R.A. Dougal, An Overview of SMES
Applications in Power and Energy Systems, IEEE Trans. on
Sustainable Energy, Vol. 1, Issue 1, 2010, pp. 38-47.
[5] D. Sutanto and K.W. E. Cheng, Superconducting magnetic energy
storage systems for power system applications, Procd. Int. Conf. on
Applied Superconductivity and Electromagnetic Devices 2009 (ASEMD
2009), pp. 377 380, Sept. 2009.
[6] P. F. Ribeiro, Aysen Arsoy and Yilu Liu, Transmission Power Quality
benefits realized by a SMES-FACTS controller, Procd. of Int. Conf. on
Harmonics and Quality of Power, vol. 1, 1-4, pp. 307-312, Oct. 2000.
[7] A. K. Dahiya, R. Dahiya and D. P. Kothari, Fuzzy Controlled
STATCOM-SMES for Enhancing Transient Stability of SMIB, IJESC,
Vol. 2, No. 2, pp. 81-88, 2010.
[8] A. B. Arsoy, Y. Liu, P. F. Rebeiro and F. Wang, STATCOM-SMES,
Industry Applications Magazine, IEEE, vol. 9, Issue 2, pp. 21-28. MarApr 2003.
[9] M. G. Molina, P. E. Mercado and E. H Watanabe, Dynamic
Performance of a Static Synchronous Compensator with
Superconducting Magnetic Energy Storage, IEEE 36th Conf. on Power
Electronics Specialists Conference 2005, pp. 224230, June 16, 2005.
[10] M. H. Ali, T. Murata and J. Tamura, A Fuzzy Logic-Controlled
superconducting Magnetic Energy Storage for Transient Stability
Augmentation, IEEE Transaction on Control System technology, vol.
15, Issue 1, pp. 114-150, 2007.
[11] D. P. Kothari, Application of neural networks to power systems, IEEE
Proc. of International Conference on Industrial Technology 2000, Vol.
1, pp. 621-626, 2000.
[12] A. M. Hemeida, Artificial Neural Network PI Controlled
Superconducting Magnetic Energy Storage, SMES for Augmentation of
Power Systems Stability, Power System Conference, 2008. MEPCON
2008, 12th International Middle-East, March 2008, pp. 187191, 2008.
[1]

Figure 8. Comparison of active power

Figure 9. Comparison of active power

VII. CONCLUSION
Lyapunove second method is used to include the effect of
STATCOM-SMES on the stability of a SMIB power system
with Automatic Voltage Regular. The LF is energy-type and
the influence of each of the control devices appears on the
energy, synchronization torque, and damping torque. The
method applied to the SMIB system considering the effect of
SMES, LF formulation has shown very effective result with
respect to oscillation damping. During the fault SMES is
capable to absorb the excess electrical energy of the system
which is the main cause of instability of the system hence
increasing the critical clearing time. This excess energy is
stored in SMES and can be utilized during peak demand
hours.
The transient stability of SMIB system connected
with STATCOM-SMES also has been analyzed through the
simulation using SimPowerSystems of MATLAB. The
analysis of results reveal that system is stabile when subjected
to three phase to ground fault. The performances of various
controllers (PI, Fuzzy and ANN) used in STATCOM-SMES
also have been studied. The performances of intelligent
controllers (Fuzzy and ANN) have been found better than PI

APPENDIX
DATA USED:
M=0.0544 , D=0.0054 s;

X d = X q =0.7245 pu;

X ' d =0.1327 pu; K R =31; TR =0.06 s; X e =0.4 pu;,

T ' d 0 5.35s; Pe0 =1.5pu; V=0.9945 pu; VT0 =1.0pu
Lsm 0.5H , I sm0 0.2018 pu,
Vsm 0 , Tdc 0.026 , K s 1.060

46

International Journal of Science and Advanced Technology (ISSN 2221-8386)

http://www.ijsat.com

Volume 1 No 3 May 2011

Anil Kumar Dahiya is graduated in 1990 from M.M.M.

Engg. College, Gorakhpur, India and received M.Tech degrees in
Electrical Power Systems from REC Kurukshetra in 1995. He has
served at various technical institutes and industry. He is currently an
Assistant Professor in the Dept. of Elect. Engg, NIT, Kurukshetra. His
fields of interest are Control and applications of FACTS devices.

Ratna Dahiya is graduated in 1982 from G.B. Pant

University, India and received M.Tech and P.hD degrees in Electrical
Enginnering from REC Kurukshetra in 1988 and 2002 respectively. She
is currently an Associate Professor in the Dept. of Elect. Engg, NIT,
Kurukshetra. Her fields of interest include Power System, Power
Electronics and FACTS devices.

D.P. Kothari is Director General of Vindhya Institute of

Technology & Science, Indore, India. Former Vice-Chancellor of VIT
University Vellore Tamilnadu, Director I/C IIT Delhi, Principal VREC
Nagpur, Professor and Head of the Centre for Energy Studies IIT Delhi
India. He is Fellow of IEEE, National Academy of Engineering, and
National Academy of Sciences. His fields of interest include Power
System, Optimization, Reliability and Energy Conservation.

47