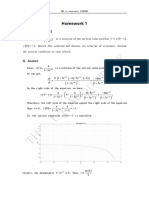
Homework 12 - Solution

(p. 462: 9.37)

Let X1, X2, ..., Xn denote n iid Bernoulli random variables such that
P(Xi = 1) = p and P(Xi = 0) = 1 - p,
for each i = 1, 2, ..., n. Show that i 1 X i is sufficient for p by using the factorization criterion
n

given in Theorem 9.4.

Solution:
xi
The likelihood function is L( p ) p (1 p ) n xi . By theorem 9.4, in1 X i is sufficient for p
X i
with g ( i 1 X i , p ) p
n
(1 p ) n X i and h(y) = 1.

(p. 462: 9.38)

Let Y1, Y2, ..., Yn denote a random sample from a normal distribution with mean and variance 2.
(a) If is unknown and 2 is known, show that Y is sufficient for .
(b) If is known and 2 is unknown, show that i 1 (Yi ) is sufficient for 2.
n 2

(c) If and 2 are both unknown, show that i 1Yi and i 1Yi are jointly sufficient for and 2.
n n 2

[Thus, it follows that Y and S2 are also jointly sufficient for and 2.]

Solution:
For this exercise, the likelihood function is given by

L 1
( 2 ) n / 2 n
n 2

exp[ i1 (2yi 2 ) ] (2 ) n / 2 n exp 21 2 in1 yi 2 ny n 2
2

(a) When 2 is known, Y is sufficient for by Theorem 9,4 with

g ( y , ) exp 2 ny n 2
2 2
and h(y) (2 ) n / 2
n exp[ 21 in1 yi 2 ]
2

(b) When is known, use Theorem 9.4 with

n 2
g ( in1 ( yi ) 2 , 2 ) ( 2 ) n / 2 exp[ i1 (2yi 2 ) ] and h(y ) (2 ) n / 2 .
(c) When and 2 are both unknown, the likelihood can be written in terms of the two statistics

U1 in1Yi and U 2 in1Yi 2 . Let

g (U1 , U 2 , , 2 ) (2 2 ) n / 2 exp( 2U22 ) exp[ 2n 2 ( Un1 ) 2 ] and h(y ) 1

in1Yi and in1Yi 2 are jointly sufficient for and 2.

Y and S2 are also jointly sufficient for and 2 since they can be written in terms of U1 and U2.

(p. 481: 9.80)

Suppose that Y1, Y2, ..., Yn denote a random sample from the Poisson distribution with mean .
(a) Find the MLE for .
(b) Find the expected value and variance of .
(c) Show that the estimator of part (a) is consistent for .
(d) What is the MLE for P(Y = 0) = e-?

Solution:
(a) For the Poisson distribution, the likelihood function would be

L i 1 e yi!
n yi

n y
e n i 1 i
in1 yi !

and the log-likelihood function would be

ln L ln e n y !
n
n i 1yi

i1 i
n i 1 yi ln i 1 ln yi !
n n

Now take the derivative of it with respect to and set it to 0,

yi
n i1 0
n
ln L

Solving it for , we get

Y .
Since the second derivative of the log-likelihood function evaluated at Y is less than 0,
1 Y is the MLE for .
(b) By sampling distribution E ( ) and V ( ) / n .
(c) Since is unbiased and has variance that goes to 0 with increasing n, it is consistent.
Y
(d) By the invariance property, the MLE for P(Y = 0) = e- is e .

(p. 481: 9.81)

Suppose that Y1, Y2, ..., Yn denote a random sample from an exponential distributed population
with mean . Find the MLE of the population variance 2.

Solution:
For the exponential distribution, the likelihood function would be

L i 1 1 e yi /
n

in1yi /
e
n

Then the log-likelihood function is

ln L ln e n
i 1yi / n

i 1 yi / n ln
n

Now take the derivative of it with respect to and set it to 0,

 n
n i12 i 0
ln L y

Solving it for , we get

Y .
Since the second derivative of the log-likelihood function evaluated at Y is less than 0, the
MLE is Y . By the invariance property of MLEs, the MLE of 2 is Y .
2