Академический Документы
Профессиональный Документы
Культура Документы
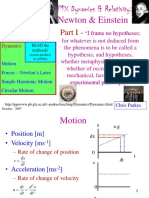
! V + V + V ! A + A + A: Important Reminders Kinematics: Description of Motion
Загружено:
JoØrsh Ênrique Tu Xikytø NînîØflowИсходное описание:
Оригинальное название
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
! V + V + V ! A + A + A: Important Reminders Kinematics: Description of Motion
Загружено:
JoØrsh Ênrique Tu Xikytø NînîØflowАвторское право:
Доступные форматы
Last Lecture Important Reminders Kinematics: Description of Motion
Kinematics - describing 1D motion
All measurements require an origin, a coordinate
Relative velocity (yes, more vectors!) Pset #2 due here tomorrow at 10 am system, and units
Today Next complication is reference frame, the term used to
describe the motion of observer
More dimensions Finish Mastering Physics #3 before next Monday at
Constant velocity is OK, accelerated observer is not
More examples 10pm
Basic definitions:
More vectors
Position
Important Concepts Exam #1 is next Friday at 10am Distance versus displacement
Change=derivative=slope Velocity - change of position
Multiple dimensions are as independent as many objects Speed is the magnitude of velocity
Think carefully about directions (changes the +/- sign) Acceleration - change of velocity
More complicated situations Vector Connections Multi-dimensional Kinematics Problems
More objects ! ! ! Need to think carefully about directions (signs!)
! dr ! dv d 2 r
Write an additional set of equations
v= a= = Need to think carefully about initial conditions
More dimensions dt dt dt 2 Write separate equations for each dimension
Write an additional set of equations
! Read problem carefully to understand the specific
v =
dx dv
a = x = 2
d2x v = vx2 + vy2 + vz2 constraint to use to solve
x dt x dt dt
!
v =
dy
a =
dv 2
y d y
= 2
a = ax2 + ay2 + az2
y dt y dt dt
Special Case of Constant Acceleration Extra special case Super special case
x = x0 + v0 x t + 12 ax t 2 Trajectories with gravity near the surface of the Earth
and no air resistance or other drag forces
Range of a projectile near the surface of the Earth
and no air resistance or other drag forces
vx = v0 x + ax t v0
Y x0 = 0 y0 = 0 y final = 0 x final = Range
y = y0 + v0 yt + 12 ayt 2
X v02 sin(2! )
Range =
vy = v0 y + ayt
g
Physics ax = 0 ay = !g
You should immediately forget you ever saw this formula
Initial conditions v0 x = v0 cos(! ) v0 y = v0 sin(" ) but remember the technique used to find it.
Quadratic Equations Summary
Study special cases (like range of a projectile) but
understand the assumptions that go into all formulas
ax + bx + c = 0
2
Position, velocity, and acceleration are ALL vectors
and need to be manipulated using either arrows
!b b ! 4ac 2
(qualitative) or components (quantitative)
x=
2a Directions (or signs in 1D) of position, velocity, and
acceleration can all be different
Important property: Such equations can have 0, 1, or 2 solutions
depending on the value of b2 -4ac.
Negative: 0 solutions Zero: 1 solution Positive: 2 solutions
Warning: Only one of the 2 solutions may be physical!
Вам также может понравиться
- Green's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)От EverandGreen's Function Estimates for Lattice Schrödinger Operators and Applications. (AM-158)Оценок пока нет
- Fizik4 BölümДокумент13 страницFizik4 BölümHuseyin ERENОценок пока нет
- The Equidistribution Theory of Holomorphic Curves. (AM-64), Volume 64От EverandThe Equidistribution Theory of Holomorphic Curves. (AM-64), Volume 64Оценок пока нет
- Chapter 03 PDFДокумент23 страницыChapter 03 PDFMihir PatelОценок пока нет
- On the Tangent Space to the Space of Algebraic Cycles on a Smooth Algebraic Variety. (AM-157)От EverandOn the Tangent Space to the Space of Algebraic Cycles on a Smooth Algebraic Variety. (AM-157)Оценок пока нет
- P1X Dynamics & Relativity: Newton & Einstein: PartiДокумент26 страницP1X Dynamics & Relativity: Newton & Einstein: PartiavgОценок пока нет
- DynamicsДокумент26 страницDynamicsNikhil Panikkar100% (1)
- Kinematics in Two Dimensions: Projectile MotionДокумент26 страницKinematics in Two Dimensions: Projectile MotionTakudzwa MiltonОценок пока нет
- Notes 01Документ7 страницNotes 01cicin8190Оценок пока нет
- MIT5 73F18 Lec1Документ10 страницMIT5 73F18 Lec1Faradila DanisОценок пока нет
- 4 MSC AFM Governing EquationДокумент61 страница4 MSC AFM Governing Equationhonar.yaseenОценок пока нет
- Day1 TutorialДокумент7 страницDay1 TutorialLouis JohnsonОценок пока нет
- 2 UndeterminedCoefficients SДокумент39 страниц2 UndeterminedCoefficients SRivalelo HeavymanОценок пока нет
- Chapter 2 Motion Part 2Документ19 страницChapter 2 Motion Part 2Mircea PanteaОценок пока нет
- Motion Along A Straight LineДокумент8 страницMotion Along A Straight LineMohamed MohamedОценок пока нет
- Integral Differensial Vektor PDFДокумент9 страницIntegral Differensial Vektor PDFKamenriderОценок пока нет
- Kinematics Formulas and ProblemsДокумент6 страницKinematics Formulas and Problems10B29-viswa DeepakОценок пока нет
- Formulas FinalДокумент2 страницыFormulas FinalTam AdıОценок пока нет
- Chapter 2 Motion Along A Straight LineДокумент11 страницChapter 2 Motion Along A Straight Lineajaysahu1441Оценок пока нет
- Modern PhysicsДокумент63 страницыModern Physicsapi-26870484100% (4)
- Y - Q Y+ y y - : CalculusДокумент17 страницY - Q Y+ y y - : CalculusAarav ShahОценок пока нет
- Chapter 02 Motion in One DimensionДокумент31 страницаChapter 02 Motion in One DimensiongideonmknОценок пока нет
- II Dynamics: Without Reference To The Cause of The MotionДокумент22 страницыII Dynamics: Without Reference To The Cause of The MotionosamaОценок пока нет
- 1 0-KinamaticДокумент49 страниц1 0-KinamaticSfyr sfyrОценок пока нет
- Lecture 10SДокумент17 страницLecture 10SSATISH PATIОценок пока нет
- Differential Equations NoteДокумент25 страницDifferential Equations NoteSumudu DilshanОценок пока нет
- Relativistic Kinematics: Raghunath Sahoo Indian Institute of Technology Indore, India-452020Документ41 страницаRelativistic Kinematics: Raghunath Sahoo Indian Institute of Technology Indore, India-452020aleacunia87Оценок пока нет
- Physics Lecture NotesДокумент8 страницPhysics Lecture NotesbluesОценок пока нет
- 03b Motion2DДокумент7 страниц03b Motion2DMandy KernОценок пока нет
- Mathematics For Engineers PDF Ebook-1006-1010Документ5 страницMathematics For Engineers PDF Ebook-1006-1010robertodjoko001Оценок пока нет
- Motion in One Dimension: 2.1 The Important StuffДокумент26 страницMotion in One Dimension: 2.1 The Important StuffCurieCleous Ann EustaquioОценок пока нет
- Section 3-4: Arc Length With Parametric Equations: X FT y GT TДокумент5 страницSection 3-4: Arc Length With Parametric Equations: X FT y GT Tkahob821Оценок пока нет
- Introduction To Computational Fluid Dynamics: Lecture 2: CFD DiscretizationДокумент63 страницыIntroduction To Computational Fluid Dynamics: Lecture 2: CFD DiscretizationKhayrulIslamОценок пока нет
- Lecture4 8 29Документ6 страницLecture4 8 29Solomon Kaleb GebreabОценок пока нет
- 121 Wi23 EquationSheet MT2Документ3 страницы121 Wi23 EquationSheet MT2于一阳Оценок пока нет
- Fick Second LawДокумент9 страницFick Second LawJohnny WoodsОценок пока нет
- Cinética de La PartículaДокумент48 страницCinética de La PartículaOrlando HsОценок пока нет
- Hdout Chap 2 5210Документ42 страницыHdout Chap 2 5210park ji hyeОценок пока нет
- 210-02 Rectilinear Motion of ParticlesДокумент5 страниц210-02 Rectilinear Motion of ParticlesReggy SeptaОценок пока нет
- Ph-3502 Nandita Mam NoteДокумент16 страницPh-3502 Nandita Mam NoteAnand PrajapatiОценок пока нет
- Chapter 2 Motion Part 1Документ20 страницChapter 2 Motion Part 1Mircea PanteaОценок пока нет
- Uniform Acceleration: 6.1 Events at The Same Proper Distance From Some EventДокумент22 страницыUniform Acceleration: 6.1 Events at The Same Proper Distance From Some Eventsayandatta1Оценок пока нет
- ME230 2014S Homework 02 SolutionДокумент12 страницME230 2014S Homework 02 SolutionNefer PitouОценок пока нет
- 2 Rectilinear Motion (Updated)Документ46 страниц2 Rectilinear Motion (Updated)sefieilgua100% (1)
- Lecture4 Discretization TechniqueДокумент25 страницLecture4 Discretization TechniqueTin DangОценок пока нет
- Chapter 4: Fluids Kinematics: Velocity and Description MethodsДокумент21 страницаChapter 4: Fluids Kinematics: Velocity and Description MethodsADIL BAHОценок пока нет
- Revision Notes3Документ3 страницыRevision Notes3pratyaksh_bharadwajОценок пока нет
- 1.2 Homogeneous EquationДокумент3 страницы1.2 Homogeneous EquationNasir AiyubОценок пока нет
- March 2ndДокумент53 страницыMarch 2ndRucille RamlalОценок пока нет
- Lecture 9: Linear Programming Duality: 1.1 Max FlowДокумент6 страницLecture 9: Linear Programming Duality: 1.1 Max FlowMukesh KumarОценок пока нет
- Diffeq PDFДокумент4 страницыDiffeq PDFGhenoiu PaulОценок пока нет
- 07 Kinematics TransparanciesДокумент22 страницы07 Kinematics TransparanciesMokhampanyane RamokalelaОценок пока нет
- 11 Physics Chapter 2 Comprehensive Notes P3Документ2 страницы11 Physics Chapter 2 Comprehensive Notes P3Keerthe BalaОценок пока нет
- BENG 221 Mathematical Methods in BioengineeringДокумент19 страницBENG 221 Mathematical Methods in Bioengineeringsimona_constantine_3Оценок пока нет
- Odes: Basic Methods: Phys 416/517 Garcia, Chapter 2Документ22 страницыOdes: Basic Methods: Phys 416/517 Garcia, Chapter 2jck23216Оценок пока нет
- Lecture 3 - Fluid Kinematics STДокумент39 страницLecture 3 - Fluid Kinematics SToialjarah13Оценок пока нет
- lctr04 05 0910 0912 HandoutДокумент12 страницlctr04 05 0910 0912 HandoutETHIOPIA INFOОценок пока нет
- Lecture 1 - Numerical Solution of Differential EquationsДокумент50 страницLecture 1 - Numerical Solution of Differential EquationsAli ًSameerОценок пока нет
- Chapter 8 Further Applications of IntegrationДокумент3 страницыChapter 8 Further Applications of Integration祈翠Оценок пока нет
- Happy Holidays! Happy New Year! Welcome Back! Important Reminders Complete Description of MotionДокумент2 страницыHappy Holidays! Happy New Year! Welcome Back! Important Reminders Complete Description of MotionJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- I Important Rem Nders: Energy and Momentum of RotationДокумент1 страницаI Important Rem Nders: Energy and Momentum of RotationJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Important Reminders Complete Description of Motion: " # ! " !! !R " !F ! R F Sin (#)Документ2 страницыImportant Reminders Complete Description of Motion: " # ! " !! !R " !F ! R F Sin (#)JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Prs 01 09 06solДокумент1 страницаPrs 01 09 06solJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Important Reminders Problem-Solving Strategy 4-StepsДокумент5 страницImportant Reminders Problem-Solving Strategy 4-StepsJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Lec 31Документ1 страницаLec 31JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Lec 30Документ2 страницыLec 30JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Lec 12Документ1 страницаLec 12JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Lec 13Документ1 страницаLec 13JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Lec 20Документ1 страницаLec 20JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Block A Collides With Block B. After The Collisions The Two Blocks Stick Together. Which of The Following Is True?Документ2 страницыBlock A Collides With Block B. After The Collisions The Two Blocks Stick Together. Which of The Following Is True?JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Lec 29Документ1 страницаLec 29JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- I Important Rem Nders: G NM KGДокумент1 страницаI Important Rem Nders: G NM KGJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- I Important Rem Nders: A Due To On AДокумент2 страницыI Important Rem Nders: A Due To On AJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- ) Important Reminders Blast From The Past (Early Exam ReviewДокумент2 страницы) Important Reminders Blast From The Past (Early Exam ReviewJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Prs 11 03 05solДокумент1 страницаPrs 11 03 05solJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Prs 11 01 05sol PDFДокумент1 страницаPrs 11 01 05sol PDFJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- I Important Rem Nders: 0 V Cos (!) !G V Sin (")Документ2 страницыI Important Rem Nders: 0 V Cos (!) !G V Sin (")JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- I Important Rem Nders: Note Distinction Between Mass and WeightДокумент2 страницыI Important Rem Nders: Note Distinction Between Mass and WeightJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Prs 11 01 05solДокумент1 страницаPrs 11 01 05solJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Prs 11 08 05solДокумент3 страницыPrs 11 08 05solJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Sit Anywhere. Assigned Seats Will Start This Friday. Pset#1 Due Here Tomorrow at Start of Class. Last LectureДокумент1 страницаSit Anywhere. Assigned Seats Will Start This Friday. Pset#1 Due Here Tomorrow at Start of Class. Last LectureJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- I Important Rem Nders: Constant Velocity Is OK, Accelerated Observer Is NotДокумент2 страницыI Important Rem Nders: Constant Velocity Is OK, Accelerated Observer Is NotJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Prs 11 17 05solДокумент1 страницаPrs 11 17 05solJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Moves Down The Incline. Which of The Does Not Move at All. Which of TheДокумент2 страницыMoves Down The Incline. Which of The Does Not Move at All. Which of TheJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Prs 11 22 05solДокумент3 страницыPrs 11 22 05solJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Lec 2Документ2 страницыLec 2JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Displacement Versus Distance Velocity and Acceleration: Velocity Equal To Zero?Документ2 страницыDisplacement Versus Distance Velocity and Acceleration: Velocity Equal To Zero?JoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Prs 11 29 05solДокумент1 страницаPrs 11 29 05solJoØrsh Ênrique Tu Xikytø NînîØflowОценок пока нет
- Drag On A Circular Cylinder: Instructed byДокумент12 страницDrag On A Circular Cylinder: Instructed byKasun Weerasekara100% (1)
- Sine Rule and Cosine RuleДокумент35 страницSine Rule and Cosine RuleOrtigas Aileen Grace100% (1)
- CH - 03 Mechanical Systems V-07 PDFДокумент72 страницыCH - 03 Mechanical Systems V-07 PDFKld HamedОценок пока нет
- Rotational KinematicsДокумент21 страницаRotational KinematicsRe Zi LeОценок пока нет
- Chapter Test A: Teacher Notes and Answers SoundДокумент5 страницChapter Test A: Teacher Notes and Answers SoundWengОценок пока нет
- Sma 2322 Fluid Mechanics 1Документ2 страницыSma 2322 Fluid Mechanics 1xtnnjrОценок пока нет
- Motion With Uniform AccelerationДокумент3 страницыMotion With Uniform AccelerationShidevОценок пока нет
- Relative Velocity - Wikipedia, The Free EncyclopediaДокумент6 страницRelative Velocity - Wikipedia, The Free EncyclopediaZaw Moe KhineОценок пока нет
- I I R R 7 20 I: 1971 Applied Maths Higher Level Questions 1Документ4 страницыI I R R 7 20 I: 1971 Applied Maths Higher Level Questions 1dawnОценок пока нет
- Projectile PDFДокумент6 страницProjectile PDFSlim ShaddysОценок пока нет
- Ch.02 Modeling of Vibratory SystemsДокумент17 страницCh.02 Modeling of Vibratory SystemsanleОценок пока нет
- Aircraft Stability and Control - Lec04Документ14 страницAircraft Stability and Control - Lec04Akeel AliОценок пока нет
- Investigating The Properties of SoundДокумент15 страницInvestigating The Properties of SoundMaria Rosalia B. ApostolОценок пока нет
- Waves in A Resonance TubeДокумент3 страницыWaves in A Resonance TubeMohammad Al AbdullaОценок пока нет
- Work & EnergyДокумент2 страницыWork & EnergyDerick PeraltaОценок пока нет
- LES For Acoustics by Wei Shyy and Michael J. RycroftДокумент471 страницаLES For Acoustics by Wei Shyy and Michael J. RycroftPeshala GamageОценок пока нет
- Physics Laboratory Activity 2Документ4 страницыPhysics Laboratory Activity 2Mylene NerioОценок пока нет
- Mid-Term Examination - Summer 2021Документ1 страницаMid-Term Examination - Summer 2021Md. Imran AhmedОценок пока нет
- Markscheme: November 2011Документ16 страницMarkscheme: November 2011Ahmad OmarОценок пока нет
- WEEK 3 - Motion in 1D (Graphs of Motion)Документ55 страницWEEK 3 - Motion in 1D (Graphs of Motion)Jhen Ivy100% (1)
- Figuras de Interferencia HiáxicasДокумент19 страницFiguras de Interferencia HiáxicasLeo Alvarez RomeroОценок пока нет
- Chap 05Документ152 страницыChap 05noscribdyoucantОценок пока нет
- Physics MCAT PDFДокумент23 страницыPhysics MCAT PDFZakir HossainОценок пока нет
- Physics Formula SheetДокумент4 страницыPhysics Formula Sheetraheemadom87Оценок пока нет
- Photo Electric Effect by Dr. BCS TewariДокумент22 страницыPhoto Electric Effect by Dr. BCS TewariAdity AОценок пока нет
- Mechanics PowerpointДокумент12 страницMechanics PowerpointRoy MarkОценок пока нет
- MIT2 003SCF11 Pset2 SolДокумент16 страницMIT2 003SCF11 Pset2 SolproflaruscoОценок пока нет
- Problem 1) : Homework No. 3 Instructor: Ali BakhshiДокумент4 страницыProblem 1) : Homework No. 3 Instructor: Ali Bakhshiplamss asawdОценок пока нет
- Turbomachinery (ME-209) : Dr. Sumit Kumar Singh Guest Faculty, Mechanical Engineering Department Tezpur UniversityДокумент28 страницTurbomachinery (ME-209) : Dr. Sumit Kumar Singh Guest Faculty, Mechanical Engineering Department Tezpur UniversityR HОценок пока нет
- Chap2 SHM - Student VersДокумент64 страницыChap2 SHM - Student Vers范其平Оценок пока нет