Академический Документы
Профессиональный Документы
Культура Документы
Families of Curves
Загружено:
Mariz Ellaine BaltazarИсходное описание:
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Families of Curves
Загружено:
Mariz Ellaine BaltazarАвторское право:
Доступные форматы
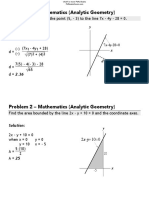
FAMILIES OF CURVES 4. Straight line with slope and x-intercept equal.
Obtain the differential equation of the family of plane curves y
described.
1. Straight lines through the origin.
y
x
x
m=a
General Equation:
y = m(x - a)
where m = slope = arbitrary constant
General Equation: Subst. a = m,
y = mx y = m(x - m)
where m = slope = arbitrary constant dy = m dx
Differentiate, dy
m= = y
dy dx
y = m or m = Substitute,
dx
Substitue m, y = y (x - y)
dy y = xy (y)2
y= x
dx
(y)2 = xy y
y dx = x dy
y dx x dy = 0
5. Circles with centers at the origin.
2. Straight lines through the fixed point (h,k) ; h and k not to be
y General Equation :
eliminated.
x2 + y 2 = r 2
2x dx + 2y dy = 0
y
r x dx + y dy = 0
x
(h,k)
6. Circles with center on the x-axis.
y
General Equation :
General Equation:
(y - k) = m (x - h)
(x-h)2 + y2 = r2
Where m = slope = arbitrary constant
r Differentiate
Differentiate,
x 2(x + h) + 2yy = 0
dy = mdx
dy x h + 2yy = 0
m=
dx Differentiate
Substitute, 1 + (yy + yy) = 0
dy
(y - k) =
dx
(x - h) yy + (y)2 + 1 = 0
(y - k) dx = (x - h) dy
(y - k) dx - (x - h) dy = 0 6. Parabolas with vertex on the x-axis, with axis parallel to the y-axis,
and with distance from focus to vertex fixed as a.
3. Straight lines with slope and y-intercept equal.
y y
m=b x
General Equation :
y = mx + b General Equation:
where m = slope = arbitrary constant (x - h)2 = 4a (y - k)
Substitute b = m, Subst. k = 0
Y = mx + m (x - h)2 = 4ay EQ1
Differentiate, h = arbitrary constant
dy = m dx Differentiate,
dy 2(x - h) = 4ay
m=
dx (x - h) = 2ay
Substitute,
dy dy
(x - h)2 = 4a2 (y) 2
y= x+ Subst. in EQ1
dx dx
y dx = x dy + dy 4a2 (y) 2 = 4ay
y dx - (x + 1) dy = 0 a(y) 2 = y
Вам также может понравиться
- Families of CurvesДокумент2 страницыFamilies of CurvesJoshua RodriguezОценок пока нет
- Integrating Factors Found by InspectionДокумент14 страницIntegrating Factors Found by InspectionGelbert Silot50% (2)
- 11 Substitution Suggested by The EquationДокумент11 страниц11 Substitution Suggested by The EquationMia Manalo100% (1)
- Elimination of Arbitrary ConstantsДокумент6 страницElimination of Arbitrary ConstantsElaine Bicol100% (2)
- Sample Problems - Mech 1Документ26 страницSample Problems - Mech 1Heart VenturanzaОценок пока нет
- Differential EquationsДокумент73 страницыDifferential EquationsJhemson ELis100% (1)
- Diff Eq ModuleДокумент105 страницDiff Eq ModuleRiccalhynne MagpayoОценок пока нет
- D.E 3rd EditionДокумент33 страницыD.E 3rd Editionken100% (2)
- Engineering Economy Lecture 1 PDFДокумент2 страницыEngineering Economy Lecture 1 PDFMichael Angelo Jugador Bas100% (1)
- Enigneering Mechanics 1 Solution ManualДокумент93 страницыEnigneering Mechanics 1 Solution ManualFelicito Espiritu III100% (1)
- Rainville and Bedient Elementary Differential Equations SolutionsДокумент6 страницRainville and Bedient Elementary Differential Equations SolutionsJehu5% (38)
- MODULE 3 Engineering EconomyДокумент34 страницыMODULE 3 Engineering EconomyJohn Carlo Bacalando IIОценок пока нет
- Bernoullis EquationДокумент2 страницыBernoullis EquationMoktar Pandarat Maca-arab100% (1)
- Ch1 - Laplace Transform L.T. - 26 Pgs PDFДокумент26 страницCh1 - Laplace Transform L.T. - 26 Pgs PDFMohamad Duhoki100% (1)
- Elimination of Arbitrary ConstantДокумент5 страницElimination of Arbitrary ConstantMaria Gella Perez100% (1)
- Math 4 Prelim CoverageДокумент41 страницаMath 4 Prelim CoverageZen MarkОценок пока нет
- FRICTIONSДокумент9 страницFRICTIONSKandee Marie ApiОценок пока нет
- MEASUREMENTS WITH TAPE. The Sides of A Rectangular Parcel of PropertyДокумент2 страницыMEASUREMENTS WITH TAPE. The Sides of A Rectangular Parcel of PropertyshemalОценок пока нет
- Analytic Geometry Problems With SolutionsДокумент8 страницAnalytic Geometry Problems With SolutionsMercedita Ginoo100% (1)
- Estiven Gier Problem Sets 1 & 2Документ55 страницEstiven Gier Problem Sets 1 & 2Estiven Gier100% (7)
- Differential EquationsДокумент18 страницDifferential EquationsMargaret FloresОценок пока нет
- Es 23 CouplesДокумент12 страницEs 23 CouplesFranz ValenciaОценок пока нет
- Simple CircuitsДокумент5 страницSimple CircuitsPaolo PerezОценок пока нет
- Eeco 120313Документ21 страницаEeco 120313Argel Linard Francisco Mabaga100% (1)
- Chapter 3Документ62 страницыChapter 3Billy Jake CorpuzОценок пока нет
- Elementary Differential Equations 7th Edition (Ch1-12) Rainville and Bedient PDFДокумент133 страницыElementary Differential Equations 7th Edition (Ch1-12) Rainville and Bedient PDFDarvy Ong55% (11)
- Statically Indeterminate ProblemsДокумент16 страницStatically Indeterminate ProblemsJake CanlasОценок пока нет
- Engineering Econ FinalsДокумент10 страницEngineering Econ FinalsIvan Morise AtienzaОценок пока нет
- D.E. QuestionsДокумент9 страницD.E. Questionsrobertz_tolentino0140% (1)
- Dynamics of Rigid BodiesДокумент14 страницDynamics of Rigid BodiesFelichi Dacumos BalajadiaОценок пока нет
- Differential CalculusДокумент8 страницDifferential CalculusCheyenne El Cabillon100% (1)
- Math WD Solns 3Документ23 страницыMath WD Solns 3Chemuel Mardie G. Obedencio100% (6)
- Lesson 1Документ7 страницLesson 1Ma Aaron Gwyneth BalisacanОценок пока нет
- Strain: 2.5 Statically Indeterminate Problems Illustrative Example 2.6 The Concrete Post in Fig. (A) Is ReinforcedДокумент3 страницыStrain: 2.5 Statically Indeterminate Problems Illustrative Example 2.6 The Concrete Post in Fig. (A) Is ReinforcedJoshua John JulioОценок пока нет
- Softcopy Thermo BastroДокумент29 страницSoftcopy Thermo BastroLester Alfred M. Olasiman100% (1)
- Economics AnnuityДокумент2 страницыEconomics AnnuityGeodetic Engineering FilesОценок пока нет
- Problem Set 10 Partition of Land1 PDFДокумент14 страницProblem Set 10 Partition of Land1 PDFsairin parkОценок пока нет
- Enhancement Review Fluid Mech. Set CДокумент10 страницEnhancement Review Fluid Mech. Set Cᜎᜒᜌᜓᜈᜒᜎ᜔ ᜄ᜔ᜏᜇᜒᜈ᜔Оценок пока нет
- Engineering Mechanics (Rectilinear Motion and Sample Problems)Документ7 страницEngineering Mechanics (Rectilinear Motion and Sample Problems)Kay Mae Lim Pascua40% (5)
- Engiana Quiz 1Документ3 страницыEngiana Quiz 1Ivy SanchezОценок пока нет
- Problem Solving in Dynamics PDFДокумент16 страницProblem Solving in Dynamics PDFAnonymous hK0I8Kwjm100% (2)
- L4 Examples - Exact Differential Equations PDFДокумент16 страницL4 Examples - Exact Differential Equations PDFCarlo EdolmoОценок пока нет
- Solutions To Problems in Statics of Rigid BodiesДокумент34 страницыSolutions To Problems in Statics of Rigid BodiesPaul Gerard AguilarОценок пока нет
- Differential Equation - Examples of Coefficients Linear in Two VariablesДокумент5 страницDifferential Equation - Examples of Coefficients Linear in Two VariablesAimi Najwa ZailanОценок пока нет
- Problem Set No. 1: Ee 420: Basic Electrical and Electronics EngineeringДокумент16 страницProblem Set No. 1: Ee 420: Basic Electrical and Electronics EngineeringWingel Lullaby100% (1)
- MomentДокумент10 страницMomentAngeloLorenzoSalvadorTamayo50% (2)
- Math 121 - MODULE 3Документ18 страницMath 121 - MODULE 3Quines Queenie100% (1)
- System: Problem ExerciseДокумент3 страницыSystem: Problem ExerciseAnnaliza Alcazar ApostolОценок пока нет
- Module 1Документ5 страницModule 1arzОценок пока нет
- 2019 8N DifferentiationДокумент12 страниц2019 8N DifferentiationmitoОценок пока нет
- Linear Equations of The First OrderДокумент1 страницаLinear Equations of The First OrdereulaОценок пока нет
- 2019 8N Differentiation2Документ12 страниц2019 8N Differentiation2加卡内-张进哲Оценок пока нет
- Differential Equations - I - 18.08Документ6 страницDifferential Equations - I - 18.08Sanjoy BrahmaОценок пока нет
- University of Kirkuk College of Engineering Department of Mechanical EngineeringДокумент13 страницUniversity of Kirkuk College of Engineering Department of Mechanical EngineeringMustafa hisham.sОценок пока нет
- Lesson 29 PDFДокумент7 страницLesson 29 PDFShubham KothariОценок пока нет
- Unit IIДокумент50 страницUnit IIapi-352822682100% (1)
- Module2 Topic3 Week4 Differential EquationДокумент4 страницыModule2 Topic3 Week4 Differential EquationCHEZANIE MIYA ASUNCIONОценок пока нет
- 06 Differential EquationДокумент16 страниц06 Differential EquationGeeta MОценок пока нет
- L8 Differential Equation 01Документ3 страницыL8 Differential Equation 01WIIGEENОценок пока нет
- Tables of The Legendre Functions P—½+it(x): Mathematical Tables SeriesОт EverandTables of The Legendre Functions P—½+it(x): Mathematical Tables SeriesОценок пока нет
- Prestressed ConcreteДокумент15 страницPrestressed ConcreteMariz Ellaine BaltazarОценок пока нет
- Tutorial 4Документ17 страницTutorial 4Mariz Ellaine BaltazarОценок пока нет
- Riders Digest 2015Документ140 страницRiders Digest 2015Mariz Ellaine BaltazarОценок пока нет
- Beam DeflectionДокумент37 страницBeam DeflectionMariz Ellaine Baltazar100% (1)
- StrainДокумент1 страницаStrainMariz Ellaine BaltazarОценок пока нет
- Shear and Moment in BeamsДокумент1 страницаShear and Moment in BeamsMariz Ellaine BaltazarОценок пока нет
- Simple StressДокумент2 страницыSimple StressMariz Ellaine BaltazarОценок пока нет
- Non Structural ElementsДокумент72 страницыNon Structural ElementsMariz Ellaine BaltazarОценок пока нет
- Exact EquationsДокумент1 страницаExact EquationsMariz Ellaine BaltazarОценок пока нет
- Families of CurvesДокумент1 страницаFamilies of CurvesMariz Ellaine Baltazar87% (15)
- Introducing The Role of The Quantity Surveyor: Alistair Seel - Partner QS SquaredДокумент21 страницаIntroducing The Role of The Quantity Surveyor: Alistair Seel - Partner QS SquaredMariz Ellaine BaltazarОценок пока нет
- Earthquake Design IntroДокумент26 страницEarthquake Design IntroMariz Ellaine BaltazarОценок пока нет
- Equivalent Lateral Force ProcedureДокумент2 страницыEquivalent Lateral Force ProcedureMariz Ellaine BaltazarОценок пока нет
- Hay 1993 Calculating Solar Radiation For Inclined Surfaces Practical ApproachesДокумент8 страницHay 1993 Calculating Solar Radiation For Inclined Surfaces Practical ApproachesJuan Carlos GonzálezОценок пока нет
- Landslide Hazard Evaluation and Zonation Mapping in Mountainous TerrainДокумент9 страницLandslide Hazard Evaluation and Zonation Mapping in Mountainous TerrainGeologians DUОценок пока нет
- IB MAA SL Calculus PracticeДокумент13 страницIB MAA SL Calculus PracticeXiyue ChenОценок пока нет
- 5 FB e 1stДокумент5 страниц5 FB e 1stYan Hao NamОценок пока нет
- Math 9 Curriculum ChecklistДокумент2 страницыMath 9 Curriculum Checklistapi-506766912Оценок пока нет
- Coordinate Geometry, Relations, Functions, Graphs and VariationsДокумент30 страницCoordinate Geometry, Relations, Functions, Graphs and VariationsAnthony BensonОценок пока нет
- CH12Документ52 страницыCH12blackhawk00001Оценок пока нет
- Entry Test Quick Solution Maths ShortcutsДокумент91 страницаEntry Test Quick Solution Maths Shortcutsfarhan92% (48)
- Nptel Gabion Wall PDFДокумент49 страницNptel Gabion Wall PDFsdutta2591100% (2)
- Astm D 4595 - 17Документ13 страницAstm D 4595 - 17Muhamad HamandiОценок пока нет
- CalculusДокумент4 страницыCalculusClare Anne Therese EsbietoОценок пока нет
- Mark Scheme (Results) January 2023Документ11 страницMark Scheme (Results) January 2023khaled ahmedОценок пока нет
- Year I-Unit 5 Test: IB Mathematics HLДокумент6 страницYear I-Unit 5 Test: IB Mathematics HLnadia sykesОценок пока нет
- Lesson 6-Rectangular Coordinate System and Linear Equation in Two VariablesДокумент35 страницLesson 6-Rectangular Coordinate System and Linear Equation in Two VariablesEliza CalixtoОценок пока нет
- Taleem City Test Series For 12 Class: Objective TypeДокумент9 страницTaleem City Test Series For 12 Class: Objective TypeAhm MalikОценок пока нет
- M1 Statics PDFДокумент12 страницM1 Statics PDFHasharaОценок пока нет
- Nda+2020 +Application+of+Derivatives+in+1+Shot+Документ94 страницыNda+2020 +Application+of+Derivatives+in+1+Shot+yashgalgat319Оценок пока нет
- Unit 15 STRAIGHT LINES AND PAIR OF LINES-1Документ34 страницыUnit 15 STRAIGHT LINES AND PAIR OF LINES-1RonnyОценок пока нет
- Reading 8 Grades, Batters and Longitudinal SectionsДокумент20 страницReading 8 Grades, Batters and Longitudinal SectionsHassan FarhatОценок пока нет
- The Tangent LineДокумент27 страницThe Tangent LineKrisvi Cassandra AlvizОценок пока нет
- Chapter 2: Standard of Presentation: Drafting and Design Presentation Standards Volume 3: Structural Drafting StandardsДокумент30 страницChapter 2: Standard of Presentation: Drafting and Design Presentation Standards Volume 3: Structural Drafting StandardsopulitheОценок пока нет
- CPD Reference Manual: Page 1/31Документ31 страницаCPD Reference Manual: Page 1/31ususariОценок пока нет
- Maths SS 2 WK 3Документ2 страницыMaths SS 2 WK 3Jerry OgugoОценок пока нет
- Specialist Methods T 16-20Документ49 страницSpecialist Methods T 16-20Saquib KhanОценок пока нет
- Differential Calculus: Differentiation. Geometrically, The Derivative at A Point Is TheДокумент10 страницDifferential Calculus: Differentiation. Geometrically, The Derivative at A Point Is TheNirmal BhowmickОценок пока нет
- Highway I Spring 2023 1Документ40 страницHighway I Spring 2023 1Hellin DelОценок пока нет
- Lecture Notes On Mathematics For Business: International School of Business, UEH, VietnamДокумент171 страницаLecture Notes On Mathematics For Business: International School of Business, UEH, VietnamPhuong AnhОценок пока нет
- CE BOARD NOV 2020 Structural Analysis Set 2Документ1 страницаCE BOARD NOV 2020 Structural Analysis Set 2Eugenio Genesis AbadОценок пока нет
- Chapter 6 Practice Answers PDFДокумент10 страницChapter 6 Practice Answers PDFMinson SimОценок пока нет
- MATH 8 Quarter 2 Week 5 Problems Involving Linear Functions Example 1Документ2 страницыMATH 8 Quarter 2 Week 5 Problems Involving Linear Functions Example 1Alfie BurbosОценок пока нет