Measuring Quantum Geometries via Quasi-Coherent States

Introduction
 Structure of spacetime is expected to be quantum at very short distances like at
plank scale.
 One of examples of such geometries is matrix geometries realized by non-trivial
solutions by Yang-Mills models like IKKT or BFSS.
 These geometries (configurations) are defined by set of Hermitian matrices in
the target space.
 These matrices are interpreted as quantized coordinates in target space
equipped with a metric.
 Fuzzy Sphere and Fuzzy Tori are some good examples (Fuzzy Spaces).

Aim
 To differentiate non-geometric and geometric configurations
 And also measure this geometry
Method

 To look for optimally localized states with small dispersion

 Then X (matrices) can almost be simultaneously measured and their expectation
values provide location of some Variety M embedded in the target space R.

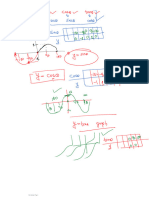
Quasi-Coherent States

 The ground states of matrix Laplacian or matrix Dirac operators in the presence
of point like test brane in the target space.
 The eigenvalues of matrix Laplacian or matrix Dirac operators are interpreted as
displacement energy (energy of the strings stretching between test brane and
the background brane).

Hierarchy of Eigenvalues of Hessian

 For matrix backgrounds which define some approximate semi-classical brane

geometry, the eigenvalues of H must exhibit a clear hierarchy between small
eigenvalues corresponding to tangential directions and eigenvalues O(1) which
correspond to directions transversal to the brane in target space.
Comparison between matrix Laplacian or matrix Dirac operators realizations

 For matrix Laplacian operator ground state energy is strictly positive and
provide information about local dispersion and geometric uncertainty.
 For matrix Dirac operator location of state is recovered form exact zero modes.


Main Points

 To determine the coherent states

 To find Quasi Minimum of displacement energy E