Chapter 9: Tutorial 1 Midpoint and Trapezoid Rules Sec. 9.

Many definite integrals that occur in practical problems cannot be evaluated directly and
therefore, we must use numerical methods to get an approximate answer to the value of the
definite integral.

In this tutorial, we show how Excel can be used to approximate definite integrals.

Midpoint Rule

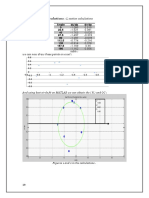
Example Approximate the area under the curve f(x)=1/(1+exp(x)) from x=0 to x=2 using
10 equal subintervals and the midpoints of the subintervals to construct the
rectangles.

Solution We construct a table as follows - since the interval is 2 units, each subinterval is
be of length 0.2 (why?). The midpoints will then be 0.1,0.3 ,...,1.9 (again, why?).

x_i delta_x f(x_i) f(x_i)*delta_x

0.1 0.2 0.475020813 0.0950041625
0.3 0.2 0.425557483 0.0851114966
0.5 0.2 0.377540669 0.0755081338
0.7 0.2 0.331812228 0.0663624456
0.9 0.2 0.289050497 0.0578100995
1.1 0.2 0.249739894 0.0499479789
1.3 0.2 0.214165017 0.0428330034
1.5 0.2 0.182425524 0.0364851048
1.7 0.2 0.154465265 0.030893053
1.9 0.2 0.130108474 0.0260216949

Area ------> 0.5659771729

The approximate area is therefore 0.56598, rounded to five decimal places.

Note that all we had to do to get the answer was sum the last column, since
that corresponds to the Midpoint Rule given in Section 9.4.

U Try It Modify the table above to find the approximate the area under the curve of
f(x)=1/(1+x^2), from x=0 to x=1. Use the midpoint rule with n=10 subintervals.
Be careful with the values for x_i, f(x_i) and delta (they will NOT be the same as
the example).

Trapezoid Rule

Example Approximate the area under the curve f(x)=1/(1+exp(x)) from x=0 to x=2 using
10 equal subintervals and the trapezoidal rule.

Solution We construct a table as follows - since the interval is 2 units, each subinterval is
be of length 0.2 (why?). We then apply the trapezoid rule as given in Section 9.4.

Page 1 of 6 (c) 2003 Prentice Hall, Upper Saddle River, NJ

 i x_i f(x_i)
0 0 0.5
1 0.2 0.450166003
2 0.4 0.40131234
3 0.6 0.354343694
4 0.8 0.310025519
5 1 0.268941421
6 1.2 0.231475217
7 1.4 0.197816111
8 1.6 0.167981615
9 1.8 0.141851065
10 2 0.119202922

Delta_x 0.2

Trap. Rule
Total -----> 0.566702889

Recall that the trapezoid rule is given by T=

0.5*delta_x(f(x_0) +2 (f(x_1) +f(x_2) +...+ f(x_n-1)) + f(x_n))

Question Can you write down the formula for the Trapezoid Rule total above using
the cell references? Check your answer by clicking into the Trap. Rule
Total cell.

U Try It Modify the table above to find the approximate the area under the curve of
f(x)=1/(1+x^2), from x=0 to x=1. Use the trapezoid rule with n=10 subintervals.
Be careful with the values for x_i, f(x_i) and delta (they will NOT be the same as
the example).

Problems #7-14, Sec. 9.4. You should use more subintervals than those suggested by
the text since you have a computer.

Page 2 of 6 (c) 2003 Prentice Hall, Upper Saddle River, NJ

Chapter 9: Tutorial 2 Simpson's Rule Sec. 9.4

We continue the example in Chapter 9, Tutorial 1 - this time we use Simpson's

Rule to approximate the integral.

Simpson's Rule

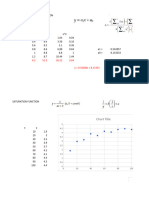
Example Approximate the area under the curve f(x)=1/(1+exp(x)) from x=0 to x=2 using
10 equal subintervals and Simpson's rule.

Solution We construct a table as follows - since the interval is 2 units, each subinterval is
be of length 0.2 (why?). We then apply Simpson's rule as given in Section 9.4.

Method A Note that Simpson's Rule also uses the midpoints of each subinterval, in addition
to the endpoints. Rather than implement the formula (4) in Section 9.4, we can
use the fact that S = 2/3 M + 1/3 T, where M and T are the approximations
using the midpoint and trapezoid rules, respectively.

We next give the tables for the midpoint and trapezoid rules as generated in the
previous tutorial.
Midpoint Rule

x_i delta_x f(x_i) f(x_i)*delta_x

0.1 0.2 0.475021 0.095004163
0.3 0.2 0.425557 0.085111497
0.5 0.2 0.377541 0.075508134
0.7 0.2 0.331812 0.066362446
0.9 0.2 0.28905 0.057810099
1.1 0.2 0.24974 0.049947979
1.3 0.2 0.214165 0.042833003
1.5 0.2 0.182426 0.036485105
1.7 0.2 0.154465 0.030893053
1.9 0.2 0.130108 0.026021695

M ------> 0.565977173
Trapezoid Rule

i x_i f(x_i)
0 0 0.5
1 0.2 0.450166
2 0.4 0.401312
3 0.6 0.354344
4 0.8 0.310026
5 1 0.268941
6 1.2 0.231475
7 1.4 0.197816
8 1.6 0.167982
9 1.8 0.141851

Page 3 of 6 (c) 2003 Prentice Hall, Upper Saddle River, NJ

 10 2 0.119203

Delta_x 0.2

Trap. Rule
T ------> 0.566703

Now, we just apply the formula for S to get

Simpson's Rule
S -------> 0.566219

Method B We can also implement Formula(4) from Section 9.4 directly using the following
table. Note that you need the midpoints as well the endpoints of the subintervals.

i x_i a_i f(x_i) f(a_i)

0 0 0.5
1 0.1 0.2 0.475021 0.450166003
2 0.3 0.4 0.425557 0.40131234
3 0.5 0.6 0.377541 0.354343694
4 0.7 0.8 0.331812 0.310025519
5 0.9 1 0.28905 0.268941421
6 1.1 1.2 0.24974 0.231475217
7 1.3 1.4 0.214165 0.197816111
8 1.5 1.6 0.182426 0.167981615
9 1.7 1.8 0.154465 0.141851065
10 1.9 2 0.130108 0.119202922

Note that the x_i are the midpoints of each

Delta_x 0.2 subinterval and a_i are the endpoints of the
subintervals.

Simpson's Rule
S -------> 0.566219

Question Can you write down the formula for the Simpson's Rule S above using
the cell references? Check your answer by clicking into the Simpson's Rule
S cell.

The answers for both methods of calculation for Simpson's Rule are the same,
as they ought to be.

Problems #21-24, Sec. 9.4. You should use more subintervals than suggested
since you're using a computer.

Page 4 of 6 (c) 2003 Prentice Hall, Upper Saddle River, NJ

Chapter 9 : Project 1 Error Analysis for Approximate Integration

Consider the area under the of f(x) =1/x from x=1 to x=3.

(1) Express the area as a definite integral and evaluate it exactly. The exact answer will
be referred to as I in the following parts.

(2) Use the trapezoid rule with 10, 20 and 40 subintervals to approximate I. For each
set of subintervals, determine the error | T - I |, where T is an approximation using the
trapezoid rule. Summarize the information in a table like the one below:

# subintervals | T- I |
10
20
40

(3) Examining the table in part (2), what do you notice about the error as the number of
subintervals is doubled? How does this corroborate the statement in Section 9.4 about
the effect on the error of doubling the number of subintervals?

(4) Repeat parts (2) and (3) using Simpson's rule. You may want to review Tutorial 1 and 2 of
this chapter to set up the computations properly.

Page 5 of 6 (c) 2003 Prentice Hall, Upper Saddle River, NJ

Chapter 9 : Project 2 Estimating Distance Traveled by a Rocket

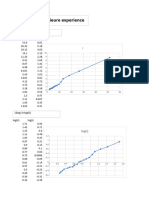
Upon takeoff, the velocity readings of a rocket noted every second for 10 seconds were as
follows: (Problem 27, Section 9.4)

t (sec.) v(t) (ft/sec)

0 0
1 30
2 75
3 115
4 155
5 200
6 250
7 300
8 360
9 420
10 490

(1) Plot the velocity function as a function of time - use X-Y Scatter with only the point plot
option (i.e. do not connect the dots).

(2) Estimate the distance traveled by the rocket during the first 10 seconds using the trapezoid
rule.

(3) Use your graph in part(1) to indicate (with pen on paper) the area corresponding to using the
trapezoid rule in part (2). (See problem 31 in Section 9.4 for more information about the
trapezoid rule.)

(4) To believe in the result given by the trapezoidal rule approximation in part(2), what are
we assuming about the behavior of the velocity function in between the times that the readings
of the velocity are taken?

Page 6 of 6 (c) 2003 Prentice Hall, Upper Saddle River, NJ