This document is marked Internal. Do not distribute outside of the organization.

A satellite dish is a perfect

example of the reflective
properties of parabolas mention
earlier. The signals that are
received are directly sent to the
focus, which are then correctly
reflected to a receiver (signals are
sent out parallel to the axis).

If one is to observe suspension

bridges, the shape of the cables
which suspend the bridge
resemble a parabolic curve. There
has been sufficient confusion
about whether the cables are
suspended in a parabola or a
catenary. Studies show that the
shape is nearer to a parabola. The
cables would have been
hyperbolic, but when a uniform
load (the horizontal deck) is
present, they get deformed like a
parabola.

Fountains spray water in the air,

the water jet propels upwards
reaching a specific altitude, and
then comes back. Again the path
traced by the stream of water is
similar to a parabola.

This document is marked Internal. Do not distribute outside of the organization.

 Take the example of any object
thrown up in the air. It goes up in
the air till its highest attainable
height or point and then comes
down back to the ground. If one is
to trace the path of the object, the
resulting curve obtained is a
parabola. The point at which you
release the ball and the altitude
forms a line (Y axis on a graph).
The midpoint of this line is
bisected by a perpendicular from
the vertex of the parabola. The
speed and air resistance might
distort the shape sometimes.

This is the same principle like the

one used in a torch. The inner
surface is smooth and made of
glass which makes it a powerful
reflector. The principle used here
is that the light source is at the
focus, and the light rays will be
reflected parallel to the axis. This
is the reason one can see a thick
focused beam of light emitting
from a headlight.

This document is marked Internal. Do not distribute outside of the organization.

WHAT IS A PARABOLA? WHAT ARE THE IMPORTANT
THINGS WE NEED TO REMEMBER?

 The graph of a quadratic function is a U-shaped curve called a

parabola.

 The sign on the coefficient a of the quadratic function affects

whether the graph opens up or down. If a<0a<0, the graph makes a
frown (opens down) and if a>0a>0 then the graph makes a smile
(opens up).

 The extreme point (maximum or minimum) of a parabola is called

the vertex, and the axis of symmetry is a vertical line that passes
through the vertex.

 The x-intercepts are the points at which the parabola crosses the x-
axis. If they exist, the x-intercepts represent the zeros, or roots, of
the quadratic function.

This document is marked Internal. Do not distribute outside of the organization.

WHAT ARE THE PROPERTIES OF A PARABOLA?
The eccentricity of any parabola is 1.

The parabola is symmetric about its axis.

The axis is perpendicular to the directrix.

The axis passes through the vertex and the focus.

This document is marked Internal. Do not distribute outside of the organization.

 WHAT ARE THE EQUATIONS OF A PARABOLA?
The standard form of a parabola with Vertex at the origin 𝑉(0,0)

𝐹(0, 𝑐) directrix ℓ: 𝑦 = −𝑐 𝑥 2 = 4𝑐𝑦

𝐹(𝑐, 0) directrix ℓ: 𝑦 = 𝑐 𝑦 2 = 4𝑐𝑥

The standard form of a parabola with Vertex at 𝑉(ℎ, 𝑘)

(𝑥 − ℎ)2 = 4𝑐(𝑦 − 𝑘)

𝐹 (ℎ, 𝑘 + 𝑐)
ℓ: y = k − c

(𝑦 − 𝑘)2 = 4𝑐(𝑥 − ℎ)
𝐹 (ℎ + 𝑐, 𝑘)

ℓ: y = h − c

This document is marked Internal. Do not distribute outside of the organization.

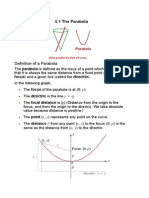
 PARTS OF THE PARABOLA
 Vertex: The point at which a parabola changes direction,
corresponding to the minimum or maximum value of the quadratic
function.
 Axis of symmetry: A vertical line drawn through the vertex of a
parabola around which the parabola is symmetric.
 The latus rectum of a conic section is the chord (line segment) that
passes through the focus, is perpendicular to the major axis and has
both endpoints on the curve.
 A parabola is set of all points in a plane which are an equal distance
away from a given point and given line. The point is called
the focus of the parabola.
 Directrix of a conic section is a line such that ratio of the distance of
the points on the conic section from focus to its distance from
directrix is constant.

This document is marked Internal. Do not distribute outside of the organization.

 NOW THAT YOU ALREADY KNOW THE EQUATIONS OF A
PARABOLA, I’LL GIVE SOME EXAMPLE FOR YOU TO UNDERSTAND
IT THOROUGHLY!
A satellite dish shaped like a paraboloid has its receiver located at the focus.
How far is the receiver from the vertex if the dish is 10 ft. across and 3 ft.
deep at the center?

The equation is 𝑥 2 = 4𝑐𝑦 because the parabola opens upward.

We will use (5,3) so it will be easier.

Let’s substitute the (5,3) to the equation. It will be 52 = 4𝑐(3)

25 = 12𝑐
25 12𝑐
12
= 12
25 1
12
= 𝑐 or 2 12 ft.
1
The receiver is 2 12 ft from the vertex.

This document is marked Internal. Do not distribute outside of the organization.

A certain bridge is supported by a reinforced parabolic arc. The bridge deck,
being the directrix of the parabola arc, has the equation y=24, where 24
represents its vertical clearance of 24 ft. from the surface of the river. The
bridge deck is 6 ft. above the peak of the arc. If the tallest column in the left
represents the y-axis and is 60 ft. away from the corresponding column to
the right, find the coordinates of the vertex, focus, and the general
equation that describes the arc.

The parabolic open downwards, so the equation is of the form of

(𝑥 − ℎ)2 = −4𝑐(𝑦 − 𝑘).

The distance between the bridge deck and the peak of the parabola is 6 ft.,
which gives us the value of 𝑐 = 6.

Since the bridge deck is 24 ft above the surface of the river, the
y−coordinate of the vertex is 18. The distance between the two
corresponding columns is 60 ft. Since the structure and its parabolic arc is
symmetric, the vertex must be midway between the two columns. Its
x−coordinate should be then 30.

Thus, the vertex is located at (30,18)

Plugging in the value of c and the coordinates of the vertex into the
equation, we now have the equation (𝑥 − 30)2 = 24(𝑦 − 18).

The focus os 6 ft below the vertex; hence, its coordinates are (30,12).

The endpoints of the latus rectum are 12 ft both to the left and to the right,
giving us the coordinates (18,12) & (42,12)

This document is marked Internal. Do not distribute outside of the organization.

Hailey wants to know the graph of the parabola using the given below.
What will be the focus and the directrix? Find them without using an
equation.

𝑉(0,0) 𝐿𝑅 = 6 (−3,4), (3,4)

Answer: 𝐹(0,4) 𝑦 = −4

James was given a focus and a directrix, if 𝐹(3,2) and ℓ: 𝑦 = −2, what will
be the equation of the parabola?

Since the distance between the vertex and the focus is equal to the distance
between the vertex and the directrix, the vertex is aligned in the x-axis which
is 𝑉(3,0).

|𝑐| = |𝐹𝑉| = |2 − 0| 𝑐 = 2
(𝑥 − ℎ)2 = 4𝑐(𝑦 − 𝑘)

(𝑥 − 3)2 = 4(2)(𝑦 − 0)

Answer: (𝑥 − 3)2 = 8𝑦

Sean was given an equation. What will be the Vertex, Focus, Directrix, Axis
of Symmetry and the endpoints of the Latus Rectum if the equation is

𝑦 2 = −16(𝑥 − 3)?

𝑉(3,0)
𝐹: 4𝑐 = 16 𝑐 = 4 𝐹(3 − 4,0) = (−1,0)

𝐷: 𝑥 = 3 + 4 𝑥=7
𝐴𝑥𝑖𝑠 𝑜𝑓 𝑆𝑦𝑚𝑚𝑒𝑡𝑟𝑦: 𝑦 = 0
𝐿𝑅1 = (−1,8) 𝐿𝑅2 = (−1, −8)

This document is marked Internal. Do not distribute outside of the organization.