CLL261-Dynamic characteristics of more complicated

process
Hariprasad Kodamana
IIT DELHI

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 1 / 24

Poles of a TF

Consider a transfer function

K
G(s) = (1)
s(τ1 s + 1)(τ22 + 2ζτ2 s + 1)

Denominator of a TF is called characteristic polynomial

Roots of the characteristic polynomial are called poles
Poles of (1):
q q
−1 −ζ (1 − ζ 2 ) −ζ (1 − ζ 2 )
s1 = 0, s2 = , s3 = +j , s4 = −j
τ1 τ2 τ2 τ2 τ2
(2)

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 2 / 24

Poles of a TF

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 3 / 24

Zeros

The dynamics of a process are affected not only by the poles of

G(s)
THey are also affected by the values of s that cause the
numerator of G(s) to become zero
These values are called the zeros of G(s)
For a general transfer function:

bm s m + · · · + b1 s1 + b0 bm (s − z1 ) · · · + (s − zm )
G(s) = n
=
a n s + · · · + a 1 s1 + a 0 an (s − p1 ) . . . (s − pn )
(3)

where zi and pi are the poles ans zeros, respectively.

m ≤ n for system to be physically realizable

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 4 / 24

Inverse response

K(1 + t 3 s )
G(s) =
(1 + t 1s )(1 + t 2 s ) slope (t = 0) ¹ 0
If t3 > 0 ….fast response
t 3 < 0 ....inverse response
t 3 : zero of transfer function

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 5 / 24

Inverse response -example

An inverse response can occur in a distillation column when the

steam pressure to the reboiler is suddenly changed
However, the initial effect usually is to increase the amount of
frothing on the trays immediately above the reboiler, causing a
rapid spillover of liquid from these trays into the reboiler below
This initial increase in reboiler liquid level, is later overwhelmed
by a decrease due to the increased vapor boil-up.

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 6 / 24

Two parallel first order systems

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 7 / 24

Process with time delays

Also called dead time or transport delays

Generally occurs due to
Fluid flow in a pipe
Transport of solid material (e.g., conveyor belt)
Chemical analysis
Sampling line delay
Time required to do the analysis (e.g., on-line gas
chromatograph)

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 8 / 24

Time delay
A time delay, θ , between an input u and an output y results in
the following expression:

0 for t < θ
y (t) = (4)
u(t − θ) for t ≥ 0
Y (s) −θs
G(s) = e (5)
U(s)

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 9 / 24

Polynomial approximations of time delay
The exponential form of G(s) = YU(s)
(s) −θs
e is a nonrational
transfer function
It cannot be expressed as a rational function, a ratio of two
polynominals
Consequently, it cannot be factored into poles and zeros, a
convenient form for analysis
Approximating e −θs using Taylor series expansion
θ2 s 2 θ3 s 3
e −θs ≈ 1 − θs + − (6)
2! 3!
Approximating e −θs using a 1/1 Pade approximation:

−θs 1 − 2θ s
e ≈ G1 (s) = (7)
1 + 2θ s

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 10 / 24

Polynomial approximations of time delay
Approximating e −θs using a 2/2 Pade approximation:
θ2 s 2
−θs 1 − 2θ s + 12
e ≈ G2 (s) = θ2 s 2
(8)
1 + 2θ s − 12

First prder plus time delay system

Ke −θs
G(s) = (9)
τs + 1

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 11 / 24

Approximation of higher order transfer functions

By first order Taylor series

e θ0 s ≈ 1 − θ0 s (10)

Hence,

1 1
e −θ0 s = ≈ (11)
e θ0 s 1 + θ0 s
where the time constant has a value of θ0
These expressions can be used to approximate the pole or zero
term in a transfer function

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 12 / 24

Skogestad’s half rule

Skogestad (2002) has proposed an approximation method for

higher-order models that contain multiple time constants.
He approximates the largest neglected time constant in the
following manner:
One half of its value is added to the existing time delay (if any)
and the other half is added to the smallest retained time
constant.
Time constants that are smaller than the ”largest neglected
time constant” are approximated as time delays using:
1 1
e −θ0 s = ≈ (12)
e θ0 s 1 + θ0 s

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 13 / 24

Approximation of higher order transfer functions

Consder the following transfer fuction:

K (−0.1s + 1)
G(s) = (13)
(5s + 1)(3s + 1)(0.5s + 1)

Aprroximate (13) using (i) Taylor series (ii) Skogestad’s half rule

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 14 / 24

Approximation of higher order transfer functions

Solution

(a) The dominant time constant (5) is retained. Applying

the approximations in :

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 15 / 24

Approximation of higher order transfer functions
(b) To use Skogestad’s method, we note that the largest neglected
time constant in has a value of three.

• According to his “half rule”, half of this value is added to the

next largest time constant to generate a new time constant

• The other half provides a new time delay of 0.5(3) = 1.5.

• The approximation of the RHP zero in provides an additional
time delay of 0.1.
• Approximating the smallest time constant of 0.5 in by
produces an additional time delay of 0.5.
• Thus the total time delay in is,

θ = 1.5 + 0.1 + 0.5 = 2.1

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 16 / 24

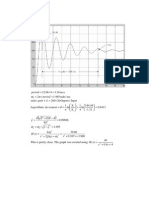
Approximation of higher order transfer functions
The normalized step responses for G(s) and the two approximate
models are shown.
Skogestad’s method provides better agreement with the actual
response.
Chapter 5

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 17 / 24

Non-interacting systems

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 18 / 24

Non-interacting systems

H10 (s) K1 Q 0 (s) 1

= , 10 = (14)
Qi0 (s) τ1 s + 1 Hi (s) K1
H20 (s) K2 0
Q (s) 1
= , 10 = (15)
Q10 (s) τ1 s + 1 H1 (s) K2
H20 (s) 0 0 0
H2 (s) Q1 (s) H1 (s) K2
= 0 0 0
= (16)
Qi (s) Q1 (s) H1 (s) Qi (s) (τ1 s + 1)(τ2 s + 1)
Hn0 (s) Kn
= Qn (17)
Qi0 (s) i=1 τn s + 1
Qn0 (s) 1
= Qn (18)
Qi0 (s) i=1 τn s + 1

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 19 / 24

Interacting systems

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 20 / 24

State-space models

ẋ = Ax + Bu + Ed (19)
y = Cx (20)

x state vector; u is the input vector of manipulated variables; d is the

disturbance vector; and y is the output vector of measured variables.
The elements of x are referred to as state variables. The elements of
y are typically a subset of x , namely, the state variables that are
measured. In general, x , u, d and y are functions of time.

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 21 / 24

Stability of state space models

A state space model is said to be stable if the response x (t) is

bounded for all u(t) and d(t) that are bounded
The state-space model will exhibit a bounded response x (t) for
all bounded u(t) and d(t) if and only if all of the eigenvalues of
A have negative real parts
Note that stability is solely determined by A; the B, C , and E
matrices have no effect

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 22 / 24

Relationship between state space and transfer
function
State space model:

ẋ = Ax + Bu + Ed (21)
y = Cx (22)

By taking Laplace transform:

sX (s) = AX (s) + BU(s) + ED(s) (23)

Y (s) = CX (S) (24)

If Y (s) = Gp (s)U(s) + Gd (s)D(s), then Gp (s) = C (sI − A)−1 B

and Gd (s) = C (sI − A)−1 E

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 23 / 24

 Thank you!

HK (CHE IITD ) CLL261-PDC 20-OCT-2020 24 / 24