Plane Electromagnetic Waves

Electromagnetics
Plane Waves
Plane Electromagnetic Waves Plane waves in lossless media Plane waves in lossy media Group velocity Flow of electromagnetic power Poynting vector Incidence at conducting boundary Incidence at dielectric boundary Incidence at multiple dielectric interfaces
C-N Kuo, Winter 2004
Electromagnetics
Plane Waves
Energy Transmission
Energy stored in the static electric and magnetic fields. Electromagnetic waves carry with the electromagnetic power. Energy is transported through space (media) to distant receiving points by electromagnetic waves.
1 2E E 2 =0 2 c t
2
Electromagnetics
Plane Waves
Maxwells Equation
Differential Form E = B t Integral Form Significance Faraday's Law Ampere's Circuital Law Gauss' s Law No Isolated Magnetic charge
E dl =
c
d dt
D H = J + t D = B = 0
D H dl = I + t ds c S
D ds = Q
S
B ds = 0
S
Electromagnetics
Plane Waves
For a source free medium, EM relations:
H E = t E = 0
E H = t H = 0
1 2E 2 E 2 2 = 0 c t 1 2H 2 H 2 =0 2 c t
( H ) 2E E = = 2 t t E = ( E ) 2 E = 2 E 2E 2 E 2 = 0 t 1 2E if c = 1 / 2 E 2 2 = 0 c t
Electromagnetics
Plane Waves
Time-Harmonic Fields
Arbitrary periodic time functions can be expanded into Fourier series of harmonic sinusoidal components; and transient nonperiodic functions can be expressed as Fourier Integral Maxwells equations are linear differential equations, sinusoidal time variations of source functions of a given frequency will produce sinusoidal variations of E and H with the same frequency in the steady state. Thus, for source functions with an arbitrary time dependence, electrodynamics fields can be source functions.
E ( x, y, z , t ) = Re[ E ( x, y, z )e jt ] E = jH H = jE E = H = 0
= 0(source free)
5
Electromagnetics
Plane Waves
Source-Free Fields
For free-space (simple, non-conducting source-free medium), Helmholtzs equation
r r 2 E + ko E = 0
2
r r 2 H + ko H = 0
2
where free-space wavenumber
k o = o o =
ko =
where c =
o o
3 10 8 ( m / sec)
o =
2 ko
In Cartesian coordinates, each field component follows this equation. Consider the E field component in the x direction.
2Ex 2 2 2 2 2 ( 2 + 2 + 2 + k o ) E x ( x , y , z ) = 0 uniform plane wave + ko E x = 0 E x ( x, y , z ) = E x ( z ) x y z z 2

Consider uniform plane wave with z-dependence
C-N Kuo, Winter 2004 6
Electromagnetics
Plane Waves
Plane Waves in Lossless Media

Solutions of wave equation are traveling waves (unique solution).
+ E x ( z ) = E x ( z ) + E x ( z )
= Eo+ e jko z + Eo e + jko z

+z direction -z direction
Constants are determined by B.C. Instantaneous fields
E x+ ( z , t ) = Eo+ cos(t ko z )
Electromagnetics
Plane Waves
Traveling Waves
At successive times the curve effectively travels in the positive z direction. For a point of a particular phase (fixed phase),
t ko z = const
Phase velocity in free space the velocity of propagation of an equi-phase front.
dz up = = = dt ko
o o
=c
Electromagnetics
Plane Waves
Magnetic Field
Associated magnetic field can be determined by curl E.
Consider only Ex component exists.
ax E = 0
+ Ex ( z)
ay 0 0
az + + = j o (a x H x + a y H y + a z H z+ ) z 0
+ k 1 E x ( z ) 1 1 + Hy = = ( Eo+ e jko z ) = o Eo+ e jko z = E x+ j o z j o z o o
note:
H y ( z) =
E x ( z )
Intrinsic impedance for free-space. (real number)
o =
o
ko
o = 120 377 () o
9
Electromagnetics
Plane Waves
Example 8-1
Uniform plane wave propagates in a lossless simple medium in the +zdirection.
Write the instantaneous expression for E for any t and z. Write the instantaneous expression for H. Determine the locations where Ex is a positive maximum when t=10^-8(s)
r E = ax Ex
r = 4, r = 1, = 0
f = 100MHz , E x ,max = 10 4 (V / m) at t = 10 -8 & z =
1 8
10
Electromagnetics
Plane Waves
Example 8-1 (cont)

wavenumber and wavelength.
k o = =
2 3 = (m) k 2
2 10 8 r r = 3 10 8
4=
4 ( rad / m ) 3
Expression for E field.
r E = a x E x = a x 10 4 cos(t kz + )
8
1 k maximum @ 2 10 0 k + = 0 = = (rad ) 8 8 6 r 4 x 10 4 cos(2 108 t E=a z+ ) 3 6 4 1 ( z )] = a x 10 4 cos[2 108 t 3 8

Electromagnetics
Plane Waves
Example 8-1 (cont)

Expression for H field.
r Ey H ( z, t ) = a y H y = a y
o = 60 () r
10 4 4 1 = ax cos[2 108 t ( z )] 60 3 8
At t=10^-8 (sec)
8
maximum of cosine function occurs at

4
4 1 2 10 (t = 10 ) ( z ) = 2n 3 8 13 3 13 z = n = n n = 0,1,2 K 8 2 8
Electromagnetics
Plane Waves
Transverse Electromagnetic Waves

A transverse electromagnetic (TEM) wave is a wave for which the electric and magnetic field vectors lie in a plane which is transverse or perpendicular to r r jkz the axis of propagation.
E ( z ) = Eo e
Phasor expression for a general form.
r r jk x jk y y jk z E ( x , y , z ) = Eo e x e e z
r r 2 E+k E =0 r 2 2 2 2 ( 2 + 2 + 2 + k ) E ( x, y , z ) = 0 x y z
2
r H
r E
2 where k x2 + k y + k z2 = 2 = k 2
13
Electromagnetics
Plane Waves
Constant Phase Plane

Define wavenumber vector.
r k = a x k x + a y k y + a z k z = kan r R = ax x + a y y + az z
r r r r r jkr R r jka R n E ( R ) = Eo e = Eo e
Constant phase plane.
r r r k R = kan R = constant
14
Electromagnetics
Plane Waves
Characteristic of Plane-wave Solution

r r In charge-free region, E = 0 E (e jk R ) = 0 o
Since
(e jk R ) = (a x
jk y + ay + a z )(e jk x x e y e jk z z ) x y z
jk y y jk z z
= j (a x k x + a y k y + a z k z )e jk x x e = jkan e jk R
r r jk R Eo ( jkan e ) = 0 Eo a n = 0
E field is transverse to the direction of propagation.
15
Electromagnetics
Plane Waves
TEM Waves
Uniform plane wave is a TEM wave with E and H field perpendicular to each other. Express H field in terms of E field.
r r r r r r 1 1 H ( R) = E ( R ) = an E ( R ) j
Express E field in terms of H field.
r r r r jkr R H ( R) = H o e
r r r r jka R 1 n H ( R ) = ( a n Eo ) e
r r r r r r 1 E ( R) = H ( R) = an H ( R) j
Electromagnetics
Plane Waves
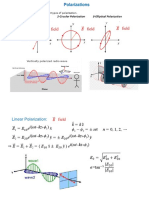
Polarization
The polarization of a uniform plane wave describes the time-varying behavior of the electric field intensity vector at a given point in space. Linear polarization.
Field is fixed in one direction (in space quadrature, but in time phase).
Circular polarization.
Superposition of two linearly polarized waves (both in space and time quadrature).
General expression. r time harmonic field
E ( z ) = a x E1 ( z ) + a y E2 ( z ) = a x E10 e jkz a y jE20 e jkz (*assume E2(z) leads E1(z)by 90 0 r E ( z , t ) = Re{[a x E1 ( z ) + a y E2 ( z )]e jt }
instantaneous field
= a x E10 cos(t kz ) + a y E20 cos(t kz ) 2

Electromagnetics
Plane Waves
Circular Polarization
Observe field at z=0.
r E (0, t ) = a x E1 (0, t ) + a y E2 (0, t ) = a x E10 cos(t ) + a y E20 sin(t )

angular velocity
18
Electromagnetics
Plane Waves
Circular Polarization (cont)

Right-hand (positive circularly polarized wave)
Finger of the right hand follow the direction of the rotation of E, the thumb points to the direction of wave propagation. Counterclockwise direction. r
E ( z ) = a x E1 ( z ) + a y E2 ( z )
= a x E10 e jkz a y jE20 e jkz

Left-hand (negative circularly polarized wave)
Clockwise direction.
r E ( z ) = a x E1 ( z ) + a y E2 ( z ) = a x E10 e jkz + a y jE20 e jkz
19
Electromagnetics
Plane Waves
Linear Polarization
If E2(z) and E1(z) are in space quadrature, but in time phase.
r E (0, t ) = (a x E10 + a y E20 ) cos t
General expression.
r E ( z , t ) = a x E10 cos(t kz ) + a y E20 cos(t kz )

Note: the reception of transmitted signal must be coincident with the polarization.
20
Electromagnetics
Plane Waves
Example 8-3
Decomposition of linearly polarized plane wave into a right-hand circularly polarized wave and a left-hand circularly polarized wave of equal amplitude.
r E ( z ) = a x E0 e jkz = E0 E (a x ja y )e jkz + 0 (a x + ja y )e jkz 2 2

left-hand circular polarization
right-hand circular polarization
21
Electromagnetics
Plane Waves
Plane Waves in Lossy Media

In a source-free lossy medium, the homogeneous vector Helmholtzs equation:
2 E + kc E = 0
2
kc =
c = ( ' j " ) =
1+ j
Define propagation constant
= jk c = j c " = j ' 1 j = j 1 + ' j = + j phase constant

attenuation constant
Electromagnetics
Plane Waves
Low-Loss Dielectrics
Low-loss dielectric is a good but imperfect insulator with a nonzero equivalent conductivity.
= + j j '[1 j "
(Np/m) 2 ' 1 " 2 '[1 + ( ) ] (rad/m) 8 ' " 1 / 2 " c = (1 j ) (1 + j ) ' ' ' 2 '
" 1 " 2 + ( ) ] 2 ' 8 '
complex impedance implies E and H fields are not in time phase.
1 1 " 2 up = [1 ( ' ) ] ' 8
23
Electromagnetics
Plane Waves
Good Conductors
A good conductor is a medium for which
>> 1
= j 1 +
= = f
j j
f,
= j
j =
1+ j 2
c =
= (1 + j )
f = (1 + j )
magnetic field intensity lags behind the electric field intensity by 45 deg.
2 up =
Electromagnetics
Plane Waves
Skin Depth
At very high frequencies the attenuation constant tends to be very large for a good conductor. The amplitude of a wave will be attenuated by the factor z
The distance through which the amplitude of a traveling plane wave 1 decreases by a factor of e , or 0.368, is called the skin depth, or the depth of penetration of a conductor. conductor
1 f
(m)
interface
penetration depth
(m)
25
Electromagnetics
Plane Waves
Skin Depth of Various Materials
26
Electromagnetics
Plane Waves
Current Distribution
At high frequencies, electric current distribution is no longer uniform due to the effect of skin depth. Cross-sectional view of a good conductor.
high frequency
27
Electromagnetics
Plane Waves
Ionized Gases
Gases become ionized due to high energy excitation, e.g., ionosphere. The electron and ion densities in the individual ionized layers of the ionosphere are essentially equal called plasmas. When electromagnetic waves passing through the ionosphere, the electrons are accelerated by the electric fields more than positive ions. Assume the intensity of plasmas is low and ignore the collisions between the electrons and the gas atoms.
28
Electromagnetics
Plane Waves
Ionized Gases
An electron of charge e and mass m in a time-harmonic electric field E in the x-direction at an angular frequency experiences a force eE.
Such a displacement gives rise to an electric dipole moment:
d 2x e eE = m 2 = m 2 x x = E 2 dt m
Ne 2 D = 0 E + P = 0 (1 )E 2 m 0
p = ex
p = 0 (1 2 ) E ( p =
p is called plasma angular frequency
Ne 2 ) m 0
p 1 fp = = 2 2
Ne 2 m 0
2 fp p2 p = 0 (1 2 ) = 0 (1 2 ) f
29
Electromagnetics
Plane Waves
Ionized Medium
Consider wave propagation in an ionized medium:
= o 1 ( f p / f ) 2 =
At =p, =0.
1 ( p / ) 2
no propagation.
At =p, propagation is possible.
c up = = c 2 1 ( p / )
ug = 1 = c 1 ( p / ) 2 c d / d
u p ug = c2
30
Electromagnetics
Plane Waves
Wave Velocity
Phase velocity is defined as the velocity of propagation of an equi-phase wavefront. Group velocity is defined as the velocity propagation of the wave-packet envelope.
ug =
1 d / d
up =
1 = /
31
Electromagnetics
Plane Waves
Time-Harmonic Traveling Waves

Consider a wave packet that consists of two traveling waves having equal amplitude and slightly different angular frequencies.
E ( z , t ) = Eo cos[(o + )t ( o + ) z ] + Eo cos[(o )t ( o ) z ] = 2 Eo cos(t z ) cos(ot o z )

amplitude of slow variation with an angular frequency Phase velocity: u p =
dz = = dt k
ug = dz 1 = = dt /
1 d / d
Group velocity: t z = const. u g =
32
Electromagnetics
Plane Waves
Diagram
For plane waves in a lossless medium, phase constant is a linear function of . As a consequence, phase velocity is a constant. In general, phase constant is not a linear function of . Dispersion: waves of the component frequencies travel with different phase velocities, causing a distortion in the signal wave shape.
Fast wave region
Slow wave region
33
Electromagnetics
Plane Waves
Ionized Medium
Consider wave propagation in an ionized medium:
= o 1 ( f p / f ) 2 =
At =p, =0.
1 ( p / ) 2
no propagation.
At =p, propagation is possible.
c up = = c 2 1 ( p / )
ug = 1 = c 1 ( p / ) 2 c d / d
u p ug = c2
34
Electromagnetics
Plane Waves
General Relation
General relation between the group and the phase velocities.
d d 1 du p = ( )= 2 d d u p u p u p d
ug =
up
du p 1 u p d
du p d =0
Three possible cases: No dispersion (independent of frequency) Normal dispersion Anomalous dispersion
ug = u p
du p d du p d
<0 >0
ug < u p
ug > u p
35
Electromagnetics
Plane Waves
Flow of Electromagnetic Power

Relation between the rate of energy transfer and the electric and magnetic field intensities associated with a traveling electromagnetic wave. r r
r r r r r r r r r B r r r D ( E H ) = H ( E ) E ( H ) = H EJ E t t
In a simple medium,
r B E = t
r r D H = J + t
r r r r r B r ( H ) 1 ( H H ) 1 H =H = = ( H 2 ) t t 2 t t 2 r r r D r (E ) 1 2 E = E = ( E ) t t t 2 r r E J = E 2
36
Electromagnetics
Plane Waves
Flow of Electromagnetic Power

r r r r r B r r r D EJ E (E H ) = H t t 1 2 1 = ( E + H 2 ) E 2 t 2 2
The integral form
r r r 1 1 ( E H ) ds = ( E 2 + H 2 )dv E 2 dv S V t V 2 2
Time-rate of change of the energy stored in the electric and magnetic fields. rate of decrease of the electric and magnetic energies stored The Ohmic power dissipated in the volume
37
Electromagnetics
Plane Waves
Poynting Vector
To be consistent with the law of conservation of energy, the LHS must equal to the power leaving the volume through the surface. Poynting vector is defined to represent the power flow per unit area (leaving the enclosed volume) r r r in the direction normal = E H (W/m 2 ) to both E and H Poyntings theorem
r r P ds = ( we + wm )dv + P dv S V t V
this term vanishes in a static situation
this term vanishes if the region of concern is loseless

38
Electromagnetics
Plane Waves
Example 8-7
Find the Poynting vector on the surface of a long, straight conducting wire (of radius b and conductivity ) that carries a direct current I. DC situation; uniform current distribution over the cross-sectional area.
r I J = az 2 b
r r J E = = az
r I I H = a 2 b 2b
on the surface
r r r = E H = ar
I2 2 2b 3
I2 2 2b l ) = I 2R b 2
39
To verify Poynting theorem.
r r r P ds = P ar ds =
S S
2bl = I 2 ( 3
Electromagnetics
Plane Waves
Where the previous equation, the resistance of a straight wire, R=l/S, has been used. The above result affirms that the negative surface integral of the Poynting vector is exactly equal to the I2R ohmic power loss in the conducting wire.
40
Electromagnetics
Plane Waves
Instantaneous Power Densities

Care with nonlinear operations on phasor expressions.
r r E ( z , t ) = Re[ E ( z )e jt ] = a x Eo cos(t z ) r r E H ( z , t ) = Re[ H ( z )e jt ] = a y o e z cos(t z ) | |

Note:
r r r r jt jt Re[ E ( z )e ] Re[ H ( z )e ] Re[ E ( z ) H ( z )e jt ]
Instantaneous power density.
r r r r r j t P( z , t ) = E ( z , t ) H ( z , t ) = Re[ E ( z )e ] Re[ H ( z )e jt ]
41
Electromagnetics
Plane Waves
Instantaneous Power Densities

Power density vector.
r r r jt P ( z , t ) = Re[ E ( z )e ] Re[ H ( z )e jt ] = az = az
On the other hand.
Eo2
e 2z cos(t z ) cos(t z ) e 2z [cos + cos(2t 2 z )]
Eo2
not the same!
r r Eo2 2z Re[ E ( z ) H ( z )e jt ] = a z e cos(t z )
42
Electromagnetics
Plane Waves
Average Power Densities

As far as the power transmitted by an electromagnetic wave is concerned, the average value is a more significant quantity than the instantaneous value.
r 1 Pav ( z ) = T
r Eo2 2z P( z , t )dt = a z e cos 2
Make use of this identity.
1 1 1 * * Re[ A] Re[ B ] = ( A + A ) ( B + B ) = Re[ A B * + A B] 2 2 2
r 1 Pav ( z ) = T
r r r jt P( z , t ) = Re[ E ( z )e ] Re[ H ( z )e jt ] r r* r r 1 = Re[ E ( z ) H ( z ) + E ( z ) H ( z )e j 2t ] 2
r r r* 1 P( z, t )dt = Re[ E ( z ) H ( z )] 2
43
Electromagnetics
Plane Waves
Bounded Region
In practice, waves propagate in bounded regions where several media with different constitutive parameters are present. When an electromagnetic wave traveling in one medium impinges on another medium with a different intrinsic impedance, it experiences a reflection. Two cases will be considered:
normal incidence oblique incidence.
(lossless)
(perfect conductor)
44
Electromagnetics
Plane Waves
Normal Incidence
Assume the phasors of the incident fields inside medium 1.
Ei ( z ) = a x Eio e j1z H i ( z) = ay Eio
j1 z
take z=0 Eio is the magnitude of field intensity @ z=0.
Pi ( z ) = Ei ( z ) H i ( z )
Inside medium 2 (PEC), both electric and magnetic fields vanish. is transmitted across the boundary into the z>0 region. no wave
The incident wave is reflected, giving rise to a reflected wave (Er, Hr).
Er ( z ) = a x Ero e + j1 z
Electromagnetics
Plane Waves
Normal Incidence
The total field in medium 1.
E1 ( z ) = Ei ( z ) + Er ( z ) = a x ( Eio e j1 z + Ero e + j1 z )
Boundary condition (continuity of the tangential components) at z=0 demands that
E1 (0) = a x ( Eio + Ero ) = E2 (0) = 0 Ero = Eio
E1 ( z ) = a x Eio (e j1z e + j1z ) = a x j 2 Eio sin 1 z

The magnetic field intensity Hr of the reflected wave is related to Er:
H r ( z) = = 1
anr Er ( z ) =
j1 z
a z Er ( z ) e j1z
46
a y Er 0 e
= ay
Ei 0
Electromagnetics
Plane Waves
H1 ( z ) = H i ( z ) + H r ( z ) = a y 2

Ei 0
cos 1 z
No average power is associated with the total eletromagnetic wave in medium 1, since are E1(z) in H1(z) phase quadrature. Instantaneous electric and magnetic field intensities:
E1 ( z , t ) = Re E1 ( z )e jt = a x 2 Eio sin 1 z sin t E jt x 2 io cos 1 z cos t H1 ( z , t ) = Re H1 ( z )e =a
( (
While 1z = -n , or z = -n n = 0,1,2,...........
, zero of E1 ( z , t ) maxi. of H1 ( z , t )
While 1z = -(2n + 1) , or z = -(2n + 1) n = 0,1,2,............

, 4 maxi. of E1 ( z , t ), zero of H1 ( z , t )
47
Electromagnetics
Plane Waves
Standing Wave
48
Electromagnetics
Plane Waves
Oblique Incidence at a Plane Conducting Boundary

Perpendicular polarization, Ei is perpendicular to the plane of incidence. (i, angle of incidence).
ani = a x sin i + a z cos i

Ei ( x, z ) = a y Ei 0 e j1ani R = a y Ei 0 e j1 ( x sini + z cosi ) H i ( x, z ) = = Ei 0 1
[ani Ei ( x, z )]
1 i i
[ ax cos i + az sin i ]e j ( x sin + z cos )
49
Electromagnetics
Plane Waves
For the reflected wave:
anr = a x sin r a z cos r where r is the angle of reflection.

Er ( x, z ) = a y Er 0 e j1 ( x sin r z cos r ) at z = 0 : E1 ( x,0) = Ei ( x,0) + Er ( x,0) = a y ( Ei 0 e j1 x sin i + Er 0 e j1 x sin r ) = 0 Ei 0 = Er 0 and i = r
Snells law of reflection: the angle of reflection equals to the angle of incidence.
50
Electromagnetics
Plane Waves
Er ( x, z ) = a y Ei 0 e j1 ( x sin i z cos i )
H r ( x, z ) = = Ei 0 1
[anr Er ( x, z )]
1 i i
[ ax cos i az sin i ]e j ( x sin z cos )

H1 ( x, z ) = 2
j1 x sin i
E1 ( x, z ) = Ei ( x, z ) + Er ( x, z ) = a y Ei 0 (e
j1 z cos i
Ei 0
j1 z cos i
)e
[a x cos i
= a y j 2 Ei 0 sin( 1 z cos i )e j1 x sin i
cos( 1 z cos i )e j1x sin i + a z j sin i sin( 1 z cos i )e j1x sini ]
51
Electromagnetics
Plane Waves
Along the z-direction, E1y and H1x maintain standing wave patterns. No average power is propagated. Along the x-direction, E1y and H1z are in both time and space phase and propagate with a phase velocity. u u1x = = = 1 1x 1 sin i sin i 2 1x = = 1 1x sin i The propagating wave in x-direction is a nonuniform plane wave because its amplitude varies with x. When
1 z cos i =
z cos i = m ,
m = 1,2,3.....................
E1=0 for all x since
sin( 1 z cos i ) = 0
A transverse electric (TE) wave (E1x=0) would bounce back and forth between the conducting planes and propagate in the x-direction.
52
Electromagnetics
Plane Waves
OA' =
1
2
OA = b =
2 cos i
1 1
The traveling wave in the parallel - waveguide has a guide wavelength equal to 2OA " : OA' = 1 > 1 sin i sin i
g = 2OA" = 2
i = 0, no wave propagating along x axis
53
Electromagnetics
Plane Waves
H-Polarization Incidence
Ei ( x, z ) = Ei 0 [a x cos i a z sin i ]e j1 ( x sin i + z cos i ) H i ( x, z ) = a y Ei 0
Incidence wave
e j1 ( x sin i + z cosi )
Er ( x, z ) = Er 0 [a x cos r + a z sin r ]e j1 ( x sin i z cos i ) H r ( x, z ) = a y

at z = 0 :
Reflective wave
Er 0
e j1 ( x sin r z cos r )
Eix ( x,0) + Erx ( x,0) = 0 ( Ei 0 cos i )e j1x sin i + ( Er 0 cos r )e j1x sin r = 0 Ei 0 = Er 0 and i = r
Electromagnetics
Plane Waves
E1 ( x, z ) = Ei ( x, z ) + Er ( x, z ) = a x Ei 0 cos i (e j1 z cos i e j1z cos i )e j1x sini a z Ei 0 sin i (e j1z cos i e j1z cosi )e j1 x sin i = 2 Ei 0 [a x j cos i sin( 1 z cos i ) + a z sin i cos( 1 z cos i )]e j1 x sin i H 1 ( x, z ) = H i ( x, z ) + H r ( x, z ) = ay 2 Ei 0 cos( 1 z cos i )e j1x sin i
55
Electromagnetics
Plane Waves
Along the z-direction, E1x and H1y maintain standing wave patterns. No average power is propagated. Along the x-direction, E1z and H1y are in both time and space phase and propagate with a phase velocity. u u1x = = = 1 1x 1 sin i sin i 2 1x = = 1 1x sin i The propagating wave in x-direction is a nonuniform plane wave because its amplitude varies with x. When 2
1 z cos i =
z cos i = m ,
m = 1,2,3.....................
E1x=0 for all x since
sin( 1 z cos i ) = 0
A transverse magnetic (TM) wave (H1x=0) would bounce back and forth between the conducting planes and propagate in the x-direction.
56
Electromagnetics
Plane Waves
Normal Incidence at Plane Dielectric Boundary

Incidence Wave
Ei ( z ) = a x Eio e j1z H i ( z) = a y
Eio
Reflective Wave
e j1z
Er ( z ) = a x Ero e j1z H r ( z ) = a z
Er ( z )
= a y
Ero
e j1z
Transmitted Wave
Er ( z ) = a x Eto e j 2 z H t ( z ) = az
Et ( z )
= ay
Eto
e j 2 z , Eto = Et ( z = 0)
57
Electromagnetics
Plane Waves
B.C. :Tangential components of the electric and magnetic field intensities must be continuous:
Ei (0) + Er (0) = Et (0) Ei 0 + Er 0 = Et 0

H i (0) + H r (0) = H t (0) ( Ei 0 + Er 0 ) = 1 2 2 1 Er 0 = Ei 0 2 + 1 1 Et 0
2 2 Et 0 = Ei 0 2 + 1
Definitions:
Transmission coefficient =
Et 0 2 2 = Ei 0 2 + 1
Er 0 2 1 Reflection coefficient = = Ei 0 2 + 1
+1 =
58
Electromagnetics
Plane Waves
and may themselves be complex in the general case. A complex or simply means that a phase shift is introduced at the interface upon reflection or transmission: Example: if medium 2 is a perfect conductor, 2=0. Then, =-1 and =0. Thus, Er0=-Ei0., and Et0=0. The incident wave will be totally reflected, and a standing wave will be produced in medium 1. If medium 2 is not a perfect conductor, partial reflection will result.
E1 ( z ) = Ei ( z ) + Er ( z ) = a x Ei 0 (e j1z + e j1z ) = a x Ei 0 [(1 + )e j1 z + (e j1z e j1z )] = a x Ei 0 [e j1 z + ( j 2 sin 1 z )]
Ei 0 : traveling wave
2 Ei 0 : standing wave
Electromagnetics
Plane Waves
j1 z
E1 ( z ) = a x Ei 0 e
(1 + e
2 j1 z
H1 ( z ) = a y
Ei 0
>0, (2 > 1):
e j1 z (1 e 2 j1z )
The maximum value of E1(z) is Ei0(1+) occurs when 21zmax=-2n (n=0,1,2,3) zmax= -n/ 1=-n1/2, n=0,1,2,3 The minimum value of E1(z) is Ei0(1-) occurs when 21zmin=-(2n+1) (n=0,1,2,3) zmax= -(2n+1)/ 21=-(2n+1)1/4, n=0,1,2,3 The maximum value of E1(z) is Ei0(1-) occurs when 21zmax=(2n+1) (n=0,1,2,3) zmax=-(2n+1)/ 21=-(2n+1)1/4, n=0,1,2,3 The minimum value of E1(z) is Ei0(1+) occurs when 21zmin=-2n (n=0,1,2,3) zmax= -n/ 1=-n1/2, n=0,1,2,3
<0, (2 < 1):
In a dissipationless medium, is real; and H1(z) will be a minimum at locations where E1(z) is a maximum, and vice versa. In medium 2:
E2 ( z ) = a xEi 0 e
j 2 z
, H 2 ( z) = a y Ei 0 e j z 2
2
60
Electromagnetics
Plane Waves
Standing Wave Ratio

Definition: the ratio of the maximum value to the minimum value of the electric field intensity of a standing wave.
S=
Emax Emin
1+ 1
While the value of ranges from 1 to +1, the value of S ranges from 1 to . The standing wave ratio in decibels is 20 log10 S.
S=220log102=6.02 dB. =1/3 SWR:2dB S=1.26, =0.015
S 1 S +1
61
Electromagnetics
Plane Waves
Normal Incidence at Multiple Dielectric Interfaces

X-polarized incident field:
E1 = a x ( Ei 0 e j1 z + Er 0 e j1 z )
The reflected field in medium 1:
The field reflected from the interface at z=0 as the incident wave impinges on it The field transmitted back to medium 1 from medium 2 after a first reflection from the interface at z=d The field transmitted back into medium 1 from medium 2 after a second reflection at z=d And so on How to determine it?
62
Electromagnetics
Plane Waves
Er0 can be solved base the following procedure:

Write down the electric and magnetic field intensity vectors in all three regions Apply the B.C. to solve the equations.
E1 = a x ( Ei 0 e j1 z + Er 0 e j1 z ) 1 H1 = a y ( Ei 0 e j1 z Er 0 e j1 z )
BC.s (tangential component continuous) At z = 0, E1 (0) = E2 (0) H 1 ( 0) = H 2 ( 0) At z = d, E2 (d ) = E3 (d ) H 2 (d ) = H 3 (d )
E2 = a x ( E2 e H 2 = ay 1
+ j 2 z +
+ E2 e
j 2 z
2
+
( E2 e j 2 z E2 e j 2 z )
E3 = a x E3 e j 3 z H 2 = ay 1
E3 e j 3 z
63
Electromagnetics
Plane Waves
Wave Impedance of The Total Field

Wave Impedance of the total field: the ratio of the total electric field intensity to the total magnetic field intensity at any plane parallel to the plane boundary. For instance, a z-dependent uniform plane wave as shown in the previous figure, we write, in general:
Total E x ( z ) Z ( z) = Total H y ( z )
For previous case (normal incidence)
E1x ( z ) Ei 0 (e j1 z + e j1z ) = Z1 ( z ) = H1 y ( z ) Ei 0 (e j1z e j1z )
e j1z + e j1 z = 1 j1 z e e j1z
Electromagnetics
Plane Waves
Z = l
2 cos 1l + j1 sin 1l E1x (l ) e j1l + e j1l Z1 (l ) = = 1 j1l = 1 j1l 1 cos 1l + j 2 sin 1l H1 y (l ) e e 2 1 = 2 + 2

Which correctly reduces to 1 when 2=1. In that case there is no discontinuity at z=0; hence there is no reflected wave and the total-field wave importance is the same as the intrinsic impedance of the medium. If the plane boundary is perfectly conducting, 2 =0 and =-1, and
Z1 (l ) = j1 tan 1l
Which is the same as the input impedance of a transmission line of length l that has a characteristic impedance 1 and terminates in a short circuit.
65
Electromagnetics
Plane Waves
Impedance Transformation with Multiple Dielectrics

The total field in medium 2 is the result of multiple reflections of the two boundary planes at z=0 and z=d; but it can be grouped into a wave traveling in the +z direction and another traveling in the z direction. The wave impedance of the total field in medium 2 at the left-hand interface z=0 can be found from the right side by replacing 2 by 3 , 1 by 2 , 1 by 2 , and l by d. thus,
Z 2 (0) = 2
3 cos 2 d + j 2 sin 2 d 2 cos 2 d + j3 sin 2 d
The effective reflection coefficient at z=0 for the incident wave in medium 1 is
0 =
Er 0 H Z (0) 1 = r0 = 2 Ei 0 H i 0 Z 2 (0) + 1
0 differs from only in that has been replaced by Z2(0)
66
Electromagnetics
Plane Waves
Example
A dielectric layer of thickness d and intrinsic impedance 2 is placed between media 1 and 3 having intrinsic impedances 1 and 3 , respectively. Determine d and 2 such that no reflection occurs when a uniform plane wave in medium 1 impinges normally on the interface with medium2. Sol:
z = 0, 0 = 0, or Z 2 (0) = 1
2 (3 cos 2 d + j 2 sin 2 d ) = 1 ( 2 cos 2 d + j3 sin 2 d ) 3 cos 2 d = 1 cos 2 d

and 2 sin 2 d = 13 sin 2 d
2
3 = 1 or cos 2 d = 0 2 d = (2n + 1) n = 0,1,2,3......

or d = (2n + 1)
2
4
Electromagnetics
Plane Waves
On the other hand, 2 sin 2 d = 13 sin 2 d

2
2 = 3 = 1 or sin 2 d = 0 2 d = n or d = n n = 0,1,2,3......
When 1= 3 , we require d=n2/2, n=0,1,2. That the thickness of the dielectric layer be a multiple of a half-wavelength in the dielectric at the operating frequency. Such a dielectric layer is referred to as a half-wave dielectric windows. Since 2 =up2/f=1/f, where f is the operating frequency, a half-wave dielectric window is a narrow-band device. When 1 3 . We require 2 = 1 3, and d=(2n+1)2/4, n=0,1,2. When media 1 and 3 are different, 2 should be the geometric mean of 1 and 3 , and d should be an odd multiple of a quarter wavelength in the dielectric layer operating frequency in order to eliminate reflection. Under these conditions the dielectric layer acts like a quarter-wave impedance transformer.
2
2
68
Electromagnetics
Plane Waves
Oblique Incidence at a Plane Dielectric Boundary

Line AO, O' A' , O' B are the intersecti on of the wavefronts (surface of constant phase) of the incident, reflected, and transmitt ed wave, respective ly, with the plane of incidence. Since both the incident and the reflected waves propagate in medium 1 with the same phase velocity u p1 , OA' = AO ' OO' sin r = OO ' sin i r = i The angle of reflection is equal to the angle of incidence, which is Snell' s law of reflection .
Electromagnetics
Plane Waves
In medium 2 : OB AO ' OB OO ' sin t u p 2 = = = u p 2 u p1 AO ' OO ' sin i u p1 sin t u p 2 1 n1 = = = sin i u p1 2 n2 where n1and n2 are the indices of refraction for media 1 and 2
Snells law of refraction: at an interface between two dielectric media, the ratio of the sine of the angle of refraction (transmission) in medium2 to the sine of the angle of incidence in medium1 is equal to the inverse ratio of indices of refraction n1/n2. In medium 2 :
For nonmagneti c media, 1 = 2 = 0 sin t 1 r1 n1 1 = = = = sin i 2 r 2 n2 2

Electromagnetics
Plane Waves
Total Reflection
Setting : t =
sin c =
2 1
c : incidence angle (which corresponding to the threshold of total reflection : t = ) is called the critical angle. c = sin 1
? If i > c sin t =
2 2 n = sin 1 ( 2 ) 1 n1
1 sin i > 1 2 1 2 sin i 1 2

71
cos t = 1 sin 2 t = j
Electromagnetics
Plane Waves
In medium 2, the unit vector ant ant = a x sin t + a z cos t , Both Et and H t vary spatially e -j2ant R = e -j2 ( x sin t + z cost ) For i > c e 2 ze j 2 x x , 2 = 2
1 2 sin i 1, 2 x = 2 1 sin i 2 2
The positive sign has been abandoned because it would lead to the impossible result of an increasing field as z increase. For i> c an evanescent wave exists along the interface (in the x-direction), which is attenuated exponentially in medium 2 in the normal direction (zdirection). This wave is tightly bound to the interface and is called a surface wave. Obviously, it is a nonuniform plane wave. No power is transmitted into medium 2 under these conditions.
72
Electromagnetics
Plane Waves
Example
The permittivity of water at optical frequencies is 1.750. It is found that an isotropic light source at a distance d under water yields an illuminated circular area of a radius 5 m. Determine d.
The refractive index of water nw = 1.75 = 1.32 The radius of illuminated area, O'P = 5m
c = sin 1 (
Thus, d =
1 1 ) = sin 1 ( ) = 49.2o nw 1.32 O'P 5 = = 4.32m tan c tan 49.2o
73
Electromagnetics
Plane Waves
Example
A dielectric rod or fiber of a transparent material can be used to guide light or an electromagnetic wave under the conditions of total internal reflection. Determine the minimum dielectric constant of the guiding medium so that a wave incident on one end at any angle will be confined within the rod until it emerges from the other end.
sin 1 sin c ,
1 =
t cos t sin c , 1
sin t =
r1
sin i 1
r1
sin 2 i
1 r0 = r1 r1
which requires : r1 1 + sin 2 i the dielectric constant of the guiding medium to be at least 2 n1 = 2 glass and quartz can be satisfied.
Electromagnetics
Plane Waves
Perpendicular Polarization
Incidence wave
Ei ( x, z ) = a y Ei 0 e j1 ( x sin i + z cos i ) H i ( x, z ) =
Ei 0
(a x cos i + a z sin i )e j1 ( x sini + z cosi )
Reflective wave
Er ( x, z ) = a y Er 0 e j1 ( x sin r z cos r ) H r ( x, z ) =
Er 0
(a x cos r + a z sin r )e j1 ( x sin r z cos r )
Transmitted wave
Et ( x, z ) = a y Et 0 e j 2 ( x sin r + z cos r ) H t ( x, z ) = Et 0
(a x cos t + a z sin t )e j 2 ( x sint + z cos t )

75
Electromagnetics
Plane Waves
B.C.: tangential components of E and H be continuous at the boundary z=0
Ei (0) + Er (0) = Et (0) Ei 0 e j1x sin i + Er 0 e j1x sin r = Et 0 e j 2 x sin t

H i (0) + H r (0) = H t (0)
( Ei 0 cos i e j1x sin i + Er 0 cos r e j1x sin r ) =
Et 0 cos t e j 2 x sin t
For all x, all three exponential factors that are functions of x must be equal (phase matching)
1 x sin i = 1 x sin r = 2 x sin t

Snells law of reflection and refraction
i = r
sin t u p 2 1 n1 = = = sin i u p1 2 n2
76
Electromagnetics
Plane Waves
Ei (0) + Er (0) = Et (0) and H i (0) + H r (0) = H t (0)
2 2 1 Er 0 2 cos i 1 cos i cos t cos i = = = 2 Ei 0 2 cos i + 1 cos i + 1 cos t cos i =

2 2 cos i 2 2 cos i Et 0 = = 2 Ei 0 2 cos i + 1 cos i + 1 cos t cos i
Ei 0 + Er 0 = Et 0 and
( Ei 0 Er 0 ) cos i =
Et 0 cos t
When i=0, making r= t=0 these expressions reduce to those for normal incidence
77
Electromagnetics
Plane Waves
1 + =
If medium 2 is a perfect conductor, 2 =0. We have
= 1, Er 0 = Ei 0 , = 0, ( Et 0 = 0)
Now, we inquire whether there is a combination of 1 , 2 and i, which makes = 0 for no reflection. Denoting this particular i by B
2 cos B = 1 sin t
n12 cos t = 1 sin t = 1 2 sin 2 i n2
2
sin 2 B =
1 1 2 2 1 1 ( 1 2 ) 2
The angle B is called the Brewster angle of no reflection for the case of perpendicular
Electromagnetics
Plane Waves
For nonmagnetic media, 1= 2 = 0 B does not exist. In the case of 1= 2, 1 2 :
sin B =
1 1 + ( 1 2 )
79
Electromagnetics
Plane Waves
Parallel Polarization
Incidence wave
Ei ( x, z ) = Ei 0 (a x cos i a z sin i )e j1 ( x sin i + z cos i ) H i ( x, z ) = a y
Ei 0
e j1 ( x sin i + z cos i )
Reflective wave
Er ( x, z ) = Er 0 (a x cos r + a z sin r )e j1 ( x sin r z cos r ) H r ( x, z ) = a y
Er 0
e j1 ( x sin r z cos r )
Transmitted wave
Et ( x, z ) = Et 0 (a x cos t a z sin t )e j 2 ( x sin r + z cos r ) H t ( x, z ) = a y Et 0
e j 2 ( x sint + z cost )
80
Electromagnetics
Plane Waves
B.C.: tangential components of E and H be continuous at the boundary z=0, also lead to snells law of reflection and refraction:
Ei (0) + Er (0) = Et (0) and H i (0) + H r (0) = H t (0) ( Ei 0 + Er 0 ) cos i = Et 0 cos t ,

Er 0 2 cos t 1 cos i // = = Ei 0 2 cos t + 1 cos i
( Ei 0 Er 0 ) =
Et 0
// =
Et 0 2 2 cos i = Ei 0 2 cos t + 1 cos i
cos t 1 + // = // cos i

81
Electromagnetics
Plane Waves
If medium 2 is a perfect conductor, 2 =0. We have
// = 1, // = 0, making the tangential component of the total E field on the surface conductor vanish.
> // for all i except i = 0 Polaroid sunglass.

2 2
Now, we inquire whether there is a combination of 1 , 2 and i, which makes // = 0 for no reflection. Denoting this particular i by B
2 cos t = 1 sin B // 1 2 1 1 2 sin 2 B // = 1 ( 1 2 ) 2 The angle B // is called the Brewster angle of no reflection for the case of parallel
82
Electromagnetics
Plane Waves
1= 2
sin B // =
1 1 + ( 1 2 )
1
B // = tan
2 1 n2 = tan n 1 1
Because of the difference in the formulas for Brewster angles for perpendicular and parallel polarizations, it is possible to separate these two types of polarization in an unpolarized wave.
83

Plane Electromagnetic Waves

Загружено:

Сведения о документе

Исходное описание:

Авторское право

Доступные форматы

Поделиться этим документом

Поделиться или встроить документ

Параметры публикации

Этот документ был вам полезен?

Это неприемлемый материал?

Авторское право:

Доступные форматы

Plane Electromagnetic Waves

Загружено:

Авторское право:

Доступные форматы

Electromagnetics

C-N Kuo, Winter 2004

C-N Kuo, Winter 2004

C-N Kuo, Winter 2004

For a source free medium, EM relations:

where free-space wavenumber

2Ex 2 2 2 2 2 ( 2 + 2 + 2 + k o ) E x ( x , y , z ) = 0 uniform plane wave + ko E x = 0 E x ( x, y , z ) = E x ( z ) x y z z 2

Plane Waves in Lossless Media

= Eo+ e jko z + Eo e + jko z

Constants are determined by B.C. Instantaneous fields

C-N Kuo, Winter 2004

C-N Kuo, Winter 2004

+ k 1 E x ( z ) 1 1 + Hy = = ( Eo+ e jko z ) = o Eo+ e jko z = E x+ j o z j o z o o

Intrinsic impedance for free-space. (real number)

C-N Kuo, Winter 2004

Example 8-1 (cont)

Expression for E field.

1 k maximum @ 2 10 0 k + = 0 = = (rad ) 8 8 6 r 4 x 10 4 cos(2 108 t E=a z+ ) 3 6 4 1 ( z )] = a x 10 4 cos[2 108 t 3 8

Example 8-1 (cont)

maximum of cosine function occurs at

Transverse Electromagnetic Waves

Phasor expression for a general form.

C-N Kuo, Winter 2004

Constant Phase Plane

Constant phase plane.

C-N Kuo, Winter 2004

Characteristic of Plane-wave Solution

E field is transverse to the direction of propagation.

C-N Kuo, Winter 2004

General expression. r time harmonic field

= a x E10 cos(t kz ) + a y E20 cos(t kz ) 2

r E (0, t ) = a x E1 (0, t ) + a y E2 (0, t ) = a x E10 cos(t ) + a y E20 sin(t )

C-N Kuo, Winter 2004

Circular Polarization (cont)

= a x E10 e jkz a y jE20 e jkz

r E ( z ) = a x E1 ( z ) + a y E2 ( z ) = a x E10 e jkz + a y jE20 e jkz

C-N Kuo, Winter 2004

r E (0, t ) = (a x E10 + a y E20 ) cos t

r E ( z , t ) = a x E10 cos(t kz ) + a y E20 cos(t kz )

C-N Kuo, Winter 2004

r E ( z ) = a x E0 e jkz = E0 E (a x ja y )e jkz + 0 (a x + ja y )e jkz 2 2

right-hand circular polarization

C-N Kuo, Winter 2004

Plane Waves in Lossy Media

Define propagation constant

= jk c = j c " = j ' 1 j = j 1 + ' j = + j phase constant

" 1 " 2 + ( ) ] 2 ' 8 '

complex impedance implies E and H fields are not in time phase.

1 1 " 2 up = [1 ( ' ) ] ' 8

C-N Kuo, Winter 2004

C-N Kuo, Winter 2004

Skin Depth of Various Materials

C-N Kuo, Winter 2004

C-N Kuo, Winter 2004

C-N Kuo, Winter 2004

Such a displacement gives rise to an electric dipole moment:

p is called plasma angular frequency

C-N Kuo, Winter 2004

At =p, propagation is possible.

C-N Kuo, Winter 2004

C-N Kuo, Winter 2004

Time-Harmonic Traveling Waves

E ( z , t ) = Eo cos[(o + )t ( o + ) z ] + Eo cos[(o )t ( o ) z ] = 2 Eo cos(t z ) cos(ot o z )