Академический Документы
Профессиональный Документы
Культура Документы
Randy A. Bartels Et Al - Learning From Learning Algorithms: Application To Attosecond Dynamics of High-Harmonic Generation
Загружено:
PocxaИсходное описание:
Оригинальное название
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Randy A. Bartels Et Al - Learning From Learning Algorithms: Application To Attosecond Dynamics of High-Harmonic Generation
Загружено:
PocxaАвторское право:
Доступные форматы
PHYSICAL REVIEW A 70, 1 (2004)
Learning from learning algorithms: Application to attosecond dynamics of high-harmonic generation
Randy A. Bartels
Department of Electrical and Computer Engineering, Colorado State University, Ft. Collins, Colorado, USA
Margaret M. Murnane* and Henry C. Kapteyn
JILA, University of Colorado, Boulder, Colorado 80309-0440, USA
Ivan Christov
Department of Physics, Soa University, Soa, Bulgaria
Herschel Rabitz
Department of Chemistry, Princeton University, Princeton, New Jersey, USA (Received 15 January 2004) Using experiment and modeling, we show that the data set generated when a learning algorithm is used to optimize a quantum system can help to uncover the physics behind the process being optimized. In particular, by optimizing the process of high-harmonic generation using shaped light pulses, we generate a large data set and analyze its statistical behavior. This behavior is then compared with theoretical predictions, verifying our understanding of the attosecond dynamics of high-harmonic generation and uncovering an anomalous region of parameter space. DOI: XXXX PACS number(s): 32.80.Qk, 42.62. b, 89.20. a
Experiments that study the dynamics of quantum systems, such as optical studies of atomic and molecular dynamics, often employ a pump-probe conguration where a pump pulse perturbs a system, and a probe pulse at varying time delay probes its evolution [1]. However, this technique corresponds to a simplied case of the more-general stimuliresponse experiment, where by observing the dynamical response of a system to varying stimulus, one can compare experiment with hypothesis. Often, in the case where the physics of a system is relatively simple, a pump-probe experiment can provide the most-readily interpretable data. However, pump-probe experiments can be difcult to interpret in the case of a complex quantum system, where the full dynamics are not already understood. Therefore devising new approaches to uncover and understand the dynamics of quantum systems is very important, in particular in the case of complex chemical and biological systems. Another area that requires a more sophisticated approach is the emerging eld of attosecond science where subfemtosecond electron dynamics in atoms and molecules are observed. In this area, experimental constraints limit the applicability of a straightforward pump-probe experiment, and instead experiments infer various light source properties and electronic dynamics, using various comparisons of experimental observations with theoretical models [25]. The more general case of a stimulus-response experiment was discussed by Rabitz [6] for the case of optically probed quantum (i.e., atomic, molecular, or electronic) systems. He suggested that the use of learning algorithms could both
*Fax: (303) 492-5235. Electronic address: murnane@jila.colorado.edu
1050-2947/2004/70(4)/1(5)/$22.50
accomplish coherent control over a quantum system to obtain a desirable outcome [712], as well as provide information about the quantum system itself. In past work, we demonstrated the power of learning algorithms to selectively optimize the generation of coherent extreme-ultraviolet light using high-harmonic generation (HHG) [2]. By adjusting the phase of the laser eld guided by a learning algorithm, we manipulated and optimized the quantum interferences that occur during the HHG process to achieve selective optimization of a single harmonic order. A comparison of theory with experiment was used to identify the mechanism behind the optimization: an optimally shaped light pulse allowed the phase of the radiating electron wave function to be adjusted on 10 20 attosecond time scales to selectively optimize a single harmonic order [13,14]. Both the optimization result itself that allowed selective maximization of a particular harmonic, as well as the mechanism behind the optimization, were not anticipated in advance of the experiment. Therefore new approaches that allow further validation of theoretical models used in optimal control experiments are highly desirable. In this work we show that by analyzing the statistical behavior of the trial solutions generated during the process of optimizing high-harmonic generation, we can independently corroborate the mechanism behind the optimization, as well as uncover interesting behavior for a quantum system. The learning algorithm nds and probes an interesting, unexpected, and previously unobserved region of parameter space where a single harmonic order is selectively optimized, and where the chirps of adjacent harmonics have opposite sign. All previous work demonstrated adjacent harmonic orders to have similar chirps [15,16]. This anomalous chirp behavior found by the learning algorithm leads to an observed anticor2004 The American Physical Society
70 1-1
BARTELS et al.
PHYSICAL REVIEW A 70, 1 (2004)
relation in intensity between adjacent harmonic orders that can be used to validate theory through a statistical analysis of the data set. More generally, our analysis [17] and recent parallel work on other systems [18,19] show that the entire data set acquired during an optimization process is useful for understanding the physical system under investigation. In a learning algorithm experiment, the algorithm iteratively performs thousands of experiments and observes the results of each. Thus in the process of training the experimental apparatus to optimize a quantum process we acquire a great deal of information about the dynamics of the quantum system. An analysis of the optimization pathway itself thus serves to probe the dynamics and can be used to independently compare with theoretical predictions. Understanding what can be learned from optimal control data sets is particularly useful in the case of nonperturbative, high-eld phenomena that are not well understood. HHG is a coherent, nonlinear, optical process. In HHG, a large number of visible-energy photons from an intense laser pulse are combined into a single high-energy photon. The semiclassical theory of HHG considers an atom irradiated by an intense, ultrashort light pulse. At intensities approaching 1014 W cm2, the optical eld is sufciently strong that the Coulomb barrier binding the outermost electron to the atom is suppressed. Electrons can then tunnel through the barrier, leading to eld ionization of the atom. This process occurs twice per optical cycle as the optical eld strength peaks. Once ionized, the electrons oscillate in the light eld and some fraction of the ionized electrons recollide with the parent ion and recombine with it, releasing their kinetic energy as a high-energy photon. The shape of the driving laser pulse determines the trajectory of the electron as it oscillates in the laser eld, and hence the quantum phase accumulated during its trajectory, as well as the interferences that occur between different adjacent electron trajectories. This quantum phase in turn determines the harmonic phase and ultimately the spectrum of the generated high-harmonic radiation. In our experiment, mJ-energy pulses from a 1-kHz repetition-rate laser system [20] were focused into a 175 - m-diameter argon-lled hollow waveguide. This creates a phase-matched comb of harmonics containing the 23rd31st orders [21]. The waveguide geometry creates an extended region of high laser intensity and long coherence length to efciently generate the high-harmonic radiation, which is observed using a spectrometerx-ray charge-coupled device camera system. A deformable mirror pulse shaper [22] and an evolutionary strategy algorithm were then used to selectively optimize the 27th harmonic, while simultaneously suppressing the 25th and 29th orders. The optimum pulse shape is found after about 100 iterations of the learning algorithm, each of which consists of about 100 trials. Although the learning process is fundamentally trial and error, this does not mean that the pathway the learning algorithm takes toward optimization is a random one. In particular, there are very signicant changes in the statistical behavior of the optimum solution as the optimization proceeds, reecting the guidance provided by the learning algorithm. Figure 1(a) shows the peak intensity of the 25th, 27th, and 29th harmonic orders for the optimal pulse shape from each iteration of the learning algorithm, where the learning
1-2
FIG. 1. (a) Peak brightness of the 25th, 27th, and 29th, harmonic orders from an experiment to selectively optimize the 27th order. A correlation map of the 25th and 29th harmonic orders for the rst (b), second (c), and third (d) fractions of the learning algorithm experiment.
algorithm tness function, f = 1 b25 + b29 / 2b27, is constructed to selectively optimize the 27th harmonic, increasing the intensity contrast between the 27th and the neighboring harmonic orders. Here bi is the brightness of the ith harmonic. The correlation between the intensities of the 25th and 29th harmonic orders is plotted in Figs. 1(b)1(d) for the rst, second, and third fractions of the data set. Initially, [Fig. 1(b)] the pulse shapes that correspond to the trial population are random. However, after a few iterations there exists a population of shapes that largely do generate a highharmonic spectrum. Furthermore, the initial pulse shapes generally do not selectively enhance a particular harmonic order in comparison with the relative harmonic magnitudes obtained from a transform-limited pulse. In this early stage, the intensity of all harmonic orders uctuates together; i.e., the intensities are correllated. However, by the end of the optimization process [Fig. 1(d)], the intensity of the 27th harmonic has been enhanced, and the intensities of the 25th and 29th harmonics are strongly anticorrelated. We can quantify this relationship by using Spearmans rhoa correlation function that enumerates correlated trends in pairwise data [23]. If both monotonically increase, the correlation is 1, while if one increases and the other decreases, the value is 1 (anticorrelated case). The value of Spearmanns rho for the rst four iterations of the learning algorithm is +0.80 and +0.54 for the rst six generations, indicating the neighboring harmonic orders exhibit a strong positive correlation. This positive correlation between the neighboring harmonic orders indicates that the brightness of both of the neighboring harmonic orders either increase or decrease in response to pulse shape perturbations. However, as the algorithm progresses, it begins to nd pulse shapes that exhibit the desired harmonic-order selectivity, and this is also accompanied by changes in the statistical correlations of the HHG spectra, in which the 25th and 29th order harmonics become anticorrelated. This indicates that the learning algorithm has found a different region of parameter space for
LEARNING FROM LEARNING ALGORITHMS:
PHYSICAL REVIEW A 70, 1 (2004)
FIG. 2. (a) Correlation of the 25th and 29th experimental harmonic brightness as a moving window (15 generations wide) is scanned along algorithm generations (triangles) and the corresponding average tness value (points). (b) Correlations plotted vs the average tness value for the data in (a), where the color is graded from dark to light for high to low condence in the correlation result.
driving HHG. We can observe this transition by calculating Spearmanns rho for a moving window across the data set as shown in Fig. 2(a) (triangles); note that the window width of 15 was chosen to maximize the average condence of the statistical analysis (most of the statistics exhibited a condence of 90% in the calculated correlation value) across the data set. After only ten generations, the data become anticorrelated. This anticorrelation is accompanied by an increase in the tness [Fig. 2(a), points], indicating that the harmonic selectivity is associated with the anticorrelated behavior. This relationship between the correlation and tness is better elucidated by plotting their relationship, as shown in Fig. 2(b), where the color is graded from dark to light for high to low condence in the correlation result. We see a steady change in the correlation from positive to negative values that coincides with an increasing tness value. The discussion above shows that as the learning algorithm nds pulses that preferentially enhance the 27th harmonic, the intensity uctuations of the 25th and 29th harmonic orders due to perturbations of the trial pulse shapes become anticorrelated. The algorithm was very effective at increasing the intensity of the 27th harmonic by nearly an order of magnitude, by means of a process we have termed intraatomic phase matching (IAPM), described elsewhere [14]. As explained above, the HHG emission phase is determined by the quantum phase that the electron wave packet accumulates during its free trajectory in the laser eld, and depends on the integral history of the amplitude and phase over the fraction of the driving laser pulse when the electron is free. Thus, by controlling the laser pulse shape with sub-opticalcycle sensitivity, we control the recollision times of the electron wave function during different half cycles of the laser pulse. This controls the phase of the harmonic emission from each half cycle. A properly sculpted driving pulse will ensure that the 27th-harmonic radiation generated in each half-cycle of the driving eld interferes constructively for the ten half
1-3
FIG. 3. Physical mechanism behind the anticorrelated intensity behavior observed for neighboring harmonic orders with small pulse shape perturbations about the optimal pulse shape for selective optimization of the 27th order. Black points: calculated distribution of the harmonic emission phases for each recollision event for an optimal pulse shape that can select a single harmonic order. In this case, the target harmonic order phases are well aligned (maximum harmonic intensity) while neighboring orders have opposite signs of curvature (yielding lower intensity harmonics). Gray points: a slight perturbation in the laser pulse shape has little effect on the target harmonic. However, the higher (29th) harmonic order emission from each recollision event becomes more in phase, which will lead to an increase in intensity, while the lower harmonic order (25th) will decrease in intensity. This will result in an anticorrelation in the brightness of neighboring harmonic intensities in response to optimal pulse shape perturbations.
cycles that contribute to the harmonic. This increases the intensity of the 27th order. On the other hand, simulations also predict that for the same optimized pulse shape, the adjacent 25th and 29th harmonic orders are generated with a phase variation of hundreds of attoseconds and with opposite chirp. These calculations are shown in Fig. 3 (black points). The ability to enhance HHG using shaped light pulses via IAPM is consistent with our understanding of the physics of HHG. During the leading edge of a transform-limited laser pulse, the increasing laser intensity leads to the generation of harmonics with increasing values of negative chirp, as a result of the intensity-dependent phase acquired by the propagating electron [15,16]. This chirp can be partially compensated for by adjusting the chirp of the laser. However, only by nding a nonlinearly chirped laser pulse using the learning algorithm can a relatively at harmonic phase and signicant enhancements of the harmonic intensity be obtained [2,13,14]. Moreover, because the harmonic phase increases slightly from harmonic to harmonic, the optimal laser pulse can achieve selective optimization of a single harmonic order. Finally, since the harmonic chirp varies monotonically with increasing harmonic order, if one harmonic is optimized for at phase, then adjacent harmonics will have opposite chirps. As a result, small variations in laser pulse chirp (as a result of small variations in laser phase about the optimal
BARTELS et al.
PHYSICAL REVIEW A 70, 1 (2004)
pulse shape to select a single harmonic order) can lead to an anticorrelated intensity behavior for the adjacent harmonic orders. Thus the data of Figs. 1 and 2 further validate the IAPM mechanism. The physical mechanism behind the anticorrelated behavior for the adjacent harmonic orders is show in Fig. 3, which shows the harmonic phases corresponding to the optimal pulse (black points) as well as those corresponding to an example perturbation (gray points) about the optimal point. As the learning algorithm probes parameter space to reshape the driving laser pulse after the optimized pulse shape is found, it effectively shifts the relative timing of the electron recollision events by small amounts. This timing shift is similar for all harmonic orders. Pulse shape perturbations that make a particular recollision event become more out of phase for the 25th order will move the timing of that recollision event more in phase for the 29th order, and vice versa as indicated in Fig. 3 (gray points). Therefore, the intensities of the 25th and 29th orders should be anticorrellated, for some small pulse shape perturbations about the optimal point for selective enhancement of the 27th order. Thus a statistical analysis of the data can validate the mechanism for optimization. This behavior was not known or predicted previously; but rather was discovered by the optimization process, both experimentally and theoretically, and validated by the statistical behavior of the data. Previously, there was no mechanism for selective optimization of a single harmonic order, or for imparting different phases and chirps on adjacent harmonic orders, or for observing anticorrelated intensity behavior. We also carried out numerical simulation of the learning experiment and performed identical statistics on the simulated data, in order to show that both experiment and theory reproduce the same statistical behavior and to further validate the IAPM mechanism. Our numerical models for high harmonic generation are described elsewhere [14]. Figure 4(a) shows the calculated peak intensity of the 25th, 27th, and 29th harmonic orders for each trial pulse shape from each iteration of the learning algorithm simulation. The correlation between the 25th and 29th harmonic orders from the entire set of simulated data is plotted in Figs. 4(b)4(d) for the rst, second, and third fractions of the data set. These data demonstrate that the statistical changes in the 25th and 29th harmonic intensities are similar to that observed experimentally. Note that because of the different number of theory data points, different initial conditions, noise levels and mutation rates in the experiment and theory, the appearance of Figs. 1 and 4 are somewhat different. This is also expected because the theoretical phases that are added to the pulse can be more varied than the experimental values, because of the imperfect nature of the pulseshaper that likely limits the available pulse shapes to those with relatively low-order phase variations. This will lead to a more pronounced anti correlation behavior for the experimental data, since many high-order phase variations will not lead to atter phase for one harmonic and thus will not exhibit any anticorrelation in the intensities. Figure 5(a) shows the moving window Spearmanns rho for the simulated data; note the window width of 100 was chosen to maximize the average condence value across the
1-4
FIG. 4. (a) Peak brightness of the 25th, 27th, and 29th, harmonic orders from a learning algorithm simulation designed to selectively optimize the 27th harmonic. A correlation map of the 25th and 29th harmonic orders for the rst (b), second (c), and third (d) fractions of the learning algorithm simulation.
data set. The anticorrelated behavior [Fig. 5(a), triangles], is evident in the simulation as the optimization proceeds, and is again accompanied by an increase in the tness [Fig. 5(a), points], indicating selectivity of harmonic orders occurs for pulse shapes that exhibit anticorrelated behavior. The relationship between the correlation and tness for the simulated data is shown in Fig. 5(b), where again the color is graded from dark to light for high to low condence in the correlation result. The agreement between the statistical behavior of experiment and theory in Figs. 2 and 5 demonstrates the use of learning algorithms to uncover interesting and unexpected dynamics in complex quantum systems. When comparing experiment and theory from Figs. 2(b)
FIG. 5. (a) Correlation of the 25th and 29th theoretical harmonic brightness as a moving window is scanned along algorithm generations (triangles) and the corresponding average tness value (points). (b) Correlations plotted vs the average tness value for the data in (a), where the color is graded from dark to light for high to low condence in the correlation result.
LEARNING FROM LEARNING ALGORITHMS:
PHYSICAL REVIEW A 70, 1 (2004)
and 5(b), the dark data points should be used. These are the data points for which there is a high degree of condence in the correlation result. Experimentally in Fig. 2(b), the 25th and 29th harmonic orders start out slightly correlated, and become strongly anticorrelated. Theoretically in Fig. 5(b), the 25th and 29th harmonic orders start out correlated, and become anticorrelated. The difference between theory and experiment at the start of the optimization can be explained by varying initial conditions, and small positive correlations could be due to overall pulse duration and intensity uctuations. At the end of the optimization (which can occur over a different number of iterations for theory and experiment), when the tness is high indicating selective optimization, the 25th and 29th harmonics show anticorrelated behavior for both theory and experiment for those points (dark) that have a high degree of condence in the correlation results. Thus there is good agreement between theory and experiment, even in the detailed statistical behavior of the optimization. One would not expect perfect agreement because the noise
levels, mutation rates, and accessible pulse shapes are not the same for theory and experiment. In conclusion, this analysis represents a different demonstration of extracting the temporal dynamics of a high-eld quantum process by studying the ensemble behavior of the populations involved in a learning control optimization procedure. Analyses of the complete data sets were used to study the global behavior of the attosecond dynamics and control of free electron wave packets and to validate the mechanism behind selective optimization of high-harmonic generation. Moreover, the learning control algorithm automates the study of the parameter space, and selects an interesting and useful region for investigation. The authors gratefully acknowledge support for this work from the National Science Foundation and from the Chemical Sciences, Geosciences and Biosciences Division of the Ofce of Basic Energy Sciences, U.S. Department of Energy.
[1] P. Barbara, J. Fujimoto, W. Knox, and W. Zinth, Ultrafast Phenomena X (Springer-Verlag, Berlin, 1996). [2] R. Bartels, S. Backus, E. Zeek, L. Misoguti, G. Vdovin, I. P. Christov, M. M. Murnane, and H. C. Kapteyn, Nature (London) 406, 164 (2000). [3] G. G. Paulus, F. Grasbon, H. Walther, P. Villoresi, M. Nisoli, S. Stagira, E. Priori, and S. De Silvestri, Nature (London) 414, 182 (2001). [4] M. Drescher, M. Hentschel, R. Kienberger, G. Tempea, C. Spielmann, G. A. Reider, P. B. Corkum, and F. Krausz, Science 291, 1923 (2001). [5] P. M. Paul, E. S. Toma, P. Breger, G. Mullot, F. Auge, P. Balcou, H. G. Muller, and P. Agostini, Science 292, 1689 (2001). [6] H. Rabitz, R. de Vivie-Riedle, M. Motzkus, and K. Kompa, Science 288, 824 (2000). [7] D. Meshulach and Y. Silberberg, Nature (London) 396, 239 (1998). [8] D. Oron, N. Dudovich, D. Yelin, and Y. Silberberg, Phys. Rev. Lett. 88, 063004 (2002). [9] R. J. Levis, G. M. Menkir, and H. Rabitz, Science 292, 709 (2001). [10] J. L. Herek, W. Wohlleben, R. J. Cogdell, D. Zeidler, and M. Motzkus, Nature (London) 417, 533 (2002). [11] A. Assion, T. Baumert, M. Bergt, T. Brixner, B. Kiefer, V. Seyfried, M. Strehle, and G. Gerber, Science 282, 919 (1998). [12] T. C. Weinacht, R. Bartels, S. Backus, P. H. Bucksbaum, B. Pearson, J. M. Geremia, H. Rabitz, H. C. Kapteyn, and M. M.
Murnane, Chem. Phys. Lett. 344, 333 (2001). [13] R. Bartels, S. Backus, I. Christov, H. Kapteyn, and M. Murnane, Chem. Phys. 267, 277 (2001). [14] I. P. Christov, R. Bartels, H. C. Kapteyn, and M. M. Murnane, Phys. Rev. Lett. 86, 5458 (2001). [15] Z. Chang, A. Rundquist, H. Wang, I. Christov, H. C. Kapteyn, and M. M. Murnane, Phys. Rev. A 58, R30 (1998). [16] P. Salieres, P. Antoine, A. de Bohan, and M. Lewenstein, Phys. Rev. Lett. 81, 5544 (1998). [17] E. Gibson, A. Paul, N. Wagner, S. Backus, M. M. Murnane, H. C. Kapteyn, R. A. Bartels, and I. P. Christov, in 3rd International Workshop on Optimal Control of Quantum Dynamics: Theory and Experiment (Ringberg, Germany, 2003). [18] J. L. White, B. J. Pearson, and P. H. Bucksbaum, e-print quantph/0401018. [19] C. Daniel, J. Full, L. Gonzalez, C. Lupulescu, J. Manz, A. Merli, S. Vajda, and L. Woste, Science 299, 536 (2003). [20] E. Zeek, R. Bartels, M. M. Murnane, H. C. Kapteyn, S. Backus, and G. Vdovin, Opt. Lett. 25, 587 (2000). [21] A. Rundquist, C. G. Durfee III, S. Backus, C. Herne, Z. Chang, M. M. Murnane, and H. C. Kapteyn, Science 280, 1412 (1998). [22] E. Zeek, K. Maginnis, S. Backus, U. Russek, M. Murnane, G. Mourou, H. Kapteyn, and G. Vdovin, Opt. Lett. 24, 493 (1999). [23] M. Hollander and D. A. Wolfe, Nonparametric Statistical Methods (Wiley, New York, 1973).
1-5
Вам также может понравиться
- Theory of Quantum and Classical Connections in Modeling Atomic, Molecular and Electrodynamical SystemsОт EverandTheory of Quantum and Classical Connections in Modeling Atomic, Molecular and Electrodynamical SystemsОценок пока нет
- Applications of Quantum and Classical Connections in Modeling Atomic, Molecular and Electrodynamic SystemsОт EverandApplications of Quantum and Classical Connections in Modeling Atomic, Molecular and Electrodynamic SystemsОценок пока нет
- Ultrarelativistic Nanoplasmonics As A New Route Towards Extreme Intensity Attosecond PulsesДокумент15 страницUltrarelativistic Nanoplasmonics As A New Route Towards Extreme Intensity Attosecond Pulsesnasrin49Оценок пока нет
- Coherently Driving A Single Quantum Two-Level System With Dichromatic Laser PulsesДокумент18 страницCoherently Driving A Single Quantum Two-Level System With Dichromatic Laser Pulses鍾宗霖Оценок пока нет
- Quantum Computational Advantage Using Photons: Cylu@ustc - Edu.cn Pan@ustc - Edu.cnДокумент23 страницыQuantum Computational Advantage Using Photons: Cylu@ustc - Edu.cn Pan@ustc - Edu.cnkerblaОценок пока нет
- A Mathematical Model For The Transient Lightning Response From Grounding SystemsДокумент15 страницA Mathematical Model For The Transient Lightning Response From Grounding SystemsGilberto MejiaОценок пока нет
- W. G. Noid, Gregory S. Ezra and Roger F. Loring - Optical Response Functions With Semiclassical DynamicsДокумент18 страницW. G. Noid, Gregory S. Ezra and Roger F. Loring - Optical Response Functions With Semiclassical DynamicsOmasazzОценок пока нет
- Density Functional Theory and Solvation ModelДокумент37 страницDensity Functional Theory and Solvation Modelsiska tasyaОценок пока нет
- Report - Ab Initio and Semiempirical1Документ15 страницReport - Ab Initio and Semiempirical1Elisha NiñaОценок пока нет
- Spectroscopic and Theoretical AspectsДокумент123 страницыSpectroscopic and Theoretical AspectsMPCОценок пока нет
- Quantum Mechanics: MethodsДокумент5 страницQuantum Mechanics: MethodsLuis CapaОценок пока нет
- Multiscale Modeling With Carbon Nanotubes: A. MaitiДокумент44 страницыMultiscale Modeling With Carbon Nanotubes: A. MaitiAlessio GagliardiОценок пока нет
- Quantum Model Simulations of Attosecond Electron Di: Science ChinaДокумент18 страницQuantum Model Simulations of Attosecond Electron Di: Science ChinaJingrui LiОценок пока нет
- Exact MappingДокумент21 страницаExact MappingReember CanoОценок пока нет
- C.-L. Chang Et Al - Production of A Monoenergetic Electron Bunch in A Self-Injected Laser-Wakefield AcceleratorДокумент10 страницC.-L. Chang Et Al - Production of A Monoenergetic Electron Bunch in A Self-Injected Laser-Wakefield AcceleratorVasmazxОценок пока нет
- Orbit HarmonicДокумент21 страницаOrbit HarmonicMartín FigueroaОценок пока нет
- An Introduction To Molecular ModelingДокумент10 страницAn Introduction To Molecular ModelingVidya MОценок пока нет
- Vaschetto 1999Документ13 страницVaschetto 1999lionelОценок пока нет
- Lattice 2008 099Документ7 страницLattice 2008 099Red GluonОценок пока нет
- Falk Richter Et Al - Time-Dependent Wavepacket Study On Trans-Cis Isomerization of HONO With An External FieldДокумент50 страницFalk Richter Et Al - Time-Dependent Wavepacket Study On Trans-Cis Isomerization of HONO With An External FieldTreaxmeAОценок пока нет
- Latest - CLRI Internship ReportДокумент17 страницLatest - CLRI Internship ReportAdil KollanОценок пока нет
- Srep 07892Документ7 страницSrep 07892ResalatFaruqueNuhОценок пока нет
- Superposition P-WPS OfficeДокумент2 страницыSuperposition P-WPS OfficeCarrizz Laurie Wasian DaysaОценок пока нет
- N. Renaud, M. A. Ratner and C. Joachim - A Time-Dependent Approach To Electronic Transmission in Model Molecular JunctionsДокумент11 страницN. Renaud, M. A. Ratner and C. Joachim - A Time-Dependent Approach To Electronic Transmission in Model Molecular JunctionsHumdsОценок пока нет
- Thomas Pfeifer Et Al - Heterodyne Mixing of Laser Fields For Temporal Gating of High-Order Harmonic GenerationДокумент4 страницыThomas Pfeifer Et Al - Heterodyne Mixing of Laser Fields For Temporal Gating of High-Order Harmonic GenerationPocxaОценок пока нет
- Statement of Research Interests-Example 3Документ7 страницStatement of Research Interests-Example 3NedelcuGeorgeОценок пока нет
- Control Fields PDFДокумент42 страницыControl Fields PDFREDIL KATALОценок пока нет
- Alessandro Troisi and Mark A. Ratner - Inelastic Insights For Molecular Tunneling Pathways: Bypassing The Terminal GroupsДокумент7 страницAlessandro Troisi and Mark A. Ratner - Inelastic Insights For Molecular Tunneling Pathways: Bypassing The Terminal GroupsHumdsОценок пока нет
- Carmen Herrmann Et Al - Ghost Transmission: How Large Basis Sets Can Make Electron Transport Calculations WorseДокумент17 страницCarmen Herrmann Et Al - Ghost Transmission: How Large Basis Sets Can Make Electron Transport Calculations WorseGomsajОценок пока нет
- DFT TsunedaДокумент207 страницDFT Tsunedaunknown159Оценок пока нет
- Krug 2009Документ18 страницKrug 2009asteriОценок пока нет
- Nicholson ShainДокумент18 страницNicholson ShainFrancisco SalgadoОценок пока нет
- Particle-Vibration Coupling Within Covariant Density Functional TheoryДокумент41 страницаParticle-Vibration Coupling Within Covariant Density Functional TheoryBayer MitrovicОценок пока нет
- Non-Newtonian Topological Mechanical Metamaterials Using Feedback ControlДокумент6 страницNon-Newtonian Topological Mechanical Metamaterials Using Feedback ControlKutjePutjeОценок пока нет
- E. Hertz Et Al - Probing Attosecond Pulse Trains Using Phase-Control'' TechniquesДокумент4 страницыE. Hertz Et Al - Probing Attosecond Pulse Trains Using Phase-Control'' TechniquesPocxaОценок пока нет
- Energy States of MoleculesДокумент12 страницEnergy States of MoleculesBenjamín Marc Ridgway de SassouОценок пока нет
- Efthymios Kallos Et Al - A Multibunch Plasma Wakefield AcceleratorДокумент3 страницыEfthymios Kallos Et Al - A Multibunch Plasma Wakefield AcceleratorVasmazxОценок пока нет
- Spectral Calculations With DFTДокумент28 страницSpectral Calculations With DFTCristián MaulénОценок пока нет
- ETP PDF Final 2014Документ8 страницETP PDF Final 2014Jaime Guerra ValenciaОценок пока нет
- Atomic Scale FemДокумент16 страницAtomic Scale FemAgnitra GhoshОценок пока нет
- Spontaneous and Stimulated Radiative Emission of Modulated Free-Electron Quantum Wavepackets - Semiclassical AnalysisДокумент49 страницSpontaneous and Stimulated Radiative Emission of Modulated Free-Electron Quantum Wavepackets - Semiclassical AnalysisMuhammad AsgharОценок пока нет
- Excitation Spectra and Brightness Optimization of Two-Photon Excited ProbesДокумент11 страницExcitation Spectra and Brightness Optimization of Two-Photon Excited ProbesCLPHtheoryОценок пока нет
- A Novel Fundamental and Harmonics Detection Method Based On State-Space Model For Power Electronics SystemДокумент11 страницA Novel Fundamental and Harmonics Detection Method Based On State-Space Model For Power Electronics SystemJosé Júlio M. MelazzoОценок пока нет
- Christian Beck Et Al - Highly Excited Vibrational States of HCP and Their Analysis in Terms of Periodic Orbits: The Genesis of Saddle-Node States and Their Spectroscopic SignatureДокумент17 страницChristian Beck Et Al - Highly Excited Vibrational States of HCP and Their Analysis in Terms of Periodic Orbits: The Genesis of Saddle-Node States and Their Spectroscopic SignatureImasmzОценок пока нет
- An Introduction To Molecular Orbital TheoryДокумент24 страницыAn Introduction To Molecular Orbital TheoryvellarineОценок пока нет
- First Physics News From The Cms Experiment at The LHCДокумент14 страницFirst Physics News From The Cms Experiment at The LHCperica21Оценок пока нет
- Heat and ChargeДокумент18 страницHeat and ChargeBhanu PrakashОценок пока нет
- 2006 MKS NPA RRD-EFs-O+TbДокумент22 страницы2006 MKS NPA RRD-EFs-O+TbUnnati GuptaОценок пока нет
- Introduction To Computational ChemistryДокумент16 страницIntroduction To Computational ChemistryBruno OliveiraОценок пока нет
- Algorithm For Raman Backward PumpingДокумент8 страницAlgorithm For Raman Backward PumpingBharath LagishettyОценок пока нет
- Computational Study of Amino Acids, Order To Simulation of Membrane Protein Channels Using by Theoretical MethodsДокумент6 страницComputational Study of Amino Acids, Order To Simulation of Membrane Protein Channels Using by Theoretical MethodsMhemeydha Luphe YudhaОценок пока нет
- MicromachinesДокумент21 страницаMicromachinessvfОценок пока нет
- Modelos DFTДокумент17 страницModelos DFTAlberto Núñez CardezoОценок пока нет
- Methods of Exploring Energy Diffusion in Lattices With Finite TemperatureДокумент20 страницMethods of Exploring Energy Diffusion in Lattices With Finite TemperatureJeanette AmayaОценок пока нет
- Electron Beam Waves in Microwave Tubes: H. A. HausДокумент46 страницElectron Beam Waves in Microwave Tubes: H. A. Hausjk556Оценок пока нет
- Electronic Spectra of Cyanine Dyes: A Particle in The Box ModelДокумент6 страницElectronic Spectra of Cyanine Dyes: A Particle in The Box ModelMurad AlDamenОценок пока нет
- AbstractsДокумент4 страницыAbstractsapi-248830768Оценок пока нет
- Andrew K. Henrick, Tariq D. Aslam and Joseph M. Powers - Simulations of Pulsating One-Dimensional Detonations With True Fifth Order AccuracyДокумент19 страницAndrew K. Henrick, Tariq D. Aslam and Joseph M. Powers - Simulations of Pulsating One-Dimensional Detonations With True Fifth Order AccuracyNikeShoxxxОценок пока нет
- Separacao Spin CargaДокумент12 страницSeparacao Spin CargaMatheus MendesОценок пока нет
- Magneto HydrodynamicsДокумент32 страницыMagneto HydrodynamicsNitin PooniaОценок пока нет
- Gennady Shvets - Beat-Wave Excitation of Plasma Waves Based On Relativistic BistabilityДокумент4 страницыGennady Shvets - Beat-Wave Excitation of Plasma Waves Based On Relativistic BistabilityPocxaОценок пока нет
- E. Hertz Et Al - Probing Attosecond Pulse Trains Using Phase-Control'' TechniquesДокумент4 страницыE. Hertz Et Al - Probing Attosecond Pulse Trains Using Phase-Control'' TechniquesPocxaОценок пока нет
- Science at Ultra-Brieftime Periods From The Attosecond To The PetawattДокумент8 страницScience at Ultra-Brieftime Periods From The Attosecond To The PetawattPocxaОценок пока нет
- G.V. Stupakov and M. S. Zolotorev - Ponderomotive Laser Acceleration and Focusing in Vacuum For Generation of Attosecond Electron BunchesДокумент4 страницыG.V. Stupakov and M. S. Zolotorev - Ponderomotive Laser Acceleration and Focusing in Vacuum For Generation of Attosecond Electron BunchesPocxaОценок пока нет
- Design of Combinational Circuit For Code ConversionДокумент5 страницDesign of Combinational Circuit For Code ConversionMani BharathiОценок пока нет
- Training For Humans Guide: FAQ's How Many Sets/reps Should I Do Per Exercise?Документ28 страницTraining For Humans Guide: FAQ's How Many Sets/reps Should I Do Per Exercise?Paulo Pires100% (1)
- Ra 9272Документ6 страницRa 9272janesamariamОценок пока нет
- FIRST SUMMATIVE EXAMINATION IN ORAL COMMUNICATION IN CONTEXT EditedДокумент3 страницыFIRST SUMMATIVE EXAMINATION IN ORAL COMMUNICATION IN CONTEXT EditedRodylie C. CalimlimОценок пока нет
- Meno's Paradox of Inquiry and Socrates' Theory of RecollectionДокумент10 страницMeno's Paradox of Inquiry and Socrates' Theory of RecollectionPhilip DarbyОценок пока нет
- How To Block HTTP DDoS Attack With Cisco ASA FirewallДокумент4 страницыHow To Block HTTP DDoS Attack With Cisco ASA Firewallabdel taibОценок пока нет
- Applied Economics 2Документ8 страницApplied Economics 2Sayra HidalgoОценок пока нет
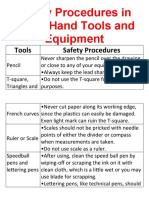
- Safety Procedures in Using Hand Tools and EquipmentДокумент12 страницSafety Procedures in Using Hand Tools and EquipmentJan IcejimenezОценок пока нет
- Rifle May 2015 USAДокумент72 страницыRifle May 2015 USAhanshcОценок пока нет
- PresentationДокумент27 страницPresentationMenuka WatankachhiОценок пока нет
- MultiLoadII Mobile Quick Start PDFДокумент10 страницMultiLoadII Mobile Quick Start PDFAndrés ColmenaresОценок пока нет
- Rajiv Gandhi University of Health Sciences, Bengaluru, KarnatakaДокумент9 страницRajiv Gandhi University of Health Sciences, Bengaluru, KarnatakaNavin ChandarОценок пока нет
- Chapter 4 Achieving Clarity and Limiting Paragraph LengthДокумент1 страницаChapter 4 Achieving Clarity and Limiting Paragraph Lengthapi-550339812Оценок пока нет
- Music 10 (2nd Quarter)Документ8 страницMusic 10 (2nd Quarter)Dafchen Villarin MahasolОценок пока нет
- Listen and Arrange The Sentences Based On What You Have Heard!Документ3 страницыListen and Arrange The Sentences Based On What You Have Heard!Dewi Hauri Naura HaufanhazzaОценок пока нет
- Head Coverings BookДокумент86 страницHead Coverings BookRichu RosarioОценок пока нет
- ELEVATOR DOOR - pdf1Документ10 страницELEVATOR DOOR - pdf1vigneshОценок пока нет
- 7TH Maths F.a-1Документ1 страница7TH Maths F.a-1Marrivada SuryanarayanaОценок пока нет
- UT Dallas Syllabus For Govt4396.002.08s Taught by Gregory Thielemann (Gregt)Документ2 страницыUT Dallas Syllabus For Govt4396.002.08s Taught by Gregory Thielemann (Gregt)UT Dallas Provost's Technology GroupОценок пока нет
- Health Post - Exploring The Intersection of Work and Well-Being - A Guide To Occupational Health PsychologyДокумент3 страницыHealth Post - Exploring The Intersection of Work and Well-Being - A Guide To Occupational Health PsychologyihealthmailboxОценок пока нет
- Advanced Chemical Engineering Thermodynamics (Cheg6121) : Review of Basic ThermodynamicsДокумент74 страницыAdvanced Chemical Engineering Thermodynamics (Cheg6121) : Review of Basic ThermodynamicsetayhailuОценок пока нет
- DLP - Light Science 7Документ6 страницDLP - Light Science 7Samara M. SalacayanОценок пока нет
- CHAPTER 1 SBL NotesДокумент13 страницCHAPTER 1 SBL NotesPrieiya WilliamОценок пока нет
- LP For EarthquakeДокумент6 страницLP For Earthquakejelena jorgeoОценок пока нет
- (1921) Manual of Work Garment Manufacture: How To Improve Quality and Reduce CostsДокумент102 страницы(1921) Manual of Work Garment Manufacture: How To Improve Quality and Reduce CostsHerbert Hillary Booker 2nd100% (1)
- Evolution Army 3 R DadДокумент341 страницаEvolution Army 3 R DadStanisław DisęОценок пока нет
- Quiz 140322224412 Phpapp02Документ26 страницQuiz 140322224412 Phpapp02Muhammad Mubeen Iqbal PuriОценок пока нет
- Physics Education Thesis TopicsДокумент4 страницыPhysics Education Thesis TopicsPaperWriterServicesCanada100% (2)
- Escaner Electromagnético de Faja Transportadora-Steel SPECTДокумент85 страницEscaner Electromagnético de Faja Transportadora-Steel SPECTEdwin Alfredo Eche QuirozОценок пока нет
- The Covenant Taken From The Sons of Adam Is The FitrahДокумент10 страницThe Covenant Taken From The Sons of Adam Is The FitrahTyler FranklinОценок пока нет