Академический Документы
Профессиональный Документы
Культура Документы
Particle Tracking Notes
Загружено:
Pejman ShoИсходное описание:
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Particle Tracking Notes
Загружено:
Pejman ShoАвторское право:
Доступные форматы
From the SelectedWorks of Kari Myhnen
January 2008
Modeling of dispersed phase by Lagrangian
approach in Fluent
Contact
Author
Start Your Own
SelectedWorks
Notify Me
of New Work
Available at: http://works.bepress.com/kari_myohanen/5
Modeling of Dispersed Phase
by Lagrangian Approach in Fluent
Theory and simulation of dispersed-phase multiphase flows, Autumn 2007 Spring 2008
11 March 2008
Kari Myhnen
kari.myohanen@lut.fi
Pr esent at i on Out l i ne
Introduction
Modeling options and limitations in Fluent
Model theory
Solution strategies
Example calculation
I nt r oduct i on
The discrete phase model (DPM) in Fluent follows the Euler-Lagrange approach.
The fluid phase (gas or liquid, continuous phase) is treated as a continuum by
solving the time-averaged Navier-Stokes equations (Eulerian reference frame).
The dispersed phase is solved by tracking a number of particles through the
calculated flow field of continuous phase (Lagrangian reference frame).
The particles may be taken to represent solid particles in gas or liquid, liquid droplets
in gas or bubbles in liquid.
The dispersed phase can exchange momentum, mass and energy with the fluid
phase.
Di scr et e Phase Model i ng Opt i ons i n Fl uent
Fluent provides the following discrete phase modeling options:
Calculation of the particle trajectories using a Lagrangian formulation that includes:
Discrete phase inertia
Hydrodynamic drag
Force of gravity
Other forces
pressure gradient, thermophoretic, rotating reference frame, brownian motion,
Saffman lift, and user defined forces
Steady state and transient flows.
Turbulent dispersion of particles.
Heating and cooling of the discrete phase.
Vaporization and boiling of liquid droplets.
Combusting particles, including volatile evolution and char combustion to simulate
coal combustion.
Optional two-way coupling of the continuous phase flow and the discrete phase.
Wall film modeling.
Spray model (droplet collision and breakup).
Li mi t at i ons i n Fl uent
Particle-particle interactions are neglected.
Assumption: dispersed phase is sufficiently dilute.
Fluent manual provides a hand rule volume fraction usually less than 10-12%.
In general, this limit is far too high and does not fulfill the requirement of ratio
between the momentum response time and collisional time
V
/
C
< 1
(see lecture notes, session 1).
The DPM model is however often used for dense dispersed flows as well. Care
should be taken when interpreting the results.
The steady state DPM model cannot be applied for continuous suspension of particles
The particle streams should have well-defined entrance and exit conditions.
For cases, in which the particles are suspended indefinetely in the continuum (e.g.
stirred tanks), the unsteady DPM modeling should be used instead.
If the dispersed phase model is used with Eulerian-Eulerian multiphase model the
coupling is defined with the primary phase only.
Several restrictions when using DPM model with other Fluent models
Limitations with parallel computing, streamwise periodic flows, combustion
models, sliding meshes, etc. See Fluent manual for details.
Regi mes of Di sper sed Tw o- Phase Fl ow s
Sommerfeld (2000), based on Elghobashi (1994).
fluidparticle fluidparticle
fluidparticle particle
Moment um Equat i on
The force balance of particle in Lagrangian reference frame defines the
movement of the particles.
The momentum equation for i-direction:
Drag Gravity Additional acceleration
due to other forces
(force/unit particle mass)
Acceleration
Dr ag Coef f i ci ent
For smooth spherical particles, Fluent uses equation by Morsi and Alexander (1972):
The constants a
1
, a
2
and a
3
are
determined for different ranges of Re:
For nonspherical particles, the equation by Haider and Levenspiel (1989) is used:
Shape factor
Surface area of sphere with same volume
Actual surface area
Compar i son of Dr ag Coef f i ci ent Equat i ons
The discrete phase and the continuous phase can be coupled in a number of ways.
In Fluent, the one-way or two-way coupling are possible to model.
One-way coupling
The continuous phase affects the discrete phase, but there is no reverse effect.
In Fluent, this is referred as uncoupled approach.
The discrete phase is solved once after the continuous phase flow has been
solved.
Two-way coupling
Both phases affect each other (exchange of momentum, mass and energy).
In Fluent, this is referred as coupled approach.
The continuous phase flow field is impacted by the discrete phase and the
calculations of the continuous phase and dispersed phase equations are
alternated until the solution is converged (hopefully).
Three-way coupling
Particle disturbance of the fluid locally affects
another particles motion, e.g. drafting of a trailing particle.
Four-way coupling
Particle collisions affect motion of individual particles.
Coupl i ng
Tw o- Way Coupl i ng i n Fl uent
Momentum exchange
Drag Other interaction forces
Heat exchange
(without chemical reactions)
Vaporization
and pyrolysis
Sensible heat
Mass exchange
Par t i cl e Types and Law s i n Fl uent
Particle type Description Requirements Laws activated
Inert inert/heating or cooling Available for all models 1, 6
Droplet heating/evaporation/
boiling
Energy equation.
Minimum two chemical species or the
nonpremixed or partially premixed
combustion model.
Gas phase density by ideal law.
1, 2, 3, 6
Combusting heating; evolution of
volatiles/swelling;
heterogeneous surface
reaction
Energy equation.
Minimum three chemical species or
the nonpremixed combustion model.
Gas phase density by ideal law.
1, 4, 5, 6
Multicomponent multicomponent
droplets/particles
Energy equation.
Min. two chemical species.
Use volume weighted mixing law to
define define particle mixture density.
7
Law 1: Particle temperature below vaporization temperature.
Law 2: Droplet vaporization.
Law 3: Droplet boiling.
Law 4: Devolatilization of combusting particle.
Law 5: Surface combustion.
Law 6: Volatile fraction of the particle consumed.
Law 7: Multicomponent particle definition
Ex ampl e of Law s Appl i ed f or a Dr y i ng Dr opl et
T
e
m
p
e
r
a
t
u
r
e
Particle time
Law 1:
Inert heating
before vaporization
Law 2:
Vaporization
Law 3:
Boiling
T
bp
T
vap
T
injection
Law 6:
Volatile fraction
consumed
Different energy and mass transfer equations are applied during different laws.
Mass transfer (molar flux of vapor)
Mass and Ener gy Tr ansf er of Dr y i ng Dr opl et
Law 1:Inert heating before vaporization
Law 6: Volatile fraction consumed
Law 2: Vaporization
Law 3: Boiling
Heat transfer
Convection Radiation
Vapor concentration at droplet surface / bulk gas
Vapor pressure
must be correctly
defined
Diffusion coefficient
given by user
Particle temperature is constant.
Energy required for vaporization appears as energy sink for gas phase
Evaporation
Mass transfer without radiation
with radiation
Heat transfer
Par t i cl e- Wal l I nt er act i on
Different particle boundary conditions can be defined for walls, inlets and outlets:
volatile fraction
flashes to vapor
Escape
Reflect Trap
For particle reflection, a restitution coefficient e is specified:
Normal component:
Tangential component:
Tur bul ent Di sper si on of Par t i cl es
In Fluent, the dispersion of particles due to continuous phase turbulence can be modeled by
a stochastic tracking model (random walk model, eddy interaction model), or
a particle cloud model.
In the random walk model, the instantaneous continuous phase velocity is formed
of mean velocity and fluctuating component:
The fluctuating component varies randomly during a particle track.
Each particle injection is tracked repeatedly in order to generate a statistically
meaningful sampling.
The cloud model uses statistical methods to trace the turbulent dispersion of particles
about a mean trajectory
Mean trajectory is calculated from the ensemble average of the equations of motion
for the particles represented in the cloud.
Distribution of particles inside the cloud is represented by a Gaussian PDF.
Eddy I nt er act i on Model
The stochastic tracking model in Fluent is based on eddy interaction model.
The discrete particle is assumed to interact with a succession of eddies.
Each eddy is characterized by
a Gaussian distributed random velocity fluctuation u
i
a time scale (life time of eddy)
e
a length scale (size of eddy) L
e
During interaction, the fluctuating velocity is kept constant.
The interaction lasts until time exceeds the eddy lifetime or the eddy crossing time.
Literature presents several theories for determining the above values (see Graham and James (1996)).
The following presents the equations used in Fluent with k- turbulence model.
Fluid Lagrangian integral time Coefficient C
L
defined by user. Default value C
L
= 0.15.
Characteristic life time of eddy
Eddy length scale
(based on Karema(2008))
Notice: in literature, the length scale and life time are often linked:
In Fluent, this seems to be:
c
2 3 /
L e
k
C L =
k
L
e
e
2
1
=
t
3
2k L
e
e
=
t
Eddy crossing time Velocity response time
t
18
2
p p
d
=
Fluctuating velocity
For k- turbulence model:
= Gaussian distributed random number
(standard normal distribution)
or alternatively random variation:
, ) r ln T
L e
= t
r = uniform random number [0...1]. Notice:
, )
L e
T r ln = = t 1
I nj ect i on Set up
Particle injections can be defined by various methods:
Single: a particle stream is injected from a single point.
Group: particle streams are injected along a line.
Cone: streams are injected in a hollow conical pattern.
Solid cone.
Surface: particle streams are injected from a surface
(one stream from each cell face).
Atomizer: streams are injected by using various predefined
atomizer models.
File: injection locations and initial conditions are defined
in an external file.
For each injection, the following data are defined:
Particle type (inert, droplet, combusting, multicomponent)
Material (from database)
Initial conditions (particle size, velocity, etc.)
Destination species for reacting particles.
Evaporating material for combusting particles.
DPM Concent r at i on
Fluent can report a DPM concentration in a coupled calculation. This is a total
concentration of the discrete phase in a continuous cell.
The mass flow of a particle track is determined based on particle mass and
mass flow at the particle injection and particle mass at current location.
The particle mass can change due to evaporation and other phase changes.
The discrete phase concentration inside a cell can be determined from the
residence time and mass flow.
Inside a cell, the particle stream is tracked with n particle time steps. The
residence time of one particle track is the sum of these time steps.
The total concentration is summed over all particle tracks.
The particle-particle interaction is neglected, thus when multiple
particle tracks cross the cell, the calculated concentration can
exceed the bulk density of solids or even solid density
(volume fraction of solids above 1). These results are not
physically sensible but they can show areas, where the particle
loading is high and the assumption of dilute flow is not valid.
t
0
t
N
m
p
Sol ut i on St r at egi es: Par t i cl e Tr ack i ng
The particle tracks are calculated in steps. The step length factor determines
approximately the number of steps per fluid cell. The default value is 5, but it should
preferably be higher: 10 20.
Increasing the step length factor (i.e. decreasing the step length) can improve stability of
heat and mass exchange (e.g. when calculating vaporization).
The max. number of steps limits the number of calculated time steps. This should be
large enough so that the particles can travel from entrance to exit.
If particles remain suspended in the model (tracking incomplete), then steady state
solution is questionable and transient tracking should be used instead. The transient
calculations in Fluent can be performed in a number of ways and combinations. This
presentation is focused on steady state calculation.
Sol ut i on St r at egi es: Tw o- Way Coupl i ng
The solution of the continuous field without coupling is usually the starting point.
In most cases, the continuous flow does not have to be fully converged before
the coupling is started, because the particle tracks will have a large effect on the
continuous flow.
In a coupled calculation, additional source terms appear in discretized flow
equations of continuous phase. During particle tracking, each particle is seeing
a fresh cell and makes no notice of particles already visited and marked the
cell with their source terms. This leads to overprediction of the source terms and
bad convergence behaviour with evaporation, combustion and radiation.
Use solution limits to limit the temperature in the domain.
Increasing the number of trajectories (especially with random walk model) will
smooth the particle source terms, which should help convergence.
The discrete phase source terms can be under-relaxed (e.g. 0.5). The flow
equations may need to be under-relaxed as well (energy and species).
The number of continuous phase calculations between the trajectory
calculations can either be small (< 3) or high (>15). In the first choice, the
dispersed and continuous flow are closer coupled and the solution of both
should slowly convergence. In the second choice, the flows are decoupled and
the solution of continuous field remains better converged and the calculation is
more stable. In the latter case, the continuous phase may appear to be
converged, but the discrete phase is not.
If the dispersed phase is not dilute, then convergence is very difficult to achieve
in coupled calculations.
C a l c u l a t e
c o n t i n u o u s
p h a s e
C a l c u l a t e
p a r t i c l e
t r a c k s
U p d a t e
s o u r c e
t e r m s
Model i ng Ex ampl e
The model geometry is shown below.
Hot air flows in a 200 mm diameter duct.
Wet limestone particles are injected from the top of the duct
(inlet d = 50 mm) at location 500 mm before a 90bend.
Air inlet: 10 m/s, 270C, D= 0.2 m
Particle inlet: 0.1 kg/s, 0.1 m/s, d
p
=200 m,
p
=2700 kg/m3, H
2
O=30%
Average volume fraction of
solids in the duct:
dilute, two-way coupling
(but only as average)
Mesh
Gas Pr oper t i es
Sol i d Pr oper t i es ( Li mest one)
Model Par amet er s
Sol ut i on of Cont i nuous Phase
The continuous phase was first solved without the particles.
The convergence was good.
Uncoupl ed Mean Par t i cl e Tr ack s
The mean particle tracks were solved without two-way coupling.
The particle tracks are thus calculated only once after the continuous phase was solved.
The following images present particle tracks colored by mass, which indicates evaporation.
Initial mass 1.13E-8 kg
Fully evaporated 7.92E-9 kg
Uncoupl ed Tur bul ent Tr ack s
Random walk model with 50 stochastic tracks (total 2400) was used with default C
L
= 0.15.
Uncoupled solution, ie. one-way coupled calculation of dispersed phase.
Turbulence effects are fairly small, but can be noticed in the track images.
Initial mass 1.13E-8 kg
Fully evaporated 7.92E-9 kg
Sol ut i on of Coupl ed Cal cul at i on
Two-way coupled solution did not converge well.
Different step length factors, under-relaxation parameters and number of continuous phase
iterations were tried.
In the final calculations, the step length factor was 20 and the number of continuous phase
iterations between dispersed phase calculations was 20. The residuals were indicating poor
convergence.
Coupl ed Par t i cl e Tr ack s
The particle tracks show that some of the particle streams circulate for long times before
reaching the outlet.
The solution of flow is much different from uncoupled solution.
The images do not show all particle tracks.
Initial mass 1.13E-8 kg
Fully evaporated 7.92E-9 kg
Ef f ect on Cont i nuous Fl ow Fi el d
In the coupled calculation, the particle tracks affect the continuous phase flow.
In this case, the effect is considerable.
DPM Concent r at i on
The DPM concentration shows the total concentration of dispersed phase.
Results indicate that in the bend, the dispersed phase is not dilute (
max
= 0.094).
Reaching a converged solution in this case would be impossible.
The results should be utilized with caution.
Vi sual i zat i on of Resul t s
Different process variables can be easily visualized: pressure, velocities, temperature,
concentration of species, turbulence variables, ...
Summar y
The DPM model in Fluent can be used for studying one-way or two-way
coupled dilute dispersed flows, including effects of turbulence.
The basic model is easy to use and physics are clear and simple.
The limitations of the DPM model should be carefully considered when
analyzing the results.
The model neglects particle-particle interaction, thus it is valid for dilute
dispersed phase only.
The one-way coupling is valid for very dilute flow only. The two-way coupled
solution can be much different from the one-way coupled solution.
The average flow can be dilute, but it can contain regions, in which the
dispersed phase is dense. In these regions, the model results are false.
Moreover, the convergence is poor, if the dispersed phase is dense and the
momentum, mass and energy exchange to continuous phase is strong.
Despite the limitations, the DPM model can be (and is) successfully used for
modeling various applications.
Ref er ences
Bakker, A. (2006). Lecture notes, Computational Fluid Dynamics, Dartmouth College.
http://www.bakker.org/dartmouth06/engs150/.
Elghobashi, S. (1994). On predicting particle-laden turbulent flows, Appl. Sci. Res. 52, pp. 309
329.
Fluent 6.3 Documentation (2008).
Fluent Training Material (2008). http://www.fluentusers.com.
Graham D. I. and James P.W. (1996). Turbulent dispersion of particles using eddy interaction
models. Int. J. Multiphase Flow, 22-1, pp 157-175.
Haider, A. and Levenspiel, O. (1989). Drag Coefficient and Terminal Velocity of Spherical and
Nonspherical Particles.Powder Technology, 58, pp. 6370.
Jalali, P. (2007). Lecture notes, Theory and simulation of dispersed-phase multiphase flows,
Lappeenranta University of Technology. http://www2.et.lut.fi/ttd/Dispersed2007/Dispersed.htm
Karema, H. (2008). Discussions with Hannu Karema (Process Flow), January 2008.
Loth, E. (2008). Computational Fluid Dynamics of Bubbles, Drops and Particles (draft).
http://www.ae.uiuc.edu/~loth/CUP/Loth.htm
Morsi, S. and Alexander A. (1972), An investigation of particle trajectories in two-phase flow
systems, Journal of Fluid Mechanics 55, pp. 193208.
Sommerfeld, M. (2000). Theoretical and Experimental Modelling of Particulate Flows. Lecture
Series 2000-06, von Karman Institute for Fluid Dynamics.
http://www-mvt.iw.uni-halle.de/download.php?id=571340,326,2
Вам также может понравиться
- Process Flow Diagram Design CriteriaДокумент16 страницProcess Flow Diagram Design CriteriaGabriele GabrieleОценок пока нет
- Marshall Mix Design ProcedureДокумент31 страницаMarshall Mix Design Procedurebraackw100% (2)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceОт EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceРейтинг: 4 из 5 звезд4/5 (890)
- Thermodynamics, Heat Transfer, and Fluid Flow Handbook: Fluid Flow Continuity EquationДокумент300 страницThermodynamics, Heat Transfer, and Fluid Flow Handbook: Fluid Flow Continuity EquationGanesh BangarОценок пока нет
- The Yellow House: A Memoir (2019 National Book Award Winner)От EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Рейтинг: 4 из 5 звезд4/5 (98)
- Measuring Instrument For Drilling MudДокумент12 страницMeasuring Instrument For Drilling Mudrony asmОценок пока нет
- The Little Book of Hygge: Danish Secrets to Happy LivingОт EverandThe Little Book of Hygge: Danish Secrets to Happy LivingРейтинг: 3.5 из 5 звезд3.5/5 (399)
- Partition Curve - An Overview - ScienceDirect TopicsДокумент38 страницPartition Curve - An Overview - ScienceDirect TopicsnarendrasinghsjsОценок пока нет
- PTZ-BOX FCD - IOM - Oct 2009 PDFДокумент49 страницPTZ-BOX FCD - IOM - Oct 2009 PDFtareq.sefatОценок пока нет
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeОт EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeРейтинг: 4 из 5 звезд4/5 (5794)
- Manual Threaded Balancing Valves: Product Data SheetДокумент20 страницManual Threaded Balancing Valves: Product Data SheethalackОценок пока нет
- Never Split the Difference: Negotiating As If Your Life Depended On ItОт EverandNever Split the Difference: Negotiating As If Your Life Depended On ItРейтинг: 4.5 из 5 звезд4.5/5 (838)
- Direct Shear Test Lab ManualДокумент6 страницDirect Shear Test Lab Manualmm0% (1)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureОт EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureРейтинг: 4.5 из 5 звезд4.5/5 (474)
- Geosynthetic Institute: 475 Kedron Avenue Folsom, PA 19033-1208 USA TEL (610) 522-8440 FAX (610) 522-8441 GRI GII GEIДокумент12 страницGeosynthetic Institute: 475 Kedron Avenue Folsom, PA 19033-1208 USA TEL (610) 522-8440 FAX (610) 522-8441 GRI GII GEIГригорий ЛевашовОценок пока нет
- Microscopic Analysis of Activated Sludge. Training Manual-EPA PDFДокумент248 страницMicroscopic Analysis of Activated Sludge. Training Manual-EPA PDFjvan migvelОценок пока нет
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryОт EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryРейтинг: 3.5 из 5 звезд3.5/5 (231)
- Copper MIMДокумент12 страницCopper MIMRamachandra KulkarniОценок пока нет
- Astm B488 PDFДокумент8 страницAstm B488 PDFmunnizza64100% (1)
- The Emperor of All Maladies: A Biography of CancerОт EverandThe Emperor of All Maladies: A Biography of CancerРейтинг: 4.5 из 5 звезд4.5/5 (271)
- Gravitation Formula SheetДокумент3 страницыGravitation Formula SheetimkushofficialОценок пока нет
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreОт EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreРейтинг: 4 из 5 звезд4/5 (1090)
- Gummy BearДокумент3 страницыGummy Bearapi-265813360Оценок пока нет
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyОт EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyРейтинг: 3.5 из 5 звезд3.5/5 (2219)
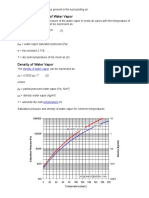
- Vapor Pressure of WaterДокумент3 страницыVapor Pressure of WaterDương Hoàng100% (1)
- Team of Rivals: The Political Genius of Abraham LincolnОт EverandTeam of Rivals: The Political Genius of Abraham LincolnРейтинг: 4.5 из 5 звезд4.5/5 (234)
- Case Study of The Changi East Land Reclamation Project SingaporeДокумент13 страницCase Study of The Changi East Land Reclamation Project SingaporeVictoria JungОценок пока нет
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersОт EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersРейтинг: 4.5 из 5 звезд4.5/5 (344)
- P 1Документ16 страницP 1Chaos GamingОценок пока нет
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaОт EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaРейтинг: 4.5 из 5 звезд4.5/5 (265)
- Che 321 Lecture Note PDFДокумент78 страницChe 321 Lecture Note PDFChigozie Francolins UzohОценок пока нет
- Stress Analysis of GRP - GRE - FRP Piping System Using Caesar II - What Is PipingДокумент23 страницыStress Analysis of GRP - GRE - FRP Piping System Using Caesar II - What Is PipingHazimОценок пока нет
- European Pharmacopoeia Optical Rotation and Refractive IndexДокумент1 страницаEuropean Pharmacopoeia Optical Rotation and Refractive IndexAlejaMedranoОценок пока нет
- ACI 229R 99 Controlled Low Strength MaterialsДокумент15 страницACI 229R 99 Controlled Low Strength MaterialsLuis Alberto Sonel GonzalezОценок пока нет
- Cosasco Two-Inch System: CORROSION COUPONS (Alloy Specimens) & Coupon Holder AssembliesДокумент17 страницCosasco Two-Inch System: CORROSION COUPONS (Alloy Specimens) & Coupon Holder AssembliesArifinОценок пока нет
- American Cinematographer 1923 Vol 2 No 28 PDFДокумент28 страницAmerican Cinematographer 1923 Vol 2 No 28 PDFbrad_rushingОценок пока нет
- The Unwinding: An Inner History of the New AmericaОт EverandThe Unwinding: An Inner History of the New AmericaРейтинг: 4 из 5 звезд4/5 (45)
- Materials Engineer Reviewer 1 With Answer KeyДокумент22 страницыMaterials Engineer Reviewer 1 With Answer KeymcpayodОценок пока нет
- CHM170L Exp2 DensityДокумент6 страницCHM170L Exp2 DensityKaiser SaltoОценок пока нет
- Calculation Method For Design Silos and Hoppers - Silos and Hopper Flow of Powder - Flowability Issues Solving - Discharge Throughput (Beverloo Equation)Документ19 страницCalculation Method For Design Silos and Hoppers - Silos and Hopper Flow of Powder - Flowability Issues Solving - Discharge Throughput (Beverloo Equation)SOURAVОценок пока нет
- Anorganische Chemie Fuer SchuelerДокумент478 страницAnorganische Chemie Fuer SchuelerFranke SchifflerОценок пока нет
- TDS Na2CO3Документ2 страницыTDS Na2CO3Darío Díaz de LeónОценок пока нет
- D 3014 - 99 - Rdmwmtqtukve PDFДокумент7 страницD 3014 - 99 - Rdmwmtqtukve PDFsusanaОценок пока нет
- Performance of Coconut Shell As Coarse Aggregate inДокумент46 страницPerformance of Coconut Shell As Coarse Aggregate inBiprajit Saha100% (1)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)От EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Рейтинг: 4.5 из 5 звезд4.5/5 (119)