Академический Документы
Профессиональный Документы
Культура Документы
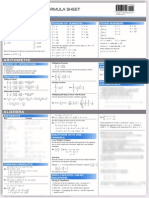
Revising Algebra Skills: Jackie Nicholas
Загружено:
علي برادةИсходное описание:
Оригинальное название
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Revising Algebra Skills: Jackie Nicholas
Загружено:
علي برادةАвторское право:
Доступные форматы
Mathematics Learning Centre
Revising algebra skills Jackie Nicholas
c 2005
University of Sydney
Mathematics Learning Centre, University of Sydney
1
1.1
Revision of Algebraic Skills
Why use algebra?
Algebra is used extensively throughout the sciences and economics. It allows us to examine relationships between two or more variables. For example, Sn = P (1 + r)n gives the formula for the amount, Sn , available on maturity when a principal, P , is invested for n years at a rate of r per annum. Lets suppose we have 10, 000 to invest for 3 years at an interest rate of 5.25% per annum. Then, S3 = 10000(1 + 0.0525)3 = 11659.13. So, at the end of 3 years we will have $11,659.13 in the account. One advantage of expressing this formula algebraically is that we can vary our values of P , r and n and use the formula again and again. Another advantage of having the algebraic formula, is that we can recongure it and ask a dierent question. For example, suppose we are have a sum of money left to us as an inheritance. We want to spend some now but also set aside enough to buy a new car in 3 years time. How much money would we need to put into a savings account earning 6% per annum now in order to have $25,000 in 3 years time. In this example, we know Sn = 25000, r = 0.06 and n = 3, but we do not know P . We can nd P by reconguring the equation, P = That is P = Sn . (1 + r)n
25000 25000 25000 = 20990.48. = = (1 + 0.06)3 1.063 1.191016
So, we would need to put $20990.48 into an account now in order to have $25,000 available for a car in 3 years time. We used algebra to work this out. In this lecture we will revise some general algebra skills.
1.2
1.2.1
General rules of algebra
Some general rules
In this section we present some general rules of algebra, with an example where appropriate. We will not attempt to justify them here. If you are interested in this or want more examples to practise then there are many elementary algebra books available. x + x + x = 3 x = 3x.
Mathematics Learning Centre, University of Sydney
x x = x2 . So, 3ab3 = 3 a b3 = 3 a b b b.
The following rules hold where n and m are real numbers and for all x where xn and xm are dened. xn xm = xn+m . For example, x3 x2 = x5 . xn xm = xnm . For example, p6 p4 = p64 = p2 . (xn )m = xnm . For example, (x4 )2 = x42 = x8 . x0 = 1, for any x other than 0, since xn xn = xnn = x0 = 1. 1 . This is a consequence of the above rule for division, as x3 x5 = x35 = n x x3 1 2 x , but x3 x5 = 5 = 2 . x x 1 1 n x = n . For example, x = x 2 . x xn =
1.2.2
Collecting like terms
Express 4p 3q + r 2q + p 5r in its simplest form. Here we can collect like terms together and simplify as follows: 4p 3q + r 2q + p 5r = 4p + p 3q 2q + r 5r = 5p 5q 4r. Note that the signs can be thought of as belonging to the pronumeral, p, q or r that follows the sign. Example Express 5xy 2 8x2 y + 10xy 3x2 y 3xy in its simplest form. Solution We can rewrite the equation as follows: 5xy 2 8x2 y + 10xy 3x2 y 3xy = 5xy 2 8x2 y 3x2 y + 10xy 3xy = 5xy 2 11x2 y + 7xy. 1.2.3 Removing brackets
There are many instances where we use brackets in mathematics for grouping parts of expressions. For example in the formula Sn = P (1 + r)n , the brackets tell us to add 1 and r rst, (1 + r), and then raise the result to the power of n. There are rules for their removal and some traps to avoid. Simple brackets In an expression like (2x 3) + (x + 1) the brackets can be removed straightforwardly to get 2x 3 + x + 1 = 3x 2.
Mathematics Learning Centre, University of Sydney
However in an expression like (2x 3) (x + 1), we must realise that we are substracting the whole expression x + 1 and take this into account when we remove the brackets. (2x 3) (x + 1) = 2x 3 x 1 = x 4. Notice that when we removed the bracket around the second term, we got x and 1. The distributive law An expression like 5(x + 1) means that we take x and add 1 and multiply the result by 5. When removing the bracket, we multiply each of the symbols inside the bracket by 5. That is 5(x + 1) = 5 x + 5 1 = 5x + 5. This is an application of the distributive law, a(x + y) = ax + ay. Examples Remove the brackets and simplify the following expressions: 1. 6(3a 1) + 4(a 5), 2. 2(4b 1) (b + 3), 3. 3a(a b) + b(a + 3). Solutions 1. 6(3a 1) + 4(a 5) = 18a 6 + 4a 20 = 22a 26. 2. 2(4b 1) (b + 3) = 8b + 2 b 3 = 9b 1. 3. 3a(a b) + b(a + 3) = 3a2 3ab + ab + 3b = 3a2 2ab + 3b. We can use the distributive law to multiply out the product of two (or more) brackets. For example, expand (y + 3)(5y 2). To use the distributive law here we distribute (y + 3) through the second bracket to get (y + 3)(5y 2) = (y + 3)5y + (y + 3)(2) = 5y 2 + 15y 2y 6 = 5y 2 + 13y 6. This is the same as taking each term in the rst bracket and multiplying through the second bracket term by term as follows: (y + 3)(5y 2) = 5y 2 2y + 15y 6 = 5y 2 + 13y 6. We can then extend this to more complex expressions. For example, (2p 4)(p2 + 3p 1) = 2p3 + 6p2 2p 4p2 12p + 4 = 2p3 + 2p2 14p + 4.
Mathematics Learning Centre, University of Sydney
1.2.4
Factorising
Extracting factors from algebraic expressions is the reverse process of expanding brackets. The distributive law says that a(x + y) = ax + ay. We can turn it around and write it as ax + ay = a(x + y). In this case we say that ax + ay is expressed as a product of factors a and (x + y). For example, 3p2 12pq = 3p(p 4q) and 66 36ab = 6(11 6ab). In each case we looked for a common factor in each term of the expression and extracted it as a factor. The other factor is what is left when we divide each term by that common factor. It is always a good idea to check your answer by multiplying out the bracket again in your head. Dierence of two squares The following equation can be using to factorise the dierence of two squares, x2 y 2 = (x + y)(x y). For example, a2 9b2 = (a + 3b)(a 3b). 1.2.5 Algebraic fractions
The rules of fractions also apply to algebraic fractions. For addition and subtraction, write each fraction as an equivalent fraction using a common denominator if necessary. a + 3a 4a a 3a + = = = a. 4 4 4 4 x x 4x 3x x = = . 3 4 12 12 For multiplication, multiply the numerators together and multiply the denominators together and then cancel any common factors (or cancel the common factors rst). 3m 2n 3m 2n 6mn 6m = = = . n l nl nl l For division, invert the fraction in the denominator and multiply. (You are in eect multiplying both the numerator and the denominator by the reciprocal of the donominator.) 2p 9q 2p 8p = 3q 9q 3q 8p 2p 9q = 3q 8p 18pq = 24pq 3 . = 4
Mathematics Learning Centre, University of Sydney
1.3
Substituting into formulae
We are often in the situation where we need to substitute values into a formula. In each case we replace the variable with its value and the form of the equation will determine the way we evaluate it. We will give some examples here from economics or statistics to illustrate this. 1. A demand equation is given by p = 600 2q where p is the unit price of a good and q is number of units of the good that the consumers will demand at that price during a given time period. Find the value of p when q = 100. Here we can substitute q = 100 straight into the equation as follows: p = 600 2q = 600 2(100) = 600 200 = 400. Notice that we multiplied q = 100 by 2 and then subtracted the result from 600. This is what the formula told us to do in this situation. 2. A rms total cost of production (T C) is given as a function of output q by the equation T C = q 3 20q 2 + 220q. Find the total cost of production when q = 10. Again we can substitute into the equation as follows: T C = q 3 20q 2 + 220q = (10)3 20(10)2 + 220(10) = 1000 2000 + 2200 = 1200. 3. When we take a sample of size n from an (innitely) large population, the formula for a 95% condence interval for population proportion is ps 1.96 ps (1 ps ) . n
If ps = 0.4, and n = 100, nd the 95% condence interval for population proportion. ps 1.96 ps (1 ps ) (0.4)(0.6) = 0.4 1.96 = 0.4 1.96 0.0024 = 0.4 0.0960. n 100
4. An exponential model with a seasonal component is tted to time series data and is given by: Y = b0 bXi bQ1 bQ2 bQ3 . 1 2 3 4 Find Y when b0 = 6, b1 = 0.5, b2 = 0.1, b3 = 0.2, b4 = 0.2, Xi = 10, Q1 = Q3 = 0 and Q2 = 1. Here we have Y = b0 bXi bQ1 bQ2 bQ3 = 6(0.510 )(0.10 )(0.21 )(0.20 ) = 6(0.000976)(0.2) = 0.001172. 1 2 3 4 Note that 0.10 = 0.20 = 1. (Dont worry about what each of the symbols represent.)
Mathematics Learning Centre, University of Sydney
1.4
Equations
It is often necessary to solve equations in economics and statistics. For example, we may be given a demand equation p = 600 2q but need to rewrite it as an equation q = f (p), ie so q is the subject. In this case p p 600 (1)(p 600) 600 p 600 2q 2q 2q 2q 600 p q = 2 p = 300 . 2 = = = =
How do we know what to do at each stage? One way to approach this is to write down the operations we went through to get from q to p, and then backtrack to get from p to q. (If you have another method that you learned in school that gives you the correct answer, then use that method.) q
2
2q
2q
+600
600 2q = p.
To get from p back to q we do the operation that undoes each of these operations in the reverse order, ie we do the last one rst. Of course, to keep an equivalent equation we do each operation to both sides of the equation. p p 600 (1)(p 600) 600 p 600 2q 2q 2q 2q 600 p q = 2 p = 300 . 2 = = = =
subtract 600 multiply by 1 divide by 2
In statistics, the following formula is well known: Z= X .
We often wish to rewrite it so that it is in the form X = . . . in which case our analysis gives X X X = Z. Working backwards undoing each operation we get:
Mathematics Learning Centre, University of Sydney
X Z = X Z + = X. Z =
multiply by add
So, X = + Z. Here is another formula from statistics: SE(p) = p(1 p) n
If we want an expression where n is the subject, our analysis gives:
take reciprocal
1 n
p(1p)
p(1 p) n
take square root
p(1 p) = SE(p). n
Note that the reciprocal of n is
a b 1 , and the reciprocal of is . n b a
Working backwards undoing each operation we get:
SE(p) = SE(p)2 =
p(1 p) n p(1 p) n square both sides divide by p(1 p) take reciprocal
1 SE(p)2 = p(1 p) n p(1 p) = n. SE(p)2
So, n =
p(1 p) . SE(p)2
Mathematics Learning Centre, University of Sydney
1.5
Solving quadratic equations
Any equation of the form p = aq 2 + bq + c where a = 0, b and c are constants, is a quadratic equation. For example, p = 4 + 5q q 2 is quadratic. If we want to nd a solution for the equation aq 2 + bq + c = 0 (ie p = 0) then we can use the (well known) formula: b b2 4ac q= . 2a (Note: If b2 4ac is a negative number, then there are no real solutions to the equation aq 2 + bq + c = 0.) Example Solve the equation 4 + 5q q 2 = 0. Solution First of all, rewrite the equation so that the coecient of q 2 is positive, q 2 5q + 4 = 0. Then, q = = (5) 5 (5)2 4(1)(4) 2 25 16 2
5 9 = 2 = giving us two solutions, q =
5+3 2
53 2 = 4 and q =
53 2
= 1.
1.6
1.6.1
Exercises
General algebraic skills
1. Applying the general rules Simplify the following expressions using the general rules: a. 2p3 5p2 q b. 4x3 8x2 c. (2a2 )4 .
Mathematics Learning Centre, University of Sydney
2. Collecting like terms Simplify the following expressions: a. 3x2 2xy y 3 + 5xy + 4y 3 b. 5 2ab3 + 4ab2 a3 8 5ab2 + 6a2 b 10 c. 4pq 6q 2 12 + 2p3 8qp + q 2 6. 3. Removing brackets In the following exercises, remove the brackets and simplify if appropriate: a. (2p 3q 2 ) (4q 4 5p + 4) b. 2x(x2 y 2 2xy + x y) + (x + y)(x y) c. (x 2)(x + 3) (x + 1)(1 x). 4. Factorising Factorise the following expression: a. 3p3 q 12pq + 36p2 q 2 b. ax + a bx b c. 9p2 16q 2 . 5. Algebraic fractions Simplify the following algebraic fractions pq a. 2 2 p q 2pq ab b. 1 2 a b2 x2 2xy y1 c. . 2y y x 2y 1.6.2 Substituting into formulae
1. The Variance Inationary Factor (V IFj ) is given by the formula, V IFj = Evaluate V IFj when Rj = 0.8. 2. A rms prot, , is given as a function of output, q, by the equation = 80q 4q 2 200. Find the value of when q = 10. 3. The Geometric Mean (GM ) is given by the formula, GM =
n
1 . 2 (1 Rj )
X1 X2 Xn .
Find the value of the Geometric Mean if n = 6 and X1 = 1.04, X2 = 1.15, X3 = 0.97, X4 = 1.12, X5 = 1.08 and X6 = 1.14.
Mathematics Learning Centre, University of Sydney
10
1.6.3
Equations
1. q = 400 2p. Rewrite this formula making p the subject. 2. Z= X
n
is another formula from statistics. Rewrite this formula making X the subject. 3. The Variance Inationary Factor (V IFj ) is given by the formula, V IFj = 1 . 2 (1 Rj )
Assuming that Rj 0, rewrite this equation making Rj the subject (ie as Rj = . . . ). 4. Solve the following quadratic equations using the quadratic formula. a. q 2 + q 12 = 0 b. 5x 6x2 1 = 0 c. 80q 4q 2 200 = 0
1.7
1.7.1
Answers to exercises
General algebraic skills
1. Applying the general rules a. 10p5 q b. x 2 c. 16a8 2. Collecting like terms a. 3x2 + 3xy + 3y 2 b. 2ab3 ab2 + 6a2 b a3 13 c. 2p3 4pq 5q 2 18 3. Removing brackets a. 7p 3q 2 4q 4 4 b. 2x3 2xy 2 4x2 y + 3x2 2xy y 2 c. 2x2 + x 7 4. Factorising a. 3pq(p2 + 12pq 4) b. (a b)(x + 1) c. (3p + 4q)(3p 4q)
Mathematics Learning Centre, University of Sydney
11
5. Algebraic fractions 1 a. (pq 2) a+b1 b. a+b x c. y 1.7.2 Substituting into formulae
1. V IFj = 2.7778 to 4 decimal places 2. = 200 3. GM = 1.0815 to 4 decimal places 1.7.3 Equations
1. p = 200
q 2 z 2. X = + n 3. Rj = 1 1 V IFj
(Here we were told that Rj is positive, so we took the positive square root as our solution.) 4. a. q = 4 or q = 3 b. x =
1 2
or x =
1 3
c. q = 17.0711 or q = 2.9289
Вам также может понравиться
- A Level Core Pure Maths by Michael Cook PDFДокумент188 страницA Level Core Pure Maths by Michael Cook PDFhpant100% (1)
- MC Ty Completingsquare2 2009 1Документ8 страницMC Ty Completingsquare2 2009 1Helen Guey-HerngОценок пока нет
- Real Numbers: Exercise 1.1Документ40 страницReal Numbers: Exercise 1.1MarasharaoОценок пока нет
- Sigma Notation: 1. 2 2. Some Examples 3 3. Writing A Long Sum in Sigma Notation 5 4. Rules For Use With Sigma Notation 6Документ10 страницSigma Notation: 1. 2 2. Some Examples 3 3. Writing A Long Sum in Sigma Notation 5 4. Rules For Use With Sigma Notation 6DarwinОценок пока нет
- Algebra Test SolutionsДокумент4 страницыAlgebra Test SolutionsJennifer Jai Eun HuhОценок пока нет
- Completing SquareДокумент8 страницCompleting SquareliverpoolengineerОценок пока нет
- Binomial TheoremДокумент9 страницBinomial TheoremIan Lester Toledo100% (1)
- RegressionДокумент6 страницRegressionmirelaasmanОценок пока нет
- Assignment 1Документ4 страницыAssignment 1JackA89Оценок пока нет
- Ipmat Indore 2021 Official Paper 02760aa991f7bДокумент23 страницыIpmat Indore 2021 Official Paper 02760aa991f7bSamir Shiva ReddyОценок пока нет
- Unit I-Collection of Numbers: Lesson 3-Operation On SetДокумент9 страницUnit I-Collection of Numbers: Lesson 3-Operation On SetAnonymous 2Jl89uОценок пока нет
- Cmi Sample Problems & Solutions: WWW - Ctanujit.inДокумент12 страницCmi Sample Problems & Solutions: WWW - Ctanujit.inaanbalanОценок пока нет
- Ujses Sctirh: Guess The Word Out of A Scrambled Letters Given. ExampleДокумент16 страницUjses Sctirh: Guess The Word Out of A Scrambled Letters Given. ExampleAlen Joy CamachoОценок пока нет
- SequencesДокумент13 страницSequencesDefault AccountОценок пока нет
- Em04 IlДокумент10 страницEm04 Ilmaantom3Оценок пока нет
- Maths Note P1 and P3Документ188 страницMaths Note P1 and P3Afeefa SaadatОценок пока нет
- Maths Model Test Paper For Summative Assessment - 1Документ13 страницMaths Model Test Paper For Summative Assessment - 1Apex InstituteОценок пока нет
- Stage 3 Revision Sheet HigherДокумент9 страницStage 3 Revision Sheet Highercozzy'mozzy..dozzy.;Оценок пока нет
- CRT ExampleДокумент5 страницCRT ExampleSagar JaikarОценок пока нет
- Quadratic Equations: Completing The SquareДокумент9 страницQuadratic Equations: Completing The SquareSarah Ossama MaharemОценок пока нет
- Ab Means A × B A A: AlgerbraДокумент9 страницAb Means A × B A A: AlgerbraNoor NoorОценок пока нет
- Obj. 4 Rational and Radical Equations (Presentation)Документ18 страницObj. 4 Rational and Radical Equations (Presentation)Sandra MillerОценок пока нет
- SigmaДокумент10 страницSigmaAlphaОценок пока нет
- ELEMENTARY ALGEBRA Final Project For Final SemДокумент21 страницаELEMENTARY ALGEBRA Final Project For Final SemJulita AleonarОценок пока нет
- Mathematics: Quarter 3 - Module 4Документ10 страницMathematics: Quarter 3 - Module 4Miguel June100% (2)
- Math 1 - Chapter 2 - Algebraic ExpressionsДокумент7 страницMath 1 - Chapter 2 - Algebraic ExpressionsJose Arnaldo Bebita DrisОценок пока нет
- Real Numbers and Their PropertiesДокумент31 страницаReal Numbers and Their PropertiesFaist Name Last NameОценок пока нет
- SMO 2009 Open SolutionДокумент13 страницSMO 2009 Open SolutionwmdsgОценок пока нет
- Higher Eng Maths 9th Ed 2021 Solutions ChapterДокумент23 страницыHigher Eng Maths 9th Ed 2021 Solutions ChapterAubrey JosephОценок пока нет
- Math Study Guide Notes For Final Exam MCR3U Grade 11 FunctionsДокумент31 страницаMath Study Guide Notes For Final Exam MCR3U Grade 11 FunctionsSujith NimalarajОценок пока нет
- Summation NotesДокумент9 страницSummation NotesnunterhunterОценок пока нет
- DifferentiationДокумент30 страницDifferentiationPranjal Sharma100% (1)
- CrapДокумент8 страницCrapvincentliu11Оценок пока нет
- CBSE Class 10 Maths Paper SolutionДокумент25 страницCBSE Class 10 Maths Paper SolutionSantanuОценок пока нет
- Trial Paper 1Документ7 страницTrial Paper 1MuhandiramalageОценок пока нет
- Real Counterexample.Документ10 страницReal Counterexample.mandilipОценок пока нет
- DivisibilityДокумент0 страницDivisibilityFabiano FerreiraОценок пока нет
- BMM10233 - Chapter 4 - Theory of EquationsДокумент19 страницBMM10233 - Chapter 4 - Theory of EquationsMohanakrishnaОценок пока нет
- SAT Subject Math Level 2 FactsДокумент11 страницSAT Subject Math Level 2 FactsSalvadorОценок пока нет
- Adventures in PrecalculusДокумент72 страницыAdventures in PrecalculusDr Srinivasan Nenmeli -KОценок пока нет
- CMC Exam Paper and AnswersДокумент5 страницCMC Exam Paper and AnswersNikita AgrawalОценок пока нет
- 6.3 Exponential Equations and Inequalities: X 7 X 7 X 7 X 7 XДокумент11 страниц6.3 Exponential Equations and Inequalities: X 7 X 7 X 7 X 7 XMam MJ RosasОценок пока нет
- Mathematics: Problem Solving in MathematicsДокумент17 страницMathematics: Problem Solving in MathematicsRedzuan SaidiОценок пока нет
- Inmo-Sol-2000 Previous Year Question Papers of Indian National Mathematical Olympiad (INMO) With SolutionsДокумент5 страницInmo-Sol-2000 Previous Year Question Papers of Indian National Mathematical Olympiad (INMO) With SolutionsAkshay PandeyОценок пока нет
- Miscellaneous Topics in First Year Mathematics: WwlchenДокумент14 страницMiscellaneous Topics in First Year Mathematics: WwlchenAnonymous 9kzuGaYОценок пока нет
- Mathematics 9 - Introduction To Quadratic EquationsДокумент5 страницMathematics 9 - Introduction To Quadratic EquationsJames Russel MariОценок пока нет
- RegressionДокумент6 страницRegressionmalp23Оценок пока нет
- M InvestДокумент21 страницаM InvestNinja MentroОценок пока нет
- MathДокумент36 страницMathRobert EspiñaОценок пока нет
- Class 10 Formula IcseДокумент9 страницClass 10 Formula IcseAdarsh Dongare100% (4)
- GMAT Math Formula Sheet Preview PDFДокумент4 страницыGMAT Math Formula Sheet Preview PDFm1u2a3b413% (30)
- Treemath Mock AIME SolutionsДокумент11 страницTreemath Mock AIME SolutionsHarry GaoОценок пока нет
- EuclidДокумент4 страницыEuclidayoyaОценок пока нет
- Maths AnualДокумент11 страницMaths Anualjainmanan852Оценок пока нет
- A-level Maths Revision: Cheeky Revision ShortcutsОт EverandA-level Maths Revision: Cheeky Revision ShortcutsРейтинг: 3.5 из 5 звезд3.5/5 (8)
- Factoring and Algebra - A Selection of Classic Mathematical Articles Containing Examples and Exercises on the Subject of Algebra (Mathematics Series)От EverandFactoring and Algebra - A Selection of Classic Mathematical Articles Containing Examples and Exercises on the Subject of Algebra (Mathematics Series)Оценок пока нет
- Trigonometric Ratios to Transformations (Trigonometry) Mathematics E-Book For Public ExamsОт EverandTrigonometric Ratios to Transformations (Trigonometry) Mathematics E-Book For Public ExamsРейтинг: 5 из 5 звезд5/5 (1)
- ECU MS 4 Sport ManualpdfДокумент26 страницECU MS 4 Sport ManualpdfLucas DuarteОценок пока нет
- Beg 2018 XXДокумент42 страницыBeg 2018 XXFranz Gustavo Vargas MamaniОценок пока нет
- Adherence Tradeoff To Multiple Preventive Therapies and All-Cause Mortality After Acute Myocardial InfarctionДокумент12 страницAdherence Tradeoff To Multiple Preventive Therapies and All-Cause Mortality After Acute Myocardial InfarctionRoberto López MataОценок пока нет
- Soil ResistivityДокумент6 страницSoil ResistivityAnonymous EP0GKhfОценок пока нет
- Model-Checking: A Tutorial Introduction: January 1999Документ26 страницModel-Checking: A Tutorial Introduction: January 1999Quý Trương QuangОценок пока нет
- Lecture # 3 Introduction To JqueryДокумент88 страницLecture # 3 Introduction To JqueryDanial AhmadОценок пока нет
- Clavija L5-30P Ref 2611Документ3 страницыClavija L5-30P Ref 2611CristianDuarteSandovalОценок пока нет
- People Vs CorreaДокумент2 страницыPeople Vs CorreaRmLyn Mclnao100% (1)
- Awareness On Stock MarketДокумент11 страницAwareness On Stock MarketBharath ReddyОценок пока нет
- Ed508-5e-Lesson-Plan-Severe Weather EventsДокумент3 страницыEd508-5e-Lesson-Plan-Severe Weather Eventsapi-526575993Оценок пока нет
- Jackson R. Lanning: Profile StatementДокумент1 страницаJackson R. Lanning: Profile StatementJacksonLanningОценок пока нет
- Freedom SW 2000 Owners Guide (975-0528!01!01 - Rev-D)Документ48 страницFreedom SW 2000 Owners Guide (975-0528!01!01 - Rev-D)MatthewОценок пока нет
- Bhakra Nangal Project1Документ3 страницыBhakra Nangal Project1Sonam Pahuja100% (1)
- Focus: Optimised Efficiency For The Paper IndustryДокумент24 страницыFocus: Optimised Efficiency For The Paper IndustryZoran BadurinaОценок пока нет
- Lagundi/Dangla (Vitex Negundo)Документ2 страницыLagundi/Dangla (Vitex Negundo)Derrick Yson (Mangga Han)Оценок пока нет
- SOLIDWORKS 2022 Whitepaper UsingDesignAutomationtoReduceCostsIncreaseProfitability FinalДокумент10 страницSOLIDWORKS 2022 Whitepaper UsingDesignAutomationtoReduceCostsIncreaseProfitability FinalAlba R.Оценок пока нет
- 3.6.4 Details of Courses For Nuclear Medicine TechnologyДокумент2 страницы3.6.4 Details of Courses For Nuclear Medicine TechnologyhemendrasingОценок пока нет
- Mock MeetingДокумент2 страницыMock MeetingZain ZulfiqarОценок пока нет
- The Little MermaidДокумент6 страницThe Little MermaidBobbie LittleОценок пока нет
- 1 - CV - SwarupaGhosh-Solutions Account ManagerДокумент2 страницы1 - CV - SwarupaGhosh-Solutions Account ManagerprabhujainОценок пока нет
- Visco GraphДокумент4 страницыVisco GraphwamlinaОценок пока нет
- 2017-Process Tracing in Social SciencesДокумент28 страниц2017-Process Tracing in Social SciencesTudor CherhatОценок пока нет
- 3500 Ha027988 7Документ384 страницы3500 Ha027988 7Gigi ZitoОценок пока нет
- Everyday Life - B1 - ShoppingДокумент7 страницEveryday Life - B1 - ShoppingAmi BarnesОценок пока нет
- Improving Radar Echo Lagrangian Extrapolation Nowcasting by Blending Numerical Model Wind Information: Statistical Performance of 16 Typhoon CasesДокумент22 страницыImproving Radar Echo Lagrangian Extrapolation Nowcasting by Blending Numerical Model Wind Information: Statistical Performance of 16 Typhoon CasesLinh DinhОценок пока нет
- Barclays Personal Savings AccountsДокумент10 страницBarclays Personal Savings AccountsTHОценок пока нет
- Vocabulary: ExileДокумент5 страницVocabulary: ExileWael MadyОценок пока нет
- Banking Adbl EnglishДокумент74 страницыBanking Adbl Englishdevi ghimireОценок пока нет
- The Art of Starting OverДокумент2 страницыThe Art of Starting Overlarry brezoОценок пока нет
- PCI20107, Overview of Boiler Commissioning and Startup PDFДокумент17 страницPCI20107, Overview of Boiler Commissioning and Startup PDFMarc AnmellaОценок пока нет