Академический Документы
Профессиональный Документы
Культура Документы
Maths Chance Planner
Загружено:
LaurencassarИсходное описание:
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Maths Chance Planner
Загружено:
LaurencassarАвторское право:
Доступные форматы
MATHEMATICS / UNIT PLANNER LEVEL:__2____
TERM :___3_____
WEEK:__5-7_______
VOCABULARY: Certainly, maybe, never, outcomes, random, possible outcomes, chance, experiment, test, select, record, equal, same chance, repeated, fair, unfair. Other unfamiliar probability vocabulary. MATERIALS: Masking Tape, language cards, Twister, 2x altered spinners, Smarties, paper bags, Smartie worksheet, 15x 20 sided Die and standard die, cubes to make own die, numbers 1-6, counters, horse sheet (large) and individual x 15, work sheets and spinner. Lesson MATH TOOLS WHOLE CLASS INDEPENDENT TARGET SHARE TIME AND ASSESSMENT OBJECTIVE SESSION FOCUS LEARNING TEACHING TEACHER STRATEGIES GROUP SUMMARY Students are to: Assessment of Discussion of Use a different In groups discuss why Discuss strategies for - Students work is to 1 students prior chance spinners. spinner, but dont they think the spinner tallying. be completed and knowledge. Where they have show class. looks that way. Discuss thought collect for assessment seen them in the Spin 10 times. Students write on their process on dividing and revision. real word or in Student record and sheets why they chose the spinner. other games. draw what they think to divide their spinner Show the students the Discuss properties the spinner looks like. the way they did. real spinner and of a spinner. Spin 10 more times Compare strategies for consider the and from the 20 spins tallying. possibilities and the student draws a difference with their new spinner. own.
- use and understand chance expressions. - be able to record numerous possible outcomes for chance events.
Language Line. Students place phrases on a student line, and discuss why they should be placed there. -discuss other terms that may not be familiar
Pose Question: Jack and Jill went up the hill to fetch a pail of water. Jack fell down and broke his crown And Jill. Teaching Strategy: - Use nursery rhyme book as this will assist those students who have no prior experience of the Jack and Jill nursery rhyme.
Using the key words, certainly, maybe or impossible list what you think happened to Jill. Prompt: Whats one thing that definitely happened to Jill? Whats one thing that maybe happened to Jill? Whats one thing that could not have happened to Jill? Extend: Graph which events are more or less likely to have happened? Why?
Give some guidance for children who need some assistance in engaging with the task using questions such as: What happened to Jack?
Students read out statements. Discuss which ones are most likely and which ones probably wouldnt occur. Why? Discuss the notion of numerous outcomes, possible to have numerous outcomes for the same event. Place chance line on board with labels, chose five students to rewrite their statements and ask students where they should be placed on the chance line. Why?
Listen to the language used, has it altered as a result of examining it. Ability to order items according to degrees of certainty. Do they give numerous creative possibilities? Do children justify answers? Question students on the likelihood of events.
3&4
- identify some events as having a greater or lesser chance of occurring. - realizing that the chance of an outcome occurring can be presented using numbers and fractions.
Guess my rule. In pairs students are given an answer and a rule. One student begins stating the stating number, then reads out a rule, the student with the answer to that rule must state the answer and then their rule. Using mental calculations students must work out whether they have the answer to the rule that has been previously read out.
Using a large colorful spinner introduce students to the idea of the denominator and numerator, there purposes and what they suggest about chance, model this using the spinner. Alter the spinner (change colors, numbers of pieces) and discuss how such events effect the numerator and denominator, again model and represent the chance in fraction form. Discuss what the fraction suggests.
Using the prepared counter bags (3 colours, 15 counters or 2 colours for lower students) and student work sheet students are to firstly record each colours fraction (chance of being pulled out) and then take one counter out of the bag each time. After each counter has been removed students are to record the new fraction of each colour and predict what colour will be chosen next by using the new fractions recorded.
Work with a group of children who need some assistance to get started.
- Identify activities where there is an equal chance of an outcome occurring.
Bingo. Students draw their own game board. 20 sided die is rolled. Students cross there numbers out. - why do you think .won? - why didntwin. - could his numbers have had an impact on him winning.
Pose Question: A spinner company wants to design a spinner where the chance of spinning any of the colors is equal. What might the spinner look like? (Allow students to design their own spinner.) Altered from dice to spinner due to the unavailability of blank dice. - Relate to fractions Numerator and Denominator.
Work in pairs or individually. Create own spinner. Prompt: A spinner company wants to design a spinner where the chance of spinning a red is . What might the dice look like? Extend: A dice company wants to design an equality spinner, where the chance of spinning any color is equal. However there must be at least five colors on this spinner. What might the spinner look like?
Prompt students if experiencing difficulty. Create a teacher focus group based on student need.
What denominator did you begin with? Did that alter during the activity? Why did that happen? What numerators did you begin with? Why were they all different? How did they alter during the activity? What were the fractions telling you? How did you predict what colour would be chosen? Why did you use the fractions? Who got their prediction right all the time? Who got them some of the time? Why were some predictions incorrect? Students show created spinner. Discuss what equal means proportion. Make comparisons between spinners. Note colour differences and ratios. How do you know its equal? How did you work it out? What happens if I added another colour to the dice spinner, what would need to occur? Summary: Some events have an equal chance of occurring because each part it of equal proportion.
Listen to the language used. Sharing of strategies. Where fractions evident? Did they alter after every round? Collect sheets? Did predictions suggest that students were choosing colours based on the altered fractions?
Listen to language used Note insights on annotated class list. Do children justify answers? Do they give numerous creative possibilities? Take pictures of students spinners and get them to articulate what they did and why.
- Identify that different outcomes may occur for the same event. - understand that events can be random and independent of each other.
Heads or Tails. Students are given a coin, they are to predict what they will flip (head or tail) they then carry out the investigation. They continue doing this numerous times with a partner.
Pose Question: If Paul rolls two dice, what numbers might be rolled? (Allow student to roll dice however try and get them to guess first)
Work in pairs or individually to create a list of numerous possibilities. Prompt: If Paul rolls one die, what numbers might be rolled? Extend: If Paul rolls three dice, what numbers might be rolled? What numbers are impossible for Paul to roll? What if Paul rolled two 24 sided die, what numbers might he roll? Individual and group work. Prompt: Design a spinner where it is easier for you to win against one other opponent? Extend: Design a spinner where there is only a slight chance of other opponents winning against you?
Stop students half way and discuss strategies for working out the problem.
- understand that some events can be classified as fair, unfair or be persuade by bias. - realise how an outcome can be influenced.
Horse game. Modeled and students play in pairs.
Pose Question: Design a spinner where it is easier for you to win against other opponents? (Allow students have some experience with a spinner and then design their own.)
Prompt students if experiencing difficulty with understanding the properties of a spinner.
Discuss what occurred. What numbers might Paul have rolled? How many different combinations could Paul have rolled? Are there any numbers that Paul couldnt have rolled? How did you work that out? Are there any other strategies used? Which strategy would have been faster? How did you tally your results? Could there have been a faster way? Show spinners Discuss colours and proportions. Chose three different spinners and ask, which one is more likely to spin a red? What makes this an unfair spinner? Why? When deciding on coloring and separating the spinner what were you thinking? Why did you think that? Discuss the difference in the predicted graphs and results graph. Discuss individual graph compared to the class graph Examine the idea that results are more
Listen to language used Are numerous possibilities listed? Do children justify answers? Question students about the randomness of events. Can they identify how the events are independent. Note on class list what techniques students utilize to work out answers. - Are they systematic? - Do they use concrete materials? - Do they draw? Note which spinners are more or less rigged. Take pictures of students spinners and get them to articulate what they did and why. Do students use ratio or other unexpected tools to assess the fairness or unfairness of their spinner? Peer assessment of effectiveness of spinners. Is fairness described in qualitative terms?
Findings can be illustrated in graphical form.
Greedy Pig Play greedy pig and reflect on the strategies students used for the game.
Pose Question:
Shanae and Ryan rolled a die 30 times and then graphed their results. What do you think their graph looked like? Why?
Individual and group work. Extend: What do you think the graph looked like? Create a class graph of students die rolls.
Focus on students who are having trouble with graph features.
Question students about the possibility of outcomes. Are suggestions made by students reasonable or expected.
Shanae and Ryan rolled a die 30 times find out what their results were? (Allow student to roll a die 20 times and collect results) (Create a class graph and allow each student to place their rolled numbers on the graph)
likely to occur when doing lots of trials. Discuss features of a graph Discuss strategies for tallying results. Was there a quicker method? What is the graph showing? Why did we graph our results? Give students a sheet with results on it from coins, dice and a spinner. Students draw what they think the coin, dice or spinner looks like. In groups discuss why they think the spinner looks that way. Students write on their sheets why they chose to divide their spinner the way they did. Compare strategies for tallying. Lower ability group.
Collect student reflected graphs and display. Are graphs correctly labeled? Were students able to utilize an appropriate recording method for comparison of the data collected?
- realizing that the chance of an outcome occurring can be presented using numbers and fractions. Assessment of students gained chance knowledge.
Write down multiple fractions for students to decide which colour is likely to be spun. Revise properties of a spinner. Spin unseen spinner 10 times. Allow a 1 minute compulsory reflective period for students to reflect on the results.
Revise fractions denominator and numerator. Why we use fractions. Relate to spinner results. Spin 10 more times and from the 20 spins the student draws a new spinner. Again allow a 1 minute compulsory reflective period for students to reflect on the results before they begin.
- Students work is to
be completed and collect for assessment and comparison.
10
Whole class- Use prompting questioning.
Discuss strategies for tallying. Discuss thought process on dividing the spinner. Show the students the real spinner and consider the possibilities and difference with their own.
- Students work is to
be completed and collect for assessment and comparison.
Вам также может понравиться
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceОт EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceРейтинг: 4 из 5 звезд4/5 (894)
- The Yellow House: A Memoir (2019 National Book Award Winner)От EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Рейтинг: 4 из 5 звезд4/5 (98)
- The Little Book of Hygge: Danish Secrets to Happy LivingОт EverandThe Little Book of Hygge: Danish Secrets to Happy LivingРейтинг: 3.5 из 5 звезд3.5/5 (399)
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeОт EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeРейтинг: 4 из 5 звезд4/5 (5794)
- Never Split the Difference: Negotiating As If Your Life Depended On ItОт EverandNever Split the Difference: Negotiating As If Your Life Depended On ItРейтинг: 4.5 из 5 звезд4.5/5 (838)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureОт EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureРейтинг: 4.5 из 5 звезд4.5/5 (474)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryОт EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryРейтинг: 3.5 из 5 звезд3.5/5 (231)
- The Emperor of All Maladies: A Biography of CancerОт EverandThe Emperor of All Maladies: A Biography of CancerРейтинг: 4.5 из 5 звезд4.5/5 (271)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreОт EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreРейтинг: 4 из 5 звезд4/5 (1090)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyОт EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyРейтинг: 3.5 из 5 звезд3.5/5 (2219)
- Team of Rivals: The Political Genius of Abraham LincolnОт EverandTeam of Rivals: The Political Genius of Abraham LincolnРейтинг: 4.5 из 5 звезд4.5/5 (234)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersОт EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersРейтинг: 4.5 из 5 звезд4.5/5 (344)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaОт EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaРейтинг: 4.5 из 5 звезд4.5/5 (265)
- The Unwinding: An Inner History of the New AmericaОт EverandThe Unwinding: An Inner History of the New AmericaРейтинг: 4 из 5 звезд4/5 (45)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)От EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Рейтинг: 4.5 из 5 звезд4.5/5 (119)
- A Review of The Path To ConsistencyДокумент8 страницA Review of The Path To ConsistencyCAD16Оценок пока нет
- Problem Set 5 Saf PDFДокумент2 страницыProblem Set 5 Saf PDFtrols sadОценок пока нет
- Generate Random Paragraphs with a ClickДокумент5 страницGenerate Random Paragraphs with a Clickjuan eyronОценок пока нет
- Intervensi DomainДокумент92 страницыIntervensi DomainSylvia DamayantiОценок пока нет
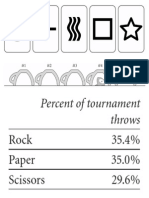
- Rock Breaks Scissors - Reference GuideДокумент45 страницRock Breaks Scissors - Reference GuidePRABUICE100% (1)
- 25 NT TR 604 Uncertainty From Sampling A NORDTEST HandbookДокумент91 страница25 NT TR 604 Uncertainty From Sampling A NORDTEST HandbookVictor Nuñez YsiqueОценок пока нет
- Statistics of Discrete Random VariablesДокумент29 страницStatistics of Discrete Random VariablesDaryl Sharen Mae Sause100% (1)
- Mathematics 10Документ11 страницMathematics 10NamanОценок пока нет
- Probability of drawing balls of different colorsДокумент5 страницProbability of drawing balls of different colorsbsudheertecОценок пока нет
- Finding possible values of random variables (≤40 charsДокумент2 страницыFinding possible values of random variables (≤40 charsAndrea Marie LaquiñaОценок пока нет
- Monte Carlo Simulation of Bike ProductionДокумент4 страницыMonte Carlo Simulation of Bike ProductionswapnadipОценок пока нет
- Aide MATLab Sur Les Algorithmes GénétiquesДокумент21 страницаAide MATLab Sur Les Algorithmes GénétiquesJes Nard100% (2)
- Theory of ProbabilityДокумент100 страницTheory of ProbabilityMeet100% (2)
- 03.probability Level (1 To 4) Ex. Module-6-AДокумент17 страниц03.probability Level (1 To 4) Ex. Module-6-ARaju SinghОценок пока нет
- Personalized Question Bank Research Based On Particle Swarm OptimizationДокумент5 страницPersonalized Question Bank Research Based On Particle Swarm OptimizationShivendraSaurabhОценок пока нет
- Statistics: Random Variables and Probability DistributionsДокумент41 страницаStatistics: Random Variables and Probability DistributionsChanty100% (1)
- Probability Review: WorksheetДокумент3 страницыProbability Review: WorksheetAmy JonesОценок пока нет
- Implement simple random number generator tests using stdlib randДокумент4 страницыImplement simple random number generator tests using stdlib randRabia ShahОценок пока нет
- Quality Control and Process CapabilityДокумент9 страницQuality Control and Process CapabilityAbdAllah KhodaryОценок пока нет
- Procedural Dungeon DesignДокумент7 страницProcedural Dungeon Designapi-323170246Оценок пока нет
- Census Vs Sample Enumeration: Comparison ChartДокумент12 страницCensus Vs Sample Enumeration: Comparison ChartNaman LadhaОценок пока нет
- Elementary Statistics Chapter 1Документ15 страницElementary Statistics Chapter 1Marion AlyssaОценок пока нет
- Full Text 01Документ199 страницFull Text 01huberОценок пока нет
- Introduction To Probability With Mathematica - Kevin J. Hasting PDFДокумент466 страницIntroduction To Probability With Mathematica - Kevin J. Hasting PDFJoel Santiago100% (3)
- Statistics For Management and Economics 10th Edition Gerald Keller Test Bank DownloadДокумент50 страницStatistics For Management and Economics 10th Edition Gerald Keller Test Bank DownloadPhillip Rees100% (20)
- Teach Yourself StatisticsДокумент242 страницыTeach Yourself Statisticsaashoo70100% (11)
- Block-1 MCO-3 Unit-4Документ23 страницыBlock-1 MCO-3 Unit-4Tushar SharmaОценок пока нет
- Subject: Quantitative Techniques PGDM 2nd Trimester Topic: Sampling Techniques Submitted To: Sowmya MamДокумент8 страницSubject: Quantitative Techniques PGDM 2nd Trimester Topic: Sampling Techniques Submitted To: Sowmya MamHarsh ShrivastavaОценок пока нет
- An Automation PCI Allocation Method For eNodeB and Home eNodeB CellДокумент4 страницыAn Automation PCI Allocation Method For eNodeB and Home eNodeB CellurfriendlyjoeОценок пока нет
- Aps 6 2 NotesДокумент4 страницыAps 6 2 Notesapi-261956805Оценок пока нет