Regression Equation

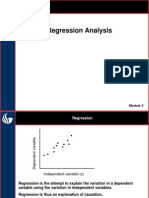
Regression Equation
Regression Equation:
A mathematical equation that allows us to predict values of one dependent variable from
known values of one or more independent variables is called regression equation.

Type of Regression Equation:
There are following ------------- type of equations.
1. Simple linear regression equation
2. Exponential regression equation
3. Multiple regression equation
4. General linear model

What is Simple Linear Regression Equation (SLR)?

A mathematical equation that allows us to predict value of one dependent variable from known
value of one independent variable is called simple linear regression equation.
The predict equation
, by which we can predict the value of y on the basis of

predictor x.

The parametric simple linear regression equation is represented by the equation

, where are called parameters of regression coefficients. Where a and b are the
point estimators for , respectively, we can then estimate
by
from the sample

regression line
.
If we let
represent the vertical deviation from the

i
y points to the
i
Y
regression line, the

method of least squares yields formulae for calculating a and b so that the sum of the
squares of these deviations is a minimum. This sum of the squares of the deviations is called the
sum of squares of the errors about the regression line and is denoted by SSE.

= =
=
n
i
n
i
i i i
bx a y e
1 1
2 2
) (

Given the sample {(x,y); I = 1,2,3,..,n}, the least-square method estimates of the parameters in
the regression line are obtained from the formula:

x b y a
x x n
y x y x n
S
S
x Var
y x Cov
b
n
i
n
i
i i
n
i
i
n
i
i
n
i
i i
x
xy
=
|
.
|
\
|
|
.
|
\
|
|
.
|
\
|
= = =

= =
= = =
1
2
1
2
1 1 1
2
) (
) , (

Now for any fixed value of x, each observation
in our sample satisfies the relation

i
yix i
y c + =
Where
i
c is a random error representing the vertical deviation of the point from the population
regression line (parametric regression equation). From previous assumptions on
i
y ,
i
c must
necessarily be a value of a random variable having a mean of zero and the variance
2
o . In terms of the
sample regression line, we can also write:

i i i
e y y + =
An essential part of regression analysis involves the construction of confidence intervals for and and
testing hypothesis concerning these regression coefficients. The hypothesis for testing the coefficients
are =0 and =0. However the unknown variance
2
must be estimated from the data. An unbiased
estimate of
2
with n-2 degree of freedom, denoted by
2
e
S , is given by the formula:

2
) (
2 2
2 2
2
=

n
y y
n
e
n
SSE
S
i i i
e

In usual the sample variance formula we use to take one degree of freedom, provide an unbiased
estimate of the population variance, since only is replaced by the sample mean in our calculations.
Here, it is necessary to take 2 degree of freedom in the formula for
2
e
S because 2 degree of freedom are
lost by replacing and by a and b in our calculation of the s y
i
' .The simple formula for the
calculation of SSE are as follows:

) 1 (
) (
) 1 (
) (
) )( 1 (
1 1
2 2
2
1 1
2 2
2
2 2 2
=
=

= = = =
n n
y y n
andS
n n
x x n
S
Where
S b S n SSE
n
i
n
i
i i
y
n
i
n
i
i i
x
x y

Test for Linearity of Regression Equation
OR
Validity of the Regression Model

We define the regression to be linear when all the means of y corresponding to each
fall on a straight
line. One can always prefer a linear regression model over non linear model. We can test the linearity of
the regression equation by using the ANOVA test. If the linearity will be confirm than we can say that
regression model is valid and then we develop the model.

Calculation of ANOVA:

Values of x
50 55 65 70
Values of
corresponding to
each X
74.893 79.378 88.348 92.833
74.893 79.378 88.348 92.833
79.378 88.348 92.833
79.378
Sum 149.786 317.512 265.044 278.499 1010.841
Square of sum 22435.85 100813.9 70248.32 77561.69 1021800
Square of sum/n
i
11217.92 25203.47 23416.11 25853.9 85149.96

Regression sum of square = (11217.92+25203.47+23416.11+25853.9)- 85149.96

Regression sum of square = 541.69
Residual sum of square = SSE = 186.557 and
2
e
S = 18.656

ANOVA
b

Model Sum of Squares df Mean Square F Sig.
1 Regression 541.693 1 541.693 29.036 .000
a

Residual 186.557 10 18.656

Total 728.250 11

a. Predictors: (Constant), TestScore
b. Dependent Variable: CheScore
Here the significance value of 0.000 < 0.05 which means that the Ho of ANOVA is significant
means that the Ho reject.
Inference: Ho = all means are equal; which is rejected means Regression line is not
horizontal that implies that line with some slope and slope shows the correlation between the
predictor and the estimator.

Inferences Concerning the regression coefficients:
Confidence interval for

A (1-)100% confidence interval for the parameter in the regression line
is

) 1 ( ) 1 (
1
2
2
1
2
2
+ < <

= =
n n S
x S t
a
n n S
x S t
a
x
n
i
i e
x
n
i
i e o o
o
Note that the symbol is being used here in two totally unrelated ways, first as the level of
significance and then as the intercept of the regression line.

Confidence interval for

A (1-) 100% confidence interval for the parameter in the regression line
is

) 1 ( ) 1 (
2 2
+ < <
n S
S t
b
n S
S t
b
x
e
x
e o o
|
Note that the symbol is being used here in two totally unrelated ways, first as the level of
significance and then as the intercept of the regression line.

Predictions
The equation
may be used to predict the mean response

o
x y
at x = xo, where, xo
is not necessarily one of the pre-chosen values, or it may be used to predict a single value
of
the variable
when
. We would expect the error of the prediction to be higher in the

case of a single predicted value than in the case where a mean is predicted. This, then, will
affect the width of our confidence intervals for the values being predicted.

Predictions for
o
x y

A (1-) 100% confidence interval for the mean
o
x Y
is given by:
2
2
2
2
2
2
) 1 (
) ( 1
) 1 (
) ( 1
x
o
e o x Y
x
o
e o
S n
x x
n
S t y
S n
x x
n
S t y
o
+ + < <
+
o o

Predictions for
o
y
A (1-) 100% confidence interval for the single value
o
y when
is given by:
2
2
2
2
2
2
) 1 (
) ( 1
1
) 1 (
) ( 1
1
x
o
e o o
x
o
e o
S n
x x
n
S t y y
S n
x x
n
S t y
+ + + < <
+ +
o o

What is the necessary condition for Simple linear regression?

The necessary condition for simple linear regression is that the test must be run between two
scale variable.
The variable must be correlated with each other.

How to run the test?

For the understanding we take the example from the book wall pole page no. 347.
In this example the two variables are IQ test score and Chemistry test score. Both are scale
measurement and theoretically they have correlation with each other.

Interpretation of output:

Descriptive Statistics

Mean Std. Deviation N
Chemistry test score 84.2500 8.13662 12
IQ test score 60.4167 7.82140 12

The descriptive of the variables

Correlations

Chemistry test
score IQ test score
Pearson Correlation Chemistry test score 1.000 .862
IQ test score .862 1.000
Sig. (1-tailed) Chemistry test score . .000
IQ test score .000 .
N Chemistry test score 12 12
IQ test score 12 12

The independent and dependent variable having correlation with each other therefore test can
be run.
The significant value 0.000 which means that the test is significant. The hypothesis for the test
is there is no correlation between the two study variables which is rejected and test become
significant.

Model Summary
b

Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .862
a
.744 .718 4.31923
a. Predictors: (Constant), IQ test score
b. Dependent Variable: Chemistry test score
(18.656)^0.5 = 4.319 (sum of the square of error term or residual
R-square = 0.744 this means 74.4% variation is explained by the predictors of the model.

ANOVA
b

1 Regression 541.693 (no. of predictors)1 541.693 29.036 .000
a

Residual 186.557 10 18.656

Total 728.250 (N-no. of predictors)11

a. Predictors: (Constant), IQ test score
b. Dependent Variable: Chemistry test score

The value of F-statistic is 29.036 which is very high and the p-value (or the sig value) is 0.000
which is less than 0.05 ( level of significance) this implies that the test of ANOVA is significant
and the model is valid from the given predictors. (See page # 365 for study)
Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 (Constant) 30.043 10.137

2.964 .014 7.458 52.629

IQ test
score
.897 .167 .862 5.389 .000 .526 1.268 1.000 1.000
a. Dependent Variable: Chemistry test score
1. t-values are calculated by taking the ratio between and the standard error. (e.g.
30.043/10.137 = 2.964)
2. as far as standard error is increases the t-value is decreases and as t-value decreases the
significant value (p-value) will increases and if p-value become more than the level of
significance which is usually 0.05 than the predictor become insignificant or less
important for the model
3. Here the significance value (the p-value) is less than 0.14 and 0.000; both are less than
0.05 which means that the constant term as well as the coefficient of x both is significant
for model.
4. Standardized Coefficients of Beta: it can be calculated by taking standardized values of
all the predictors and then run the test of regression analysis. In this context, whatever
be the value of be calculated that will be the Standardized Coefficients of Beta.
5. If there are more than one predictors, Standardized Coefficients of Beta will rank the
importance of the predictors. The bigger value will be more important predictor as
compare to the one which has the smaller value.
6. It shows that 95% confidence Interval which fall between 7.458 and 52.629. It means
researcher is 95% confident that minimum value for 30.043 may be 7.458 and maximum
may be 52.629. (See page no. 358 to 360 of wall Pole for further study).
7. As in this model which is simple linear regression model where only one predictor
therefore the explanation of tolerance and VIF cannot be explain well. It will discuss
when we discuss multiple regression model.

Variable which is save during run of the test is RES_1, which shows the residual value we can
check by taking the difference between predicted value (PRE_1) and actual (chemistryScore)

The variables 7, 8 and 9, 10 show the confidence interval of 95% for the predicted value of y at
specific value of x on the basis of mean of sample and on the individual basis. See page 361 to
363 of Wall Pole; for further understanding. Here this is important to understand that the range
of individual is more than mean. Because, it depends upon sample and its mean

Final Regression model
x Y 897 . 0 043 . 30
+ =
The predictor explaining 74.4% (R-Square = 0744) of the model.

Exponential regression equation
Or
Log Transformation
If a set of data appears to be best represented by a nonlinear regression curve, we must then try to
determine the form of the curve and estimate the parameters. Non linear regression curve means
the mean values of ys corresponding to each value of x are not fall on a straight line which
shows that the curve is nonlinear. In that situation we mostly apply exponential curve of the
form:

x
x y
o =
Where and o are parameters to be estimated from the data. Denoting these estimates by c and
d, respectively, we can estimate
x y
by y from the sample regression curve.

x
cd y =
Taking log base 10 on both sides
x d c y ) (log log log + =
And each pair of observations in th sample satisfies the relation

i i i
i i i
e bx a y
e x d c y
+ + =
+ + =
log
) (log log log

Where a = log c and b = log d. Therefore, it is possible to find a and b by the formulas discussed
above and then find c and d by taking the anti-log of the values.

Note: the log transformation is usually a good transformation technique for addressing the
nonlinearity of
x y
.

Multiple regression equation
What is Multiple Regression Equation?
Multiple regression equation is a linear regression model with one independent and multiple
numbers of dependent variables. It is a dependence technique.
c | | | | o + + + + =
r r x x x Y
x x x x
r
.........
3 3 2 2 1 1 ....
, 2 , 1

Why is Multiple Regression Analysis?
Multiple regression analysis is a statistical technique that can be used to analyze the relationship
between a single dependent (criterion) variable and several independent (predictors) variables.
The objective of multiple regression analysis is to use the independent variables whose values
are known to predict the single dependent value selected by the researcher.

When Multiple Regression Analysis?
- It will carry out when all the variables are scale in measurement.
- Some time, the variable with ordinal measurement may also use in MLR but without changing
the measurement.
- In SLR can be effective with a sample size of 20, but in multiple regression requires a minimum
sample of 50 and preferably 100 observations for most research situations.
- The minimum ratio of observations to variables is 5:1, but the preferred ratio is 15:1 or 20:1,
which should increase when stepwise estimation is used.
- As the structure of y and error term are same therefore we study the structure of error
term instead of y , because it is easy to study.
- For the study of MLR, the following assumptions about the error term should not violate:
Error term must hold the Normality
Variables are Identical
All predictors are Independent or lack of multi-collinearity or Independency
Error term structure holds the linearity

Important terms to understand the discussion

How to perform Multiple Regression Analysis (MLR) on SPSS?
There are two steps involve in the analysis.
1. To run the test in SPSS
2. To understand and interpret the output of the test.
How to run the test in SPSS?
For running the test we consider the file of car_sales.sav from the sample files of system file.
In the beginning remove all the variables from variable no. 15 till end ( these are transformed or
standardized variables which is not useful during the initial level of MLR)

Make a correction in the measurement of the variable type from ordinal to nominal.

Out of 11 scale variables sales in thousand is dependent variable, while all other scale
variables (10 in number) are independents. In other words we can say that there are 10 predictors
which estimate the car sales.
Here we are using enter method.

Do continue and ok

How to understand the output of the test?

Descriptive Statistics

Mean Std. Deviation N
Sales in thousands 59.11232 75.058933 117
4-year resale value 18.03154 11.605632 117
Price in thousands 25.96949 14.149699 117
Engine size 3.049 1.0552 117
Horsepower 181.28 58.592 117
Wheelbase 107.326 8.0506 117
Width 71.190 3.5302 117
Length 187.718 13.8499 117
Curb weight 3.32405 .597177 117
Fuel capacity 17.813 3.7946 117
Fuel efficiency 24.12 4.404 117
Descriptive of all the variables

Correlations

Sales in
thousands
4-year
resale
value
Price in
thousands
Engine
size Horsepower Wheelbase Width Length
Curb
weight
Fuel
capacity
Fuel
efficiency
Pearso
n
Correlat
ion
Sales in
thousands
1.000 -.275 -.252 .038 -.153 .407 .178 .272 .067 .138 -.067
4-year resale
value
-.275 1.000 .955 .527 .773 -.054 .178 .025 .363 .325 -.399
Price in
thousands
-.252 .955 1.000 .649 .853 .067 .301 .183 .511 .406 -.480
Engine size .038 .527 .649 1.000 .862 .410 .672 .537 .743 .617 -.725
Horsepower -.153 .773 .853 .862 1.000 .226 .507 .401 .599 .480 -.596
Wheelbase .407 -.054 .067 .410 .226 1.000 .676 .854 .676 .659 -.471
Width .178 .178 .301 .672 .507 .676 1.00
0
.743 .736 .672 -.600
Length .272 .025 .183 .537 .401 .854 .743 1.000 .684 .563 -.466
Curb weight .067 .363 .511 .743 .599 .676 .736 .684 1.000 .848 -.819
Fuel capacity .138 .325 .406 .617 .480 .659 .672 .563 .848 1.000 -.809
Fuel efficiency -.067 -.399 -.480 -.725 -.596 -.471 -.600 -.466 -.819 -.809 1.000
Sig. (1-
tailed)
Sales in
thousands
. .001 .003 .342 .050 .000 .028 .001 .236 .069 .237
4-year resale
value
.001 . .000 .000 .000 .283 .027 .393 .000 .000 .000
Price in
thousands
.003 .000 . .000 .000 .236 .000 .024 .000 .000 .000
Engine size .342 .000 .000 . .000 .000 .000 .000 .000 .000 .000
Horsepower .050 .000 .000 .000 . .007 .000 .000 .000 .000 .000
Wheelbase .000 .283 .236 .000 .007 . .000 .000 .000 .000 .000
Width .028 .027 .000 .000 .000 .000 . .000 .000 .000 .000
Length .001 .393 .024 .000 .000 .000 .000 . .000 .000 .000
Curb weight .236 .000 .000 .000 .000 .000 .000 .000 . .000 .000
Fuel capacity .069 .000 .000 .000 .000 .000 .000 .000 .000 . .000
Fuel efficiency .237 .000 .000 .000 .000 .000 .000 .000 .000 .000 .
The first column shows the correlation between the dependent variable sales in thousands and
other independent variables. So high correlation in this column and low level of significant (p-
value) shows that those variables are important for the model otherwise the variable is
insignificant and less important for the model. On the other hand the high correlation in the other
columns shows that the independent variables are highly correlated with each other. This shows
the property of multicollinearity is exist between the independent variables. Multicollineartity
violate the assumption of the independency among predictors. The advantage which one can
observe that, when we remove the variable which has the multicollineartity than the R-square of
the model will increase which is also a good sign for the model. One of the solutions of this
problem is to make the factors or components by factor analysis before the regression analysis.

Model Summary
b

Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .565
a
.319 .255 64.798014
a. Predictors: (Constant), Fuel efficiency, 4-year resale value, Length,
Width, Engine size, Fuel capacity, Wheelbase, Curb weight,
Horsepower, Price in thousands
b. Dependent Variable: Sales in thousands

R-Square (Coefficient of determination) is equals to 0.319 or 31.9%. It means that all the 10
predictors explain the 31.9% of the variation in the estimators.

ANOVA
b

1 Regression 208454.878 10 20845.488 4.965 .000
a

Residual 445070.963 106 4198.783

Total 653525.841 116

a. Predictors: (Constant), Fuel efficiency, 4-year resale value, Length, Width, Engine size, Fuel
capacity, Wheelbase, Curb weight, Horsepower, Price in thousands
The test of ANOVA is significant which show that the model will be valid.

Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 (Constant) -225.116 191.901

-1.173 .243 -605.579 155.347

4-year resale
value
.011 2.253 .002 .005 .996 -4.456 4.478 .053 18.890
Price in
thousands
-.015 2.146 -.003 -.007 .994 -4.269 4.239 .039 25.464
Engine size 37.640 15.588 .529 2.415 .017 6.735 68.545 .134 7.474
Horsepower -.612 .342 -.477 -1.788 .077 -1.290 .067 .090 11.095
Wheelbase 6.391 1.787 .685 3.576 .001 2.848 9.934 .175 5.718
Width -.375 3.120 -.018 -.120 .905 -6.561 5.811 .298 3.352
Length -.437 1.077 -.081 -.406 .686 -2.573 1.698 .163 6.149
Curb weight -69.476 29.602 -.553 -2.347 .021 -128.165 -10.787 .116 8.633
Fuel capacity -.157 3.697 -.008 -.043 .966 -7.487 7.172 .184 5.437
Fuel efficiency -2.608 2.931 -.153 -.890 .376 -8.418 3.203 .217 4.602
a. Dependent Variable: Sales in thousands
All such predictors which are insignificant should remove one by one from the model start from
the highest significant valued variable.
NOTE:
One should advise to study the residual structure and apply the appropriate transformation before
the removal of the variable. The reason of this practice is just to find out the true significant
variables otherwise it is quite possible that during the process of enter and remove one can
remove the significant variable.

Study of the residual Structure:

Usually we perform the analysis of residual structure by drawing the graph (scatter plot) between
unstandardized predicted value and standardized residual value (the variables unstandardized
predicted value and standardized residual value generates when researcher runs the test
conditionally when we give the option of save during the running the test)
If the predicted values are very large than residuals will also be very large, and as a result
analysis of residual structure becomes difficult. Therefore we use standardized or studentized
residual values. The Standardized residual (taking on y-axis or dependent) and un-standardized
predicted value (taking on x-axis or independent)

Do OK

The graph shows that the variation between the two variables initially less but later on it will
increase. Compare with the following set of graph.

Here the graph which we form shows the resemblance with the graph of C. as shown below
Graph-1

It means that the graph has the heteroscedasticity. Heteroscedasticity means that the variance
pattern between the values of y for the different predictors is not same. So transformation
requires lifting the assumption violation.

Method of Transformations:

When Data Transformation require?
The data transformation require when the study of residual structure tells us that it is not
following or violating the assumptions of the model. The assumptions are listed below:
Linearity of the phenomenon measured (through scatter plot of the error term).
Constant variance of the error terms (Homoscedasticity).
Independence of the error term (multicollineartity). All predictors are
Independent.
Normality of the error term distribution.

Why Data Transformation require?
Data transformation gives us two benefits:
1. Two correct the violations of the statistical assumption mentioned above for the
multivariate technique.
2. To improve the relationship between the study variable and the predictors.
3. Transformation shows the correct picture of the significant variables. Sometime we may
find such few variables which are insignificant but after transformation it deduces that the
variable was actually significant.
How to do Data Transformation?
Criterion for the transformation
Figure
Violation of assumption
Situation of
Violation
Remedy
a Null Plot All the
assumptions of
the model are
met.
No remedy is required.
b Non Normality Flat pattern Inverse transformation
(1/y)
Negatively
Skewed
Squared or Cubed (y
2
or
y
3
)
Positively
Skewed
Square root or log
transformation (y or ln
y)
C Heteroscedasticity Cone shape
distribution
Inverse transformation
(1/y)
opens rightward
Opens leftward Square root
transformation (y)
D,H Heteroscedasticity A diamond shape
pattern shows
that the high
variance in the
middle while at
the end the
variance are less.
It means it is
nonlinearity is
also exist.
Usually log
transformation is
advisable. It is often
happened that when we
address one of the
violation the other will
also adjusted
simultaneously.
E Time base dependence
F Event base dependence
G Normal
Numerous procedures are available for achieving linearity between two variables but most
simple nonlinear relationships can be placed in one of four categories in the figure below. If the
relationship looks like figure a, then either variable can be squared to achieve linearity. When
multiple transformation possibilities are shown, start with the top method in each figure and then
move downward until linearity is achieved.

How to perform transformation:
Stepwise transformation are shown below.

The dependent variable sales has been transformed as variable name TransformedSales
Now see the effect of transformation shown below.
Before seeing the effect of transformation, run the regression test again by taking the dependent
variable transformedSales. After that draw the scatter plot of Standardized residual and
Unstandardized predicted value.

Result of transformation

Before Transformation After transformation
Model Summary
b

Mod
el R
R
Square
Adjusted R
Square
Std. Error
of the
Estimate
1 .565
a
.319 .255 64.798014
a. Predictors: (Constant), Fuel efficiency, 4-year
resale value, Length, Width, Engine size, Fuel
capacity, Wheelbase, Curb weight, Horsepower,
Price in thousands

Model Summary
b

Mode
l R
R
Square
Adjusted R
Square
Std. Error of
the Estimate
1 .634
a
.402 .345 1.08253
a. Predictors: (Constant), Fuel efficiency, 4-year
resale value, Length, Width, Engine size, Fuel
capacity, Wheelbase, Curb weight, Horsepower,
Price in thousands
b. Dependent Variable: TransformedSales

Conclusion:
1. R-Square improved from 31.9% to 40.2%
2. The scatter plot also show that this is looks like the null plot.

Enter and Remove the Predictors (Before transformation)
Here we perform the removal of insignificant variable from the model one by one we perform
this exercise without the transformation. The removal of the variable will take place in
descending order on the basis of significant values. The variable which has the highest sig value
will remove first continue this procedure one by one.
Note: It is quite possible that the researcher can think about any particular variable as an
important factor but statistical may not support his/her idea. It does not matter, if researcher
thinks to include that variable to be a part of the model so it can be.

0. Without removing any variable (Consider all predictors)

Model Summary
Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .565
a
.319 .255 64.798014

Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence Interval
for B
B Std. Error Beta Lower Bound Upper Bound
1 (Constant) -225.116 191.901

-1.173 .243 -605.579 155.347
4-year resale
value
.011 2.253 .002 .005 .996 -4.456 4.478
Price in
thousands
-.015 2.146 -.003 -.007 .994 -4.269 4.239
Engine size 37.640 15.588 .529 2.415 .017 6.735 68.545
Horsepower -.612 .342 -.477 -1.788 .077 -1.290 .067
Wheelbase 6.391 1.787 .685 3.576 .001 2.848 9.934
Width -.375 3.120 -.018 -.120 .905 -6.561 5.811
Length -.437 1.077 -.081 -.406 .686 -2.573 1.698
Curb weight -69.476 29.602 -.553 -2.347 .021 -128.165 -10.787
Fuel capacity -.157 3.697 -.008 -.043 .966 -7.487 7.172
Fuel efficiency -2.608 2.931 -.153 -.890 .376 -8.418 3.203

1. Remove variable 4-year resale value
Model Summary
b

Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .560
a
.314 .270 58.895390
a. Predictors: (Constant), Fuel efficiency, Length, Price in thousands,
Width, Fuel capacity, Engine size, Wheelbase, Curb weight,
Horsepower

The value of R-Square is slightly drop (i.e. 0.005)

Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
for B
1 (Constant) -214.894 152.450

-1.410 .161 -516.258 86.471
Price in
thousands
-.441 .731 -.092 -.604 .547 -1.886 1.004
Engine size 34.469 11.271 .525 3.058 .003 12.189 56.750
Horsepower -.563 .250 -.464 -2.254 .026 -1.056 -.069
Wheelbase 4.729 1.317 .529 3.590 .000 2.125 7.333
Width -.222 2.428 -.011 -.092 .927 -5.022 4.577
Length -.129 .748 -.025 -.173 .863 -1.608 1.349
Curb weight -50.079 19.946 -.462 -2.511 .013 -89.508 -10.649
Fuel capacity .460 2.719 .026 .169 .866 -4.916 5.835
Fuel efficiency -1.172 2.266 -.073 -.517 .606 -5.653 3.308
After the removal of 4-year resale value the significance value of the variables are addressed
few are increase and few are decrease. The variable horse power which was initially
insignificant, but now become significant.

2. Remove variable width

Model Summary
b

Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .560
a
.314 .275 58.690836
Fuel capacity, Engine size, Wheelbase, Curb weight, Horsepower
This time there is no change in the value of R-square.

Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients t Sig.
for B
1 (Constant) -224.403 111.287

-2.016 .046 -444.383 -4.423
Price in
thousands
-.433 .722 -.090 -.599 .550 -1.860 .995
Engine size 34.277 11.036 .522 3.106 .002 12.463 56.091
Horsepower -.565 .248 -.466 -2.283 .024 -1.054 -.076
Wheelbase 4.712 1.299 .527 3.628 .000 2.144 7.279
Length -.141 .734 -.028 -.192 .848 -1.592 1.310
Curb weight -50.374 19.616 -.465 -2.568 .011 -89.148 -11.600
Fuel capacity .447 2.706 .026 .165 .869 -4.902 5.796
Fuel efficiency -1.181 2.257 -.074 -.523 .602 -5.642 3.280
After this run only 4 variables are now left as insignificant while the constant becomes
significant itself.
3. Remove variable Fuel Capacity

Model Summary
b

Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .560
a
.313 .280 58.492268
Engine size, Wheelbase, Curb weight, Horsepower
Again R-square is dropped slightly i.e. only 0.001

Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
for B
1 (Constant) -221.857 109.840

-2.020 .045 -438.963 -4.750
Price in
thousands
-.423 .718 -.089 -.590 .556 -1.842 .995
Engine size 34.347 10.990 .523 3.125 .002 12.624 56.070
Horsepower -.569 .245 -.469 -2.320 .022 -1.054 -.084
Wheelbase 4.767 1.250 .534 3.815 .000 2.297 7.238
Length -.151 .729 -.030 -.207 .836 -1.592 1.290
Curb weight -48.971 17.621 -.452 -2.779 .006 -83.801 -14.142
Fuel efficiency -1.310 2.111 -.082 -.620 .536 -5.482 2.863
4. Remove variable Length

Model Summary
b

Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .560
a
.313 .285 58.298917
a. Predictors: (Constant), Fuel efficiency, Price in thousands,
Wheelbase, Engine size, Curb weight, Horsepower
No change in the value of R-square

Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
for B
1 (Constant) -223.549 109.174

-2.048 .042 -439.327 -7.771
Price in
thousands
-.384 .690 -.080 -.556 .579 -1.747 .979
Engine size 34.172 10.922 .520 3.129 .002 12.586 55.759
Horsepower -.582 .237 -.480 -2.455 .015 -1.050 -.113
Wheelbase 4.585 .884 .513 5.189 .000 2.839 6.331
Curb weight -49.726 17.184 -.459 -2.894 .004 -83.689 -15.762
Fuel efficiency -1.421 2.035 -.089 -.698 .486 -5.443 2.602
5. Remove variable Price in thousand

Model Summary
b

Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .560
a
.313 .290 57.965284
a. Predictors: (Constant), Fuel efficiency, Wheelbase, Horsepower,
Curb weight, Engine size
No change in the value of R-square

Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence Interval for
B
1 (Constant) -224.038 108.178

-2.071 .040 -437.823 -10.253
Engine size 36.113 10.310 .549 3.503 .001 15.737 56.489
Horsepower -.682 .156 -.563 -4.382 .000 -.990 -.374
Wheelbase 4.746 .830 .531 5.715 .000 3.105 6.386
Curb weight -53.227 15.946 -.491 -3.338 .001 -84.739 -21.715
Fuel efficiency -1.541 2.006 -.096 -.768 .444 -5.506 2.424
6. Remove variable Fuel efficiency

Model Summary
b

Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .556
a
.309 .291 57.595036
a. Predictors: (Constant), Curb weight, Horsepower, Wheelbase,
Engine size
This time R-square dropped by 0.004 unit but it is still predictors explain the estimator by 30.9%.

Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence Interval for
B
1 (Constant) -288.879 73.316

-3.940 .000 -433.745 -144.012
Engine size 36.856 9.985 .561 3.691 .000 17.127 56.585
Horsepower -.669 .154 -.552 -4.354 .000 -.973 -.365
Wheelbase 4.747 .820 .531 5.787 .000 3.126 6.367
Curb weight -46.288 13.208 -.427 -3.505 .001 -72.386 -20.190
Now only significant variables are left.

Enter and Remove the Predictors (After Transformation)
0. First output with considering all the variables.
Model Summary
b

Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .634
a
.402 .345 1.08253
b. Dependent Variable: LogSale

Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 (Constant) -1.097 3.206

-.342 .733 -7.453 5.259

4-year resale
value
-.012 .038 -.101 -.311 .757 -.086 .063 .053 18.890
Price in
thousands
-.036 .036 -.385 -1.015 .312 -.107 .035 .039 25.464
Engine size .310 .260 .244 1.190 .237 -.206 .826 .134 7.474
Horsepower -.003 .006 -.118 -.470 .639 -.014 .009 .090 11.095
Wheelbase .093 .030 .559 3.111 .002 .034 .152 .175 5.718
Width -.026 .052 -.068 -.492 .624 -.129 .078 .298 3.352
Length -.018 .018 -.188 -1.008 .316 -.054 .018 .163 6.149
Curb weight .262 .495 .117 .530 .597 -.718 1.242 .116 8.633
Fuel capacity -.059 .062 -.166 -.949 .345 -.181 .064 .184 5.437
Fuel efficiency .026 .049 .087 .538 .592 -.071 .123 .217 4.602
a. Dependent Variable: LogSale
1. Remove variable 4-year resale value
The variable 4-year resale value having the heighest sig value i.e. 0.757 so remove it first.

Model Summary
b

Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .678
a
.459 .425 1.01072
Width, Fuel capacity, Engine size, Wheelbase, Curb weight,
Horsepower

Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 (Constant) -.414 2.616

-.158 .874 -5.586 4.758

Price in
thousands
-.057 .013 -.616 -4.542 .000 -.082 -.032 .207 4.835
Engine size .408 .193 .321 2.110 .037 .026 .791 .164 6.095
Horsepower -.004 .004 -.151 -.828 .409 -.012 .005 .114 8.760
Wheelbase .061 .023 .355 2.711 .008 .017 .106 .222 4.499
Width -.049 .042 -.127 -1.175 .242 -.131 .033 .325 3.080
Length -.003 .013 -.028 -.217 .828 -.028 .023 .226 4.418
Curb weight .424 .342 .202 1.238 .218 -.253 1.100 .142 7.019
Fuel capacity -.026 .047 -.077 -.560 .576 -.118 .066 .200 4.991
Fuel efficiency .047 .039 .153 1.218 .225 -.030 .124 .241 4.144
Coefficients
a

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 (Constant) -.414 2.616

-.158 .874 -5.586 4.758

Price in
thousands
-.057 .013 -.616 -4.542 .000 -.082 -.032 .207 4.835
Engine size .408 .193 .321 2.110 .037 .026 .791 .164 6.095
Horsepower -.004 .004 -.151 -.828 .409 -.012 .005 .114 8.760
Wheelbase .061 .023 .355 2.711 .008 .017 .106 .222 4.499
Width -.049 .042 -.127 -1.175 .242 -.131 .033 .325 3.080
Length -.003 .013 -.028 -.217 .828 -.028 .023 .226 4.418
Curb weight .424 .342 .202 1.238 .218 -.253 1.100 .142 7.019
Fuel capacity -.026 .047 -.077 -.560 .576 -.118 .066 .200 4.991
Fuel efficiency .047 .039 .153 1.218 .225 -.030 .124 .241 4.144
After removal of the first insignificant variable, the value of R-square is increases by 0.57 or
5.7% and variable price in thousand and engine size become significant.
2. Remove Constant term

Model Summary
c,d

Model R R Square
b

Adjusted R
Square
Std. Error of the
Estimate
1 .961
a
.924 .919 1.00727
a. Predictors: Fuel efficiency, Price in thousands, Engine size, Fuel
capacity, Horsepower, Curb weight, Wheelbase, Width, Length
b. For regression through the origin (the no-intercept model), R Square
measures the proportion of the variability in the dependent variable about
the origin explained by regression. This CANNOT be compared to R
Square for models which include an intercept.
c. Dependent Variable: LogSale
d. Linear Regression through the Origin

Coefficients
a,b

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 Price in
thousands
-.057 .012 -.498 -4.603 .000 -.082 -.033 .045 22.048
Engine size .413 .190 .376 2.174 .031 .038 .789 .018 56.259
Horsepower -.004 .004 -.194 -.836 .405 -.012 .005 .010 101.939
Wheelbase .061 .022 1.848 2.720 .007 .017 .105 .001 870.319
Width -.053 .030 -1.072 -1.757 .081 -.114 .007 .001 702.034
Length -.003 .013 -.141 -.209 .834 -.028 .023 .001 859.164
Curb weight .424 .341 .410 1.241 .216 -.251 1.098 .005 205.739
Fuel capacity -.027 .046 -.138 -.574 .567 -.118 .065 .009 109.013
Fuel efficiency .044 .034 .304 1.299 .196 -.023 .112 .010 102.955
b. Linear Regression through the Origin
3. Remove variable Length

Model Summary
c,d

Model R R Square
b

Adjusted R
Square
Std. Error of the
Estimate
1 .961
a
.924 .920 1.00392
a. Predictors: Fuel efficiency, Price in thousands, Engine size, Fuel
capacity, Horsepower, Curb weight, Wheelbase, Width

Coefficients
a,b

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 Price in
thousands
-.057 .012 -.492 -4.703 .000 -.080 -.033 .048 20.811
Engine size .411 .189 .374 2.173 .031 .037 .785 .018 56.089
Horsepower -.004 .004 -.205 -.904 .367 -.012 .004 .010 97.349
Wheelbase .058 .017 1.755 3.432 .001 .025 .091 .002 495.998
Width -.055 .030 -1.096 -1.833 .069 -.114 .004 .001 678.380
Curb weight .410 .334 .397 1.228 .221 -.250 1.070 .005 198.513
Fuel capacity -.026 .046 -.133 -.558 .578 -.117 .065 .009 108.047
Fuel efficiency .043 .033 .294 1.288 .200 -.023 .109 .010 99.044

4. Remove variable Fuel Capacity

Model Summary
c,d

Model R R Square
b

Adjusted R
Square
Std. Error of the
Estimate
1 .961
a
.924 .920 1.00154
a. Predictors: Fuel efficiency, Price in thousands, Engine size, Curb
weight, Horsepower, Wheelbase, Width

Coefficients
a,b

Model
Unstandardized
Coefficients
Standardized
Coefficients t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 Price in
thousands
-.057 .012 -.499 -4.814 .000 -.081 -.034 .049 20.521
Engine size .410 .189 .372 2.172 .031 .037 .783 .018 56.081
Horsepower -.003 .004 -.188 -.841 .402 -.012 .005 .010 95.713
Wheelbase .055 .016 1.680 3.413 .001 .023 .087 .002 461.716
Width -.057 .030 -1.135 -1.916 .057 -.115 .002 .001 669.012
Curb weight .334 .304 .323 1.098 .274 -.267 .934 .006 164.991
Fuel efficiency .050 .031 .343 1.632 .105 -.011 .111 .012 84.344

5. Remove variable Horse Power

Model Summary
c,d

Model R R Square
b

Adjusted R
Square
Std. Error of the
Estimate
1 .961
a
.924 .920 1.00053
a. Predictors: Fuel efficiency, Price in thousands, Engine size, Curb
weight, Wheelbase, Width

Coefficients
a,b

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 Price in
thousands
-.065 .008 -.566 -8.443 .000 -.080 -.050 .117 8.584
Engine size .308 .145 .280 2.128 .035 .022 .595 .030 33.125
Wheelbase .055 .016 1.662 3.383 .001 .023 .087 .002 460.831
Width -.062 .029 -1.235 -2.132 .035 -.119 -.004 .002 641.711
Curb weight .403 .292 .390 1.381 .169 -.174 .980 .007 152.731
Fuel efficiency .053 .031 .362 1.732 .085 -.007 .113 .012 83.408
6. Remove variable Curb weight
Model Summary
c,d

Model R R Square
b

Adjusted R
Square
Std. Error of the
Estimate
1 .961
a
.923 .920 1.00022
a. Predictors: Fuel efficiency, Price in thousands, Engine size,
Wheelbase, Width

Coefficients
a,b

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 Price in
thousands
-.062 .007 -.542 -8.407 .000 -.077 -.047 .125 7.975
Engine size .332 .143 .303 2.317 .022 .049 .615 .030 32.794
Wheelbase .063 .015 1.930 4.265 .000 .034 .093 .003 393.006
Width -.049 .027 -.989 -1.793 .075 -.103 .005 .002 583.801
Fuel efficiency .027 .024 .186 1.125 .262 -.021 .075 .019 52.739

7. Remove variable Fuel efficiency

8. Remove variable Width
Model Summary
c,d

Model R R Square
b

Adjusted R
Square
Std. Error of the
Estimate
1 .960
a
.922 .921 .99940
a. Predictors: Wheelbase, Price in thousands, Engine size
Model Summary
c,d

Model R R Square
b

Adjusted R
Square
Std. Error of the
Estimate
1 .961
a
.923 .921 .99628
a. Predictors: Width, Price in thousands, Engine size, Wheelbase
Coefficients
a,b

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 Price in
thousands
-.062 .007 -.541 -8.480 .000 -.077 -.048 .125 8.005
Engine size .223 .106 .203 2.094 .038 .013 .432 .054 18.427
Wheelbase .061 .015 1.849 4.161 .000 .032 .090 .003 388.695
Width -.031 .022 -.630 -1.398 .164 -.076 .013 .003 399.409

Coefficients
a,b

Model
Unstandardized
Coefficients
Standardized
Coefficients
t Sig.
95.0% Confidence
Interval for B
Collinearity
Statistics
B Std. Error Beta
Lower
Bound
Upper
Bound Tolerance VIF
1 Price in
thousands
-.064 .007 -.559 -8.913 .000 -.078 -.050 .130 7.684
Engine size .221 .107 .202 2.078 .039 .011 .432 .054 18.426
Wheelbase .041 .003 1.237 16.255 .000 .036 .046 .088 11.328
Conclusion
After all these exercise we conclude that there are three predictors; (1) price in thousand, (2)
engine size and (3) wheel base are the significant predictors but the VIF of engine size is very
high that is 18.426 so it shows the effect of multicollinearity exist here although it is significant
coefficient. So it depends upon the researcher and theory, whether to include or not to include
this variable in the regression model. On the other hand, when the test was run before the
transformation we find the other four variables with constant term was (1) engine size (2) horse
power (3) wheel base and (4) curb weight. After transformation we get theoretically more logical
predictors as compare to the result of before transformation while the value of R-Square is also
much better than before.
Finally the regression equation will be:
Logsale = - 0.064 (price in thousands) + 0.041(Wheelbase)
Enter & Remove by Backward Method
The same test and approximately the same result can calculate by using the backward method.
We validate the result of before and after transformation by backward method.

How to perform Backward Method? (Without transformation)

Variables Entered/Removed
b

Model
Variables
Entered
Variables
Removed Method
1 Fuel efficiency,
4-year resale
value, Length,
Width, Engine
size, Fuel
capacity,
Wheelbase, Curb
weight,
Horsepower,
Price in
thousands
a

. Enter
2 . 4-year resale
value
Backward
(criterion:
Probability of F-
to-remove >=
.100).
3 . Price in
thousands
Backward
(criterion:
Probability of F-
to-remove >=
.100).
4 . Fuel capacity Backward
(criterion:
Probability of F-
to-remove >=
.100).
5 . Width Backward
(criterion:
Probability of F-
to-remove >=
.100).
6 . Length Backward
(criterion:
Probability of F-
to-remove >=
.100).
7 . Fuel efficiency Backward
(criterion:
Probability of F-
to-remove >=
.100).
a. All requested variables entered.

Model Summary
Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .565
a
.319 .255 64.798014
2 .565
b
.319 .262 64.494517
3 .565
c
.319 .269 64.195246
4 .565
d
.319 .275 63.900650
5 .565
e
.319 .282 63.614616
6 .563
f
.317 .287 63.398826
7 .556
g
.309 .285 63.486236
b. Predictors: (Constant), Fuel efficiency, Length, Width, Engine size,
Fuel capacity, Wheelbase, Curb weight, Horsepower, Price in
thousands
c. Predictors: (Constant), Fuel efficiency, Length, Width, Engine size,
Fuel capacity, Wheelbase, Curb weight, Horsepower
d. Predictors: (Constant), Fuel efficiency, Length, Width, Engine size,
Wheelbase, Curb weight, Horsepower
e. Predictors: (Constant), Fuel efficiency, Length, Engine size,
Wheelbase, Curb weight, Horsepower
f. Predictors: (Constant), Fuel efficiency, Engine size, Wheelbase, Curb
weight, Horsepower
g. Predictors: (Constant), Engine size, Wheelbase, Curb weight,
Horsepower

Coefficients
a

Model
Unstandardized Coefficients
Standardized
Coefficients
t Sig. B Std. Error Beta
1 (Constant) -225.116 191.901

-1.173 .243
4-year resale value .011 2.253 .002 .005 .996
Price in thousands -.015 2.146 -.003 -.007 .994
Engine size 37.640 15.588 .529 2.415 .017
Horsepower -.612 .342 -.477 -1.788 .077
Wheelbase 6.391 1.787 .685 3.576 .001
Width -.375 3.120 -.018 -.120 .905
Length -.437 1.077 -.081 -.406 .686
Curb weight -69.476 29.602 -.553 -2.347 .021
Fuel capacity -.157 3.697 -.008 -.043 .966
Fuel efficiency -2.608 2.931 -.153 -.890 .376
2 (Constant) -224.919 186.969

-1.203 .232
Price in thousands -.006 .991 -.001 -.006 .996
Engine size 37.627 15.300 .529 2.459 .016
Horsepower -.611 .339 -.477 -1.801 .074
Wheelbase 6.392 1.769 .686 3.613 .000
Width -.374 3.099 -.018 -.121 .904
Length -.438 1.046 -.081 -.419 .676
Curb weight -69.529 27.528 -.553 -2.526 .013
Fuel capacity -.154 3.619 -.008 -.043 .966
Fuel efficiency -2.610 2.878 -.153 -.907 .367
3 (Constant) -225.048 184.706

-1.218 .226
Engine size 37.654 14.496 .529 2.597 .011
Horsepower -.613 .213 -.478 -2.881 .005
Wheelbase 6.392 1.758 .686 3.636 .000
Width -.371 3.057 -.017 -.121 .904
Length -.437 1.019 -.081 -.429 .669
Curb weight -69.586 25.500 -.554 -2.729 .007
Fuel capacity -.156 3.590 -.008 -.043 .966
Fuel efficiency -2.613 2.827 -.153 -.924 .357
4 (Constant) -225.414 183.665

-1.227 .222
Engine size 37.728 14.328 .530 2.633 .010
Horsepower -.614 .211 -.479 -2.906 .004
Wheelbase 6.364 1.619 .683 3.929 .000
Width -.395 2.993 -.019 -.132 .895
Length -.424 .967 -.078 -.438 .662
Curb weight -70.015 23.394 -.557 -2.993 .003
Fuel efficiency -2.561 2.557 -.150 -1.002 .319
5 (Constant) -242.535 129.494

-1.873 .064
Engine size 37.238 13.775 .523 2.703 .008
Horsepower -.611 .209 -.477 -2.919 .004
Wheelbase 6.346 1.607 .681 3.949 .000
Length -.460 .924 -.085 -.498 .619
Curb weight -70.466 23.039 -.561 -3.059 .003
Fuel efficiency -2.554 2.545 -.150 -1.004 .318
6 (Constant) -247.393 128.688

-1.922 .057
Engine size 36.371 13.619 .511 2.671 .009
Horsepower -.626 .207 -.489 -3.031 .003
Wheelbase 5.745 1.057 .616 5.436 .000
Curb weight -71.956 22.767 -.572 -3.161 .002
Fuel efficiency -2.831 2.475 -.166 -1.144 .255
7 (Constant) -353.714 89.146

-3.968 .000
Engine size 39.752 13.313 .559 2.986 .003
Horsepower -.638 .207 -.498 -3.087 .003
Wheelbase 5.556 1.045 .596 5.315 .000
Curb weight -56.888 18.597 -.453 -3.059 .003

At the end we find the same significant variables which we find in enter and remove method
with approximately the same level of significant values.

How to perform Backward Method? (After transformation)

Variables Entered/Removed
b

Model Variables Entered
Variables
Removed Method
1 Fuel efficiency, 4-year resale value, Length,
Width, Engine size, Fuel capacity, Wheelbase,
Curb weight, Horsepower, Price in thousands
a

. Enter
2 . 4-year resale value Backward (criterion: Probability of F-to-
remove >= .100).
3 . Horsepower Backward (criterion: Probability of F-to-
remove >= .100).
4 . Width Backward (criterion: Probability of F-to-
remove >= .100).
5 . Fuel efficiency Backward (criterion: Probability of F-to-
remove >= .100).
6 . Curb weight Backward (criterion: Probability of F-to-
remove >= .100).
7 . Length Backward (criterion: Probability of F-to-
remove >= .100).
8 . Engine size Backward (criterion: Probability of F-to-
remove >= .100).
9 . Fuel capacity Backward (criterion: Probability of F-to-
remove >= .100).
a. All requested variables entered.

Model Summary
Model R R Square
Adjusted R
Square
Std. Error of the
Estimate
1 .634
a
.402 .345 1.08253
2 .633
b
.401 .351 1.07796
3 .632
c
.400 .355 1.07419
4 .631
d
.398 .360 1.07068
5 .629
e
.396 .363 1.06766
6 .628
f
.394 .367 1.06480
7 .621
g
.386 .364 1.06719
8 .618
h
.382 .365 1.06590
9 .613
i
.376 .365 1.06600
b. Predictors: (Constant), Fuel efficiency, Length, Width, Engine size,
Fuel capacity, Wheelbase, Curb weight, Horsepower, Price in
thousands
c. Predictors: (Constant), Fuel efficiency, Length, Width, Engine size,
Fuel capacity, Wheelbase, Curb weight, Price in thousands
d. Predictors: (Constant), Fuel efficiency, Length, Engine size, Fuel
capacity, Wheelbase, Curb weight, Price in thousands
e. Predictors: (Constant), Length, Engine size, Fuel capacity,
Wheelbase, Curb weight, Price in thousands
f. Predictors: (Constant), Length, Engine size, Fuel capacity,
Wheelbase, Price in thousands
g. Predictors: (Constant), Engine size, Fuel capacity, Wheelbase, Price
in thousands
h. Predictors: (Constant), Fuel capacity, Wheelbase, Price in thousands
i. Predictors: (Constant), Wheelbase, Price in thousands

Coefficients
a

Model
Unstandardized Coefficients
Standardized
Coefficients
t Sig. B Std. Error Beta
1 (Constant) -1.097 3.206

-.342 .733
4-year resale value -.012 .038 -.101 -.311 .757
Price in thousands -.036 .036 -.385 -1.015 .312
Engine size .310 .260 .244 1.190 .237
Horsepower -.003 .006 -.118 -.470 .639
Wheelbase .093 .030 .559 3.111 .002
Width -.026 .052 -.068 -.492 .624
Length -.018 .018 -.188 -1.008 .316
Curb weight .262 .495 .117 .530 .597
Fuel capacity -.059 .062 -.166 -.949 .345
Fuel efficiency .026 .049 .087 .538 .592
2 (Constant) -1.301 3.125

-.416 .678
Engine size .323 .256 .255 1.264 .209
Horsepower -.003 .006 -.124 -.497 .620
Wheelbase .092 .030 .553 3.108 .002
Width -.027 .052 -.071 -.516 .607
Length -.017 .017 -.175 -.968 .335
Curb weight .317 .460 .141 .689 .493
Fuel capacity -.062 .060 -.176 -1.027 .307
Fuel efficiency .029 .048 .095 .599 .551
3 (Constant) -1.344 3.113

-.432 .667
Engine size .238 .188 .187 1.262 .210
Wheelbase .094 .029 .564 3.210 .002
Width -.028 .052 -.073 -.537 .592
Length -.019 .017 -.199 -1.147 .254
Curb weight .377 .442 .168 .853 .395
Fuel capacity -.062 .060 -.175 -1.024 .308
Fuel efficiency .031 .048 .103 .653 .515
4 (Constant) -2.502 2.239

-1.117 .266
Engine size .204 .177 .161 1.153 .251
Wheelbase .094 .029 .565 3.224 .002
Length -.022 .016 -.228 -1.380 .170
Curb weight .354 .439 .158 .806 .422
Fuel capacity -.068 .059 -.192 -1.150 .253
Fuel efficiency .029 .047 .096 .617 .539
5 (Constant) -1.553 1.622

-.958 .340
Engine size .167 .166 .132 1.006 .316
Wheelbase .096 .029 .579 3.340 .001
Length -.021 .016 -.218 -1.331 .186
Curb weight .262 .411 .117 .637 .526
Fuel capacity -.083 .053 -.236 -1.556 .123
6 (Constant) -1.771 1.581

-1.120 .265
Engine size .199 .158 .157 1.256 .212
Wheelbase .098 .029 .589 3.425 .001
Length -.019 .015 -.196 -1.226 .223
Fuel capacity -.063 .042 -.177 -1.473 .143
7 (Constant) -2.338 1.515

-1.542 .126
Engine size .125 .147 .099 .852 .396
Wheelbase .070 .017 .422 4.011 .000
Fuel capacity -.050 .041 -.141 -1.205 .231
8 (Constant) -2.593 1.484

-1.747 .083
Wheelbase .073 .017 .441 4.292 .000
Fuel capacity -.040 .040 -.113 -1.011 .314
9 (Constant) -1.920 1.326

-1.448 .150
Wheelbase .061 .012 .369 4.980 .000
As here, only the two variables that is price in thousand and wheelbase are the two significant variables while
the constant term is insignificant for the model.
Finally, the regression equation will be:
logSale = - 0.049(price in thousands) + 0.061(Wheelbase)
The result which we generate by enter method is mentioned below.
Logsale = - 0.064 (price in thousands) + 0.041(Wheelbase)
After the study of the two regression model we find that both the method gives us the same variable with
slightly different in the coefficients. So it is possible that may find a minor difference in the beta coefficients.

Tolerance and Variance Inflation factor (VIF)
The tolerance and VIF are reciprocal to each other. It use for the measurement of independency
of the independent variables or one can say that to measure the multicollinearity among the
independent variables. multicollinearity measure expressing the degree of explanation or
variation of one independent variable in the model due to other independent variable in the
model. This can be calculated as to take one of the independent variable as a dependent
variable and rest of the independent variables as predictors and then to regress them. The
regression will tell us the value of R
2
, the percentage which is explained by the other variable.
This R
2
is called as R
2*
, the amount of independent variable which is explained by the other
independent variable.
Tolerance is calculated as 1-R
2*
, It means that as far as the value of tolerance becomes high, the
multicollinearity will be low.
Variance inflation factor (VIF) is calculated as 1/Tolerance. VIF is the degree to which the
standard error has been increased due to multicollinearity.
R
2*
increases then tolerance will decrease this implies VIF will increase this means
multicollinearity is increases.

Regression Equation

Загружено:

Сведения о документе

Исходное описание:

Авторское право

Доступные форматы

Поделиться этим документом

Поделиться или встроить документ

Параметры публикации

Этот документ был вам полезен?

Это неприемлемый материал?

Авторское право:

Доступные форматы

Regression Equation

Загружено:

Авторское право:

Доступные форматы

Regression Equation

, by which we can predict the value of y on the basis of

from the sample

represent the vertical deviation from the

regression line, the

in our sample satisfies the relation

may be used to predict the mean response

. We would expect the error of the prediction to be higher in the

Вам также может понравиться