1

Signal Processing
Mike Doggett
Staffordshire University
2

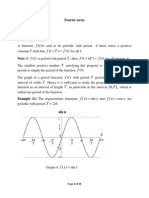
FOURIER SERIES (F.S.)

Fouriers Theorem states that any periodic
function of time, f(t), (i.e. a periodic signal) can
be expressed as a Fourier Series consisting of:

A DC component the average value of f(t).

A component at a fundamental frequency and
harmonically related components, collectively
the AC components.

ie f(t) = DC + AC components.
3
The Fourier Series for a periodic signal may be
expressed by:






f t a a n t b n t n n
n
( ) { cos sin } = + +
=

0
1
e e
DC or average component
AC components
Fundamental frequency (n=1)
at rads per second.

4
a
0
, a
n
and b
n
are coefficients given by:


a
T
f t dt
T
T
0
2
2
1
=

+
}
( )
}
+

=
2
2
cos ) (
2
T
T
tdt n t f
T
n
a e
tdt n t f
T
n
b
T
T
e
}
+

=
2
2
sin ) (
2
5
NOTE
The function must be periodic, i.e. f(t) = f(t+T).
Periodic time = T. Frequency f = Hz.
If f(t) = f(-t) the function is EVEN and only cosine
terms (and a0) will be present in the F.S.










time
6
If f(t) = -f(-t) the function is ODD and only sine
terms (and a
0
) will be present in the F.S.






The coefficients a
n
and b
n
are the amplitudes
of the sinusoidal components.
For example, in general, a
n
cos nt










time
7
The component at the lowest frequency
(excluding the DC component) is when n = 1,

i.e. a
1
cos t

This is called the fundamental or first
harmonic. The component for n = 2 is called
the second harmonic, n = 3 is the third
harmonic and so on.
8
FOURIER SERIES FOR A UNIPOLAR
RECTANGULAR PULSE TRAIN

Consider the rectangular pulse train below.











time
t=0
2
T

2
T

Pulse width
E



0
9
Pulse width seconds, periodic time T seconds,
amplitude E volts (unipolar).

As shown, the function is chosen to be even, ie
f(t) = f(-t) so that a DC term and cosine terms
only will be present in the F.S.

We define f(t) = E,


And f(t) = 0, elsewhere
2 2
t t
s s t
10
As noted, the Fourier Series for a periodic signal
may be expressed by:





Applying to find
f t a a n t b n t n n
n
( ) { cos sin } = + +
=

0
1
e e
}
+

=
2
2
1
0
t
t
Edt
T
a
| |
2
2
0
t
t
= t
T
E
a
11





The a
n
coefficients are given by
T
E
a
t
=
0
}
+

=
2
2
cos ) (
2
T
T
tdt n t f
T
n
a e
12







Since sin(-A) = -sinA
2
2
2
2
sin 2
cos
2
t
t
t
t
e
e
e

+

= =
}
n
t n
T
E
tdt n E
T
n
a
(

|
.
|

\
|
=
2
sin
2
sin
2 et et
e
n n
T n
E
n
a
|
.
|

\
|
=
2
sin
4 et
e
n
T n
E
n
a
13
In this case it may be show that b
n
= 0 (because
the choice of t = 0 gives an even function).

Hence:






and
T
E
a
t
=
0
|
.
|

\
|
=
2
sin
4 et
e
n
T n
E
n
a
0 =
n
b
14
Simplifying, by noting

substituting back into the F.S. equation:
T
t
e
2
=
|
.
|

\
|
=
|
|
|
|
.
|

\
|
=
|
.
|

\
|
=
T
n
n
E
T
n
T
T
n
E n
T n
E
n
a
tt
t
t
t
t
et
e
sin
2
2
2
sin
2
4
2
sin
4

=
+ =
1
0 cos ) (
n
n t n a a t f e
15
Fourier Series for a unipolar pulse train.





But NOTE, it is more usual to convert this to a
Sinc function.

ie Sinc(X) =
t n
n
T
n
n
E
T
E
t f e
tt
t
t
cos
1
sin
2
) (

=
|
.
|

\
|
+ =
X
X sin
16






Note the trick, i.e multiply by


This reduces to
|
.
|

\
|
|
.
|

\
|
|
.
|

\
|
=
|
.
|

\
|
=
2
.
2
2
sin
4
2
sin
4 et
et
et
e
et
e
n
n
n
T n
E n
T n
E
n
a
2
2
et
et
n
n
|
.
|

\
|
=
2
2 et t n
Sinc
T
E
n
a
17
Hence




This is an important result, the F.S. for a periodic
pulse train and gives a spectrum of the form
shown below:
t n
n
n
Sinc
T
E
T
E
t f e
et t t
cos
1
2
2
) (

=
|
.
|

\
|
+ =
18

























Sinc envelope
frequency
19
FOURIER SERIES (F.S.) Review
We have discussed that the general FS for an
Even function is:


Fourier Series for a unipolar pulse train.

=
+ =
1
cos ) (
0
n
t n
n
a a t f e
t n
n
T
n
n
E
T
E
t f e
tt
t
t
cos
1
sin
2
) (

=
|
.
|

\
|
+ =
t n
n
n
Sinc
T
E
T
E
t f e
et t t
cos
1
2
2
) (

=
|
.
|

\
|
+ =
20
The Sinc function gives an envelope for the
amplitudes of the harmonics.

The Sinc function, in conjunction with

gives the amplitudes of the harmonics.

Note that Sinc(0) =1. (As an exercise, justify this
statement).
T
Et 2
21
The amplitudes of the harmonic components are
given by:



To calculate, it is usually easier to use the form
|
.
|

\
|
=
2
2 et t n
Sinc
T
E
n
a
|
.
|

\
|
=
T
n
T
E
n
a
et t
sin
2
22
The harmonics occur at frequencies n radians
per second.

We normally prefer to think of frequency in
Hertz, and since = 2f, we can consider
harmonics at frequencies nf Hz.

The periodic time, T, and frequency are related

by f = Hz.
T
1
23

Rules of Thumb

The following rules of thumb may be deduced
for a pulse train, illustrated in the waveform
below.











E
volts

T
E
volts
24
Harmonics occur at intervals of f =

OR f, 2f, 3f, etc.

Nulls occur at intervals of


If = x is integer, then nulls occur every xth

harmonic.
.
3
,
2
,
1
,
1
etc
T T T
ie Hz
T
etc ie Hz ,
3
,
2
,
1
,
1
t t t t
t
T
25
For example if T = 10 ms and = 2.5 ms, then

= 4 and there will be nulls at the 4th
harmonic, the 8th harmonic, the 12th harmonic and so
on at every 4th harmonic.

As is reduced, ie the pulse gets narrower, the first and
subsequent nulls move to a higher frequency.

As T increases, ie the pulse frequency gets lower, the
first harmonic moves to a lower frequency and the
spacing between the harmonics reduces, ie they move
closer together.
t
T
26
Exercise Q1. Label the axes and draw the pulse
waveform corresponding to the spectrum below.























frequency
4 kHz
27
Q2. What pulse characteristic would give this
spectrum?


















frequency
1 kHz
28
Q3.
Suppose a triac firing circuit produces a narrow
pulse, with 1 nanosecond pulse width, and a
repetition rate of 50 pulses per second.

What is the frequency spacing between the
harmonics?

At what frequency is the first null in the spectrum?

Why might this be a nuisance for radio reception?
29

COMPLEX FOURIER SERIES

Up until now we have been considering
trigonometric Fourier Series.

An alternative way of expressing f(t) is in terms
of complex quantities, using the relationships:
2
cos
t jn
e
t jn
e
t n
e e
e

+
=
j
t jn
e
t jn
e
t n
2
sin
e e
e

=
30
Since the trig form of F.S. is:




, then this may be written in the complex form:

=
+ + =
1
} sin cos {
0
) (
n
t n
n
b t n
n
a a t f e e

=
(
(

|
|
.
|

\
|

+
|
|
.
|

\
|

+
= =
1
2 2
0
) (
n
j
t jn
e
t jn
e
n
b
t jn
e
t jn
e
n
a a t f
e e e e
31
The complex F.S. may be written as:






where:

=
=
n
t jn
e
n
C t f
e
) (
( )
n
jb
n
a
n
C =
2
1
dt
t jn
e t f
T
n
C
T
T
}

=
2
2
) (
1
e
32
When n = 0, C
0
e
j0
= C
0
is the average value.

n = 1, n = 2, n = 3 etc represent pairs of
harmonics.

These are general for any periodic function.

33
In particular, for a periodic unipolar pulse
waveform, we have:





OR
|
.
|

\
|
=
T
n
n
E
n
a
tt
t
sin
2
|
.
|

\
|
=
2
2 et t n
Sinc
T
E
n
a
34
Hence



Alternative forms of complex F.S. for pulse train:
|
.
|

\
|
=
|
.
|

\
|
= =
2
sin
2
1 et t tt
t
n
Sinc
T
E
T
n
n
E
n
a
n
C
t jn
e
n
T
n
n
E
t f
e
tt
t

=
|
.
|

\
|
= sin ) (
t jn
e
n
Sinc
n
T
E
t f
e
et t
|
.
|

\
|

=
=

2
) (
35
Example
Express the equation below (for a periodic pulse
train) in complex form.





NOTE, we change the cos term, We DONT
change the Sinc term.
t n
n
n
Sinc
T
E
T
E
t f e
et t t
cos
1
2
2
) (

=
|
.
|

\
|
+ =
36
Since:




By changing the sign of the -n and summing
from - to -1, this may be written as:
2
cos
t jn
e
t jn
e
t n
e e
e

+
=
2
1
2
2
) (
t jn
e
t jn
e
n
n
Sinc
T
E
T
E
t f
e e
et t t

+

=
|
.
|

\
|
+ =

t jn
e
n
Sinc
n
T
E
t jn
e
n
n
Sinc
T
E
T
E
t f
e
et t
e
et t t
|
.
|

\
|
=
+

=
|
.
|

\
|
+ =


2
1
2
) (
1
37


We the have and


We want


We need to include the term for n = 0 and may

show that for n = 0, the term results.

=
1
n

=1 n

= n
T
Et
38
Consider when n = 0

Sinc(0) = 1 and e
j0
= 1,

ie = when n = 0


Hence we may write:
t jn
e
n
Sinc
T
E
e
et t
|
.
|

\
|
2
t jn
e
n
Sinc
T
E
e
et t
|
.
|

\
|
2
T
Et
t jn
e
n
Sinc
n
T
E
t f
e
et t
|
.
|

\
|

=
=

2
) (
39
Comments
Fourier Series apply only to periodic functions.

Two main forms of F.S., Trig F.S. and Complex
F.S. which are equivalent.

Either form may be represented on an Argand
diagram, and as a single-sided or two-sided
(bilateral) spectrum.

The F.S. for a periodic function effectively allows a
time-domain signal (waveform) to be represented
in the frequency domain, (spectrum).
40
Exercise
Q1.
A pulse waveform has a ratio of

= 5.

Sketch the spectrum up to the second null
using the rules of thumb.
t
T
41
Q2.
A pulse has a periodic time of T = 4 ms and a
pulse width = 1 ms.

Sketch, but do not calculate in detail, the single-
sided and two-sided spectrum up to the second
null, showing frequencies in Hz.
42
Q3.

With T = 4 ms and = 1 ms as in Q2, now
calculate, tabulate and sketch the single-sided
and two-sided spectrum.
43
Q4.

Convert the trig FS to complex by using the
substitution :
2
cos
t jn
e
t jn
e
t n
e e
e

+
=