Академический Документы
Профессиональный Документы
Культура Документы
Measure of Central Tendency
Загружено:
CY100%(1)100% нашли этот документ полезным (1 голос)
391 просмотров13 страницMeasure of Central Tendency
Авторское право
© © All Rights Reserved
Доступные форматы
PPT, PDF, TXT или читайте онлайн в Scribd
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документMeasure of Central Tendency
Авторское право:
© All Rights Reserved
Доступные форматы
Скачайте в формате PPT, PDF, TXT или читайте онлайн в Scribd
100%(1)100% нашли этот документ полезным (1 голос)
391 просмотров13 страницMeasure of Central Tendency
Загружено:
CYMeasure of Central Tendency
Авторское право:
© All Rights Reserved
Доступные форматы
Скачайте в формате PPT, PDF, TXT или читайте онлайн в Scribd
Вы находитесь на странице: 1из 13
Measure of Central
Tendency
Mean
Mode
Median
Mean of Ungrouped Data
Mean of ungrouped data is the sum of all data
divided by the number of data.
x
xi
i 1
or
Example 1: Find the mean of the set of numbers 4, 6, 1, 8, 6, 3,
7, 6
If the frequencies of the data are given, then
n
x
Example 2:
f i xi
i 1
n
fi
or
fx
x
f
i 1
Number of siblings, x
Number of students, f
10
11
Mean of grouped data
The mid-point, x, of each class is used to represent the
class.
Example 3:
Number of durians
collected daily
Number of days
fx
x
f
120
124
125
129
130
134
135
139
140
144
144
149
26
13
Mean of grouped data
A useful technique:
Start with an assumed mean, k.
Find the difference, y, between each mid-point and k,
i.e
y = x - k.
Find fy.
Then
fy
xk
f
If we wish to further reduce the magnitudes of the numbers involved,
we can use a scaling factor, h.
So,
y = (x k)/h
fy
And the mean is given by x k h
Median of ungrouped data
The median is the middle value of a set of n numbers
arranged in order of magnitude.
For raw data, arrange the data in order of magnitude.
th
If n is odd, then the median is
n
value
If n is even, then the median is arithmetic mean of the
n
2
th
value and
n
1
2
th
value
Median of ungrouped data
Example:
Find the median of each of these set of data:
(a) 1, 9, 6, 7, 12, 8, 3, 10, 11.
(b) 2, 5, 1, 6, 7, 11, 13, 8.
Arrange the data in order of magnitude:
(a) 1, 3, 6, 7, 8, 9, 10, 11, 13
median = 8
(b) 1, 2, 5, 6, 7, 8, 11, 13
median = (6 + 7)/2 = 6.5
Median of ungrouped data
For ungrouped frequency distribution, determine the median from the
cumulative frequency distribution.
For example: Number of cars
0 1 2
Number of families
3 5 11 10 4
Cumulative frequency distribution:
Number of Cumulative
cars
frequency
0
19
20
33
35
As n = 35,
the median = [(35+1)/2]th value.
i.e. the 18th value.
Thus, the median = 2.
Median of grouped data
Once the data has been grouped, we have
lost the original information of the raw data.
So we can only estimate a value for the
median.
This can be done by one of the following
methods
(i) By interpolation
(ii) From a cumulative frequency curve
(iii) From a histogram
Median of grouped data
(i) By interpolation
B
C
m LB 2
fm
where LB is the lower boundary of the median class,
FB is cumulative frequency before median class,
fm is the frequency of the median class,
C is the width of the median class
Median of grouped data
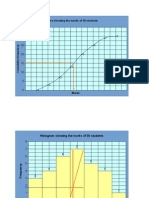
(ii) Draw the cumulative frequency curve and read off
the observation for (f).
(iii) From the histogram,
determine the median class,
draw the horizontal line for (f) N,
where N is the cumulative frequency before the
median class,
draw the diagonal for the median class
estimate the median from the point of
intersection of these two lines
Mode of ungrouped data
The mode of a set of data is the observation
which occurs most often.
For raw data, arrange in the order of
magnitude so that the mode can be identified.
Example: Find the mode for 4, 5, 5, 1, 2, 6, 7,
2, 5.
Rearranging: 1, 2, 2, 4, 5, 5, 5, 6, 7.
Mode = 5
Mode of grouped data
(i) Drawing a histogram
(ii) By calculation
d1
c
d1 d 2
m0 a
where d1 = difference between the frequency of
the modal class and the class before the modal class,
d2 = difference between the frequency of
the modal class and the class after the modal class,
a = lower boundary of the modal class,
c = width of the modal class.
Relative frequency distribution
To compare two or more sets of data, it is
sometimes useful to calculate the relative
frequency for every class in a set of data.
Relative frequency can be expressed either
as a fraction (total 1) or in percentage (total
100%).
Вам также может понравиться
- Research Purposive Final 5Документ16 страницResearch Purposive Final 5Danilo Fronda Jr.100% (1)
- Teaching Mathematics in The Primary Grades FinalsДокумент1 страницаTeaching Mathematics in The Primary Grades FinalsRamer Garaes CardeñoОценок пока нет
- Medieval Mathematics PPT ReportДокумент20 страницMedieval Mathematics PPT ReportJemuel VillaОценок пока нет
- Grade 7: Measures of VariabilityДокумент11 страницGrade 7: Measures of VariabilityBernaliza Caser100% (1)
- Exercises WilcoxonДокумент7 страницExercises WilcoxonRohaila RohaniОценок пока нет
- Assessment and Evaluation in Math - Module 1Документ43 страницыAssessment and Evaluation in Math - Module 1naribarbonОценок пока нет
- DLL Sept 5 CircleДокумент3 страницыDLL Sept 5 CircleLamette AyongОценок пока нет
- 32 Teaching Strategies in MathДокумент15 страниц32 Teaching Strategies in MathLeslye Somarriba PinedaОценок пока нет
- 3 Statistical Description of DataДокумент76 страниц3 Statistical Description of DataAnonymous rkGhCUhОценок пока нет
- Effect of T Math Modules To The Numeracy Level of Grade 6 Learners of Patabog Elementary SchoolДокумент12 страницEffect of T Math Modules To The Numeracy Level of Grade 6 Learners of Patabog Elementary SchoolPsychology and Education: A Multidisciplinary JournalОценок пока нет
- Knowledge Skills Attitudes ValuesДокумент4 страницыKnowledge Skills Attitudes ValuesAmbass EcohОценок пока нет
- Lesson4.2 Deciles and PercentileДокумент9 страницLesson4.2 Deciles and PercentileSmiley UyОценок пока нет
- Difficulties and Coping Strategies of BSED Mathematics College Students in Dealing With Worded ProblemsДокумент9 страницDifficulties and Coping Strategies of BSED Mathematics College Students in Dealing With Worded ProblemsPsychology and Education: A Multidisciplinary JournalОценок пока нет
- A Correlational Analysis On Math Anxiety and Mathematical Performance of Grade 10 Students in Morong National High SchoolДокумент10 страницA Correlational Analysis On Math Anxiety and Mathematical Performance of Grade 10 Students in Morong National High SchoolPsychology and Education: A Multidisciplinary JournalОценок пока нет
- Lesson Plan - Unit 4 Lesson 6 Exponential EquationsДокумент7 страницLesson Plan - Unit 4 Lesson 6 Exponential Equationsapi-528997236Оценок пока нет
- Mean Median Mode Lesson PlanДокумент3 страницыMean Median Mode Lesson Planapi-283375352Оценок пока нет
- Measure of Skewness - Lesson 7Документ16 страницMeasure of Skewness - Lesson 7Gemmavi DulnuanОценок пока нет
- Chapter II Normal DistributionДокумент39 страницChapter II Normal DistributionMaricris Jagto-calixtoОценок пока нет
- Final Cyclic GroupsДокумент8 страницFinal Cyclic GroupsRaquel disomimbaОценок пока нет
- Mean, Median and Mode Grouped DataДокумент9 страницMean, Median and Mode Grouped DataTheo ParrottОценок пока нет
- Normal Distribution LPДокумент4 страницыNormal Distribution LPJomar Ed CañesoОценок пока нет
- 2022 Stat Analysis Module 4 Parametric Test RДокумент18 страниц2022 Stat Analysis Module 4 Parametric Test RArsenio N. RojoОценок пока нет
- Measures of Central Tendency: Mean Median Mode Weighted MeanДокумент20 страницMeasures of Central Tendency: Mean Median Mode Weighted MeanKrysstal Geronga100% (1)
- Lesson 1 Probability BingoДокумент4 страницыLesson 1 Probability Bingoapi-253261408Оценок пока нет
- Quiz On Normal DistrributionДокумент2 страницыQuiz On Normal Distrributiongulafshan100% (1)
- 3 Two Sample Independent TestДокумент5 страниц3 Two Sample Independent TestMarven LaudeОценок пока нет
- Using Multibase Dienes For Basic Six Pupils of Assin NkranДокумент41 страницаUsing Multibase Dienes For Basic Six Pupils of Assin NkranAiman UsmanОценок пока нет
- Module 5 Neutral Geometry Projective Geometry and Differential GeometryДокумент12 страницModule 5 Neutral Geometry Projective Geometry and Differential GeometryDanilyn SukkieОценок пока нет
- Lesson Plan With Assure ModelДокумент4 страницыLesson Plan With Assure Modelapi-511774279Оценок пока нет
- Alg1 Jigsaw LessonДокумент15 страницAlg1 Jigsaw LessonCacait RojanieОценок пока нет
- Lesson Plan 2 Limits at InfinityДокумент5 страницLesson Plan 2 Limits at Infinityapi-438162770Оценок пока нет
- Educational Psychology - Module 2 PDFДокумент24 страницыEducational Psychology - Module 2 PDFMulenga Levy ChunguОценок пока нет
- FS 1 Activity 13.1-13.4Документ4 страницыFS 1 Activity 13.1-13.4SWEET JEAN CASABALОценок пока нет
- Grade 6 LP Data Handling 070918Документ1 страницаGrade 6 LP Data Handling 070918Pooja SharmaОценок пока нет
- Drills A-Strategy-In-Improving-The-Numeracy-Skills-On-Operations of Integers-Of-Grade-8-StudentsДокумент7 страницDrills A-Strategy-In-Improving-The-Numeracy-Skills-On-Operations of Integers-Of-Grade-8-StudentsErliza PerezОценок пока нет
- Lesson 1: Revisiting The Cartesian Coordinate SystemДокумент60 страницLesson 1: Revisiting The Cartesian Coordinate SystemFlorence TangkihayОценок пока нет
- A LESSON PLAN For Mean of Ungrouped DataДокумент6 страницA LESSON PLAN For Mean of Ungrouped DataCarissa Grace DironОценок пока нет
- Lesson Plan 2Документ3 страницыLesson Plan 2api-281594404Оценок пока нет
- QuestionnairesДокумент3 страницыQuestionnairesPatricia TorrecampoОценок пока нет
- Importance of History of Mathematics in Math LearningДокумент8 страницImportance of History of Mathematics in Math LearningHaniz RadziОценок пока нет
- Abesar PrelimДокумент73 страницыAbesar PrelimMary Jhane Tegolo50% (2)
- Detailed Lesson Plan Day2Документ4 страницыDetailed Lesson Plan Day2Abegail VillanuevaОценок пока нет
- Aurora Turmelle - Rubric For GraspsДокумент4 страницыAurora Turmelle - Rubric For Graspsapi-434662376Оценок пока нет
- SAMPLE ReserachДокумент44 страницыSAMPLE ReserachPatrick RodriguezОценок пока нет
- MMC104 - Logic and Set TheoryДокумент7 страницMMC104 - Logic and Set TheoryGreg Recto CayabyabОценок пока нет
- Effect of Peer Tutoring Strategy On Problem Solving Ability, Inter-Group Relations and Academic Achievement in Mathematics For VII Grade StudentsДокумент23 страницыEffect of Peer Tutoring Strategy On Problem Solving Ability, Inter-Group Relations and Academic Achievement in Mathematics For VII Grade Studentsmukesh abrcОценок пока нет
- Assessment Is a-WPS OfficeДокумент3 страницыAssessment Is a-WPS Officejsjjsjs ksksndОценок пока нет
- Effective Teaching Strategies in MathematicsДокумент3 страницыEffective Teaching Strategies in MathematicsJudea Mae Canuto AnteroОценок пока нет
- Mcnemars TestДокумент20 страницMcnemars TestMiaОценок пока нет
- Edited LESSON PLAN IN MATHEMATICS 6 Adding IntegersДокумент5 страницEdited LESSON PLAN IN MATHEMATICS 6 Adding Integersarvin fernando paulinОценок пока нет
- Compare and Distinguish 2-Dimensional Shapes According To Features Such As Sides and Corners.Документ3 страницыCompare and Distinguish 2-Dimensional Shapes According To Features Such As Sides and Corners.Mary Grace De QuirozОценок пока нет
- LE Math 10 Multidisciplinary ApproachДокумент14 страницLE Math 10 Multidisciplinary ApproachJason LaroaОценок пока нет
- Budget of Works For The Most Essential Learning CompetenciesДокумент37 страницBudget of Works For The Most Essential Learning CompetenciesNyliram CariagaОценок пока нет
- Mean Deviation of Grouped Data - LPДокумент4 страницыMean Deviation of Grouped Data - LPKishi Nissi Dela CruzОценок пока нет
- Module 6 - Normal CurveДокумент9 страницModule 6 - Normal CurveAdrianОценок пока нет
- Chapter 2Документ15 страницChapter 2Art BrandОценок пока нет
- Lesson Plan in Mathematics 10Документ4 страницыLesson Plan in Mathematics 10Jerson YhuwelОценок пока нет
- EDUC 8 - Module 3 (Assessment in Student Learning 1)Документ3 страницыEDUC 8 - Module 3 (Assessment in Student Learning 1)Luis Santos Amatosa Jr.Оценок пока нет
- Add Math StatisticsДокумент14 страницAdd Math Statisticskamil muhammadОценок пока нет
- Chapter 7: Statistics 7.1 Measures of Central Tendency 7.1.1 MeanДокумент13 страницChapter 7: Statistics 7.1 Measures of Central Tendency 7.1.1 MeanShafiqah Samsuri100% (1)
- OBSERVEДокумент6 страницOBSERVECYОценок пока нет
- OBSERVEДокумент6 страницOBSERVECYОценок пока нет
- OBSERVEДокумент6 страницOBSERVECYОценок пока нет
- 1.2 Functions: Many To One Relation Are FunctionДокумент3 страницы1.2 Functions: Many To One Relation Are FunctionCYОценок пока нет
- OBSERVEДокумент6 страницOBSERVECYОценок пока нет
- Kimia Bab 10Документ38 страницKimia Bab 10CYОценок пока нет
- OBSERVEДокумент6 страницOBSERVECYОценок пока нет
- Set MM f4 SPM Paper 2editedДокумент9 страницSet MM f4 SPM Paper 2editedCYОценок пока нет
- Do It YourselfДокумент2 страницыDo It YourselfCYОценок пока нет
- Experiment 1:: Heating of NaphthaleneДокумент3 страницыExperiment 1:: Heating of NaphthaleneCYОценок пока нет
- Chapter 5Документ23 страницыChapter 5CYОценок пока нет
- Chapter 4 Mathematical ReasoningДокумент26 страницChapter 4 Mathematical ReasoningGaya GayaОценок пока нет
- Graph: Student Performance Graph For Chemistry 2017Документ1 страницаGraph: Student Performance Graph For Chemistry 2017CYОценок пока нет
- Chapter 8: Circular Measure 8.0 Concept MapДокумент1 страницаChapter 8: Circular Measure 8.0 Concept MapCYОценок пока нет
- The Upper Tail Probability Q (Z) For The Normal Distribution N (0, 1) ZДокумент2 страницыThe Upper Tail Probability Q (Z) For The Normal Distribution N (0, 1) ZCYОценок пока нет
- Quadratic EquationsДокумент6 страницQuadratic EquationsCYОценок пока нет
- PC Functions Basic FunctionsДокумент16 страницPC Functions Basic FunctionsHector R.Оценок пока нет
- Vol 1 Chapter 1Документ4 страницыVol 1 Chapter 1Jm'' GarrickОценок пока нет
- Ogive Showing The Masses of 100 StudentsДокумент4 страницыOgive Showing The Masses of 100 StudentsCYОценок пока нет
- MT Kedah STPM Trial 2008Документ12 страницMT Kedah STPM Trial 2008CYОценок пока нет
- Trigonometric EquationsДокумент7 страницTrigonometric EquationsCYОценок пока нет
- Histogram Showing The Speed of Vehicles Passing Through A CheckpointДокумент4 страницыHistogram Showing The Speed of Vehicles Passing Through A CheckpointCYОценок пока нет
- Technique of Integration - ChartДокумент1 страницаTechnique of Integration - ChartCYОценок пока нет
- Ogive Showing The Marks of 30 StudentsДокумент4 страницыOgive Showing The Marks of 30 StudentsCYОценок пока нет
- Measures of DispersionДокумент27 страницMeasures of DispersionCYОценок пока нет
- Conditional & Independent EventsДокумент15 страницConditional & Independent EventsCYОценок пока нет
- Data Representation: Discrete & Continuous Data Ungrouped & Grouped Data Stem Plots Histogram Cumulative Frequency CurveДокумент10 страницData Representation: Discrete & Continuous Data Ungrouped & Grouped Data Stem Plots Histogram Cumulative Frequency CurveCYОценок пока нет
- Histogram Showing The Blood Pressures of 100 PatientsДокумент2 страницыHistogram Showing The Blood Pressures of 100 PatientsCYОценок пока нет
- Events & ProbabilitiesДокумент9 страницEvents & ProbabilitiesCYОценок пока нет
- Statistics For Managers NotesДокумент57 страницStatistics For Managers NotesRishi vardhiniОценок пока нет
- Measures of Dispersion: HapterДокумент17 страницMeasures of Dispersion: HapterMd IbrahimОценок пока нет
- Study of The Old Stacking ContainerДокумент8 страницStudy of The Old Stacking ContainerIr. Baginda Sitto Siregar, STОценок пока нет
- Research-Paper-Updated 2Документ74 страницыResearch-Paper-Updated 2Daniel MacaspacОценок пока нет
- Bachelor of Business Administration (BBA) : Q.T. in BusinessДокумент4 страницыBachelor of Business Administration (BBA) : Q.T. in BusinessRaghav PokharelОценок пока нет
- Syallabus For B.com SemesterДокумент41 страницаSyallabus For B.com SemesterPawan NabiyalОценок пока нет
- Michael S. Lewis-Beck-Data Analysis - An Introduction, Issue 103-SAGE (1995)Документ119 страницMichael S. Lewis-Beck-Data Analysis - An Introduction, Issue 103-SAGE (1995)ArletPR100% (1)
- Mean Grouped DataДокумент17 страницMean Grouped DataKath AnaretaОценок пока нет
- Descriptive ResearchДокумент5 страницDescriptive Researchnagire_9100% (1)
- Chapter 4 - Numerical Descriptive MeasuresДокумент68 страницChapter 4 - Numerical Descriptive MeasuresRaaj RTОценок пока нет
- Ch3 Numerical Descriptive MeasuresДокумент18 страницCh3 Numerical Descriptive MeasuressameerОценок пока нет
- Research PaperДокумент10 страницResearch PaperSujeet KawdeОценок пока нет
- Lecture 1 PDFДокумент49 страницLecture 1 PDFPorkkodi Sugumaran0% (1)
- Course Outline - StatДокумент3 страницыCourse Outline - StatProf Dr Md Saifur Rahman0% (1)
- 2023 BSC Stochastik Skript enДокумент481 страница2023 BSC Stochastik Skript enMelina SandrinОценок пока нет
- Lec 1Документ31 страницаLec 1Umair GurmaniОценок пока нет
- StatisticsДокумент272 страницыStatisticsAnonymous hYMWbA100% (2)
- Mba Semester 1 Mb0040 - Statistics For Management-4 Credits (Book ID: B1129) Assignment Set - 1 (60 Marks)Документ10 страницMba Semester 1 Mb0040 - Statistics For Management-4 Credits (Book ID: B1129) Assignment Set - 1 (60 Marks)amarendrasumanОценок пока нет
- Chap6.1 Statistics 1Документ46 страницChap6.1 Statistics 1Skrrtt SkrrttОценок пока нет
- Numerical Descriptive MeasuresДокумент27 страницNumerical Descriptive MeasuresRyan Ador Dionisio CastilloОценок пока нет
- UNITДокумент143 страницыUNITmudit bhargavaОценок пока нет
- Omtex - Classes: "The Home of Text"Документ3 страницыOmtex - Classes: "The Home of Text"AMIN BUHARI ABDUL KHADERОценок пока нет
- Mth001 Final Term by Vu Expert SolutionsДокумент11 страницMth001 Final Term by Vu Expert SolutionsMuhammad TalhaОценок пока нет
- Hbaf 3105Документ94 страницыHbaf 3105Abdi Ahmad Maalim100% (2)
- Stats Sample CommerceДокумент20 страницStats Sample Commercesimranarora2007Оценок пока нет
- S3 - Measures of Central Tendency of Grouped DataДокумент24 страницыS3 - Measures of Central Tendency of Grouped DataJoboy FritzОценок пока нет
- Statistics and ProbabilityДокумент141 страницаStatistics and Probabilitykhamru7823100% (7)
- Statistic Sample Question IiswbmДокумент15 страницStatistic Sample Question IiswbmMudasarSОценок пока нет
- Bit 3 LessonДокумент20 страницBit 3 LessonKalum PalihawadanaОценок пока нет