Академический Документы
Профессиональный Документы
Культура Документы
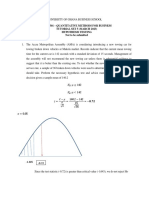
Diagnostic Tests
Загружено:
zkИсходное описание:
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Diagnostic Tests
Загружено:
zkАвторское право:
Доступные форматы
Autocorrelation and
Heteroskedasticity
Introduction
Assess the main ways of remedying
autocorrelation
Describe the problem of non-constant
error terms
Assess the main test for heteroskedasticity
Examine the main remedies for
heteroskedasticity
Introduce the multivariate approach to
regression analysis
Cochrane-Orcutt methodology
This approach to remedying
autocorrelation relies on the generalised
difference equation approach
It is an iterative procedure, the estimates
of the parameters converge towards their
actual value.
It assumes the autocorrelation follows a
first order autoregressive process
(simplest form)
Cochrane-Orcutt Procedure
t t t
t t t
u u
u x y
c
| o
+ =
+ + =
1
Procedure (Based on previous
slide)
Run regression and collect the error term
(u).
Run a second regression of u against u(t-
1) to obtain an estimate of .
Form the generalised difference equation,
to obtain new estimates of the parameters
Re-run this equation, obtain u and repeat
process until there is no significant
difference from one iteration to the next.
Restricted Version of the GDE
The generalised difference equation
can be written in the following form,
which includes a restriction, the
product of the coefficients on y(-1) and
x is equal to the negative of the
coefficient on x(-1) :
t t t t t
x x y y c | | o + + + =
1 1
) 1 (
Unrestricted version of the GDE
In the unrestricted version of the equation in
the previous slide, there are no restrictions
on the values of the coefficients:
t t t t t
x x y y c o o o o + + + + =
1 3 2 1 1 0
The Common Factor Test
To determine whether the restricted or unrestricted
versions are best, we can use the common factor test,
under the null hypothesis that the restriction holds, the
test statistic is:
squares of sum sidual RSS
ns observatio of number T
RSS
RSS
T
unres
res
e
Re
log
Heteroskedasticity
This occurs when a Gauss-Markov
assumption is broken, it indicates non-
constant variance of the error term.
It is often caused by variables which have
substantial differences in the values of the
observations, i.e. GDP differing between
the USA and Cuba
With heteroskedasticity the estimator is no
longer BLUE, as it is not the best.
Tests for Heteroskedasticity
Goldsfeldt-Quandt test (not used much
now)
Whites Test (used in E-views computer
software).
LM test (Similar to the LM test for
heteroskedasticity)
Whites Test
This test follows a similar pattern to the LM test
for autocorrelation discussed earlier.
Based on the same first equation as in slide 4,
we estimate the model and collect the residual u.
Square the residual to form the variance of the
residual
Run a secondary regression of the squared
residual on the explanatory variable and this
variable squared
Whites Test
This secondary regression appears like the
following:
t t t t
x x u c o o o + + + =
2
2 1 0
2
Whites Test
Collect the R-squared statistic and multiply by
the number of observations to obtain the test
statistic.
This follows a chi-squared distribution, the d of f
equal the number of parameters in the
secondary regression (i.e. 2 in above example)
The null hypothesis is no heteroskedasticity.
If there were 2 explanatory variables, you could
include the cross product of these variables, in
the secondary regression.
Remedies for heteroskedasticity
If the standard deviation of the residual is
known, the heteroskedasticity can be removed
by dividing the regression equation through by
the standard deviation of the residual (weighted
Least Squares)
If this is not known, as is likely, we need to
stipulate what the standard deviation is equal to.
We can then divide the regression equation
through by this variable to obtain a constant
variance residual.
Remedying Heteroskedasticity
If we assume the error variance is
proportional to x, the explanatory variable
and we have the usual model:
t t t
t t
u x y
x u E
+ + =
=
| o
o
2 2
) (
Remedying Heteroskedasticity
If we divide our model through by the
square root of x:
t
t
t
t
t t
t
x
u
x
x
x x
y
+ + = |
o
Remedying Heteroskedasticity
Taking the new error term, we can show it is
no longer suffering from heteroskedasticity
by proving it is now constant:
2
2 2
2
2
2
) (
) (
) (
) ( o
o
= = = =
t
t
t
t
t
t
t
t
x
x
x
u E
x
u E
x
u
E
Multivariate Regression
Regressions with more than one explanatory
variable are similar to the bi-variate case, we
can interpret the coefficients and t-statistics in
much the same way as before.
We now have a potential problem with
multicollinearity, when the explanatory variables
are correlated
The formula for the contains an expression for
the covariance between the explanatory
variables.
Multivariate Regression Analysis
The regression coefficients are more likely to be
accurate, the less closely related are the explanatory
variables
This allows testing for the significance of groups of
variables
The R-squared increases with the more explanatory
variables
We need to consider whether all relevant effects are
included in the model
When estimating the t-tests, we need to account for the
extra degrees of freedom
There is a trade off between the number of explanatory
variables and the ease of interpreting the model
Conclusion
The common factor test can be used to
determine the best solution to the problem
of autocorrelation
In the presence of heteroskedasticity, the
estimator is no longer BLUE.
Whites test is the most common test for
heteroskedasticity
Weighted Least Squares can be used to
remedy the heteroskedasticity problem.
Вам также может понравиться
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeОт EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeРейтинг: 4 из 5 звезд4/5 (5794)
- Working Time in 28 Countries Website VersionДокумент24 страницыWorking Time in 28 Countries Website VersionzkОценок пока нет
- The Little Book of Hygge: Danish Secrets to Happy LivingОт EverandThe Little Book of Hygge: Danish Secrets to Happy LivingРейтинг: 3.5 из 5 звезд3.5/5 (399)
- Existence of Walrasian Equilibrium: Proof For The Two-Goods CaseДокумент3 страницыExistence of Walrasian Equilibrium: Proof For The Two-Goods CasezkОценок пока нет
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryОт EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryРейтинг: 3.5 из 5 звезд3.5/5 (231)
- BehaviouralCharacteristicsChecklistOfMathematicallyGiftedStudentsAppI&II 2Документ8 страницBehaviouralCharacteristicsChecklistOfMathematicallyGiftedStudentsAppI&II 2zkОценок пока нет
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceОт EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceРейтинг: 4 из 5 звезд4/5 (894)
- Entrepreneurship Policy Digest June 2014Документ2 страницыEntrepreneurship Policy Digest June 2014zkОценок пока нет
- The Yellow House: A Memoir (2019 National Book Award Winner)От EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Рейтинг: 4 из 5 звезд4/5 (98)
- The Impact of Monetary Regime On The Exchange Rate Pass-Through Under Exchange Rate Volatility (Dynamic Panel Data Approach)Документ16 страницThe Impact of Monetary Regime On The Exchange Rate Pass-Through Under Exchange Rate Volatility (Dynamic Panel Data Approach)zkОценок пока нет
- Harnessing research to inform data-driven hiring and increase student achievementДокумент15 страницHarnessing research to inform data-driven hiring and increase student achievementzkОценок пока нет
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureОт EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureРейтинг: 4.5 из 5 звезд4.5/5 (474)
- Writing Economics DukeДокумент67 страницWriting Economics DukezkОценок пока нет
- Never Split the Difference: Negotiating As If Your Life Depended On ItОт EverandNever Split the Difference: Negotiating As If Your Life Depended On ItРейтинг: 4.5 из 5 звезд4.5/5 (838)
- Useful Stata CommandsДокумент50 страницUseful Stata CommandszkОценок пока нет
- Labor Economics Chapter 1: Labor SupplyДокумент81 страницаLabor Economics Chapter 1: Labor SupplyzkОценок пока нет
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaОт EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaРейтинг: 4.5 из 5 звезд4.5/5 (265)
- 4 CHAUDHARY Trade Instability and Economic GrowthДокумент17 страниц4 CHAUDHARY Trade Instability and Economic GrowthZaheer AhmedОценок пока нет
- Stata CommandsДокумент2 страницыStata CommandszkОценок пока нет
- 1 Sustainable Growth in The Creative Industries PDFДокумент9 страниц1 Sustainable Growth in The Creative Industries PDFzkОценок пока нет
- The Emperor of All Maladies: A Biography of CancerОт EverandThe Emperor of All Maladies: A Biography of CancerРейтинг: 4.5 из 5 звезд4.5/5 (271)
- TOEFLSpeaking Practice PDFДокумент9 страницTOEFLSpeaking Practice PDFzkОценок пока нет
- Behavior ChecklistДокумент11 страницBehavior ChecklistzkОценок пока нет
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersОт EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersРейтинг: 4.5 из 5 звезд4.5/5 (344)
- Wickens Questions3Документ229 страницWickens Questions3zkОценок пока нет
- Team of Rivals: The Political Genius of Abraham LincolnОт EverandTeam of Rivals: The Political Genius of Abraham LincolnРейтинг: 4.5 из 5 звезд4.5/5 (234)
- Changing Demographics and Economic Growth in PakistanДокумент16 страницChanging Demographics and Economic Growth in PakistanzkОценок пока нет
- Wickens Questions3Документ229 страницWickens Questions3zkОценок пока нет
- ManagerialEconomics 2013 FoldedДокумент56 страницManagerialEconomics 2013 FoldedzkОценок пока нет
- IJCAS v6 n5 pp.639-650Документ12 страницIJCAS v6 n5 pp.639-650zkОценок пока нет
- Validity of Scandura and Ragins (1993) Multidimensional MentorinДокумент40 страницValidity of Scandura and Ragins (1993) Multidimensional MentorinzkОценок пока нет
- The Unwinding: An Inner History of the New AmericaОт EverandThe Unwinding: An Inner History of the New AmericaРейтинг: 4 из 5 звезд4/5 (45)
- 2sls Note PDFДокумент18 страниц2sls Note PDFzkОценок пока нет
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyОт EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyРейтинг: 3.5 из 5 звезд3.5/5 (2219)
- Validity of Scandura and Ragins (1993) Multidimensional MentorinДокумент40 страницValidity of Scandura and Ragins (1993) Multidimensional MentorinzkОценок пока нет
- 1 s2.0 S0161893811000743 MainДокумент11 страниц1 s2.0 S0161893811000743 MainzkОценок пока нет
- Laws of Cricket PDFДокумент115 страницLaws of Cricket PDFMohamed SultanОценок пока нет
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreОт EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreРейтинг: 4 из 5 звезд4/5 (1090)
- Lantz FrederickДокумент19 страницLantz FrederickzkОценок пока нет
- Thomson Voluntary Health Insurance and Health System PDFДокумент261 страницаThomson Voluntary Health Insurance and Health System PDFzkОценок пока нет
- Tax ImplicationsДокумент21 страницаTax ImplicationszkОценок пока нет
- The Accuracy of Demand Forecast Models As A Critical Factor in The Financial Performance of The Food IndustryДокумент24 страницыThe Accuracy of Demand Forecast Models As A Critical Factor in The Financial Performance of The Food IndustryzkОценок пока нет
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)От EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Рейтинг: 4.5 из 5 звезд4.5/5 (119)
- Energy Consumption, Economic Growth and Environmental Pollutants in IndonesiaДокумент11 страницEnergy Consumption, Economic Growth and Environmental Pollutants in IndonesiazkОценок пока нет
- 751 764Документ14 страниц751 764zkОценок пока нет
- POLC 6314 - Homework 4 - DELAOДокумент16 страницPOLC 6314 - Homework 4 - DELAOKaty DОценок пока нет
- Supervised Learning With Scikit-Learn: Introduction To RegressionДокумент31 страницаSupervised Learning With Scikit-Learn: Introduction To RegressionNourheneMbarekОценок пока нет
- Pengaruh Metode Permainan Find Your Mate Terhadap Peningkatan Pengetahuan Kader Posyandu Tentang Lima Meja Di Puskesmas Klasaman Kota SorongДокумент5 страницPengaruh Metode Permainan Find Your Mate Terhadap Peningkatan Pengetahuan Kader Posyandu Tentang Lima Meja Di Puskesmas Klasaman Kota SorongAesthetic GirlОценок пока нет
- The Kruskal-Wallis H TestДокумент7 страницThe Kruskal-Wallis H TestNic OleОценок пока нет
- MNPMДокумент15 страницMNPMJdPrzОценок пока нет
- ECONOMICS SEM 4 Notes SakshiДокумент10 страницECONOMICS SEM 4 Notes SakshiSakshi MutturОценок пока нет
- Assignment - 3Документ2 страницыAssignment - 3Priyanka AlmiaОценок пока нет
- BBS10 PPT ch01Документ19 страницBBS10 PPT ch01cleofecaloОценок пока нет
- Sample Exam PDFДокумент4 страницыSample Exam PDFAnkit RadiaОценок пока нет
- TChap2-sampling Dist & Confidence IntervalДокумент3 страницыTChap2-sampling Dist & Confidence IntervalNurulFatimahalzahraОценок пока нет
- Exercises Ch9 Type of ErrorsДокумент15 страницExercises Ch9 Type of ErrorsAhmad MalakОценок пока нет
- Introduction To Simulations in R: Charles Dimaggio, PHD, MPH, Pa-CДокумент48 страницIntroduction To Simulations in R: Charles Dimaggio, PHD, MPH, Pa-CKo DuanОценок пока нет
- Chapter One: Foundations of BiostatisticsДокумент9 страницChapter One: Foundations of BiostatisticsFiza MushtaqОценок пока нет
- Measures of VariationДокумент31 страницаMeasures of VariationMerjie A. NunezОценок пока нет
- Overfitting and Solution SovlveДокумент3 страницыOverfitting and Solution SovlveLoc TranОценок пока нет
- Trend Based Forecasting Methods (P2)Документ26 страницTrend Based Forecasting Methods (P2)mohammed aliОценок пока нет
- Evaluation of Proficiency Test Data by Different Statistical Methods ComparisonДокумент10 страницEvaluation of Proficiency Test Data by Different Statistical Methods Comparisonbiologyipbcc100% (1)
- Two Sample Hotelling's T SquareДокумент30 страницTwo Sample Hotelling's T SquareJoselene MarquesОценок пока нет
- Bastidas HW 4 Chap 2Документ5 страницBastidas HW 4 Chap 2Jenifer Lopez SuarezОценок пока нет
- Official Status and DocId for USP Chapter 1010Документ29 страницOfficial Status and DocId for USP Chapter 1010alexanderaristizabal100% (1)
- Digital Notes on Probability & StatisticsДокумент200 страницDigital Notes on Probability & StatisticsLingannaОценок пока нет
- Statistics With Economics and Business Applications: Chapter 4 Useful Discrete Probability DistributionsДокумент30 страницStatistics With Economics and Business Applications: Chapter 4 Useful Discrete Probability DistributionsTos HernandoОценок пока нет
- Elementary Statistics Triola 11th Edition Solutions ManualДокумент36 страницElementary Statistics Triola 11th Edition Solutions Manualheartzoutcho4yu100% (40)
- Mastering Statistical Quality Control With MinitabДокумент7 страницMastering Statistical Quality Control With MinitabBrian PrestonОценок пока нет
- Files-2-Presentations Malhotra Mr05 PPT 16Документ53 страницыFiles-2-Presentations Malhotra Mr05 PPT 16Needmaterial123Оценок пока нет
- Coefficient Alpha, A Basic Introduction From The Perspectives of Classical Test TheoryДокумент21 страницаCoefficient Alpha, A Basic Introduction From The Perspectives of Classical Test TheorySilvia Jasminne Carmona CusquisibanОценок пока нет
- Andrew Rosenberg - Lecture 18: Gaussian Mixture Models and Expectation MaximizationДокумент34 страницыAndrew Rosenberg - Lecture 18: Gaussian Mixture Models and Expectation MaximizationRoots999Оценок пока нет
- Sol Tutorial Set 5 - HypothesisДокумент4 страницыSol Tutorial Set 5 - Hypothesisfather strechОценок пока нет
- Assignment 1.1 - Jupyter NotebookДокумент4 страницыAssignment 1.1 - Jupyter NotebookSHWETABH KUMAR100% (1)
- Effect of blended learning and i-think strategy on student motivation and interestДокумент6 страницEffect of blended learning and i-think strategy on student motivation and interestlimОценок пока нет