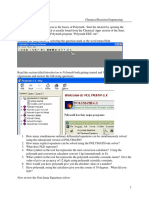
Академический Документы
Профессиональный Документы
Культура Документы
Complex Numbers 2
Загружено:
Tilak PatidarИсходное описание:
Авторское право
Доступные форматы
Поделиться этим документом
Поделиться или встроить документ
Этот документ был вам полезен?
Это неприемлемый материал?
Пожаловаться на этот документАвторское право:
Доступные форматы
Complex Numbers 2
Загружено:
Tilak PatidarАвторское право:
Доступные форматы
Complex Numbers 2
www.mathxtc.com
Complex Numbers
Complex Numbers
What is truth?
Complex Numbers
Who uses them
in real life?
Complex Numbers
Who uses them
in real life?
Heres a hint.
Complex Numbers
Who uses them
in real life?
Heres a hint.
Complex Numbers
Who uses them
in real life?
The navigation system in the space
shuttle depends on complex numbers!
Can you see a problem here?
Who goes first?
Complex numbers do not have order
What is a complex number?
It is a tool to solve an equation.
What is a complex number?
It is a tool to solve an equation.
It has been used to solve equations for the
last 200 years or so.
What is a complex number?
It is a tool to solve an equation.
It has been used to solve equations for the
last 200 years or so.
It is defined to be i such that ;
2
1 i =
What is a complex number?
It is a tool to solve an equation.
It has been used to solve equations for the
last 200 years or so.
It is defined to be i such that ;
Or in other words;
2
1 i =
1 i =
Complex
i is an imaginary
number
Complex
i is an imaginary
number
Or a complex number
Complex
i is an imaginary
number
Or a complex number
Or an unreal number
Complex?
i is an imaginary
number
Or a complex number
Or an unreal number
The terms are inter-
changeable
complex
imaginary
unreal
Some observations
In the beginning there were counting
numbers
1
2
Some observations
In the beginning there were counting
numbers
And then we needed integers
1
2
Some observations
In the beginning there were counting
numbers
And then we needed integers
1
2
-1
-3
Some observations
In the beginning there were counting
numbers
And then we needed integers
And rationals
1
2
-1
-3
0.41
Some observations
In the beginning there were counting
numbers
And then we needed integers
And rationals
And irrationals
1
2
-1
-3
0.41
2
Some observations
In the beginning there were counting
numbers
And then we needed integers
And rationals
And irrationals
And reals
1
2
-1
-3
0.41
2
t
0
So where do unreals fit in ?
We have always used them. 6 is not just 6 it is
6 + 0i. Complex numbers incorporate all
numbers.
1
2
-1
-3
0.41
2
t
3 + 4i
2i
0
A number such as 3i is a purely imaginary
number
A number such as 3i is a purely imaginary
number
A number such as 6 is a purely real number
A number such as 3i is a purely imaginary
number
A number such as 6 is a purely real number
6 + 3i is a complex number
A number such as 3i is a purely imaginary
number
A number such as 6 is a purely real number
6 + 3i is a complex number
x + iy is the general form of a complex
number
A number such as 3i is a purely imaginary
number
A number such as 6 is a purely real number
6 + 3i is a complex number
x + iy is the general form of a complex
number
If x + iy = 6 4i then x = 6 and y =
-
4
A number such as 3i is a purely imaginary
number
A number such as 6 is a purely real number
6 + 3i is a complex number
x + iy is the general form of a complex
number
If x + iy = 6 4i then x = 6 and y =
4
The real part of 6 4i is 6
Worked Examples
1. Simplify
4
Worked Examples
1. Simplify
4
2
4 4 1
4
2
i
i
=
=
=
Worked Examples
1. Simplify
2. Evaluate
4
2
4 4 1
4
2
i
i
=
=
=
3 4 i i
Worked Examples
1. Simplify
2. Evaluate
4
2
4 4 1
4
2
i
i
=
=
=
3 4 i i
2
3 4 12
12 1
12
i i i =
=
=
Worked Examples
3. Simplify
3 4 i i +
Worked Examples
3. Simplify
3 4 i i +
3 4 7 i i i + =
Worked Examples
3. Simplify
4. Simplify
3 4 i i +
3 4 7 i i i + =
3 7 4 6 i i + +
Worked Examples
3. Simplify
4. Simplify
3 4 i i +
3 4 7 i i i + =
3 7 4 6 i i + +
3 7 4 6 13 i i i + + = +
Worked Examples
3. Simplify
4. Simplify
5. Simplify
3 4 i i +
3 4 7 i i i + =
3 7 4 6 i i + +
3 7 4 6 13 i i i + + = +
(3 7)(3 7) i i +
Addition Subtraction
Multiplication
3. Simplify
4. Simplify
5. Simplify
3 4 i i +
3 4 7 i i i + =
3 7 4 6 i i + +
3 7 4 6 13 i i i + + = +
(3 7)(3 7) i i +
( )
2
2
(3 7)(3 7) 3 7 9 49 58 i i i + = = =
Division
6. Simplify
2
3 7 i +
Division
6. Simplify
The trick is to make the denominator real:
2
3 7 i +
Division
6. Simplify
The trick is to make the denominator real:
2
3 7 i +
2 3 7 2(3 7)
3 7 3 7 58
(3 7)
29
7 3
29
i i
i i
i
i
=
+
=
Solving Quadratic Functions
) ( 2 3
2
1 16 6
2
16 6
2
52 36 6
0 13 6 . 7
2
Conjugates solutions complex i x
x
x
x
x x Solve
=
=
=
=
= +
Powers of i
=
=
=
=
=
=
=
7
6
5
4
3
2
i
i
i
i
i
i
i i
Powers of i
( )
=
=
=
=
=
= =
=
7
6
5
4
3
2
2
1 1
i
i
i
i
i
i
i i
Powers of i
( )
=
=
=
= =
= =
= =
=
7
6
5
4
3
2
2
1 1 1
1
1 1
i
i
i
i
i i i
i
i i
Powers of i
( )
i i
i
i i
i
i i i
i
i i
=
=
=
= =
= =
= =
=
7
6
5
4
3
2
2
1
1 1 1
1
1 1
Powers of i
1
1
16 12 8 4
15 11 7 3
14 10 6 2
13 9 5 1
= = = =
= = = =
= = = =
= = = =
i i i i
i i i i i
i i i i
i i i i i
Developing useful rules
2 2
2
2 2
2
2
) )( (
2
) )( (
2
2
) (
b abi a
bi a bi a z
b bi a
bi a bi a z
bi z z
a z z
Conjugate bi a z and bi a z Consider
=
=
+ =
+ + =
=
= +
= + =
Developing useful rules
2 2
2 2
2
2 2
2
) (
) (
) (
) (
) )( (
) (
b a
b abi a
bi a
bi a
bi a
bi a
z
z
z
b a
bi a bi a z z
Conjugate bi a z and bi a z Consider
+
+
=
+
+
+
=
=
+ =
+ =
= + =
Developing useful rules
( )
=
= +
+ = + =
2 1
2 1
2 1
. 2
. 1
z z
z z
di c z and bi a z Consider
Developing useful rules
( )
( )
2 1 2 1
2 1 2 1
2 1
. 2
. 1
z z z z
z z z z
di c z and bi a z Consider
=
+ = +
+ = + =
Argand Diagrams
Jean Robert Argand was a Swiss amateur
mathematician. He was an accountant
book-keeper.
Argand Diagrams
Jean Robert Argand was a Swiss amateur
mathematician. He was an accountant
book-keeper.
He is remembered for 2 things
His Argand Diagram
Argand Diagrams
Jean Robert Argand was a Swiss amateur
mathematician. He was an accountant
book-keeper.
He is remembered for 2 things
His Argand Diagram
His work on the bell curve
Argand Diagrams
Jean Robert Argand was a Swiss amateur
mathematician. He was an accountant
book-keeper.
He is remembered for 2 things
His Argand Diagram
His work on the bell curve
Very little is known about Argand. No
likeness has survived.
Argand Diagrams
x
y
1 2 3
1
2
3
2 + 3i
Argand Diagrams
x
y
1 2 3
1
2
3
2 + 3i
We can represent complex
numbers as a point.
Argand Diagrams
x
y
1 2 3
1
2
3
Argand Diagrams
x
y
1 2 3
1
2
3
We can represent complex
numbers as a vector.
O
A
1
2 z i OA = + =
Argand Diagrams
x
y
1 2 3
1
2
3
1
2 z i OA = + =
2
2 3 z i OB = + =
O
A
B
Argand Diagrams
x
y
1 2 3
1
2
3
1
2 z i OA = + =
2
2 3 z i OB = + =
O
A
B
3
4 4 z i OC = + =
C
Argand Diagrams
x
y
1 2 3
1
2
3
1
2 z i OA = + =
2
2 3 z i OB = + =
O
A
B
3
4 4 z i OC = + =
C
1 2
z z OA AC
OC
+ = +
=
Argand Diagrams
x
y
1 2 3
1
2
3
1
2 z i OA = + =
2
2 3 z i OB = + =
O
A
B
3
4 4 z i OC = + =
C
? BA =
Argand Diagrams
x
y
1 2 3
1
2
3
1
2 z i OA = + =
2
2 3 z i OB = + =
O
A
B
3
4 4 z i OC = + =
C
? BA =
Argand Diagrams
x
y
1 2 3
1
2
3
1
2 z i OA = + =
2
2 3 z i OB = + =
O
A
B
3
4 4 z i OC = + =
C
OB BA OA + =
Argand Diagrams
x
y
1 2 3
1
2
3
1
2 z i OA = + =
2
2 3 z i OB = + =
O
A
B
3
4 4 z i OC = + =
C
OB BA OA
BA OA OB
+ =
=
Argand Diagrams
x
y
1 2 3
1
2
3
1
2 z i OA = + =
2
2 3 z i OB = + =
O
A
B
3
4 4 z i OC = + =
C
1 2
OB BA OA
BA OA OB
z z
+ =
=
=
De Moivre
Abraham De Moivre was a
French Protestant who moved
to England in search of
religious freedom.
He was most famous for his
work on probability and was an
acquaintance of Isaac Newton.
His theorem was possibly
suggested to him by Newton.
( )
cos sin cos sin
n
i n i n u u u u + = +
De Moivres Theorem
This remarkable formula works for
all values of n.
Enter Leonhard Euler..
Euler who was the first to use i for complex
numbers had several great ideas. One of them
was that
e
iu
= cos u + i sin u
Here is an amazing proof.
1
Let sin
sin
y
y
u
u
=
=
1
2
Let sin
sin
1
, now let so
1
y
y
dy y iz dy idz
y
u
u
u
=
=
= = =
(
(
]
( )
1
2
2
Let sin
sin
1
, now let so
1
1
1
y
y
dy y iz dy idz
y
idz
iz
u
u
u
=
=
= = =
(
(
]
(
(
]
( )
1
2
2
2
Let sin
sin
1
, now let so
1
1
1
1
1
y
y
dy y iz dy idz
y
idz
iz
i dz
z
u
u
u
=
=
= = =
=
+
(
(
]
(
(
]
(
(
]
( )
1
2
2
2
Let sin
sin
1
, now let so
1
1
1
1
1
y
y
dy y iz dy idz
y
idz
iz
i dz
z
u
u
u
=
=
= = =
=
+
(
(
]
(
(
]
(
(
]
( )
2
2
1
1
ln 1 [standard integral]
i dz
z
i z z
u
u
=
+
= + +
(
(
]
( )
2
2
1
1
ln 1 [standard integral]
sin
now
i dz
z
i z z
y
y iz z
i i
u
u
u
=
+
= + +
= = =
(
(
]
( )
2
2
2
1
1
ln 1 [standard integral]
sin
now
sin sin
ln 1
i dz
z
i z z
y
y iz z
i i
i
i i
u
u
u
u u
u
=
+
= + +
= = =
| |
| |
= + + |
|
|
\ .
\ .
(
(
]
( )
( )
2
2
2
2
1
1
ln 1 [standard integral]
sin
now
sin sin
ln 1
ln 1 sin sin
i dz
z
i z z
y
y iz z
i i
i
i i
i i
u
u
u
u u
u
u u
=
+
= + +
= = =
| |
| |
= + + |
|
|
\ .
\ .
=
(
(
]
( )
( )
2
2
2
2
1
1
ln 1 [standard integral]
sin
now
sin sin
ln 1
ln 1 sin sin
i dz
z
i z z
y
y iz z
i i
i
i i
i i
u
u
u
u u
u
u u
=
+
= + +
= = =
| |
| |
= + + |
|
|
\ .
\ .
=
(
(
]
( )
( )
2
2
2
2
1
1
ln 1 [standard integral]
sin
now
sin sin
ln 1
ln 1 sin sin
i dz
z
i z z
y
y iz z
i i
i
i i
i i
u
u
u
u u
u
u u
=
+
= + +
= = =
| |
| |
= + + |
|
|
\ .
\ .
=
(
(
]
( )
( )
2
ln 1 sin sin
ln cos sin
i i
i i
u u u
u u u
=
=
( )
( )
( )
( )
2
1
ln 1 sin sin
ln cos sin
ln cos sin
ln cos sin
i i
i i
i i
i i
u u u
u u u
u u u
u u u
=
=
=
=
( )
( )
( )
( )
2
1
ln 1 sin sin
ln cos sin
ln cos sin
ln cos sin
1
ln
cos sin
1 cos sin
ln
cos sin cos sin
i i
i i
i i
i i
i
i
i
i
i i
u u u
u u u
u u u
u u u
u
u u
u u
u
u u u u
=
=
=
=
| |
=
|
\ .
+
| |
=
|
+
\ .
( )
( )
( )
( )
2
1
ln 1 sin sin
ln cos sin
ln cos sin
ln cos sin
1
ln
cos sin
1 cos sin
ln
cos sin cos sin
i i
i i
i i
i i
i
i
i
i
i i
u u u
u u u
u u u
u u u
u
u u
u u
u
u u u u
=
=
=
=
| |
=
|
\ .
+
| |
=
|
+
\ .
1 cos sin
ln
cos sin cos sin
i
i
i i
u u
u
u u u u
+
| |
=
|
+
\ .
( )
1 cos sin
ln
cos sin cos sin
ln cos sin
i
i
i i
i i
u u
u
u u u u
u u u
+
| |
=
|
+
\ .
= +
( )
1 cos sin
ln
cos sin cos sin
ln cos sin
cos sin
i
i
i
i i
i i
e i
u
u u
u
u u u u
u u u
u u
+
| |
=
|
+
\ .
= +
= +
( )
1 cos sin
ln
cos sin cos sin
ln cos sin
cos sin
i
i
i
i i
i i
e i
u
u u
u
u u u u
u u u
u u
+
| |
=
|
+
\ .
= +
= +
One last amazing result
Have you ever thought about i
i
?
One last amazing result
What if I told you that i
i
is a real
number?
now cos sin
2 2
i i
t t
= +
2
now cos sin
2 2
but cos sin
so cos sin
2 2
i
i
i i
e i
e i i
u
t
t t
u u
t t
= +
= +
= + =
2
2
now cos sin
2 2
but cos sin
so cos sin
2 2
i
i
i
i
i
i i
e i
e i i
e i
u
t
t
t t
u u
t t
= +
= +
= + =
| |
=
|
\ .
2
2
2
2
2
now cos sin
2 2
but cos sin
so cos sin
2 2
i
i
i
i
i
i
i
i
i i
e i
e i i
e i
e i
e i
u
t
t
t
t
t t
u u
t t
= +
= +
= + =
| |
=
|
\ .
=
=
i
i
= 0.20787957635076190855
2
5
2
3
2
3
2
3
2
3 3
now cos sin
2 2
but cos sin
3 3
so cos sin
2 2
i
i
i
i
i
i
i
i
i i
e i
e i i
e i
e i
e i
u
t
t
t
t
t t
u u
t t
= +
= +
= + =
| |
=
|
\ .
=
=
i
i
= 111.31777848985622603
So i
i
is an infinite number of
real numbers
The
End
Вам также может понравиться
- The Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeОт EverandThe Subtle Art of Not Giving a F*ck: A Counterintuitive Approach to Living a Good LifeРейтинг: 4 из 5 звезд4/5 (5794)
- The Little Book of Hygge: Danish Secrets to Happy LivingОт EverandThe Little Book of Hygge: Danish Secrets to Happy LivingРейтинг: 3.5 из 5 звезд3.5/5 (399)
- A Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryОт EverandA Heartbreaking Work Of Staggering Genius: A Memoir Based on a True StoryРейтинг: 3.5 из 5 звезд3.5/5 (231)
- Hidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceОт EverandHidden Figures: The American Dream and the Untold Story of the Black Women Mathematicians Who Helped Win the Space RaceРейтинг: 4 из 5 звезд4/5 (894)
- The Yellow House: A Memoir (2019 National Book Award Winner)От EverandThe Yellow House: A Memoir (2019 National Book Award Winner)Рейтинг: 4 из 5 звезд4/5 (98)
- Elon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureОт EverandElon Musk: Tesla, SpaceX, and the Quest for a Fantastic FutureРейтинг: 4.5 из 5 звезд4.5/5 (474)
- Never Split the Difference: Negotiating As If Your Life Depended On ItОт EverandNever Split the Difference: Negotiating As If Your Life Depended On ItРейтинг: 4.5 из 5 звезд4.5/5 (838)
- Devil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaОт EverandDevil in the Grove: Thurgood Marshall, the Groveland Boys, and the Dawn of a New AmericaРейтинг: 4.5 из 5 звезд4.5/5 (265)
- The Emperor of All Maladies: A Biography of CancerОт EverandThe Emperor of All Maladies: A Biography of CancerРейтинг: 4.5 из 5 звезд4.5/5 (271)
- The Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersОт EverandThe Hard Thing About Hard Things: Building a Business When There Are No Easy AnswersРейтинг: 4.5 из 5 звезд4.5/5 (344)
- Team of Rivals: The Political Genius of Abraham LincolnОт EverandTeam of Rivals: The Political Genius of Abraham LincolnРейтинг: 4.5 из 5 звезд4.5/5 (234)
- The Unwinding: An Inner History of the New AmericaОт EverandThe Unwinding: An Inner History of the New AmericaРейтинг: 4 из 5 звезд4/5 (45)
- The World Is Flat 3.0: A Brief History of the Twenty-first CenturyОт EverandThe World Is Flat 3.0: A Brief History of the Twenty-first CenturyРейтинг: 3.5 из 5 звезд3.5/5 (2219)
- The Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreОт EverandThe Gifts of Imperfection: Let Go of Who You Think You're Supposed to Be and Embrace Who You AreРейтинг: 4 из 5 звезд4/5 (1090)
- The Sympathizer: A Novel (Pulitzer Prize for Fiction)От EverandThe Sympathizer: A Novel (Pulitzer Prize for Fiction)Рейтинг: 4.5 из 5 звезд4.5/5 (119)
- Matematik 1449 Nota Akhir SPMДокумент6 страницMatematik 1449 Nota Akhir SPMWan FadhОценок пока нет
- Larry Jay B. Valero, LPTДокумент36 страницLarry Jay B. Valero, LPTChristine Shane MagraciaОценок пока нет
- Real Number SystemsДокумент18 страницReal Number SystemsEdgar M. TorresОценок пока нет
- Ntse Sat Mathematics Trigonometry Important QuestionsДокумент12 страницNtse Sat Mathematics Trigonometry Important QuestionsKukresh TanveeraОценок пока нет
- Poly LinearДокумент5 страницPoly LinearUtkarsh RathoreОценок пока нет
- Uos BSC Gen Maths A AllДокумент16 страницUos BSC Gen Maths A AllAatir HashmiОценок пока нет
- Answer Key For College Algebra & Trigonometry TestДокумент6 страницAnswer Key For College Algebra & Trigonometry TestSo AZ Cop Watch0% (1)
- Introduction to NURBS Curves and SurfacesДокумент6 страницIntroduction to NURBS Curves and SurfacesPadmaja TripathyОценок пока нет
- Elliptic Curve MapleeДокумент10 страницElliptic Curve MapleeNISRINE MRHILIОценок пока нет
- System of Linear Equations - Linear Algebra WithДокумент37 страницSystem of Linear Equations - Linear Algebra Withradhikaseelam1Оценок пока нет
- Math 8 Written Work No. 1 Quarter 1: - Encircle The Letter of The Correct AnswerДокумент8 страницMath 8 Written Work No. 1 Quarter 1: - Encircle The Letter of The Correct AnswerEthel Joy Rivera AgpaoaОценок пока нет
- Transformations (Solution)Документ12 страницTransformations (Solution)Amman ButtОценок пока нет
- Lecture 10: Impulse Response of A Differential LTI System: A Dyt DT B DXT DTДокумент6 страницLecture 10: Impulse Response of A Differential LTI System: A Dyt DT B DXT DTRoziyan HidayatОценок пока нет
- Null 1 PDFДокумент5 страницNull 1 PDFFiaz Ahmad FrazОценок пока нет
- MS-103 Calculus and Analytic Geometry CISДокумент4 страницыMS-103 Calculus and Analytic Geometry CISfaizОценок пока нет
- Math 21-2 Syllabus (Ar)Документ6 страницMath 21-2 Syllabus (Ar)Joyce CulloОценок пока нет
- Mso-203 B Assignment 1 Iit, KanpurДокумент1 страницаMso-203 B Assignment 1 Iit, KanpurgouravОценок пока нет
- Class 12 Math Chep - Chap 3 - Matrices, Chapter 4 - DeterminentsДокумент23 страницыClass 12 Math Chep - Chap 3 - Matrices, Chapter 4 - DeterminentsEr Piyush ThaganОценок пока нет
- Chapter 1 - Limits and Continuity PDFДокумент55 страницChapter 1 - Limits and Continuity PDFZack MalikОценок пока нет
- Find The Positive Root of The Equation Correct To Five Decimal PlacesДокумент5 страницFind The Positive Root of The Equation Correct To Five Decimal PlacesPramod GowdaОценок пока нет
- Elements of Linear Multilinear - Algebra - PDFДокумент152 страницыElements of Linear Multilinear - Algebra - PDFmayОценок пока нет
- Contemporary Mathematics For Business and Consumers Brief Edition 7th Edition Brechner Test Bank 1Документ36 страницContemporary Mathematics For Business and Consumers Brief Edition 7th Edition Brechner Test Bank 1amandagonzalezkejnwodxqr100% (23)
- Multipe Integrals - Engineering MathematicsДокумент26 страницMultipe Integrals - Engineering Mathematicshana faqihОценок пока нет
- POLYMATH TutorialChemical Reaction EngineeringДокумент8 страницPOLYMATH TutorialChemical Reaction EngineeringAnonymous ox8Tn9Оценок пока нет
- Fast Fourier TransformДокумент32 страницыFast Fourier Transformanant_nimkar9243100% (1)
- (448293) 10 Convert Metric Units of VolumeДокумент2 страницы(448293) 10 Convert Metric Units of VolumeJaniceОценок пока нет
- Math 8 SOL Review: Section One: Number SenseДокумент9 страницMath 8 SOL Review: Section One: Number SenseGianinne LozadaОценок пока нет
- Analytic GeometryДокумент45 страницAnalytic GeometryMC VillasencioОценок пока нет
- Cengage Book ListДокумент12 страницCengage Book ListSatya RanjanОценок пока нет
- Unit - IV: Numerical Solutions of Differential Equations (MCQ)Документ5 страницUnit - IV: Numerical Solutions of Differential Equations (MCQ)DeathSky GamingОценок пока нет